1. Introduction
The essential oils (EO) are compounds obtained from the metabolic state in plants [1, 2], and they have a diversity of applications in the cosmetic, medicinal and pesticides contexts (see [3] for a long list of applications). In the medicinal area, a renewed interest has emerged due to the antimicrobial and antioxidant effect, exhibited by the EO (see example [4], a long review about eugenol effect and its microemulsions (ME) on antimicrobiological activity). In addition, their multiple applications can be found in the literature.
In each ME, water and oil are the essential ingredients that interact rising to a tiny interface, which plays an important role when surfactants are added. These provide ME with high thermodynamic stability as long as proper conditions of adhered surfactants are maintained [5]. These ingredients and their optimal combination (water, oil and surfactants) form a transparent optical structure. Such transparency implies a characterization of its microstructure through length scales that are submicron, which is, below 100 nm. Likewise, three types of ME can be found in the literature: water in oil, oil in water and bicontinuous structures [5]. They can be formed with oil drops with geometries such as spherical, cylindrical, flat or sponge, as a consequence of having a small interfacial tension and the degree of curvature that surfactants can communicate to ME in their own interface [6].
On the other hand, this type of system has been studied through different types of simplified models [7]. Among them, there are some which deal with the context of networks (see, for example ([8-10], among others). In these models, descriptions of the ME are made with relative simplification. An interesting approach to study this type of systems is that one which regards the fractal morphometry associated with them that is directly related to the physico-geometric characteristics of such biophysical entities. For example, they are used in Ref. [11] surfactant-free emulsions, and industrially, their fractal characterization is used in the task of modifying starch and amaranth. In the Ref. [12], a study is carried out on the dielectric relaxation of the ME AOT-water-decane, close to the percolation temperature threshold. The description of such a relaxation process is made taking into account its fractal structure.
Likewise, dielectric spectroscopy is useful for obtaining information about the structure of ME at different spatial and temporal scales, as described in Ref. [13]. Another interesting contribution in the context of fractal characterization of ME conglomerates was addressed in Ref. [14], where the effect of different types of surfactants on the sizes and shapes of ME is investigated. Thus, endless applications at different contexts can be found where fractal geometry is reflected in the subject of essential oil ME.
However, isolated ME fractal morphometry (FM) is a remaining issue in the literature, which we try to address as a contribution at least as a first attempt. Achieving this first attempt at an approximate fractal characterization of individual spherical-type EO ME would increase the knowledge about their stability, taking into account that its degree of deformation is closely related to the temporary duration of such stability. Despite the fact that these types of estimates do not have a direct relevance in technological applications, their determination plays a relatively important role in the generalized physical-geometric characterization. This may allow obtaining a more realistic estimate of associated physical parameters contributing to the basic scientific knowledge. For example, achieving at least approximate form of the fractal morphometric structure of individual ME would allow us to know more explicitly about the relationship between entropy and thermal fluctuations, which contribute to the degree of instability that their curvature may have at one point. Therefore, our work was distributed as follows: In a second section, the main characteristics of the formalism associated with continuous models of fractal media with homogeneity and isotropy properties are described, which are the basis for the model proposed in the third section. The reduced model is described in the third section to obtain an approximation of the volume fractal dimension (VFD) of an isolated ME, which assumes ME are highly homogeneous systems. The application of the model is shown in the fourth section, obtaining the VFD and the fractal volume (FV) of two types of EO ME (Rosmarinus officinalis and Melaleuca alternifolia), whose effects [15] on humans’ cells and pathogens microorganisms were recently investigated to obtain the ME sizes because such physical characteristic can support to reference (visual way) their stability [16, 17]. In the fifth section, the surface fractal morphometry (SFM) is obtained for these ME. Finally, a brief discussion of the results and conclusion of the work and future perspectives are presented in the sixth and seventh sections respectively.
2. Homogeneous and Isotropic Fractal Medium
To make the proposal more self-contained, the most important characteristics of a homogeneous and isotropic continuous medium model for a fractal medium are described, within the context of non-integer dimensional spaces.
A constant density distribution is the main characteristic in every homogeneous fractal medium.
To illustrate the idea of homogeneity in a fractal medium, a three-dimensional spherical region W A of the Euclidean type can be supposed, where A is the midpoint of such region, so the volume and average density are given by [18]
where R A and M are the radius and mass from such region, respectively. On the other hand, if two regions W A and W B are considered, the fractal medium is regarded homogeneous when the relationship of volumes and average densities is fulfilled
that means, there is no effect on
On the other hand, the isotropy of a fractal material is characterized by the relationship between the mass M (W B ) of a spherical region W B of a fractal medium with radius R as follows [19]
where D is the mass dimension of the fractal medium, R 0 is a characteristic size of atoms and molecules in general.
In the case of an anisotropic fractal material, it can be characterized by the power law relationship for the mass of a parallelepiped-like region W p as follows [19]
where α k , k = 1, 2, 3 is the non-integer dimension along the Cartesian axes and L x , L y , L z are the sides of the parallelepiped.
The value of α k is related to the parameter D as follows [19]
where D is the fractal mass dimension of the anisotropic fractal medium. Also, D can be interpreted as a dimension of space.
Equations (3) and (4) allow a fractal material to be defined as a medium with a non-integer mass dimension [19]. Finally, as an application to a spherical fractal material with constant average density in a space of non-integer dimension, the volume is given by [19]
where R is the radius of that sphere in an space of non-integer dimension.
These properties of homogeneous and isotropic-anisotropic fractal materials, within the framework of a non-integer dimensional space, represent the foundation of our proposal described in the following section.
3. Model description
We supposed to have one ME, obtained in Ref. [15] and visualized at Fig. 1.
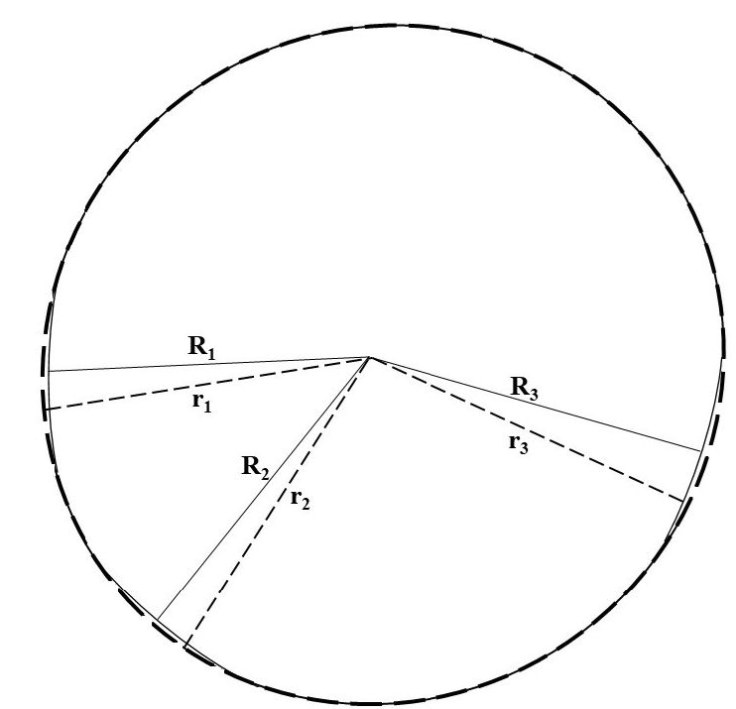
Figure 1 The amplified model of one ME shows three superficial deformations. The dashed line represents the ME without deformations, and the continuous line with them.
Where
where α j is a proportionality parameter pretty close to 1, 0.9 ≤ α j ≤ 0.99999.
The supposition (7) can guarantee when the ME are too small to achieve a thermodynamics stability (TS). Additionally, the introduction of the parameter α j under the supposition (7) guarantee a very small anisotropy, which allows to model such ME as volumetric systems, given by
Where V n represents to the ME as fractal sphere, n is its fractal dimension (FD) and R i the radii. On the other hand, considering (1) and (2) the next approximation can be made according to
where V 3D = (4/3)πr 3 is the ME modeled volume as Euclidean sphere into the 3D space.
This assumption is easy to understand, taking into account that, its almost perfect spherical formation, is due to the energetic formation of the gradient type. This perfect quasisphericity in microemulsions allows to carry out or justify the approximation (3), which is relevant because of its role to establish the present model.
The approximation (9) can be used through of the next interpretation: “An EO ME in a stable thermodynamic state can be considered as a fractal medium, homogeneous and anisotropic, where the anisotropy is very small so that the idealize volume, V 3D , can approximate to a real volume, an approximate fractal volume (AFV) V n ”.
If we consider the approximation (9) and the supposition (7), they could allow us to obtain FD of the ME resolving the equation
which may be interpreted as the representation of a “four-dimensional sphere”, being R i the physical radial variable of the ME, and n the variable of the approximate fractal dimension volume (AFDV).
4. Volumetric fractal morphology
As an application example way, using the Eq. (10), a computational code was written through the free software Wolfram Mathematica [20] to obtain the approximate fractal dimension (AFD), associated with the volume of the ME analyzed. The radio R i corresponding to these volumes were obtained from a previous article [15], that are observed in the tables through the manuscript.
The results Tables I and II are shown for the FD regards to the ME volume of essential oils from Rosmarinus officinalis and Melaleuca alternifolia, recently studied.
Table I AFDV n = n
V
=
| R i |
|
|
|
|
|
|---|---|---|---|---|---|
| 2 | 3.0000023 | 3.0000233 | 3.0002326 | 3.0023369 | 3.0244966 |
| 35 | 3.0000030 | 3.0000299 | 3.0002989 | 3.0030032 | 3.0314781 |
| 60 | 3.0000032 | 3.0000316 | 3.0003159 | 3.0031735 | 3.0332632 |
| 85 | 3.0000033 | 3.0000328 | 3.0003279 | 3.0032943 | 3.0345286 |
| 110 | 3.0000034 | 3.0000337 | 3.0003373 | 3.0033898 | 3.0355290 |
Table II AFDV n = n
V
=
| R i |
|
|
|
|
|
|---|---|---|---|---|---|
| 4 | 3.0000025 | 3.0000246 | 3.0002458 | 3.0024696 | 3.0258870 |
| 15 | 3.0000028 | 3.0000276 | 3.0002757 | 3.0027694 | 3.0290290 |
| 16 | 3.0000028 | 3.0000277 | 3.0002773 | 3.0027860 | 3.0292021 |
| 30 | 3.0000029 | 3.0000294 | 3.0002944 | 3.0029578 | 3.0310823 |
| 31 | 3.0000030 | 3.0000295 | 3.0002954 | 3.0029673 | 3.0311023 |
| 45 | 3.0000031 | 3.0000307 | 3.0003066 | 3.0030803 | 3.0322860 |
| 46 | 3.0000031 | 3.0000307 | 3.0003073 | 3.0030872 | 3.0323586 |
| 60 | 3.0000032 | 3.0000316 | 3.0003159 | 3.0031735 | 3.0332632 |
As observed in Tables I and II, clearly a small increment was more evident in FD according to the ME radii, such as the Eq. (10) predicted, being reasonable physically.
On the other hand, it is evident that
and
respectively.
Similar inequalities are obtained when we consider other α
j
. These inequalities are represented in terms of
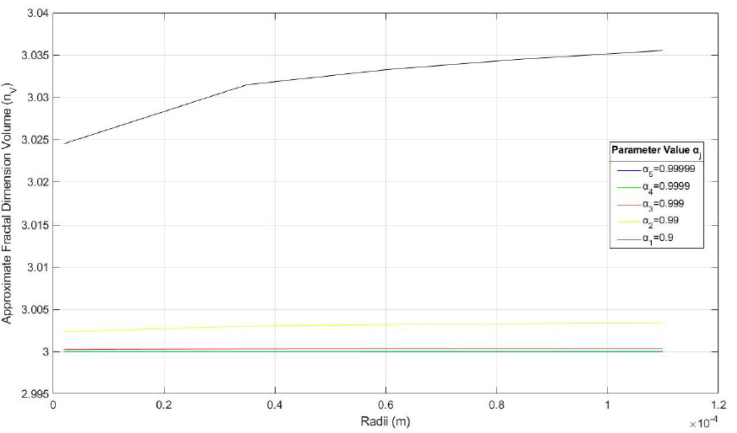
Figure 2 Graphic display of the AFDV of the ME of Rosmarinus officinalis, for the four α j models, as shown in Table I.
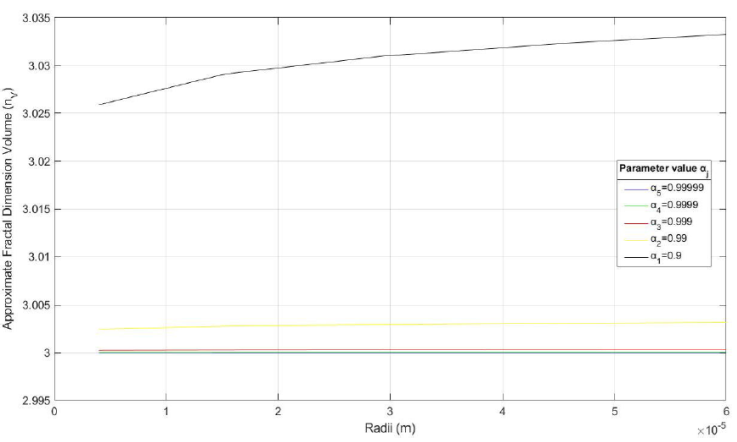
Figure 3 Graphic display of the AFDV of the ME of Melaleuca alternifolia, for the four α j models, as shown in Table II.
Similarly, using the Eq. (8), a computational code was written through the free software Wolfram Mathematica [20] to obtain the approximate fractal volume (AFV) V n associated to the analyzed ME. The results are shown in Table III and Table IV, using 5 models for the parameter α j .
Table III AFV V n , according to different ME radii of essential oil from Rosmarinus officinalis when α j {9.99999, 0.9999, 0.999, 0.99, 0.9} respectively. Radii are in μm.
| R i |
|
|
|
|
|
|---|---|---|---|---|---|
| 2 | 0.0335 × 10 -15 | 0.0335 × 10 -15 | 0.0333 × 10 -15 | 0.0325 × 10 -15 | 0.0244 × 10 -15 |
| 35 | 0.0179 × 10 -11 | 0.0179 × 10 -11 | 0.0179 × 10 -11 | 0.0174 × 10 -11 | 0.0130 × 10 -11 |
| 60 | 0.0904 × 10 -11 | 0.0904 × 10 -11 | 0.0902 × 10 -11 | 0.0877 × 10 -11 | 0.0659 × 10 -11 |
| 85 | 0.0257 × 10 -10 | 0.0257 × 10 -10 | 0.0256 × 10 -10 | 0.0249 × 10 -10 | 0.0187 × 10 -10 |
| 110 | 0.0557 × 10 -10 | 0.0557 × 10 -10 | 0.0555 × 10 -10 | 0.0540 × 10 -10 | 0.0406 × 10 -10 |
Table IV AFV V n , according to different ME radii of essential oil from Melaleuca alternifolia when α j {9.99999, 0.9999, 0.999, 0.99, 0.9} respectively. Radii are in μm.
| R i |
|
|
|
|
|
|---|---|---|---|---|---|
| 4 | 2.0000025 | 2.0000246 | 2.0002458 | 2.0024696 | 2.0258870 |
| 15 | 2.0000028 | 2.0000276 | 2.0002757 | 2.0027694 | 2.0290290 |
| 16 | 2.0000028 | 2.0000277 | 2.0002773 | 2.0027860 | 2.0292021 |
| 30 | 2.0000030 | 2.0000294 | 2.0002944 | 2.0029578 | 2.0310823 |
| 31 | 2.0000030 | 2.0000295 | 2.0002954 | 2.0029673 | 2.0311023 |
| 45 | 2.0000031 | 2.0000307 | 2.0003066 | 2.0030803 | 2.0322860 |
| 46 | 2.0000031 | 2.0000307 | 2.0003073 | 2.0030872 | 2.0323586 |
| 60 | 2.0000032 | 2.0000316 | 2.0003159 | 2.0031735 | 2.0332632 |
Likewise, for a better display of information in Tables III and Table IV, Figs. 4 and 5 are shown respectively. The source code to generate the graphs was designed in MAT-LAB Version R2018b [23] and for a better display of data, the radius was expressed in m. Here, the curves show a similar behavior, especially in the smallest radii of the ME which tend to have the most stable volumes.
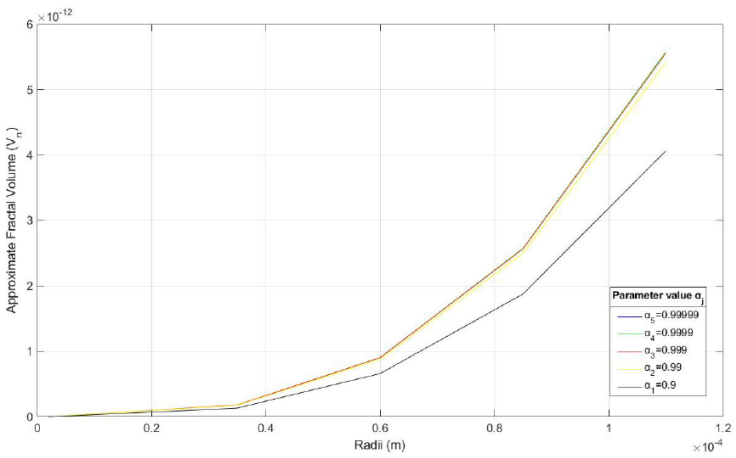
Figure 4 Graphical visualization of the AFV V n of the ME of Rosmarinus officinalis for the four models of α j , as shown in Table III.
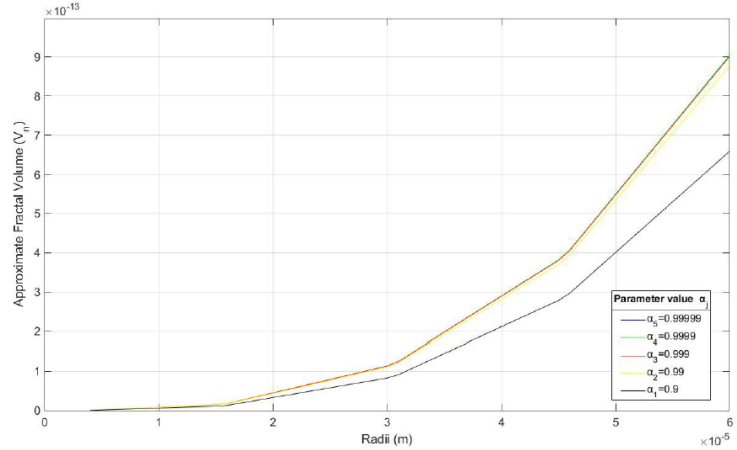
Figure 5 Graphical visualization of the AFV V n of the ME of Melaleuca alternifolia for the four models of α j , as shown in Table IV.
5. Surface fractal morphometry
In general, for a non-homogeneous fractal material, the relationship between the fractal dimension of area (FDA) n α and the fractal dimension of volume (FDV) n V given by n α = n V - 1, is not right [24]. However, the ME system analyzed in this study are considered as highly homogeneous systems, so the relationship between n α and n V shown in this paragraph can be used to estimate the fractal dimension (FD) of area associated with each ME under study, at least as an approximation.
When estimating for the FD of the area n α , interesting results are shown in Tables V and VI, using the five models for the parameter α j .
Table V FD approximation of area nα =
| R i |
|
|
|
|
|
|---|---|---|---|---|---|
| 2 | 2.0000023 | 2.0000233 | 2.0002326 | 2.0023369 | 2.0244966 |
| 35 | 2.0000030 | 2.0000299 | 2.0002989 | 2.0030032 | 2.0314781 |
| 60 | 2.0000032 | 2.0000316 | 2.0003159 | 2.0031735 | 2.0332632 |
| 85 | 2.0000033 | 2.0000328 | 2.0003279 | 2.0032943 | 2.0345286 |
| 110 | 2.0000034 | 2.0000337 | 2.0003373 | 2.0033898 | 2.0355290 |
Table VI FD approximation of area nα =
| R i |
|
|
|
|
|
|---|---|---|---|---|---|
| 4 | 2.0000025 | 2.0000246 | 2.0002458 | 2.0024696 | 2.0258870 |
| 15 | 2.0000028 | 2.0000276 | 2.0002757 | 2.0027694 | 2.0290290 |
| 16 | 2.0000028 | 2.0000277 | 2.0002773 | 2.0027860 | 2.0292021 |
| 30 | 2.0000030 | 2.0000294 | 2.0002944 | 2.0029578 | 2.0310823 |
| 31 | 2.0000030 | 2.0000295 | 2.0002954 | 2.0029673 | 2.0311023 |
| 45 | 2.0000031 | 2.0000307 | 2.0003066 | 2.0030803 | 2.0322860 |
| 46 | 2.0000031 | 2.0000307 | 2.0003073 | 2.0030872 | 2.0323586 |
| 60 | 2.0000032 | 2.0000316 | 2.0003159 | 2.0031735 | 2.0332632 |
These results on the approximate fractal dimension of area for the two types of EM, can be better visualized through Figs. 6 and 7, respectively. The source code to generate the graphs was designed in MATLAB Version R2018b [23] and, to obtain a better display of data, the radius was expressed in m. As in the cases of Figs. 2 and 3, and expected for the three of the α j models, the evolution of the AFD is remarkably close to the 2D Euclidean volumetric integer dimension, which shows the degree of importance with respect to the two remaining cases of proportionality models.
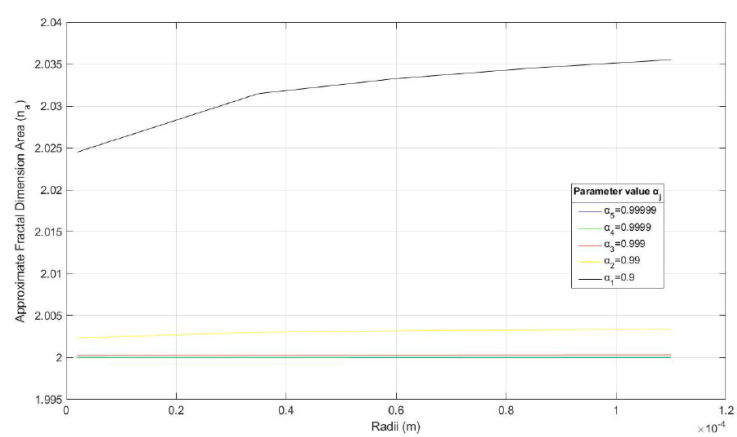
Figure 6 Graphic display of the AFD of the area of the ME of Rosmarinus officinalis, for the four α j models, as shown in Table V.
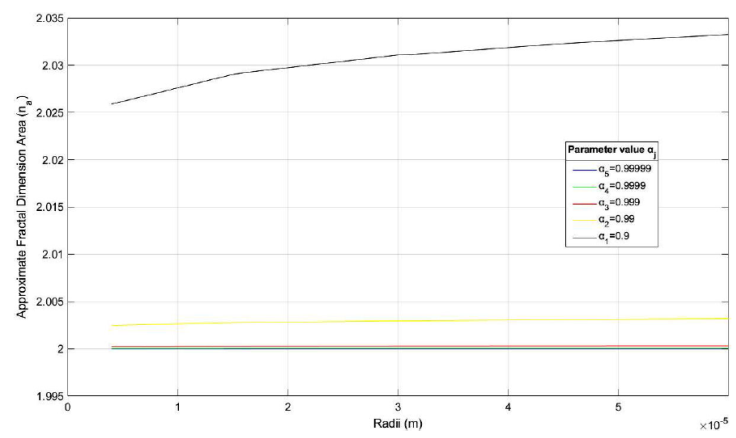
Figure 7 Graphic display of the AFD of the area of Melaleuca alternifolia, for the four α j models, as shown in Table VI.
Regarding that the ME are highly homogeneous, the approximate fractal area (AFA) is calculated as in [25]
where R = R i is the radius of the ME.
This application was carried out after writing a computational code using the Wolfram Mathematica software [20] to obtain the fractal area associated with the ME analyzed.
When applying the Eq. (5), the results for
Table VII AFA
| R i |
|
|
|
|
|
|---|---|---|---|---|---|
| 2 | 0.0502 × 10−9 | 0.0502 × 10−9 | 0.0500 × 10−9 | 0.0488 × 10−9 | 0.0369 × 10−9 |
| 35 | 0.0153 × 10−6 | 0.0153 × 10−6 | 0.0153 × 10−6 | 0.0149 × 10−6 | 0.0113 × 10−6 |
| 60 | 0.0452 × 10−6 | 0.0452 × 10−6 | 0.0451 × 10−6 | 0.0439 × 10−6 | 0.0333 × 10−6 |
| 85 | 0.0090 × 10−5 | 0.0090 × 10−5 | 0.0090 × 10−5 | 0.0088 × 10−5 | 0.0066 × 10−5 |
| 110 | 0.0152 × 10−5 | 0.0152 × 10−5 | 0.0151 × 10−5 | 0.0147 × 10−5 | 0.0112 × 10−5 |
Table VIII AFA
| R i |
|
|
|
|
|
|---|---|---|---|---|---|
| 4 | 0.0201 × 10−8 | 0.0201 × 10−8 | 0.0200 × 10−8 | 0.0195 × 110−8 | 0.0147 × 10−8 |
| 15 | 0.0282 × 10−7 | 0.0282 × 10−7 | 0.0281 × 10−7 | 0.0274 × 10−7 | 0.0208 × 10−7 |
| 16 | 0.0321 × 10−7 | 0.0321 × 10−7 | 0.0320 × 10−7 | 0.0312 × 10−7 | 0.0236 × 10−7 |
| 30 | 0.0113 × 10−6 | 0.0113 × 10−6 | 0.0112 × 10−6 | 0.0109 × 10−6 | 0.0083 × 10−6 |
| 31 | 0.0120 × 10−6 | 0.0120 × 10−6 | 0.0120 × 10−6 | 0.0117 × 10−6 | 0.0088 × 10−6 |
| 45 | 0.0254 × 10−6 | 0.0254 × 10−6 | 0.0253 × 10−6 | 0.0247 × 10−6 | 0.0187 × 10−6 |
| 46 | 0.0265 × 10−6 | 0.0265 × 10−6 | 0.0265 × 10−6 | 0.0258 × 10−6 | 0.0195 × 10−6 |
| 60 | 0.0452 × 10−6 | 0.0452 × 10−6 | 0.0451 × 110−6 | 0.0439 × 10−6 | 0.0333 × 10−6 |
Similarly, data in the Tables VII and VIII, are also shown in Figs. 8 and 9, respectively to display more clearly the behavior of the AFA. The source code to generate the graphs was designed using the MATLAB Version R2018b [23] and for better visualization, the radius was expressed in m. Here, the curves show a similar behavior, especially in the smallest radii of the EM which tend to have the most stable areas. In addition, the pattern observed is similar to those in Figs. 4 and 5, showing an increasing trend in the approximate fractal areas.
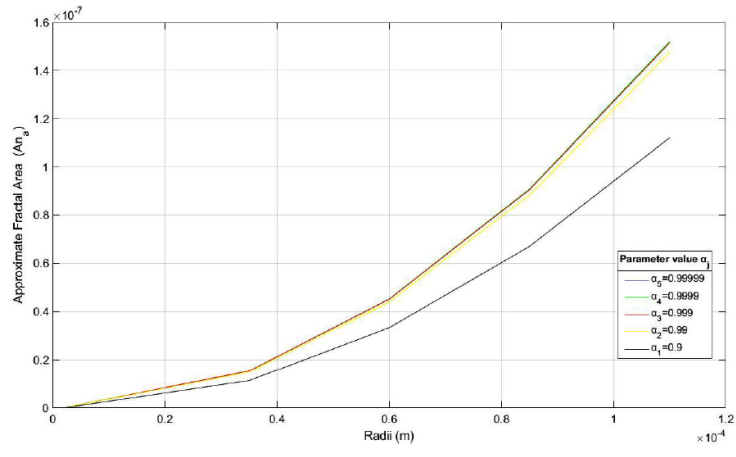
Figure 8 Graphic display of the AFA of the ME of Rosmarinus officinalis, for the four α j models, as shown in Table VII.
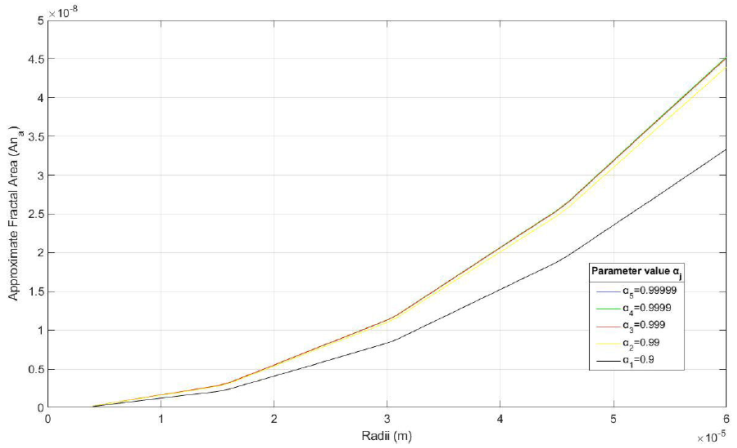
Figure 9 Graphic display of the AFA of the ME of Melaleuca alternifolia for the four α j models, as shown in Table VIII.
6. Discussion
As observed in Tables I, II, III and IV, the AFDV n V and the approximate fractal dimension area (AFDA) n α respectively, both of the ME of Rosmarinus officinalis and Melaleuca alternifolia tend to increase as their radius increase. This behavior is observed for each one of the five models of the proportionality parameter α j . This dynamics experienced by the fractal volumetric morphometry of the ME, has a relative coherence, since if volume increases, the interaction forces in the system produce higher instability tending to move away from the value 3, corresponding to the Euclidean topology associated with the ME. Likewise, the parameter α j plays an important role when α j → 1, the ME tend to behave as less complex systems with a dimension closer to the Euclidean one. On the contrary, when α j moves away from 1, the system shows an increase in fractal geometric complexity.
On the other hand, the AFV
The Fractal Dimension of Approximate Area (FDAA) and AFA parameters follow similar behaviors to those associated with volume, which is a consequence of the model proposed and already described above. They can be examined numerically through Tables V, VI, VII and VIII, respectively or graphically in Figs. 6, 7, 8 and 9, respectively. Such behavior shows that n α tends to grow as the radius of the ME grows, which is a coherent physico-geometric result. Like-wise, when the parameter α j → 1 the FDAA n α → 2, which corresponds to the area of a Euclidean sphere.
Similarly, the AFV
Also, it is important to bring up that the model needs to take into consideration more parameters associated with this type of system. Hopefully the scientific community can take into consideration a possible feedback to the model in the future.
7. Conclusions and future perspectives
The combined use of some published models about the fractal characterization of homogeneous and anisotropic media, allowed us to model the essential oil ME as geometric systems, which seem to obey this type of physical-geometric characterization. Using this, a reduced simple analytical model was developed to build an equation to be applied to the ME, and their AF, AFDA, FV and AFA were estimated respectively.
These results are a small contribution to the physical and geometric aspects associated with this type of isolated systems. Likewise, it is important to mention that although the numerical results were obtained for two types of ME (Rosmarinus officinalis and Melaleuca alternifolia), the model can be applied to any type of spherical ME in stable thermodynamic equilibrium state. On the other hand, these results were consistent with the Szpilrajn’s inequality and the experimental measurements of real physical dimension n = 3 ± 10 -6 , as mentioned in Ref. [26], which gives some support to our proposal. This value of n is supported by observational facts within the context of general relativity, as mentioned in Ref. [27]. On the other hand, as a work to be continued and future proposal, we intend to establish a system of equations of allometric scaling type for the fractal volume and fractal area, associated to each ME analyzed in order to establish a system of fractional differential equations and describe the global evolution of ME in a non-integer dimension space.











 nova página do texto(beta)
nova página do texto(beta)


