1.Introduction

Recently, there has been increasing interest in Fractional Calculus, which deals with integration/differentiation of arbitrary orders. It has been proved that the real phenomena in majority systems can be more adequately described by the fractional-order differential equations ¹. For instance, the capacitors, which are one of the most important elements in integrated circuits, are used extensively in many electronic circuits as the ideal components. It has been found by Jonscher ² and many other authors that the ideal capacitor cannot exist in nature, because an impedance of the form 1/jCω would violate causality. So, the realistic models of capacitors integrate the fractional-order form. Therefore, the integration of the notion of fractional-order in the modelling and simulation process of systems is of great importance. The fractional-order derivative is useful for the description of memory and hereditary properties of various materials and processes ¹. The list of applications of fractional calculus has been overgrowing and includes control theory, viscoelasticity, diffusion, turbulence, electromagnetism and many other physical processes ^3-7. More recently, fractional-order derivative has been used to develop mathematical models of several diseases including the novel coronavirus (2019-nCOV) and Human Immunodeficiency Virus (HIV) ^8-12. It is proved that the fractional-order models are more powerful than the ordinary order mathematical models ¹². Interestingly, the data fitting can be considered better with fractional order rather than ordinary order; the reader can refer to ^13,14 for more explanations. Provided that fractional-order derivative plays an important role, the nonlinear dynamical systems that involve fractional-order derivative are welcome. Furthermore, there are many material differences between the integer-order systems and their equivalent fractional-order models. Most of the properties or considerations of the integer-order system cannot be simply extended to the case of the fractional-order one. In this regard, several chaotic fractional-order systems have been reported including Duffing system ¹⁵, Chua circuit ¹⁶, Chen system ¹⁷, Lü system ¹⁸, unified system ¹⁹, Lorenz system²⁰, Rössler system ²¹ and so on. In this contribution, we investigate the dynamics of a Lorenz-like system called fractional-order Shimizu-Morioka system. Before focusing our attention on the proposed fractional-order Shimizu-Morioka system, it is important to make a brief recall on some interesting works related to the original Shimizu-Morioka system ²². In the latter literature, Shimizu and Morioka used the perturbation theory to calculate the analytic form of the limit cycles. Computer simulations have been able to confirm the occurrence of limit cycles predicted by the theoretical results. In Ref ²³, the dynamics of the Shimizu-Morioka is further investigated with concept of delayed feedback. They used the delay as a bifurcation parameter and proved the existence of local Hopf bifurcation in the system. Furthermore, the authors used the normal form theory and the center manifold theorem to derive the explicit formulae for determining the stability and direction of bifurcated periodic solutions. They finally showed by the numerical simulations that the delayed feedback control plays an important role in control of chaos. In addition, in Ref. ²⁴, the control of chaos in Shimizu-Morioka system is investigated by using Lie algebraic exact linearization method. The authors designed suitable controller and derived a necessary and sufficient conditions for stabilization of the system to a point as well as onto a limit cycle. Numerical simulations were performed to show the effectiveness of the proposed control method. However, these interesting works are restricted to the integer-order form of the system and make no mention of the fractional-order model counterpart. The aim of the present work is to consider the dynamics of the Shimizu-Morioka system with fractional-order derivative. We wish to inspect the effect of the fractional-order derivative on the dynamical behavior of the original Shimizu-Morioka system.

The rest of the paper is organized as follows. Section 2 deals with analysis of integer-order and fractional-order Shimizu-Morioka system. In Sec. 3, the electronic circuit design of the fractional-order Shimizu-Morioka system and PSpice-based circuit simulations are carried out in order to verify the numerical analysis. The results obtained are compared with numerical ones and a qualitative agreement is observed. Finally, we summarize our contributions and draw the conclusions of this work in Sec.4.

2.Analysis of integer- and fractional-order Shimizu-Morioka system

There are several methods to study fractional calculus ²⁵. In this work, we adopt Caputo fractional calculus, which allows the traditional initial and boundary condition assumptions. The Caputo fractional-order derivative ²⁶ of a function x(t) is defined by

where cDqt0 is the Caputo derivative operator of order q(m-1)<q≤m,m∈N t₀ and Γ(⋅) are the initial time and the gamma function, respectively.

Using the Caputo fractional-order derivative given in Eq.1, the fractional-order form of the original Shimizu-Morioka system ²² is constructed as follows:

dqxdtq=y, (1a)

dqydtq=x-γy-xz, (1b)

dqzdtq=-αz+x2, (1c)

where x, y and z are state variables; γ and α are positive constant parameters; q is the derivative order satisfying 0<q<1. The model involves six terms of which two are nonlinear. The nonlinear terms are responsible of the complex behaviors exhibited by the whole system. For background theory on fractional-order calculus, the readers should be referred to Refs. ^27-31.This model received great attention due to its ability to describe bifurcation of the associated Lorenz-like attractors. It is easy to prove that the fractional-order Shimizu-Morioka system has a natural symmetry S about z-axis since the transformation S:(x,y,z)↔(-x,-y,z) is invariant for a specific set of the system parameters. The equilibrium points of the fractional-order Shimizu-Morioka system is calculated by solving dqx/dtq=0, dqy/dtq, and dqz/dtq=0. Therefore, we found that the fractional-order Shimizu-Morioka system has three equilibrium points defined by E₀(0,0,0) and E1,2(±α,0,1) when α > 0 and only one equilibrium point defined by E₀(0,0,0) when α < 0.

2.1.Numerical investigations of integer-order Shimizu-Morioka system

Here, the dynamical behavior of integer-order Shimizu-Morioka system is investigated. In order to select the values of parameters accordingly, the two-parameter phase diagram showing the regions of different dynamical behaviors in the (γ,α) plane is computed as shown in Fig. 1 with initial conditions (x(0),y(0),z(0))=(0.1,0.2,0.3).

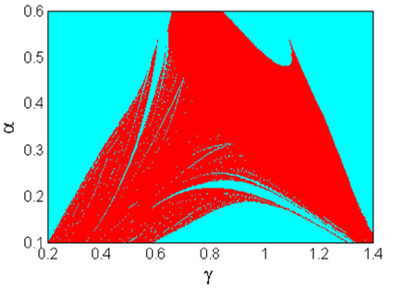
Figure 1 (Color on line) Two-parameter phase diagram showing different dynamical behaviors of integer-order Shimizu-Morioka system in the (γ; α) plane. The periodic dynamics is represented with cyan regions, while chaotic dynamics is associated to red ones. The initial conditions are (x(0); y(0); z(0)) = (0:1; 0:2; 0:3). 

From Fig.1, it can be seen that the chaotic and periodic regions intertwined intricately. The periodic and chaotic behaviors are identified by the cyan and red regions, respectively. This diagram is of great importance for a practical implementation of integer-order Shimizu-Morioka system. Indeed, it can help to choose the parameters of the system accordingly.

To analyze the effect of parameter γ on the dynamics of integer-order Shimizu-Morioka system, we fix α = 0.2 and plot the bifurcation diagram and the largest Lyapunov exponent (LLE) versus the parameter γ varying from 0.2 to 0.35 as provided in Fig. 2. Note that the largest Lyapunov exponent is computed using the algorithm proposed by Wolf and colleagues ³². The LLE helps to characterize the dynamics of a system. The system is periodic or chaotic for LLE≤0 and LLE>0, respectively.

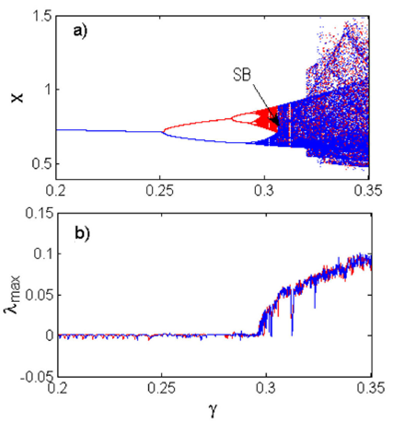
Figure 2 Forward (blue) and backward (red) bifurcation diagram a) showing the local maxima of the state variable x and corresponding graph of LLEλ_max b) versus the control parameter γ varying from 0.2 to 0.35 for α = 0:2. The initial conditions are (x(0); y(0); z(0)) = (0:1; 0:2; 0:3). The acronym SB means symmetry breaking. 

The plot of Fig. 2 has two sets of data corresponding to increasing (blue) and decreasing (red) the values of control bifurcation parameter γ. The chaotic behavior appears in integer-order Shimizu-Morioka system via well-kwon period-doubling routes. From Fig. 2, it is noticed that when the value of the bifurcation parameter γ is less than 0.306, the system displays bistable chaotic attractors. And for γ > 0.306 the bistable chaotic attractors merge to form monostable ones via the common symmetry breaking phenomenon. The illustrations of such bistable and monostable chaotic attractors are shown in Fig. 3 and 4 for respectively, two specific values of γ and α = 0.2. The initial conditions are chosen as (x(0),y(0),z(0))=(0.1,±0.2,0.3).

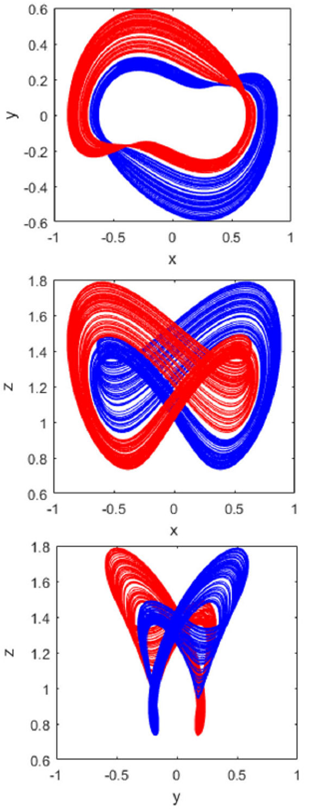
Figure 3 Bistable chaotic attractors of integer-order Shimizu- Morioka system in (x; y), (x; z) and (y; z) planes computed with α = 0:2, γ = 0:305 and initial conditions (x(0); y(0); z(0)) = (0:1;§0:2; 0:3). 

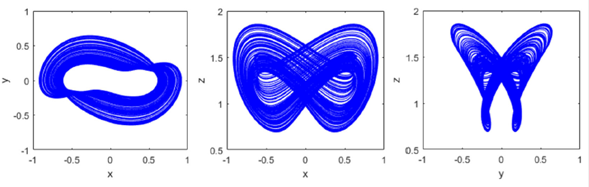
Figure 4 Monostable chaotic attractors of integer-order Shimizu-Morioka system in (x; y), (x; z) and (y; z) planes computed with α = 0:2, γ = 0:315 and initial conditions (x(0); y(0); z(0)) = (0:1; 0:2; 0:3). 

It is clearly observed from Fig. 3 and 4 that the integer-order Shimizu-Morioka system exhibits bistable and monostable chaotic attractors.

When we fix α = 0.2 and γ = 0.3012, the integer-order Shimizu-Morioka system experiences the coexistence of three different chaotic attractors (two with single band and one with double-band) for different initial conditions as displayed in Fig. 5.

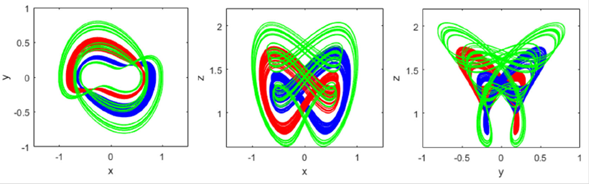
Figure 5 Coexistence of two asymetric chaotic attractors (red and blue) with one double-band chaotic attractors (green) for α = 0:2 and γ = 0:3012 in different planes. The initial conditions are (x(0); y(0); z(0)) = (0:1;§0:2; 0:3) for attractors in red and blue and (x(0); y(0); z(0)) = (1; 2; 3). for the one in green. 

2.2.Numerical investigations of commensurate fractionnal-order Shimizu-Morioka system

The numerical simulations of commensurate fractional-order Shimizu-Morioka system is carried out by using the modified Adams-Bashforth-Moulton algorithm proposed by Diethelm and collaborators ³³. The time grid is always kept Δt=10-2. The transient is totally suppressed after the sufficient long time integration of commensurate fractionnal-order Shimizu-Morioka system.

For γ = 0.35 and α = 0.2, the integer-order form of Shimizu-Morioka system exhibits chaotic behaviour (see 3) and has three equilibria E₀(0,0,0) and E1,2(±0.44721,0,1) as well. The equilibrium points and their eigenvalues are given as:

E0(0,0,0):λ1=-1.477032,λ2=-0.065, λ3=0.67703, (2a)

E1,2(±0.44721,0,1):λ1=-0.933378,×λ1,2=0.19189±062573j, (2b)

Now according to Ref. ³⁴, the equilibrium points E_1,2 are saddle points of index 2 and E₀ is saddle point of index 1. From Ref. ³⁴, we can get the following inequality in order to determine the stability condition: arg(0.19189±0.62573j)≥qπ/2⇒q<0.81056. Therefore, the necessary condition for appearance of chaos in commensurate fractional-order Shimizu-Morioka system is q≥0.81056. Since the aforementioned condition is a necessary but not sufficient condition, it does not warrant chaos itself. The bifurcation diagram showing the local maxima of the state variable x and the graph of LLE with respect to the commensurate fractional-order q varying from 0.81 to 1 are provided in Fig. 6 with γ = 0.35, α = 0.2 and initial conditions (x(0),y(0),z(0))=(0.1,0.2,0.3).

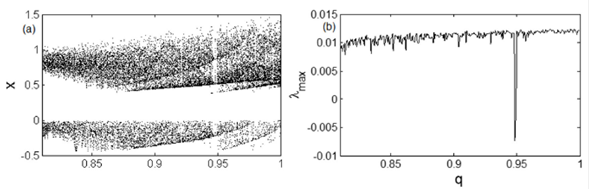
Figure 6 Bifurcation diagram a) showing the local maxima of the state variable x and LLE b) with respect to the commensurate fractionalorder varying from 0.81 to 1. The parameters are setting as γ = 0:35 and α = 0:2. The initial conditions are keep as (x(0); y(0); z(0)) = (0:1; 0:2; 0:3). 

The bifurcation diagram of the fractional-order Shimizu-Morioka system with respect to the commensurate fractional-order varying from 0.81 to 1 presents a large zone of chaotic bahavior with a tiny window of periodic orbits around q = 0.95. This diagram helps to investigate the influence of the fractional-order on the dynamics of the original Shimizu-Morioka system.

In order to examine the effect of the fractional-order on the dynamical behavior of the Shimizu-Morioka system, we select q = 0.9, α = 0.2 and plot the bifurcation diagram of fractional-order Shimizu-Morioka system versus varying from 0.2 to 0.35 as depicted in Fig. 7.

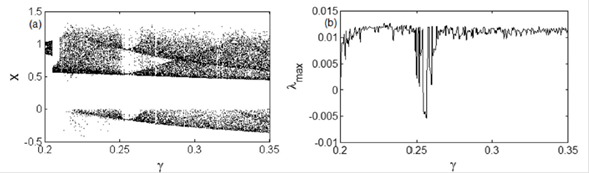
Figure 7 Bifurcation diagram of the commensurate fractional-order Shimizu-Morioka system showing the local maxima of the state variable in terms of control parameter ° varying from 0.2 to 0.35 for α = 0:2 and q = 0:9. The initial conditions are keep as (x(0); y(0); z(0)) = (0:1; 0:2; 0:3). 

From Fig.7, we can observe that the commensurate fractional-order affect considerably the dynamics of the commensurate fractional-order model of Shimizu-Morioka system. The route to chaos has been modified and the new windows of periodic and chaotic dynamics have appeared. One can see that the chaotic behavior is more abundant in commensurate fractional-order model of Shimizu-Morioka system.

As mentioned above in 2 the fractional-order Shimizu-Morioka system possesses a symmetry with respect to the z-axis. This property induces the bistability phenomenon in the system. The bistable and monostable chaotic attractors of the fractional-order form of Shimizu-Morioka system are shown in Figs. 8 and 9, respectively for γ = 0.21 and γ = 0.35. The other parameters are α = 0.2 and q = 0.9.

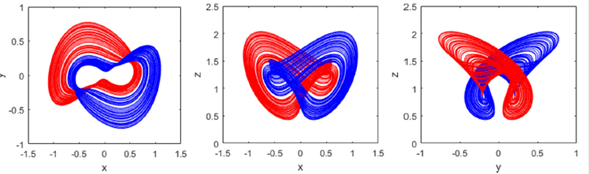
Figure 8 Bistable chaotic attractors of fractional-order form of Shimizu-Morioka system in (x; y), (x; z) and (y; z) planes computed with α = 0:2, γ = 0:21 and q = 0:9 and initial conditions (x(0); y(0); z(0)) = (0:1;§0:2; 0:3). 

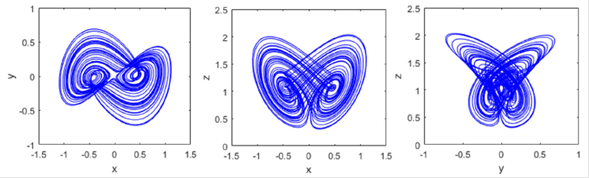
Figure 9 Monostable chaotic attractors of fractional-order form of Shimizu-Morioka system in (x; y), (x; z) and (y; z) planes computed with α = 0:2, γ = 0:35 and q = 0:9 and initial conditions (x(0); y(0); z(0)) = (0:1;§0:2; 0:3) 

It is clearly observed from Figs. 8 and 9 that the fractional-order Shimizu-Morioka system exhibits bistable and monostable chaotic attractors. The bistable chaotic attractors have been reported in many other systems with the symmetry properties.

During numerical investigations, by varying the control parameter γ in the range 0.253≤γ≤0.256, we found that commensurate fractionnal-order Shimizu-Morioka displays a provisional chaotic attractor, i.e. the chaotic attractor evolves into a periodic orbit in a finite time as shown in Fig. 10.

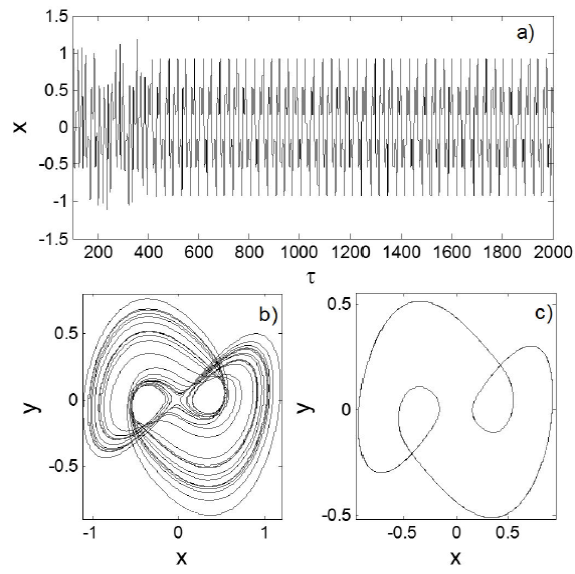
Figure 10 Time series of the state variable x illustrating the phenomenon of metastable chaos in the commensurate fractional-order Shimizu-Morioka system a); metastable chaotic attractor b) and periodic orbit in the steady state c) for for α = 0:2, γ = 0:253 and q = 0:9. The initial conditions are (x(0); y(0); z(0)) = (0:1; 0:2; 0:3). 

In Fig. 10a), we show the time series of state variable illustrating the metastable chaotic behavior in the system, while Fig. 10b) and 10c) show respectively, the transient chaotic attractor (i.e. chaotic saddle) and the periodic orbit formed after transient has been decayed for γ = 0.253. We see (Fig. 10a) that the signal appears chaotic up to certain time and then becomes periodic for all the rest of the signal. It should be stressed that the period of time that the system response takes to move from chaotic to periodic motion depends, of course, on the values of system parameters, and changes from orbit to orbit (i.e. depends on the initial states).

Detail notes on transient dynamics can be found in Ref.³⁵. The transient chaos phenomenon possesses a however, hardly observed in real laboratory experimental measurements due to its relatively short lifetime and sensitivity to noise. This unusual phenomenon of transient chaos has been observed in many physical and engineering systems ^35-39. It ought to be stressed that, to the best of authors’ knowledge, there are no similar results in reported Shimizu-Morioka system and therefore represents an enriching contribution concerning the dynamical analysis of this type of system.

Furthermore, our numerical analysis reveals also the occurrence of the periodic and chaotic spiking oscillations in the commensurate fractionnal-order Shimizu-Morioka system. This kind of dynamics is illustrated in Figs.11 and12. The periodic spiking oscillations are depicted in Fig. 11 where panel (1) presents the time traces of the state variables x, y and z and panel (2) the periodic phase portraits in planes (x,y), (z,x) and (z,y) for γ = 0.8, α = 0.008, q = 0.98 and initial conditions chosen as (x(0),y(0),z(0))=(0.1,0.2,0.3).

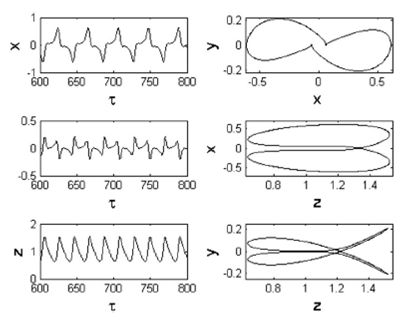
Figure 11 Periodic spiking: panel (1) time traces of the state variables x, y; and z; panel (2) phase portraits in planes (x; y), (z; x) and (z; y) for γ = 0:8, α = 0:008 and q = 0:98. The initial conditions are (x(0); y(0); z(0)) = (0:1; 0:2; 0:3). 

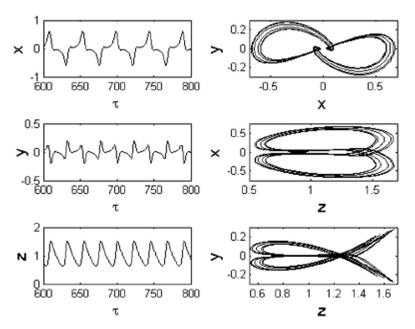
Figure 12 Chaotic spiking: panel (1) time traces of the state variables x, y and z; panel (2) phase portraits in planes (x; y), (z; x) and (z; y) for γ = 0:8, α = 0:065 and q = 0:98. and initial condition (x(0); y(0); z(0)) = (0:1; 0:2; 0:3). The state variables x and y while z is slow. 

The system exhibits chaotic spiking oscillations as shown in Fig. 12 for γ = 0.8, α = 0.065, q = 0.98 and initial conditions chosen as (x(0),y(0),z(0))=(0.1,0.2,0.3). The panel (1) presents the time traces of the state variables x, y, and z while panel (2) displays the chaotic phase portraits in planes (x,y), (z,x) and (z,y)

From Figs. 11 and 12, it is found that the state variables x and y model the dynamics of relatively fast changing processes, while the state variable describes the relatively slowly changing quantity that modulates x and y. The spiking dynamics has been observed in many fields, including neuroscience ^40-43, mathematical biology and biophysics ^44,45, chemical physics ^46,47; see also references therein.

3.PSpice-based circuit simulations

Our motivation in this section is to verify the numerical results obtained previously by performing some PSpice-based circuit simulations of system under study. Futhermore, it is important to evalute the effects of fractional-order derivative taken into account in the mathematical model, on the real behavior of a hardware prototype of the Shimizu-Morioka system. To this end, we design and simulate the circuit diagram of the proposed electronic simulator of fractonal-order Shimizu-Morioka system provided in Fig. 13.

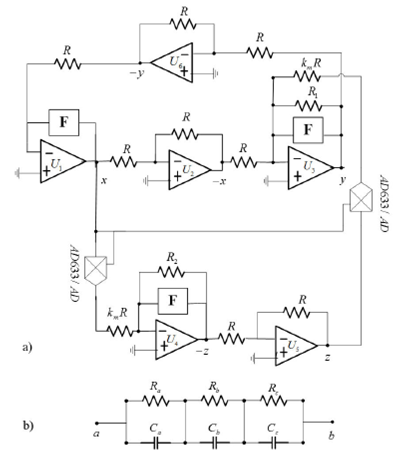
Figure 13 Electronic circuit realization of the fractional-order Shimizu-Morioka system a). The block F is a chain fractance circuit includes three resistor-capacitor pairs connected in series b). The values of electronic elements of the chain fractance circuit defined as in ³⁸ for q = 0:9 are R _a = 62:84 MΩ, R _b = 250 kΩ, R _a = 2:5 kΩ, C _a = 1:232 μF, and C _c = 1:1 μF. 

This circuit consists of resistors, capacitors, operational amplifiers (TL084), analog multiplier chips (AD633JN) and three chain fractances circuit represented by a block F ⁴⁸. Each chain fractance circuit includes three resistor-capacitor pairs connected in series. By using the Kirchhoff’s electric laws on circuit of Fig. 13, the following set of three coupled first-order nonlinear differential equations are obtained:

dqVxdtq=1RC0Vy,

dqVxdtq=1RC0Vx-1R1C0Vy-0.1RC0VxVz,

dqVzdtq=-1R2C0Vz-0.1RC0Vx2,

where V_x, V_y, and V_z are the output voltages of the operational amplifiers U₁, U₂ and U₅. The capacitor C₀ replaces the chain fractance circuit. In order to use the same sets of parameters for both numerical and electronic circuit simulations, the values of electronic components in Fig. 13 are selected as: R = 1 kΩ, R₁ = 2.851 kΩ, and R₂ = 5 kΩ. The values of the electronic components of chain fractance circuit ³⁸ are selected as R_a = 62.84 MΩ, Rb = 250 kΩ, R_a = 2.5 kΩ, C_a = 1.232 μF, C_a = 1.84 μF, C_a = 1.84 μF, and C_c = 1.1 μF in order to realize the commensurable fractional-order q = 0.9. The monostable chaotic phase portraits of respectively, integer and fractional-order form of the circuit in planes (V_x, V_y), (V_x, V_z) and (V_y, V_z) are shown in Figs. 14 and 15 with the above given values of electronic elements. The initial voltages are (Vx,Vy,Vz)=(0.1V,0.2V,0.3V).

PSpice-based circuit simulation results for integer-order as well as for fractional-order models (see Figs.14 and 15) confirm that the chaotic portraits obtained numerically (see Figs 4 and 9), can be generated by the proposed electronic circuit. This serves to validate the numerical results. The other dynamical behaviors are verified in PSpice and omitted here for brevity.

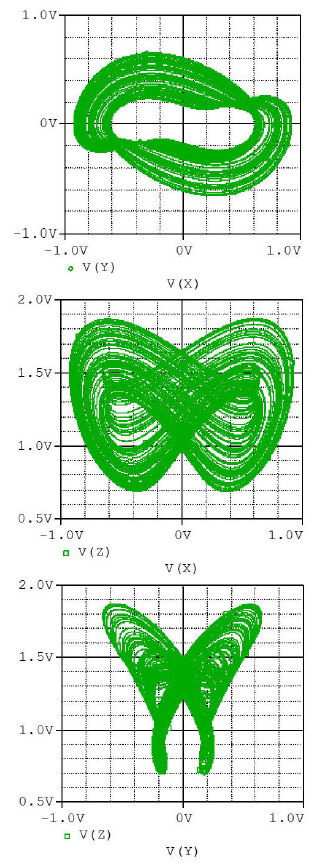
Figure 14 Chaotic phase portraits in plane (V _x ; V _y ), (V _x ; V _z ) and (V _y ; V _z ) obtained from the PSpice-based circuit simulations of integer-order Shimizu-Morioka system for R = 1 kΩ, R ₁ = 2:851 kΩ, and R ₂ = 5 kΩ. The initial voltages are (V _x ; V _y ; V _z ) = (0:1V; 0:2V; 0:3V ). 

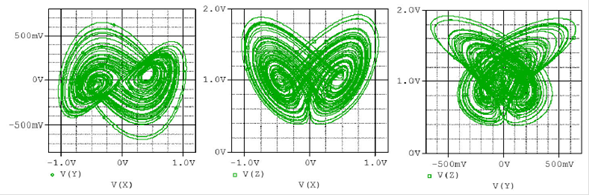
Figure 15 Monostable chaotic phase portraits in plane (V _x ; V _y ), (V _x ; V _z ) and (V _y ; V _z ) obtained from the PSpice-based circuit simulations of fractional-order Shimizu-Morioka system for R = 1 kΩ, R1 = 2:851 kΩ, R ₂ = 5 kΩ. The values of the electronic components of chain fractance circuit for q = 0:9 are R _a = 62:84 MΩ, R _b = 250 kΩ, R _a = 2:5 kΩ, C _a = 1:232 μF, Ca = 1:84 μF, and Cc = 1:1 μF. The initial voltages are (V _x ; V _y ; V _z ) = (0:1V; 0:2V; 0:3V ). 

4.Conclusion

In the present paper, an integer and fractional-order Shimizu-Morioka system was studied. The integer-order system exhibited monostable and bistable chaotic attractors, as well as their coexistence. It was revealed from the numerical simulations that fractional-order Shimizu-Morioka system exhibits very rich and complicated dynamics such as bistable chaotic attractors, metastable chaos and spiking oscillations for specific parameter settings. The implementation of an electronic circuit using chain fractance circuits for the interger- and the commensurate fractional-order Shimizu-Morioka system was performed in Orcad PSpice sotfware. A close agreement was observed between PSpice-based circuit simulations and numerical simulations.

Conflict of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.