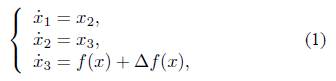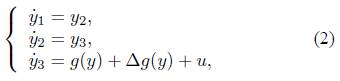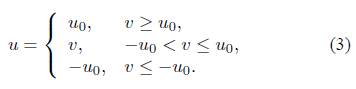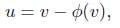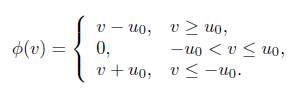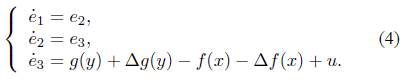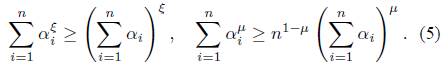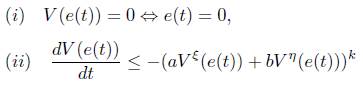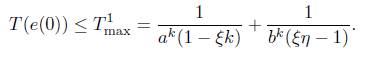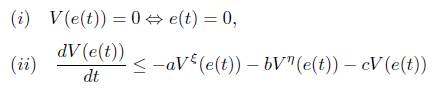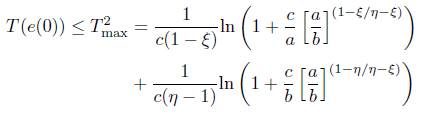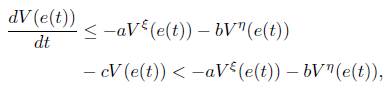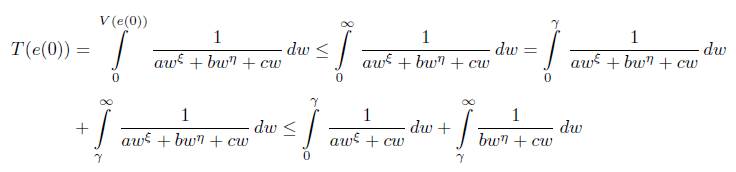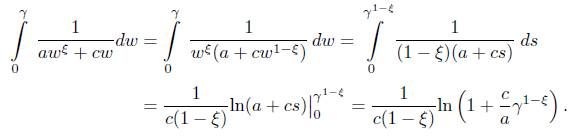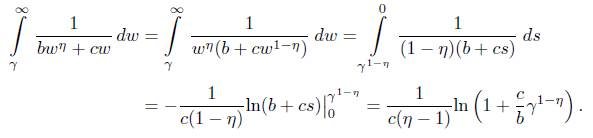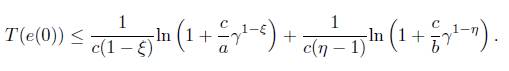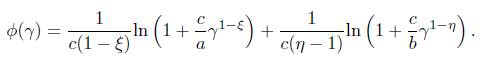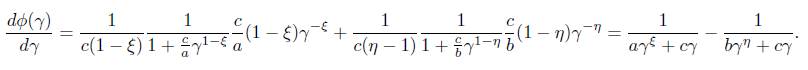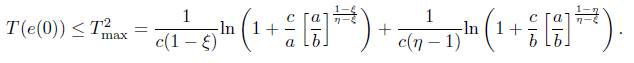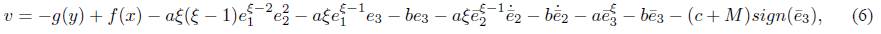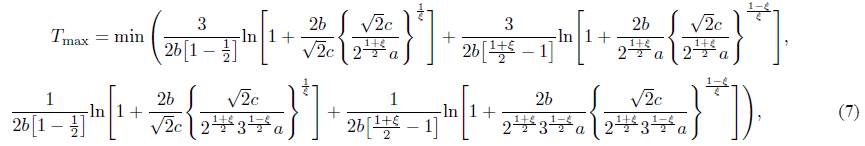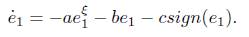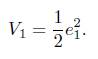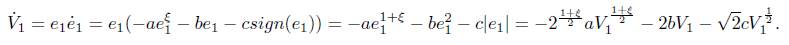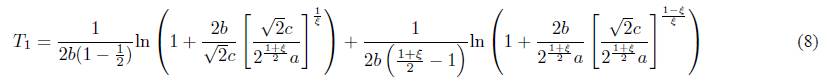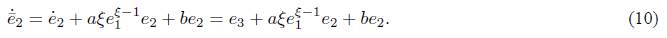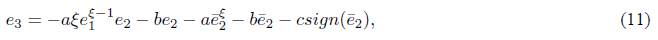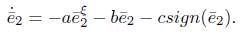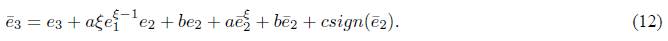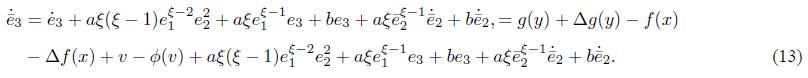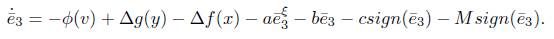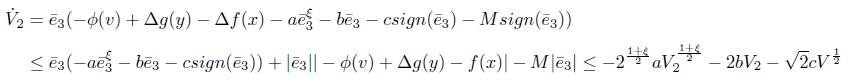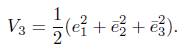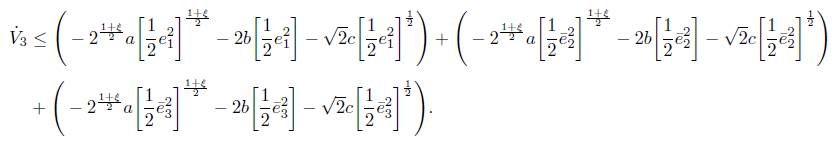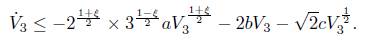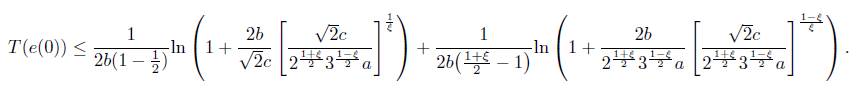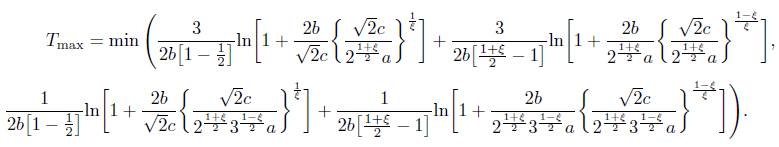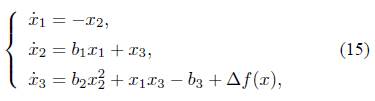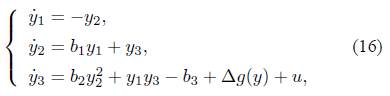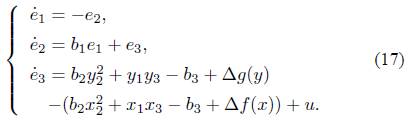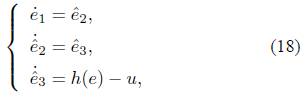1. Introduction
Synchronization behavior is a fundamental natural phenomenon widely existing in the natural world and the field of engineering. During the past decades, chaos synchronization has attracted considerable interest and been extensively studied owing to its potential applications in various fields, such as information processing, chemical reactors, physical science, secure communication, and so on. Accordingly, various control methods have been proposed to solve the synchronization problem between chaotic systems, such as linear control [1], optimal control [2], pinning control [3], sliding mode control [4], and so on. So far, many interesting results have been obtained for chaos synchronization [5-9]. However, most of the researching products are based on asymptotical synchronization, which means that chaos synchronization can only be achieved when time tends to infinity. As we all know that in reality, it is more valuable that the synchronization of chaotic systems is realized in finite time rather than infinite time. Therefore, a lot of work has been done in the research of fixed time synchronization [10-13]. Fixed time synchronization means that chaos synchronization can be achieved within a bounded time for any initial value of the studied system. Compared with asymptotical synchronization, fixed time synchronization has some excellent performances, such as faster convergence speed, better anti-interference capability, and so on. In order to observe fixed time synchronization, the error system must be stable within a fixed time. Although some results have been proposed in the literature, the study on the fixed time stability of chaotic systems is still in its infancy. So, it is of great significance to further establish some novel and effectively fixed time stability criteria. On the other hand, it is well known that the practical systems are often subject to input saturation, which could cause unsatisfactory imprecision and even instability of the controlled systems. In order to improve the synchronization performance, the effect of saturation should be further considered.
Based on the above mentions, the main aim of our paper is devoted to the fixed time stability of nonlinear systems and the fixed time synchronization of a class of chaotic systems via the backstepping control. A new fixed time stability theorem and an estimate formula of the settling time are establish firstly. Then, a novel saturation controller for the synchronization of a class of chaotic systems is derived by using the obtained fixed time stability theory. Finally, some numerical simulations are given to demonstrate the effectiveness and validity of the derived method.
This article is organized as follows. In Sec. 2, the system description and some necessary preliminaries are given. The fixed time stability of nonlinear systems and the synchronization of chaotic systems are investigated in Sec. 3. In Sec. 4, some numerical simulations are presented to show the feasibility of the theoretical results. Section 5 ends the article with conclusions.
2. The system description and preliminaries
Consider a class of chaotic systems described by the following differential equation:
where x 1 ,x 2 ,x 3 denote the state variables, f(x) is a nonlinear function, ∆f(x) describes the bounded disturbance, x = (x 1 ,x 2 ,x 3) T .
Remark 1. The system (1) includes an extensive variety of chaotic systems such as Genesio system [14], Rossler system [15], Arneodo-Coullet system [16], Wei system [17], and so on.
Remark 2. The backstepping method, which has been developed by Kristic et al. [27], is one of the most powerful nonlinear techniques of controller design. It proposes a systematic recursive algorithm specified for the class of nonlinear systems having a lower triangular form. Note that the structure of the considered model (1) is in the form of strict feedback. Therefore, in this paper, we utilize the backstepping control approach to investigate the fixed-time synchronization of the system (1).
Suppose the above system is viewed as the drive system, then the response system, which may be different from the drive system (1), is given as:
where y 1 ,y 2 ,y 3 denote the state variables, g(y) is a nonlinear function, ∆g(y) describes the bounded external disturbance, y = (y 1 ,y 2 ,y 3) T . u is the saturation control input which is defined by:
The saturation controller u can also be written as:
where
If the error between the drive system (1) and the response system (2) is defined as e = y − x, then the error system can be obtained:
Definition 1 [10]. The origin of system (4) can achieve finite-time stability, if there exists a constant T(e(0)) > 0 such that lim t→T(e(0)) ||e(t)|| = 0 and ||e(t)|| = 0 for any t > T(e(0)), where T(e(0)) is called the settling time.
Definition 2 [11]. The origin of system (4) is said to be fixed time stable if it is globally finite-time stable and the settling time T(e(0)) is bounded for any e(0) ∈ R 3 , i.e., there exists T max > 0 such that T(e(0)) ≤ T max for e(0) ∈ R 3 .
This paper aims at designing a robust reliable controller u to synchronize the drive system (1) and response system (2) in a fixed time. Based on Definition 2, we only need to design proper controller u such that the origin of system (4) is fixed time stable.
Lemma 1 [19]. If α 1 ,α 2 ,··· ,α n ≥ 0,0 ≤ ξ ≤ 1,µ > 1, then we get
Lemma 2 [11]. If there exists a continuous, positive definite, and radially unbounded function V (e(t)) : R n → R such that any solution e(t) of (4) satisfies the following two conditions:
for some α,b,η,ξ,k > 0 and ηk > 1,ξk < 1, then the origin of system (4) is fixed time stable, and the settling time T(e(0)) is estimated by
3. The synchronization scheme
In this section, the synchronization scheme between systems (1) and (2) is investigated, and some new criteria are given.
Theorem 1. If there exists a continuous, positive definite and radially unbounded function V (e(t)) : R n → R such that any solution e(t) of (4) satisfies the following two conditions:
for some α,b,c,η,ξ > 0 and η > 1,ξ < 1, then the origin of system (4) is fixed time stable, and the settling time T(e(0)) is estimated by
Proof. Since
based on Lemma 2, we know that the origin of system (4) can achieve fixed time stability.
In the following, we estimate the settling time:
a) Let s = w 1−ξ , then ds = (1 − ξ)w −ξ dw which implies that dw = (1/[1 − ξ]w −ξ )ds. Thus, we have
b) Let s = w 1−η , then ds = (1 − η)w −η dw which means that dw = (1/[1 − η]w −η )ds. Thus, we get
By a), b) we obtain
In order to find the optimal estimation of T(e(0)), set
Then
Let dφ(γ)/dγ = 0, we have αγ ξ + cγ = bγ η + cγ, i.e. αγ ξ − bγ η = 0. By solving this equation, one can get γ 1 = 0, γ 2 = (α/b) (1/η−ξ) .
If γ = 0, then φ(γ) = ∞, which
implies that the minimal
Remark 3. Some fixed time stability theorems have been proposed in papers [18-20] without considering the term cV (e(t)). The term cV (e(t)) is important since it can help to improve the convergence performances. Thus, Theorem 1 given in our paper is the extension of the fixed time stability theorems presented in papers [18-20].
Remark 4. A theorem similar to theorem 1 is investigated in paper [21]. However, the upper bound estimate formula of the settling time given in paper [21] is obtained by setting γ = 1, which means that the upper bound estimation is not optimal. Note that the upper bound of the settling time proposed in our paper is optimal, which implies that compared with the paper [21], Theorem 1 can give the settling time a more accurate estimate. Therefore, in terms of applicability, Theorem 1 has some advantages over that presented in the paper [21].
Theorem 2. For the error system (4). If
then there exists fixed time T(e(0)) ≤ T max such that lim t→Tmax e i = 0 and e i = 0,i = 1, 2, 3 for t ≥ T max, where
and α, b, c are positive constants, ξ =
(q/p) > 2, p, q > 0 are
odd integers,
Proof: After observing system (4) we know that if there exists fixed
time T such that lim
t→T
e
1 = 0 and e
1 = 0 for t ≥ T, then lim
t→T
In the following, we use the backstepping method to prove Theorem 2.
If
Let
Its derivative about time t is
Because of Theorem 1, we know there exists a fixed time
such that lim t→T1 e 1 = 0 and e 1 = 0 for t ≥ T 1.
In order to get
Then we have
If
then according to (10) and (11), we obtain
Based on Theorem 1, we know that there exists fixed time T1 such that lim
t→T
Then
Now we assume that ∆g(y), ∆f(x) are bounded which means that there exists constant M > 0 such that
Putting (6) into (13), yields
Choosing
Based on Theorem 1, we know there exists T
1 such that lim
t→T1
From the proof process of Theorem 2, it is easy to see that when t ≥ 3T 1 we have e 1 = 0. Thus, the setting time should be T(e(0)) ≤ 3T 1 .
In order to find the optimal setting time, we chose the final Lyapunov candidate as:
Taking the derivation of V 3 results in
By using Lemma 1, one gets
By Theorem 1, we know that the setting time T(e(0)) should be
Therefore, the setting time T(e(0)) should be satisfied T(e(0)) ≤ T max, where
Remark 5. Papers [21-23] have investigated the fixed time control or synchronization of nonlinear systems and proposed some control schemes without considering the input saturation. Since in the practical systems, input saturation is often encountered, so these drawbacks of the control schemes given in papers [21-23] will limit their range of application and effect of use.
Remark 6. In the literature, some papers have considered the control or synchronization of the system (1). For example, paper [24] has investigated the adaptive robust synchronization of the n-dimensional system (1) based on the Lyapunov theory. Paper [25] has studied the control of the fractional-order system (1) via the reduced-order method. It is easy to see that the synchronization and stabilization in papers [24-25] will be achieved when time goes infinity. However, in our paper, the synchronization time is bounded by a constant which is independent with regard to the initial values. In addition, papers [24-25] have not taken account of the input saturation.
4. Simulation results
In this section, some numerical simulations by using the Wei system [18] as an example are given to demonstrate the effectiveness of the proposed design schemes.
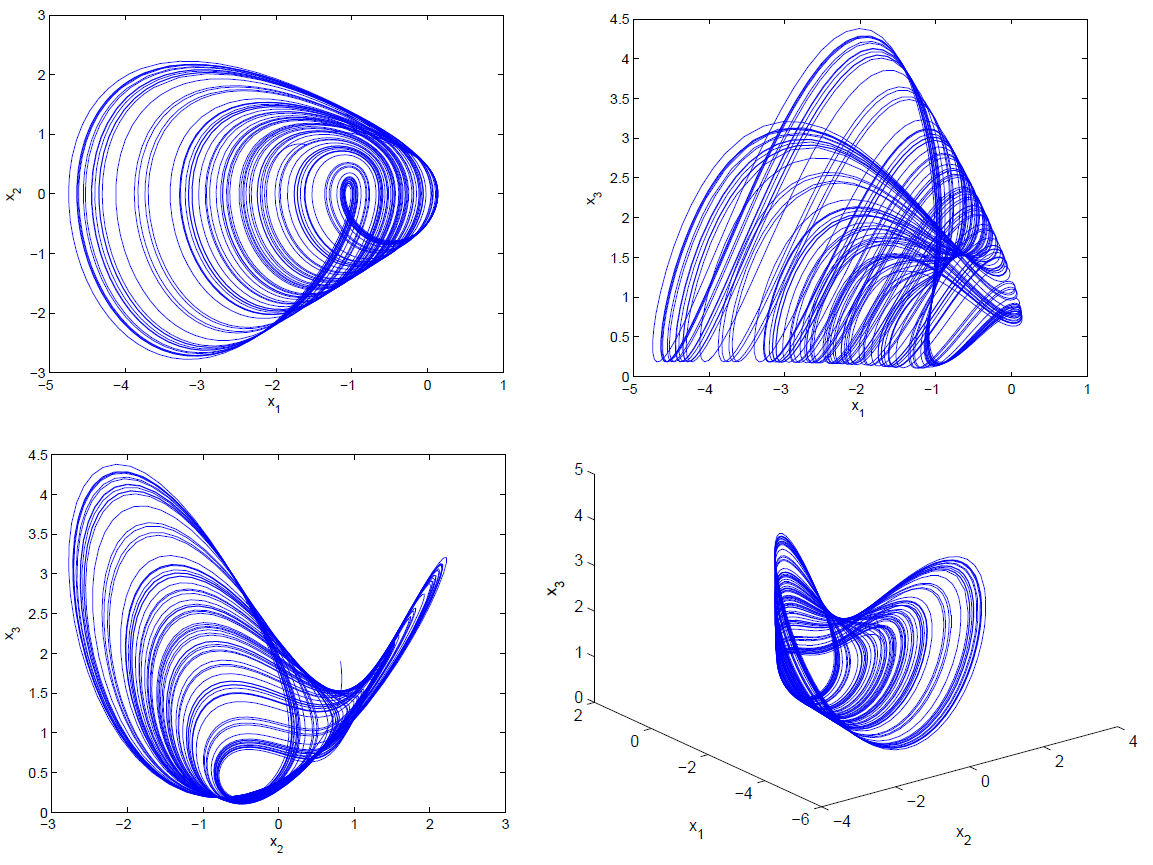
The Wei system [18] is described by:
where b 1 ,b 2 ,b 3 are the system’s parameters, ∆f(x) is the bounded disturbance. When b 2 = 3,b 1 = 1,b 3 = 0 and ∆f(x) = 0 system (15) is the Sprott D [26]; when b 2 = b 3 ,b 1 = 0 and ∆f(x) = 0 system (15) is topologically equivalent to the Falkner-Skan system [17]. Especially, when (b 2 ,b 1 ,b 3) = (2,1,0.35) and ∆f(x) = 0, system (15) is chaotic and has a single-scroll attractor with no equilibria. The phase portraits of x 1 − x 2, x 1 − x 2, x 1 − x 2 and x 2 − x 1 − x 3 are shown in Fig. 1.
Suppose system (15) is the drive system, then the response system is constructed as:
where u is the controller.
Based on (15) and (16), the error dynamic system is
It is easy to see that the structure of the system (17) is different from that of the
system (4). In order to take advantage of the obtained results, we set
where
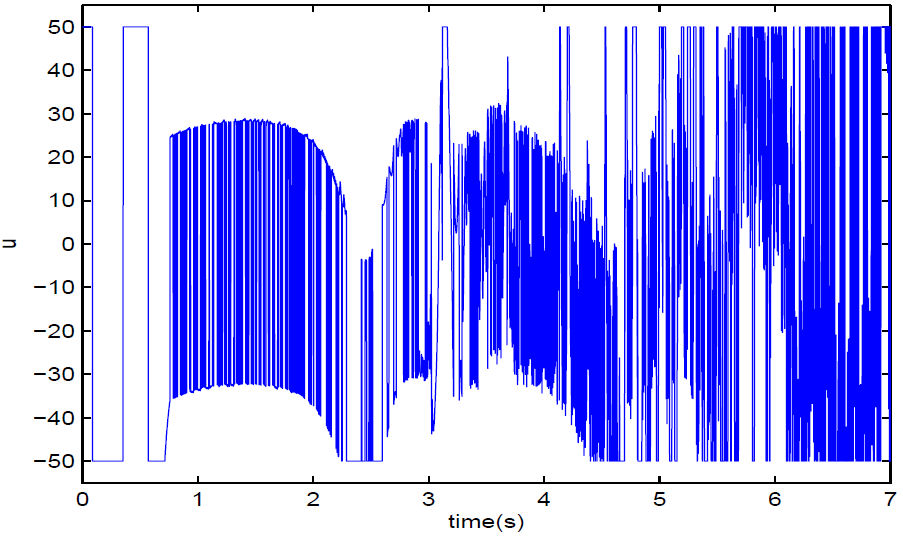
In the numerical simulation process, we suppose (b 2 ,b 1 ,b 3) = (2,1,0.35) so that system (15) has chaos attractor. The disturbances ∆f(x) and ∆g(y) are assume to be (1/2)sin(t) and (1/2)sin(t)cos(t), respectively. The controller u is designed based on (3) and (6), where α = b = 1,c = 0.01 and ξ = 3, M = 30, u 0 = 50. According to Theorem 2, systems (15) and (16) can be synchronized in fixed time. The initial conditions of simulation are taken as (x 1(0),x 2(0),x 3(0), y 1(0),y 2(0),y 3(0)) = (2,1,−4,4,−1,3). The trajectories of variables e 1 ,e 2, and e 3 are depicted in Figs. 2-4. By computation, the T max defined in (7) is T max = min{12.4619,12.1307} = 12.1307.
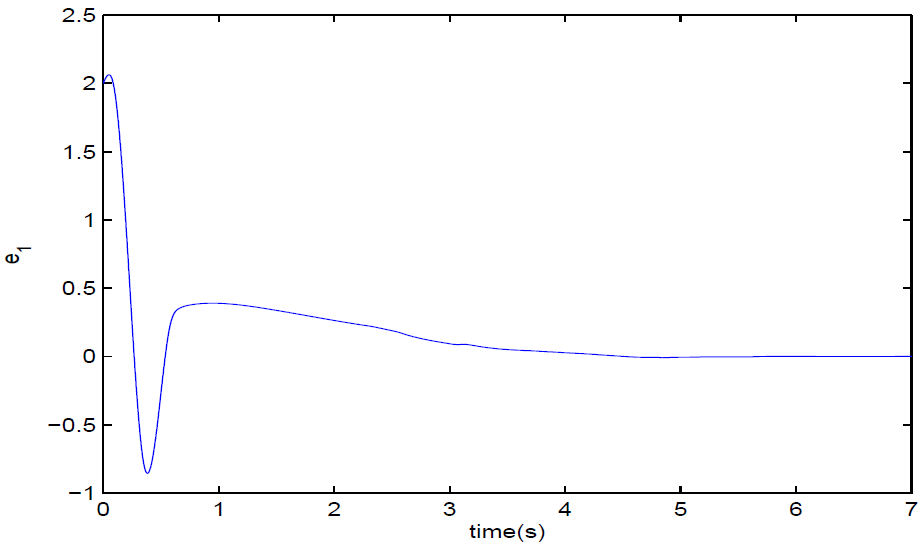
FIGURE 2 Fixed time synchronization error e 1 between the drive system (15) and the response system (16).
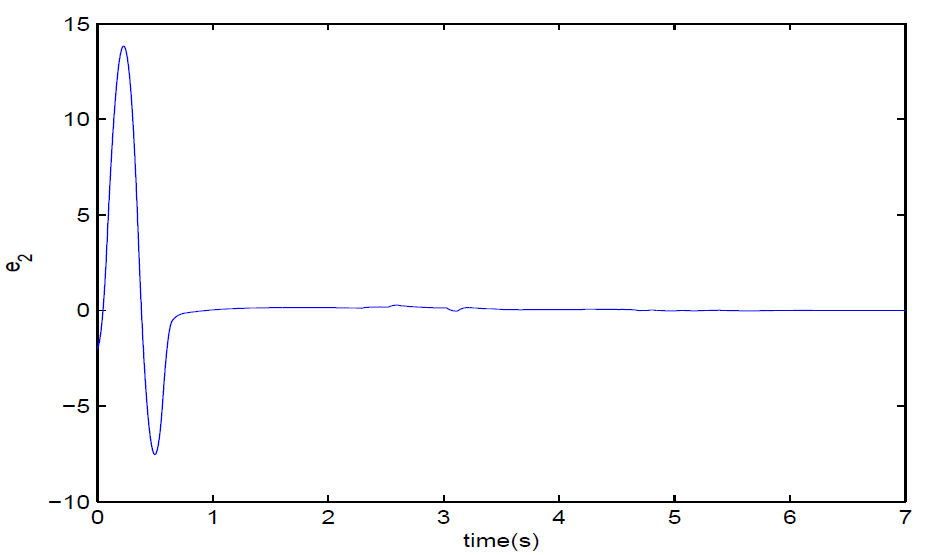
FIGURE 3 Fixed time synchronization error e 2 between the drive system (15) and the response system (16).
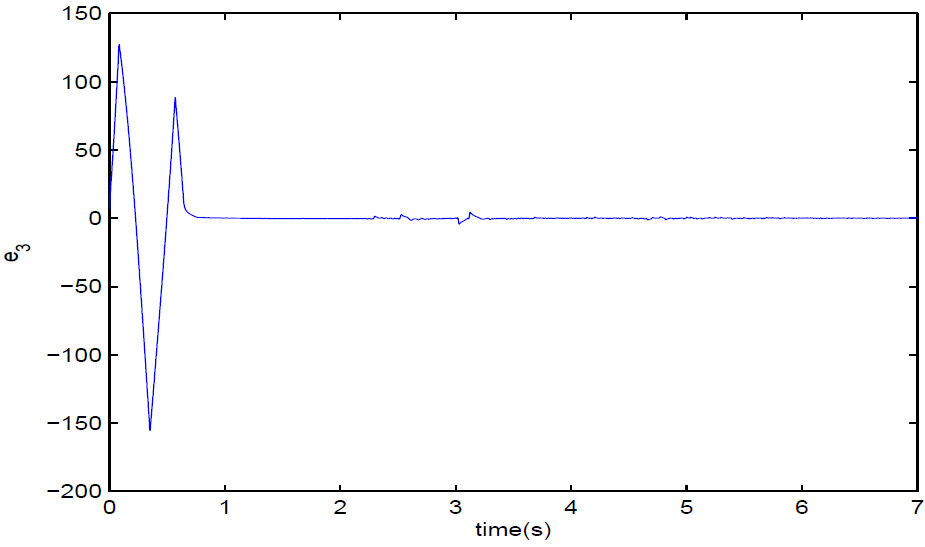
FIGURE 4 Fixed time synchronization error e 3 between the drive system (15) and the response system (16).
However, from Figs. 2-4, it is easy to see that the synchronization between systems (15) and (16) can be achieved in 6 seconds which is less than T max = 12.1307. The simulation results are in accord with the theory, which demonstrates the effectiveness of our proposed design schemes.
5. Conclusions
In this paper, we propose a new fixed time stability criterion in which the fixed time estimation formula is different from those obtained in the literature. With the assistance of the novel fixed time stability criterion, the fixed time synchronization of a class of chaotic systems is investigated by the backstepping procedure. Based on the practical application, the disturbances and input saturation are taken into consideration in this paper. Numerical simulations demonstrate the fast convergence and robust performance of the presented controller.











 nueva página del texto (beta)
nueva página del texto (beta)