1.Introduction
For the scientific community, it is known the great number of works related to the application of fractional calculation in the different areas of knowledge 1-10. In parallel, there are efforts that continue with the objective of performing physical and geometric interpretations of both the fractional derivative and the fractional integral, as shown in recent contributions. See for example: 11-14, where are shown geometric and physical interpretations of Volterra-type convolution integrals a relationship between the fractal set of Cantor and the fractional integral, the presentation of the general conformable fractional derivative, along with its physical interpretation, and the geometric interpretation of the tangent line angle of a polynomial with fractional derivative coefficients, respectively.
On the other hand, independently of the existence of diverse physical and geometric interpretations of what the fractional derivative of the function of a physical system represents, it is important to mention that its use in different sciences, as well as natural (physical) sciences, can be said to be endorsed by the formulation of the variational principles of fractional type, which describes with great success the evolution of non-conservative systems, as mentioned in the references 15,16. Likewise, in related literature, we can find several explicit applications of the fractional derivative in natural systems; for example, in 17, a model is proposed to characterize natural shapes such as neutral hydrogen emissions using the concept of a fractional derivative. Also, in 18, it is found that an approximation can be established between the concepts of relativistic kinetic energy and fractional kinetic energy. The heterogeneous semiconductor structures do not escape this multitude of applications of the fractional calculation; for example, in 19-25 just some of them can be found. Thus, taking into account the favorable effect that the fractional derivative can have on the different natural systems, our present contribution consists in the direct application of the framework developed in 14 to find, for the first time, the approximate physical and geometric effect that produces the fractional derivative of the variable the concentration of a dopant, in this case, Aluminum deposited on a substrate, the position-dependent effective mass adopted by the confined electron, and the potential energy that the electron acquires due to the semiconducting medium. It should be mentioned that we use these magnitudes in a recent contribution 26, where we use the structure formed by AlxGa1-xAs as a semiconductor. Bearing this in mind, the second section contains the description of the mathematical formalism. The third section describes the application of such formalism to the semiconductor parameters of the mentioned type and, finally, in the fourth section, a brief description of the obtained results and the consequences inferred by them are made.
2.Description of the formalism
The concept of a fractional derivative is linked to that of the minimum trajectory to go from a point (x1, f(x1)) to a point (x2, f(x2)) in a plane x, f(x), and then to get the Lagrangian of the system. From the classical theory of differential calculus and integral calculus, we can see that for a function f(x), there is an infinite sequence of derivatives and integrals 27
The fractional calculation tries to interpolate the sequence (1) in such a way that it allows generating any order from an arbitrary order. Several definitions have been proposed for the fractional derivative, among which are those of Riemann-Liouville, Grünwald-Letnikov, Weyl, Caputo, Marchaud, and Riesz. In particular, in the present work, we make use of a definition that is generated from the fractional derivative of Riemann-Liouville:
with 0 < α < 1. Integrating by parts and making a change of variable to
introduce the definition of the beta function, it can be seen that for a function of
the type
This type of fractional derivative is used in 14, where the result of

Figure 1 Graphic representation of the geometric and physical elements, described by the mathematical formalism, adopting an order of the fractional derivative of a = 1=2.
The triangular area
The value of λ is solved for the triangular area in the form
In such a way that
where
On the other hand, from the triangular area we also have that
With this information, the triangular area is expressed as
As can be seen, once the values of b and a are determined, both
As mentioned in 14, the triangular
area
3.A direct application of the formalism
Using atomic units, the concentration of the semiconductor is given by
In applying the formalism described in the previous section to x(z), m(z), V(z), respectively, is obtained
The fractional derivatives (8), (9) y (10) have a graphic structure equivalent to that described by Fig. 1, within the framework of the formalism raised above.
Taking into account the above, the areas
To solve the areas of (11), (12), and (13), respectively, it is taken into account that
where
On the other hand, from the same triangles with the areas given by (11), (12), and (13), we also have, respectively that
Therefore, substituting the angles
Once these areas are obtained, the following physical magnitudes can be constructed
The Eqs. (20), (21) y (22) represent a type of conservative magnitudes from a
geometric and physical point of view. By solving (20), (21), and (22), the constant
numerical values associated with the corresponding products are obtained between the
fractional derivatives and the respective areas, as can be observed through Tables I, II, and III, where
Table I The fractional-order a of the derivative, the
fractional derivative of the concentration
x(z) evaluated in
z = 75, the projected area
| α =α0 | D α= α0[x(z)] | Da=a
0[x(z)] |
|
| 0.1000 | 0.0634 | 0.0604 | 3.83E-03 |
| 0.2000 | 0.0475 | 0.0805 | 3.83E-03 |
| 0.3000 | 0.0366 | 0.1046 | 3.83E-03 |
| 0.4000 | 0.0287 | 0.1332 | 3.83E-03 |
| 0.5000 | 0.0228 | 0.1679 | 3.83E-03 |
| 0.6000 | 0.0182 | 0.2107 | 3.83E-03 |
| 0.7000 | 0.0145 | 0.2647 | 3.83E-03 |
| 0.8000 | 0.0115 | 0.3343 | 3.83E-03 |
| 0.9000 | 0.0090 | 0.4255 | 3.83E-03 |
Table II The fractional-order a of the derivative, the
fractional derivative of the effective mass
m(z) evaluated in
z = 75, the projected area
| α =α0 | D α= α0[m(z)] | Da=a
0[m(z)] |
|
| 0.1000 | 0.0634 | 0.0604 | 3.83E-03 |
| 0.2000 | 0.0475 | 0.0805 | 3.83E-03 |
| 0.3000 | 0.0366 | 0.1046 | 3.83E-03 |
| 0.4000 | 0.0287 | 0.1332 | 3.83E-03 |
| 0.5000 | 0.0228 | 0.1679 | 3.83E-03 |
| 0.6000 | 0.0182 | 0.2107 | 3.83E-03 |
| 0.7000 | 0.0145 | 0.2647 | 3.83E-03 |
| 0.8000 | 0.0115 | 0.3343 | 3.83E-03 |
| 0.9000 | 0.0090 | 0.4255 | 3.83E-03 |
Table III The fractional-order a of the derivative, the
fractional derivative of the confining potential V
(z) evaluated in z = 75, the
projected area
| α = α0 | Dα=α0 [V (z)] | Da=a
0[m(z)] |
|
| 0.1000 | 0.0020 | 1.9202 | 3.83E-03 |
| 0.2000 | 0.0015 | 2.5622 | 3.83E-03 |
| 0.3000 | 0.0012 | 3.3274 | 3.83E-03 |
| 0.4000 | 0.0009 | 4.2393 | 3.83E-03 |
| 0.5000 | 0.0007 | 5.3419 | 3.83E-03 |
| 0.6000 | 0.0006 | 6.7037 | 3.83E-03 |
| 0.7000 | 0.0005 | 8.4230 | 3.83E-03 |
| 0.8000 | 0.0004 | 10.6375 | 3.83E-03 |
| 0.9000 | 0.0003 | 13.5397 | 3.83E-03 |
| 1.0000 | 0.0002 | 17.4006 | 3.83E-03 |
Likewise, the semiconductor concentration function x(z) can be visualized through Fig. 2, where the triangular areas obey the formalism used in this article.
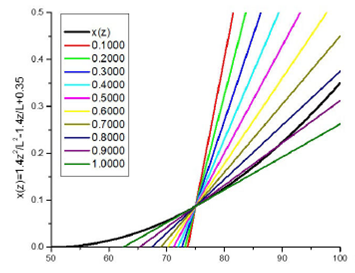
Figure 2 Graphic representation of the geometric and physical elements of the concentration x(z) described by the mathematical formalism adopting an order of the fractional derivative of α ∈ [0.1000; 1.000].
Each of the other physical magnitudes (effective mass m(z) and the
confining potential V(z)) also have geometric and physical
elements, which manifest themselves analogously to the concentration x(z). Once
obtained the numeric calculations for the effective mass and the confining
potential, it was found that the constant value associated with each of these
magnitudes was the same, i.e., it is found that
the possibility of new symmetries associated with the semiconductor system. Interestingly, the numerical coincidence of these three new invariant magnitudes could indicate that the semiconductor system has a certain self-similarity, which allows us to characterize it as a structure of fractal type.
Likewise, as we mentioned in 26,
there is a visible relationship between x(z), m(z) and V(z), which we can express as
is a linked potential. Such characteristic allows us to infer that (22) is continuous
everywhere, as shown in 28. The
fractional continuity of (22) is verified because the z coordinate
of the semiconductor crystal structure does not have a discrete value spectrum.
Likewise, such a continuity equation is a restriction to the wave function of the
confined electron, as mentioned in 28. Now, as we already mentioned, the concentration and the
mass effectively show a clear relationship with potential, and that relationship
allows us to infer that the continuity Eqs. (20) and (21) have an interpretation
similar to the continuity (22) of the potential, which is grounded since
On the other hand, from these continuity equations, it can be seen that, inside the
semiconductor, a fractional area is defined when
with 0.1000 jumps. Such an interpretation can be visualized through Fig. 3.
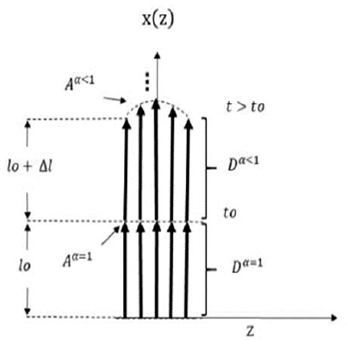
Figure 3 Visualization of the variation rate of x(z), involving an isotropic and anisotropic evolution across cross-sectional areas Euclidean and Hausdorff, respectively.
From the previous Fig. 3, you can see the
visualization of the variation rate of x(z), with dependence on the degree α of the
derivative. In the initial time t = t0, the concentration undergoes an
isotropic evolution
4.Critical points in the fractional derivative of x(z), m(z),
and
According to 14, the fractional derivative of polynomial-type functions shows critical points when the base variable and the largest exponent of the polynomial coincide. Then, to visualize some critical points in the fractional derivative of the concentration, effective mass of the electron, and potential energy of the system, it is necessary to pose the corresponding equations of the formalism for each of the magnitudes. However, as all three have the same algebraic structure, we focus only on the concentration x(z), as shown below.
If the fractional derivative of the concentration x(z) of the semiconductor under study is given by
For z = β = 2, we must then have the possibility of finding critical points. We examine this inspection in a next way
If β = 2, (12) is reduced only to the first two terms
Solving the partial derivative (13), we obtain the next equation
which is a general equation for the variable called “critical point α” y where
The solution of (26) provides us with the existence of the critical point α = 0.5,
which means that in the interval of
Table IV Critical points of the fractional derivative of the concentration x(z) evaluated in z = 2, adopting the numerical value of L = 100 for the size of the crystalline structure.
| Δα | α |
| [0.1000; 1.000] | 0.5387 |
| [2.1000; 3.000] | 2.4956 |
| [3.1000; 4.000] | 3.5729 |
| [4.1000; 5.000] | 4.6105 |
| [5.1000; 6.000] | 5.6352 |
| [6.1000; 7.000] | 6.6532 |
| [7.1000; 8.000] | 7.6671 |
| [8.1000; 9.000] | 8.6784 |
| [9.1000; 10.00] | 9.6877 |
Something interesting that we can also observe, it has to do with the numerical
coincidence shown between the critical points shown in Table IV and specific values that involve the Zeta function of
Riemann
Now, if we take into account that these series that involve the Zeta function of Riemann are produced at the same time by the generating function,
being 𝛾 the constant of Euler-Mascheroni, 30 then we could infer that the critical points predicted by (26) can be represented by a generating function like the one shown below
(31)
This coincidence allows us to strengthen the intuitive character that we have towards the self-similar behavior of the fractional derivatives of x(z), m(z), and V(z).
5.Conclusions
In the present work, we carried out an analysis of the fractional derivative applied to the concentration x(z), the effective mass m(z), and the confining potential V(z), which are magnitudes associated with a semiconductor of type AlxGa1-xAs, studied by us in a previous work. We believe that we have achieved, at least approximately, an interpretation possible with the direct application of a formalism that uses the fractional derivative of polynomial-like functions. From the results obtained in the present contribution, we can state that the new constant magnitudes found Ξ, γ, and Ω, show a self-similar process by visualizing the evolution of each of the fractional variation rates over the respective fractional areas (Eqs. (5), (6) and (7)), from an initial fractional-order α i to a final one α i , in the space of the spatial coordinate z. Also, such an evolution could be perceived, in an intuitive way, as the description of “fractional flows through fractional areas”. This result and the intuitive approach with which we approach it leads us to the equation of continuity inspected commonly in university textbooks, which has a similar structure but with the difference that the variational rates are non-fractional variational rates. In the same way, we show, numerically, that the concentration x(z) really behaves as an invariable quantity, verifying the analytical result. The same can be verified for m(z) and V(z). We also find that the fractional derivative of the concentration exhibits a set of critical points, which depend on the interval associated with the fractional order of the derivative.
Finally, it is interesting to reflect on the self-similar behavior in our system, within a given interval for the values of the order of the fractional derivative, knowing that self-similarity is a characteristic feature of a fractal, as mentioned above. This characteristic, together with the property of scale invariance and the symmetry that could be associated with each of the new magnitudes found for the semiconducting system under study, it could be studied more deeply in a future contribution.
It should be noted that the applications and topics reviewed, such as fractional calculation, fractals, and the Zeta function of Riemann, are vitally important for a great diversity of contemporary scientific research.











 nueva página del texto (beta)
nueva página del texto (beta)


