1. Introduction
Is a fundamental assumption of the economic theory of markets that the financial markets are efficient in the sense of the community of economic agents being able to discount all the possibilities of arbitrage, incorporating with it all the relevant information for the prices formation, so that it is impossible to design an (always) winning strategy for investment [1,2] i . Mathematically, this is described as a process, where a future increase or decrease of the current price is the result of a random event. Underlying such a random walk is a binomial distribution, which after a very large number of steps (price changes), converges to a normal Gaussian distribution. In turn, normal distributions are common in the description of systems in equilibrium, a stable state, small fluctuations around which decay exponentially with time. However, it seems that the financial market cannot be modeled as this kind of system; data for most financial indexes around the world are statistically described by probability distributions that exhibit a large skewness or kurtosis, relative to that of a normal distribution. It may mean that strong perturbations are not, de facto, necessary for the market entering a critical state. Recurrent significant deviations of economic variables from their average values could be just the cumulative and unavoidable result of many small-scale processes and interactions occurring within the market system, continuously subjected to a net external action like, for instance, publicly available announcements of annual earnings, stock splits, companies profits forecasts, new securities or, even more, the punctual action of agents having preferential access to restricted or confidential information.
In this regard, for years now particularly good fits to financial data have been obtained using Lévy-stable distributions [3]. Nevertheless, it is obvious that, strictly speaking, the market can neither be such a random process. First, it is unreasonable to expect data from any real (as opposed to hypothetical) process to have an infinite variance. Secondly, it is reasonable to expect data from financial transactions at a given time to have some memory of the previous transactions, i.e., the elements of the corresponding time series should not be really independent each from the others. This is easily noted, for instance, during steeped variations of the stock returns due to panic or euphoria.
Commonly there are two causes of autocorrelation in this kind of data, irregular sampling and causality determined by market microstructure. In agreement with the efficient market hypothesis, it is intuitive not to expect persistent serial dependence in price changes; otherwise, it would be used to influence the market. Consistently with this, autocorrelation is often neutralized after homogenization of the corresponding series by time averaging of subsamples. This typically results in sets with information correlated with those of daily or lower frequency data. It is for these last sets that fitting to stable distributions have already yielded remarkably good results [4-8]. More precisely, it has been verified that the actual density distribution behind the data could be a socalled Lévy-truncated [9,10] which, after sequential convolution corresponding to the sum of the values over increasing time intervals also converge to a Gaussian distribution. This convergence is ultra-slow; therefore, the truncation still allows for a relatively high probability of extreme fluctuations, which, as it was already noted, seems to be a distinctive feature of most financial markets.
Despite the success in describing markets activity as a Lévy (truncated) flight, it is widely acknowledged that the description will not be complete unless high-frequency data is also brought into the study. On the one hand, most market models are based on a variety of hypotheses regarding the long-memory features of volatility, which are difficult to extract from daily or lower-frequency data but can be observed in intraday data. For instance, as it was already mentioned, a crisis in finances may not necessarily be linked only to strong perturbations over several days, but also to the cumulative effect of intraday weaker perturbations. On the other hand, the quality of risk analysis of investment depends on the accuracy of measurement of ex-post volatility and forecast evaluation. There is evidence of the improvement in both directions thanks to the availability of high-frequency data from liquid financial markets such as the foreign-exchange, bond or equity-index markets afford [11]. Last, but not least, the analysis of the impact of sample size on the probability estimation of extreme events yields that a large volume of data is needed to determine the actual stable distribution corresponding to a given asymptotic scaling [8, 12]. This is the kind of volume that commonly characterizes the sets of highfrequency data.
It must be pointed out that market microstructure and short term interactions become relevant while analyzing intra-day fluctuations and, since they depend on local socioeconomic factors, the stylized facts of the market as a complex system can be difficult to extract. Therefore, it is very important to study different realizations of high-frequency financial data to discriminate local and universal properties of the market dynamics. It is with this intention that in this paper we report the first step into analyzing the tick-to-tick data of the Indice de Precios y Cotizaciones (IPC), the main benchmark stock index in Mexico. It has been previously shown in Ref. [8] that it can be dismissed that a normal distribution relies upon under the data of daily closing values of the IPC. On the other hand, the null hypothesis that it comes from α-stable Lévy distribution cannot be rejected´ at the 5% significance level. This implies that the daily data can safely be considered as independent and identically distributed, characterized by an infinite variance. Our aim here is to study how this conclusion changes when tick-to-tick data is analyzed.
The paper is organized as follows. In the next section, we provide a brief review of Lévy distributions, in particular of the stable and Lévy truncated distributions which we use for fitting the IPC fluctuations. The description of this data, as well as the sets derived from them and used for our analysis, is presented in Sec. 3. Next in Secs. 4 and 5, we proceed to present the analysis of the probability distribution and serial dependence of the actual fluctuations of the IPC data. We devote the last section to discuss our results and state the main conclusions.
2. Lévy distributions
As it was mentioned in the introduction, Lévy distributions are among the more frequently used to fit data from complex processes. Particularly, it has been found to be an excellent fit for the distribution of stock returns as well as other financial time series. In this section, we will briefly review the definition and properties of the stable and truncated Lévy distributions.
2.1. Stable distributions
While studying the behavior of sums of independent random variables Paul Lévy [3] introduced a skew distribution specified by scale γ, exponent α, skewness parameter β, and a location parameter µ. Since the analytical form of the Lévy stable distribution is known only for a few cases, they are generally specified by their characteristic function. The most popular parameterization is defined by Samorodnitsky and Taqqu [13] with the characteristic function:
where sign(t) stands for the sign of t. Then, the probability density function is calculated from it with the inverse Fourier transform in the form:
Lévy distributions are characterized by the property of being stable under convolution, i.e, the sum of two independent and identically Lévy-distributed random variables, is tribution), the skewness parameter β = 0. The skewness parameter must lie in the range [−1,1]. When β = +1,−1, one tail vanishes completely. The parameter γ lies in the interval (0,∞), while the location parameter µ is in (−∞,+∞).
The asymptotic behavior of the Lévy distributions is described by the expression
Hence, the variance of the Lévy stable distributions is infinite for all α < 2.
2.2. Truncated Lévy distributions
As mentioned in the previous subsection, α-stable Lévy distributions have infinite variance, hence, they have power-law tails that decay too slowly. Therefore, the fit of empirical data by Lévy stable distributions will usually overestimate the probability of extreme events. In particular, real price fluctuations have finite variance, so their distribution decays slower than a Gaussian, but faster than a Lévy-stable distribution, with the tails better described by an exponential law than by a power law. The truncated Lévy flight (TLF) was proposed by Mantegna and Stanley [9] to overcome this problem and can be defined as a stochastic process with finite variance and scaling relations in a large, but finite interval. They defined the truncated Lévy flight distribution as:
where P L (x) is a symmetric Lévy distribution. As the TLF has a finite variance, with sequential convolution, it will converge to a Gaussian process, but the convergence is very slow, as was demonstrated by Mantegna and Stanley [9]. However, the cutoff in the tail given by (4) is abrupt. This problem was solved by Koponen [10], who introduced an infinitely divisible TLF with an exponential cutoff with the characteristic function:
where c is the scaling factor, α is the stability index, and λ is the cutoff parameter. The Lévy α-stable law is restored by setting to zero the cutoff parameter. For small values of x, the truncated Lévy density described by the characteristic function (5), behaves like a Lévy-stable law of index α [14]. It was used by Matacz [15] to describe the behavior of the Australian All Ordinaries Index.
3. Data sets from IPC values
The source of the data used in this study were the databases of the National Banking and Securities Commission, the financial body of the Federal Government of Mexico. For our analysis, we used the IPC value over the period January 1999-December 2002, which comprises 4321427 transactions. Taking into account that the Mexican trading day is of six and a half hours, this gives us an average time between transactions of 5.2 seconds. To analyze the statistics of nontrivial index fluctuations, the repeated values (the intervals where no change in the returns was recorded) were filtered, and the set was reduced to N = 1164256 elements with a mean value over the period of 6209.392, a variance of 744334.3, and an excess of kurtosis of 1537.442. These ticks, Y k , are now irregularly sampled, with an average time between fluctuations of 19.3 seconds. This set is plotted in Fig. 1.

FIGURE 1 IPC tick-to-tick data after filtering repeated values. The horizontal red line corresponds to the mean value over the period.
The actual fluctuations are then taken as the difference of the Y k ,
For this study we also used sets corresponding to the convolution of the density distributions of high-frequency data {S k }, i.e., sets obtained after summing for different values of N conv,
where
It was mentioned here that after removing the inactivity from the original tick-to-tick data, it results in an irregularly sampled time series. Therefore, it is relevant to assess the effect of unevenly spaced high frequency data in our analysis and the comparison with known studies elsewhere. First, note that the ratio of the number of elements in the original set, 4321427, over the number of elements in the filtered set (N = 1164256) yields 3.71. On the other hand, for the set formed with the number of ticks between transactions with different values, it is found that the mean value is of 3.74 ticks.
The fact that these two numbers are so close each other is not trivial because it strongly depends on the way fluctuations are grouped, and it allows for the filtered data be safely represented by the mean sampling interval of 19.3 seconds. As to the impact of the irregular sampling in the convolutions, let us note that the standard deviation for the times between transactions with different values is 3.51 ticks or 18.25 seconds, which is still in the high-frequency range. Therefore, in the worst-case scenario, our time estimates are off by a factor of just 2 what, as we will see, leaves our conclusions unchanged. Even so, we have reasons for expecting ours not to be the worst case. Let us, for instance, assume that the sampling interval is 19.3 seconds, then N conv = 1200 would be the convolution corresponding to one Mexican trading day. Taking this into account we analyzed also a set of fluctuations of the IPC daily closing values (for the same period studied here) downloaded from the Yahoo Finance website. It can be observed from Table I that, even if these are different sets, the convolution with N conv = 1200 from the unevenly spaced tick-to-tick data seems to statistically describe the process at a daily frequency as well as the evenly spaced closing data.
TABLE I Statistical comparison between the fluctuations of the IPC daily closing values and the set for Nconv =1200.
| Statistics | Daily Closing Data Fluctuations |
Nconv =1200 |
| Mean | 2.20 | 2.20 |
| Std. deviation | 105.39 | 110.02 |
| Range | 993.63 | 892.47 |
| Minimum | -544.35 | -436.00 |
| Maximum | 449.28 | 456.00 |
| Sum | 2288.78 | 2122.72 |
Later in the discussion of the results presented in this manuscript, we will provide further evidence in that direction.
4. Probability distribution of IPC fluctuations
We started by analyzing the non-convoluted data. The corresponding distribution is presented in Fig. 2, where a logarithmic scale is used for the vertical axis and the horizontal axis has been rescaled, dividing by the standard deviation. The plots of best fits to a Gaussian (narrow blue curve below the data points) and a Lévy (wide red curve above the data points) distributions are also shown ii .

FIGURE 2 Distributions for N conv = 0. In the horizontal axis, Z stands for the fluctuations data or the values of the corresponding fits.
It can be observed that the probability distribution function for this data does not correspond to a normal distribution, but it neither does to a Lévy one. This is confirmed by the results of the Kolmogorov-Smirnov test shown in Table II for the best fit of data to an α-stable distribution.
TABLE II Results of the Kolmogorov-Smirnov Goodness of Fit Test (K-S test).
| Nconv | α | β | γ | δ | K-S Statistics | p-value | Reject H0? p =0.05 |
| 0 | 1.2565 | −0.0024 | 0.3796 | 0.0014 | 0.0179 | 0.0 | Yes |
| 10 | 1.5788 | 0.0056 | 2.3138 | −0.0051 | 0.0097 | 0.0 | Yes |
| 20 | 1.6107 | 0.0089 | 3.8497 | −0.0114 | 0.0076 | 0.0026 | Yes |
| 30 | 1.6296 | 0.0072 | 5.2420 | −0.0075 | 0.0081 | 0.0115 | Yes |
| 40 | 1.6539 | 0.0140 | 6.6326 | −0.03553 | 0.0099 | 0.0064 | Yes |
| 50 | 1.6523 | 0.2332 | 7.8216 | −0.0497 | 0.0108 | 0.0084 | Yes |
| 60 | 1.6594 | 0.0145 | 8.9391 | −0.0492 | 0.0100 | 0.0404 | Yes |
| 70 | 1.6647 | −0.0053 | 10.0793 | 0.0359 | 0.0078 | 0.2602 | No |
| 80 | 1.6682 | 0.0010 | 11.1893 | 0.0339 | 0.0089 | 0.2022 | No |
| 90 | 1.6688 | 0.0141 | 12.1705 | 0.0103 | 0.0102 | 0.1365 | No |
| 100 | 1.6845 | 0.0029 | 13.2942 | 0.0329 | 0.0099 | 0.2053 | No |
| 110 | 1.6916 | 0.0080 | 14.2635 | −0.0547 | 0.0123 | 0.0819 | No |
| 120 | 1.6887 | 0.0049 | 15.2096 | −0.0066 | 0.0114 | 0.1607 | No |
| 130 | 1.6826 | −0.0291 | 16.0270 | 0.2303 | 0.0131 | 0.0903 | No |
| 140 | 1.6874 | −0.0211 | 16.9094 | 0.2623 | 0.0115 | 0.2163 | No |
| 150 | 1.6909 | −0.0027 | 17.8762 | 0.1131 | 0.0107 | 0.3344 | No |
| 1200 | 1.8693 | −0.3670 | 71.8964 | 6.8822 | 0.0150 | 0.5328 | No |
| 2500 | 1.9065 | −0.6018 | 108.4828 | 12.0903 | 0.0301 | 0.7860 | No |
| 2700 | 2.0000 | 0.7973 | 122.6070 | 5.0104 | 0.0309 | 0.7985 | No |
From this table, we can also observe that as N conv reaches a value around 70, the test cannot longer reject the hypothesis of the probability density function for this data being an α-stable distribution. As it is shown in Fig. 3. Lévy scaling holds over a long range of values of N conv. For instance, in Fig. 4 is presented the data and the best fits for a normal and an α-stable distribution for N conv = 100.

FIGURE 4 Distributions for N conv =100. In the horizontal axis, Z stands for the fluctuations data or the values of the corresponding fits.
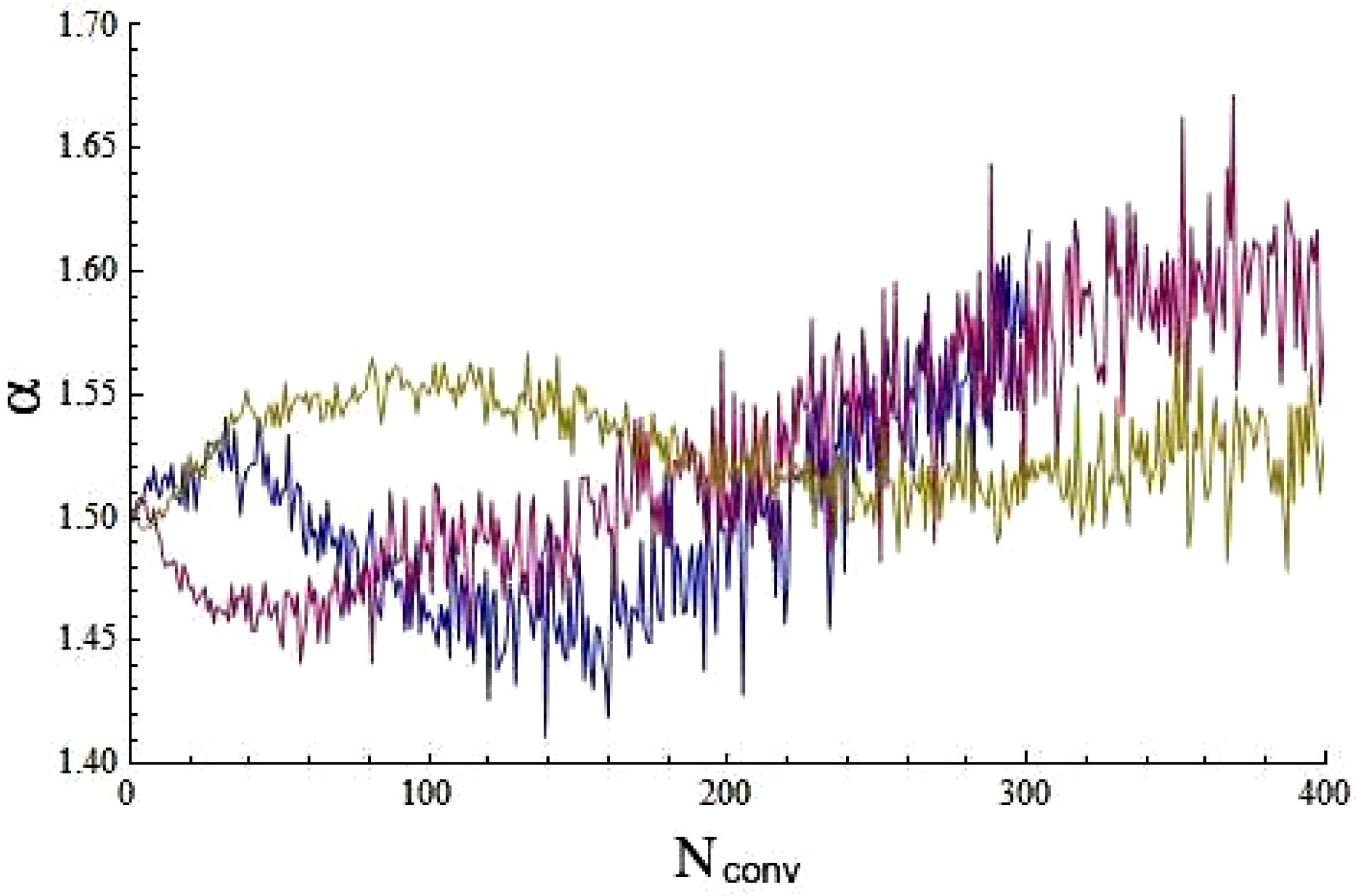
The values of α keep steadily increasing as N conv is also increased. As can be seen in Table I and it is represented in Fig. 5, the value of the stable coefficient slowly converges to 2, while the convolution involves larger blocks of data. That is, for instance, the value of α for N conv = 2700. In this case, the corresponding statistics are presented in the last row of Table I, and the distributions are plotted in Fig. 6.

FIGURE 6 Distributions for N conv =2700. In the horizontal axis Z stands for the fluctuations data or the values of the corresponding fits.
As we can see, for N conv = 2700, normal distribution and the corresponding Lévy distribution (with α = 2) give both a very good fit to the convoluted data. This is strong evidence that, indeed, the variance of the data is finite.
4.1. Convergence to α = 2
Note in Fig. 5 that α ≈ 2 for N conv around 2000 too. Also, in Table I, it can be seen that the convergence to α = 2 is not just slow, as has been noted previously [9], but it is also non-uniform. We believe that this is an effect of the finite number of elements in the sample. To verify that, we simulated data by truncating sets generated using the stable library by Nolan [16] and following expression (4). For the three sets we used the same parameters, but the length of the series is one, two, and five million elements, respectively. In Fig. 7 is plotted how the stable coefficient α for each original set (without truncation) evolves with convolution.
It is noticeable the high quality of the simulated data since in each case α converges to a value significantly different from 2 and, the larger the size of the set, the closer this value gets to the α used for generating the set.
The truncation was done by erasing out the elements of a given set with an absolute value greater than n std ×σ, where σ is the standard deviation of the corresponding data. It implies that the smaller n std , the fewer the elements remaining in the truncated set. There is a range of n std when the simulation works. For high n std (i.e., small truncation), the length of the series is not large enough for observing the convergence to α = 2, though it seems to converge to a value significantly different from the value used for generating the set, i.e., the case without convolution presented in Fig. 7. An example is given in Fig. 8. On the other hand, for low n std (i.e., large truncation), the Kolmogorov-Smirnov test rejects that the data correspond to a stable distribution. Neither it is a normal distribution, but it converges very fast to α = 2. An example is given now in Fig. 9.
Reasonable truncation can be performed, such that it can be obtained a series that for low N conv, the test cannot reject them to be stable-distributed, but with convolution converges to α = 2. The corresponding example is given in Fig. 10.
From these simulations, it can be observed that the convergence is not only slow but also non-uniform. However, the larger the number of elements in a given set, the smaller the size of the irregularities. If considering the whole population (a condition for the generalization of the Central Limit Theorem), the convergence can be expected to be uniform.
4.2. Lévy to Gaussian crossover
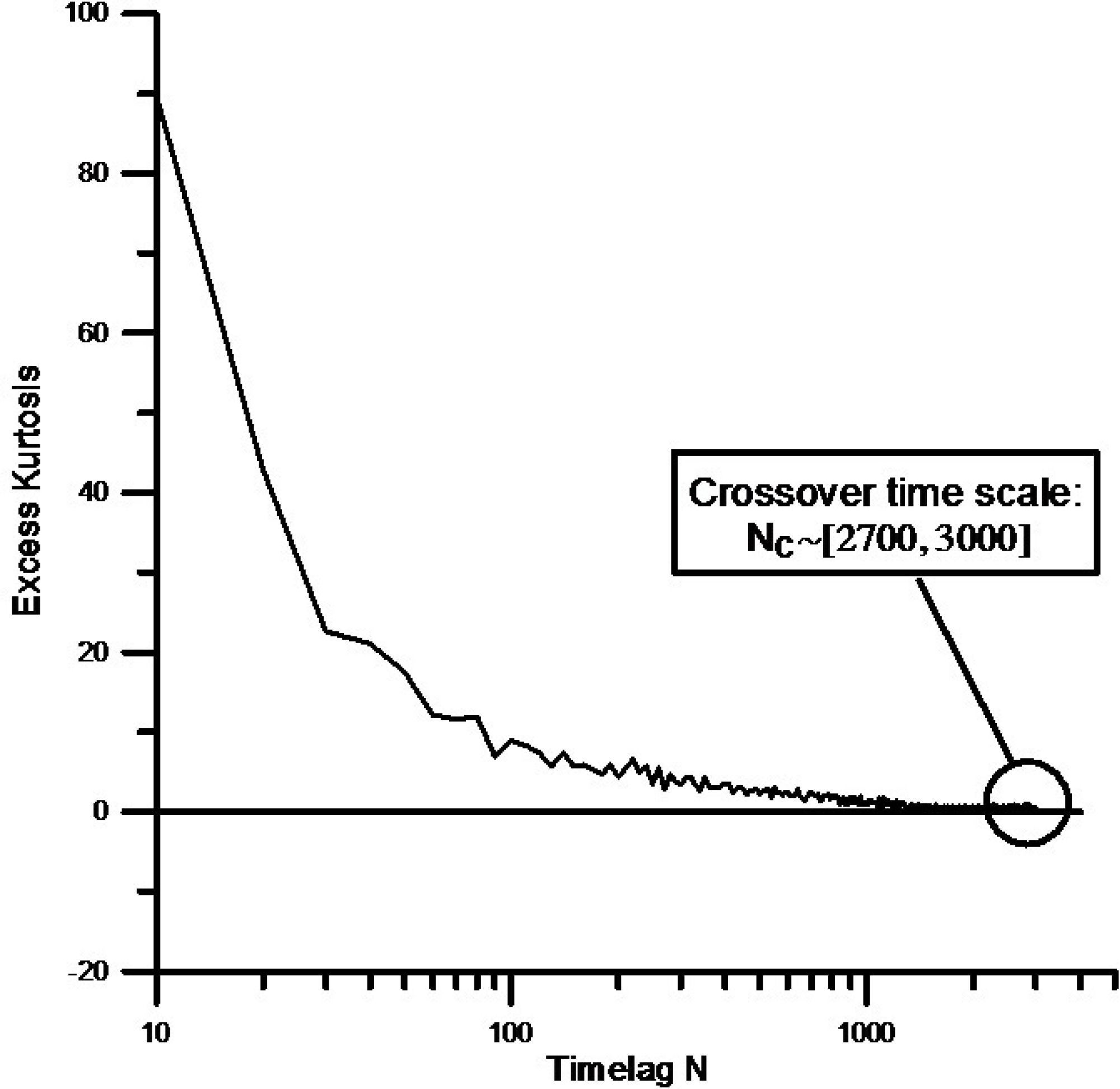
Since our sample is finite, and this affects the estimation of the parameter α, we further analyzed the transition from Lévy to the Gaussian regime by following the procedure proposed in Ref. [17]. We study the behavior of the excess kurtosis for convoluted samples, from N conv = 0 to N conv = 3000. The excess kurtosis
gives a statistical measure of the heaviness of the tail of distribution with mean value µ. A normal process shows zero excess kurtoses for the population, while it is positive for leptokurtic distributions like Lévy-stable distributions.
The results we obtained are presented in Fig. 11. It can be seen that the transition between Lévy and Gaussian regimes occurs for values of N conv between 2700 and 3000. This confirms the result discussed above for the fit of the convoluted data to a stable Lévy distribution (see Table I), which gives a value of α = 2 for N conv = 2700. This way, the crossover time can be set equal to N c = 2700. Recalling that, during the analyzed period (from January 1999 to December 2002), the average time between successive fluctuations is close to 20 seconds and that for the Mexican market, one trading day is equal to 6.5 hours, we find that the Lévy-Gaussian crossover is approximately 2.3 trading days.
The circle encloses the Lévy to Gaussian crossover.
5. Serial dependence in the IPC data
From the previous section, we concluded that for convolutions below N conv = 70 data does not fit neither a Gaussian nor any Lévy distribution. A common hypothesis for both cases is the data being independent and identically distributed. In Figs. 12 and 13 we present the results for the analysis of autocorrelation for the set {S k }. In principle, the vertical axis would cover values from −1 (full anticorrelation) to 1 (full correlation), and the values in the horizontal axis stand for the lag δ, i.e., denote the correlation between S k and S k +δ. The blue dashed lines in these figures indicate approximate limits of correlation coefficients expected under a null hypothesis of uncorrelated data. We successfully tested these limits using the simulations of truncated Lévy distributions described in Subsec. 4.1. As it can be observed, the fluctuations exhibit positive autocorrelations, which are correspondingly diluted after convoluting the series. It suggests a mild serial dependence between fluctuations within an interval of about 48 minutes.
In Figs. 14 are shown the autocorrelations for the series of absolute values of S k for a) N conv = 0 and b) N conv = 150. This is a measure of volatility, and it exhibits long-range serial dependence (beyond several months), a fact consistent with findings reported for other markets [2,7].
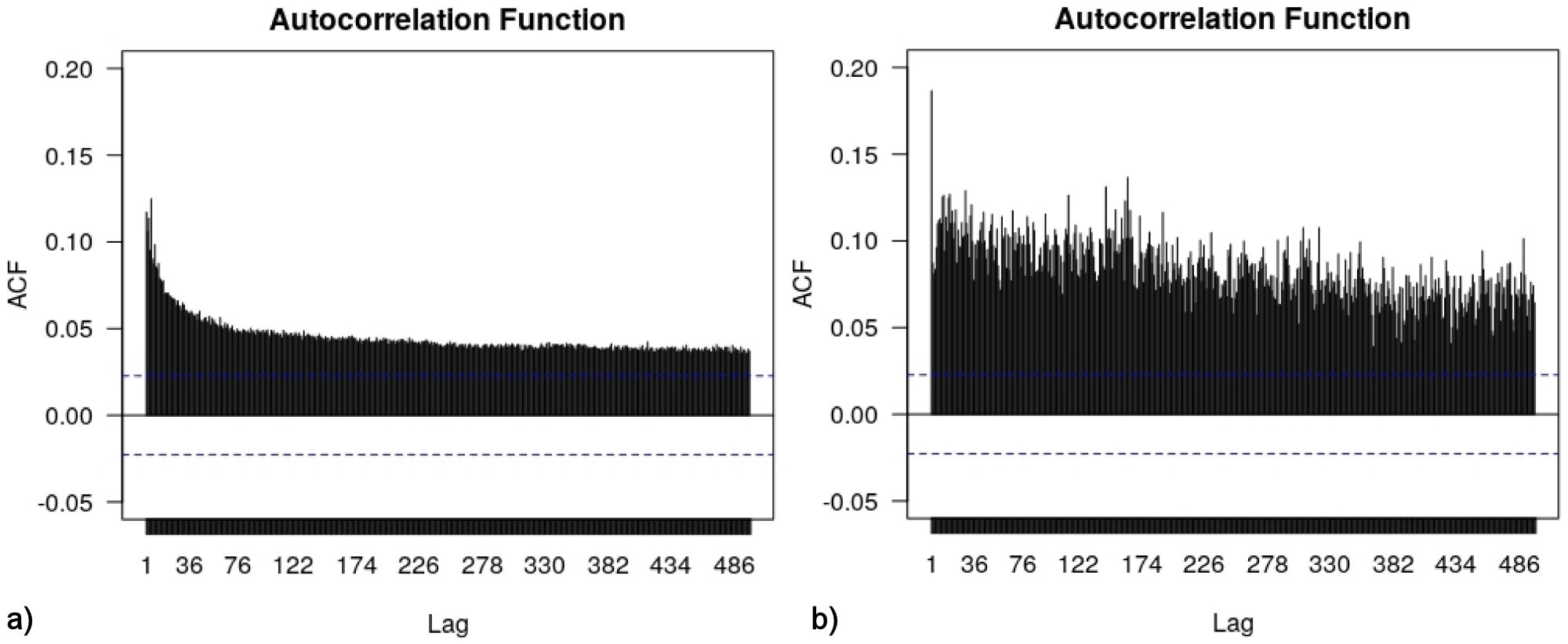
FIGURE 14 Autocorrelations for the absolute value of the returns for a) N conv =0 and b) N conv =150.
Finally, we present in Fig. 15 the autocorrelations for values and absolute values of the daily closing dataset. As can be observed, these last results are consistent with those obtained for the tick-to-tick set, where no serial dependence is present for sampling intervals above 48 minutes, including, of course, the daily frequency which corresponds to N conv = 1200. Moreover, in Fig. 15a) a mild dependence for the volatility is still observable at a lag of 300 days, which corresponds to the lag of several months observed in Fig. 15b) for the tick-to-tick data.
6. Discussion
Our results suggest that the statistical description of the Mexican market strongly depends on the time scale of interest. For the analyzed period, around 73% of the IPC tick-to-tick data, sampled every 5.2 seconds, shows no activity. Fluctuations occur, on average, every 19.3 seconds, but the underlying probability is unlikely to follow a Lévy-stable distribution, including the Gaussian. Our analysis shows that one of the reasons could be that these data are not independent. The fluctuations exhibit mild positive autocorrelations that persist for about 48 minutes before falling below the level of noise. This is, for instance, twice the value reported in Ref. [2] for the S&P500 index, sampled at a 1 min time scale, and also sometimes reported for various asset returns [7]. The autocorrelation in the IPC is diluted by convolution, i.e., the aggregation of elements of the set of fluctuations in blocks of length N conv. This is characteristic of random walks with a short memory. Conversely, in the case of a deterministic process with noise, even if autocorrelations are initially hidden, they surface and get more noticeable with convolutions. Therefore, this serial dependence seems to reflect less the internal mechanics of the market (due to the law of supply and demand) than the (complex, noisy) external action on it.
Taking all of this into account, the IPC fluctuations can be described by Lévy-stable distributions in the wide range of sampling interval from 20 seconds up to two trading days. After that time, data seems to obey normal probability distributions. We would like to note that this value for the Lévy to Gaussian crossover also differs from results obtained by other authors. For example, Mantegna and Stanley [5], for the S&P500 (during the six years from January 1984 to December 1989), estimated the crossover time to be of the order of one month; Matacz [15], for the Australian All Ordinaries, share market index for the period 1993-1997, found that the crossover time is approximately 19 trading days, and in Cuoto Miranda and Riera [17], a crossover of approximately 20 days was found for the Sao Paulo Stock Exchange Index in Brazil (IBOVESPA), during the 15 years 1986-2000.
It is worthy to note here that these results do not depend on the fact of the filtered tick-to-tick data to be unevenly sampled. After removing contiguously repeated values, the average time for fluctuations over the period is, up to a decimal of second, the same that the mean of the time values between fluctuations. This will not be the case if, for instance, all the activity happened along just one year of the whole of January 1999 to December 2002 period. Moreover, we showed that sets obtained by convolution of the IPC tick-to-tick data can be safely used to describe the activity at lower frequencies. We tested this in Table I by comparing the basics statistics for N conv = 1200, which would correspond to one trading day, with the fluctuations of the daily data from Yahoo finance for the same period. Even more, using the stability parameter α of the Lévy distribution as a quantitative and qualitative descriptor of the whole data set, from Table II we see that for N conv = 1200 the probability density decays with α = 1.8693, while for the daily closing data we obtained a close value of 1.8370. Last, but not least, the analysis of serial dependence for the fluctuations of the daily closing data (and their absolute value) presented in Figs. 15 is consistent with those for convolutions of the tick-to-tick fluctuations corresponding to frequencies above 48 minutes; there is no significant dependence at the daily frequency, while for the volatility, a mild autocorrelation persists over several months.
There are reasons for expecting the statistical description of the IPC to also depend on the period analyzed. As mentioned before, in Ref. [8] we analyzed the fluctuations of the daily closing data for the IPC covering the period from 04/09/2000 to 04/09/2010. For this whole period, we obtained α = 1.64, which is significantly lower than the value of 1.86 we obtained for the daily data over the period 01/1999 to 12/2002 studied in this paper. Both these values are still larger than, for example, the one reported by Mantegna and Stanley [5] for the S&P500 about a decade earlier. The different values of α for the two sets of IPC data we have studied, indeed reflects the details of the market behavior in the described periods. Both sets contain the years from 2000 to 2003. In the second half of the nineties, there was a spectacular rise in the stock market in the United States, specifically in the shares of companies integrated into what is known as the “new economy” or “dot-com” companies. The rate of investment in computers and other high-tech goods doubled during the last five years of that decade, and this momentum was carried into the following couple of years. Nevertheless, several events disturbed the performance of the markets in that period. Among them, the fact that Russia declared a moratorium on the payment of its debt, as well as a sudden devaluation of the ruble. At the beginning of 2001 (middle of the studied here period), a crisis arrived, with a fall in prices, especially in the United States. Fortunately, the global impact of the dot-com bubble crash was very limited, since it was mainly in the technological sphere and affected those who took the highest risk. Similarly, the disturbances in the financial market caused by the events of September 11, 2001, in New York, decayed rather quickly. Even if Mexico, as an emergent economy, was affected by the crisis of 2001, it also managed to effectively damp these perturbations. All these trends can be observed in Fig. 1. Therefore, even if the daily data for these years are not normally distributed, it is reasonable to find a value of α close enough to 2. On the other hand, the main difference between both periods is that the set studied in Ref. [8] contains the mortgage crisis of 2008. This was a financial storm of proportions much greater than the bursting of the dot-com bubble. The high level of leverage of a large number of financial assets led to a huge collapse of the world economy. The consequences in Mexico, although not as dire as in other latitudes, had a serious impact on investor confidence and the exchange rate. This increased the market volatility, leading to a higher probability of extreme fluctuations as compared with the first five years of that decade.











 nueva página del texto (beta)
nueva página del texto (beta)