1. Introduction

Quantum correlation and entanglement are some of the most considerable aspects of quantum mechanics, which has many uses in quantum information theory [¹-⁵]. Lately, it turned into a basic entrance of the quantum information theory because of its promising prospect in probing the quantum computers and other quantum information devices. In quantum information theory, the entanglement could be considered as a clue role for implementing some quantum information tasks such as quantum cryptography [⁶], quantum computations, geometric quantum computation [⁷-⁹], and dense coding [¹,¹⁰]. In the past few decades, the role of quantum correlations in dense coding and teleportation has attracted considerable attention and expanded multiple approaches not only in theories but also in experiments [¹¹-¹⁷]. Quantum teleportation and dense coding are performing with the help of prior quantum entanglement partaken by the sender and receiver.

Up to now, various entanglement measures are manipulated to quantify entanglement and to distinguish between entangled and separable (not entangled) states. Recently, it is interesting to find that spin squeezing is connected to quantum entanglement, and one can use spin squeezing to characterize entanglement. It was found that spin squeezing refers to the minimum spin fluctuation on the plane perpendicular to the mean spin direction [¹⁸-²⁰]. It is investigated for an arbitrary symmetric multi-qubit state, spin squeezing implies pairwise entanglement, for some special state, spin squeezing is equivalent to the pairwise entanglement [²¹]. Because of important applications, spin squeezing has attracted considerable attention and developed various approaches not only in theories but also in experiments [²²,²³]. Another benefit is that the spin squeezing involves no bipartition or reduction process in a many-body system, unlike some other measures of entanglement, e.g., concurrence or negativity. So, it can be easily used for every spin model, independent of size, dimension, and geometry of the system [¹⁹,²⁴,²⁵]. There are various definitions of the spin squeezing parameter; here, we exploit the most vastly studied one, determined by Kitagawa and Ueda [¹⁹].

Recent studies show that nontrivial nonclassical correlations may exist even in separable states [²⁶]. Thereby, the general nonclassical correlations are not quantitatively determined by quantum entanglement. The quantum correlations have recently emerged as a topic calling for the introduction of modern cases. In this respect, quantum discord(a measure of quantum correlation over entanglement) has been widely studied in the literature as an alternative way to characterize nonclassical correlations even in separable mixed states [²⁷-²⁹]. The investigation of this information-theoretic measure of nonclassical correlations has generated an increasing interest during the last two decades [³⁰]. Another interesting geometrical approach to describe quantum correlation is the so-called trace distance discord (TDD) [³¹,³²]. It evaluates the distance between the state under investigation and its closest zero discord states. A formalism for a special subset of two-qubit density operators named X-state is provided to calculate TDD in [³³]. TDD is one of the most successful approaches to detect not only the quantum correlations in manyspin systems but also quantum phases transition [³⁴,³⁵].

Up to now, the effect of Calogero-Moser type interaction on the quantum correlation of thermal states of a spin chain is investigated by the authors in Ref. [³⁸]. Their results imply that the quantum discord depends on the relative distance between the spins, the external magnetic field, and the temperature [³⁸]. Some authors discussed the quantum teleportation by using thermal entangled states as entanglement resource, i.e., the final two-qubit state after teleportation, and the entanglement teleportation of two qubits can be entangled [³⁶,³⁷]. Our most important motive for this study is to investigate the effect of Calogero-Moser (CM) type interactions on the thermal quantum correlations and dense coding in an anisotropic two-qubit Heisenberg XYZ system with Dzyaloshinskii-Moriya (D _z ) interaction in the presence of the external magnetic field. Temperature fluctuations lead to oscillating in the positions of spin lattices [³⁹]. It seems that the distance between spins may thus play an fundamental role in the quantum correlation of the system. Such interaction types are recognized as Calogero-Moser type interactions, acquired in the Haldane-Shastry model. Investigation the effect of Calogero-Moser type interactions on the spin quantum correlation is very important, therefore contributing to the realistic assessment of the potential of such spin systems for solid-state quantum computation and communication.

The paper is organized as follows: in Sec. 2, we describe the Hamiltonian of the systems that we want to study dense coding and quantum correlations through them. In Sec. 3 we briefly review spin squeezing and TDD, then we investigate the behavior of them by varying the model parameters. We also study thermal dense coding through this model. Finally, the main results will be summarized in Sec. 4.

2. Description of the model

The Hamiltonian of the Heisenberg model with z-component interaction parameter D _z in the presence of uniform and nonuniform magnetic fields and long-range interaction is given by

where J _z is the real spin-orbit coupling constant between the spins in z−direction, D _z is Dzyaloshinskii-Moriya (DM) coupling constants in the z direction, and σ _i are Pauli matrices of the i-th site with (i = x,y,z). The term B and b represent z-component homogeneous and inhomogeneous external magnetic fields, respectively. D _z interaction and external magnetic fields are thought to be along the z−direction. J(R) is the spin-orbit interaction coupling, which is characterized as far as CM interactions. All the parameters are dimensionless. The CM has different types of interactions in the isotropic ferromagnetic XYZ model. Here we consider Calogero-Moser type I: J(R) = (1/R ²), which is a version of the Haldane-Shastry model with exchange interaction J = (1/R ²). One can easily calculate the matrix form of H:

The above Hamiltonian is written in the standard basis of |00〉,|01〉,|10〉,|11〉. After a straightforward calculation, we obtain the eigenvectors and eigenvalues as follows:

where

We can introduce thermal fluctuations into the system, the density matrix of this two spins at thermal equilibrium is ρ=(1/Z)e-βH=Σn=14P(n)|ψn⟩⟨ψn⟩|, where P(n) = (1/Z)e ^−βEn are thermally distributed populations in the quantum states, β = 1/kT (k=1),T is the temperature. Z=∑ne-βEn is the partition function. In the standard basis, the density matrix of the system in thermal equilibrium can be written as

where

and Z=2e-Jzcosh⁡(2b2+Dz2+G2)+2e-Jzcosh⁡(2B). Now, one can investigate the entanglement of the two-qubit state ρ given in Eq. (6). In what follows, our purpose is to quantify the number of quantum correlations of the above system function of the parameters of the system.

3. Thermal quantum correlations

In this section, we study the thermal evolution of quantum correlations under the effect of the Hamiltonian parameters with multiple interactions. Thermal entanglement of the XYZ system with the Dzyaloshinskii-Moriya (Dz) interaction in the presence of the external magnetic field was considered in Ref. [¹³]. However, in this paper, we shall use three types of useful measures that are being discussed below.

3.3. Results and discussion

Using the results of the previous sections, we begin by analyzing the behavior of thermal quantum correlations under the effect of the Hamiltonian XYZ system with the Dzyaloshinskii-Moriya (D _z ) interaction in the presence of the external magnetic field in the case CM = (1/R ²). Figures 1 show the 3D plot for Fig. 1a) spin squeezing and Fig. 1b) TDD as a function of the distance R and the temperature T. It is observed from Figs. 1 that the increase of the temperature leads to very fast decaying of the TDD and having no squeezing, which implies no global entanglement. In particular, we noticed that for higher temperatures, there is not any squeezing. The system of the two atoms stays separable but contains quantum correlations that are not captured by the spin squeezing. When the temperature T = 10, the correlations reaches a minimal value at R = 0.5 with choosing D _z = B = b = J _z = 1. Also, it is observed that at any finite temperature, there is an optimal distance at which TDD reaches its deepest value; however, TDD decreases steadily as the distance is raised gradually beyond the optimal one. Moreover, we have presented plots of spin squeezing and TDD as a function of the distance R and the strength of the Dzyaloshinskii-Moriya (D _z ) interaction in Figs. 2. We can see from Figs. 2 that the increase in the value of the Dzyaloshinskii-Moriya (D _z ) interaction helps the TDD and spin squeezing to create again. Finally, it is revealed that higher D _z values correspond to lower threshold distance, deeper squeezing, and TDD.

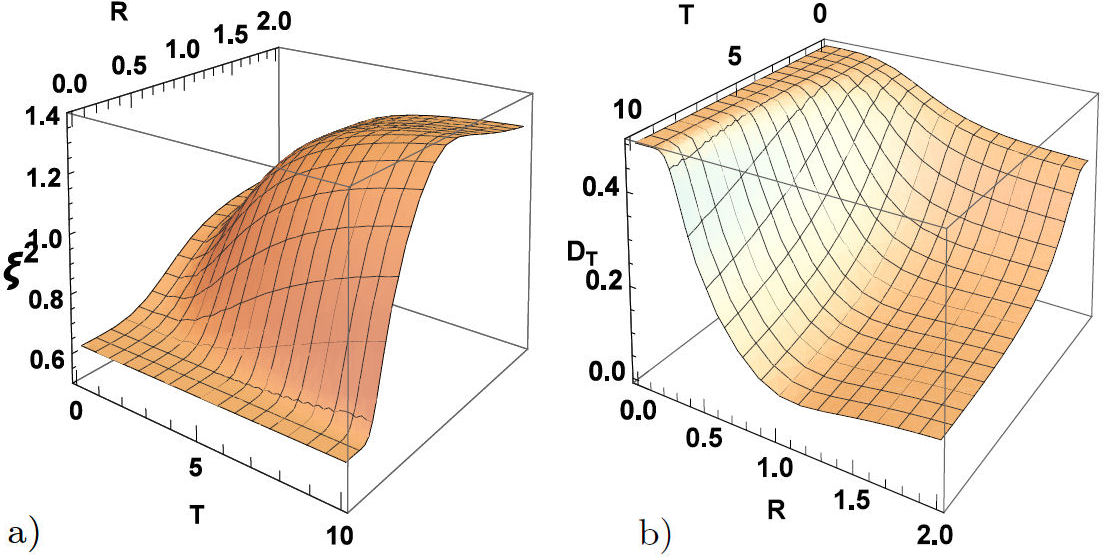
FIGURE 1 3D plot of (a) spin squeezing (ξ ²) (b) TDD as a function of R & T with D _z = B = b = J _z =1. 

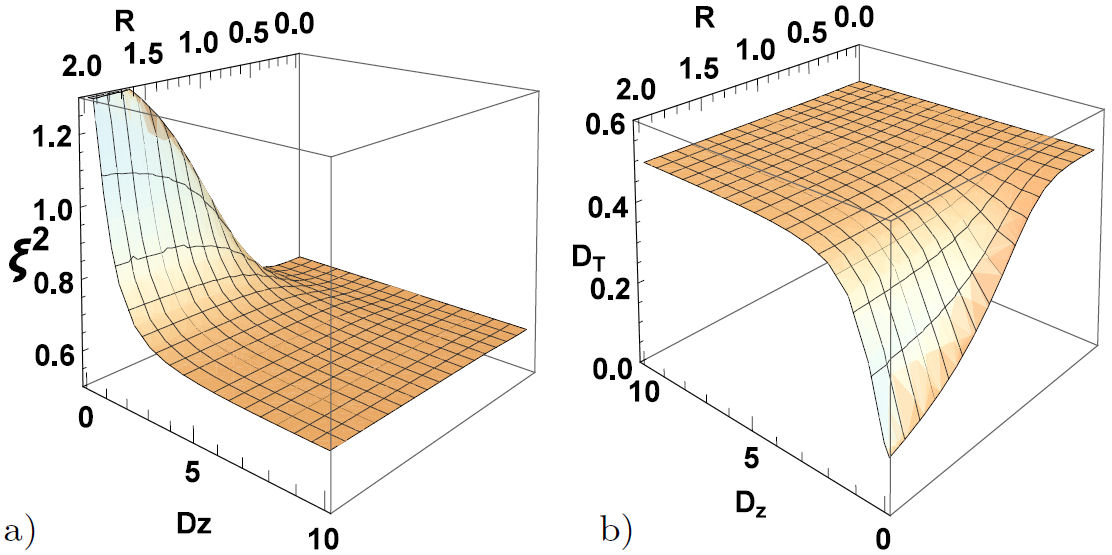
FIGURE 2 3D plot of (a) spin squeezing (ξ ²) (b) TDD as a function of R & D _z with B = b = J _z = T =1. 

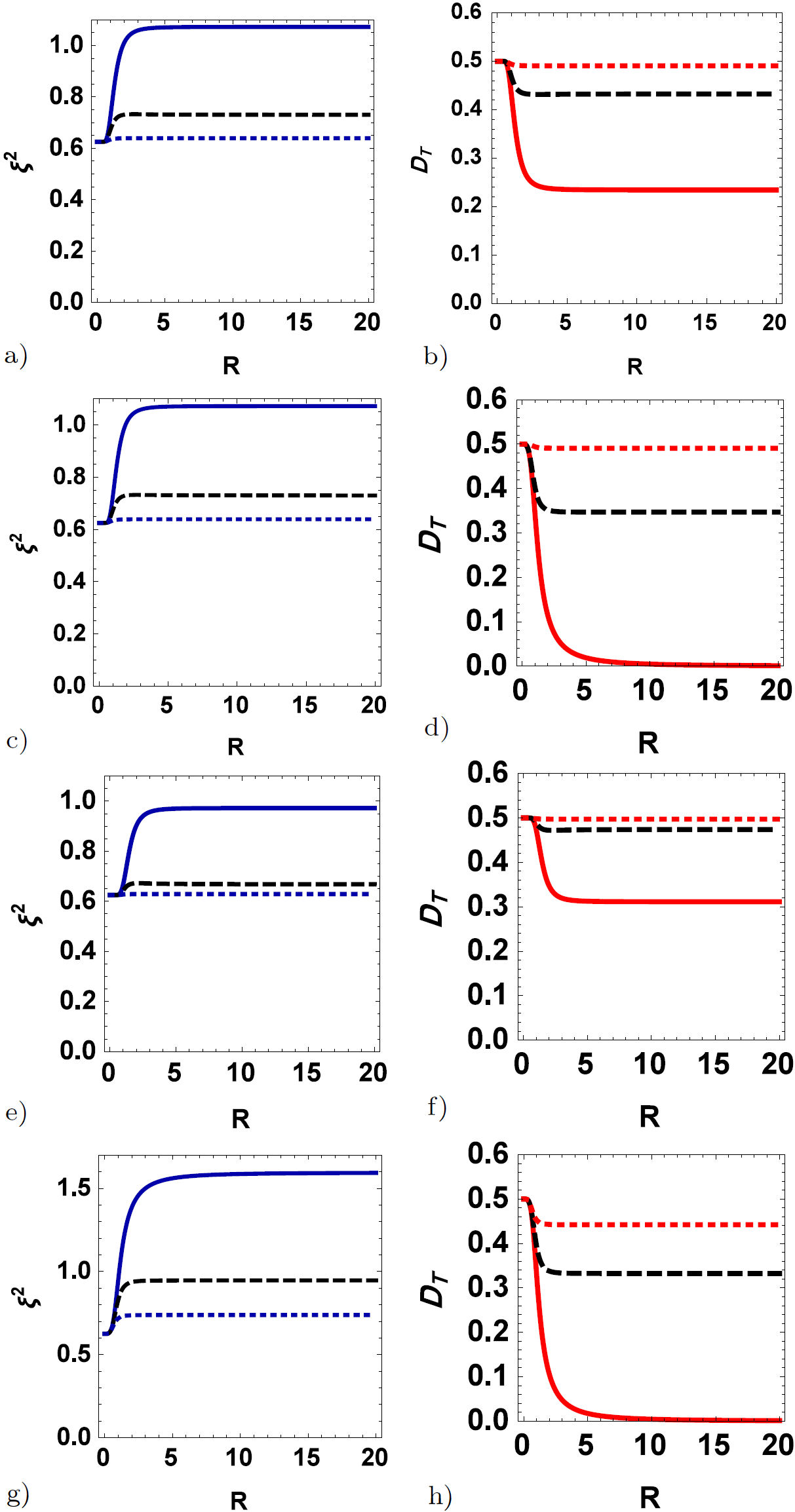
For the better description of observed behavior, we depict the thermal quantum correlations over the suggested model in Figs. 3, which is quantified by the spin squeezing a TDD under the effect of the system parameters (DzyaloshinskiiMoriya, spin-orbit coupling, Calogero-Moser type interaction, and magnetic field) in the presence and absence of a magnetic field and (T = J _z = 1). We can observe that the presence of the D _z interaction has led to the increase in the value of the quantum correlations as same as Fig. 2. It is clear that for the larger values of the Dzyaloshinskii-Moriya (D _z ) interaction, D _z = 2 gives a much better value of the TDD and deeper squeezing as observed in the dotted curve whether have a magnetic field or not it is. Also, we note that, at any fixed homogeneous magnetic field, squeezing dies down and TDD decays as the distance is increased and finally vanishes at a specific critical one. It can be observed from this figures that the homogeneous magnetic field increases the squeezing vanished very quickly, where the TDD reaches its deepest value. Moreover, in general, the magnetic field presence has a bad impact on the dynamics and the value of the TDD and spin squeezing. If we compare the results of these figures, it is easy for us to see that the presence of an inhomogeneous magnetic field increases the value of the TDD as long as it does not exceed the value of the Dzyaloshinskii-Moriya (D _z ) interaction. Also, it can maintain squeezing (see solid curves).

FIGURE 3 Spin squeezing and TDD as a function of R; the solid, dashed and dotted, curves are evaluated for D _z = 0,1,2, respectively, with J _z = T =1. (a) and (b) B =1 and b=0, (c) and (d) B =0 and b=1, (e) and (f) B = b=0 (g) and (h) B=b=1. 

4. Super Dense coding

Now we carry out the optimal dense coding with three different types of two-qubit systems as a quantum channel. For this purpose, the set of mutually orthogonal unitary transformations is necessary to be made. The set of mutually orthogonal unitary transformations for two-qubit are given as follows [¹⁰]

where|j〉 is the single-qubit computational basis (|j〉 = |0〉,|1〉). The average state of the ensemble of signal states generated by the unitary transformations Eq. (13) given by:

where 0 stands for 00, 1 for 01, 2 for 10, 3 for 11, and ρ is the density matrix of the quantum channel. If the sender does the set of mutually orthogonal unitary transformations, the maximum dense coding capacity χ can be obtained by

where S(ρ*¯) is the von Neumann entropy of the average state of the ensemble of signal states ρ*¯, and S(ρ) is the von Neumann entropy of the quantum channel. If χ > 1 dense coding is valid, and for optimal dense coding χ must be the maximum, i.e., χ _max = 2. In the following, we will use three different types of two-qubit system as a quantum channel to study optimal dense coding.

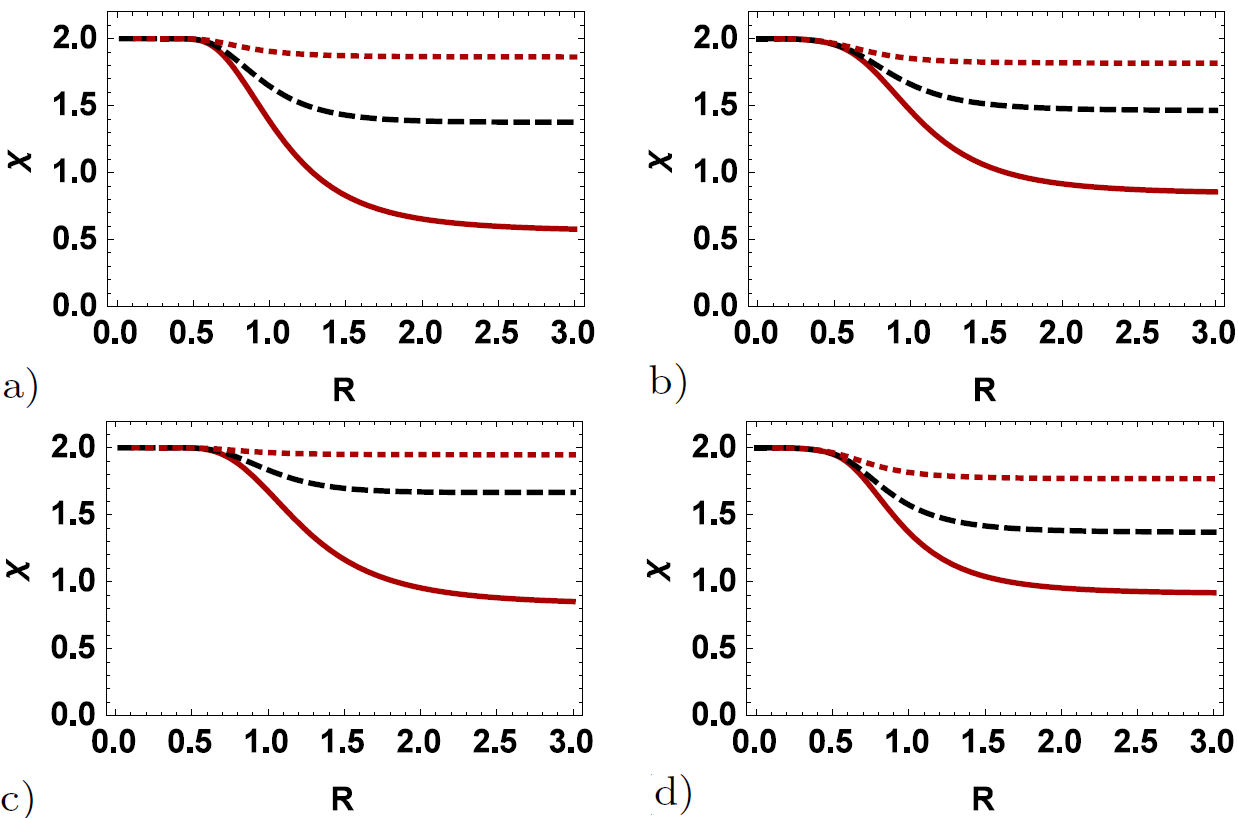
This section discusses the generated entangled channel validity in Sec. 2 to exchange the information from a spin to another. Fig. 4a) describes the effect of the temperature and Dzyaloshinskii-Moriya (D _z ) interaction on the dynamics of the dense coding capacity as a function of the distance between the spins. In this figure, dense coding capacity decreases with increasing temperature. What is interesting is that we can even see valid dense coding in the large amount of distance between the spins for the ground state (T → 0). But it is decreased from the maximum to zero in a short period of temperature and vanishes suddenly for the large amount of T. The Dzyaloshinskii-Moriya (D _z ) interaction on the behavior of dense coding has been illustrated in Fig. 4b) for B = b = J _z = 1. It can keep its valid value for some strong Dzyaloshinskii-Moriya (D _z ) interaction. Hence, the increase in the value of the Dzyaloshinskii-Moriya (D _z ) interaction helps the dense coding capacity to recover again. We can observe that D _z and T have the same effect as in the quantum correlations in Fig. 3. As shown in this figure, the critical temperature increases very rapidly with increasing D _z .

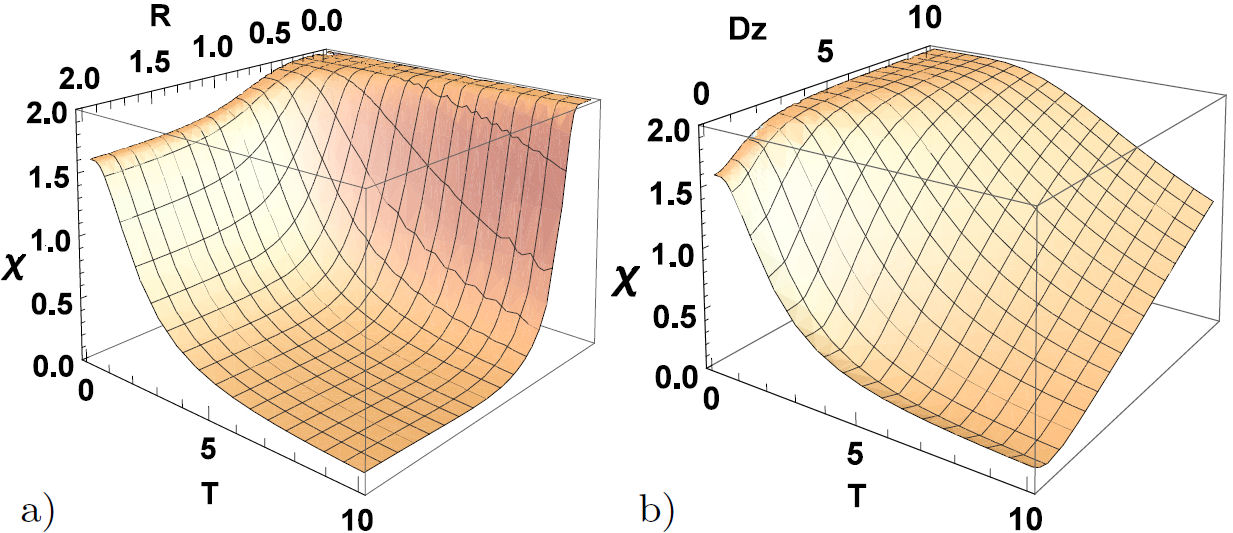
FIGURE 4 3D plot of Dense coding capacity as a function of (a) R and T with D _z = 1 (b) D _z and T with R = 1, when B = b = J _z =1. 

The behavior of dense coding capacity affected by the external magnetic field has been plotted in Figs. 5. As shown in Figs. 5, the effect of the Dzyaloshinskii-Moriya (D _z ) interaction (D _z = 0,1,2 for the solid, dashed, and dotted curve, respectively) on the dynamics of the dense coding capacity in the case that there is no effect of both uniform and nonuniform magnetic field. However, by looking at Figs. 5, they reveal that optimal dense coding values appear whether be external magnetic field or not it when D _z ≥ 1. Moreover, it can be noted that the recovery of the values of the dense coding capacity is done by increasing the D _z interaction. It can be observed from Figs. 5 that the homogeneous and inhomogeneous magnetic fields have an opposite effect on the dynamics of the dense coding capacity, where the D _z interaction increases the dense coding capacity, and the magnetic field decreases it. Also, we can understand that the effect of the inhomogeneous magnetic field is more than the homogeneous magnetic field.

FIGURE 5 Dense coding capacity as a function of R; the solid, dashed and dotted, curves are evaluated for D _z =0,1,2, respectively, with J _z = T =1. (a) B =1 and b=0, (b) B =0 and b=1, (c) B = b=0 (d) B=b=1. 

5. Conclusions

Amplification of quantum correlations and the rich dense coding capacity of the information transfer have become one of the hottest topics in quantum processors. However, it is important to identify the parameters that can cause to increase the capacity of a quantum information channel.

Our most important motivation for this study has been to analyze the impact of the distance between spins on the thermal quantum correlations and the dense coding capacity of state transfer in a two-qubit via a Heisenberg XYZ model with different D _z interactions under the effect of the external magnetic field and temperature, which can be considered as a model of the quantum processor. At first, we have provided a comprehensive quantitative analysis of spectral properties for the TDD and spin squeezing in an anisotropic two-qubit Heisenberg XYZ system. The results show that in the presence of the CM-type interactions, the thermal quantum correlations between spins have a strong behavior depending upon the magnetic field, D _z interaction, temperature, and interaction strength. It is found that the sudden death is represented at the critical distance of the TDD and spin squeezing. The dynamics of the spin squeezing and TDD have a very strong effect by varying the system parameters. Finally, we can conclude that in our model for a long-distance spin, the system can exchange information with high dense coding capacity.