1. Introduction
Quantum information theory offers many methods on how information may be stored, manipulated, and transmitted [1]. The base of quantum information theory is well known to be the quantum entanglement. It is the most fascinating feature of quantum mechanics that plays an essential role in quantum cryptographic key distribution [2], quantum teleportation [3], and quantum dense coding [4]. For example, in the original dense coding protocol, the sender can transmit two bits of classical information to the receiver by sending a single qubit if they share a two-qubit maximally entangled state. Dense coding has been investigated both experimentally [5] and theoretically [6-8]. Recently, optimal dense coding have been extensively investigated in condensed matter physics due to their good integrability and scalability in the context of quantum information processing [9, 10]. Up to now, various systems have been studied in the field of quantum processes. The spin chains have been considered as one of the most suitable candidates for the study of entanglement and quantum correlations [11-13]. Recently, the cavity quantum electrodynamics system (CQES) has received much attentions since this system offer an ideal coupling between atoms and photons [14]. As a result, it has been widely applied for engineering quantum entanglement and quantum channel [15-21]. The common result of all models show that dynamical properties of the SQD on our channel enable us to determine when and under what conditions the system is suitable for dense coding capacity [22].
Quantum correlations have been comprehensively accepted as the main resource for different quantum information processing tasks. For a long time, the study of quantum correlations has been focused on entangelement [23]. However, recent studies indicated that entanglement does not reveal quantum correlation in separable states, therefore it cannot be considered as a complete measure of quantum correlation. The present work focuses on another concept of quantum correlation, namely quantum discord (QD) [24-27]. The QD is a measure of quantumness of correlations in a bipartite state, which was introduced as the difference between two natural quantum extension of the classical mutual information. Recently, numerous works have been made toward the significance and applications of QD [28, 29]. It should be noted that discord is captured by strong measurements (projective operators). As quantum states are fragile to quantum measurements, the measurement of an arbitrary quantum state in some orthogonal basis (projective measurement) leads to the loss of its coherence. While if the measurement be done weakly, it protects the coherence of the system when we perform a measurement which couples the system and the measuring device weakly. In 1988, Aharonov, Albert and Vaidman have proposed to use weak measurements [30]. Lately, it was shown that weak measurements can also protect QD from the decoherence [31]. It is known that the weak measurement captures more quantum correlation of a bipartite system than the strong (projective) one under certain situation. In technological applications, weak measurements are important for exploring the extra quantum correlation for information processing. Actually, replacing the projective measurement with weaker one in the definition of QD, gives rise to new correlation called super quantum discord (SQD) [33, 34]. Hence, a weak measurement enforced on one of the subsystems can lead to SQD, which is always larger than the normal QD captured by the strong measurement [32].
Our most important motivation for this study is to examine the relationship between thermal properties of SQD and superdense coding. We know that entangled states have the important role in dense coding. Here we propose a two-qubit spin squeezing model as quantum channels to study the thermal dense coding capacity χ. Motivated from the recent study on the thermal of entanglement in the above model, we here devote to examining the quantum correlation properties in terms of SQD with dense coding capacity. Our results suggest that the thermal properties of SQD in the channel can accurately determine the valid dense coding. Dense coding plays a major role in quantum communication, in such a way that valid dense coding detection using the thermal properties of SQD in the channel seems to play an important role in quantum information theory. Therefore, the notion of SQD can be a more useful resource for quantum information processing tasks, quantum communication and quantum computation than QD.
The remainder of this paper is organized as follows. In Sec. 2, we introduce the Hamiltonian of the systems that we want study dense coding and quantum correlations through them. In Sec. 3 firstly, we briefly review the dense coding scheme, then we obtain the thermal super dense coding and analyze its characters. Finally, the main results will be summarized in Sec. 4.
2. Description of the model
The two-spin model under an external magnetic field and coupled to each other by a one-axis twisting spin squeezing interaction is given by [35, 36]:
where, transverse field term S z can control the strength of the external magnetic field Ω ≥ 0 in z direction. The first term includes an ensemble of N spin-1/2 particles with exchange symmetry that its dynamical properties can be described by collective operators Sα = (1/2)Σ2 i =1 σα i , (α ∈ x,y,z), and σ i α are the Pauli matrices for the i th spin. In the following, we consider N = 2. µ ≥ 0 describes the strength of the spin squeezing interaction in x direction which depends on the scattering lengths between particles and the condensate density. The interaction establishes pairwise correlations between all of individual spins in the collective spin system; in our case bipartite correlations are formed between the two spins. This model is considered as a simple one in solid state in order to generate and manipulate entangled states.
The eigenvalues E n and the corresponding eigenvectors |Ψ n 〉 of Hamiltonian Eq. (1) in the standard basis of |00〉, |10〉, |01〉, |11〉 can be easily obtained as the following forms [38]:
where
Equipped with these concepts and formulas, we are now in the status to obtain density matrix ρ(T) in the standard basis |00〉, |10〉, |01〉, |11〉,
with the element of density matrix
With knowing that density matrix is the X-state form, one can obtain the quantum correlation behaviors by using correlation measure. It is determined that the quantum correlations such as SQD and QD are more comprehensive than entanglement [37]. Recent studies indicated that at a certain temperature entanglement and quantum correlations can be increased with changing the value of the Ω and μ. The results in Ref. [13, 38] indicate that thermal quantum correlations depends on the spin squeezing interaction μ and the external magnetic interaction Ω at the same of temperature. In following, we extend the quantum dense coding to spin channel. Their study show that quantum correlations can approach a maximum value by adjusting the external magnetic field, the spin squeezing interaction and temperature.
3. Superdense Coding
Now, we carry out the thermal optimal dense coding in one-axis twisting model as a quantum channel. For this purpose, the set of mutually orthogonal unitary transformations is necessary to be made. The set of mutually orthogonal unitary transformations for two-qubit are given as follows [39]:
where |j〉 is the single qubit computational basis (|j〉 = |0〉, |1〉). The average state of the ensemble of signal states generated by the unitary transformations Eq. (4) given by:
where 0 stands for 00, 1 for 01, 2 for 10, 3 for 11, and ρ is the density matrix of the quantum channel. Eq. (4) represents the operations that Alice(sender) performs on the shared entangled state ρ. If the sender does the set of mutually orthogonal unitary transformations, the maximum dense coding capacity χ can be obtained by
where
Figure 1 (a) presents the effects of temperature on dense coding described by Eq. (4) for Ω = 1and different values of µ. We found that valid dense coding exists at T = 0, whereas with the enhancement of temperature the dense coding capacity decreases quickly to the minimum value. From Fig. 1 (a) one can see that valid dense coding vanishes with increasing µ in the limit of low temperatures. In order to transmit ρ(T)with valid dense coding, we require the value of χ to be strictly greater than 1. In Fig. 1 (b), we consider the strength of the external magnetic field µ = 2 with various values of spin squeezing interaction Ω. It can be said that valid dense coding happens with decreasing Ω at µ = 2 for the smaller values of temperature. In general from Figs. 1, the influence of Ω and µ on the valid dense coding can be obvious when the temperature is increasing from zero. The optimal dense coding vanishing occurs by increasing temperature in the a short range. By choosing the appropriate value for Ω and µ,we can preserve valid dense coding at the short range of temperature, for which exists valid dense coding by increasing Ω and µ.
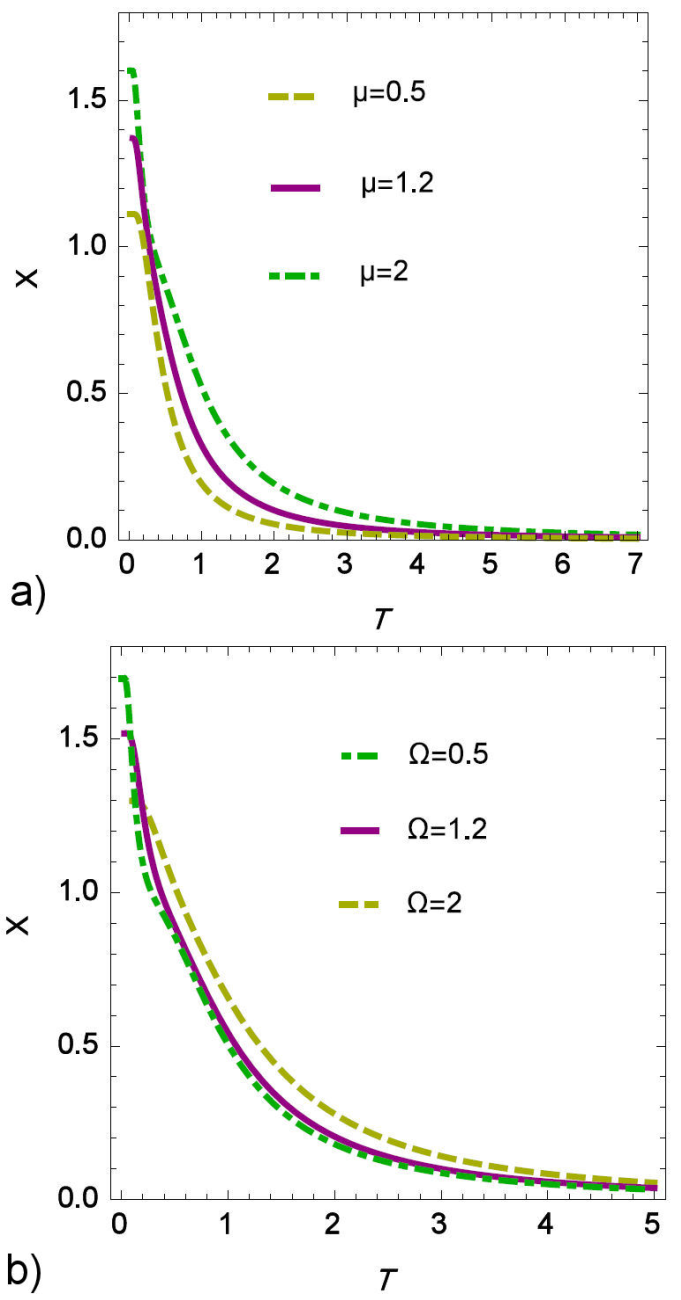
Figure 1 The super dense coding capacity as a function of temperature, (a) with external field interaction Ω = 1 and different of value for spin squeezing interaction μ, (b) with spin squeezing interaction μ = 2 and different of value for external field interaction for the spin channel.
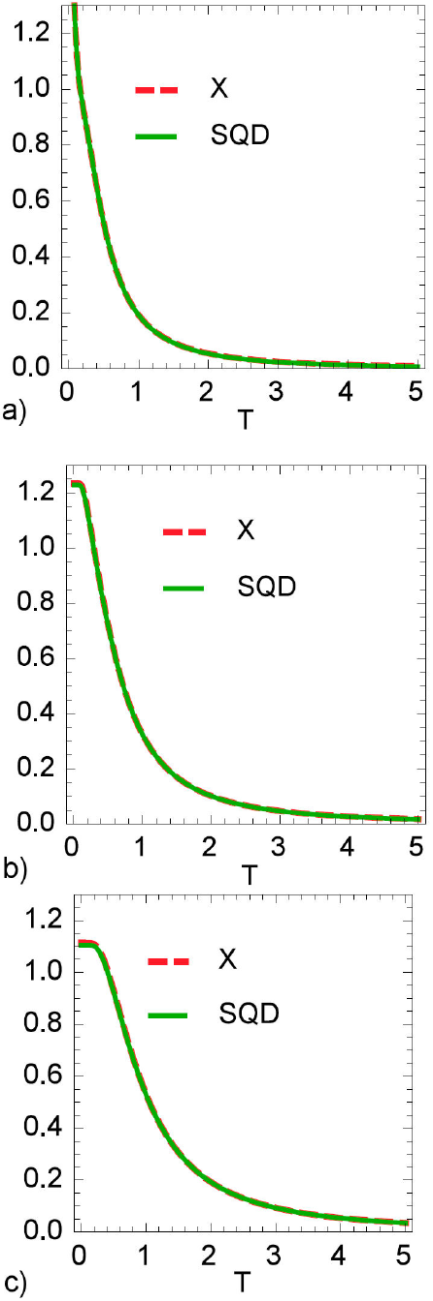
In the following, we tend to study the effects of Ω and µ on dense coding capacity at low temperature. We can identify valid dense coding with the help of calculating SQD in the quantum channel. Figure 2 indicates that the dense coding capacity is plotted as a function of Ω and µ at same temperature T = 0.5. It indicates that thermal dense coding capacity depends on the spin squeezing interaction µ and the external magnetic interaction Ω at the same of temperature. One can see clearly that there is no thermal valid dense coding when he strength of the spin squeezing or the strength of the external magnetic filed is zero. Hence, we can say that weaker or stronger external magnetic field will change the valid dense coding for the smaller value of T. We are looking for whether we can identify valid dense coding with the help of calculating the quantum correlation in the quantum channel. Formalism for a special subset of two qubit density operators named X-state is provided to calculate SQD in Refs. [32, 47, 56] or see appendix of this paper. In order to see the relationship between dynamical properties of quantum correlations and thermal dense coding capacity, in Fig. 3 we plot thermal SQD and dense coding capacity for various values of external field Ω with spin squeezing interaction µ. They show that dense coding capacity is similar to the behavior of SQD. Therefore the prediction of dense coding behavior is feasible through the thermal properties of SQD in the quantum channel. As a result through the thermal properties of SQD, we can determine when and under what conditions the channel is suitable for dense coding. Moreover, we can see the value of valid dense coding with the dencreasing of external field in µ = 1.
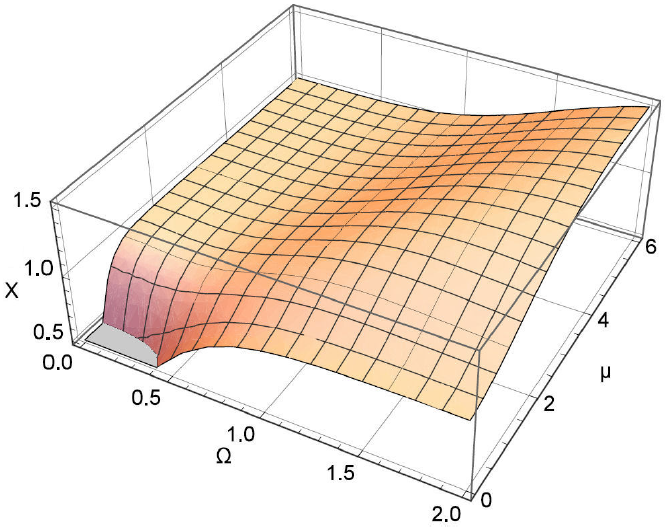
Figure 2 The super dense coding capacity as a function of external magnetic interaction Ω, spin squeezing interaction μ for the spin channel in T = 0.5.
4. Conclution
In this work, we have studied the thermal valid dense coding in a system of two spins under an external magnetic field and coupled to each other by a one-axis twisting spin squeezing. We investigated that the thermal properties of SQD how can have important role in predictng valid dense coding. We turn to the main goal of our study, first we investigated the role of squeezing interaction and the external magnetic interaction on dense coding capacity. The results showed that dense coding capacity decreases by increase of temperature. Also, the spin squeezing interaction and the external magnetic interaction have an important role in thermal valid dense coding. Comparing thermal properties of the quantum channel and dense coding capacity leads to an interesting outcome. That we can identify valid dense coding with the help of calculating the SQD in the quantum channel.











 nueva página del texto (beta)
nueva página del texto (beta)