1. Introduction

One of the processes which plays a fundamental role in quantum information science is quantum teleportation [^1-3]. Quantum teleportation, which was firstly proposed by Bennet et al, is the process of transmitting an unknown quantum state from a sender (Alice) to a remote receiver (Bob) using a quantum channel via local operations and classical communications [^4,5]. Moreover, this process can play a key role for quantum computing [⁶] and quantum networks [⁷]. Various quantum systems have been evaluated as possible candidates for quantum teleportation such as photons [^8,9,23], single atoms [¹⁰], cavity-quantum-electrodynamics systems [^11,12], Jaynes-Cummings models [¹³] and chiral graphenes [¹⁴].

The obligation of a maximally entangled quantum channel connecting Alice and Bob is very difficult to obtain or preserve in practice since the influences of decoherence from the environment reduces the entanglement of the quantum state shared between them [¹⁵]. We are going to consider this model as a quantum channel in the next section and discuss teleportation through it. Hence, it is very interesting and necessary to study the effect of decoherence on the evolution of quantum correlations and fidelity for teleported state. Recently the handling on dynamics of pairwise entanglement have been made significant progress in different fields. One of the simplest and most important models in quantum mechanics is the symmetric multi-qubit system. Recently with the help of this model, researchers have been able to investigate many of the major quantum phenomena including: spin squeezing [¹⁶], pairwise entanglement [¹⁷], entanglement teleportation [¹⁸] and pairwise quantum discord (QD) for different types of noisy channels [¹⁹]. Therefore, it is of interest and importance to investigate how the pairwise correlations for teleported state are affected by decoherence channels. In order to quantify the quantum correlations of a bipartite system, no matter whether it is separable or entangled, one can use the QD measure and the super quantum discord (SQD). QD have been considered as an informational-theoretical measure of the quantumness of correlations which was proposed by Ollivier and Zurek [²⁰]. QD can be described as a difference between classical correlation and quantum mutual information which is captured by the strong (projective) measurements. Then, when quantum and classical correlations are the same, QD is zero. On one hand, it is well known that non-zero QD is sufficient to teleport quantum information even when there is no entanglement [²¹]. However, when the system is perturbed slowly making possible not to lose its coherence completely, a rand-new quantum correlation will be constructed due to the weak measurement. [²²]. A Weak measurement performed on one of the subsystems can lead to a SQD always larger than the QD. In this paper, our attention is mainly focused on what happens to the pairwise quantum correlations for a teleported state via symmetric multi-qubit system. We calculate the concurrence, the QD and the SQD of the replica state and the fidelity between the input and the output states because it is important to know how much the entanglement is transferred to the replica state, and how close this replica state is to the original unknown state. We will find out that measurement strength and the number of qubit channel can be quantum information controllers for teleported state.

The layout is as follows: We present symmetric multi-qubit system in Sec. 2. We calculate the quantum correlations and average fidelity for the teleportated state and analyze the parameters on the teleportated entanglement in Sec. 3. Finally, the main results will be summarized in Sec. 4.

2. Description Model

We consider the Hamiltonian of one-axis twisting spin squeezing interaction [⁴⁰],

This term includes an ensemble of N spin- 1/2 particles with exchange symmetry whose dynamical properties can be described by collective operators, where

are the collective spin operators, and σⁱ _α are the Pauli matrices for the i^th spin. X describes the strength of the spin squeezing interaction in x direction. The interaction establishes pairwise correlations between all of individual spins in the collective spin system. In this paper, we choose the initial symmetry state, which can be prepared by the product state |10〉_N = |00…0〉, thus the wave function at time t is obtained as

To calculate quantum correlation, we first need to calculate the two-body reduced density matrix. According to [¹⁷], a state with exchange symmetry and parity ensures that its two-qubit reduced state can be extracted randomly from this state. In the {|00〉, |01〉, |10〉, |11〉} basis, the two-quibt reduced density matrix can be written form X-state, as follows:

The elements of the two-quibt reduced density matrix can be represented by the local expectation values of the one-axis twisting state [⁴¹]:

For example, by calculating 〈σ_1z〉 = Tr〈ρσ_1z〉 and 〈σ_1z σ_2z 〉 = Tr(ρσ_1zσ_2z), it can be easily verified that the relationship ρ₁₁ = (1/4)(1+2〈σ_1z〉+〈σ_1z σ_2z 〉) is true. Expectation values for the one-axis twisting state are obtained:

Where μ = 2χt. As we will exhibit soon, these spin pairs can be considered as good quantum channels for teleportation. There are several measures for quantum entanglement, among them concurrence is a measure of entanglement of bipartite states. For state (3), the quantum entanglement can be measured by the concurrence [⁴²],

where λ₁ > λ₂ > λ₃ > λ₄ and λ_i are the eigenvalues, ρ(σ₂ ⊗ σ₂)ρ*( σ₂ ⊗ σ₂) σ₂ is a Pauli matrix for the two-level systems and ρ* denotes the complex conjugate of ρ. The values of the concurrence range go from zero for an unentangled state to unity for a maximally entangled state. We are going to consider this model as a quantum channel in the next section and discuss teleportation through it.

3. Teleportationn

In this section, we’re going to consider the previous model as a quantum channel and in this way we will carry out the QD, the SQD the and entanglement teleportation. It is important to discuss how the number of particles in a channel have an effect on the quantum correlations dynamics of the teleported state. Let us assume that we have two users, Alice and Bob, who share an entangled state given by Eq. (3). Alice is in a pure state ρ_in = |ψ_in 〉〈ψ_in |, where,

with 0 ≤ θ ≤ π and 0 ≤ ψ ≤ 2π. The entanglement of the input state can be measured by the concurrence and it is given by C_in = 2|sin(θ/2)cos(θ/2)|. The aim of Alice is to send this state to Bob using Eq. (3). The output state is calculated as follows [⁴³]:

where P_μν = Tr[E^μ ρ^AB] Tr[E^ν ρ^AB], Σ_μν P_μν = 1 σ_ν (μ, ν = 0,x,y,z) are the three components of the Pauli matrix and σ₀ is the identity matrix. Here,

where

and

are bell states. Using the computational basis, |00〉, |11〉 |10〉, |01〉, the density operator on Bob’s hand (out state), ρ_out, is given by:

the elements of this matrix are:

By knowing the input states and the output states, we intend to characterize the quality of the teleportated state Eq. (16) using quantum correlations and fidelity. From Eq. (A.12), we recognize that SQD explicitly depend on the measurement strength. In the following, therefore, we first detect how the measurement strength affects the SQD teleportation. For this purpose, we assume that Eq. (14) is the maximum entanglement. From Fig. 1, we know that the strength influences and the number of qubit are not only the amplitude of the SQD teleportation but also its survival time. SQD teleportation can be exploited directly by the measurement strength and the number of qubit channel, since the dynamical evolutions of SQD teleportation and its stable value are closely depended on the measurement strength and the number of qubit channel.A even-qubit states for a quantum channels make the quantum correlation amplitude higher than odd-qubit states in μ =3.

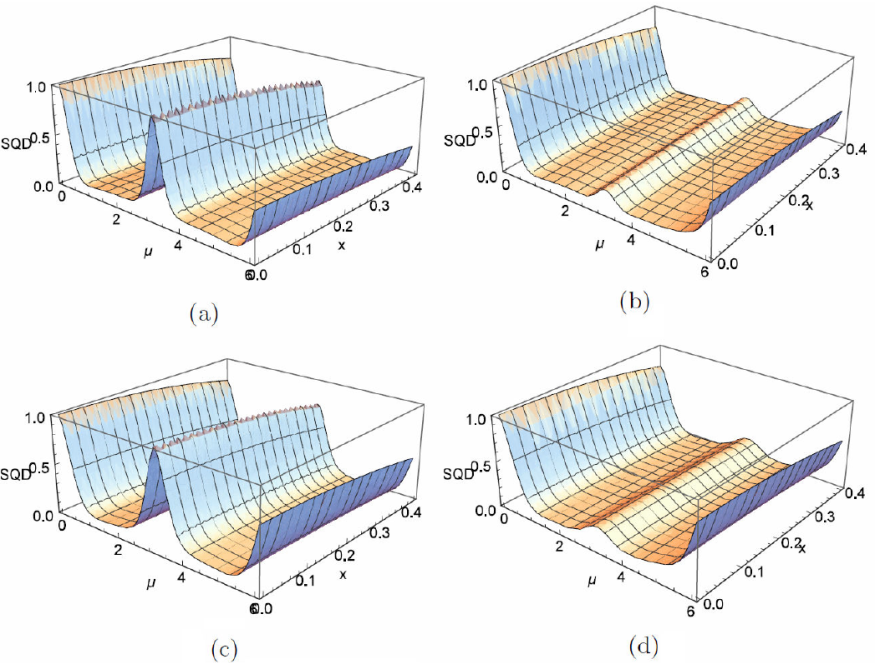
Figure 1 Teleported super quantum discord versus µ and x for the (a) N=10 (b) N=9 (c) N=6 (d) N=5 with the fixed value θ = (π/2) and ψ = 0. 

The quality of Bob’s state will be measured in terms of the fidelity and quantum correlations. Fidelity measures how close the final state is to the initial state which is defined by [⁴⁴]:

It is a useful indicator of the teleportation performance of a quantum channel when the input state is a pure one. Since the transported state is a pure state, the efficiency of quantum communication is characterized by the average fidelity, which describes the fidelity averaged over all possible pure input states in Bloch sphere formulated as:

If our model is used as quantum channel for teleportating an entanglement state, Fa can be expressed as:

In common situation, 0 ≤ F _a ≤ 1, information is distorted to some extent after being transmitted. For quantum communication, F _a can be larger than (2/3), which is the maximum of classical communication [⁴⁵]. So that in order to transmit |ψ _in 〉 with better fidelity than any classical communication protocol, we require the value of F _a to be strictly greater than (2/3).

In the following, we are interesting in pairwise entanglement and pairwise quantum correlations properties of teleported states in terms of concurrence, QD, SQD and average fidelity for pairs of particles extracted from a symmetric state of multi-qubit systems. Continuing our discussion, we will focus on a specific case that the teleported state Eq. (14) is located at maximum entanglement C _in = 1. In Figs. 2(a-d) we provide concurrence, QD, SQD and average fidelity for teleported state as a functions of scaled time μ = 2χt in different number of particles for fixed θ = (π/2) and for an arbitrary amount of ψ. The results numerically indicate the dependence of the teleported states Eq. (14) on the number of qubits. As seen from Fig. 2, concurrence, QD, SQD and average fidelity of teleported state oscillate with scaled time μ and have the same behavior. But the values of QD and SQD, which approximately are the same, are always greater than those of average fidelity and concurrence. Also, we observe that the concurrence, QD, SQD and average fidelity are symmetric with respect to μ = π. The important point is that concurrence, QD and average fidelity behavior are different depending on the number of qubits whether odd or even at μ = π. However, SQD approximately have the same behavior for the number of qubits both odd or even at μ = π. Therefore, quantum correlations and average fidelity differ when the number of qubits state is initially odd or even. From Figs. 2, one has found that entanglement can fall abruptly to zero and will remain zero for a period of time, which is called entanglement sudden death [⁴⁶]. Several investigations have focused on this subject [⁴⁷]. But QD and SQD decay continuously with respect to time, they tend to zero and then gradually evolve to their maximum values for even-qubit states. This means that QD and SQD do not show a phenomenon of sudden death for teleportad state. But for odd-qubit states SQD intends to revive unlike QD and entanglement in μ = π. From these figures, one finds that QD, SQD and average fidelity always coincide with each other in the dynamical evolutions. By comparing the behavior of the concurrence, QD, SQD with average fidelity under the same condition, we can say that QD, SQD can be a good measure to get information from the teleported states as well as fidelity.

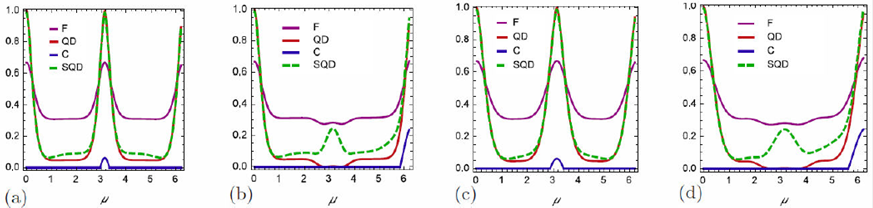
Figure 2 Teleported concurrence (blue, solid), average fidelity (purple, solid), quantum discord (red, solid) and super quantum discord (green,dot-dashed) versus µ for the (a) N=10 (b) N=9 (c) N=6 (d) N=5 with the fixed value x = 0.1, θ = (π/2) and ψ = 0. 

To better see the effect of the number of qubits in the teleported states, we plot Figs. 3 similar to as in Figs. 2 but with more qubits. The results are similar to the previous one with the difference that the death and revival quantum correlations and average fidelity happen quickly for teleported states. Therefore, the length of the chain a quantum channel can have a significant impact on the amount of data transferred via teleport stated. Also, Figs. 2 and 3 reflect where the SQD is stable through the whole process under channel decoherence. Therefore, SQD is promising to be a nice option for quantum information resource in the teleportation.

Figure 3 Teleported concurrence (blue, solid), average fidelity (purple, solid), quantum discord (red, solid) and super quantum discord (green, dot-dashed) versus µ for the (a) N=100 (b) N=99 (c) N=98 (d) N=97 with the fixed value x = 0.1, θ = (π/2) and ψ = 0. 

4. Conclusion

In summary, we have investigated quantum correlation teleportation via symmetric multi-qubit system as a quantum channel. Using QD and SQD to quantify quantum correlations for teleported state, some analytical and numerical results are presented. The results show that they are sensitive to any change in the degree of measurement strength and the number of qubit channel. In addition, we investigated the effect of the above parameters on the average fidelity in detail and we compared them with quantum correlation teleportation. When enlarging the measurement strength, SQD firstly decreases quickly to a minimum value and it then increases abruptly to a maximum value as the μ is reached approximately to π. The important point is that its value at μ = π depends on whether the number of qubits of the channel is odd or even. By comparing QD, SQD, average fidelity and concurrence, we observed that QD and SQD are good measures for quantum information processing via teleported state. Moreover, the results indicate that SQD can be better than QD in order to maintain the exchanged quantum data through the quantum channel.