1. Introduction
Flow over a converging and diverging channel is an important phenomenon for physical models due to its broad applications including mechanical, environmental, chemical, civil, bio-mechanical and aerospace engineering branches. For instance, flows through nozzles, reducers and diffusers are encountered in processing of polymers. The drawing-cold process in polymer industry is dependent on flows through converging channels. Another important implication of such flows is molten polymer extrusion through converging dye. Human blood flow in arteries and capillaries is another important implication of converging or diverging channel flow. The basic theory of diverging/ converging channel was reported by Jeffrey and Hamel [1,2]. After the basic works, few investigations on the phenomenon of diverging/ converging channel were presented. For example, Motsa et al. [3] presented the flow analysis induced by inclined walls. Asadullah et al. [4] initiated hydromagnetic Jeffery fluid flow in diverging/converging channel. Muhammad et al. [5] addressed the implication of least square technique on problem of heat transportation in converging and diverging channel. The magneto nanofluid flow generated by convergent/divergent channel was discussed by Syed et al [6].
The evaluation of heat transport in porous medium has increased tremendously in the present world of engineering and industrial application. Typical examples of these applications include production of crude oil, nuclear waste disposal, grain storage, petroleum reservoirs, porous insulation, packed bed reactors, groundwater pollution and resin transfer modeling. The term of square velocity in Darcian velocity equation was added by Forchheimer [7]. Muskat [8] presented the homogeneous fluid flows through porous media by employing Forchheimer theory. Seddeek [9] analyzed the involvement of viscous heating in Darcy-Forchheimer flow combined with convection in porous media. Hydromagnetic and diffusion features in Darcy-Forchheimer flows were described by Pal and Mondal [10]. Some important discussions on Darcy-Forchheimer flows can be seen in [12-15].
The terminology of nanofluid is used for the liquids formulated by the dispersion of the nanometer sized particles of metallic/non-metallic materials in the conventional thermal fluids. Choi [16] initially described the model of nanofluid and remarked that the factors of Brownian movement and thermophoresis are responsible for the augmentation of heat transportation. Later on, Kuznetsov and Nield [17] employed the model of Choi for boundary-layer viscous fluid flow induced by movement of the plate. Magnetohydrodynamics slip flow of viscous fluid over a vertical surface is addressed by Das et al. [18]. In recent years, various investigations are published on nanofluid [19-28]. In these research works, the authors have used different types of nanoparticles. Here, we used the Titanium dioxide (TiO2) type nanoparticles which are very close to ideal semiconductors for photocatalysis. TiO2 nanoparticles have lower cast, much safer and with high stability. Such particles are available in the nanodots and nanocrystals forms and exhibit magnetic features.
The investigations on implementation of magnetic field on boundary-layer flows is a hot topic of research due to its abundant applications in technology, industry and geothermal processes, for example, nuclear reactors cooling, high temprature plasmas, metal-liquid fluids, magnetohydrodynamic accelerators and generators. As a consequence, great interest of researchers has been devoted to address the nature of electrically conducting fluids include water-mixture with little acid and liquid-metal under applied magnetic field. In addition, the phenomenon of Joule heating has key role in thermal transportation of a fluid. In fact, Joule heating is generated by excess of heating in fluid due to applied magnetic fields or direct currents. Having all these in mind, we considered the electrically conducting fluid flow in presence of Joule heating phenomenon.
The present effort models heat transfer augmentation in water-based TiO2 nanoparticles through a converging/diverging channel. Joule heating, viscous dissipation and magnetic field are implemented. Heat transfer characteristics are studied through converging/diverging channel. To conserve the dimensional quantities into the dimensionless form, the similarity equation has been employed. The RKF-45 order technique has been implemented to treat the non-dimensional mathematical problem.
2. Mathematical Formulation
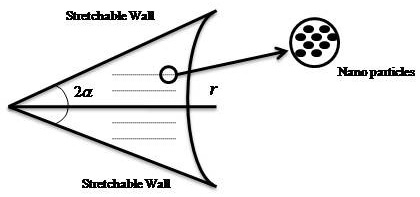
We considered the flow through the source and sink which intersects both plane walls and makes an angle 2α. Figure 1 represents the geometry of the present problem. The walls are shrinked/stretched at rate c and the velocity at the wall is expressed as (û)r = U w = c/r. Further, the channel is assumed to be saturated by nanoparticles with base-fluid (water) and TiO2 nanoparticles. The thermal equilibrium situation is considered between base-fluid and nanoparticles.
A system of polar coordinates (r, Θ) is adopted to model the flow problem. Velocity field can be described in the form V = [û, 0,0], in which ûr is a function of r and Θ. Here, the continuity, momentum and energy relations are expressed as follows [5]:
Equation (1) is the law of conservation of mass or continuity equation, Eqs. (2) and (3) are the law of conservation of momentum or momentum equations and Eq. (4) is the law of conservation of energy and is known as energy equation.
In above expressions, k is the porous medium permeability, F = cb /(rk1/2) is the non-uniform inertia factors of porous medium, cb is the coefficient of drag, σ is the electrical conductivity, B0 is the strength of electromagnetic induction. Further, knf (ρCp)nf, μnf and ρnf represent the thermal conductivity, heat capacity, dynamic viscosity and density of liquid, respectively:
where ϕ is the solid volume-fraction, ρf is the base-liquid density, ρs is density of nanoparticle, μf is the hosting liquid dynamic viscosity, (ρCp)f represents the heat capacity of hosting fluid, (ρCp)s denotes the heat capacity of nanoparticle, kf is the thermal conductivity of hosting fluid and ks is the nanoparticles’ thermal conductivity.
The following are boundary conditions for flow model:
in which U denotes the channel centerline velocity and
The radial velocity pure depiction can be described by Eq. (1) as:
The non-dimensional variables can be expressed as:
The elimination of pressure expression from Eqs. (2) and (3), and the implementation of the above defined variables lead to the following equations:
The non-dimensional conditions can be written as:
In the above expressions, c denotes the shrinking and stretching
constraint where c>0 defines the stretching wall, while
c>0 defines the shrinking walls. Re =
Ucα/νf
is the Reynolds number, the convergent channel is represented by
α>0 and the divergent channel is defined by
α>0, Kp =
νf
/kUc is the porosity parameter,
Fr = cb
/k1/2 is the inertia coefficient,
The interesting quantities from the physical point of view are the skin friction coefficients and Nusselt number which may be expressed as [5,6]:
In the above expressions, TrΘ is the wall shear stress and qw represents the wall heat flux. The non-dimensional forms of the above expressions are:
3. Results and Discussion
The non-dimensional Eqs. (12) and (13) with the boundary conditions (14) are solved by employing the RKF-45 scheme together with shooting methodology. The water is assumed as hosting fluid containing TiO2 nanoparticle suspensions. Numerical results of fluid velocity and temperature for some selected values of constraints are demonstrated with help of graphs. Numerical benchmark for friction-factors and local Nusselt number quantities are displayed and explained.
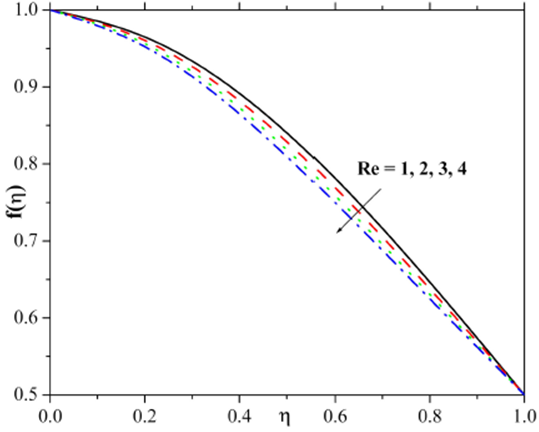
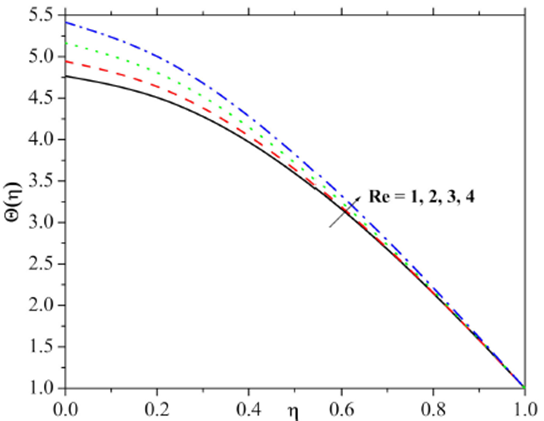
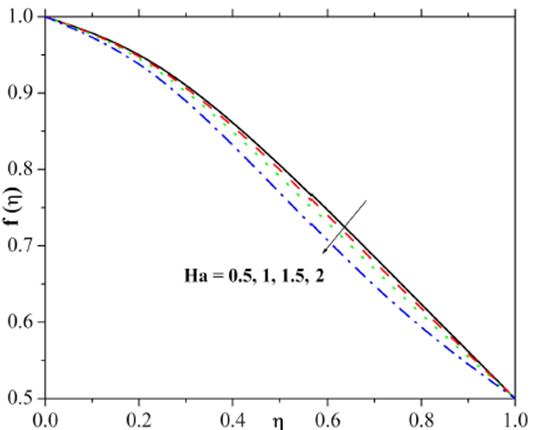
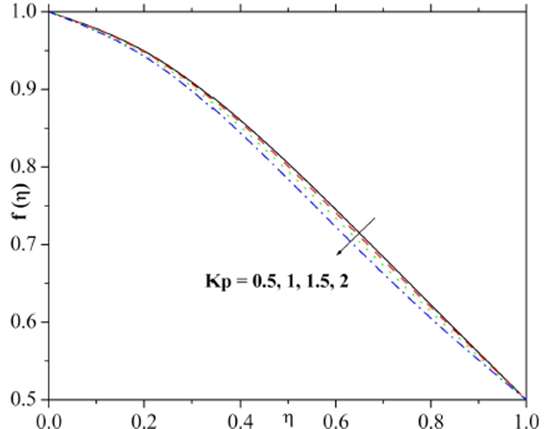
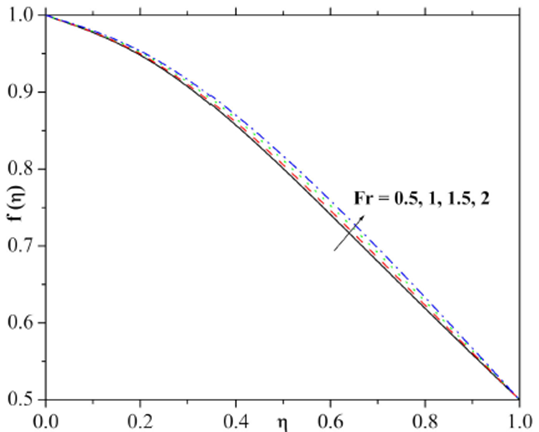
The influence of the Reynolds number on the velocity and the temperature fields has been demonstrated in Fig. 2 and 3. Figure 2 illustrates that the retardation in the velocity distribution and its interrelated thickness is noticed for the higher Reynolds number. Figure 3 depicts that Larger values of Re result in higher temperature distribution and thicker thermal boundary layer. The variation of the velocity field as a function of the Ha is presented in Fig. 4 and it is clear from the results that the higher estimation of the Ha gradually decays the velocity field and reduces the momentum thickness. From the physical point of view, an external electric field becomes stronger for larger Hartman number which consequently maximizes the velocity. Figure 5 captures the response in velocity distribution for varying porosity constraint. Here the velocity field decayed through larger estimation of porosity constraint. Physically, it justifies that the porous media increase the resistance to the fluid flow that may create a reduction in velocity. Figure 6 is displayed to explore the impact of varying inertia coefficient parameter on the velocity field. From the figure, it is evident that the stronger velocity field and momentum layer thickness accru when the inertia coefficient parameter rises gradually.
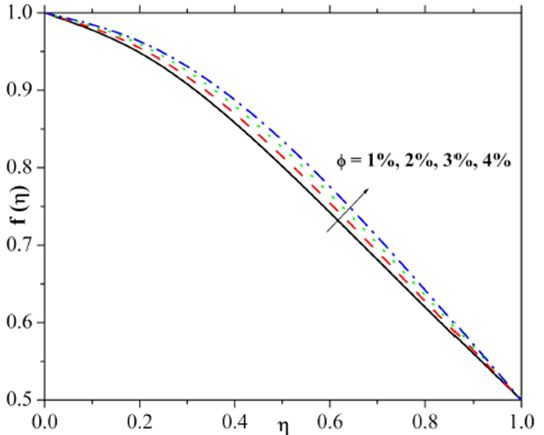
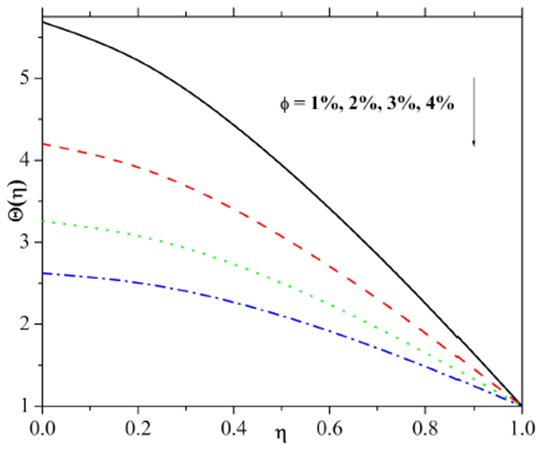
In order to investigate the impact of nanoparticle volume-fraction on both the velocity and temperature filed results are presented in Fig. 7 and 8. Figure 7 explicitly describes that the velocity field is prominently enhanced by an increase in nanoparticle concentration. Figure 8 indicates that the decreasing trend of the temperature field and the thermal layer thickness are due to the reduction on the nanoparticle concentration.
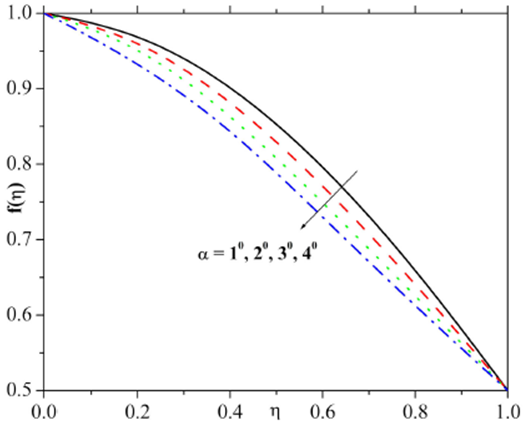
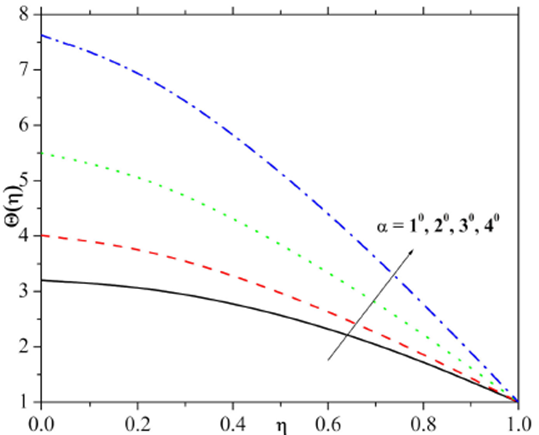
Figures 9 and 10 are plotted to analyze the effect of opening angle parameter on the velocity and temperature fields. From Fig. 9 it is scrutinized that, larger estimation of opening angle parameter scales back the velocity profile and momentum layer thickness. Moreover, the velocity field is dominant in the center of the channels. Figure 10 demonstrates the effect of opening angle on temperature distribution. Here, reduction in temperature and its correspondences boundary layer is noticed for enhancing values of opening angle parameter.
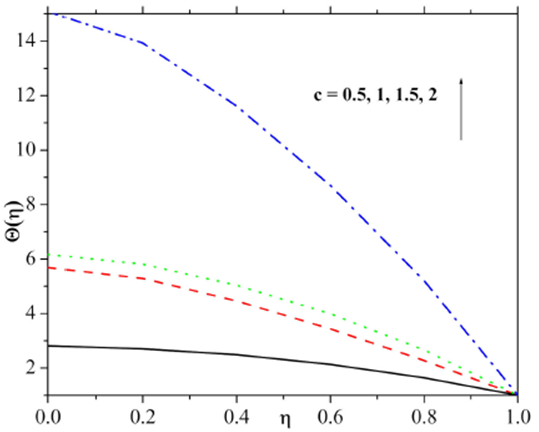
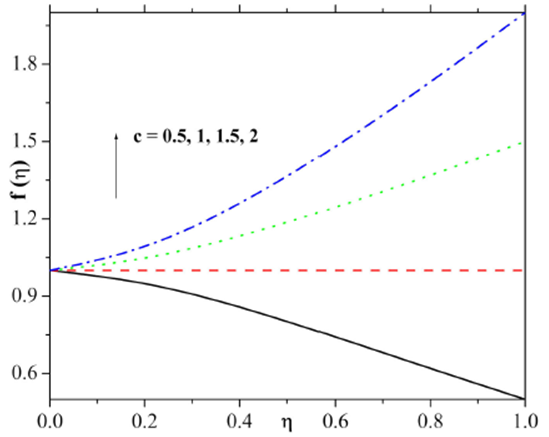
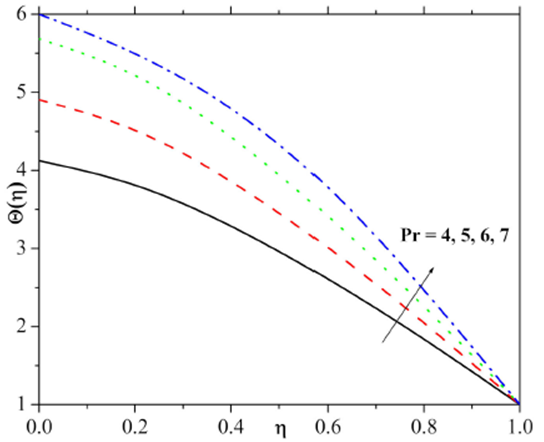
Figure 11 and 12 are displaying the nature of stretching constraint on both velocity and temperature fields. From these figures, it is observed that the velocity and temperature fields are enhanced by the increment in stretching constraint. Figure 13 disclosed the behaviour of Eckert number on temperature profile. Here thermal layer and temperature field are enhanced for larger Eckert number. This is because of the fact that viscous dissipation plays a role of the internal heat source that enhances the thermal energy and thus heats the regime. Prandtl number impact on temperature is pictured in Fig. 14. Temperature is decreased significantly with the use of larger Prandtl number.
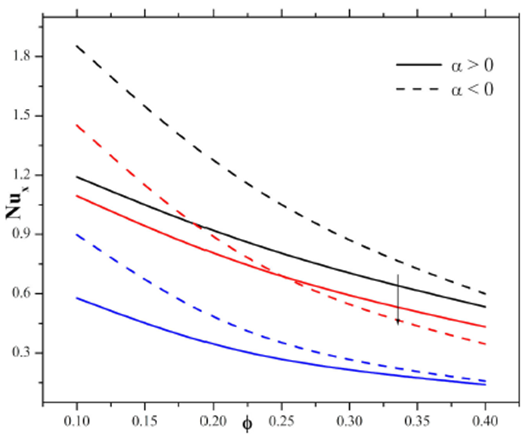
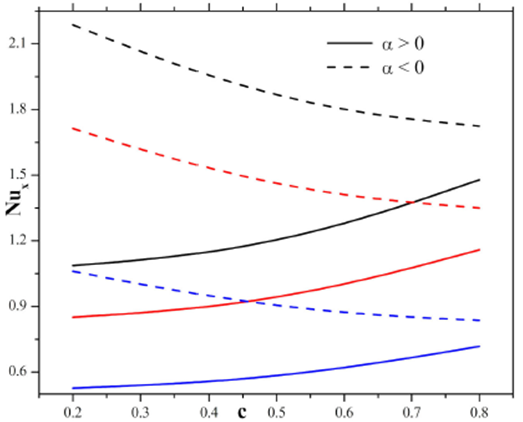
The influence of the nanoparticle concentration and the stretching ratio parameter on the Nusselt number is analyzed in Fig. 15 and 16. From Fig. 15, it is noticed that the Nusselt number is reduced in presence of nanoparticle concentration for both the converging and diverging channel. Further, from these figures it is noticed that the rate of heat transfer is maximum in converging channel when compeered to the diverging channel. In Fig. 16, considering the higher values of stretching ratio parameter, Nusselt number enhances in the diverging channel and decays in converging channel.
Table I displays the quantities of thermal and physical importance associated to nanoparticles and base-fluid. Table II describes the values of ReCf and Nu for distinct values of existing constraints. It is noticed that ReCf decreases for the Kp, α, Ha, Re and c but it improves for enhancing values of Fr and Φ. While, Nu decreases for Fr, c, Φ and increases for the persisting parameters. Table III depicts the numeric data of ReCf and Nu by employing the distinct values of emerging constraints for both diverging channel converging channel cases. Here, the rate of heat transportation is enrich in diverging channel case as comparative to converging channel situation and surface drag force is weaker in diverging channel. Table IV is displayed to see the behavior of shrinking and stretching wall on ReCf and Nu for different values of parameters, which makes clear that the rate of heat transfer is optimizing in stretching wall situation in comparison to the shrinking wall case.
Table I Thermo-physical features of Cu-water nanoparticles
| ρ(Kg/m3) | Cp (j/Kgk) | k(W/mk) | |
| H2O | 997.1 | 4179 | 0.613 |
| TiO2 | 686.2 | 4250 | 8.95 |
Table II Numerical values of ReCf and Nu for different physical constraints
| α | Ec | Kp | Fr | Ha | Pr | Re | c | Φ | ReCf | Nu |
| 1 | 083583 | 6.13521 | ||||||||
| 2 | 0.60444 | 10.79808 | ||||||||
| 3 | 0.420334 | 19.31117 | ||||||||
| 0.5 | 0.675547 | 5.506156 | ||||||||
| 1 | 0.675547 | 16.51847 | ||||||||
| 1.5 | 0.675547 | 16.51847 | ||||||||
| 0.5 | 0.699539 | 8.686828 | ||||||||
| 1 | 0.667372 | 8.856013 | ||||||||
| 1.5 | 0.613084 | 9.218566 | ||||||||
| 0.5 | 0.664872 | 8.872043 | ||||||||
| 1 | 0.678211 | 8.794897 | ||||||||
| 1.5 | 0.691502 | 8.723668 | ||||||||
| 1 | 0.693279 | 8.723668 | ||||||||
| 2 | 0.657729 | 8.913268 | ||||||||
| 3 | 0.621806 | 9.153657 | ||||||||
| 5 | 0675547 | 7.341541 | ||||||||
| 6 | 0.675547 | 8.809849 | ||||||||
| 7 | 0.675547 | 10.27816 | ||||||||
| 2 | 0.807336 | 8.182623 | ||||||||
| 3 | 0.750935 | 8.312023 | ||||||||
| 4 | 0.707969 | 8.532242 | ||||||||
| 0.2 | 0.994613 | 17.91076 | ||||||||
| 0.4 | 0.790819 | 11.21332 | ||||||||
| 0.6 | 0.552698 | 6.972496 | ||||||||
| 0.1 | 0.675547 | 8.809849 | ||||||||
| 0.2 | 0.878988 | 8.256998 | ||||||||
| 0.3 | 0.948244 | 7.925904 |
Table III Comparative analysis of values of ReCf and Nu for both convergent and divergent cases with different physical constraints
| Ec | Kp | Fr | Ha | Pr | Re | c | Φ | ReCf | Nu | ||
| α<0 | α>0 | α<0 | α>0 | ||||||||
| 0.5 | 1.868445 | 0.675547 | 14.07865 | 5.506156 | |||||||
| 1 | 1.868445 | 0.675547 | 28.1573 | 11.01231 | |||||||
| 1.5 | 1.868445 | 0.675547 | 42.23594 | 16.51847 | |||||||
| 0.5 | 1.910353 | 0.699539 | 23.75582 | 8.686828 | |||||||
| 1 | 1.854132 | 0.667372 | 22.12291 | 8.856013 | |||||||
| 1.5 | 1.758676 | 0.613084 | 19.65349 | 9.218566 | |||||||
| 0.5 | 1.850748 | 0.664872 | 22.02682 | 8.872043 | |||||||
| 1 | 1.872855 | 0.678211 | 22.65205 | 8.794897 | |||||||
| 1.5 | 1.894817 | 0.691502 | 23.29182 | 8.723668 | |||||||
| 1 | 1.899433 | 0.693279 | 23.29182 | 8.723668 | |||||||
| 2 | 1.837228 | 0.687729 | 21.65816 | 8.913268 | |||||||
| 3 | 1.774057 | 0.621806 | 20.02622 | 9.153657 | |||||||
| 5 | 1.868445 | 0.675547 | 18.77153 | 7.341541 | |||||||
| 6 | 1.868445 | 0.675547 | 22.52584 | 8.809849 | |||||||
| 7 | 1.868445 | 0.675547 | 26.28014 | 10.27816 | |||||||
| 2 | 1.238775 | 0.807336 | 10.40009 | 8.182623 | |||||||
| 3 | 1.416122 | 0.750935 | 12.69167 | 8.312023 | |||||||
| 4 | 1.626097 | 0.707969 | 16.50499 | 8.532242 | |||||||
| 0.2 | 2.663474 | 0.994613 | 38.77703 | 17.91076 | |||||||
| 0.4 | 2.15923 | 0.790819 | 27.95821 | 11.21332 | |||||||
| 0.6 | 1.550879 | 0.552698 | 17.27545 | 6.972496 | |||||||
| 0.1 | 1.868445 | 0.675547 | 22.52584 | 8.809849 | |||||||
| 0.2 | 1.784015 | 0.878988 | 10.24096 | 8.256998 | |||||||
| 0.3 | 1.864591 | 0.948344 | 5.901852 | 7.925904 | |||||||
Table IV Comparative analysis of values of ReCf and Nu for both stretching and shrinking wall cases with different physical parameter.
| α | Ec | Kp | Fr | Ha | Pr | Re | Φ | ReCf | Nu | ||
| c<0 | c>0 | c<0 | c>0 | ||||||||
| 1 | 2.474032 | 0.83583 | 25.79104 | 6.13521 | |||||||
| 2 | 1.572095 | 0.50444 | 34.74097 | 10.79808 | |||||||
| 3 | 0.839433 | 0.420334 | 51.49354 | 19.31117 | |||||||
| 0.5 | 1.572095 | 0.675547 | 21.71311 | 5.506156 | |||||||
| 1 | 1.572095 | 0.675547 | 43.42622 | 11.01231 | |||||||
| 1.5 | 1.572095 | 0.675547 | 65.13932 | 16.51847 | |||||||
| 0.5 | 1.942165 | 0.699539 | 2973111 | 8.686828 | |||||||
| 1 | 1.436527 | 0.667372 | 37.12064 | 8.856013 | |||||||
| 1.5 | 0.26309 | 0.613084 | 70.36885 | 9.218566 | |||||||
| 0.5 | 1.512817 | 0.664872 | 35.74421 | 8.872043 | |||||||
| 1 | 1.586752 | 0.678211 | 34.50157 | 8.794897 | |||||||
| 1.5 | 1.659109 | 0.691502 | 33.3697 | 8.723668 | |||||||
| 1 | 1.874842 | 0.693279 | 30.48154 | 8.717145 | |||||||
| 2 | 1.236773 | 0.657729 | 41.16595 | 8.913268 | |||||||
| 3 | 0.363945 | 0.621806 | 66.59736 | 9.153657 | |||||||
| 5 | 1.572095 | 0.675547 | 28.95081 | 7.341541 | |||||||
| 6 | 1.572095 | 0.675547 | 34.74097 | 8.809849 | |||||||
| 7 | 1.572095 | 0.675547 | 40.53113 | 10.27816 | |||||||
| 2 | 1.816693 | 0.807336 | 31.66933 | 8.182623 | |||||||
| 3 | 1.731966 | 0.750935 | 32.57276 | 8.312023 | |||||||
| 4 | 1.650576 | 0.707969 | 33.59878 | 8.532242 | |||||||
| 0.1 | 1.226586 | 0.675547 | 74.65561 | 8.809849 | |||||||
| 0.2 | 1.710947 | 0.878988 | 65.36394 | 8.256998 | |||||||
| 0.3 | 2.358251 | 37.19683 | 37.19683 | 7.925904 | |||||||
4. Conclusion
The simultaneous impacts of Joule dissipation and viscous heating in MHD heat transfer flow between the convergent/divergent channel in the presence of H2 O-TiO2 nanoparticles are numerically studied. Particular attention is paid to examine the Darcy-Forchheimer flow, strong magnetic field and Joule heating on velocity and temperature distribution. Present flow problem is studied in two cases- for converging and diverging channel condition. The main findings of the present problem include:
The rapid decrease in velocity field is visualized for various Kp and Ha.
Momentum and thermal thicknesses of boundary-layer thickness are enhancing function of suction constraint.
Larger values of Reynolds number scale back the velocity field and augment the temperature distribution.
Variations of the Reynolds number show the reverse changes in velocity and temperature fields.
The thermal thickness rapidly reduces by enhancing values of Pr and Ec.
Eckert number enhances the liquid temperature for all circumstances.
Larger estimation of α and c shows the opposite behaviour on the velocity profile.











 text new page (beta)
text new page (beta)