1. Introduction

The increasing capacity of processing and storage of computers is reaching its limit with the current technology of transistors, based on the flow of electrons. In order to overcome these technological frontiers, it is necessary to go beyond charge states and consider the freedom degree of spin instead.

Nowadays, many studies, both theoretical and experimental, are carried out in order to control the spin of the electrons ^[1,2] and thus allowing to use it in the manufacture of a new type of very powerful computers. This task is not easy, however. It has been suggested the use of nanostructures, specially quantum dots (QD’s) for this purpose ^[3,4]. As shown in other works ^[5], an external magnetic field perpendicular to the direction of QD’s growth modifies the carrier spectra, however, there are few works mentioning how the wave functions are modified when the spin is included. It is important to see how the wave functions are modified because they determine matrix elements, for example. Regarding to the carrier energies, a factor that can also alters them is the addition, often accidental and uncontrollable during the QD’s growth, of impurities that lead to the modification of the expected confinement energies. With the aim of determining how much these impurities affect the carrier states we have analyzed the effect of a single impurity in the studied systems. This is important for some applications such as optical devices and solar cells ^[6-9].

In order to have a better understanding of the QD’s behavior, in this paper we analyze the effect of the magnetic field, as a way to control the spin, and the role of impurities on the carrier band structure of InAs/GaAs ^[10,11] and GaN/AlN ^[12,13] self assembled quantum dots (SAQD’s). Both systems are studied in the framework of the eight-band k⋅p model ^[14,15], which includes a conduction band and 3 valence bands (heavy holes, light holes and the split-off band), the strain, a consequence of the self-assembly process also is considered. It has been proven in multiple studies, that strain may strongly modify the energy of the carriers, since it manifests as an additional potential ^[16-18].

The impurity is considerated also as an additional potential and for simplicity, neglecting its volume and mass. It is assumed that intrinsic potentials such as deformation or piezoelectric ones are not affected by it. Specifically, we study the inclusion of an impurity in small QD’s, to see its effects on the carrier states of the nanostructures.

The paper is organized as following: In Sec. 2 a brief description of the k⋅p model is presented and also the description of the impurity model used in the calculation. In Sec. 3 the results for both systems of QD’s are shown, first under the action of a magnetic field and then the effect of impurities. In Sec. 4 the conclusions are included.

2. k⋅p model

It is well known that the multi-band k⋅p model includes the interaction between the valence and conduction bands. Depending on the material and the interactions considered there are models from 1 up 14 bands or more ^[15,18,19]. In our case, because the materials of which the QD’s are made from have s and p external orbitals. Thus, it is only necessary to consider the conduction band and the three highest energy valence band. Adding spin leads to the 8-band model. The inclusion of the magnetic field is an arduous task, and in this work the Hamiltonian for the zinc blende structure, in the anysotropic model including the strain and magnetic field, it is taken from Ref. ^[20] for the InAs/GaAs system as

while for the wurtzite structure as in GaN/AlN QD’s, following Ref. ^[21], we use

where Vp(x,y,z)=g0μBσ⋅B for the magnetic field, or Vp(x,y,z)=Vimp(r) when the impurity is included, g0 is the free-electron Landé g-factor (g0=2), μB is the Bohr magneton and σ is a Pauli matrix. Vstrain and Vpiezo are the strain and piezoelectric potentials, respectively, calculated as in Refs. ^[16,17], where it is assumed a 3D periodic system of quantum dots embedded in a matrix. The strain and piezoelectric potential are calculated in the reciprocal space (ξ) using the Eqs. (3) and (4)

where χ̃QD is the characteristic function, which contains the geometry of the nanostructure, λ and μ are the Lamé constants, ε0 is the vacuum dielectric constant and εr is the electric constant of the material of the quantum dot, for InAs(GaN) εr=14.55 ^[20] (9.6) ^[16], Plspont and Plstrain are the terms of the piezoelectric potential due to the spontaneous polarization and the strain, respectevely. The Eqs. (3) and (4) should be converter in the real space with the equation

where V(r) is the Vstrain or Vpiezo in the real space.

An uniform magnetic field B=Bk^ is assumed along the growth direction of the quantum dots, that is, along the z axis. This, in order to reduce the complexity of the Hamiltonian. Moreover, from the practical point of view it is easier to produce and measure a homogeneous magnetic field along some direction. Notice that spin-orbit effects are neglected for simplicity.

Quantum dots, also known as artificial atoms due to their discrete energy levels, are very susceptible to change their confining energies due to various aspects, such as: the material that make them up, their size and shape, the distribution of the intrinsic deformation potential in these systems, piezoelectric field and dislocations ^[22]. Here it is analyzed another way to modify their energy levels, besides the magnetic field, by means of the presence of impurities. They play an important role as mentioned before. The effect of an impurity has been included by means of a potential in the diagonal of the Hamiltonian and the potential used for Vimp in this paper is Coulombic type ^[23], given by

where q is the fundamental charge for which we consider both types, the positive and negative case, and R is the position of the impurity in the QD.

3. Results

The Hamiltonian described in the previous section is solved by means of the finite element method ^[24]. We first present results corresponding to QD’s of InAs embedded in GaAs, under the action of a magnetic field, with a typical geometry of quadrangular pyramid whose base has 8 nm side and the height is 8 nm long ^[15,18]. Due to its crystalline structure (zinc blende), these materials do not have a considerable piezoelectric field, so in this calculation it was disregarded. Subsequently, similar results will be presented for GaN/AlN QD’s which have a geometry of truncated hexagonal pyramid ^[16,25] with dimensions from vertex to opposite vertex 18(8) nm in its lower(upper) part, a height of 4.1 nm and a wetting layer of 1 nm. Finally, the results obtained by including impurities in both systems are given.

3.1 InAs/GaAs QD’s under magnetic field

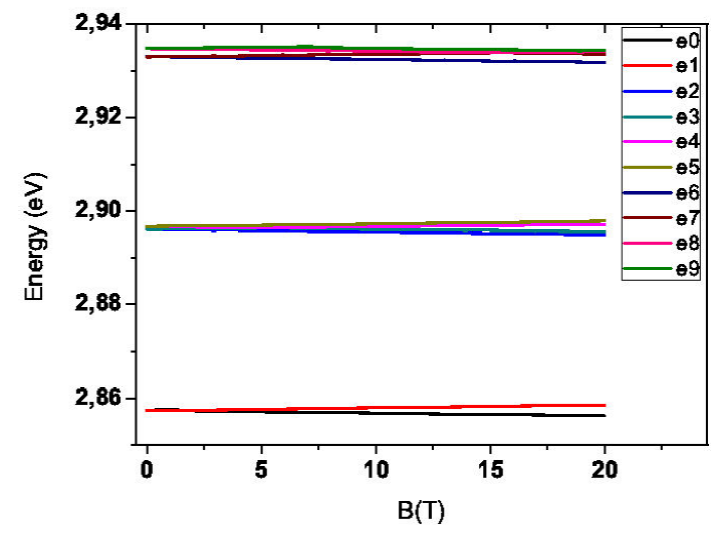
Figure 1 shows the effect of the magnetic field on the distribution probability of the first four electron states in the InAs/GaAs QD’s for B=20T. It is observed that the ground state and the first excited state have the same distribution (type s), which indicates that the conduction band is Zeeman splitted into two similar states with their respective spin up and down, the second and third state (type p) show similar splitting in two bands with spin up and spin down, with respect to the states 3 and 6. Observe that the second and fourth states are originally degenerated, similar to the third and fifth state. The weak interaction of the conduction band with the valence band favors lack of change in the distribution of the electrons respect to the case B=0 T (not shown), i.e., the distribution of the density probability for the case B=0T and B=20T are very similar. Figure 2 shows that by increasing B the carrier energy, the eigenvalues of Eq. ([hamiltonian]) increases linearly, i.e., the electrons are independent of holes, it can be seen that the states are almost overlap, due a small difference of energy in the superior states (indicated with diferent colors) with respecto to e0 and e1. Typical Zeeman effect appears as in similar results reported in previous works ^[5,26-28].

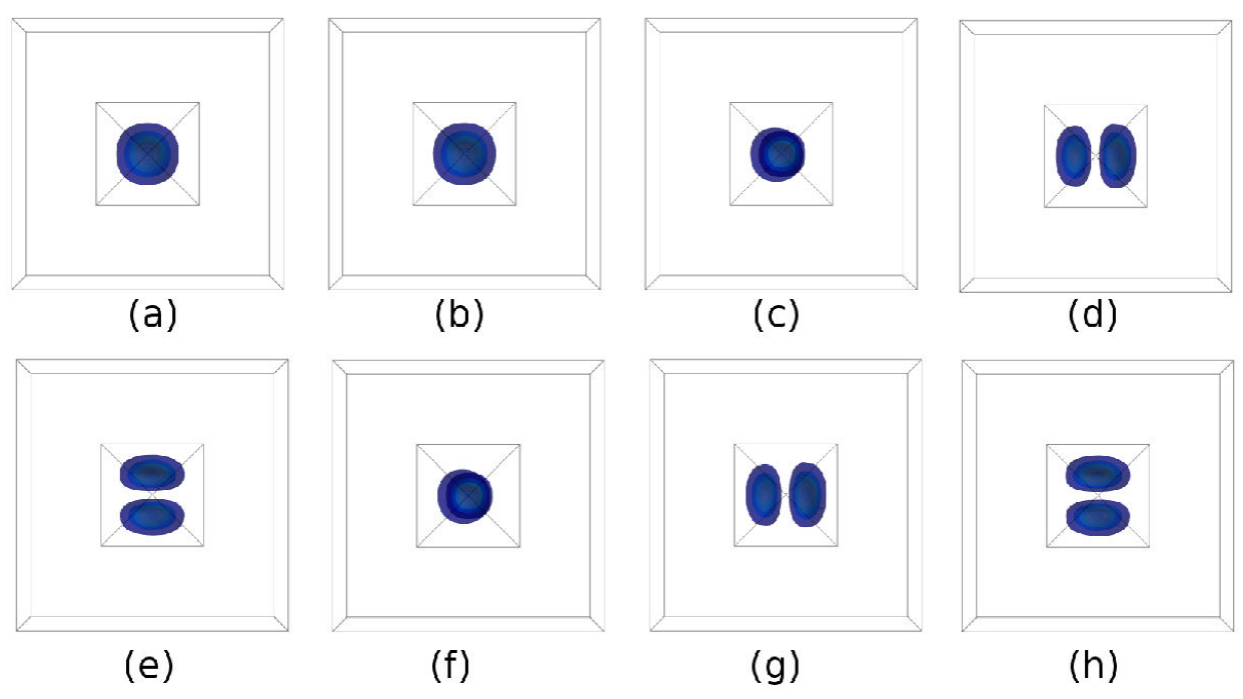
Figure 1 Top view of the electronic probability density for the first eight states: (a) e0, (b) e1, (c) e2, (d) e3, (e)e4, (f) e5, (g) e6 and (g) e7 state in InAs/GaAs QD’s with B = 20T. 

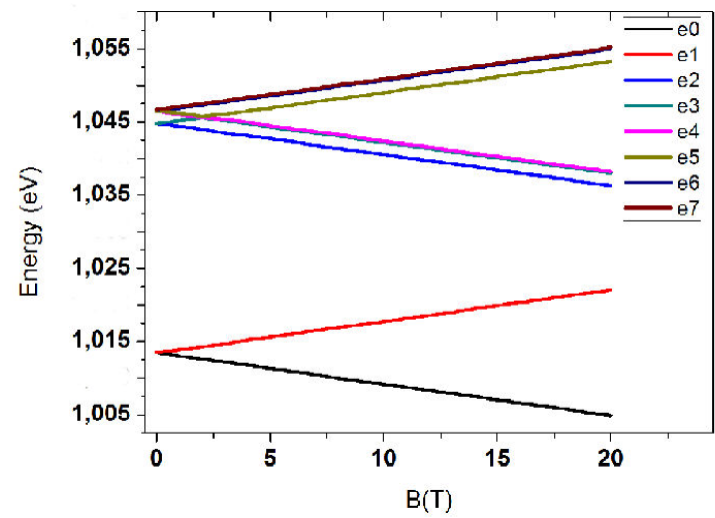
Figure 2 Carrier energy for the first 8 states of electrons in InAs/GaAs QD’s, varying the magnetic field B from 0T to 20T. Notice that the e3, e4 and e6, e7 almost overlap. 

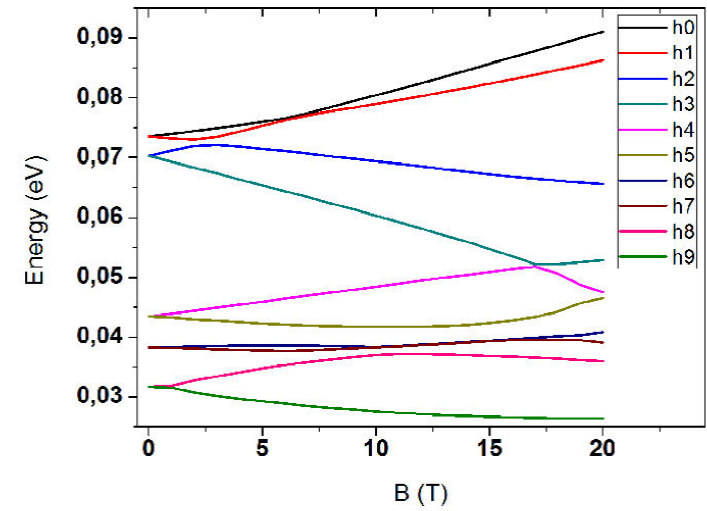
A quite different behavior is presented by the valence bands. In Fig. 3 the first four states corresponding to the heavy-hole band are shown, under the effect of a magnetic field at different intensities. Two main characteristics are observed: The states do not present a typical distribution of s or p states, and the magnetic field modifies the distribution probability and energy of the holes. The explanation is that, in contrast to electrons, a strong interaction exists between the different hole bands, that is, the heavy holes, the light holes, and the split-off bands. This interaction causes small changes in energy (remember that at the point Γ the heavy and light holes have the same energy ^[29]) and modifies the distribution of the carriers. The deformation potential and the magnetic field admixture the states modifying the distribution of the holes within the QD’s.

Figure 3 Top view of hole probability density of InAs/GaAs QDs for the first four states with values of magnetic field as show: (a) h0, (b) h1, (c) h2, and (d) h3. 

The confinement levels in Fig. 4 also show Zeeman behavior, i.e., the energy of the carriers with spin down decreases, and the opposite occurs for the spin up as the intensity of B increases, as previously reported ^[5,26]. However, this behavior changes at magnetic fields around of 10T for lower energy states, presenting an anti-crossing ^[30]. This is probably due to the change in the effective mass as modified by the magnetic field ^[1]. It can seen that the energy of the holes changed in a way very difference that the electrons, due the high interaction between the holes indicated by different colors to clarity.

Figure 4 Carrier energy for the first 10 states of holes, in InAs/GaAs QD’s, as a function of the magnetic field. Notice the Zeeman splitting and the anti-crossing. 

3.2 GaN/AlN QD under magnetic field

Now we analyze the effect of the magnetic field in a GaN/AlN QD. We begin with the analysis of the energy of the heavy holes. In Fig. 5 a very slight increase is observed as the magnetic field is increased, unlike the holes in InAs QD, this is due to the strong confinement that both carriers experience in the nitride system caused by the piezoelectric potential, which is as approximately 10 times bigger that the kinetic energy ^[16], depending of the position inside the QD and the carrier, (as seen in Fig. 8 below), which is small in InAs/GaAs QD. As in this latter system, an anti-crossing is present around 13 T between the states h7 and h8, it is important observe that the energy of all the states is similar.

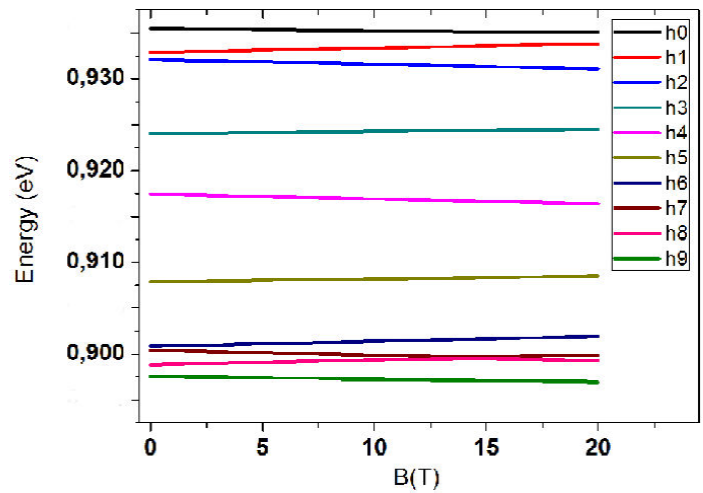
Figure 5 Carrier energy for the first 10 states of holes in GaN/AlN QD’s, as a function of the magnetic field B. Zeeman splitting is very small indicating strong confinement caused by the intrinsic piezoelectric potential. 

The energy levels of the electrons have a very similar behavior shown by the holes, as seen in Fig. 6. It is important to note the bands are almost superimposed, showing a small effect of the magnetic field compared to the strong intrinsic piezoelectric field. The states e0-e1, e2-e5, e6-e7, and e8-e9 are degenerated in B=0, but it can be seen that those degenerated states fall down when the magnetic field increases.

Figure 6 Carrier energy of electrons for the first 10 states of GaN/AlN QD’s varying the magnetic field B. Strong confinement by the piezoelectric potential is also observed. 

3.3 Impurity in QD

As mentioned before, negative or positive impurities were included in both QD’s systems, which correspond to a donor or an acceptor respectively. They were placed at half the maximum height, with x=y=0.

Table I shows the carriers energies in the different QD’s systems considering the cases with and without impurities, the eigenvalues of Eq. (2). As it is observed, when the impurity is negative the carrier energy of the electrons for both systems decreases, with respect to the case without impurity. This is because the potential of the negative impurity repels the electrons, decreasing the effect of confinement, and in consequence its energy. On the other hand, the positive impurity attracts the electron, increasing the confinement effect and its respective energy. It happens the opposite to the holes, that is, the negative impurity decreases the carrier energy and the positive impurity increases it.

Table I Carrier energies for the different quantum dots with and without impuritites. Energy is given in eV. 

System		InAs/GaAs		GaN/AlN
carrier		electron	hole	electron	hole
Type of Impurity	State	e0, e1, e2, e3	h0, h1, h2, h3	e0, e1, e2, e3	h0, h1, h2, h3
		1.0135	0.073539	2.8574	0.93286
No impurity		1.0449	0.073539	2.8961	0.93210
		1.0463	0.070252	2.8967	0.91746
		1.0467	0.070248	2.9330	0.90042
		0.9824	0.042249	2.7747	0.88951
Negative		1.0036	0.042246	2.8302	0.88854
		1.0042	0.024144	2.8307	0.87564
		1.0281	0.024142	2.8721	0.85989
		1.0549	0.13066	2.9321	0.97667
Positive		1.0800	0.13066	2.9575	0.97609
		1.0804	0.11111	2.9585	0.95977
		1.1067	0.06831	2.9879	0.94119

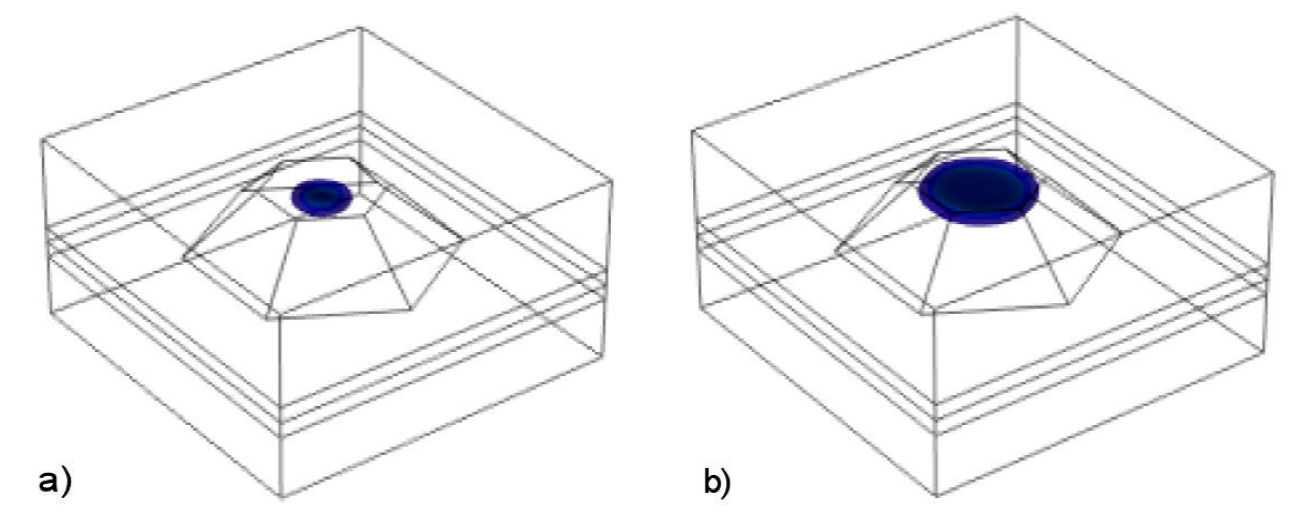
Figure 7 shows a lateral view of the probability density of the ground state of electrons and heavy holes, without and with both types of impurities in a InAs/GaAs QD. It can be observed (Fig. 7a) that for the holes the charge distributions are slightly changed when the negative impurity is added, since they are strongly confined on the bottom of the QD and the impurity potential is not strong enough to deform the distribution. On the other hand, the repulsion of the positive impurity increases the energy of the holes and these are now confined into the region where the potential has a maximum energy, in this case, near of the top of the QD.

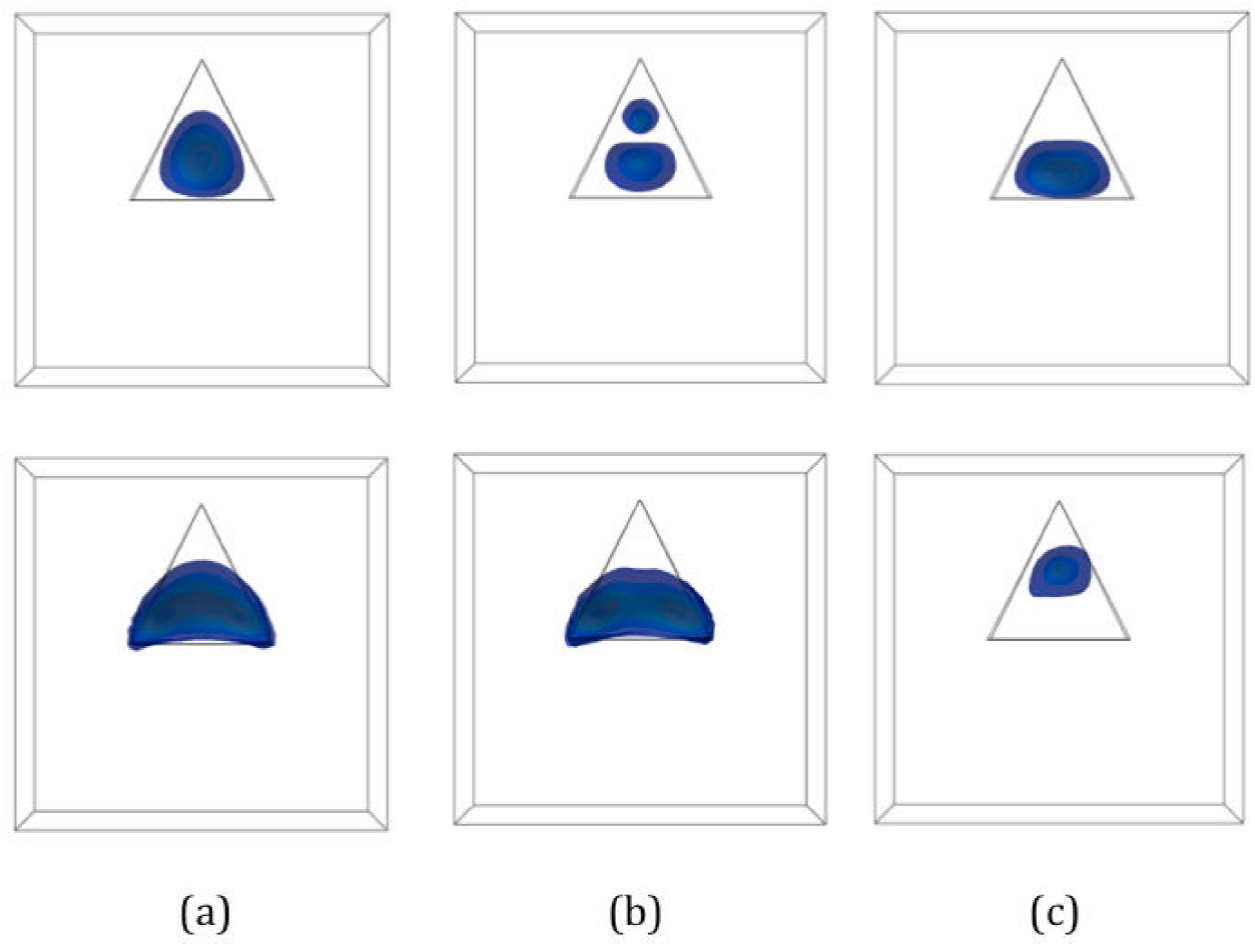
Figure 7 Lateral view of probability density isosurfaces for the first states for electrons (first row) and holes (second row) in InAs/GaAs QD’s: (a) without, with, (b) negative and (c) positive impurity. Calculated with B = 0. 

On the contrary, electrons spread on the QD, such that a negative impurity splits the distribution in two lobes (Fig. 7b) while the positive impurity creates a spherical well potential with leads to a complex competition between the confinement and the strain, causing the wavefunction to be confined at the bottom of the QD. This redistribution of the wavefunctions may affect the response of the QD. In the Table II several matrix elements involving the states e0, h0 and h1 are shown. These matrix elements play an important role in the analysis of emission spectra, for example, since they are related to the rate transitions in the dipole approximation. The matrix element represents the probability transition of the electron in the conduction band to the valence band with the emission of a photon through the coupling of an external electric field, i.e., a larger matrix element indicates that is more likely a emission, if the electric field is parallel to the corresponding direction x, y or z. Small differences alons x and y are due to of the anisotropy of the strain for the cubic system while for both pyramids the z we found a significant increase. Changes of up to one order of magnitude can be found in the arsenide, as shown in the first three columns. The matrix element <e0|z|h0> is larger when a negative impurity is included, confirming that electrons are more strongly confined.

Table II Matrix elements for the state e0, h0 and h1 considering a negative, positive and without impurity 

	InAs/GaAs			GaN/AlN
Matrix element	Without impurity	Negative impurity	Positive impurity	Without impurity	Negative impurity	Positive impurity
<e0|x|h0>	0.0101	0.1527	0.0185	2.2750×10−3	2.48-0×10−4	1.2141×10−2
<e0|y|h0>	0.0028	8.88 × 10−4	9.55×10−4	1.5610×10−4	4.1569 × 10−4	5.4893×10−5
<e0|z|h0>	0.1480	0.1527	0.0381	1.7845	2.5315	1.7720
<e0|x|h1>	0.0021	0.0013	0.0062	4.0588×10−5	3.8031×10−6	4.0140×10−4
<e0|y|h1>	0.0049	0.0080	3.1630×10−4	1.4668×10−5	2.3963×10−6	5.0957×10−5
<e0|z|h1>	0.1445	0.1501	0.0111	3.687×10−2	1.288×10−2	7.9369×10−2

In the case of the GaN/AlN system, the addition of impurities does not modify the probability density, this is again due to the fact that the piezoelectric field is very intense and creates confinement potentials in very specific areas, for the holes this zone is located below the QD within the wetting layer, and for the electrons it is located in the upper part of the QD (as reported in Ref. ^[16]). Figure 8 shows the probability density of electrons and holes calculated with zero magnetic field. Results are similar to those reported in previous works ^[1,5], where impurities are not included, confirming their almost null effect.

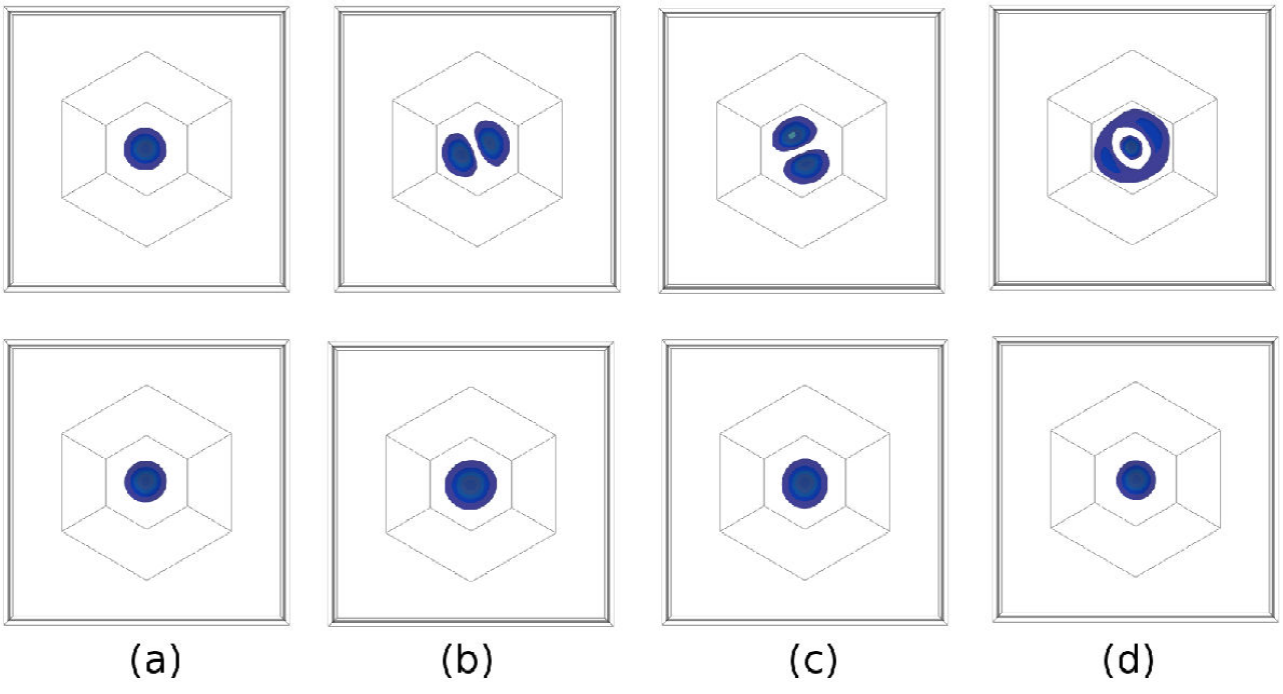
Figure 8 Top view of probability density for the first four states for electrons(up row) and holes(down row) in GaN/AlN QD’s: (a) e0/h0, (b) e1/h1, (c) e2/h2, and (d) e3/h3. Calculated with B = 0, considering a negative impurity. 

Table II also shows the matrix elements for the GaN/AlN QD’s. We can see that the probability is very small along the x and y direction, this is due the strong confinement of the carriers. But the inclusion of the negative impurity increases the value of the matrix element, because the confinement of the holes is reduced.

Finally we can see the effect of the position of a negative impurity on the electronic probability distribution inside the QD. In the Fig. 9(a) the impurity is at the center of the QD, with an energy of 2,4777eV, meanwhile in Fig. 9(b) is at the top of the QD, in this case the energy is 3.0062 ev. It is clear that the wavefunction in the latter case suffers a scattering due the repulsion between chargers.

Figure 9 Effect of the position of the impurity in the wavefunctions in GaN/AlN QDs, with a negative impurity at (a) x = 0, y = 0, z = 2 nm and (b) x = 0, y = 0, z = 4 nm. 

4. Conclusions

The magnetic field provides a form to change the energy of the carriers. However, should be taken care at high values where anti-crossings appear, which may cause a disadvantage. We have observed the Zeeman splitting in both carriers as expected. However, the energy of the carriers in the system GaN/AlN presents only a small change, due to the strong piezoelectric confinement in this system, as compared with the InAs/GaAs QD’s, for which the effect is weak. Thus, energies of the InAs/GaAs QD’s change easily with the inclusion of the magnetic field, conversely the energy of the system of nitride QD it remains almost constant as the magnetic field increases.

Another form to change the carrier energy is through the inclusion of one impurity. Its effect depends on where it is located and on its type. As observed in the InAs/GaAs system, the probability density of both carriers without the impurity spreads almost around the entire interior of the QD. When a negative/positive impurity is inserted, its potential attracts/repels holes, or in opposite form, to the electrons. This causes a redistribution of the carriers, i.e., the effect of the impurities is similar to apply a low electric field ^[31-33].

The counterpart, the GaN/AlN QD system, presents a strong intrinsic confinement due to the piezoelectric field. The probability density is not affected by the inclusion of the impurity, since the effect of the impurity is small compared to the confinement. However, if the impurity is located close to the regions where electrons or holes are confined, it affects the distribution of one of the carriers only and the confinement energy is slightly changed, which makes the GaN/AlN QD’s less sensitive to the effects of the impurities, as long as these are not located in the zones of maximum confinement of the carriers. This is confirmed with the matrix elements, which change accordingly.

The magnetic field present a feasible way to modify the confinement energy and the probability density of the carriers in zinc-blende systems, which could be used in applications as quantum computing. The effect of the impurities is also important because it could explain some shifts in the photoluminescence spectrum in the quantum dots ^[25,34-36].