1. Introduction

The interaction of a strong laser field with atoms and molecules resulted in a variety of phenomena ^[1,2]. Because of that, particular attention has been dedicated to this “problem”, both theoretical and experimental ^[3,4]. The theoretical approaches are based on the numerical solution of the time-dependent Schrodinger equation (TDSE) ^[5,6], the strong-field approximation (SFA) ^[7], and the semiclassical model for the strong-field ionization ^[8].

In this paper, we consider the case when the conditions for the semiclassical approximation are satisfied (low frequency and field intensity in the range of I>1014 Wcm-2). The first one who introduced this approach was Keldysh ^[9]. It is also well known by Keldysh parameter, γ, (γ=(ω2Ip/F, where ω is the angular frequency of the laser field, Ip, is the ionization potential, and F is the field strength in Wcm-2, introduced to separate two regimes of photoionization: tunneling and multiphoton. For γ≪1, the tunneling is dominant, while for γ≫1 multiphoton. Here, it is interesting to note that according to ^[10] tunnel and multiphoton ionization in strong laser field co-exist as two channels of ionization. Keldysh’s theory is improved by Perelomov, Popov, and Terentev (PPT) ^[11], and later extended by Ammosov, Delone, and Krainov (ADK) ^[12]. The ADK theory is one of the most used ones.

Here we will deal with elliptical polarization of the laser pulses. Compared with the case of linear (the most often used), the electron kinematics in elliptically polarized laser field are quite different. With elliptical polarization, an emitted electron is pulled away transversely because of the additional polarization direction and its trajectory becomes elliptical, reducing the probability of recolliding with its parent ion.

The quasistatic tunneling theory in an elliptically polarized laser field for a small Keldysh parameter has been very successful in explaining experimental data ^[18]. However, as the Keldysh parameter increases to the intermediate range, it was shown that the ADK theory quantitatively deviates from the experimental results ^[19]. The reason for this deviation lies in the fact that above mentioned theory is based on the independent particle (single active electron). So, in order to avoid this problem, it is necessary to extend the quasistatic tunneling theory with the presence of electron interaction in the system ^[20,21].

Zon ^[22] introduced the idea ofinelastic “tunneling”, whereby the parent ion can be left in an excited state following the ionization of one electron. Release of the electron through the process of photoionization may leave the residual positive ion either in the ground state or in an excited state of higher energy in which at least one electron is promoted to some empty orbital. Excitation is entirely caused due to electron-electron interaction and probes the electron correlation in the ground and final state.

In this paper, we introduced the excitation as well as electron-electron correlation, and as a result we obtained the formula for transition rate and energy distribution for the simultaneous core ionization and core-excitation of a helium atom (K-2Vi process) in an elliptically polarized laser field. We compared our results with those obtained experimentally and showed that ellipticity plays an important role and that inclusion of additional processes significantly influences the transition rate, as well as the energy distribution of the ejected photoelectrons ^[23,24]. We observed a non-relativistic domain in which the influence of the magnetic field can be neglected ^[23]. That is reason why the transition rate and the energy distribution of the ejected photoelectrons are determined by the electric component of the laser field.

2. Theorical Concept

One of the most used theory for description of the ionization process of atoms in a laser field, the ADK theory, is based on the tunneling of an electron through the suppressed potential barrier of the combined atomic field and the external electric field. For a monochromatic, elliptically polarized laser field, the atomic tunneling ionization rate can be calculated using the following formula ^[12]:

where n*=Z/2Ip is the effective quantum number ^[25], F is the field strength in Wcm-2, Z is the ion charge, a(x)=e-xJ0(x), J0(x) is the Bessel function of imaginary argument and a(x) is a monotonically decreasing function: a(0)=1, a(x)∼(2πx)-1)/2 for x≫1. The parameter ε is the polarization vector in the interval 0≤ε≤1 which for ε=0 describes the linearly, and for ε=±1, circularly polarized wave.

But, this theory neglected many aspects of the mentioned process, such as correlation ^[23]. But, it is fact that an atom with more than one electron is a complex system of mutually interacting electrons moving in the field of the nucleus. Because of that, we reported theoretical calculations concerning electrons correlation. Additionally, according to ^[26], parallel with ionization there is an excitation process. So, based on that, we modified the aforementioned formula by treating the ionization rate as a cumulative contribution of simultaneous processes, ionization and excitation, as a sequence of events.

We calculated a helium (and helium like) atoms within 1014-1015 W/cm-2 range of the laser intensities, with elliptically polarized pulses and without recollision. The atomic system of units e=me=ℏ=1 is used throughout this paper ^[27]. We assumed that the electron velocity is small compared to the speed of light and applied a nonrelativistic calculation.

At the end, based on obtained formula, we formulated the expression for the energy distribution. As we said, we considered the general case of a monochromatic wave, with elliptical polarization, F(t)=F(e⃗xcosωt±ε⃗e⃗ysinωt). In the previous inline equation, ε is the polarization vector, ε⃗=e⃗xcos(ξ/2)+ie⃗ysin(ξ/2), where the ellipticity parameter, ξ, describes all degrees of elliptical polarization. This parameter varied in the range π/2≤ξ≤π/2, and for ξ=0 and ξ=π/2 correspond to linear and circular polarization, respectively.

We started with the adiabatic Landau-Dykhne approximation ^[28] of the saddle-point method for estimating the time integrals in the quantum theory of transitions in an external AC field. In order for this approximation be valid, it is necessary that the photon energy of the was small compared to the ionization potential Ip(t). If this condition is fulfilled, according the aforementioned approximation, the transition rate between the initial bound state i with energy Ei(t) and final, continuum state f with energy Ef(t) is given by the well-known Landau-Dykhne formula ^[9,29] (with exponential accuracy):

i.e. the transition rate Wif, is the exponential function of the imaginary part of the action, S(τ). Here, the final energy is expressed as Ef(t)=(1/2)[p-((A⃗(t)/c)]2, where A⃗(t) is the vector potential of the external electromagnetic field, A(t)=-cF/ω[sinωτ-εcosωτ], c is the speed of light (c=137.06 in atomic unit), τ is the complex turning point in the plane of complex time and p is the generalized momentum of the ejected electron. In general, the final energy can be written as Ef(t)=(1/2)[p-((A⃗(t)/c)]2+U(r) ^[30], where last term denotes the electron’s energy in the core field.

We applied the described formalism on a two-electron transition in a helium (and helium like) atoms after the absorption of a single photon. Also, we analyzed the photoelectron distribution from K-2V states that correspond to simultaneous 1s ionization and 1s→ valence excitation (1s→2s or 1s→2p excitation), as well as the energy distribution of the ejected photoelectrons.

We firstly considered the excitation process. Simultaneous excitation ionization is only possible due to electron-electron correlations ^[31]. To introduce it into transition’s formula, we included the correlation effect into the initial energy, which now can be written as:

where the second term describes the correlation effect ^[32]. Here, we omit the Stark shift of the initial binding state. Applied laser field causes a shift of the atom’s energy levels and this displacement of the energy level is determined by expression Ist=1/2(αN-α1)F2 where αN is the static polarizability of the atom and α1 of its ion ^[33]. Also, we included the ponderomotive potential which correlates to the oscillating movement of charged particles in the final expression for the initial energy:

Now, we incorporated excitation of the second electron by modifying the final energy, Ef(t), with the energy’s terms which describes excitation processes, E±=Ip+J(1s,2s)±K(1s,2s) ^[34], and the Coulomb interaction, Ec, ^[35], where the terms J(1s,2s) and K(1s,2s) represent the Coulomb repulsion and the exchange integrals respectively ^[36]. The lower sign describes the state of lower energy, thus making the configuration 1s2s of the triplet state lower in energy than the singlet state. So, the final energy now has the following form:

For the correlation of two electrons, the Coulomb repulsion and exchange integrals have the following form: J(1s,2s)=17/81ZEh, K(1s,2s)=16/729ZEh, (Eh is the energy of a two-electrons atom given by the formula Eh=(2Z2)/n2) ^[36]. Additionally, the Coulomb interaction is described as Ec=(2n2+∣m∣+1)/η2Ip ^[37], where η is the parabolic coordinate, n2 is parabolic and m is magnetic quantum number. With all aforementioned, the resultant energy for the final state becomes:

In Eq. 6, τ is the complex turning point in the plane of complex time and it can be determined from the condition Ei(τ)=Ef(τ) ^[28]:

We used some simple transformations and Maclaurin expansion in order to express the turning point, τ. The obtained solution for the τ is complex and it has the following form:

here, Ipeff is some kind of the effective energy, Ipeff=2Ip+Z3/(5n2)(4±2/5)-2((2n2+|m|+1)/η)2Ip. It is obvious that it contains correction of the binding energy, Ip, in regard to the electron-electron correlation and the Coulomb interaction effects incorporated through the initial and final energy.

In the interest of calculating the action, S(τ), we substituted Eq. 3 and Eq. 6 into Eq. 2. As a result, we obtained a sum of four terms:

Following Wif∝exp[-2ImS(τ)], we integrated Eq. 9 over the time. After integration, we separated real and imaginary parts and obtained the action, S(τ), in the form:

We would like to note that Eq. 10 strongly depends, among other, on the momentum p of the ejected electrons. The momentum p can be expressed as: p=1/2(Fη-1+1/ηFη-1) ^[37], where η is the parabolic coordinate, η>1/F ^[38]. The momentum is conserved along the classical path, pη=p ^[29] when a system’s total energy is independent of the parabolic coordinate η.

Finally, in order to obtain the expression for the ionization rate we incorporated Eq. (8) and Eq. (10) into already mentioned formula Wif∝exp[-2ImS(τ)]. As a result, the ionization rate with simultaneous contribution of ionization and excitation processes were obtained:

For the sake of optimizing Eq. (11) we introduced the effective Keldysh parameter γ*=ωIpeff as well as the new effective quantum number n**=Z/2Ipeff and obtained:

During our calculation, we supposed that the term p2 affect the ionization rate the most, and for that reason, the terms of pn order, n>2, can be neglected.

Next, we were interested to examine how mentioned effects influence the energy distribution spectra. We started from the expression for the energy distribution spectra ^[40]: W(p∥)=W(0)exp[-(p∥2ω2(2Ip)3/2/3F2)], where W(0) presents considered tunneling ionization rate, Welip for standard and Wie for our case. The exponential part of inline equation describes the energy spectrum of ejected electrons along the polarization direction, and p∥ is the electron momentum along the field polarization direction. Because the energy spectrum of the ejected electrons along the polarization is wider than in the case of perpendicular direction, we chose the energy spectrum of ejected electrons along the polarization direction ^[30]. Combined with the well-known expressions for longitudinal energy of the ejected electron E=(p∥2)/2 ^[40], the energy distribution of the ejected photoelectrons for standard ADK formula can be written as:

while our theoretical result based on Eq. (12), takes the form:

Eq. (13) and Eq. (14) describes the exponential dependence of the energy distribution on the amplitude of the laser field, F, unperturbated ionization potential, Ip, as well as the effective Keldysh parameter, γ*, and the new effective quantum number, n**. Additional terms, which can be seen in the Eq. (14), compared to the standard ADK formula, Eq. (13), are directly related to the included electron excitation process.

3. Results and Discussion

In this section we investigated the ratio between the transition rate and the energy distribution spectra of the ejected photoelectrons, obtained based on our analytical formula for the ionization rate and the energy distribution (Eq. (12) and Eq. (14), respectively) and the standard formula (Eq. (1) and Eq. (13)), for single ionized helium atom, He, Z=1. The calculations were made for the linearly, circularly and elliptically polarized laser pulses obtained by Ti:sapphire laser which provides pulses of a wavelength λ=800 nm (ω=0.05696). Additionally, we assumed that the ejected photoelectrons have the initial momentum, p, p≠0.

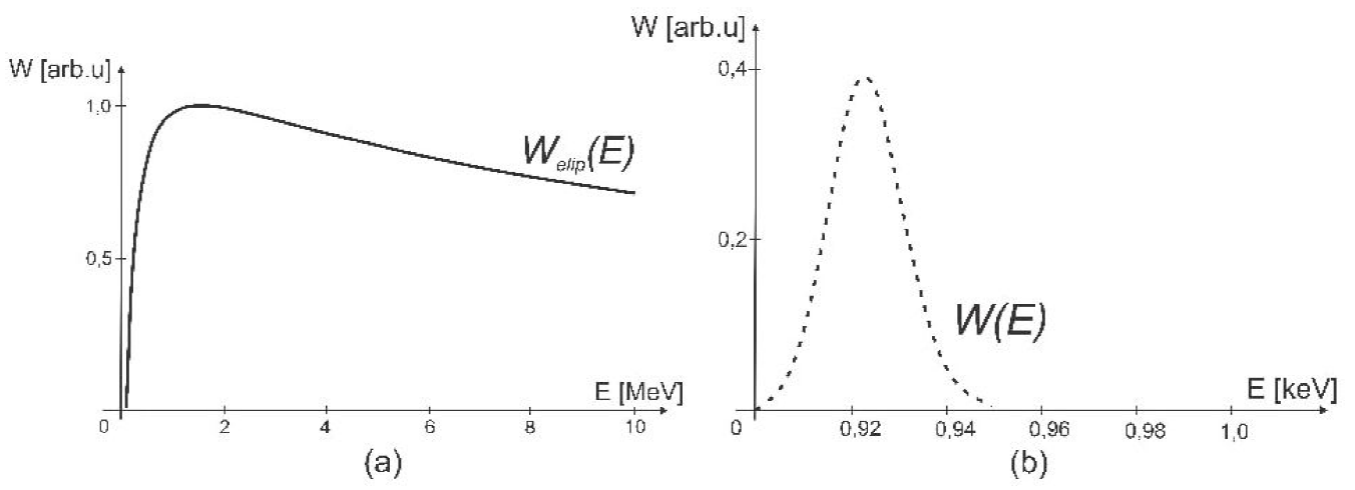
We started from the comparative review of the energy distribution spectra obtained based on the standard ADK formula, Eq. (13), (left plot) and our formula, Eq. (14), (right plot), for limiting case of the laser field polarization, ε=0, which corresponds to the linearly polarized laser field. In order to present the energy distribution, we transformed the intensity axis into units of energy. In a limited case, the energy shift of the continuum is equal to the ponderomotive energy, the cycle averaged kinetic energy of an electron in a laser field, ΔE∞=Up. For a peak intensity, I, in Wcm-2 and wavelength, in μm, the ponderomotive energy can be estimated in electron volts (eV) using the relation 9.33×10-14Iλ2.

From Fig. 1, it can be seen that both theoretical curves are qualitatively similar. They continuously increase, reach prominent peak and then decrease, but on the different energy range. The theoretical ADK curve reaches a peak at E∼1MeV, while our at around E∼0.96 keV. After reaching the maximum the ADK curve gradually decreases, while our decreases considerably faster in comparison to the ADK.

Figure 1 Comparative calculation of the energy distribution of photoelectrons (in arbitrary units) versus energy, for the limiting case of an elliptically polarized laser field, ε= 0, obtained based on: a) the ADK theory, We _lip (E), b) our formula, W(E). The parabolic coordinate is set on η= 20. 

One can observe the shift to the lower intensity of the curve obtained based on our formula, which is in accordance with^[41] where this movement to lower field intensity was distinguished. Also, its energy range is significantly narrower. This is in accordance with ^[42]. The ADK curve lies above our curve by a few orders of magnitude. Significant deviation of the ADK curve in comparison to experimental results was observed in ^[43], where it was concluded that ADK theory often overestimates the ionization rate ^[23,43]. This is in accordance to our results for the same range of intensities. Also, our curve follows the trend of the experimental data and has a similar shape to ^[44] .

Next, we repeated procedure for the case of a circularly polarized laser field, ε=1. As a result, we obtained the line graphs on Fig. 2. As in previous, we gave the comparative review of the ADK and our curve.

Figure 2 Comparative calculation of the energy distribution of photoelectrons in a circularly polarized laser field obtained based on: a) the ADK theory, We _lip (E), b) our formula, W(E). The parabolic coordinate is set on η= 20. 

Unlike the previous, Fig. 2 shows significantly different behavior of the observed theoretical curves. For both curves is common that they decline after reaching their maximum values. The difference between these curves lies in the fact that the ADK curve decreases slowly, compared to ours which approaches to the energy axis on about E∼0.94 keV. The ADK curve has a maximum at E∼1 MeV, while our at around E∼0.92 keV and it is obvious that has a defined energy range. For both graphs, under the same conditions, we observed a shift to the lower values of energy. We attribute this shift to additional processes that we considered (electron correlation, excitation), and their influence on tunneling of electron. It is important to highlight that these energies are still above the low energy range which is in accordance to ^[42,45]. It is also important to note that the curves for the case of circularly polarized laser field are a few magnitudes higher that in the case of linear ^[24].

Next, we examined how the ellipticity influences the transition rate and the energy distribution range of the ejected photoelectrons. Figure 3 displays theoretical curves obtained based on our formula for the transition rate, Eq. (12), (left plot) and the energy distribution, Eq. (14), (right plot), for ellipticities in the range of 0.2≤ε≤0.7.

Figure 3 The transition rate as a function of field intensity (left plot) and the energy distribution as a function of energy (right plot) for the different ellipticities. In order from left to right: a) ε= 0:6, ε = 0:5, ε = 0:4, ε = 0:3; b) ε = 0:7, ε = 0:6, ε = 0:5, ε = 0:4. The field intensity varies within the range I = 1 x 10¹⁴ -2 x 10¹⁵ Wcm ^-2 (left plot), while energy E = 0 - 21 keV (right plot). The parabolic coordinate is fixed on η= 20. 

As we said, on the left graph, we considered transition rates curves, in the given ellipticity range. For the higher values of ellipticity ε=0.6, 0.5 curves are symmetrical with very prominent peaks, but for the smaller, ε=0.4, 0.3 they become asymmetrical and their peaks are less prominent. Also, with the decrease of ellipticity, curves shift to higher value of the field intensity, but the transition rate is noticeably smaller ^[46]. From the first curve on the left with the ellipticity ε=0.6 to the last one with ε=0.3, our curves reach the maximum on the following field intensities, I: 7×1014 Wcm-2, 1×1015 Wcm-2, 1.5×1015 Wcm-2, 2.8×1015 Wcm-2. This is in accordance with ^[47]. In the Fig. 3 (right plot), we presented how the change in ellipticity affects observed energy distribution spectra. It is obvious that the shape of the curves is maintained with the change of ellipticity. For ellipticities until approximately ε=0.4 the laser field is considered to be near linearly polarized. One can observe a rapid shift to lower energies around this value of ellipticity ^[45,46]. Described curve’s behavior is in accordance with experimental investigation by Chen et al. ^[44] and Dietrich et al. ^[48]. Based on all aforementioned, our results are closer to experimental data than those by the standard ADK. Conclusion is that additional processes (which we included in our formula), lead to better agreement between theoretical and experimental results. That is why the behavior of our curves is consistent with ^[23,44,48].

In Fig. 4, we wanted to show how the energy distribution depends from two parameters. First, on left plot, we displayed the 3D graph which demonstrates the transition rate obtained from our analytical formula, Eq. (14), as a function of the energy, E, and ellipticity, ε, while parabolic coordinate η was fixed. Next, on right plot, we fixed ellipticity, ε and showed the 3D dependence from the energy, E, and parabolic coordinate, η.

Figure 4 3D graphs for W(E) as a function of: a) the parabolic coordinate η = 20 - 21 and the energy, E = 4 - 9 keV. Ellipticity is fixed on ε = 0:6, and b) the ellipticity ε = 0:5 - 0:51 and the energy, E = 5 - 21 keV. The parabolic coordinate is fixed on η = 20. 

From Fig. 4 (left plot), it can be seen that 3D curve raises faster for the change of the parabolic coordinate, η. Its peak is prominent and the approximately same value of energy E∼7 keV is kept. For fixed parabolic coordinate (right plot), this effect is even more drastic. It can be seen that a small change of ellipticity affects strongly the energy distribution spectra. In some definite range of the energy, 3D curve raises exponentially until reaching maximum at around E∼10.5 keV, then rapidly decreases, and approaches to energy axis. Also, with increase of ellipticity, the maximum of the energy distribution shifts to higher values of energy ^[46].

From all aforementioned, we can conclude that the photoelectron energy distribution spectra is very sensitive to the parabolic coordinate and ellipticity.

4. Conclusion

In conclusion, by applying a semiclassical model, we observed the tunneling ionization process in an elliptically polarized laser field. We presented results for the transition rate and energy distribution spectra with the contribution of additional processes, such as excitation and electron-electron correlation. The obtained results substantially deviate from the predictions of the ADK tunneling theory. We attributed the difference in results to the electrons correlation and excitation. Related to the influence of laser field polarization on the energy distribution spectra, we showed that it plays an important role.