1. Introduction
More than four decades ago, the possibility of distributing high energy over a large volume to restore broken symmetries of the physical vacuum creating abnormal states of nuclear matter was raised [1]. Very early, it was pointed out that the asymptotic freedom property of QCD implies the existence of a high-density matter formed by deconfined quarks and gluons [2], and the exponential increase of the hadron Hagedorn spectrum was connected with the existence of a different phase [3]. The thermalized phase of quarks and gluons was called Quark Gluon Plasma (QGP) [4], and the evaluations of the required high density showed that it could be reached in relativistic heavy ion collisions [5,6] and several signatures of QGP were proposed. Quarkonium suppression [7], the excess of photons and jet quenching [8,9] were some of them. At this time, it was pointed out the relevance of percolation in the study of the phase transitions of hadronic matter [10,11].
From the experimental side, there were large facilities to study the properties of
large density matter starting by the AGS and ISR, experiments later followed by SPS,
RHIC, and LHC. At SPS already several signatures hinted the onset of QGP formation
[12]. The RHIC data show a
collective elliptic flow which pointed out a very low shear viscosity over entropy
density ratio
On the other hand, the data on quarkonium confirm the validity of combined picture of
a subsequent melting of the different resonances, together the recombination of
heavy quarks and antiquarks at high energy [30-32]. The departure of linear dependence on the
multiplicity of the
On the theoretical side, in addition to the hydrodynamics studies, the Color Glass
Condensate (CGC) approach [38-42] gives a good description of most of the experimental data
and is derived directly from QCD. In QCD, the gluon density
This dense system, called CGC, has a very high occupation number
In high energy physics experiments, the colliding objects move at velocities close to the speed of light. Due to the Lorentz contraction, the collision of two nuclei can be seen as a that of two sheet of colored glass where the color field in each point of the sheets is randomly directed. Taking these field as initial conditions, one finds that between the sheets, longitudinal color electrical and magnetic fields are formed. The number of these color flux tubes between the two colliding nuclei is forming the called Glasma [46], which has been extensively compared with the experimental data.
Another approach to the initial state is the percolation of strings [47-51] which is not so popular as the CGC because
cannot be derived directly from QCD although it is inspired in it, and most of its
results, are a direct consequence of properties of QCD. In this approach, the
multi-particle production is described in terms of older strings stretched between
the partons of the projectile and target. These strings decay into
In string percolation, the basic ingredients are the strings, and it is necessary to know its number, rapidity extension, fragmentation and number distribution. All that requires a model and therefore, string percolation is model dependent. However, most of the QCD inspired models give similar results for most of the observables in such a way that the predictions are, by a large measure, independent of the model used.
The string percolation and the Glasma are related to each other [55]: in the limit of high density, there is a
correspondence between the physical quantities of both approaches. The number of
color flux tubes in Glasma picture,
The observed densities of our world have large differences which expand over many
orders of magnitude, from 10-6 nucleons/cm3 in average in the
Universe to 1038 nucleons/cm3 inside a nucleus and
1039 nucleons/cm3 in a neutron star. The study of the
high-density limit, i.e., the study of de-confinement of quarks and
gluons can be regarded as the place where high energy collision of two bodies probes
the short distances and meets the thermodynamics (many body) of this short distance
limit [56]. The lattices studies
have shown that at low chemical potential
In finite
Note that
Below the critical temperature
which measures the constituent quark masses obtained from a Lagrangian with massless quarks. At high temperature this mass melts, therefore:
Here,
The energy densities resulting from lattice QCD are shown in Fig. 2 (up), indicating that even for
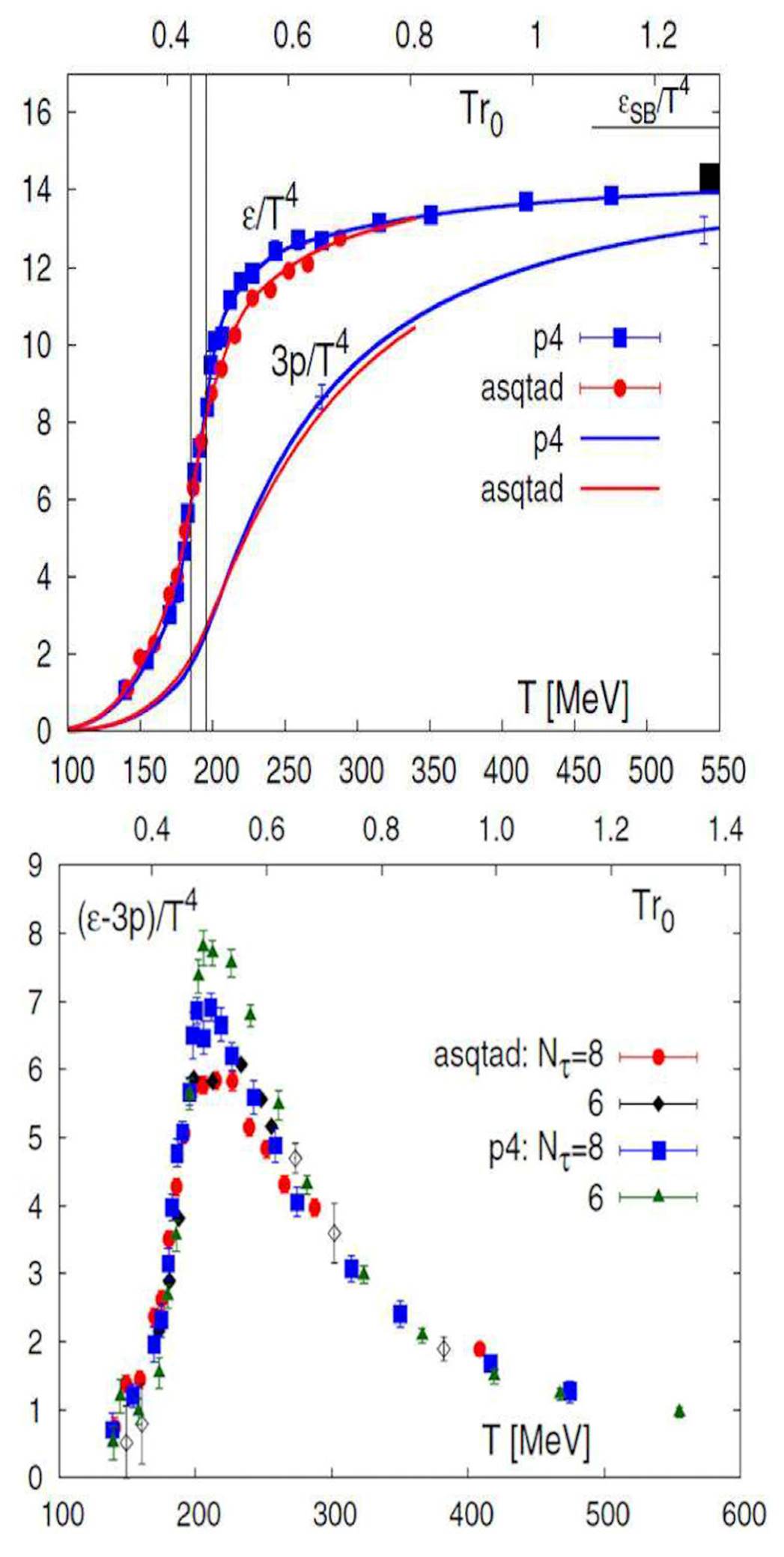
Figure 2 The energy density and the pressure as the function of temperature (up). The energy density shows a sharp rise in the temperatura region 170-200 MeV. The interaction measure calculated using different staggered fermion actions (bottom)[58].
where
Moreover, the trace of the energy momentum tensor:
is
2. Percolation model
Let us distribute small discs of area
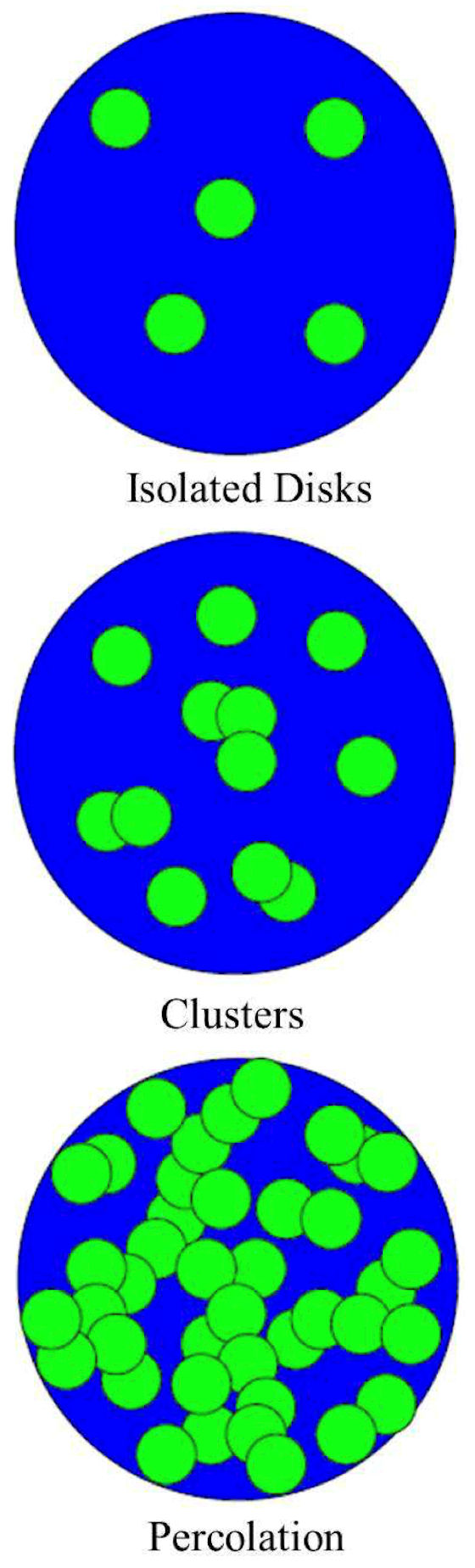
Figure 3 Up panel: Disconnected discs, Middle: Cluster formation, Bottom panel: Over-lapping discs forming a spanning cluster[56].
The critical density for the onset of continuum percolation is determined by numerical and Monte Carlo simulations, which in the 2-dimensional case gives:
In the thermodynamical limit,
It also gives the total fraction of the plane covered by discs in
where
In SU(3) Gauge theory, spatial clusters can be identified as those where the local
Polyakov loops
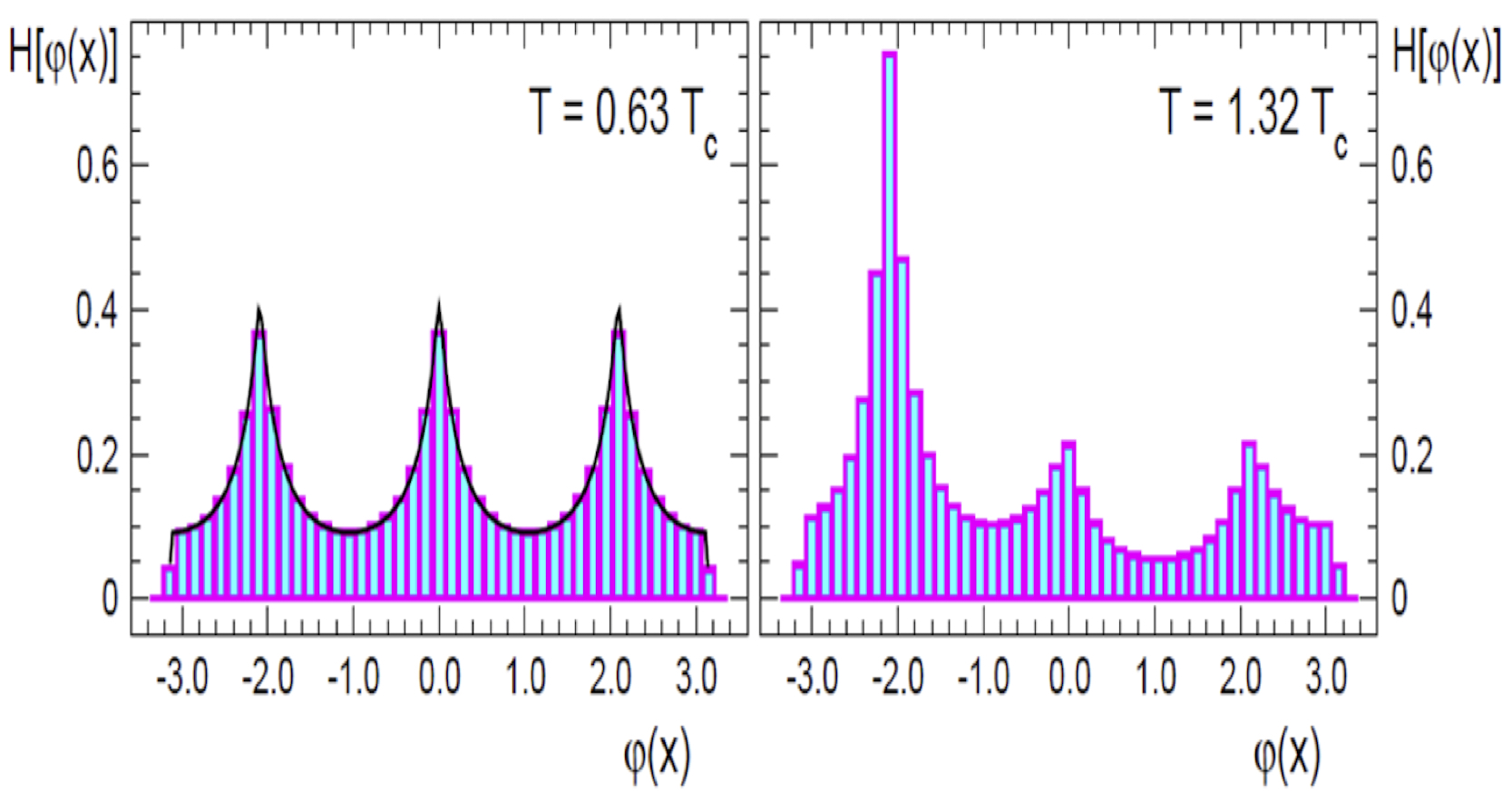
Figure 4 Histograms for the distributions of the phase
In high energy collisions, we expect that color strings were formed between the projectile and target partons. These color fields must have a small transverse size due to confinement. In this way, the strings, in the transverse plane, are small discs in the surface of the collisions. As the number of strings grows with energy and centrality degree of the collision, the strings start to overlap forming clusters which eventually percolate. The phenomenological consequences in relation to SPS, RHIC, and LHC, p+p, pA and AA data are the main subject of this brief review. A more extended version can be found in Ref. [66]
3. String percolation
3.1 String models
The basic ingredient of the string percolation are the strings. Despite
differences, most of them coincide in basic postulates as the number of strings
and its dependence on energy and centrality, which is taken from the
Glauber-Gribov Model.We will concentrate in models with color exchange between
projectile and target as the Dual Parton Model (DPM) [67-69], Quark Gluon String Model (QGSM) [70], Venus and EPOS [71]. They are based on the
where
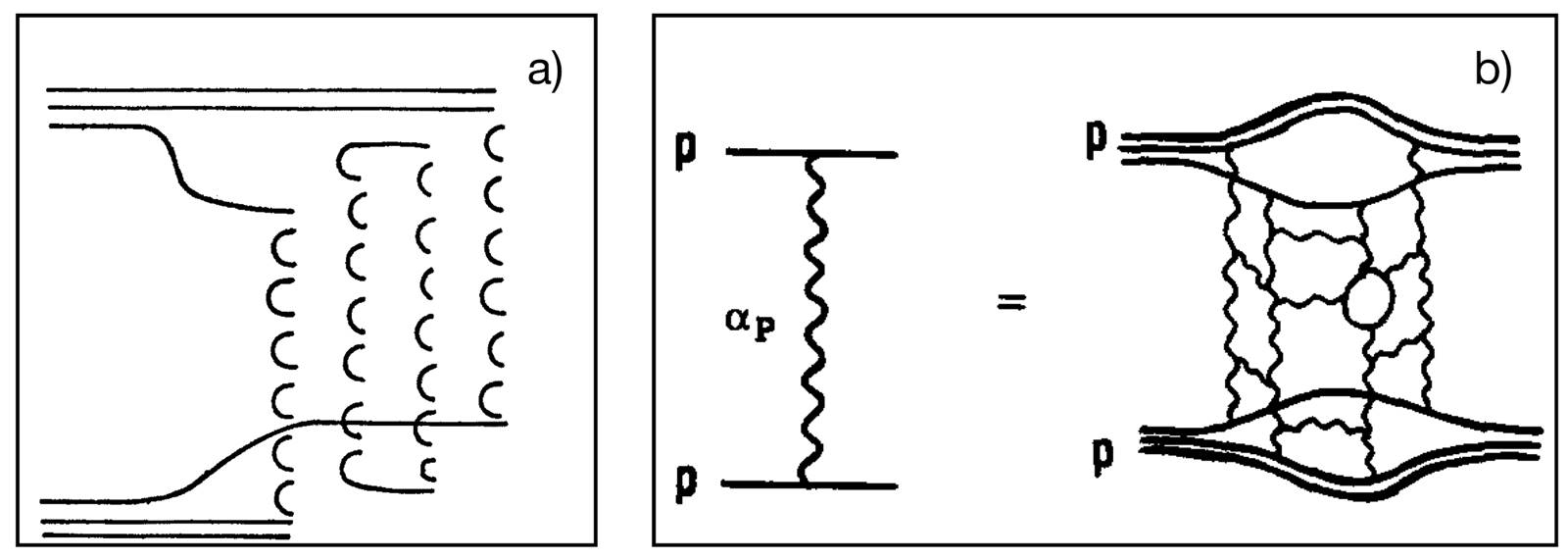
Figure 5 a) Two cut Pomeron diagram (four chain) for proton-proton collisions. b) Single Pomeron exchange and its underlying cylindrical topology. This is a dominant contribution to proton-proton elastic scattering at high energies [67].
where
The momentum distribution used for the valence quarks, valence diquarks, sea
quarks and antiquarks are
where
where:
and g is the coupling of the pomeron to the proton,
The rise of
where N is the mean multiplicity production when cutting one pomeron, therefore, the multiplicity distribution is:
where
where
where we have introduced the possibility of having k multiple
scattering in the individual nucleon-nucleon collisions, which was neglected in
Eq.(21). Notice that there is
not any reason to assume that the term proportional to
In the case of pA collisions, the Eqs. (21) and (22) transform into:
where
3.2 String fusion and percolation
As we have said before, at large energy we expect that the strings overlap in the
transverse plane. The transverse space occupied by a cluster of overlapping
strings splits into a number of areas with different number of strings overlap,
including areas where no overlapping takes place. In each area color field
coming from the overlapping strings add together. As a result, the cluster is
split in domains with different color strength. One may assume that emission of
where
and in the overlapping area each string will have color:
The total color in the overlap area will be a vector sum of the two overlapping
colors
Notice that due to the vector nature, the color in the overlap is less than the
sum of the two overlapping colors. This effect has important consequences
concerning the saturation of multiplicities and the rise of the mean transverse
momentum with multiplicity, which we will study in the next section. Thus,
assuming independent emission from the three regions of Fig. 6, we obtain for the multiplicity weighted by the
multiplicity for a single string (
and for the mean transverse momentum squares (we divide the total transverse momentum squared by the multiplicity):
where we have used the property
where the sum runs over all individual overlaps of
The total area can be easily computed in the thermodynamic limit. One finds that
the distribution of overlap strings over the total surface S in
the variable is Poissonian with mean
Finally, we can write for the mean values:
In the rest of this review, these last equations will be used extensively.
3.3 Quenching of the low
The
where E is the external electric field. This equation leads to the quenching formula:
where
which will be used to compute the harmonic of the
3.4 Multiplicity distributions
The multiplicity distributions in the DPM of QGSM in p+p and AA collisions are
given by Eqs. (12)-(13) and Eqs. (21)-(22), respectively. However, as the
energy or centrality of the collision increases one expects interaction among
strings. As discussed before, due to the randomness of the color field in color
space non-abelian field the resulting color field in a cluster of
n overlapping strings is only
where
where:
Here, the parameter
Taking into account the interaction of strings, we can write a closed formula for the multiplicity distribution in AA in terms of the multiplicity distribution of p+p, namely [85]:
where:
and
Moreover, the dependence of the multiplicity on
Notice that here a single parameter
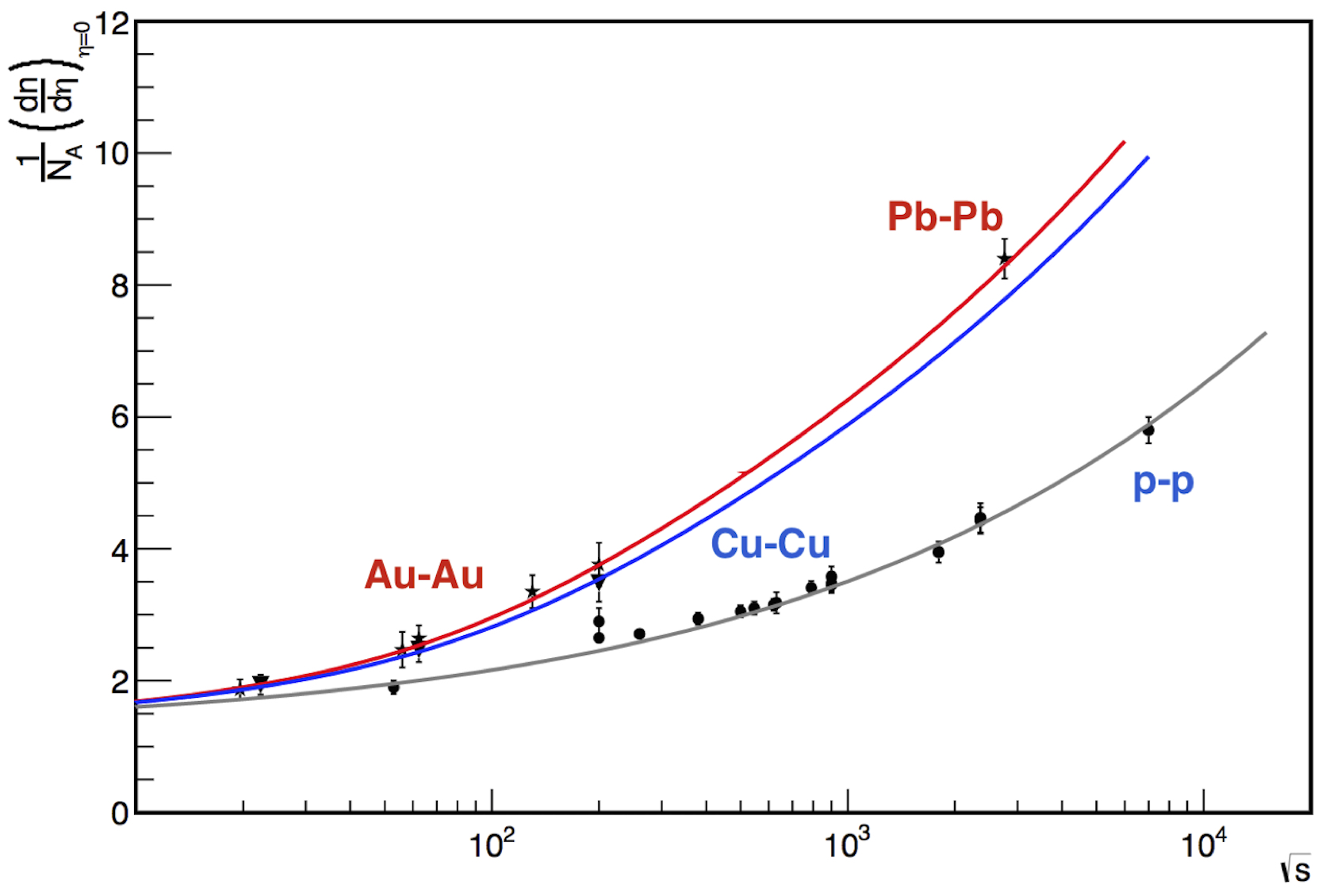
Figure 7 Comparison of the evolution of the mid-rapidity multiplicity with energy from the CSPM and data for p+p and A-A collisions. Lines are from the model for p+p (gray), Cu-Cu (blue) and red lines for Au-Au/Pb-Pb [85-89].
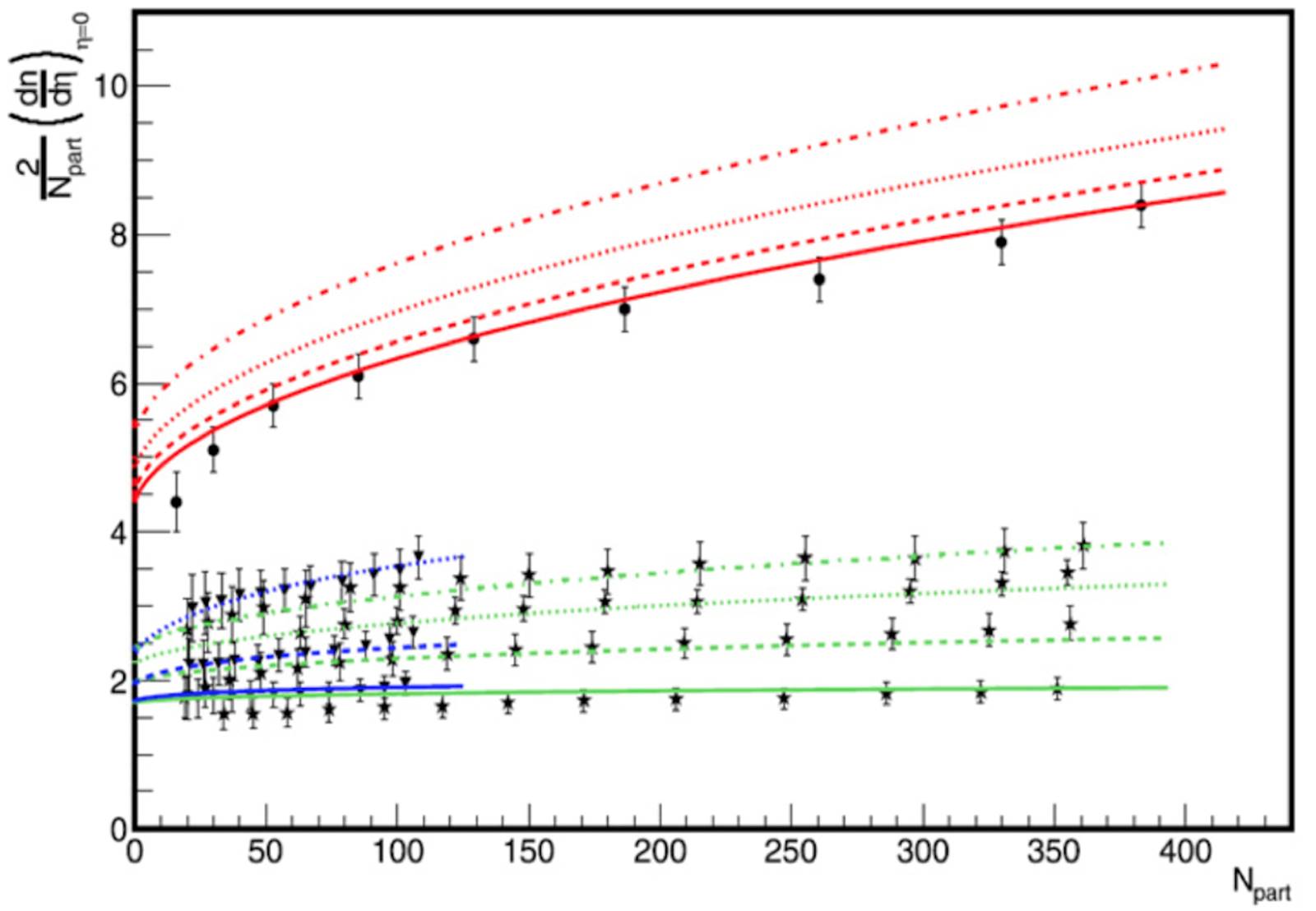
Figure 8 Multiplicity dependence on centrality (Npart). Cu-Cu (triangles), Au-Au (stars) and Pb-Pb (circles). Curves represent the model calculations. Blue line for Cu-Cu, green line for Au-Au and red for Pb-Pb.
The evolution outside the central rapidity region has been studied extensively, extending Eq.(43) to all rapidities [90-95]. The limiting fragmentation property is not satisfied exactly. In Fig. 9, we show the results together with the experimental data for p+p collisions at all rapidities at different energies [94,95] and in Fig. 10 the results for Cu-Cu, Au-Au [96] and Pb-Pb [97] together the experimental data. In Fig. 11, we compare the results [95-98] for d-Au collisions together the experimental data. A good description of all experimental data is obtained.
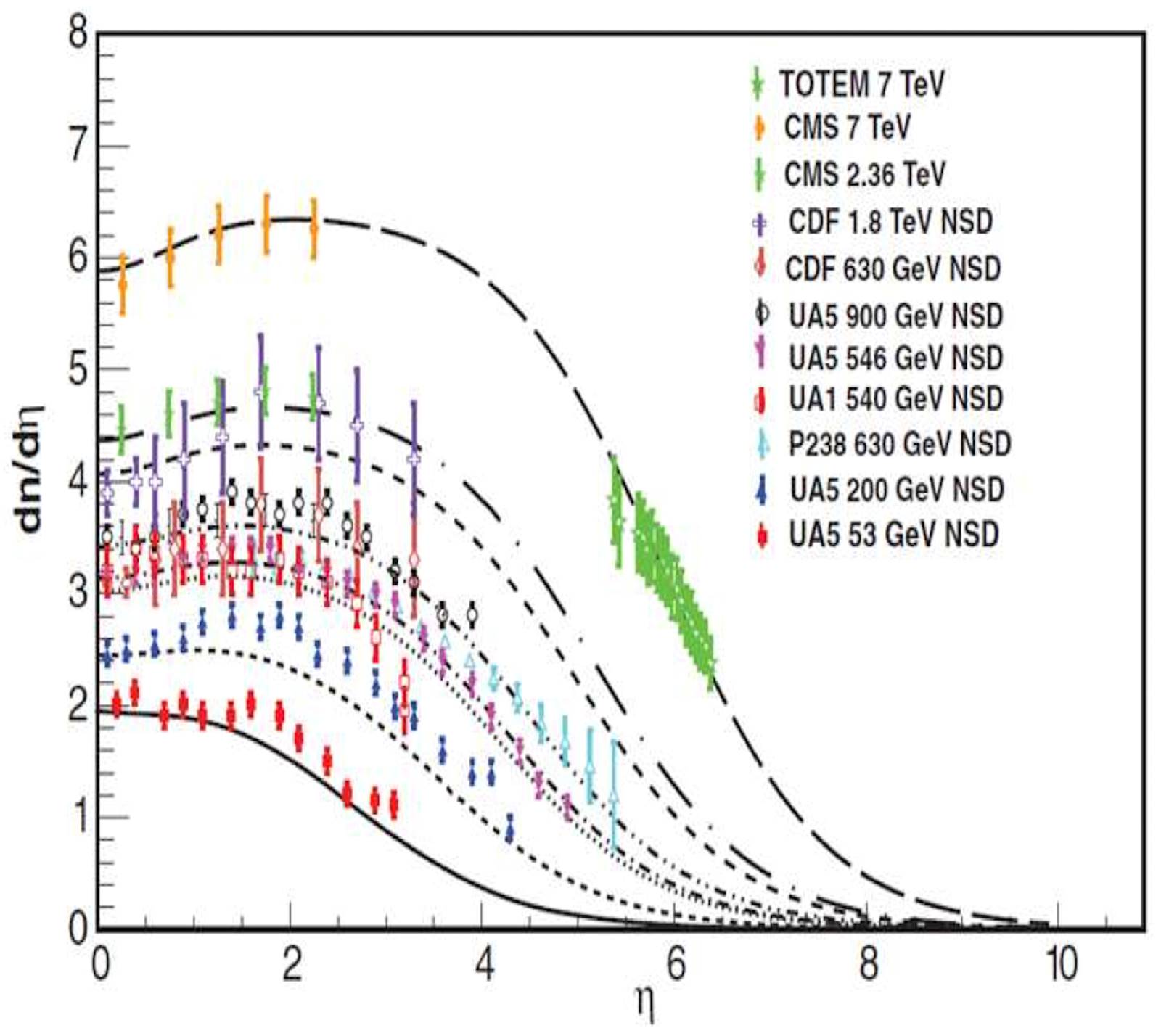
Figure 9 Comparison of results from the evolution of dnch=d´ with dependence on pseudorapidity for p+p collisions at different energies (lines).
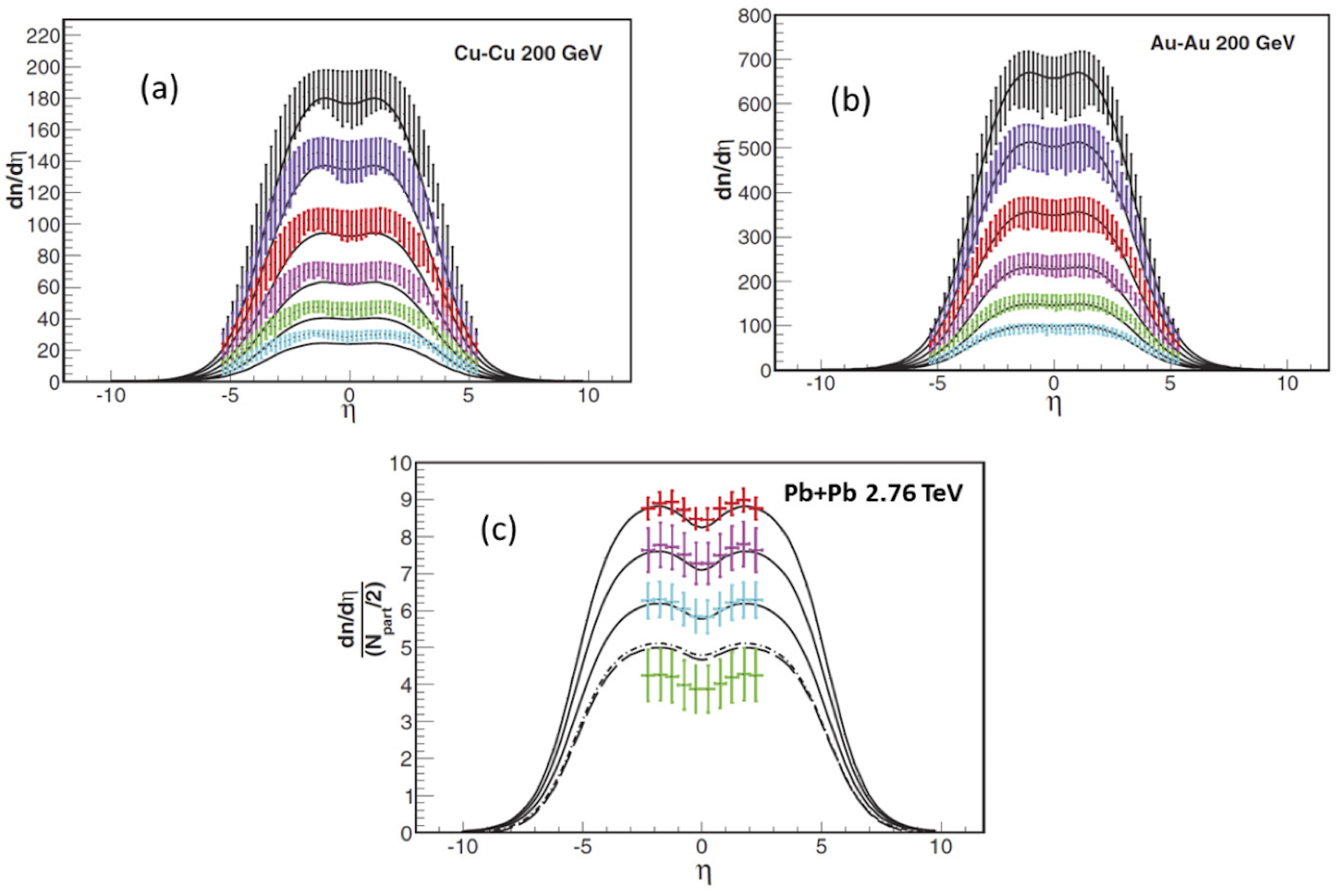
Figure 10 Comparison of results from the evolution of dn=d´ with dependence on pseudorapidity for (a) Cu-Cu at 200 GeV, (b) Au-Au 200 GeV. Plot (c) shows (dnch=´)(1=(Npart=2)) for Pb-Pb collisions at 2.76 TeV.

Figure 11 Comparison of results from the evolution of dn=d´ with dependence on pseudorapidity at different centralities for d+Au collisions at 200 GeV.
The behavior of
3.5 Multiplicity and transverse momentum distributions
Let us start considering a set of overlapping strings, which depend both on the number of strings and the overlapping area, which combine to give an average multiplicity N. We may characterize the different overlaps just by the average multiplicity that combines both the number of collisions and the area. With a lot of overlapping strings N will change practically continuously. We can introduce a probability W(N) to have overlaps with size N in a collision and write the total multiplicity distribution as:
where
The normalization conditions
For the weight function we assume the gamma distribution [99-101]:
where
Transformations of this type were studied long time ago by Jona Lasinio in
connection with the renormalization group in probabilistic theory [102], showing that the only
probability distribution function
Actually, x denotes the inverse of the color field in the cluster, which depends not only on the size but also on the degree of overlapping strings inside the cluster. Assuming that x varies continuously, one can write the total TMD, similarly to the multiplicity distribution case as:
We must realize the normalization condition:
which gives the relation:
Comparing the latter with Eq.(50b), we can make the identification
with
and:
The mean value and the dispersion of the distributions and are:
The distribution is a negative binomial distribution. Eqs.(58) and (59) are superposition of clusters
and
and:
We observe that:
Eqs.(63) and (64) give the distributions for any
projectile, target, energy and degree of centrality and are universal functions
which depend of only two parameters,
At
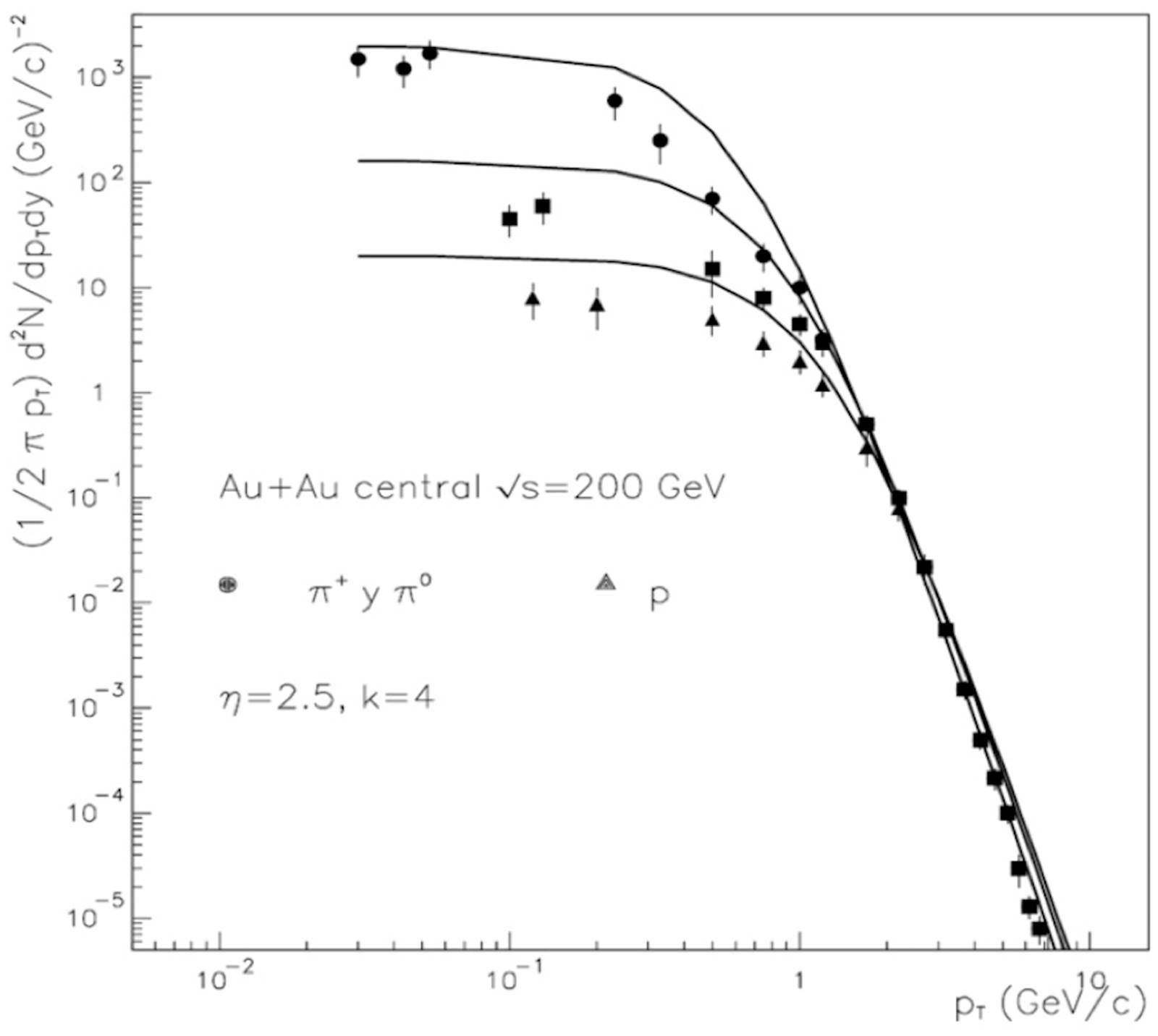
Figure 12 Experimental PHOBOS data on low pt distributions for pions, kaons
and protons along with our results for central Au-Au collisions at
Let us now discuss the interplay of low and high
The normalization on the number of collisions in the latter, essentially
eliminates
Here
which is independent of
and
At low density in the region where decreases with the string density

Figure 13 Ratios for different distributions k/π, p/π in
Au-Au collisions at
The experimental data on p+p in the range
Even though the parametrization describes well the data up to 5-10 GeV/c, most of
the considerations concerning the string fragmentation are only valid for low
and intermediate
The differences between the baryon and meson spectrum are not only due to the
mass differences, which results
In some sense, the coalescence picture of particle production is incorporated in a natural way. An effective way of taking into account these flavor considerations can be seen in Ref.[111]. Very often, it is used an exponential instead of a gaussian for the decay of one string. Indeed, the tension of a cluster fluctuates around its mean value because the chromo-electric field is not constant. Such fluctuations lead to a Gaussian distribution of the string tension [109-113]:
which give rise to the thermal distribution:
where
Now the total TMD is changed and instance of the gamma distribution in Eq (57) a Tsallis type distribution is obtained, namely:
There are several scaling properties found in TMD related to string percolation.
The experimental data for p+p collisions exhibit a universal behavior in a
suitable variable
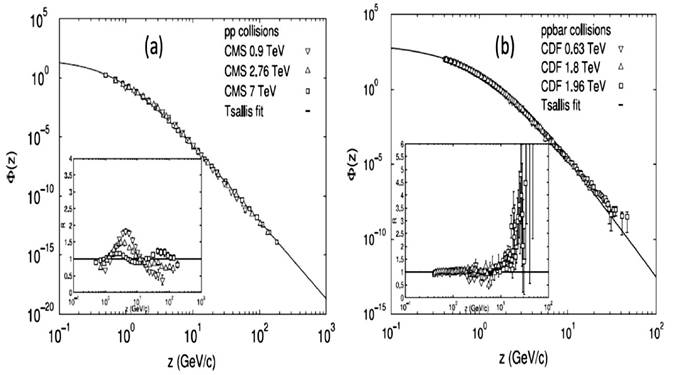
Figure 14 Scaling behavior of the charged hadron pt spectra presented in
z (a) in p+p collisions and (b)
The experimental data on the mean
3.6 Transverse momentum fluctuations
The event by event fluctuations of thermodynamical quantities as the temperature
were proposed as a probe for the deconfined phase. Due to that, the study of the
fluctuations on the mean
and the correlation between the transverse momemtum:
where
and
In Fig. 15, we show the result for
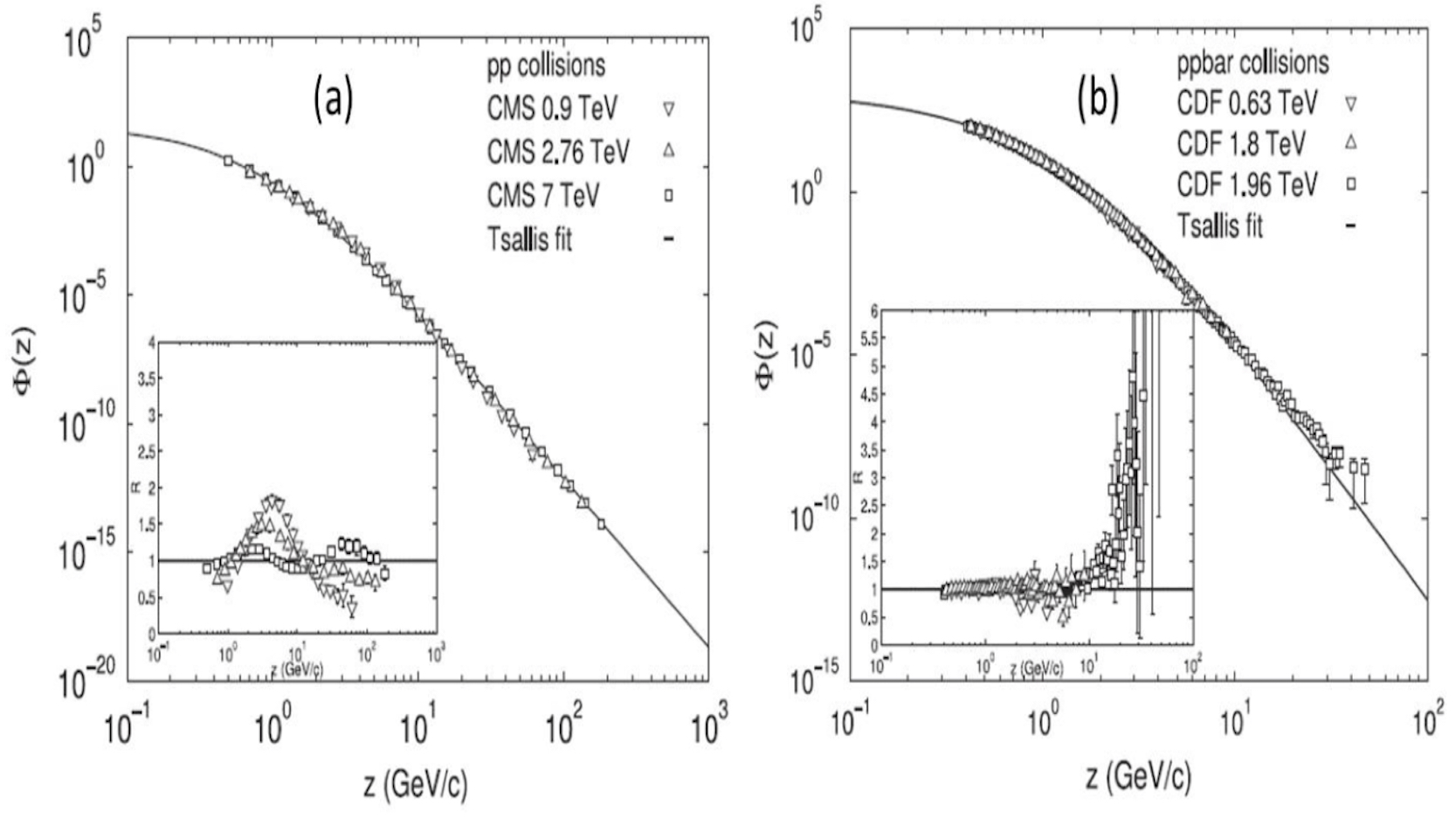
Figure 15 Scaling behavior of the charged hadron pT
spectra presented in z (a) in p+p collisions and
(b)
3.7 Forward-backward correlations
The width of the KNO scaling shape is related to the fluctuations on the number of strings or the number of clusters (independent color sources). This width is also related to the forward-backward (F-B) correlations. These correlations can be described by a linear approximation:
where
Usually, the F and B rapidity intervals are
taken separated by a central rapidity window
where
At low energy, there are not fluctuations in the number of strings,
i.e.,
As the energy or the centrality of the collisions increases,
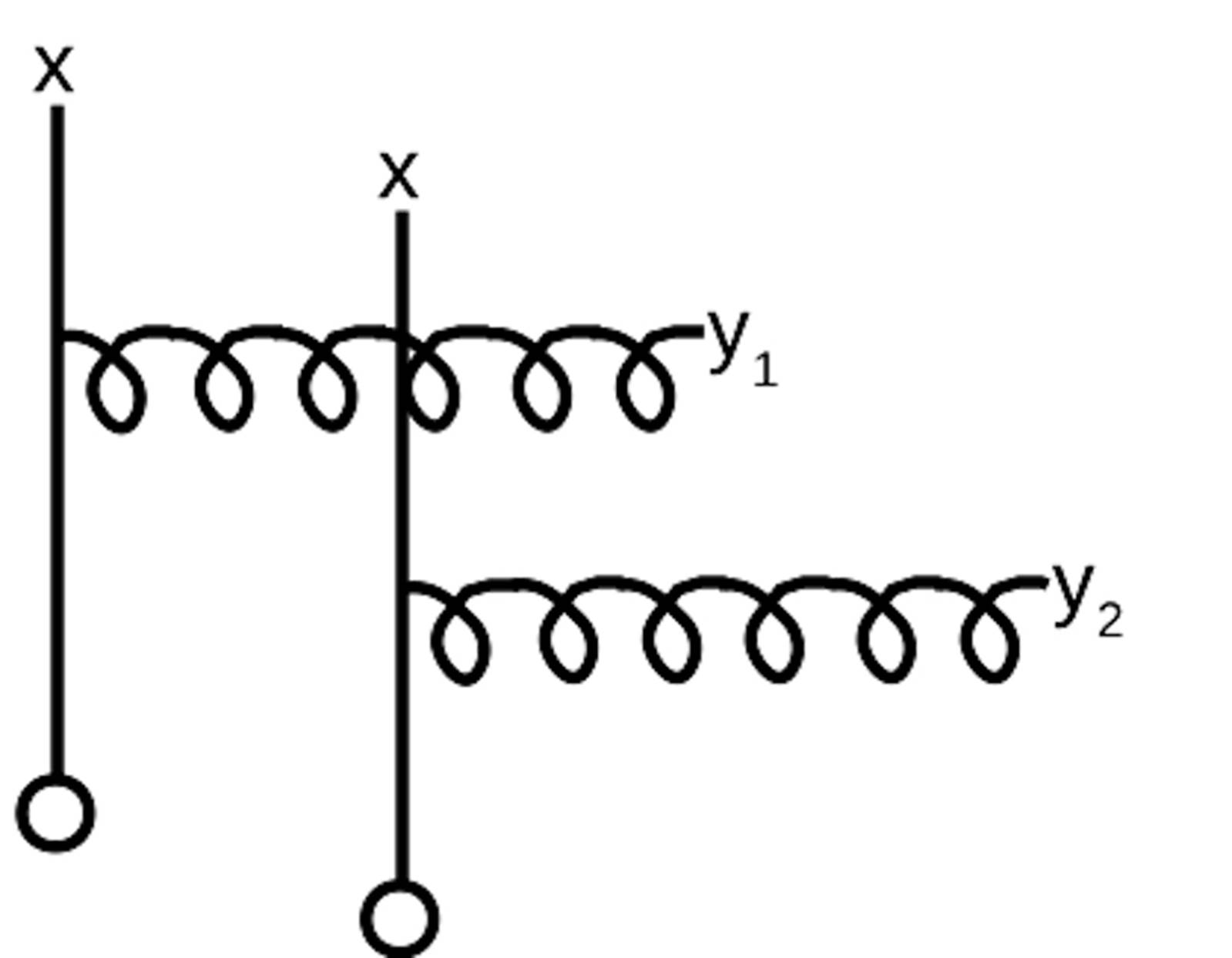
Figure 17 The leading orden diagram which induces long range correlations in rapidity. The source of one nucleus is given by the x and the other by the o. The produced gluon is denoted by the curled line.
where c is a constant independent on the energy and centrality
degree. As the strong coupling constant,
where now
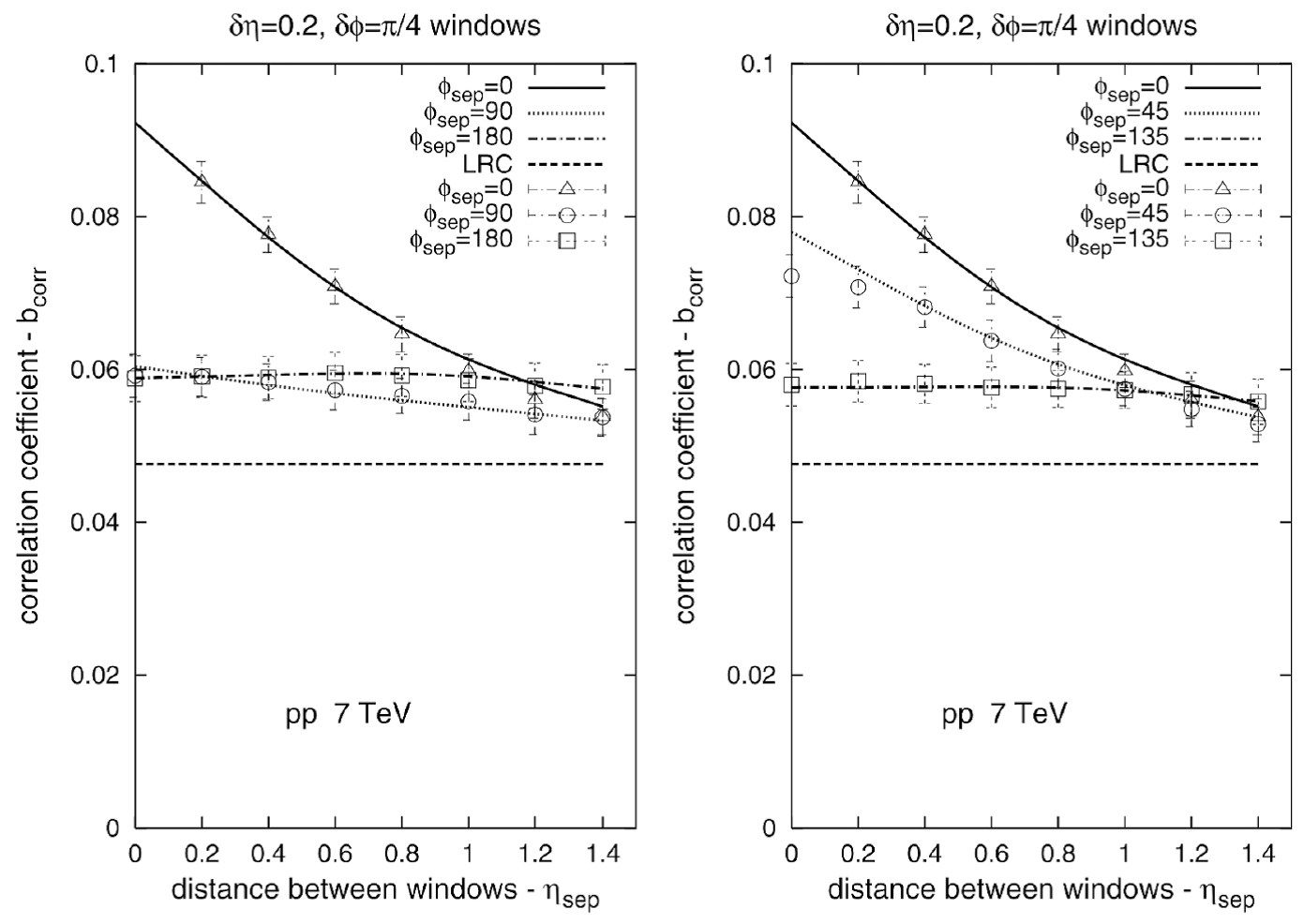
Figure 18 The forward-backward (F-B) correlation coefficient in p+p collisions at 7 TeV from reference [121].
where:
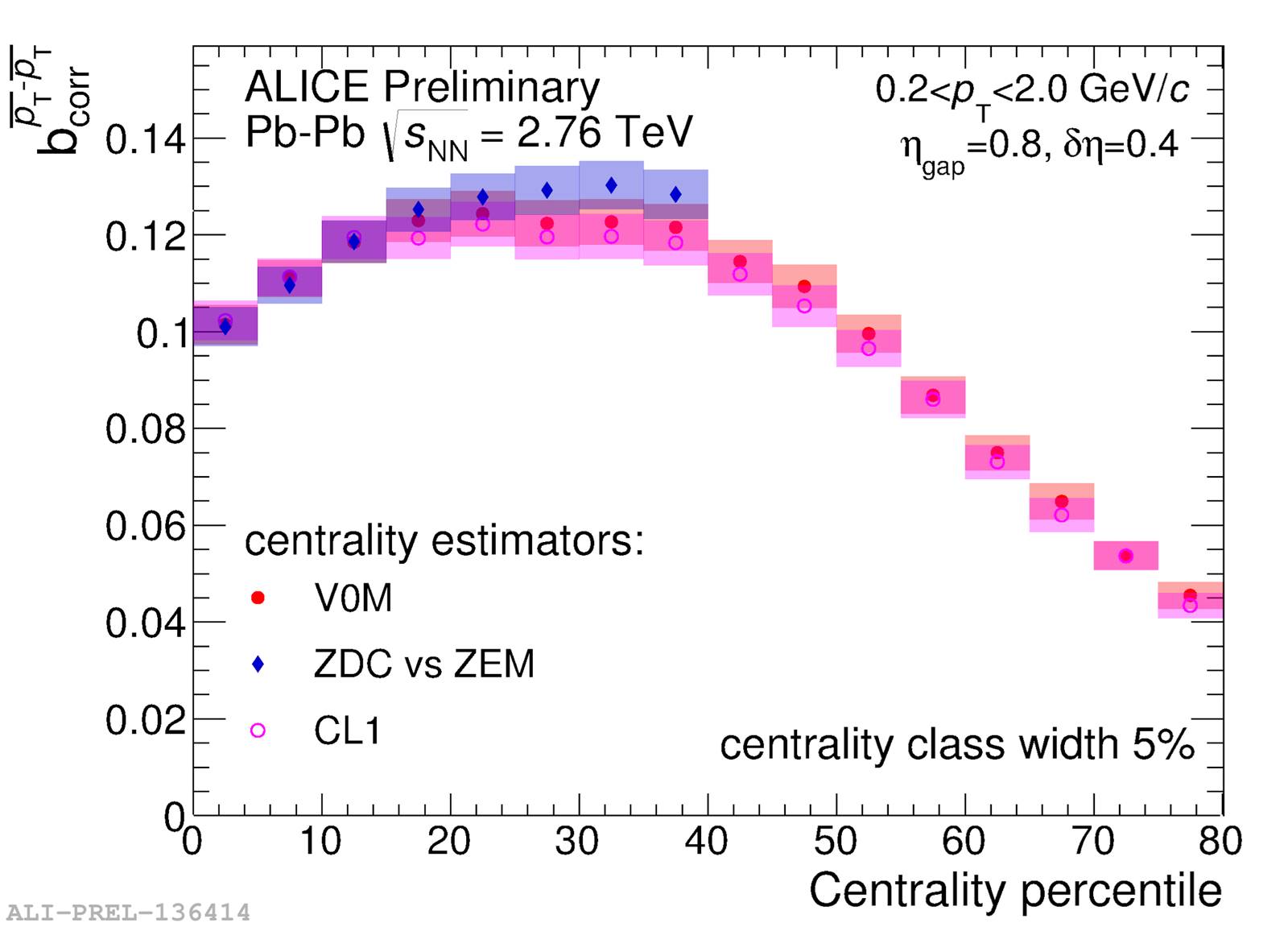
Figure 19 Dependence of
3.8 Underlying event of high
The study of the underlying effect can be useful to understand the particle
production mechanism. It has been shown that selecting events of determinate
high
If we go on the process of the selection of high
In a similar way than the one in Sec. 3.5, the only stable distributions under
these transformation are the generalized gamma function, being the gamma
function the most simple of them (see Eq.(51). This function satisfies KNO scaling if k
is independent of energy. We have seen above that k increases
with the energy for p+p collisions in the studied range, as
3.9 Bose-Einstein Correlations
The Bose-Einstein Correlations (BEC) are very interesting in order to determinate
the extension of the source of multi-particle production, as well as to know the
degree of coherence of the emitted particles. The correlation strength is
characterized by the parameter
where
and the total number of pairs of identical particles produced is:
where
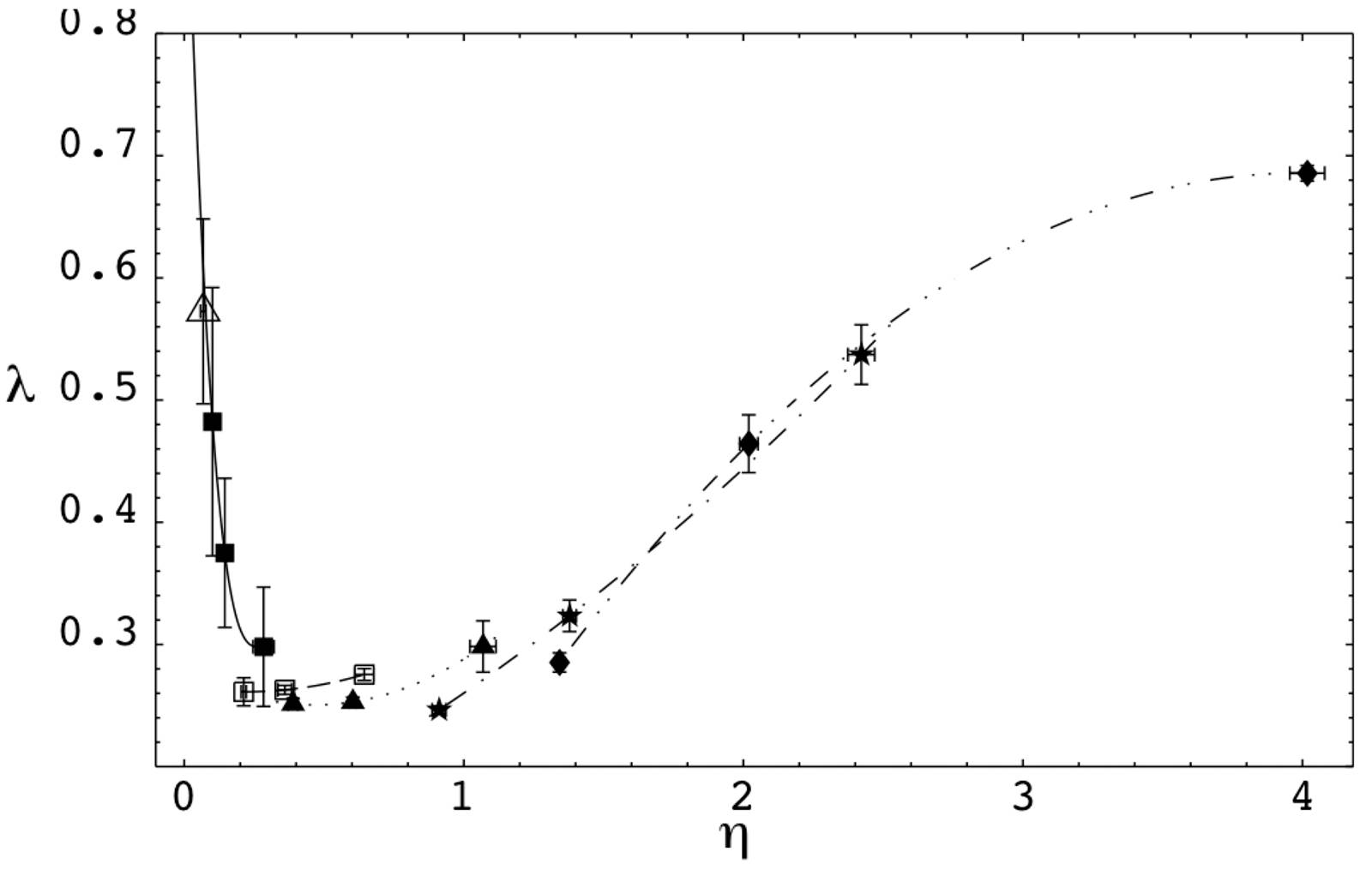
Figure 20 Dependence of λ on η for different nucleus-nucleus collisions in the percolating strings framework taking into account the energy-momentum of the strings. Each point represents a specific type of nucleus-nucleus collisions. Correlations are calculated between identical pions for y1cm = y2cm = 0:5 and mT1 = mT2 = 0:35 GeV/c 2[138].
The three body BEC have been also studied in percolation [139], predicting the strength of the three particle BEC, which is in good overall agreement with data [141].
3.10
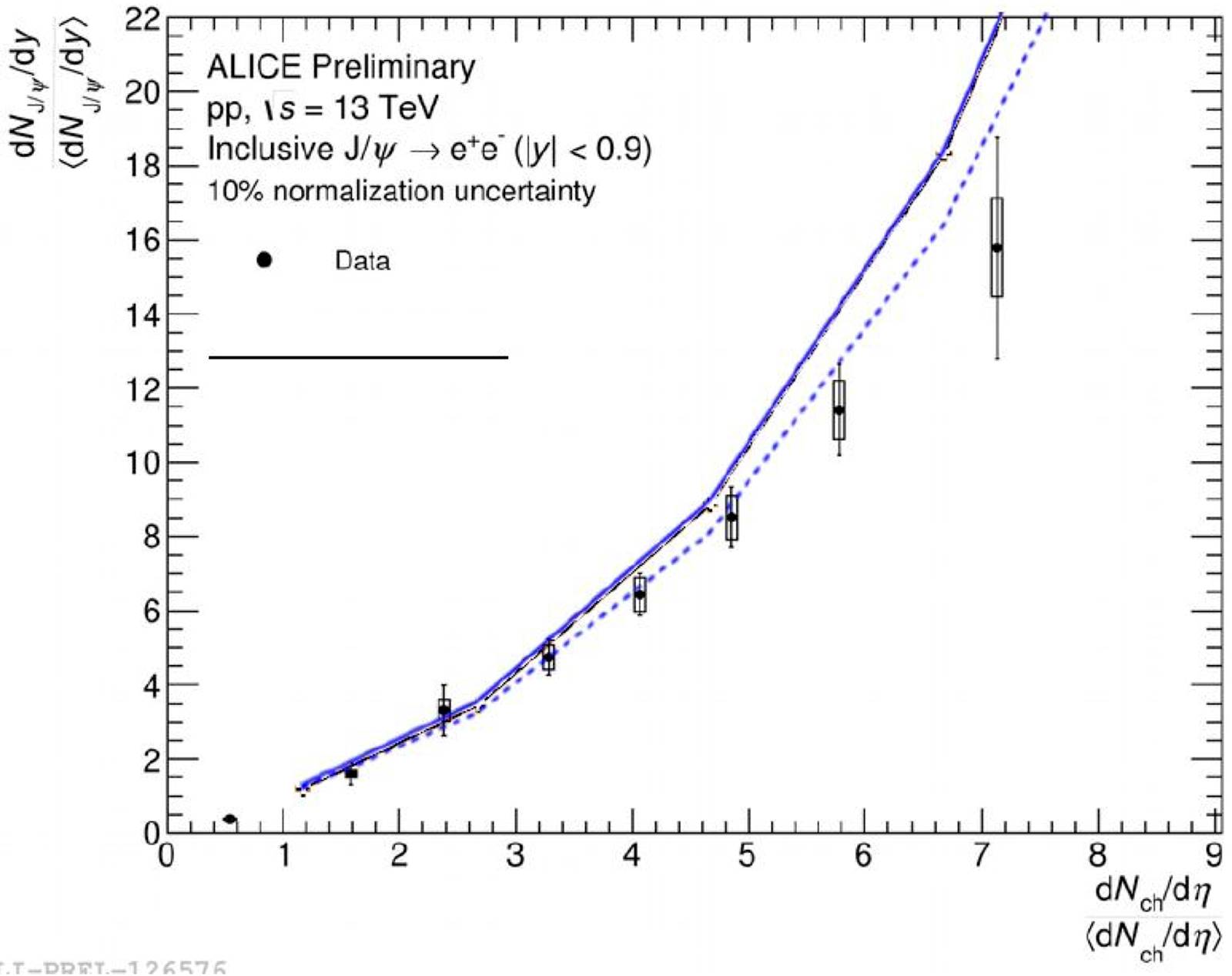
The ALICE collaboration has found a departure from linearity on the dependence of
From Eq.(35) we can write:
thus:
At low multiplicities,
therefore:
Note that the linear behavior changes to quadratic at high multiplicities. In Fig. 21, we show the results together with the experimental data [33], as well as the results for the forward rapidity region together with the experimental data. In the forward rapidity region we have less number of strings, and as a consequence, the departure from the linear behavior starts at higher multiplicity. In both cases, central and forward rapidity region, a good agreement is obtained.
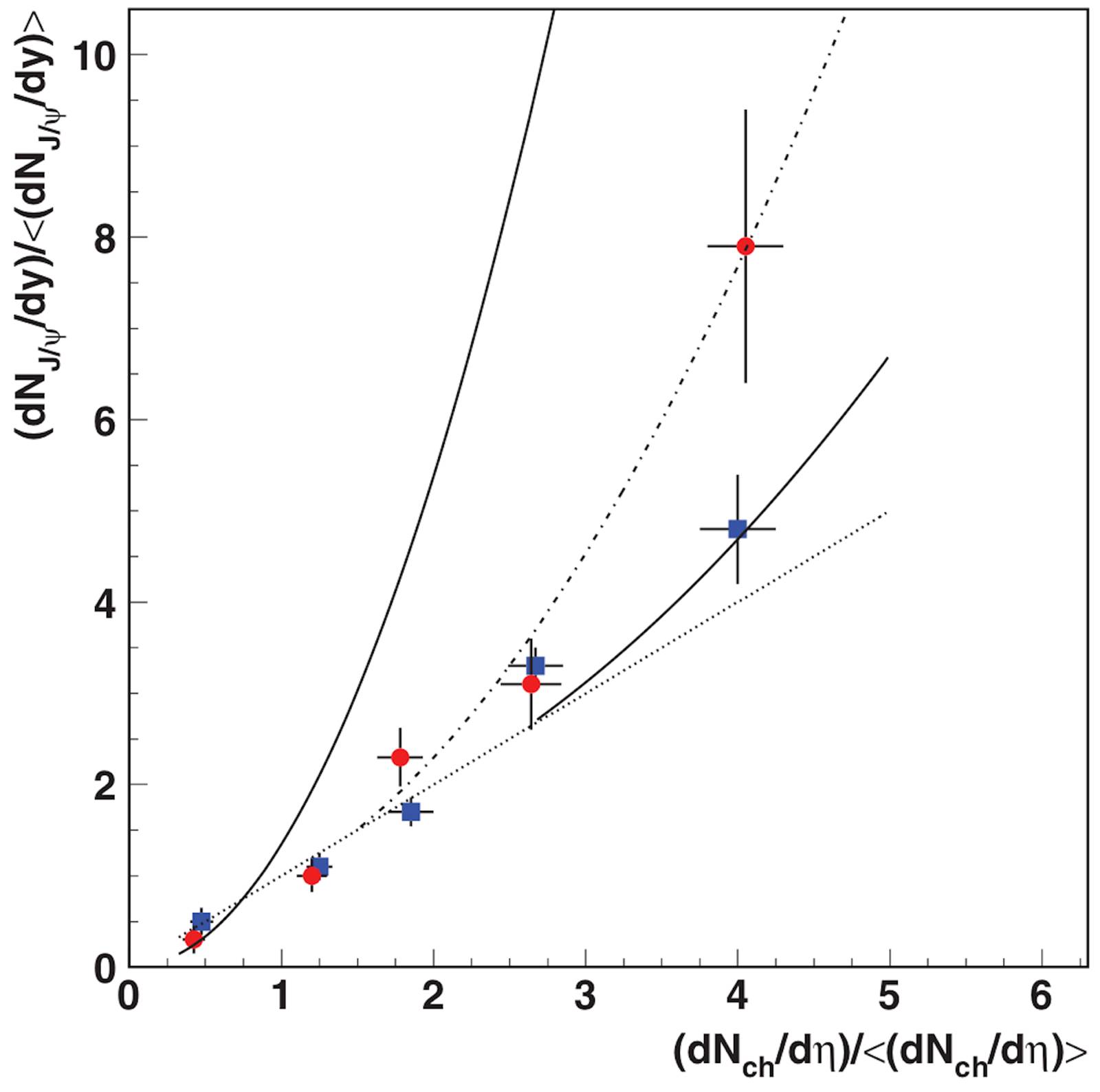
Figure 21 Results for p+p collisions in the central |y| < 0:9 rapidity range (dashed line) and forward 2:5 < y < 2:4 (dotted line), together with the experimental data for the central (circles) and forward (squares) rapidly regions from the ALICE Collaboration. The linear behavior (solid line) and the prediction for pPb collisions (dashed-dotted line) at 7 TeV are also plotted [142].
Notice that only there are two assumptions, namely, the
3.11 Incoherent
The incoherent photo production of
3.12 Strangeness enhancement
The overlapping of the strings modify the strength of the color field, and hence
the string tension of the formed cluster. Due to this, the decay of these
clusters produced naturally an enhancement of the strangeness [146-148]. In addition to this
effect, as the clusters have at their extremes complex flavor
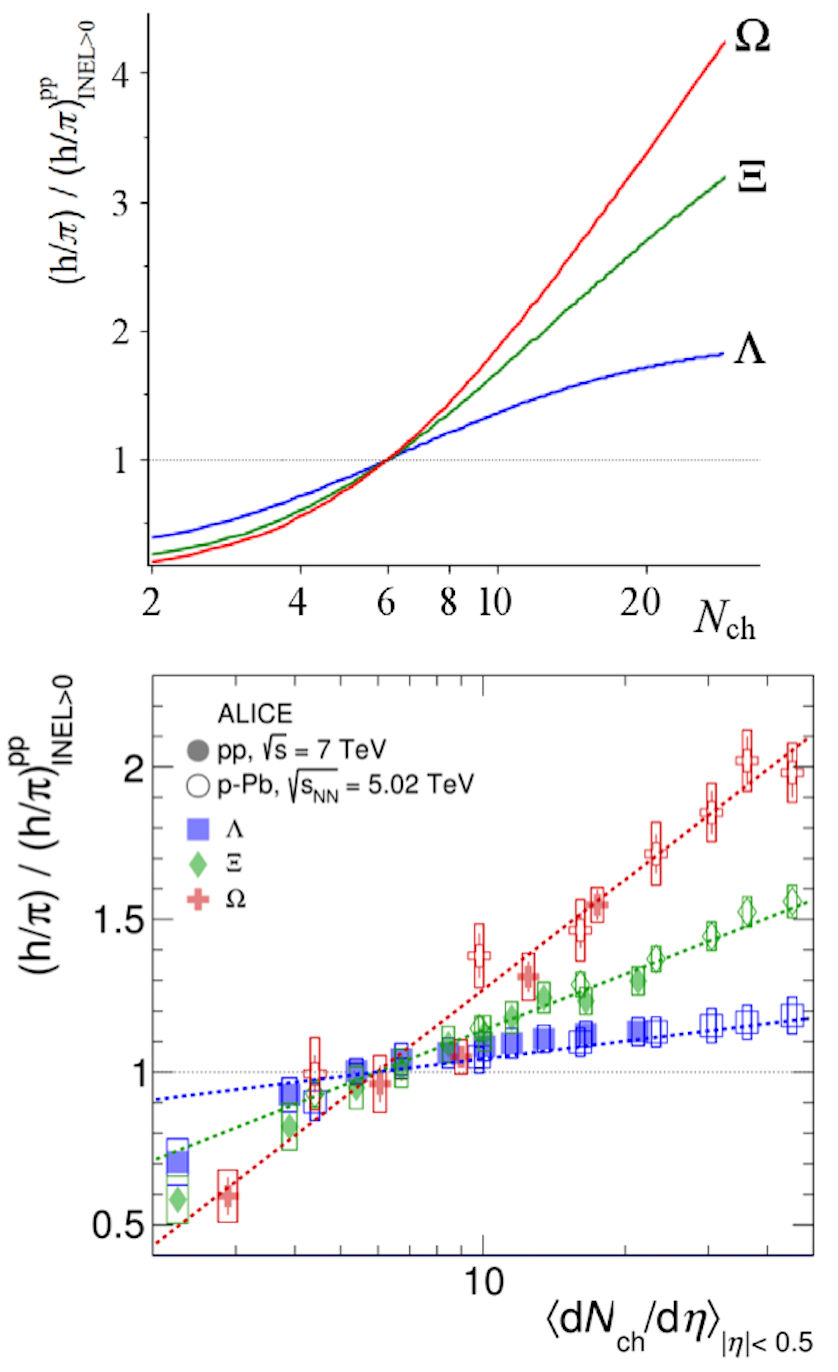
Figure 24 Comparison of the multiplicity dependence of the relative yield of Ω, Θ and Λ baryons normalized to pion multiplicity for p+p and pPb collisions for the model (up) and experimental data (bottom) [146].
4. Azimuthal dependence of the momentum distributions
4.1 Collective flow and ridge structure
The clusters formed by the strings have an asymmetric form in the transverse
plane and acquires dimensions comparable to the nuclear overlap. This azimuthal
asymmetry is at the origin of the elliptic flow in string percolation. The
partons emitted at some point inside the cluster have to pass through the strong
color field before appearing in the surface. The energy loss by the parton is
proportional to the length, and therefore, the
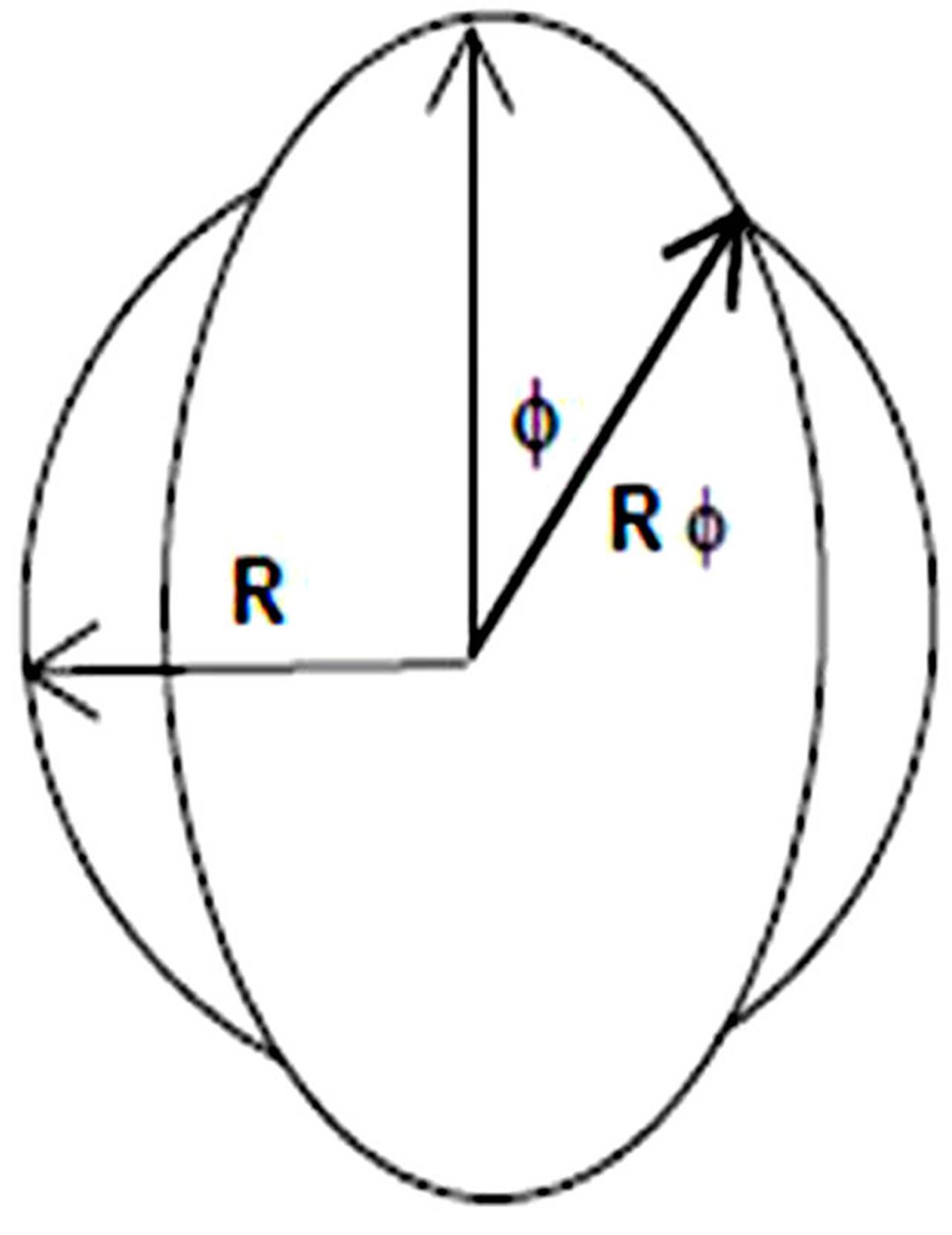
Figure 25 Scheme of the azimuthal dependence modify by the escape probability of a parton on the nuclear overlap [152].
where
Thus, the elliptic flow can be computed as follows:
Note that the latter is an analytical close expression for all energies, centralities, projectiles, and targets.
The transverse momentum dependence of
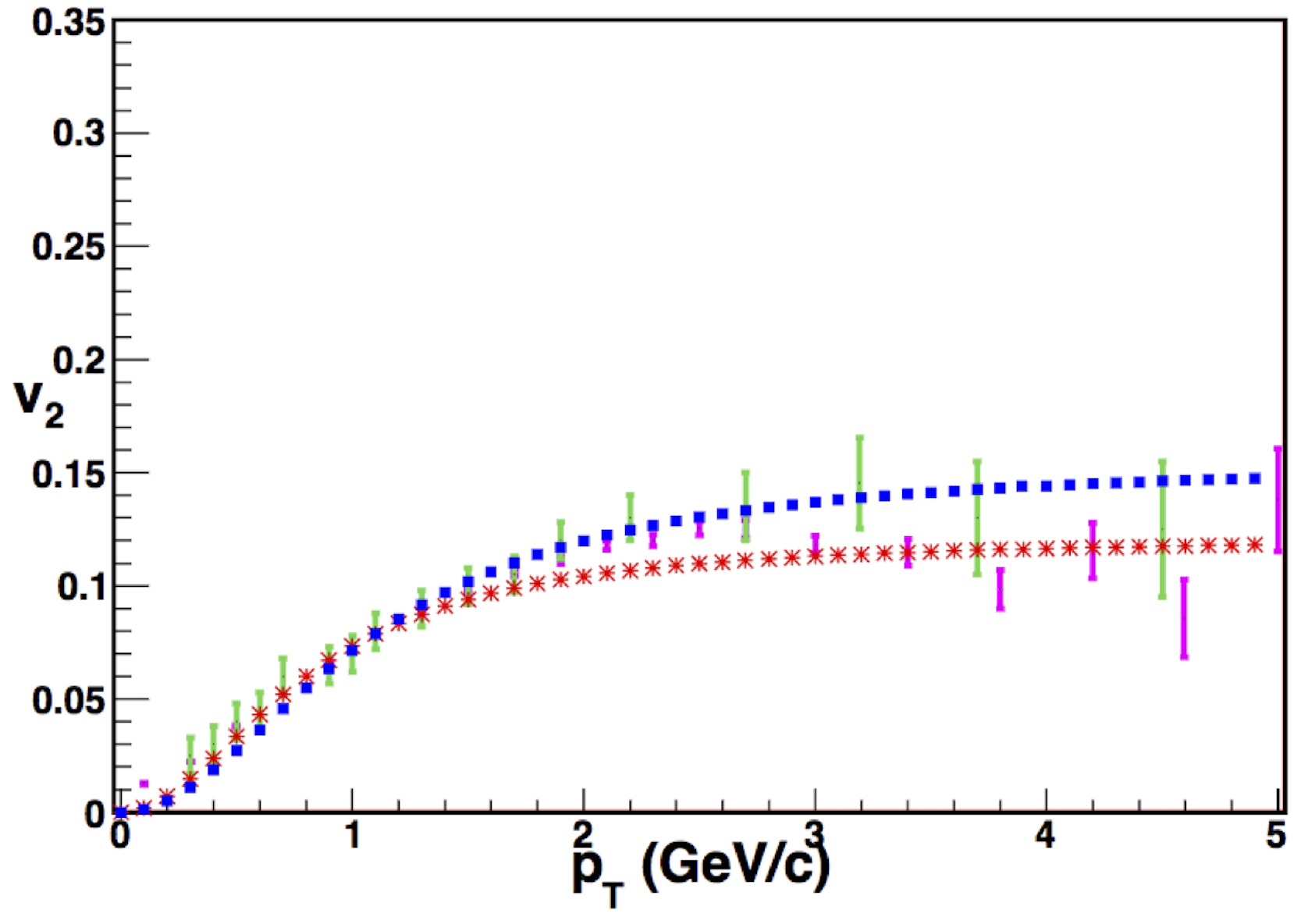
Figure 26 Comparison between the prediction of percolation model (red stars
and blue squares) and the experimental data (errorbars in green and
pink) for
In string percolation correlations can arise from the superposition of many
events with different number and type of string. In this way, there appears long
range correlations in rapidity. However, passing to the azimuthal dependence, if
the emission of strings is isotropic, the correlations due to their distribution
in different events will be also isotropic. Also in the central rapidity region,
the inclusive cross section is approximately independent of rapidity. This
generates a plateau in the
In Fig. 27, we show the results [156] for
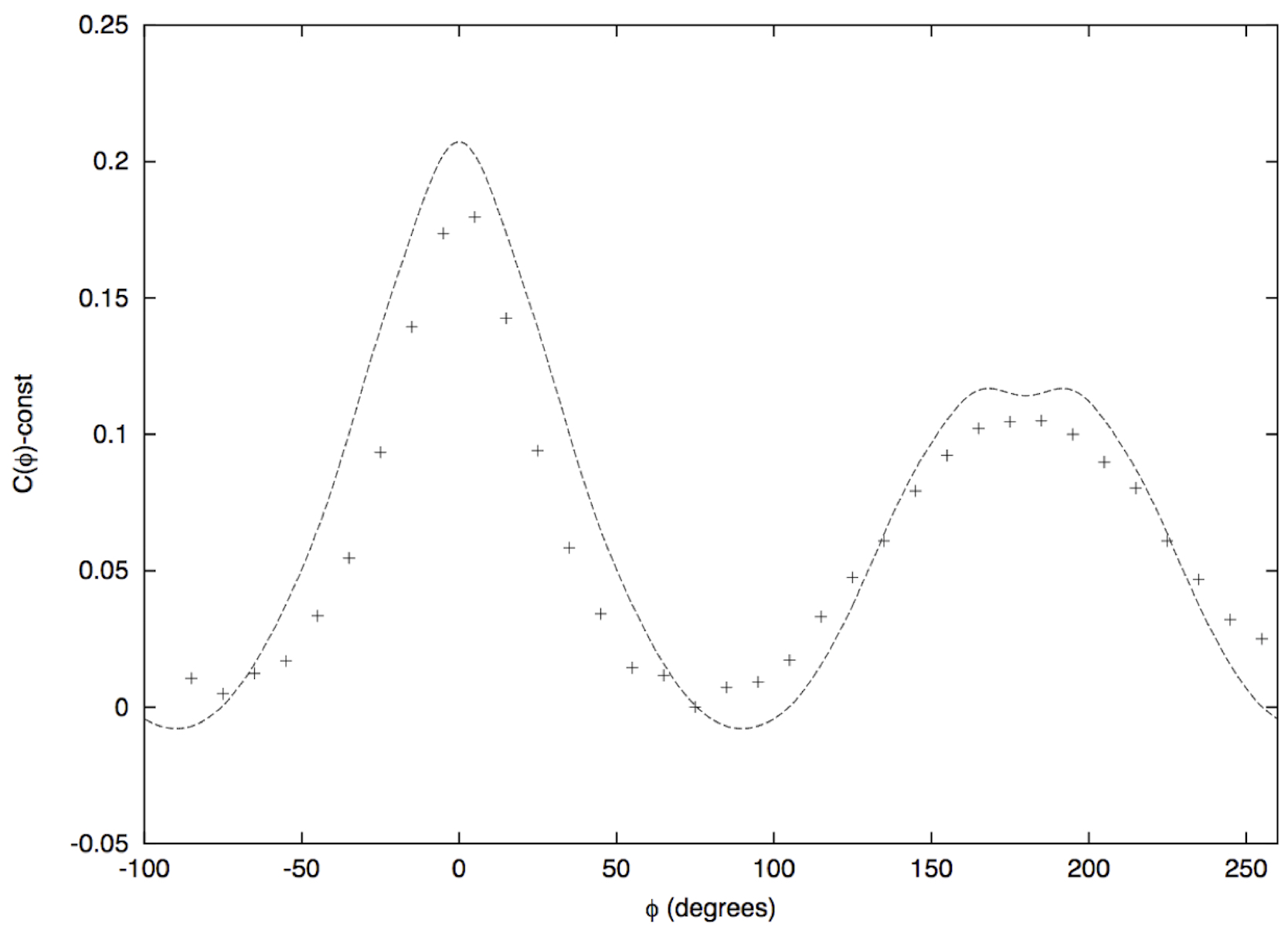
Figure 28 Correlation coefficient C(Φ) for p-Pb collisions at 5.02 TeV for central collisions compared to the data (ZYAM procedure) [156].
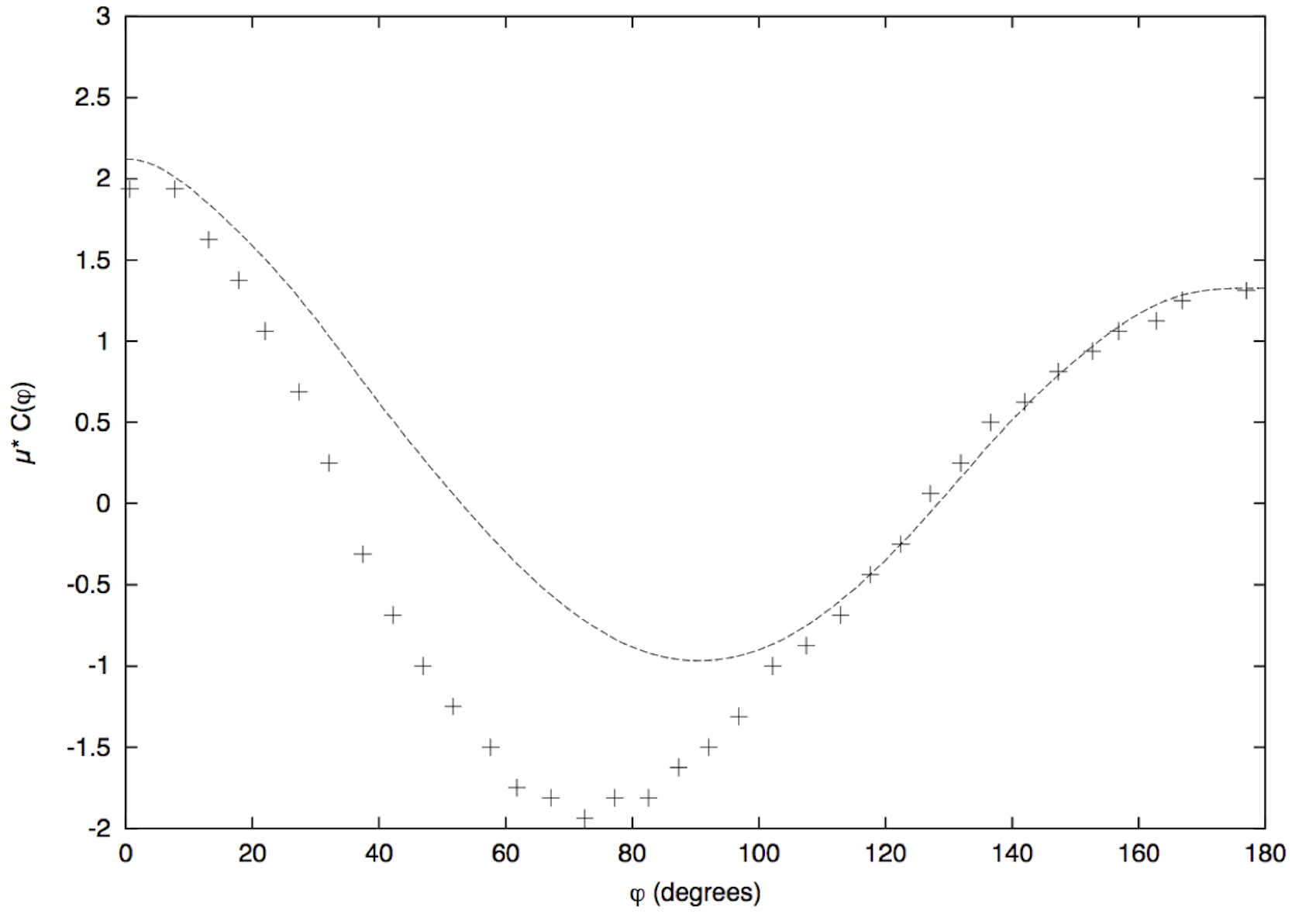
Figure 29 Correlation coefficient C(Á) for Au-Au at 200 GeV for 10% of the most central events against the experimental data [156].
In the case of p+p collisions, to obtain the ridge structure, we need to consider high multiplicity events (three times the minimum bias multiplicity shown in Fig. 29). This is due to the fluctuations needed to have sizable long correlations which are only obtained for these events. These fluctuations are also crucial to describe the higher harmonics of the azimuthal distributions.
We can conclude that string percolation is able to describe the ridge structure seen in p+p, pA and AA collisions. The ridge is obtained from the superposition of many events with different number and types of clusters of strings. There is not any essential difference between high multiplicity p+p for pA collisions and AA collisions. The collective flow is obtained from the configuration of the initial state as clusters of overlapping clusters and the interaction of the produced partons with the color field of the clusters. This interaction could be interpreted as final state interaction, but as far as the parton have these interactions before hadronization, it should be regarded as well as initial state interaction. In the production of heavy particles, due to their short formation time, they can be formed before than the parton get out the surface collision area. This is certainly true for central heavy ion collisions. In this case, the energy loss by the parton would be smaller, and thus the elliptic flow. As the elliptic flow for central collisions is small, the effect is difficult to be observed.
4.2 Elliptic flow scaling and energy loss
In Sec. 3.3, we discussed the quenching of low
Here the temperature,
We will take proportional to the product of the eccentricity of the overlap area
and
We expect that the elliptic flow were proportional to the strength of the quenching, so:
Using the dependence of
where we have choice, the scaling variable
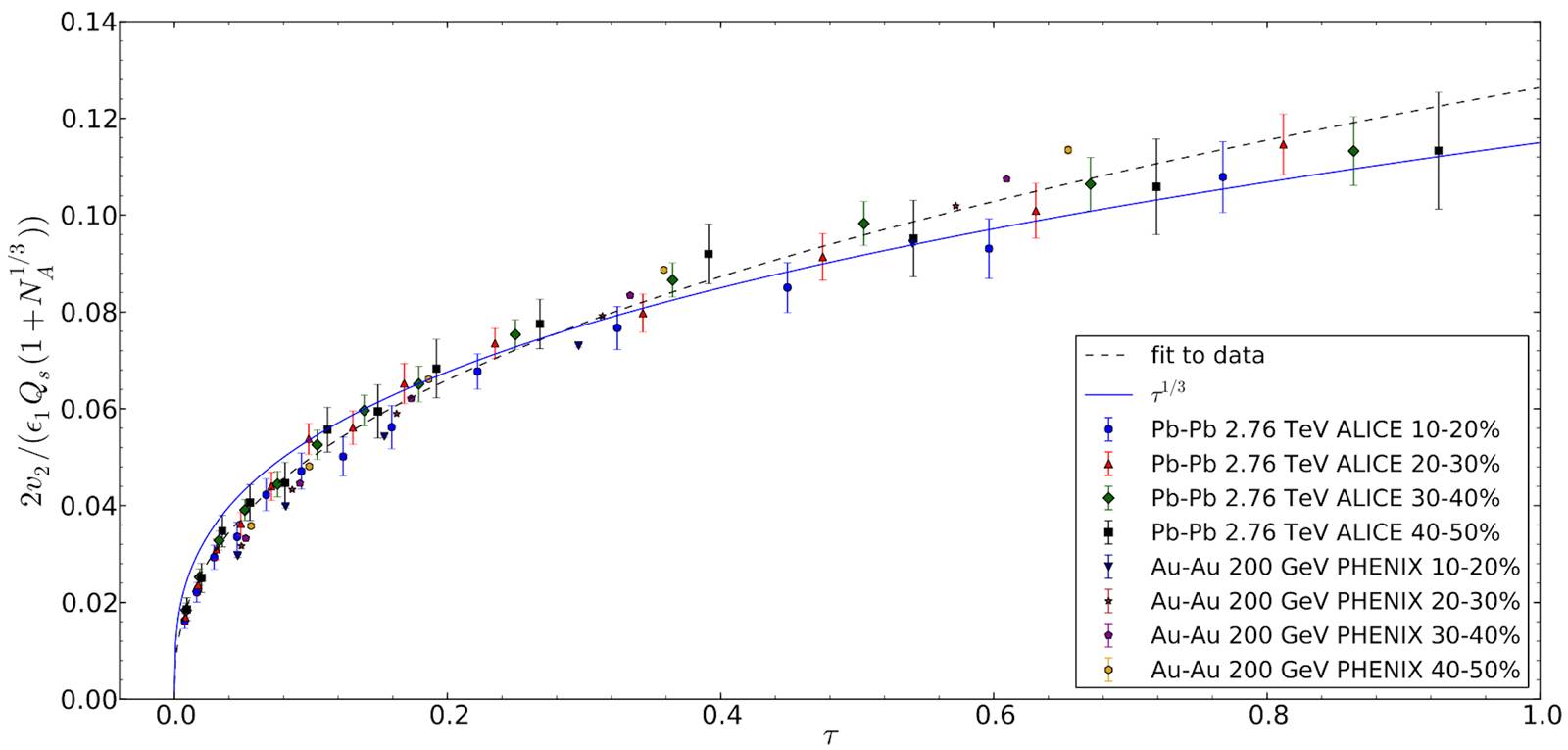
Figure 30 v2 scaled by
5. Thermodynamics of string percolation
The thermodynamics of the string percolation can be addressed by extracting the
temperature from the transverse momentum distribution. We also can extract the
suppression factor
where
In Fig. 31, we plot the obtained energy density
over
where the mean free path is
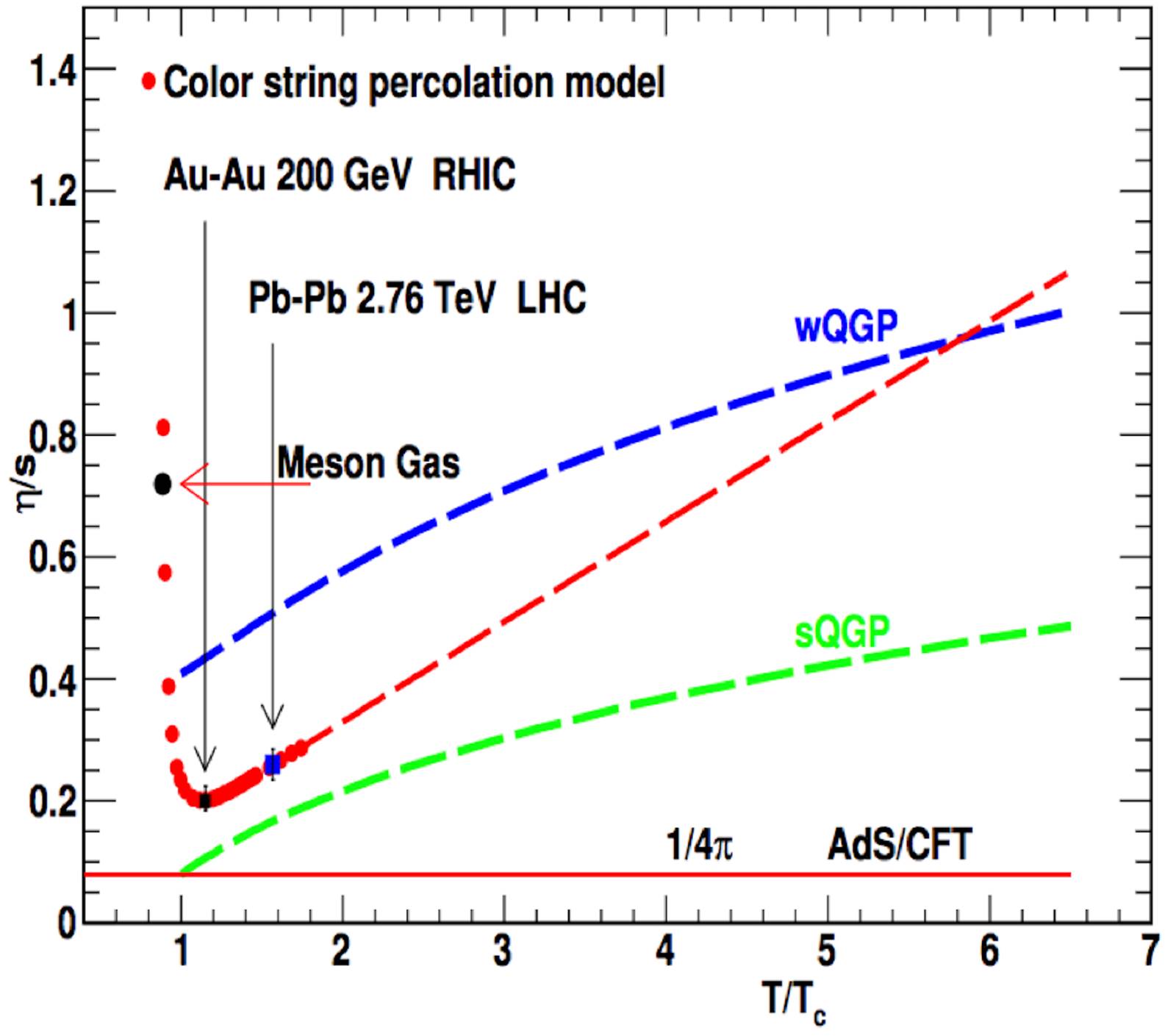
In Fig. 32, we show the behavior of
The arrows marks are the result of string percolation for Au-Au and Pb-Pb at RHIC and
LHC energies. Below
Moreover, the mean value of the trace of the energy momentum tensor
The minimum corresponds to the maximum of
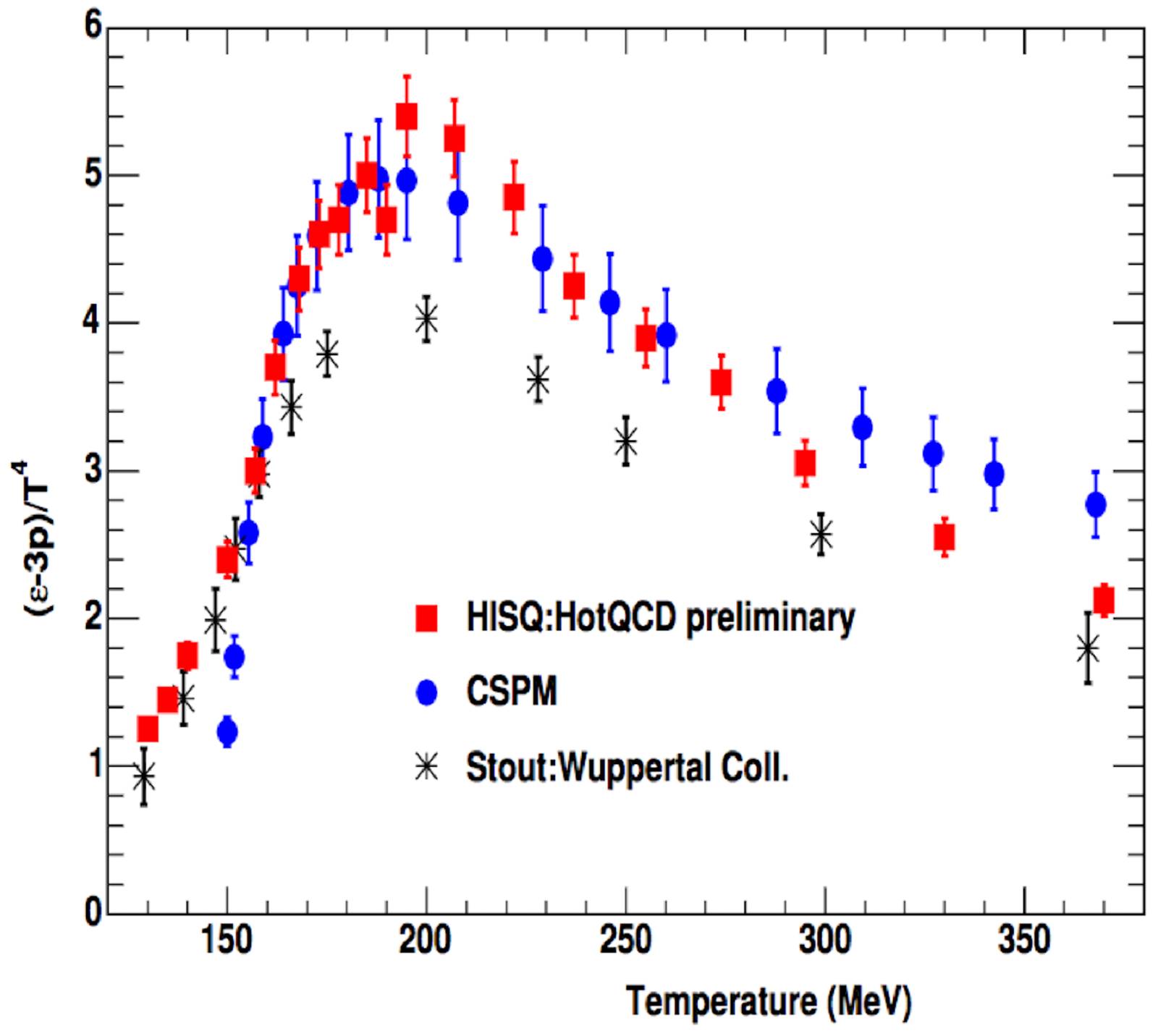
Figure 34 Comparison between the trace anomaly of the energy momentum tensor and inverse of the η/s ratio. Note that both variables have a maximum value at the same temperature point.
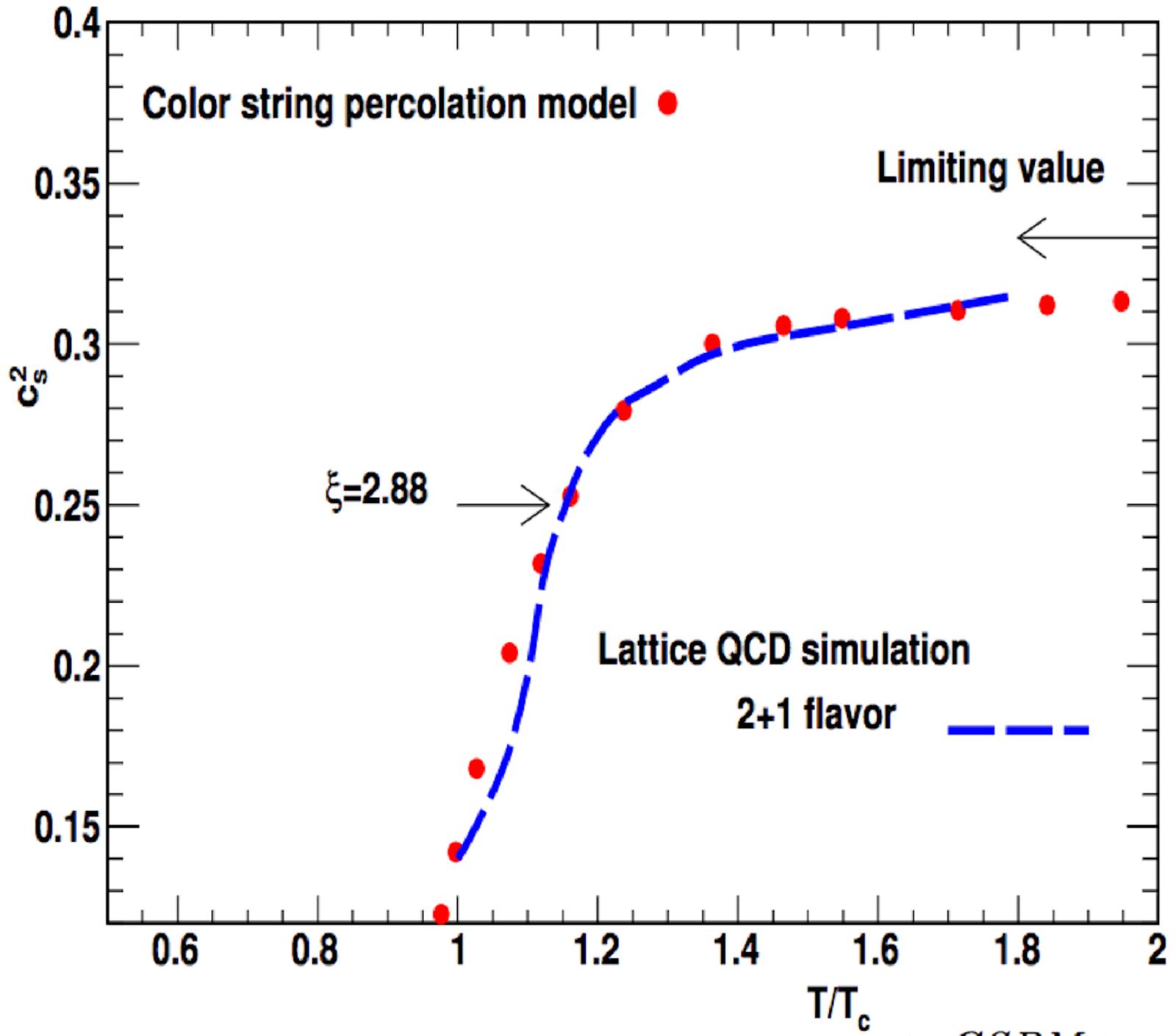
On the other hand, it is possible to determine the speed of sound,
where
From the above equations, it is possible write
where
Another interesting thermodynamic variable which can be determined is the bulk viscosity. Starting from [162]:
where
Note that this last expression depends on the sound speed, trace anomaly and entropy
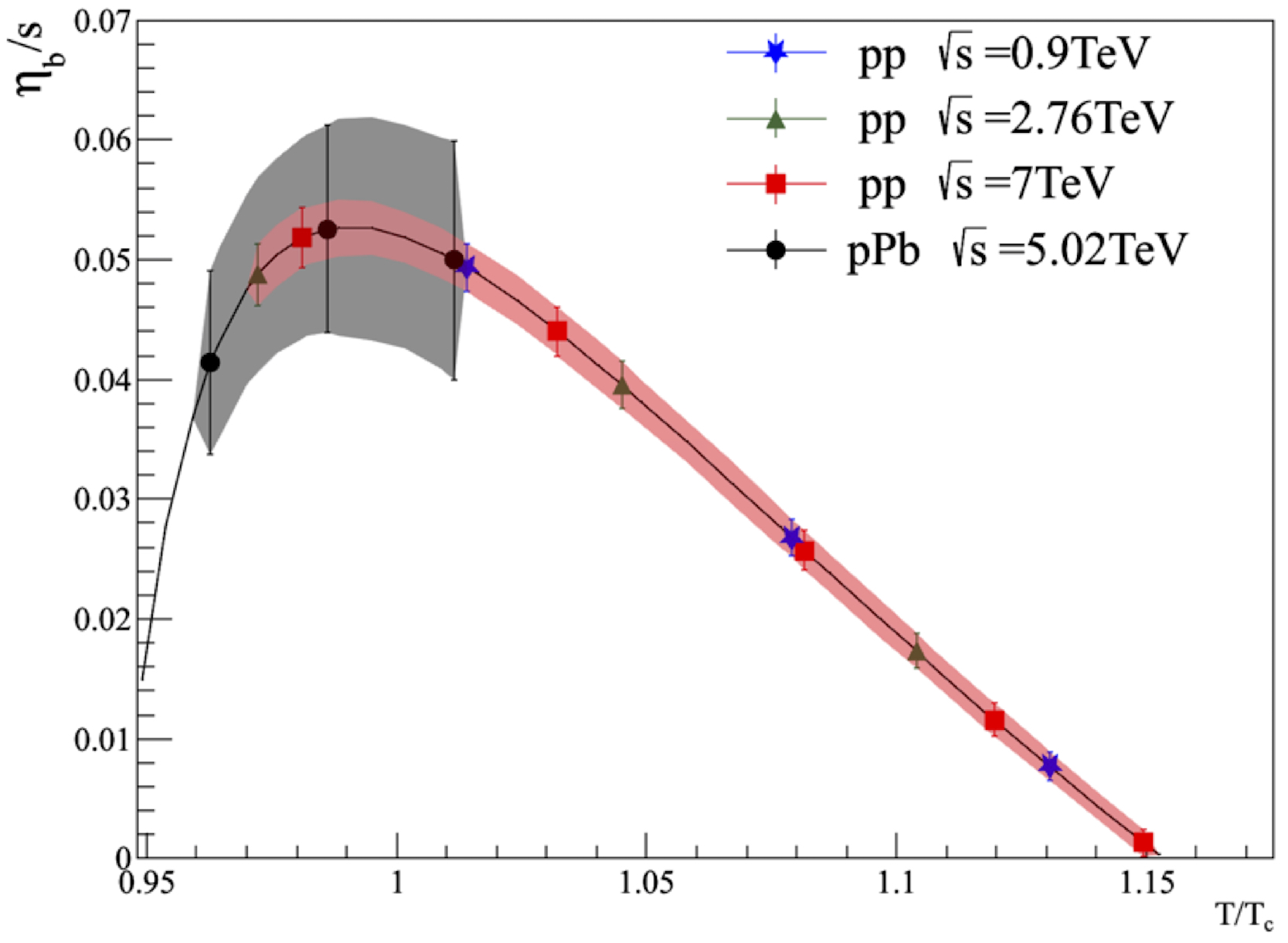
density, which has already been computed in the string percolation context. In Fig. 36, we plot the bulk viscosity over the
entropy density as a function of the temperature, which has a maximum close to
6. Summary
The string percolation describes successfully most of the experimental data in the
soft region, namely, rapidity distributions, probability distributions of
multiplicities and transverse momentum, strength of BE correlations as a function of
multiplicities, forward-backward multiplicities as
The string percolation, although is not derived directly from QCD, has a clean
physical ground and it has the fundamental QCD feature. The non abelian character is
reflected in the coherent sum of the color fields which gives rise to an enhancement
of the mean
The collective behavior of the multiparticle production has its origin in the cluster
configuration formed in the initial state of the collisions, followed by the
interactions between the produced partons with the color fields, giving rise to
energy loss. Due to that, the elliptic flow satisfies an universal scaling law valid
for all centralities and energies. At low











 text new page (beta)
text new page (beta)