1. Introduction

The discharge rate of dry, non cohesive, granular material from exits centrally located at the bottom of bins, due only to gravity action, is a very interesting phenomenon because experimental measurements show that it is independent of filling depth and non-linearly dependent on the orifice size. In this case, the first proposal of a correct phenomenological formula for the flow rate of grains from open-tops bins, m˙0, was developed by Gotthilf Hagen ^[1], a German hydraulic engineer who, in 1852, experimentally found the relationship m˙0=ρg1/2D5/2, where ρ is the bulk density, g is the acceleration due to gravity and D is the diameter of the circular orifice.

The Hagen formula constitutes the foundation of the hourglass theory ^[2-^4]. In industry, it is the basis to estimate controlled granular flows as dosage of powders and granules ^[5, ^6], among other applications. When the grain’s size is important, Hagen ^[1] and, more than a century later, Beverloo et al^[7] found experimentally that the most suitable correlation to predict the mass flow rates from bottom exits in bins, silos and hoppers is the so called Beverloo correlation, which has the form m˙0=ρg1/2D-kd5/2, where D-kd is an effective orifice size when the size of the particles becomes of the order of D, d is the mean diameter of the grain and k is a dimensionless constant (the shape-factor) with typical values k≈1-2 ^[2]. For orifices that are around 6 particle diameters (or smaller) across, the flow is intermittent, irreproducible and can be surely arrested. The Berverloo correlation should therefore not be used if D≲6d nor may it be assumed that putting the group (D-kd) equal to zero correctly predicts the orifice to particle diameter ratio at which the flow ceases. Finally, in the limit D/d≫1, the Berverloo formula yields m˙0=ρg1/2D5/2 ^[4].

Concerned with the eccentric location of single orifices in flat-bottomed bins, and in bins with vertical walls, we can distinguish two possible configurations: one is when the exit holes were made eccentric in three dimensional flat bottomed silos ^[8, ^9], and for flat bottomed quasi two-dimensional bins ^[10-^16]. In both cases, it has been found that the mass flow increases with respect to the central-hole cases. Besides, for eccentric orifices in near two-dimensional bins, the mass flow rate increases approximately as m˙= m˙01+aeb, where m˙0 is the corresponding mass flow rate for centrally located orifices ^[16, ^17], e is the dimensionless parameter of eccentricity, and a and b are nondimensional constants . The case of central orifices is recovered when e=0 . A second configuration of eccentric orifices, but now placed on the vertical sidewall of bins, was first proposed, to our knowledge, by Jamieson at the beginning of the 20th century ^[18]. However, he performed experiments using the discharge orifices on the sidewalls in the context of the grain pressures measurements and the asymmetry of pressures on the side adjacent to outlet and on opposite side.

By the way, only a few studies ^[19-^27] have been conducted to explicitly test the validity of the Hagen or the Beverloo correlations for the discharge of grains through orifices on the vertical sidewalls of bins, which we denote by m˙. To the best of our knowledge, Franklin and Johanson were the first researchers who experimentally studied the problem of the gravity driven lateral outflow of granular material from boxes. In their studies, they used galvanized metal sheet 0.238 cm thickness, and they found that the flow rate, for orifices at the vertical sidewall, scales as m˙=cρg1/2D2.93, where c is a factor dependent upon the angle of internal friction and the diameter of the particle. In such a work, non explicit consideration on the wall thickness was invoked. Later on, Bagrintsev and Koshkovskii ^[20] used oval and circular exit holes, made on the transparent plastic walls of vertical cylinders whose thicknesses were 0.1 and 0.45 cm. They found that the mass flow rate scales approximately as m˙=cρg1/2D7/2 where c is now a parameter that depends on the geometrical features of the exit hole; they also qualitatively observed that "to obtain the greatest possible outflow capacity through a circular hole in a cylindrical tube it is necessary to use a tube of minimum allowable wall thickness". Later, Chang et al^[21] and Davies and Foye ^[22] carried out experiments in rectangular vessels with rectangular exit slots. Chang et al did not report the dimensions of the wall thickness of their containers, and Davies and Foye ^[22] have reported the use of mild steel sheets 0.12 cm thick. In spite of it, all of these authors essentially found that the mass discharge obey the Beverloo relation m˙=ρg1/2(D-kd)5/2 such as Sheldon and Durian ^[23] who used circular exit holes on steel cans 0.025 cm wall thickness and square Aluminum tubings 0.03 cm wall thicknesses and also have reported that the lateral flow rate obeys the Beverloo relation.

Nevertheless, none of the previously referred works analyzed the effect of the wall thickness on m˙ systematically. In the case of wall thickness (w) comparable with the outlet diameter (D) we have reported in several studies that for single circular orifices at the sidewall, the relationship valid for the flow rate behaves as m˙=m˙0(α-θr) where m˙0=ρg1/2D5/2 when D » d^[24-^26] or m˙0=ρg1/2D-kd5/2 for cases with D∼10d ; θr is the angle of repose of the granular material and α is the angle of wall which has been defined as α = arctan (D/w). As will be shown later, the formula for m˙ predicts that when the wall thickness is very small (w « D), its dependence on w is weak but finite. The unique case where the dependence on w vanishes is in the hypothetical case w = 0, however, as will be seen later, a factor dependent upon the repose angle is maintained. Systematic experiments reported here will validate such predictions.

Experimental studies ^[28-^30] and computer simulations potapov^[31] on gravity-driven granular flows in two-dimensional hoppers discharging monodisperse granular material have shown that the flow occurs in an unsteady manner, first flowing down one side of the hopper then down the other. Moreover, in monodisperse granular material particles are arranged The strength of this packing appears to be the cause of the hopper flow instabilities. In order to avoid these undesirable effects, in our experiments we have used polydisperse materials.

It is important to comment that in the context of the outstanding applications, as the fight against hunger, of silos with lateral exit holes, the Swiss Agency for Development and Cooperation (SDC) first sponsored and introduced the manufacture and use of the metal silo, with orifices on the sidewall as an important element of its design, in some Central America countries in the 1980s, which has helped to ensure that agricultural products can be stored for personal consumption or later sale ^[32]. Between 1995 and 2007, a total of 500,143 metal silos were manufactured and sold to farmers. Commonly, manufacturing a metal silo requires galvanized iron sheet 0.5 mm thick (Gauge No 26 or 24).

Given all these facts, the main motivation of this work is to estimate accurately the flow rate of grains from orifices in bins with lateral orifices and thin vertical sidewalls, aside the error involved in the measurements when the wall thickness is not taken into account. To reach our goal, the division of this work is as follows. First, Sec. 2 we will revisit our phenomenological formula m˙=cm˙0(α-θr) ^[24-^26], to estimate the mass flow rate from orifices with thin lateral walls and we analyze the twofold limits w « D and w = 0. Then, in Sec. 3, we will report experiments of discharge rates through actual thin sidewalls. We found that the experiments fit fairly well Hagen-like or Beverloo-like correlations, both with a factor dependent linearly on w. All those results will allow us, given a geometrical interpretation of the mass flow rate formula for any thickness w, including the case when w = 0. Finally, in the last Section we will give the main remarks and conclusions of the study here tackled.

2. Correlations for thin sidewalls

Related to the lateral outflow of granular solids from vertical walls of silos, a few years ago we proposed a phenomenological formula that simultaneously spans cases of different sidewall thickness, w, and orifice diameter, D, but it was only validated experimentally when D ~ w, i.e., for thick sidewalls . This formula is unique because it encompasses, simultaneously, parameters (up to now) not related in formulas of the mass flow through bottom holes, as the wall thickness w, the angle of repose θr and the orifice diameter, D, all of them necessary to determine the minimum opening and thickness through which a stable outflow of non cohesive granular material is ensured. Despite it, the validity of such a formula has not been proved for experimental cases of very thin sidewall thickness, i.e., w « D.

As aforementioned, the wall thickness affects the granular flow when it occurs across sidewalls, i.e., w also modulates m˙, the lateral outflow, provided D>6d 5. In Fig. 1, we depict a scheme that represents the transversal region close to the exit hole of size D in vertical sidewalls of different thicknesses. In Fig. 1 (b) it becomes evident that there is a natural angle of wall α = arctan (D/w). In this same figure it can be observed that there is no flow, due to the wall thickness being large enough and therefore, the granular material contained there will attain its angle of repose. Thus, a stable outflow is kept as long as α>θr and, conversely, the outflow should be arrested if θr≥α, this is illustrated in Fig. 2 where a thick sidewall of a bin has orifices where α>θr, and there are granular flows, and others where θr≥α and there is no flow. Consequently, the mass flow rate itself must be proportional to (α-θr).

Figure 1 Schematic of a transversal view of the zone close to a vertical exit hole: (a) thin sidewall, there the granular outflow is strong, (b) no flow or arrest flow condition where the angle of wall α, meets that α<θr. 

Figure 2 Picture of a brimful bin with beach sand in contact with a sidewall. It is observed that there are four open staggered drills on an acrylic-made (transparent) thick sidewall. The larger lateral hole allows the granular flow meanwhile for the smallest of them there is no flow, due to the condition α≤θr has been reached. 

Another important feature to get a general relation for m˙T, the phenomenological approximation to the mass flow rate for lateral exit holes, is that the latter is proportional to m˙0 (the mass flow rate through bottom holes) ^[19, ^23]. Therefore, the mass flow rate dependent upon D and w is a relation of the form ^[24-^26]

where we introduced in the last part of (1) the definition of the angle of wall α = arctan (D/w). The factor ρg1/2D-kd5/2 is the Beverloo correlation valid for centered orifices at the bottom exit of silos, i.e.,

For granular solids of mean grain diameter d smaller than D, the phenomenological correlation (1) transforms into

where (2) now is

i.e., the Hagen formula. Several experimental studies have shown that formulas (1) and (3) describe pretty well the mass flow rate of granular solids crossing a vertical wall when w ~ D and D » d or when w ~ D and D ~ 10d medina4 and, if correct, it must be valid even for thin sidewalls.

Approximate rules of thumb referring to lateral flow rate across thin-walled bins can be obtained from (1) by expanding in powers series the function arctan (D/w), when w/D « 1 and D is a valid diameter; to first order in w it yields

which is a linear function on w, but it is a nonlinear function on D. Also, if the grain diameter is very small D≫d, the corresponding relation, obtained from (3), for the flow rate is now

Note that, as a direct consequence of (5), if hypothetically the wall thickness is null (w = 0) we get that

and from formula (6), for the case D≫d, is obtained

The correlation (7) ((8)) expresses that just for the case w=0, the mass flow rate for the lateral outflow essentially obeys the Beverloo (Hagen) formula, but with the numerical factor π/2-θr dependent on the type of granular sample through θr . For cases where w is small, but not zero, there must be a small influence of the thickness on the flow rates as expresses relations (5) or (6), respectively. In the next Section we will quantify how significant is the effect of the sidewall thickness on the flow rate of grains.

Finally, the achievement of a good fit among the measured mass flow rate m˙Expt and the appropriate phenomenological (calculated) formula, m˙T, given by any of relations (1)- (8), is attained if it is possible to essentially meet a relationship of the form

where A, is the discharge parameter. A very similar comparison method was discussed by Beverloo et al^[7] for bottom openings. It will be our guidance in the experimental analysis.

Experiments

In order to compare actual measurements of the mass flow rate for both, bottom and lateral orifices against the respective phenomenological values, we performed experiments with acrylic-made bins 10 x 10 cm inner cross-section and 50 cm height. On one side of the bin we are able to interchange four plates of galvanized metal 10 cm width, 50 cm height each of different thickness, w. Upon each plate we drilled five staggered circular orifices closely distributed 5 cm above of the bottom of the bin. The diameters of the five exit holes in the plates and the respective thickness of the plates, are given in Table I. Additionally, plates with the specified thicknesses were also adjusted as flat bottoms of bins with central orifices.

Experiments were performed with beach sand (angular grains), Ottawa sand (rounded and polydisperse grains) and granulated sugar (crystallized grains) representing cohesionless granular solids all of which were gently poured from the top in the bins to brimful them. The bulk properties and the mean size of the grains (median, obtained through the cumulative percentage) were measured as in and are reported in Table II. The section of the laboratory in which the experiments were carried out was climate controlled (25±1∘C and 45±10 % R.H.). The moisture contents of both, beach sand and Ottawa sand samples, were 0.50±0.06% and for granulated sugar 0.015±0.005% w.b.

The experimental setup to measure the discharge rates is sketched in Fig. 3. There, a force sensor (model Pasco CI-6537 with a resolution of 0.03 N) measures the instantaneous weight as a function of time, W(t), of the flow of particles coming from a single opened exit hole of diameter D in a removable plate of thickness w. In agreement with other previous studies , the time series of weights coming from bottom and lateral exit holes behave as linear functions of time, t, W=at, where a is a constant. Thus, the temporal derivative of the weight is dW/dt=a and, additionally, dW/dt=m˙Exptg, where m˙Expt=dm/dt is the experimental mass flow rate. Using these last relations, we can compute the mass flow rate as m˙Expt=a/g. Through this procedure we have obtained reproducible values of the mass flow rate for each pair of parameters (D,w), we repeated the weight measurement seven times for each granular material and the pair (D,w) and, after that, we averaged the respective measurements, a similar technique has been used elsewhere ^[24-^26].

Figure 3 Sketch of the experimental array for lateral grains discharge through staggered holes depicted no to scale.  

It is important to comment that in all cases, during the measurements, the minimum distance between the granular free surface and any orifice was 10 cm in order to avoid the influence of the level of filling on the flow rate. Our previous works for gravity discharge of grains from lateral orifices ^[24, ²⁶, ^27] have shown no influence on height as long as the inner funnel flow is maintained.

3.1. Beach sand discharge rates

In a first stage of the experiments, we measured the mass flow rate of beach sand for bins with bottom exits and for four plates of different thicknesses, each plate having orifices with diameters given in Table I. As in other cases already reported ^[24-^26], we have not observed any dependence of m˙Expt on w. Moreover, measurements of m˙Expt plotted against ρg1/2D5/2, correlate linearly, as established in (9), which can be written as

m˙Expt=cρg1/2D5/2, (10)

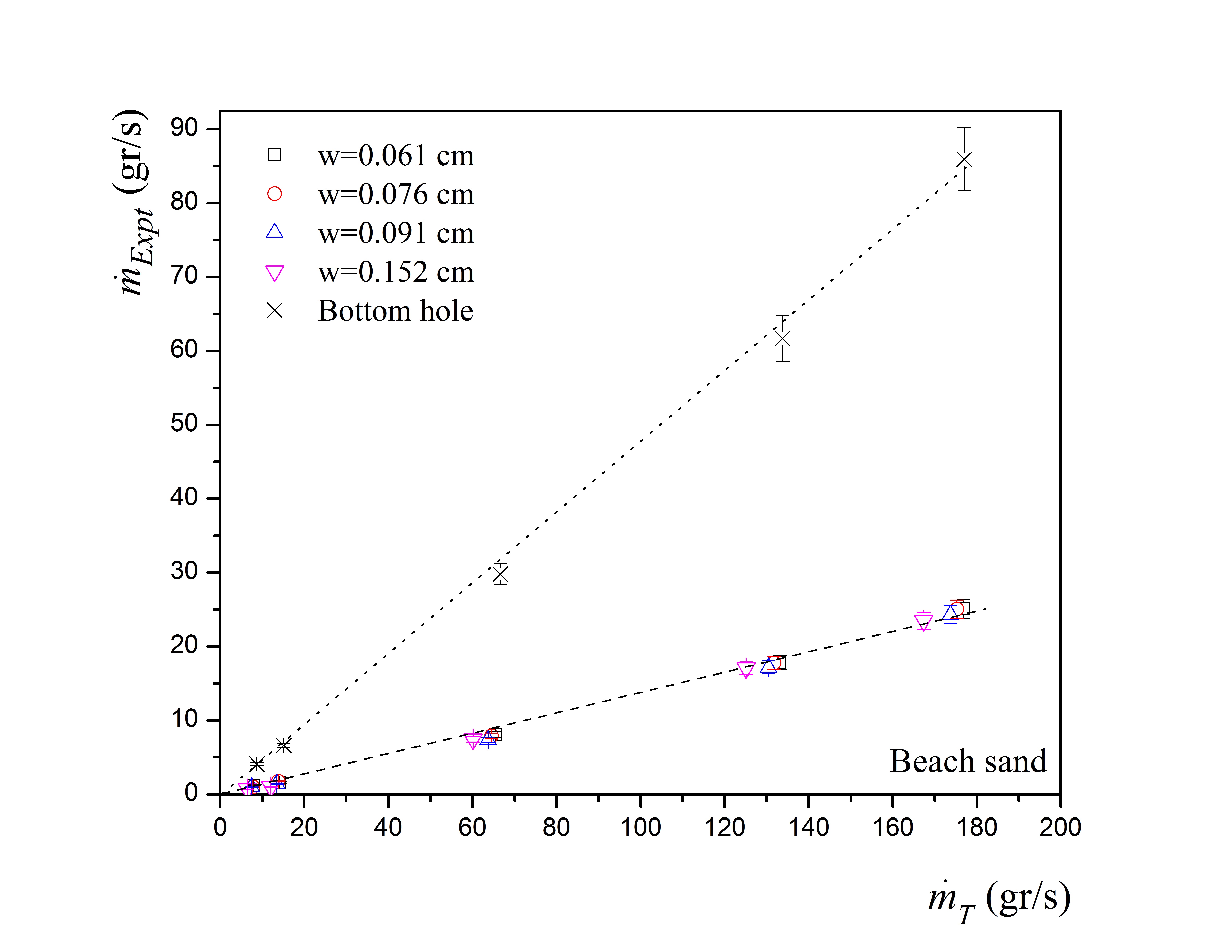
see Fig. 4, dotted straight line. In this case the discharge factor has the value c = 0.47. Clearly, the correlation (10) implies that the thickness of the bottom does not influence the flow rates and therefore the Hagen formula is satisfied.

Figure 4 Plot of m˙Expt versus m˙T=ρg1/2D5/2 for the discharge of beach sand from bins with bottom holes ( ×), the upper dotted straight line corresponds to formula (10) with c=0.47. On the other hand, color symbols correspond to the discharge of beach sand from lateral exit holes in plates of a given thickness, m˙Expt, versus m˙T defined either as in (3) (general formula) or, equivalently, as in (6) which is a linear correlation for w. In the computation of m˙T we assume given values of w (see inset). The straight line for these cases yields relations of the form m˙Expt=bm˙T where the slope has value b=0.14, formulas ( and 12. Error bars corresponding to the standard deviation are of 5%. 

The bulk density ρ=φρg, where φis the packing fraction and ρgis the grain density, is a quantity that must be introduced in the estimation of the phenomenological correlations (for instance, the term on the right hand side of (10)).

Clearly, the value of φdepends on the type of grain (angular, rounded, crystalline) used in a given experiment and the way the granular material is spilled in the bin (poured gently, ballistically deposited, poured and after vibrated, etc.). Recently, it has been experimentally shown ^[33] that in granular samples composed of amorphous grains, the packing fraction may be increased by first gently pouring the grains from the top and then introducing an overall vibration of the bin. Surprisingly, such changes on φ, and consequently the respective changes on the bulk density ρ, do not change m˙Exptdue to multiple factors that compensate each other. As aforementioned, in each one of our experiments we poured gently from the top the respective granular material obtaining a loose packing condition for the grains. Therefore, we specify that packing fractions were φ=0.58 for the beach sand, φ=0.60for Ottawa sand and φ=0.62for white sugar, values of φ which fall in the range of the reported values for sand ^[34] and sugar ^[35].

On the other hand, the corresponding measurements of the discharge rates for beach sand from lateral holes, m˙Expt, were performed first for a plate of a given thickness and for each one of the five orifices. After that, we changed the plate and for such a plate of fixed thickness we measured the respective flow rates for each orifice, and so on. After we used the four plates, with their respective holes, we have spanned the overall parametric space for the pair (D, w). In Fig. 4, to contrast the intensities of the flow rates from bottom and lateral holes, we also have plotted the respective experimental data m˙Expt for a given thickness (color symbols) against m˙T given by (6) also for a given thickness. As a result, a single line (dashed straight line) fits all experimental data which can be summarized in the correlation

m˙Expt=bρg1/2D5/2π2-θr-wD, (11)

in this case the dimensionless discharge factor b takes the value b = 0.14 . It is important to notice that the use of the complete formula (3), instead of the linear function on w (6), gives exactly the same fit for the discharge rate of small grains from thin sidewalls

m˙Expt=bρg1/2D5/2arctanDw-θr, (12)

it means that the use of both formulas is indistinct for w « D, but moreover, the leading term for the flow rate from lateral exit holes basically corresponds to the Hagen formula if (w/D) « 1 and (d/D) « 1.

To visualize the effect of the thin sidewall on the flow we plotted formulas (3) and (6) against w, now for a given diameter D. It produces once again five couples of curves (a dashed straight line and a continuous curve) shown in Fig. 5 for each value of D. The symbols in the plot correspond to the experimental data m˙Expt multiplied by a scale factor e to fit all referred curves. It yields the relationship m⋅T=em˙Expt because data fit very well the plot of each referred formula. The best fitting factor has the average value e=7.14. All this procedure along with the resulting formula (11) also let us find that e = 1/b which, in fact, is satisfied.

Figure 5 Plot of the phenomenological formulae m˙T, referred as the general formula (3) (continuous curves) and (6) (dashed straight lines) for beach sand as a function of wfor fixed values of D (see inset). The linear formula on w given by (6) only is valid for w « D. The experimental data m˙Expt were scaled to fit curves m˙T as em˙Expt where the mean value of e has the average value e = 7.14 , it corresponds to have the value b = 0.14 as is reported in Fig. 4. Error bars corresponding to the standard deviation are of 5%. 

The achievements of the present analysis merits more discussion: a) for lateral outflows data fit, in the region of thin thicknesses, both the straight lines and the curves, however the linear correlation (11) is only valid for w « D. 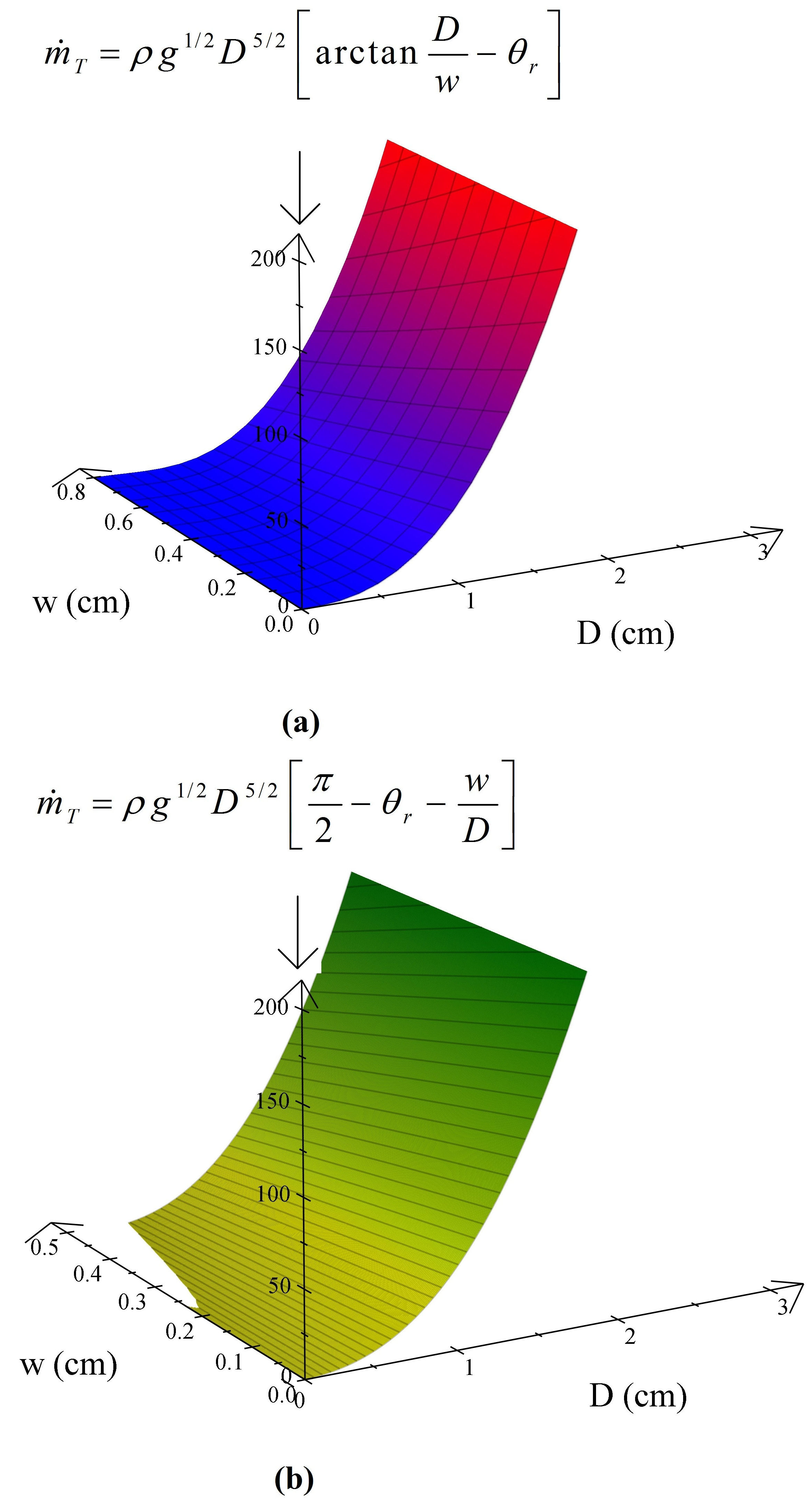On the other hand, we have plotted the curves in the overall domain of the general formula (6) since it predicts, in the limit of thick face walls, the arrest of the granular flow, just when the thickness reaches the value w=tanθr/D, which was experimentally evidenced in other studies with small and large grains; b) we have remarked in the building of plots of Fig. 5 that of course, for any curve, D must be kept constant because strictly the phenomenological formula mT=mT(D,w) is actually a two-parameters function and consequently it represents a surface in the parametric three-dimensional space.

In Fig. 6 we depict for beach sand, the plots of the phenomenological mass flow rates (surfaces) m⋅ when both D and w change, Fig. 6 (a) gives the continuous plot obtained from the general formula (3) and Fig. 6 (b) shows the continuous plot of the linear approximation on w, (6). A fundamental fact for each surface in Fig. 6 is that a mass flow rate reaches a given value, say m˙T(D,w), only for a specific couple of values of (D, w): mathematically it means that m˙T(D,w) is an injective function or one-to-one function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. It is qualitatively noticed in Fig. 6 (b) that for approximately w > 0.2 cm and small values of D it seems that there is no flow. It is an inherent error of the linear approximation because, as aforementioned, the no flow-condition follows the relationship w=tanθr/D; if we use the value θr=0.57 and the smaller diameter D = 0.51 cm, given in Table II, it yields that the minimum sidewall thickness to arrest the flow is w ≈ 0.8 cm for such a diameter (see also Fig. 5, case D = 0.51 cm). This is our main reason to limit the maximum value of w in plot of Fig. 6 (a) up to this same value. It is apparent that the Hagen and Beverloo formulas for bottom holes lack of a parametric behavior so plentiful.

Figure 6 3D plots of the phenomenological mass flow rate formulae for beach sand, m˙T, as a simultaneous function of (D, w) : (a) plot of formula (3) and (b) plot of relationship (6). 

3.2. Ottawa sand and sugar flow rates

Our goal is to reach general experimental results to validate the phenomenological formulas for thin side faces. Due to it, cases of Ottawa sand and granulated sugar lead us to situations where D∼6d (large particles in respect of the orifice size). It is the reason why granular continuous flows from the two smaller exit holes, in flat bottomed bins and in bins with lateral orifices, do not occur for both materials.

As for beach sand, neither Ottawa sand nor sugar allowed us to find any dependence of m˙Expt on w for bottom exits. Given all these facts, we have plotted for bottom exit bins the quantity m˙Expt2/5versus D in order to determine the shape-factor k for Ottawa sand and sugar (see, for instance ^[7] ). We have found for the three largest exit orifices that k=1.96 for Ottawa sand and k=1.94 for granulated sugar. Later, it is straightforward to build the plots m˙Expt as a function of ρg1/2D-kd5/2 for both materials. In Fig. 7 the best corresponding plots for bottom exits, yields

m˙Expt=cρg1/2D-kd5/2, (13)

Figure 7 Plot of m˙Expt versus m˙T=ρg1/2D-kd5/2 for the discharge of (a) Ottawa sand and (b) granulated sugar from bins with bottom holes ( ×); the upper dotted straight lines corresponds to formula (13) with c = 0.74 for Ottawa sand and c=0.69 for granulated sugar, respectively. On the other hand, color symbols correspond to the discharge of (a) Ottawa sand and (b) sugar from lateral exit holes in plates of a given thickness, m˙Expt, versus m˙T defined either as in (1) (general formula) or, equivalently, as in (5) which is a linear correlation for w. In the computation of respective m˙T we assume given values of w (see inset). The straight line yields a slope with a value b = 0.23 for Ottawa sand and b = 0.21 for granulated sugar. Error bars (standard deviation) are of 5%. 

where c = 0.74 for Ottawa sand and c=0.69 for granulated sugar. We also have plotted in Fig. 7 the experimental data of the flow rates for the lateral orifices against the quantity ρg1/2D-kd5/2arctanD/w-θr for each fix w, as indicated in the plot itself. Thus, for lateral orifices we found correlations of the form

m˙Expt=bρg1/2D-kd5/2arctanDw-θr (14)

where b = 0.23 for Ottawa sand and b = 0.21 for granulated sugar. The linear formula on w allows us to find that

m˙Expt=bρg1/2D-kd5/2π2-θr-wD, (15)

with the same values of .

The effect of the sidewall thickness on the flow rate is very similar to that found for beach sand, now we have plotted formulas (1) and (5) against w, for a given diameter D, and following the scaling for the experimental data. Thus, in Fig. 8 we show plots of the form mT=em˙Expt where e is the scale factor for each case. For Ottawa sand and sugar we found that e=4.34 (b=0.23) and e=4.76 (b=0.21), respectively. The three-dimensional plots for m˙T(D,w) for Ottawa sand or for sugar are similar to those for beach sand and we do not feature them anymore.

Figure 8 Plot of the phenomenological formulae m˙T, referred as the general formula (3) (continuous curves) and (6) (dashed straight lines) for (a) Ottawa sand and (b) for sugar, as functions of wfor fixed values of D (see inset). The linear formula on w given by ( 6) is valid only for w « D. The experimental data m˙Expt were scaled to fit curves m˙T as em˙Expt where the mean value of e has the average value e=4.34 for Ottawa sand and e=4.76 for sugar. Error bars (standard deviation) are of 5%. 

4. Remarks and conclusions

Up to now, experimental studies have bestowed little importance to thickness sidewall of vertical bins in order to estimate its influence on the flow rate of grains. Here, we have carefully checked the validity of the Hagen and Beverloo phenomenological formulas, used in bottom exit silos, following a systematic change of the wall thickness in experiments with three different granular solids. We have tested that through the use of our simple formula for the mass flow rate for lateral orifices, that encompasses variations of the orifice diameter and the wall thickness ^[24-^27], we could describe accurately the lateral outflows in the limit of thin thickness of the sidewalls (w « D).

In such cases we found that the general formula ((12) or (14) depending on the grain size) is valid for any wall thickness, and also an approximate (rule of thumb) formula ((11) or (15) depending on the grain size), is also valid for small thicknesses. Our experimental results allow us to conclude that the Hagen and Beverloo formulas were valid up to a factor of the form [arctanDw-θr]≃[;π/2-θr-w/D], i.e., the non inclusion of this factor in the estimation of the flow rate in bins with thin sidewalls involves errors quantified by such factors. Plots in Figs. 5 and 8 show visually and quantitatively actual deviations of the flow rates in bins of thin thickness w, respect to the ideal cases of zero thickness (w = 0). Physically, the effect of w on the granular discharge through lateral holes is non negligible.

An example of how to avoid the influence of the wall thickness on the mass flow rate through orifices in lateral sidewalls, of large thickness, was reported by Zhou et al^[36] who used rectangular orifices bevelled along its aperture in order to have an effective angle of wall αeff close to π/2. Strategies of this type may be obtained or justified by alluding our general formulas (1) or (3).

In an ample context, this study completes the formulation of a correlation to accurately describe the mass flow rate for lateral and circular exit holes of any diameter D and any wall thickness w. We also have shown that the geometrical representation of m˙T(D,w) allows us to show a lot of possibilities for the occurrence of granular flow across sidewalls. Finally, we believe that this study lets us reach a deeper understanding of the mechanics of the discharge of non cohesive granular materials.