1. Introduction
Yttrium aluminium borate YAl3(BO3)4 crystals(YAB) have excellent physical and chemical properties such as high laser damage threshold, good chemical stability, broad transparency range, large nonlinear optical coefficients, proper refractive index dispersion for phase matching, high thermal and mechanical resistance, and so on [1-3]. It is interesting that YAB can be expediently doped with transition or rare earth impurity ions. In general, these above properties are closely related to the local structure and electronic states of the impurity ion in the host, which can be effectively investigated by means of electron paramagnetic resonance (EPR) technique. So many related experimental and theoretical works have been done in the past years [4-8]. For instance, EPR studies were carried out for Yb3+ doped YAl3(BO3)4, the g factors g ∥ and g ⊥ and hyperfine structure constants were also measured for the trigonal Yb3+ center recently [8]. Dammk et al. calculated the EPR parameters by the method of crystal field theory. In the calculation, they directly used crystal field (CF) parameter which is not connected with the local crystal structure [9]. There are some mistakes found in their paper, for example, the wrong representation of the irreducible tensor operators lead directly to various errors in their calculation values of EPR parameters [10]. Li et al. not only recalculated the EPR values using the same CF parameters, but also theoretically studied the EPR parameters by the means of the first-principles [10]. Above theoretical results are also poor agreement with the experimental data, see Table I. As well known, the superposition model is mostly used in analysis of experimentally determined crystal field parameters. When the crystal structure of a magnetic ion is available, the SH principle is very expediently employed to study the local physical properties of the magnetic ion with its surrounding ligands. So in this paper, the EPR parameters are explained by the aid of the SH model and the perturbation formulas of 4f13 ion in trigonal symmetry. From these formulas, the EPR parameters g ∥ g ⊥ A ∥ and A ⊥ for Yb3+ center in YAl3(BO3)4 crystal are reasonably explained and the angle distortion of impurity Yb3+ center is suggested. The results are discussed.
TABLE I EPR parameters for the trigonal Yb3+ center in YAl3(BO3)4 crystal.
| g ∥ | g ⊥ | A∥ (171Yb) | A⊥ (171Yb) | A∥ (173Yb) | A⊥ (173Yb) | |
| This work | 3.6702 | 1.7014 | 959.4(30) | 441.8(16) | 263(2) | 121(1) |
| Cal. [9] | 3.257 | 2.042 | 838 | 529 | 231 | -146 |
| Cal. [10] | 4.000 | 1.391 | 1032 | 360 | 285 | 99 |
| Expt. [8] | 3.612(1) | 1.702(1) | 958(1.6) | 454(3.4) | - | - |
2. Calculation
The crystal structure of YAl3(BO3)4 belongs to the space group R32 with three molecules per unit cell [11]. In this structure, the coordination polyhedron of Y3+, Al3+, and B3+ is trigonal prism, octahedra and triangles surrounded by the oxygen ions. The Yb3+ ionic radius (0.858 A) is close˚ to that of Y3+ (0.893 Å), whereas it is much larger than that of Al3+ (0.51 Å) or B 3+ (0.23 Å) [12-13]. When Yb3+ is doped into the lattice of YAl3(BO3)4 crystal, it can substitute for the octahedral Y3+ site and conserve the local trigonal symmetry, because of their similar ionic size, and no charge compensation is required [12]. In the following, the local structures of the Yb3+ centers are to be theoretically studied from the perturbation formulas of the EPR parameters.
The free Yb3+ ion has a 4f13 electronic configuration with a 2F7/2 ground state and a 2F5/2 excited state [14]. When Yb3+ ion is located on the Y3+ site of YAl3(BO3)4 crystal, the free ion ground 2F 7/2 and excited 2F 5/2 states of free-ion splits into three and four Kramers doublets under trigonal symmetry crystal field, respectively. Because of the J-mixing between J = 7/2 and J = 5/2 states via crystalfield interaction, the basis wave function of ground doublet Γγ(or Γγ') may be gained by diagonalizing the 14 × 14 energy matrix for 4f13 ion in trigonal symmetry field. Thus, one obtains
where the subscript γ or γ’ denote the two components of Γ irreducible representation. M J1 and M J2 are halfintegers in the ranges −7/2 to 7/2 and −5/2 to 5/2, respectively [15]. The coefficients C(2 F 7/2 ; Γγ(γ’)M J1 ) or C(2 F 5/2 ;Γγ(γ’)M J2 ) can be determined by diagonalizing the 14 × 14 energy matrix containing the 2 F 7 /2 and 2 F 5 /2 states.
The perturbation Hamiltonian for the rare earth ion in the crystal under an external magnetic field can be expressed as [14]
where Ĥ SO is the spin-orbit coupling interaction and Ĥ CF is the crystal field Hamiltonian. Ĥ SO can be written as:
where ζ is the spin-orbit coupling coefficient, here ζ ≈ 2907 cm−1 [15],
The crystal-field interaction Hamiltonian Ĥ CF for a 4f13 ion may be written in terms of the irreducible tensor operators under trigonal symmetry [14]:
Where
The Zeeman interaction Ĥ Z can be expressed in terms of the Lande factor g J and the angular momentum operator Ĵ as [14]
and the hyperfine interaction term can be denoted as Ĥ
hf
= PN
J
To study the EPR spectra and the local structure for YAl3(BO3)4:Yb3+, the perturbation formulas of the SH parameters for a 4f13 ion under trigonal symmetry are adopted [16]:
Here g
J
are the Lande factors for various
2S+1
L
J
configurations, which are gained from Refs. 14 and 15. The operator Ĵ
+(= Ĵ
X
+iĴ
γ
) (or
Based on the semi-empirical superposition model [17,18], the crystal field parameters
Where the coordination factor
In the YAl3(BO3)4 crystal, the host Y3+ ion is coordinated by six nearest-neighbour O2− ions with the cationanion distance R H ≈ 2.302 Å [14], the local structure data are given as follows: θ 1 = θ 2 = θ 3 ≈ 55.188o, φ 1 ≈ −157.911o, φ 2 ≈ −37.911o, φ 3 ≈ 82.089o, θ 4 = θ 5 = θ 6 ≈ 124.812o, φ 4 ≈ −142.089o, φ 5 ≈ −22.089o, φ 6 ≈ −97.911o, [12], see Fig. 1. When a impurity ion substitutes for a host ion, R j 6= R H because of the different ionic radii of Yb3+ and the replaced Y3+ ion. The new cation-anion distance Rj can be reasonably estimated from the approximate formula [19, 20]
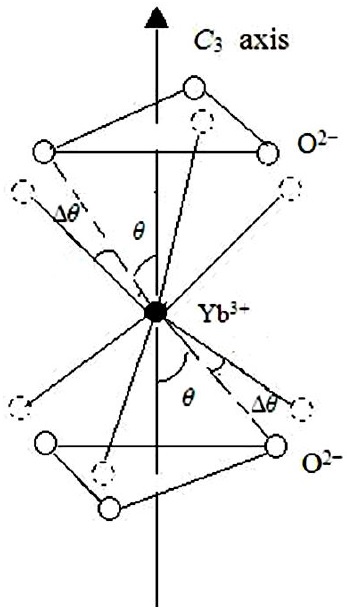
FIGURE 1 Local structure for the trigonal Yb3+ center in YAl3(BO3)4. The impurity Yb3+ on the octahedral Y3+ site experiences the angle distortion ∆θ(≈ 3.98o).
where r i and r h are the ionic radii of impurity and the host ion, respectively. For YAl3(BO3)4:Yb3+, r i ≈ 0.858 A, r h ≈ 0.893 Å [13]. Because of the covalency of Yb3+-O2− bonds, the orbital reduction factor k may be brought in, here k ≈ 0.866.
When the host cation is replaced by the impurity in YAl3(BO3)4 crystal, it can be expected that the local structure distortion ∆θ would occur. Here it is taken as an adjustable parameter. When the above superposition model intrinsic parameters are substituted into Eqs.(6-7) and matching the calculated EPR parameters to experimental results, we have ∆θ ≈ 3.98o. The comparisons between the calculated and experimental EPR parameters are shown in Table I.
3. Discussion
From Table I, one can find that by using the theoretical formulas of EPR parameters and the superposition model parameters given in this paper, the calculated results of EPR parameters g ∥, g ⊥, A ∥ and A ⊥ for Yb3+ ion at the trigonal Y3+ site in YAl3(BO3)4 crystal based on the enhancive angle distortion ∆θ show reasonable agreement with the observed data. Thus, these experimental data are reasonably explained, suggesting that the above formulas and these parameters adopted in this paper are reasonable.
Substitute the above superposition model intrinsic parameters into Eq. (8), the crystal field parameters are obtained and shown in Table II. These crystal field parameters are comparable to previous works. As mentioned before, the superposition model intrinsic parameters t k and Ā k (R 0) adopted in this paper are taken from the same impurity Yb3+ in Bi4Ge3O12 crystal. Using these parameters and diagonalizing the complete 4f13 energy matrix in the trigonal field, the energy spectra are computed, which are the foundation of further calculation, see the Table III. One can find that the calculated energy levels reasonably coincide with the experimental results. So the data of the intrinsic parameters used in this paper can be regarded as acceptable.
TABLE III The crystal-field energy levels for Yb3+ in YAl3(BO3)4 crystal (in cm−1)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Cal | 0 | 83 | 176 | 569 | 10194 | 10283 | 10666 |
| Expt. [21] | 0 | 94 | 185 | 581 | 10194 | 10277 | 10672 |
We find the local structure data of impurity Yb3+ including the cation-anion distance and the azimuthal angle of the oxygen atoms are different from those of the host Y3+ ion. The cation-anion distance of Yb3+-O2− can be reckoned by the aid of empirical equation Eq. (9). The azimuthal angle undergoes an angle distortion ∆θ ≈ 3.98o. This defect model of Yb3+ ion in YAl3(BO3)4 is similar to other rare or transition impurity ion in the same host crystal. Obviously, the theoretical result of the ∆θ as well as the hyperfine structure constants of 173Yb3+ isotopes obtained in this work still remains to be further verified with experimental studies.











 nueva página del texto (beta)
nueva página del texto (beta)


