1. Introduction
Aluminum doped zinc oxide (AZO) thin films have many important applications, principally as sensing and optoelectronic material [1]. Another interesting application is related to its use as transparent conductor [1,2] in solar cell technology. AZO films have some advantages such as higher transmittance even at near infrared wavelengths than ITO [1]. Then, the electrical characterization of someone heterojunction formed with AZO films is of great importance. One of this heterojunction is the Shottky barrier formed with a metal contact as for instance the conductive tip of an Atomic Force Microscope scanning on its surface. Few works are related with the AZO heterojunctions [3] and few talk about of the Schottky nano-contact formed with an AFM tip [4]. The leakage current of a Schottky contact strongly depends on the barrier height. A Schottky barrier of a metal-semiconductor interface must be high in order to reduce the leakage current. Then, it is also very important to research the barrier height of the Schottky nano-contact on AZO thin films by means of the C-AFM technique as is made in this work.
On the other hand, it is well known that Atomic Force Microscopy (AFM) is an
important tool in the nanotechnology as for example in the investigation of
electrical properties by means of Scanning Tunneling Microscopy or the conductive
AFM technique [5-7]. The conductive Atomic Force Microscopy (C-AFM) technique has
been widely used to measure the surface electrical current of different materials
such as conductors, semiconductors, dielectric or even biological materials [8-14].
Werner Frammelsberger et al.[8] reported electrical measurements of SiO
2. Materials and methods
2.1. Synthesis of the samples
As was detailed in a previous work [2], an
ultrasonic spray pyrolysis deposition system was used. Source solutions of
0.3032 molar concentrations of zinc acetylacetonate and 10% of aluminum
acetylacetonate (Sigma Aldrich) dissolved in N, N-dimethylformamide (N,N-DMF)
(Mallinckrodt) were prepared. A mist from the materials source solution is
produced by means of an ultrasonic generator operated at 0.8 MHz. A high purity
air at flow rate of approximately 10 l/min was used as the carrier gas in order
to transport the mist to the surface of the substrate during five minutes. A
molten tin bath was the substrate heater. Substrates of Corning 7059 glass which
were carefully cleaned using a well-known cleaning procedure [23] were used. Simultaneously, substrates
of stainless steel discs were used as well. The depositions were carried out at
substrate temperatures of 500
2.2. Atomic Force Microscopy experimental configuration
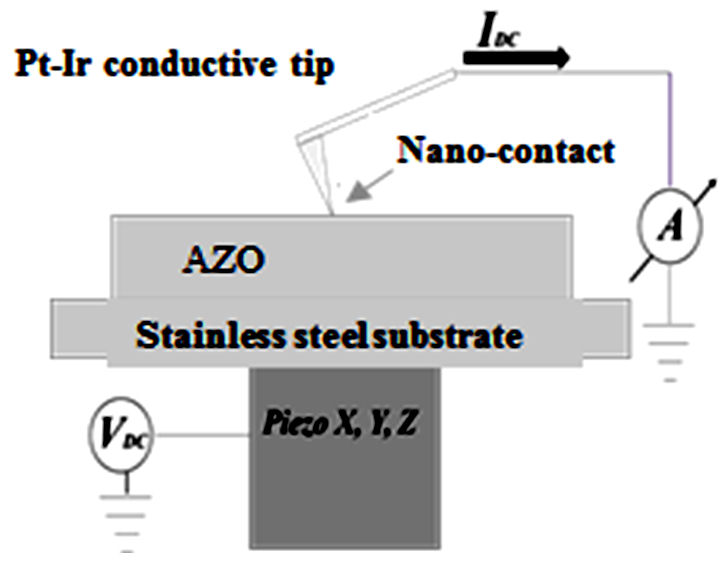
The electrical characterization was performed using a JSPM-5200 microscope
(JEOL). In order to guarantee a good electrical contact of the AZO sample, these
were deposited on stainless steel substrates, as specified in Sec. 2.1. Then,
metal-semiconductor unions or Schottky nano-contacts were formed with the
As was mentioned above, for the characterization of this nano-contact the
conductive AFM method in contact mode [8-14] was used. The used tip
was the SCM-PIT model (BRUKER) which has a nominal spring constant of

Figure 2 Scanning Electron Microscopy image of the
Now, using the method proposed by Sader [33], we proceeded to estimate the value of the constant “
Where,
The volume of the beam can be determined by means of Eq. (2):
Where
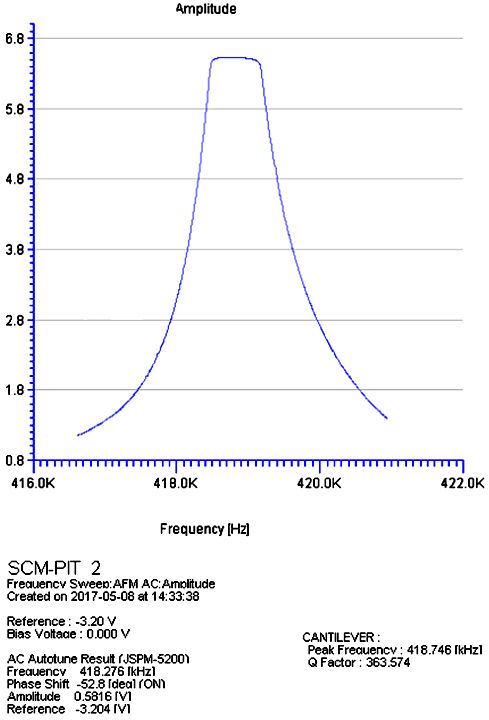
The frequency of the “
From Fig. 3, the value of
3. Methodology of the conductive AFM
Before taking the electrical measurements of the AZO thin films, it was necessary to
calibrate the conductive mode of the microscope since the I-V curve depends
drastically on the microscope parameters such as magnitude of the applied tip force
[11,24], time of scanning (clock), the control circuit gains (Pre Amp Gain
and Line Current), type of ramp and voltage range, among others [25]. Many authors do not report the
calibration of theirs measurements due to the difficulty of obtaining the optimal
software parameters of the microscope. In this section, we establish a methodology
for optimizing such parameters and set the best experimental conditions in order to
chracterize the samples. We think that the most important parameter is the magnitude
of the applied tip force. In order to adjust such parameter, a metallic copper slide
was used and also knowing that its I-V characteristics satisfies the Ohm’s law. In
the same configuration of Fig. 1, over the
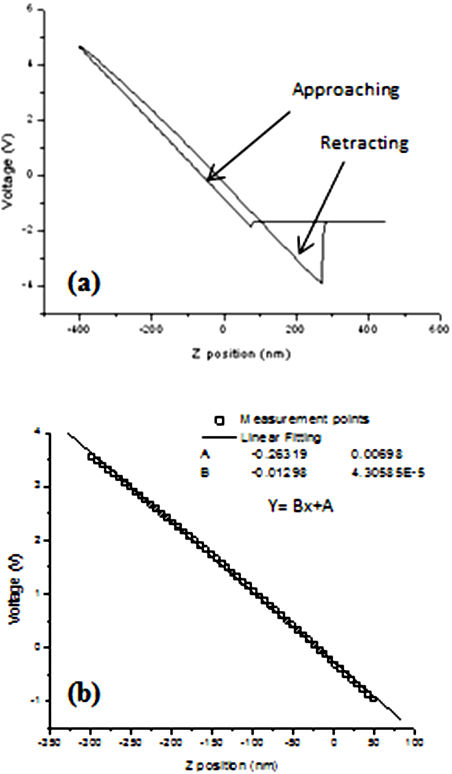
steel substrate a copper slide sample was placed. Then, the force curve (FC) was
measured using the standard contact mode of the Microscope as is shown in Fig. 4a. After that, a linear fitting in the
retraction region was performed (See Fig. 4b)
resulting a value of the slope curve equals to -0.01298 V/nm. According to the
operation manual of the microscope [25], with
the reciproc of the absolute value of the slope the sensibility parameter was
calculated, resulting in 77.0416 nm/V. Introducing in Eq. (3), the sensibility value
(a), the elastic constant (k) and the reference voltage
After the force was determined, the measurements of the I-V characteristics were
performed adjusting the electric control parameters using the same copper slide. In
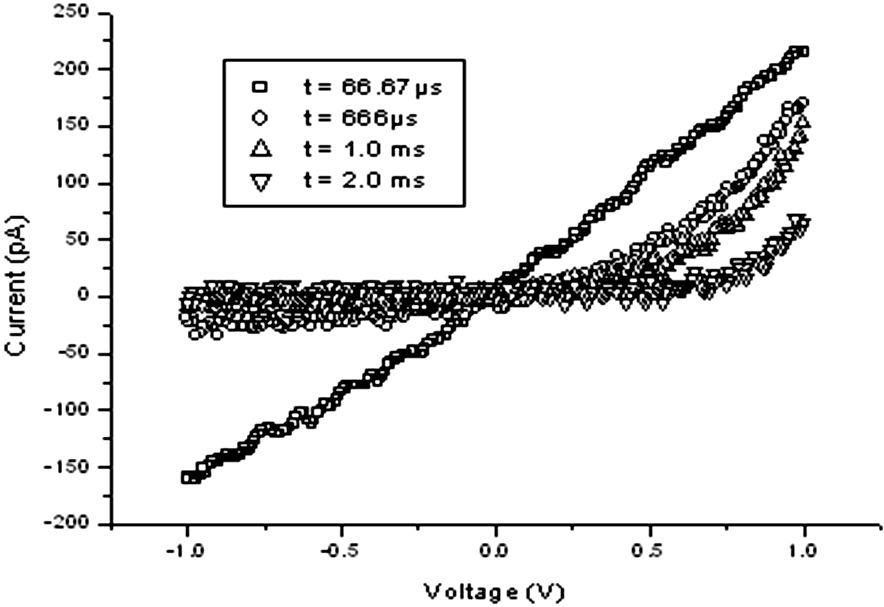
Fig. 5, it is shown the I-V curve in the
range of -0.5 to 0.5 V (Fig. 5a) and from -1 to
1 V (Fig. 5b). These curves were measured under
the following parameters conditions;
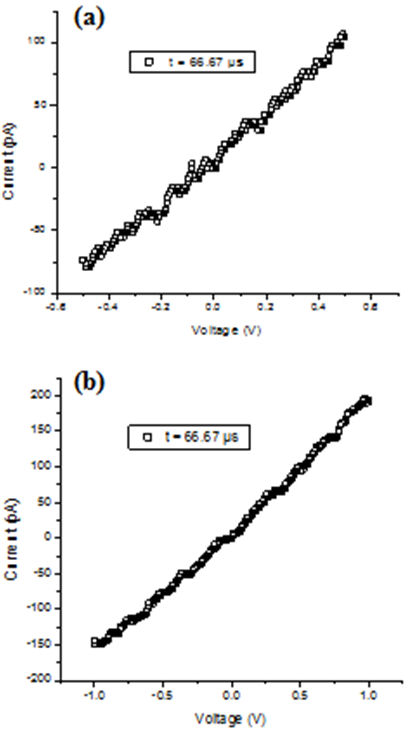
Figure 5 I-V characteristics for copper slides measured from (a)
From Fig. 5, it can be observed a linear
behavoir characteristic of the Ohm’s law for a metal such as copper. It can be
mentioned that the behavoir of the I-V characteristics is quite sensitive to the
scanning time (
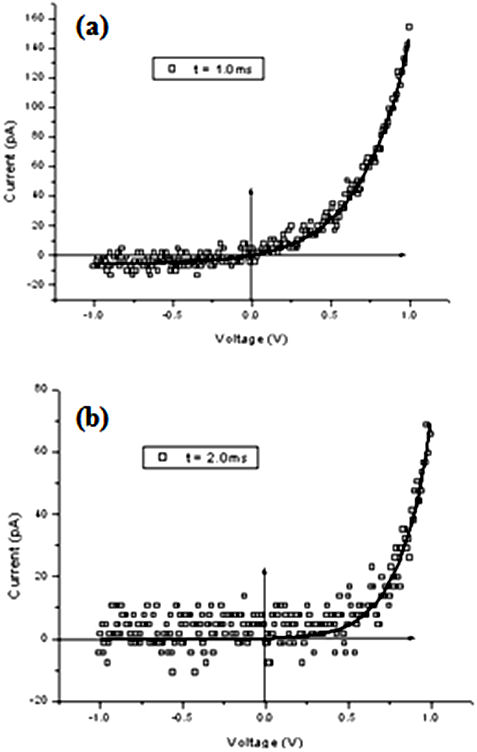
It is observed that for short scanning times of the order of
4. Results and discussion
As shown in Fig. 8, topography and linear
current images of the surface of the AZO thin films were taken at a scan area of

Figure 8 Topography (a) and their corresponding linear current image (b) of
the surface of the AZO thin films. The scanned area is
With
Where
Moreover, the value of
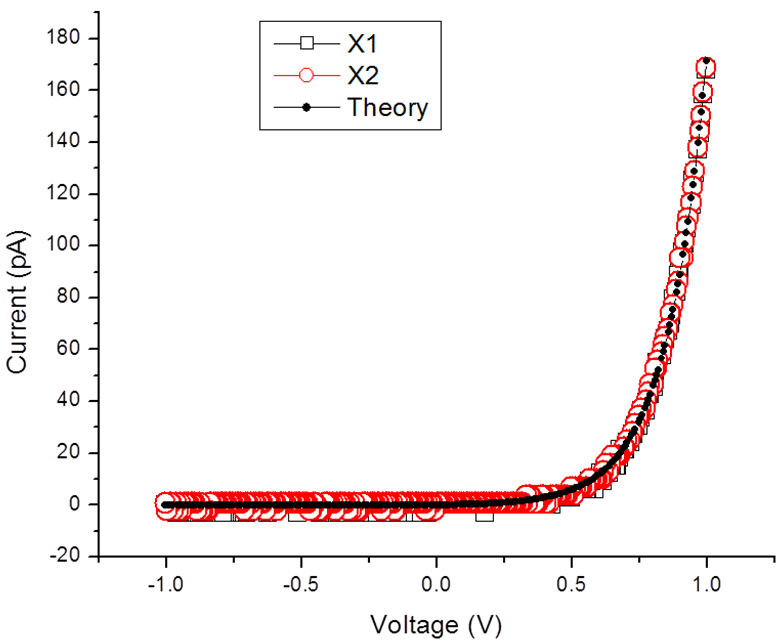
Table I Summary of the Schottky parameters results by means of the thermionic
fitting model, measurement with C-AFM, effective area
| Position | Reversecurrent I0 (A) | Ideality factor (n) | Schottky barrierheight (eV) |
|---|---|---|---|
| x 1 | 2 .05 × 10 −16 | 1.39 | 0.64 |
| x 2 | 2 .79 × 10 −16 | 1.50 | 0.63 |
| x 3 | 8 .15 × 10 −16 | 1.80 | 0.60 |
| x 4 | 1 .09 × 10 −15 | 1.91 | 0.59 |
| x 5 | 1 .71 × 10 −15 | 2.11 | 0.58 |
It is also important to mention that the
Since the 1965 year, a value of 0.75 eV of the Pt-ZnO barrier height was reported by
Mead [28], obtained using internal
photoemission yield spectroscopy. K. Ip et al.[15], reported a value of
In relation to contacts different to Pt, the Schottky barrier heights of
As was mentioned in the introduction, there are few works related to the measurement of Schottky barrier height on ZnO or AZO thin films by means of C-AFM. For instance, W. I. Park et al. [30] reported measurements for ZnO nanorods with Au coating contact tips by means of current-sensing Atomic Force Microscopy (CS-AFM). Recently, Periasamy and P. Chakrabarti [24] measured a ZnO nanoneedle array with Pd coating contact tips by means of CS-AFM resulting in 0.76 eV for the Schottky barrier height and 7.41 the value of the ideality factor. It can be noted the large value of the ideality factor, however it is in accordance with the values reported in this paper (see Table I). During I-V measurements in Ref. 24, a constant normal force of 15 nN was kept between the tip and ZnO nanoneedle array. In this work, an applied higher normal force in the order of 249.820 nN of absolute value, as was determined from the calibration of the microscope in the Sec. 2.3, is suggested. Moreover, it must be taken into account the scanning time of the order of 2 ms in order to obtain smaller reverse current as shown in Fig. 8. These suggestions should improve the measurements of the Schottky height barrier and the ideality factor. Specifically for Pt nano-contacts, Shao ZhengZheng et al. [26] reported an ideality factor of 3.2 by means of C-AFM measurements that is in accordance with the values reported in this work (see Table I).
Is important to make mention that in this experimental work, the effect of the
relative humidity was not considered on the made electrical measurements and
therefore on the height Schottky barrier estimate. However, this work proposes
considering humidity as one more factor that affects the deviation of the ideal
factor “
5. Conclusions
Values of the height of the Schottky barrier on Aluminum-doped ZnO thin films were
estimated using the conductive AFM technique. The estimated values were in the range
of











 nova página do texto(beta)
nova página do texto(beta)