1. Introduction
Fractional calculus (FC), involving derivatives and integrals of non-integer order, is the natural generalization of classical calculus, which during recent decades has become a powerful and widely used method for better modelling and control of processes in many areas of science and engineering [1-5]. The fractional derivative are non-local operators because they are defined using integrals. Therefore, the time fractional derivative contains information about the function at earlier points, thus it possesses a memory effect. Such derivatives consider the history and non-local distributed effects, which are essential for better and more accurate description and understanding of complex and dynamic system behavior [6-18]. Another peculiarity of FC is the inclusion of new degrees of freedom to the system by increasing the information that can be obtained from the nature of the phenomenon in question. Due to the lack of a consistent geometric and physical interpretation of the fractional derivative, several definitions exist [19] . The most useful definitions are the Riemann-Liouville and Caputo fractional derivatives, however, despite the accurate results obtained with the Riemann-Liouville and Caputo fractional derivatives, they have the disadvantage that their kernel has a singularity at the end point of the interval. To avoid this problem, [20] proposed the Caputo-Fabrizio derivative (CF). This is a new fractional-order derivative that does not have any singularity. The main advantage of the CF is that the singular power-law kernel is now replaced by a non-singular exponential kernel, which is easier to use in theoretical analysis, numerical calculations and real-world applications. Based on this new derivative, some interesting studies can be found in [21-26]. However, some researchers have concluded that this operator is not a derivative with fractional order, but instead a filter with fractional parameters [27] . Solutions due to an exponential kernel shows an exponential decay similar to the classical integer order model, therefore, the CF with an exponential kernel has limitations in describing phenomena with non-exponential nature, for example, anomalous relaxation [28] . To correct this deficiency, two fractional derivatives in the Caputo and Riemann-Liouville sense were defined by Atangana-Baleanu (AB) , based on the generalized stretched Mittag-Leffler function. These new derivatives have been applied to different systems in 30-33.
All definitions of fractional derivatives satisfy the property of linearity, but properties, such as the product rule, quotient rule, chain rule, mean value theorem and composition rule and so on, are lacking in almost all fractional derivatives. These inconsistencies and many more have raised many problems in real applications and have limited the possibilities to explore these fractional calculations. To avoid these difficulties, proposed to extend the ordinary limit definitions of the derivatives of a function called conformable derivative. This conformable derivative has attracted the interest of researchers, as it seems to satisfy all requirements of the standard derivative [35-43].
In this work we try to analyze the difference between the most important definitions of fractional derivatives in a simple system. In particular, we will applied the Caputo (C), Caputo-Fabrizio (CF), Atangana-Baleanu (AB) fractional derivatives and the conformable derivative (conf), in the study of a RC circuit with DC and AC sources.
2. Some definitions of fractional derivatives
The Caputo fractional derivative of order γ is defined by [44]
with
where
We have taken the normalization function properties
where
As can be seen, the Atangana-Baleanu fractional derivative (5) is the natural generalization of the Caputo-Fabrizio derivative (2). The AB derivative has a non-singular and non-local kernel, its Laplace transform is given by [29],
where
In [34], the conformable derivative definition
is given. It is defined as: Let
for all
If f is
The most important properties of this conformable derivative of order γ are given in , we only take the needed expression
if f(t) is (n+1) differentiable at t>0.
3. The ordinary RC circuit
The equation governing the behavior of the RC circuit is
where τ=RC is the time constant of the system measured in seconds,
R is the resistance measured in Ohm’s, C is
the capacitance measured in Farads, V(t) is the voltage on the capacitor and
e(t) is the source. Taking the initial condition as V(0)=0, and
assuming a constant source
This is the equation that describes the behavior (charging in our case) of a RC circuit with constant source, where its components are ideal. The solution (12) exhibits an exponential decay, when t→∞ the voltage V(t→∞)→ϵ 0, a constant. In the case of an alternating source with angular frequency ω and initial condition V(0)=0, we get
the solution is given by
4. Fractional RC circuit
Our purpose in this section is to obtain a consisting fractional differential equation corresponding to (11). In [48] a systematic way to construct fractional differential equations has been proposed. We transform the ordinary derivative in a fractional derivative in the following way
where τ=RC is the time constant measured in seconds. The term on the left in (15) has dimensions of s-1, and the one on the right is also. Substituting (15) in (11) we obtain the corresponding fractional differential equation for the RC circuit
This fractional differential equation has been studied in[49 50]. Our main aim is to analyze this differential equation using different definitions of fractional derivatives including local and non-local, make a comparison of these derivatives and give some conclusions about the way behavior of the solutions.
4.1. RC with Caputo fractional derivative
We consider the fractional differential equation (16) taking into account the
Caputo fractional derivative (1), assuming the initial condition be
and solving for
Using the Laplace inverse transform , we obtain
where
As a consequence, the Mittag-Leffler function interpolates for intermediate time
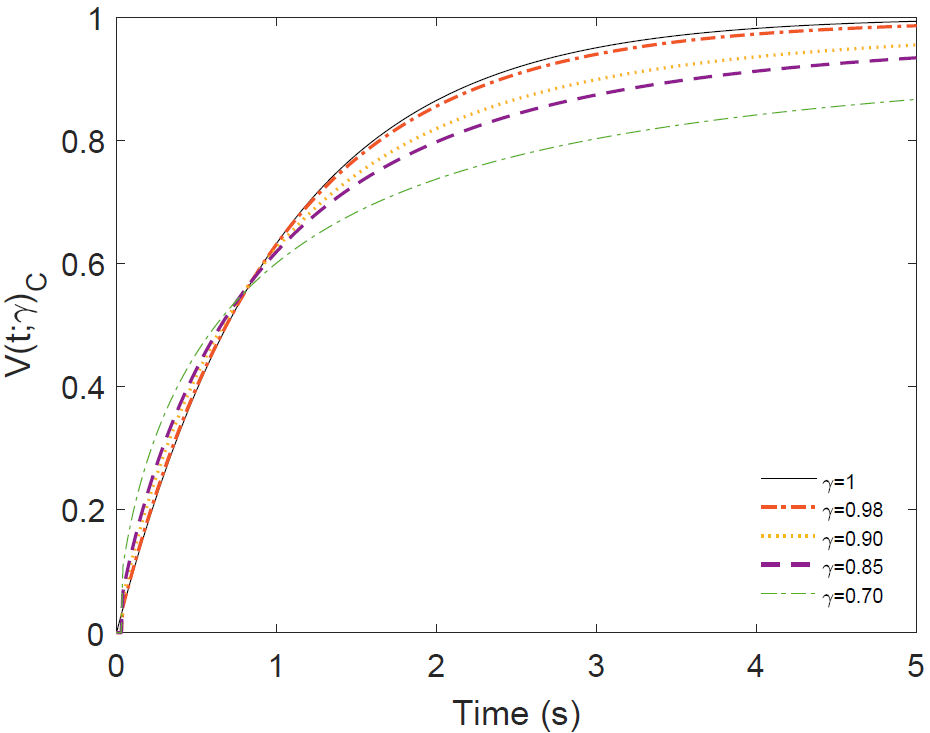
Figure 1 Plot of the equation (19) for some values of γ corresponding to voltage across the capacitor in the RC circuit of DC.
In Fig. (1), it is observed that in the case
of the fractional derivative of Caputo, when the time is between zero and very
close to 1 s, the voltage rapidly decays as a stretched exponential depending on
the value of
In the case of an oscillatory source, from (16), we have
where
We take the highest power of
Then, the inverse Laplace transform gives
4.2. RC with Caputo-Fabrizio fractional derivative
Applying the Caputo-Fabrizio derivative (2) and the Laplace transform (4) to the
fractional differential equation (16) with the same conditions
where
Then, the inverse Laplace transform gives
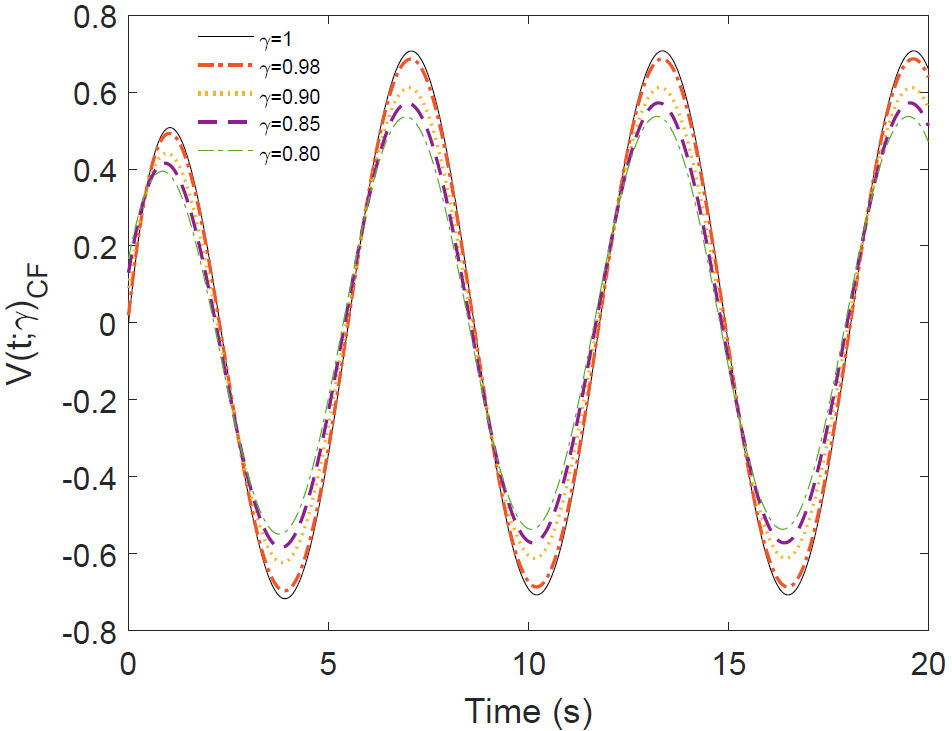
Then, the CF solution (27) exhibits an exponential decay when
In Fig. (3), similar behavior is shown as in the Caputo case, except that not all the curves start at zero and also change a little after half a second.
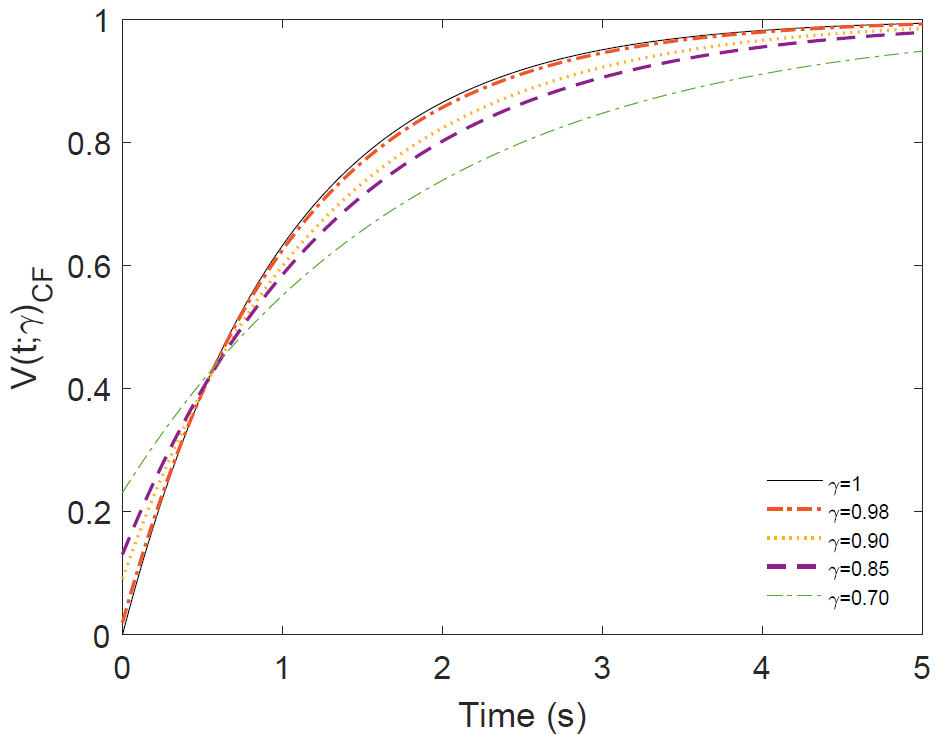
Figure 3 Plot of the Eq. (27) for some values of γ corresponding to voltage across the capacitor in the RC circuit of DC.
In the case of an oscillating source with angular frequency ω, from (16) and after applying the Laplace transform (4), we have
Solving with respect to
where
Then, the inverse Laplace transform gives the solution
5. RC with Atangana-Baleanu fractional derivative
Now, the fractional Eq. (16) is solved using the Atangana-Baleanu fractional derivative (5) and its corresponding Laplace transform (7). For the CC source we have
From here, we get
where
where
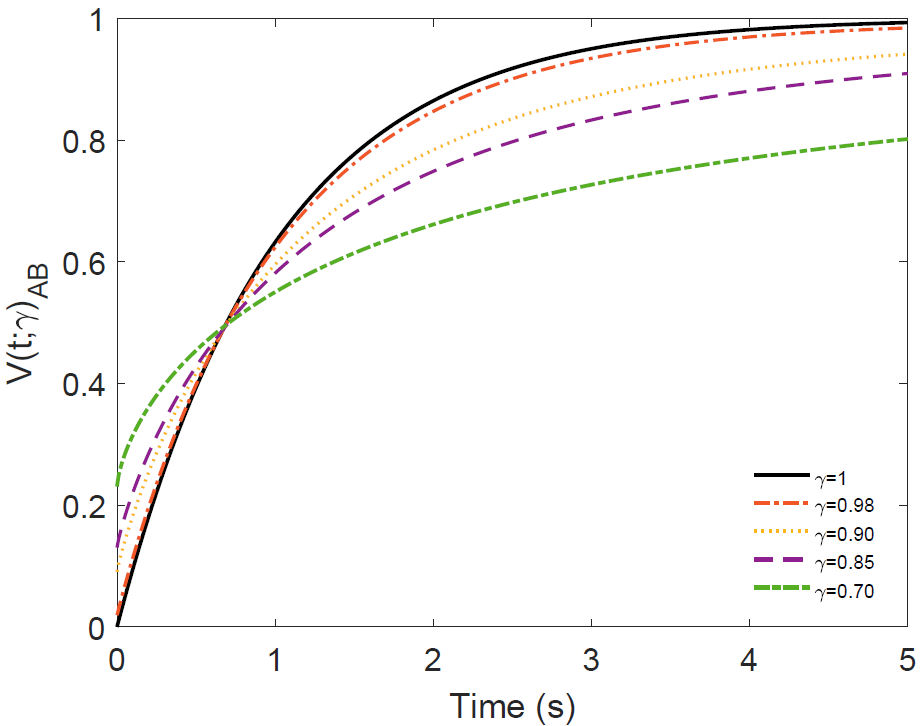
Figure 5 Numerical simulation of the Eq. (34) for some values of γ corresponding to voltage across the capacitor in the RC circuit of DC.
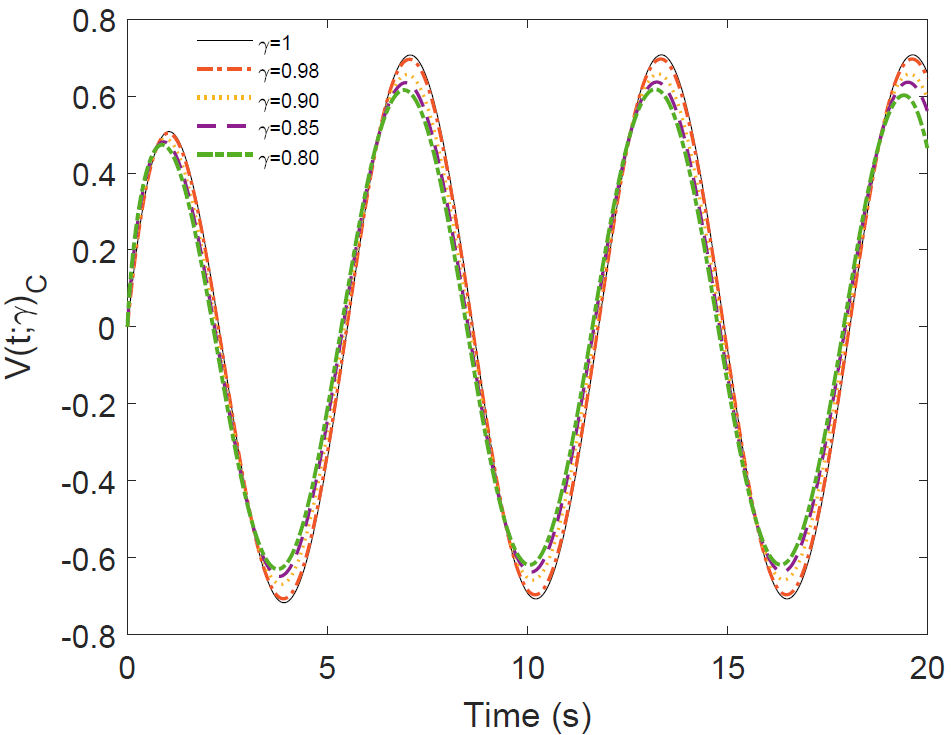
In the case of an oscillatory source, we have
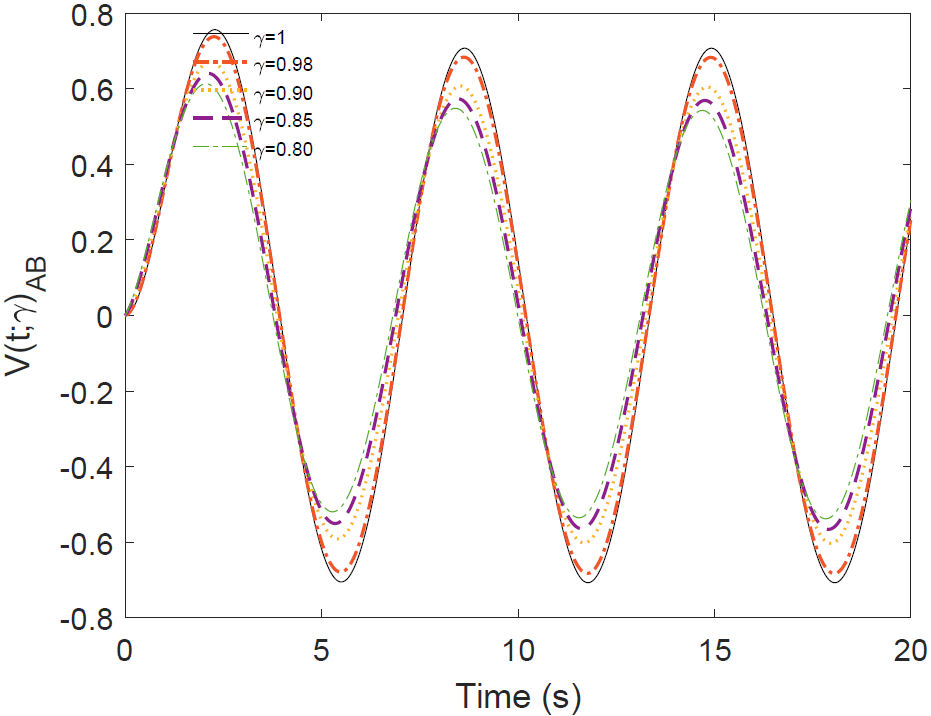
Figure 6 Numerical simulation of the Eq. (36) for some values of γ corresponding to voltage across the capacitor in the RC circuit of AC.
Solving for
6. RC with conformable fractional derivative
Finally, replacing the expression (10) in the fractional differential equation (16),
for the case
we have the conformable differential equation for the RC circuit
where
where
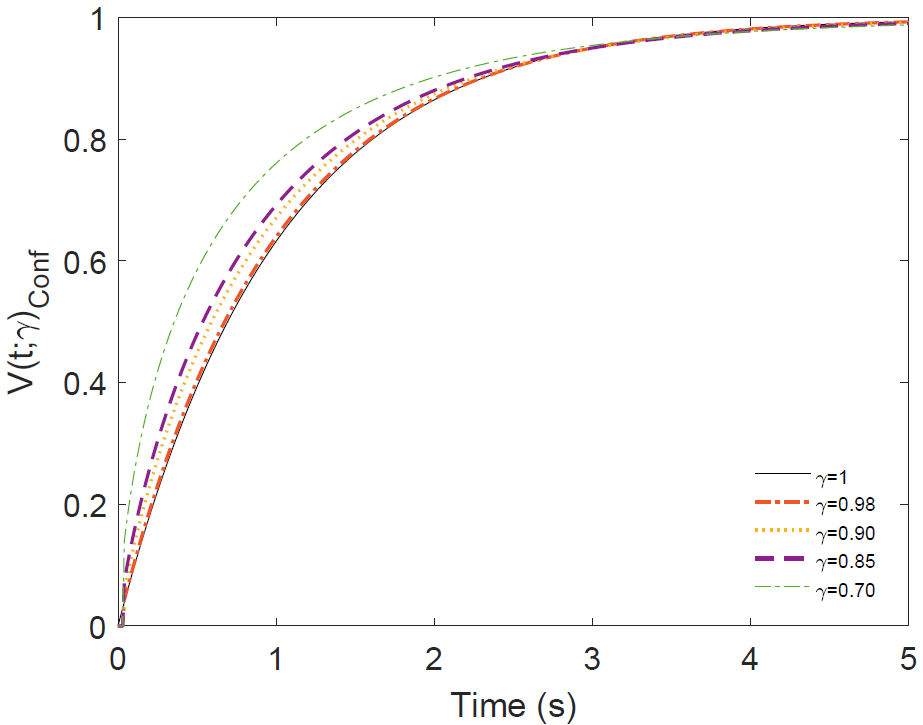
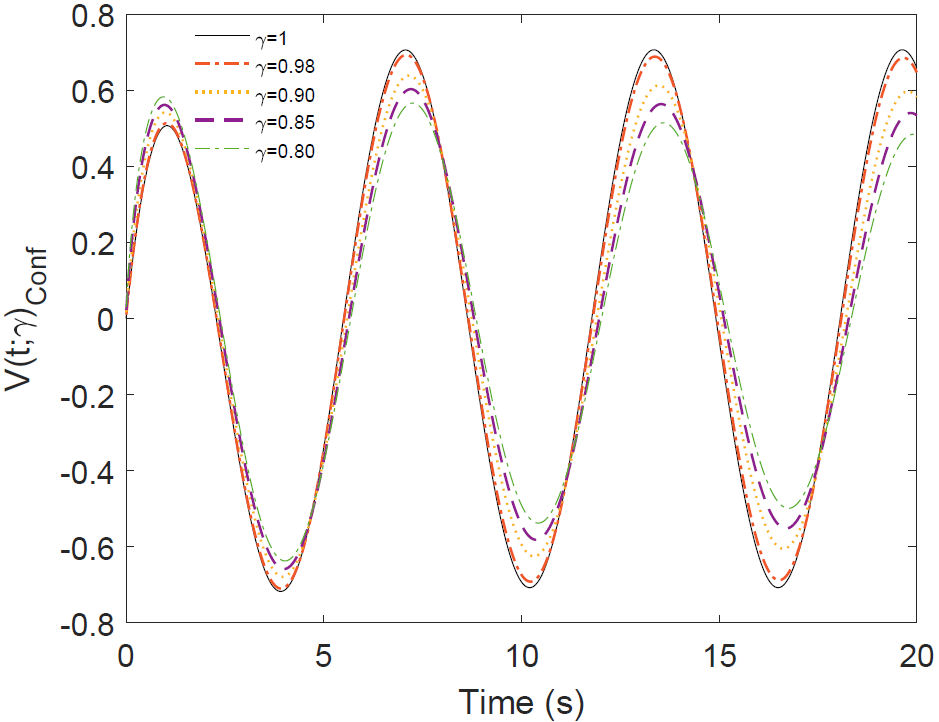
Figure 7 This graph shows the equation (39) for some values of γ corresponding to voltage across the capacitor in the RC circuit of DC.
We observe, in Fig. (7), a different behavior as
in the three previous cases. The conformable derivative strongly decays the first
three seconds, depending on the gamma order, then decays smoothly. Much slower than
the three previous cases. Stretched exponential functions are commonly observed in
disordered systems [53-59]. The possible origen of the stretched exponential is given
in [60]. It is straightforward to note, that
in the case
In the case of an oscillatory source
where,
7. Comparison
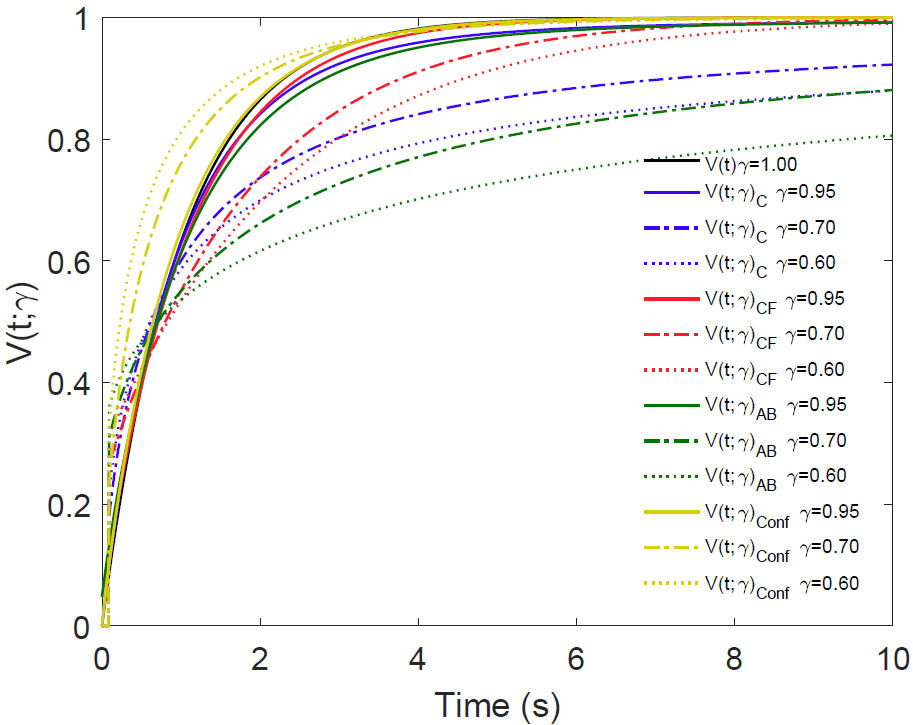
In Fig. (9), we have plotted the four solutions
given in (19), (27), (34) and (39), for different values of
8. Conclusion
In this work we have studied the behaviour of the RC electrical circuit for DC and AC sources using four different fractional derivatives. The fractional derivatives were; Caputo (C), Caputo-Fabrizio (CF), Atangana-Baleanu (AB) non-local fractional derivatives and the conformable derivative (conf). The (C) fractional derivative has the disadvantage that their kernel has a singularity at the end point of the interval, then to avoid this problem, [20] proposed the (CF) derivative. The main advantage of the CF is that the singular power-law kernel is now replaced by a non-singular exponential kernel, which is easier to use in theoretical analysis, numerical calculations and real-world applications. Solutions due to an exponential kernel shows an exponential decay, similar to the classical integer order model, (14) and (27). Therefore, the CF with an exponential kernel has limitations in describing phenomena with non-exponential nature, for example, anomalous relaxation [28] and stretched exponential relaxation physical processes [53]. To correct this deficiency, two fractional derivatives in the Caputo and Riemann-Liouville sense were defined by Atangana-Baleanu (AB) [29], based on the Mittag-Leffler function, solutions are of the form (34) with the properties (20) and (21). On the order hand, the conformable derivative was introduced in [34] . This derivative is a natural extension of the ordinary derivative, as a limit, and has the same properties as the ordinary one. This derivative can describe phenomena, such as relaxation processes in complex systems and so on [53-58]. As far as we know, the conformable derivative had not been applied to the RC circuit.
Theoretically, it was shown that the fractional derivative of Atangana-Baleanu and
the conformable derivative could describe a wider class of physical processes then
of the Caputo and Caputo-Fabrizio, Fig. 9. The
solutions are exactly equal for all four derivatives only for the case











 nueva página del texto (beta)
nueva página del texto (beta)