Research
Nonlinear damping in energy harvesters driven by colored
noise
M. Romero-Bastidaa
*
S. Cholula-Ramireza
a Sección de Estudios de Posgrado e
Investigación Escuela Superior de Ingeniería Mecánica y Eléctrica-Culhuacán,
Instituto Politécnico Nacional, Avenida Santa Ana 1000, Colonia San
Francisco Culhuacán, Delegación Coyoacan, Distrito Federal 04430,
Mexico.
Abstract
We study the performance of an electromechanical oscillator as an energy
harvester driven by finite-bandwidth random vibrations under the influence of
both a stiffness-type nonlinearity and a nonlinear damping that has recently
been found to be relevant in the dynamics of submicrometer mechanical
resonators. The device was numerically simulated and its performance assessed by
means of the net electrical power and the efficiency of the conversion of the
supplied power by the noise into electrical power for exponentially correlated
noise. We tune the parameters to achieve a good performance of the device for
non-negligible amplitudes of the nonlinearity of the oscillator and the
damping.
Keywords: Energy harvesting; nonlinear friction; wide spectrum
PACS: 05.40.Ca; 05.10.Gg; 46.65.+g; 84.60.-h
1. Introduction
Energy harvesting is the conversion of ambient energy present in the environment into
electrical energy. It is identical in principle to large-scale renewable energy
generation, for example, solar or wind power, but very different in scale. While
large-scale power generation is concerned with megawatts of power, energy harvesting
typically refers to micro- and/or milli-watts, i.e. much smaller
power generation systems. The development of energy harvesting has been driven by
the proliferation of technologies such as autonomous wireless electronic systems, a
classic example being wireless sensor nodes which combine together to form wireless
sensor networks; for this type of systems local power supply is an attractive
option. By converting ambient energy in the environment the energy harvester can
provide the required electric power for the lifetime of the wireless system which is
also free to be embedded or placed wherever it is best suited to perform its
function. Energy harvesting typically exploit kinetic, thermal, solar, or
electromagnetic radiation sources. Thermal gradients can be exploited by using
thermoelectric generators whereas solar energy is harvested using photovoltaics.
However, the most prominent type of devices are mechanical vibration energy
harvesters that convert kinetic energy via electromagnetic, electrostatic, or
piezoelectric transduction into electrical energy1-5.
Mechanical energy harvesters, also known as vibration power generators, are
typically, although not exclusively, inertial spring-mass systems where electrical
power is extracted by employing one or a combination of different transduction
mechanisms. Early studies considered linear springs and harmonic oscillators and
treated the external vibrations as sinusoidal vibrations. As most vibration power
generators are resonant systems, they generate maximum power when the resonant
frequency of the generator matches the ambient vibration frequency, known as
resonant energy harvesting1. Adaptive
generators try to minimize the difference between these two frequencies in order to
maximize the amount of generated power2, 4, 6.
Nearly all current vibration transducers operate in this regime7. This approach presents numerous drawbacks, being one of the
most important ones that the linear harvester resonant peak is necessarily very
narrow8. Thus, if the environmental
vibration frequency deviates from the harvester resonance very little power is
generated. To overcome this limitation various groups have begun to study
mass-spring systems with nonlinear springs and nonlinear oscillators9-12.
Many important results have been obtained if the broadband ambient vibrations are
modeled by Gaussian white noise. For example, it has been determined, using the
Fokker-Planck equation to describe Duffing-type energy harvesters, that the mean
power output of the device is not affected by the nonlinearity of the spring13-14.
Also the upper bounds on the power output of both linear and nonlinear energy
harvesters driven by Gaussian white noise have been obtained15. The latter ones can be advantageous since the size of the
device can be reduced without affecting the power output14. Now, while some environmental excitations exhibit the
characteristics of broadband white noise, many others have most of their energy
trapped within certain frequency bandwidths, i.e. external colored
noise. After some early experimental and simulation studies12-16 the power output
of both a monostable13 and a bistable Duffing
oscillator with a symmetric potential17
driven by Ornstein-Uhlenbeck noise was determined by approximate methods, and the
exact analytical expressions for the net electrical power and efficiency of the
conversion of the power supplied by exponentially correlated noise into electrical
power was derived for a linear electromechanical oscillator employed as an energy
harvester18.
In almost all theoretical models mentioned above, the coupling between the mechanical
oscillator and the ambient noise were supposed to be linear. This is because the
energy dissipation (damping) in previous studied systems were supposed to be linear
in general. However, damping has an important impact on the dynamic behavior of
submicrometre mechanical resonators, and recent researches have revealed that
nanostructures with high aspect ratio such as nanotubes and graphene nanoribbons can
be easily driven into nonlinear dissipation regime19. This nonlinear damping has been so far studied mainly within the
field of thermal transport in a spin-boson nanojunction20, in nonlinear two-level molecular junctions21, in a monomodal harmonic molecular junction
(a single harmonic oscillator)22, and in a
one-dimensional lattice of coupled nearest-neighbor harmonic oscillators23.
In this work we propose to study the resonator driven by colored noise studied in
Ref.18 with a nonlinear damping between
the mechanical oscillator and the source of ambient noise to explore its influence
on the performance of the device as an energy harvester. The proposed nonlinear
damping has been previously considered within the context of a micromechanical
oscillator model in Ref.19 to properly
account for various experimental observations made in mechanical resonators based on
carbon nanotubes and graphene sheets, as mentioned above.
The rest of the paper is organized as follows: in Sec. 2 we present the model as well
as our methodology. Results for both a linear and nonlinear oscillator are reported
in Sec. 3. Finally, in Sec. 4 we discuss the results so far obtained and propose
ways to further improve them.
2. Model and methodology
The herein considered energy harvester is a device that converts the power supplied
by external noise into electrical energy. This process begins with the damped
oscillator being driven by the external noise. Its kinetic energy is then converted
via a piezoelectric transducer mechanism into electrical energy that is then stored
in a capacitor. The mechanical part of the device is described by the equation for
the momentum of the stochastically driven damped oscillator of mass m, which reads as
p˙+γp+βq2p+Ftran(q,V)+ω02q+αq3=η(t),
(1)
with the dot standing for temporal derivative. In this equation ω0 is the natural frequency of the oscillator, αq3 is the so-called Duffing force, γ is the linear damping coefficient, βq2p is the nonlinear damping term, η(t) is the random driving force, and Ftran(q,V) is the transducer force due to the motion-to electricity conversion
mechanism, which depends on the geometry of the transducer and on how the circuit
that implements the energy conversion cycle operates. It opposes to the motion, just
as the friction force, and has its origin in the energy loss that occurs when
kinetic energy is converted into electric energy. The simplest expression for this
function is Ftran(q,V)=kvV, where kv>0 is a piezoelectric parameter and V(t) is the voltage. The dynamical equation for the voltage has to take into
account the load resistance RL and the capacitance C of the piezoelectric component, as well as the connecting function F(p,V) with the oscillator; all these variables are related by the equation V˙=F(p,V)-V/τp, where τp=RLC is the time associated to the charging process of the piezoelectric
element, which is larger than any other characteristic time of the system. We will
employ a connecting function of the form F(p,V)=kcp, where kc is the coupling constant of the piezoelectric sample; nonlinear
processing of the voltage delivered by the piezoelectric material in order to
enhance the electromechanical conversion has been previously considered24, but is out of the scope of the objectives
of the present work. Since our goal is to understand the effect of the nonlinear
damping on the performance of the device we have chosen simplest,
i.e. linear, expression for the connecting function in the
analysis below.
In this work we are considering a Ornstein-Uhlenbeck (OU) random force, with mean ⟨η⟩=0 and variance ⟨η(t)η(t')⟩=σexp(-|t-t'|/τc), where σ is the amplitude and τc is the correlation time. The limit τc→0 and σ→∞, with D=στc constant, corresponds to the white noise limit. In order to obtain a
closed system of equations, it is a standard procedure to employ the equation η˙=-η/τc+ξ¯(t)/τc, where ξ¯(t) is a Gaussian white noise with zero mean and correlation ⟨ξ¯(t)ξ¯(t')⟩=2στcδ(t-t'). Therefore the complete set of equations reads as
q˙=pmp˙=-ω02q-αq3-(γ+βq2)p-kvV+ηV˙=kcp-1τpVη˙=ητc+2στcξ,
(2)
with a Gaussian white noise correlation of ⟨ξ(t)ξ(t')⟩=δ(t-t').
The simulations are performed by solving numerically the Langevin equations () by
using the so-called Heun algorithm; trajectories are computed over an interval of 4×104 time units after a transient of 103 starting from a set of initial conditions given by {q(0)=p(0)=0,V(0)≡V0=1}. An ensemble average over 104 independent realizations has been performed for each set of
parameters.
Being V2(t)/RL the instantaneous power delivered to the load resistance, the measure of
performance will be the efficiency (as defined in18)
ηe=ηmeηnm=⟨V2⟩/RL⟨pη⟩/m,
(3)
where ⟨⋯⟩ implies both a time-average during the observation interval and an
ensemble average over noise realizations, ηme is the transducer’s efficiency of converting mechanical to electrical
power, and ηnm is the efficiency of power converted from the external noise to the
power transferred from the oscillator to the transducer. The explicit expressions
are reported in Ref. 18.
3. Results
In Fig. 1(a) we present the comparison of the
correlations ⟨pη⟩, ⟨p2⟩, and ⟨V2⟩ as a function of the inverse of the correlation time λ≡τc-1 for the original case reported in , i.e. α=β=0 and for α=0, β=50; the curves corresponding to α=β=50 (not shown) are indistinguishable to those reported in the above figure.
Just as in the original linear damping case, the electrical power P passes through a maximum, P*, as λ increases, whereas the efficiency decreases monotonically as λ increases. These results are reported with large α and β values because only in this range any appreciable difference can be
observed in comparison with the linear friction case. Furthermore, these differences
are only significant in the region of the maximum of each curve, being negligible as λ increases. The net effect is to reduce the height of each curve, thus
reducing the maximum power compared to the original instance, and to shift the
location of the maximum to a larger λ value. The net result, as can be appreciated in Fig. 1(b), is a reduced efficiency for all studied values of the
inverse of the correlation time, as could be expected of the dissipative nature of
the newly considered terms. We also performed further simulations with the α=-10 value and we can readily appreciate in Fig. 1(a) that the correlation ⟨p2⟩ is largely insensitive to the change in sign in the intensity of the
Duffing force. However the remaining correlations present a rather amusing behavior:
they are almost the same as those corresponding to the linear friction case. This
phenomenology results in an efficiency that is also very similar to that of the
linear damping case, as can be seen in Fig.
1(b). A possible explanation could be inferred from the fact that the
shape of the potential corresponding to the conservative forces of the system with α=-10 in the region close to the origin, i.e. for moderate
displacements, is very similar to the one corresponding to α=10, a value wherewith the efficiency of the system with a nonlinear damping
is indistinguishable from the one obtained with a system without it. This result
suggest that, if the nonlinear damping becomes relevant in any particular instance,
its negative effects in the efficiency of the device could potentially be diminished
with the inclusion of a Duffing force of negative amplitude.
Since in both considered instances the maximum efficiency does not occur when the net
electrical power is maximal and vice versa, we studied how the maximum net
electrical power P*, the efficiency at the maximum power ηe*, and the characteristic frequency of the noise at the maximum power λ* depend on the parameters τp, kc, kv, and ω0 of the energy harvester. Of these parameters the first three are related
to the electrical circuit of the transducer and the last one characterizes the
mechanical behavior of the mass-spring system. In each case the considered parameter
is varied and the rest are taken equal to 1. Considering the dependence with respect
to τp presented in Fig. 2(a)
λ* decreases mono tonically as τp increases in both instances, with a larger decay for the system with
nonlinear friction, whereas P* remains almost constant in both instances for the considered variation.
In contrast, ηe* increases for small τp values, reaches a maximum and then decreases monotonically as τp further increases; the maximum is smaller for the system with nonlinear
damping. Therefore it is convenient to take small τp values to optimize the efficiency for both types of damping. With the
value α=-10 the decay of λ* is even faster than that corresponding to the system with linear
damping, but otherwise the behavior of the other two variables is very similar to
that of the system without nonlinear damping. The behavior of P* and ηe* as the frequency ω0 changes is different in both instances, as can be inferred from the
results reported in Fig. 2(b). For the linear
damping case both variables monotonically decrease as ω0 increases, whereas in the case with nonlinear damping the behavior of
both variables is different of the aforementioned one at small frequencies,
i.e. both are weakly dependent on the frequency for ω0<1 and then slowly decreases for ω0>1. Thus in this case it is convenient to take small ω0 values to optimize the maximum net electrical power and the efficiency
at maximum power. For α=-10 we could only compute values in the ω0>1 range, and these are the same as those for the system without the
nonlinear damping term. Therefore, in this case taking the lower bound ω0=1 would be the only available choice to optimize both P* and ηe*.
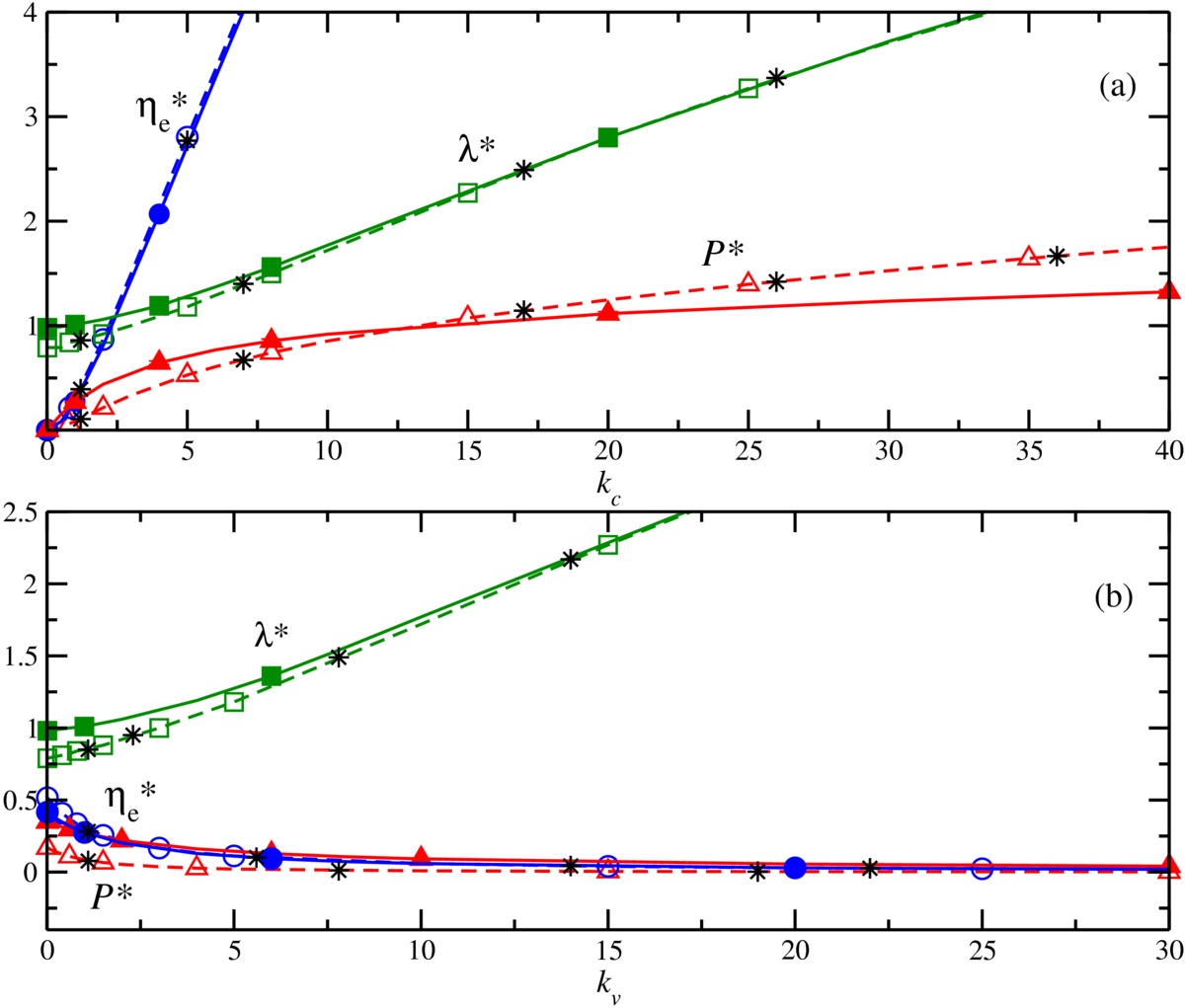
The variation with respect to kc, shown in Fig. 3(a), indicates that ηe* significantly increases for low kc in both instances, with minimal differences between them. On the other
hand, P* also increases for low kc values in both cases, being greater for the device including the
nonlinear friction term if kc<10, but rapidly approaches an asymptotic value for kc>10, unlike the case with only a linear friction term, which keeps
increasing in this value range. Thus, and considering that the physically acceptable
regime corresponds to ηe*<1, the value kc∼2.5 can be considered as an acceptable compromise to optimize the
performance of the device when the nonlinear damping is relevant. In the case in
which the variation with respect to kv is considered, depicted in Fig.
3(b), the behavior of ηe* is virtually identical in both considered cases. However, the maximum
net electrical power P* has a higher value in the low kv range for the nonlinear damping case compared to the one with linear
damping. Therefore a value of kv∼1 is adequate to optimize the values of both the maximum net electrical
power and the efficiency at the maximum power when the nonlinear damping is
relevant. For the α=-10 value the results in both panels (a) and (b) are virtually the same to
those for the corresponding cases with linear damping.
Summarizing the previous discussion, the characteristic frequency of the noise at the
maximum power λ* decreases monotonically as τp increases, see Fig. 2(a), whereas
it increases monotonically as kv and kc increase, as depicted in Figs. 3(a)
and (b). Special mention deserves the
dependence of λ* with respect to ω0 presented in Fig. 2(b), which is
very weak for low ω0 values, precisely in the value range wherein both P* and ηe* are almost independent of the natural frequency of the oscillator. In
this case our result suggest to take a ω0 value no larger than 0.5 to optimize the performance of the device, except when α=-10 is used, in which case ω0=1 has to be taken for the reasons exposed above. In all considered
instances the λ* values are higher for the case with nonlinear damping compared to the
one with linear damping. Therefore, we can conclude that to improve performance it
would be desirable to take τp,ω0<1 (ω0=1 with α=-10) for both cases, with and without nonlinear damping. As for the
remaining parameters the best value would be at around kv,kc∼2.5 since for this value the efficiency is optimized and the maximum net
electrical power P* reaches a value that is still significant compared to the one obtained
with the tuning of the remaining parameters.
4. Discussion and conclusions
Our results on the performance of a nonlinear electromechanical oscillator with a
nonlinear coupling with an external finite-bandwidth ambient noise seem to indicate
that the performance of the system as an energy harvester is only weakly affected by
the presence of the aforementioned nonlinear coupling, since the constants that
define the latter have to take exceedingly large values in order to affect in a
mensurable way the correlations that characterize the performance of the considered
energy harvester. In particular, the correlations wherewith both the maximum power
and efficiency are defined present a very weak dependence on the nonlinear
parameters of the interaction with the source of the ambient noise.
A constant among the proposed energy-harvesting devices is that the combined goals of
both maximum power and efficiency cannot be attained at the same time, being the
present one no exception. A compromise in the value of all parameters has to be
made, and thus we determined that the best performance of the energy harvester is
obtained by taking low values for the characteristic charging time of the capacitor τc and the piezoelectric parameter kv to obtain the maximum values of both P* and ηe* in each instance. For kc an intermediate value allows to obtain a significant value for the
maximum net electrical power together with a high efficiency at maximum power. The
characteristic frequency of the mechanical oscillator has to take values of ω0∼0.5 (and ω0=1 for the case α=-10) to take advantage of the fact that in this value range the maximum
power, the maximum efficiency at maximum power as well as the characteristic
frequency at maximum power have an approximately constant value. A positive
amplitude of the Duffing force has no effect on the performance of the device and,
with a negative amplitude, it was possible to minimize the adverse effects of the
nonlinear damping in the efficiency of the device. In view of this finding it would
be interesting to study the performance of an energy harvester affected by the
herein studied nonlinear coupling with the external noise source but employing a
bistable symmetric potential, which has gained attention recently, as already
mentioned9-12. We intend to investigate this particular possibility in a future
work.
Acknowledgments
M. R. B. gratefully acknowledges CONACyT, México for financial support.
References
1 S. P. Beeby, M. J. Tudor, and N. M. White, Measurement
Science and Technology 17 (2006) R175.
[ Links ]
2 S. R. Anton and H. A. Sodano, Smart Materials and
Structures 16 (2007) R1.
[ Links ]
3 J. M. Renno, M. F. Daqaq, and D. J. Inman, Journal of
Sound and Vibration 320 (2009) 386.
[ Links ]
4 A. Cammarano et al., Smart Materials and
Structures 19 (2010) 055003.
[ Links ]
5 H. S. Kim, J.-H. Kim, and J. Kim, International Journal of
Precision Engineering and Manufacturing 12 (2011)
1129.
[ Links ]
6 P. D. Mitcheson et al., Proceedings of
the IEEE 96 (2008) 1457.
[ Links ]
7 D. Spreemann and Y. Manoli, Electromagnetic Vibration
Energy Harvesting Devices: Architectures, Design, Modeling and
Optimization (Springer, Dordrecht, 2012).
[ Links ]
8 S. G. Burrow, L. R. Clare, A. Carrella, and D. Barton, in
Proceedings of the SPIE smart structures/NDE conference,
edited by M. Ahmadian (SPIE, San Diego, California, USA, 2008).
[ Links ]
9 F. Cottone, H. Vocca, and L. Gammaitoni, Phys. Rev.
Lett. 102 (2009) 080601.
[ Links ]
10 L. Gammaitoni , I. Neri, andH. Vocca , Appl. Phys.
Lett. 94 (2009) 164102.
[ Links ]
11 A. Erturk, J. Hoffmann, andD. J. Inman , Appl. Phys.
Lett. 94 (2009) 254102.
[ Links ]
12 H. Vocca , I. Neri , F. Travasso, andL. Gammaitoni ,
Applied Energy 97 (2012) 771.
[ Links ]
13 M. F. Daqaq , Journal of Sound and Vibration 329
(2010) 3621.
[ Links ]
14 P. L. Green, K. Worden, K. Atallah, and N. D. Sims,
Journal of Sound and Vibration 331 (2012)
4504.
[ Links ]
15 E. Halvorsen, Phys. Rev. E 87 (2013)
042129.
[ Links ]
16 S. D. Nguyen andE. Halvorsen , Journal of
Microelectromechanical Systems 20 (2011) 1225.
[ Links ]
17 M. F. Daqaq , Journal of Sound and Vibration 330
(2011) 2554.
[ Links ]
18 V. Méndez, D. Campos, and W. Horsthemke, Phys. Rev.
E 88 (2013) 022124.
[ Links ]
19 A. Eichler et al., Nat.
Nanotech. (2011) 339.
[ Links ]
20 D. Segal and A. Nitzan, Phys. Rev. Lett. 94
(2005) 034301.
[ Links ]
21 D. Segal andA. Nitzan , J. Chem. Phys. 122
(2005) 194704.
[ Links ]
22 D. Segal , Phys. Rev. Lett. 100 (2008)
105901.
[ Links ]
23 Y. Ming, H.-M. Li, and Z.-J. Ding, Phys. Rev. E
93 (2016) 032127.
[ Links ]
24 E. Lefeuvre et al., Sensors and
Actuators A: Physical 126 (2006) 405.
[ Links ]













 nova página do texto(beta)
nova página do texto(beta)


