Research
La turbulencia asociada con las velocidades orbitales de olas que aún
no rompen
A.O. Hernández Olivares1
F.J. Ocampo Torres1
a Departamento de Oceanografía Física,
Centro de Investigación Científica y de Educación Superior de Ensenada, B.C.
(CICESE). Carretera Ensenada-Tijuana 3918, Zona Playitas, 22860 Ensenada,
B.C. México e-mail: ocampo@cicese.mx
Resumen
Se entiende que los procesos de intercambio entre el océano y la atmósfera
determinan de manera decisiva el estado del mar, del tiempo y del clima. Con el
fin de entender mejor los procesos que aportan energı́a cinética turbulenta en
las capas de fluido en ambos lados de la superficie del mar, abordamos el caso
del oleaje y en particular el efecto de las olas que aún no rompen. Se
realizaron mediciones de las velocidades de las partı́culas de fluido inducidas
por la propagación de olas sin rompiente con el propósito de detectar la
presencia de turbulencia y su asociación con la pendiente de las olas. Se
analizaron 184 experimentos, cada uno con una duración de 3.5 minutos y olas
aproximadamente monocromáticas de diferente pendiente (0.012-0.273) . Los experimentos se realizaron en un canal con dimensiones de 12.26×0.55×0.32 m empleando un velocı́metro acústico (Vectrino Profiler, Nortek),
para medir las componentes u, v y
w de la velocidad en una columna de fluido con 3.5 cm de
longitud en 35 celdas de 1 mm de ancho, aproximadamente. En cada experimento se
obtuvo el perfil vertical de la velocidad entre 1.5 y 8.6 cm de profundidad con
respecto al nivel de agua en el canal (h=48±0.5 cm). Se consideraron las componentes u(t,z) y w(t,z) en este análisis, puesto que las olas son prácticamente
bidimensionales (v(t,z)=0). A partir de los espectros de potencia correspondientes a las
fluctuaciones turbulentas u'(t,z) y w'(t,z), se identificaron sub-rangos inerciales (turbulencia isotrópica)
independientemente de la profundidad y del valor de la pendiente de las olas.
Con los espectros de las fluctuaciones turbulentas de las velocidades se
demuestra que el tamaño de los remolinos cuya energı́a es transferida a
remolinos de menores escalas, es mayor al aumentar la pendiente de las olas.
Descriptores: Olas que aún no rompen; olas monocromáticas; velocímetro acústico; turbulencia; sub-rangos inerciales
Abstract
Ocean-atmosphere exchange processes are known to decisively determine the sea
state, the weather and our planet’s climate. With the ultimate goal of a better
understanding of the processes contributing with turbulent kinetic energy into
both boundary layers above and below the sea surface, we approach the ocean
surface wave phenomenon, and in particular we study the non-breaking waves
potential effect. Therefore, measurement of particle velocities were made in a
fluid under non-breaking waves, for the purpose of detecting turbulence and its
association with the wave steepness. A total of 184 experiments were analyzed,
each one with a duration of 3.5 minutes and the presence of approximately
monochromatic waves with varying steepness (0.012-0.273). The measurements were carried out in a wave tank with dimensions
of 12.26×0.55×0.32 m using an acoustic velocimeter (Vectrino Profiler, Nortek). The u,v and w components of velocity were measured on a 3.5 cm long fluid column
in 35 cells of 1 mm in height. During the experiments, the velocity profile
between 1.5 and 8.6 cm depth was obtained, referred to the water level in the
wave tank (h=48.6±0.5 cm). The waves propagated in deep waters (h/λ>0.5), where λ is the wave length. Only u(t,z) and w(t,z) components were considered for the analysis since, waves are
practical two-dimensional (v(t,z)=0). Power spectra were calculated in as a function of frequency
corresponding to u'(t,z) and w'(t,z) turbulent fluctuations, an inertial subrange (isotropic turbulence)
was detected in the most of the spectra, for certain depths regardless of the
wave steepness. Results from turbulent fluctuations frequency spectra show that
eddy size involved in transferring energy to smaller ones, increases with the
wave slope.
Keywords: Nonbreaking waves; monochromatic waves; acoustic velocimeter; turbulence; inertial subrange
PACS: 47, 92.10hb; 94.05.Lk
1. Introducción
La turbulencia y la mezcla en la capa superior del océano son procesos clave en la
interacción entre el océano y la atmósfera, especialmente en la transferencia de
energía, calor, momento, y masa (incluyendo gases, como el CO2). Al entender de manera más completa los mecanismos que aportan
turbulencia en la capa superficial del mar, incluyendo el efecto de las olas, se
podrá contar con los elementos necesarios y con las cantidades apropiadas para
conocer y cuantificar adecuadamente el balance de energía cinética turbulenta en
ambos lados de la superficie. Así se podrá determinar de forma más precisa el
intercambio entre el océano y la atmósfera, que es indispensable para predecir el
estado del mar, del tiempo y el clima de nuestro planeta, con menor incertidumbre en
los modelos numéricos que se utilizan. De los principales mecanismos que generan
turbulencia en la capa superior del océano se pueden citar al corte vertical de las
corrientes superficiales inducidas por viento y al rompimiento del oleaje [1,2]. El
rompimiento de las olas genera turbulencia y mezcla que es confinada a profundidades
del orden de las alturas de las olas e inclusive menores [3-6]. Sin embargo,
también se reconoce que las olas aunque no rompan, pueden generar turbulencia en la
capa superior del mar y este es el tema de investigación que se aborda en este
trabajo.
Phillips [7], propuso de manera teórica que el
movimiento de las olas (aún sin romper) puede generar turbulencia asociada con la
vorticidad del flujo, en donde el orden de magnitud de la vorticidad aleatoria
(turbulencia) es de segundo orden en los parámetros del oleaje (como la pendiente) y
por lo tanto del mismo orden que el campo promedio de la vorticidad. Posteriormente
[8,9], se encuentran evidencias de generación e intensificación de la
turbulencia, en respuesta al movimiento de las olas en ausencia de viento (oleaje
generado en tormentas lejanas), a partir de mediciones directas en el mar. En
condiciones de oleaje sin rompiente, el flujo vertical de momento horizontal debajo
de la superficie excedía el esfuerzo del viento sobre la superficie del mar.
Por otra parte, considerando la teoría lineal de las olas (teoría de Airy), Babanin
[10] establece un número de Reynolds para
olas que aún no rompen ([Rewave]2006=a2ω/ν), en donde a es la amplitud de las olas, y ω es su frecuencia angular, mientras que ν es la viscosidad cinemática. Determina un valor crítico [Rewave]2006=3000 que define la transición entre un flujo laminar y uno turbulento.
Además, se han desarrollado algunos estudios en el laboratorio (en canales de olas)
con la finalidad de demostrar que el movimiento de las partículas en un fluido
inducido por olas que aún no rompen puede generar turbulencia. Por ejemplo, Babanin
y Haus [11], calcularon el espectro de
potencia de la velocidad de las partículas de fluido en función del número de onda,
en casos con olas monocromáticas que aún no rompen, encontrando una intermitencia en
la ocurrencia de sub-rangos inerciales (Ley de -5/3 de Kolmogorov). Las velocidades fueron medidas mediante el seguimiento
de partículas en el fluido a través de secuencias de imágenes en video.
Otro ejemplo de investigación en el laboratorio es el trabajo de Dai et
al. [12], en donde cuantificaron
la mezcla inducida por olas monocromáticas (sin rompimiento), midiendo el tiempo en
que la estratificación del fluido desaparece. Utilizaron sensores de temperatura
(del tipo de agujas) colocados en la mitad de un canal de 5 m de longitud y en
diferentes profundidades, y con sus resultados demostraron que la mezcla aumenta con
la amplitud y la longitud de las olas. En otro experimento, Savelyev et
al. [13] midieron las
velocidades de las partículas de fluido en la superficie libre (η) bajo la presencia de olas sin romper, mediante velocimetría de marcado
puntual con termografía. En este método se utilizan como trazadores del movimiento
de la superficie, algunos puntos en el fluido que fueron previamente calentados con
laser (Veron et al., [14]).
Con sus resultados demostraron que las fluctuaciones observadas corresponden con
turbulencia horizontalmente anisotrópica, debido a la formación de remolinos que se
extienden en la dirección de la propagación de las olas y al aumento de su energía
cinética turbulenta con el tiempo (razón de crecimiento). Finalmente, Beyá
et al. [15] realizaron
experimentos con olas monocromáticas de amplitud finita con valores de [Rewave]2006=3000, y mediante la inyección de tinta visualizaron la mezcla inducida por la
presencia de turbulencia. Sin embargo, sus resultados no mostraron evidencias de
mezcla turbulenta por parte del movimiento de las olas, pues identificaron que la
pluma de tinta permaneció siempre visible y su grosor o espesor nominal se mantuvo
invariante con respecto al tiempo.
En este trabajo se analizan resultados experimentales sobre la presencia de
turbulencia generada por olas que aún no rompen en un fluido no estratificado. En
particular, se busca identificar sub-rangos inerciales en los espectros de potencia
de las componentes de las velocidades de las partículas del fluido, relativas al
movimiento de las olas (evidencia de una turbulencia isotrópica), así como la
cuantificación de los niveles de turbulencia generada en relación a la tasa de
disipación de la energía cinética turbulenta. Finalmente, se intenta determinar si
la frecuencia de ocurrencia de los sub-rangos inerciales, así como los niveles de
turbulencia generada, muestran alguna relación con la pendiente de las olas.
En la Sec. 2 se describen el diseño experimental, las especificaciones del
dispositivo utilizado en las mediciones, el control de la calidad de los datos
adquiridos, algunas ecuaciones fundamentales consideradas y los cálculos realizados
para la obtención de resultados. En la Sec. 3, se describen los resultados obtenidos
con relación a los espectros de potencia de las velocidades de las partículas de
fluido que tienen coherencia con la elevación de la superficie libre, y de esas
velocidades que se asocian con las fluctuaciones turbulentas. Se aborda el tema de
la identificación del sub-rango inercial en los espectros de potencia de las
velocidades detectadas como fluctuaciones turbulentas y se presentan estimaciones de
la tasa de disipación de energía cinética turbulenta en función de la pendiente de
las olas. En la Sec. 4, se discuten los resultados y se presentan las conclusiones
de nuestra investigación.
2. Experimentos en el laboratorio y procesamiento de los datos
2.1 Experimentos en el canal de olas
Los experimentos del presente trabajo se llevaron a cabo en el laboratorio de
olas de la Facultad de Ciencias Marinas (FCM) de la Universidad Autónoma de Baja
California (UABC) en Ensenada BC, en un canal de 12.26 m de largo, 0.55 m de
alto y 0.32 m de ancho. Se generaron olas aproximadamente monocromáticas (y
prácticamente planas) en condiciones de aguas profundas mediante el movimiento
de una paleta (unida al fondo del canal con una bisagra) impulsada por un motor
eléctrico. Se realizaron 184 experimentos, con duración de aproximadamente 3.5
minutos cada uno, tiempo durante el cual la amplitud y el periodo de las olas
generadas se mantuvieron relativamente constantes. Las características de las
olas generadas difieren en cada experimento: las amplitudes (a) variaron entre
0.05 y 1.69 cm, mientras que las frecuencias variaron entre 1.5 y 2.5 Hz,
reproduciendo una gama de pendientes en un intervalo entre 0.012 y 0.273.
En cada experimento se realizaron mediciones entre 315 y 525 periodos de olas
aproximadamente, lo que se considera suficiente para que olas que aún no rompen
generen turbulencia. Como referencia, se toma en cuenta que a partir de
mediciones durante unos 15 periodos de las olas [11] se logra detectar la presencia de turbulencia isotrópica
identificando sub-rangos inerciales en los espectros de potencia de las
velocidades en función del número de onda. Además, en otro trabajo con
mediciones durante los primeros 2.5 minutos de la propagación de las olas con
valores de pendientes entre 0.08 y 0.2, se reporta [12] un efecto notable de
mezcla turbulenta.
Las velocidades de las partículas del fluido bajo la presencia de olas se
midieron con un velocímetro acústico (Vectrino Profiler, Nortek) que cuenta con
una frecuencia de muestreo de 100 Hz y una resolución espacial de 1 mm en la
columna del fluido en donde se detecta el perfil vertical de las velocidades.
Las componentes u(t,z), v(t,z) y w(t,z) de la velocidad de las partículas de fluido se determinaron a lo
largo de esa columna de 3.5 cm, en 35 celdas de 1 mm de altura cada una, en
profundidades entre 1.5 y 8.6 cm con respecto al nivel medio del agua. La primer
celda se obtiene a 4 cm sobre el transductor principal del sensor. El sensor
cuenta también con un detector del fondo con una tasa de muestreo de 10 Hz, que
en este caso se utilizó como detector de la superficie del agua.
El nivel del agua en el canal fue h=48.6±0.5 cm, con lo que se determina [16] que en los experimentos realizados las olas se propagaron en
aguas profundas i.e. h/λ>0.5. Considerando h y la frecuencia del pico (fp) en los espectros de potencia de la componente u(t,z) de las velocidades (esa frecuencia coincide con la del movimiento
oscilatorio de la paleta), se determinó el número de onda (kwave) de las olas mediante la relación de dispersión.
Con relación al funcionamiento del sensor utilizado, se consideró conveniente
agregar grano de café (finamente molido) al fluido, previamente a la realización
de cada experimento, con lo que se logró obtener una mayor amplitud en la señal
acústica reflejada y valores apropiados en la razón de señal a ruido (≥35 dB).
Para reducir la reflexión de las olas al final de su propagación, en el extremo
del canal se colocó una plataforma de madera perforada (simulando una playa),
con una pendiente de 8∘ aproximadamente y cubierta con pasto sintético. El fondo y las
paredes del canal son de vidrio, por lo que pueden considerarse como superficies
lisas. El transductor del sensor utilizado se colocó en el centro del canal,
aproximadamente a 6 m de la paleta y a 0.15 m de las paredes. La distancia a la
paleta se considera suficiente para que las olas con pendientes menores que 0.3
se propaguen sin modificación visible de su perfil, mientras que la distancia a
las paredes se considera suficiente como para evitar cualquier efecto en las
mediciones de la velocidad por causa de la capa límite.
El sensor se instaló de modo que el transductor perfilara hacia arriba y con el
detector del fondo se logró determinar la elevación de la superficie libre, η(t). Las series temporales η(t), se interpolaron para obtener correspondencia con las series u(t,z), v(t,z) y w(t,z). Además, se calcularon los espectros de potencia de η(t)(Sηη(f)), y la amplitud correspondiente como A(f)=2Sηη(f)Δf
[17,18], en donde Δf es el ancho de la banda de frecuencias que describe la resolución en
el espectro. En este trabajo, la altura de las olas que se utiliza es H=2max(A(f)), donde máx es la función de valor máximo.
En cada experimento, el sensor de las velocidades se encendió aproximadamente 10
segundos después de iniciar la generación de las olas, tiempo suficiente para
que el movimiento de la paleta se considere regular. Una vez finalizado el
tiempo de medición, el generador de oleaje se apagó y se esperó que las últimas
olas generadas se disiparan por completo antes de proceder con el siguiente
experimento (aproximadamente 10 min).
2.2. Control de calidad de los datos adquiridos
Además de las mediciones de las componentes u(t,z), v(t,z) y w(t,z) de las velocidades de las partículas de fluido, el sensor
proporciona coeficientes de correlación del haz acústico (una matriz por cada
haz acústico). Estos coeficientes de correlación del haz acústico son una medida
de la similitud entre dos pulsos acústicos emitidos sucesivamente y representan
también una medida de la calidad en las mediciones de velocidad [19].
En este trabajo se consideran como ruido, los datos de velocidad cuyos valores de
correlación del haz acústico son menores que 75% en cualquiera de esas cuatro
matrices de correlación. Los valores identificados como ruido se sustituyen con
NaNs (Not a number), al igual que los valores de las velocidades fuera del
intervalo [-3σ+μ,μ+3σ], donde μ corresponde a la media temporal de la serie de tiempo y σ a su desviación estándar.
Las series de tiempo cuyo total de NaNs sea mayor que 20% del total de sus datos
originales deben descartarse. Sin embargo, en nuestros experimentos, todas las
series de tiempo fueron consideradas para su análisis puesto que el total de
NaNs fué siempre menor que 20%. Las series de datos de las velocidades se
interpolaron en el tiempo empleando el método polinómico de Hermite para
sustituir los NaNs por valores de velocidad.
Con los ángulos de Euler obtenidos a partir de las series de u(t,z), v(t,z) y w(t,z), se construyeron las matrices de rotación de coordenadas con las
cuales se corrigió la orientación e inclinación del sensor.
Con el propósito de determinar la intensidad de la posible reflexión de las olas
en el canal durante la realización de nuestros experimentos, se obtuvieron
espectros direccionales D(f,θ), en función de la frecuencia f y la dirección de propagación θ, utilizando las series de tiempo de u(t,z), v(t,z) y w(t,z) y el conjunto de rutinas computacionales denominado Directional Wave
Spectra (DIWASP) para Matlab versión 1.4, para aplicar el método extendido de
máxima entropía [20]. En cada profundidad
z en donde se midieron las velocidades, se estimó un espectro direccional D(f,θ). Me-
diante D(f,θ), se determinó la energía incidente de las olas EI y la reflejada ER
[17,18] de la forma:
EI=∫0fmaxDf,θI)df
(1)
ER=∫0fmaxD(f,θR)df
(2)
donde θI corresponde al ángulo que define la dirección incidente de las olas
i.e. la dirección correspondiente a la frecuencia del pico en D(f,θ), θR es el ángulo que define la dirección directamente opuesta a θI y fmax es la frecuencia máxima resuelta (6 Hz) en los D(f,θ), la cual es previamente definida por el usuario en las rutinas
DIWASP. Una fmax=6 Hz se considera suficiente para determinar EI y ER de las olas durante los experimentos, con lo que se calculó el
coeficiente de reflexión KR=(ER/EI)1/2
[17,18,21], correspondiente a
cada z.
Los 184 experimentos fueron considerados para el análisis de turbulencia bajo la
premisa de que KR(z)<0.15 no corresponde a una reflexión significativa de las olas. En
nuestros experimentos, los valores de KR(z) presentaron un promedio μ=0.034±0.018.
En este trabajo, únicamente se analizan las componentes u(t,z) y w(t,z) de las velocidades de las partículas del fluido, pues se considera
que el campo de las velocidades orbitales de las olas es bi-dimensional
i.e.
v(t,z)=0. Las series temporales de v(t,z) no mostraron un comportamiento característico de una velocidad
orbital y la raíz cuadrática media de v(t,z) (v(z)rms) presentó valores entre 1 y 3 órdenes de magnitud menor que u(z)rms y w(z)rms. Además, el promedio temporal de v(t,z) es prácticamente igual a cero (v(z)¯=0).
3. Aspectos teóricos fundamentales y el cálculo de características de la
turbulencia
3.1. Espectros de las velocidades en fluidos turbulentos
El espectro de potencia de la velocidad en un flujo turbulento homogéneo e
isotrópico con números de Reynolds grandes (Re>3000), presenta un intervalo característico denominado sub-rango inercial
o de Kolmogorov [22]. La densidad de
energía espectral en el sub-rango inercial, se puede expresar como:
E(k)=αε2/3k-5/3
(3)
donde 𝜉 es la tasa de disipación de la energía cinética turbulenta, k es el módulo del vector número de onda y α la constante de
Kolmogorov cuyo valor se ha determinado entre 1.4 y 2.2 [23]. En el sub-rango inercial, la energía contenida en los
remolinos turbulentos de macro-escala se transfiere a remolinos de menores
escalas en un proceso denominado cascada de energía, obedeciendo a una ley de
transferencia de energía conocida como la ley de k-5/3 o Ley de Kolmogorov.
La ley de k-5/3 se cumple en espectros unidimensionales correspondientes a una de
las componentes de la velocidad e.g.
Euu(k1)=(α1/2)ε2/3k1-5/3, donde Euu(k1) es el espectro de la componente horizontal de la velocidad en
dirección paralela al flujo medio, k1 la componente horizontal del vector número de onda k=(k1,k2,k3) y α1≈0.4 una constante denominada constante de Heisenberg [24].
La turbulencia puede considerarse como congelada, si la intensidad media de las
fluctuaciones turbulentas es al menos un orden de magnitud menor que la
intensidad de la velocidad del flujo medio i.e. u'rms, w'rms≪U, donde u'rms y w'rms son respectivamente la raíz cuadrática media (intensidad) de las
fluctuaciones turbulentas de las componentes u y
w de la velocidad y U es la velocidad del
flujo medio. En este caso, las fluctuaciones turbulentas de la velocidad se
transportan con el flujo medio a una velocidad U,
i.e. Hipótesis de Taylor[25].
Bajo las condiciones de turbulencia congelada, los espectros de potencia de las
velocidades en función del número de onda pueden ser expresados en función de la
frecuencia mediante la hipótesis de Taylor [26], tal que ω=2πf=k1Ue.g.
Euu(f)=(π/U)Euu(k1), donde Euu(f) es el espectro de la componente horizontal de la velocidad en
función de la frecuencia f y 𝜔 la frecuencia angular, así
mismo la ley de k-5/3 puede ser expresada en función de la frecuencia como f-5/3.
Benilov y Filyushkin [27] expresan el
espectro de potencia de las fluctuaciones turbulentas de las velocidades de las
partículas de un fluido bajo la presencia de olas como:
Su'u'(f)=Suu(f)-Su~u~(f)
(4)
donde Suu(f) corresponde al espectro de potencia de la componente u de las velocidades instantáneas, Su~u~(f) al espectro de potencia de la componente u~ de las velocidades orbitales asociadas con el oleaje y Su'u'(f) al espectro de potencia de la componente u' de las velocidades turbulentas.
Thornton [28] define el espectro de las
velocidades orbitales asociadas con el oleaje como:
Su~u~(f)=Suu(f)×Cuη(f)2
(5)
donde Cuη(f)2 corresponde a la coherencia espectral entre la componente u(t) de la velocidad instantánea y análogamente, el espectro de potencia
de la componente w~ de las velocidades orbitales asociadas con el oleaje se expresa como Sw~w~(f)=Sww(f)×Cwη(f)2.
A partir de las series de tiempo de las componentes u(t,z) y w(t,z) de las velocidades medidas en los experimentos realizados en el
canal de olas, se calcularon los espectros de potencia Suu(f) y Sww(f) en cada profundidad z (35 espectros Suu(f) y Sww(f) en cada experimento) con 2K=50 grados de libertad, donde k es el número de
segmentos o particiones de las series de tiempo. Se calcularon también las
respectivas coherencias espectrales con la elevación de la superficie libre η(t), (Cuη(f)2) y (Cwη(f)2) obtenida a partir de la señal del detector del fondo del sensor
utilizado. Posteriormente, considerando las expresiones (4) y de manera análoga
(5), se obtuvieron los espectros de potencia Su'u'(f) y Sw'w'(f).
Se realizó un análisis de la forma de cada espectro Su'u'(f,z) y Sw'w'(f,z) para identificar la región en el dominio de frecuencias, en donde se
presentó el sub-rango inercial tal que Su'u'(f)∼f-5/3 y Sw'w'(f)∼f-5/3. Se obtuvo un ajuste con el método de mínimos cuadrados del valor de S (en escala logarítmica) y se determinó si la pendiente
correspondiente es m=-5/3±0.04, con lo que se satisface la ley de f-5/3 (en este caso, el valor de tolerancia es ±0.04, con lo que se obtiene un 95% de confiabilidad). La identificación
de la pendiente m (-5/3±0.04) se realizó con los valores de la densidad de energía espectral, en
un rango de frecuencias ≥15 Hz (ampliando el rango hasta una frecuencia máxima en donde la
correlación entre S y f-5/3 se reduce hasta valores menores que 0.8).
Lumley y Terray [29], demostraron que la
raíz cuadrática media de las velocidades de las partículas en un fluido bajo
condiciones de olas unidireccionales en aguas profundas, resulta adecuada para
utilizar la relación de Taylor i.e.
ω=k1Uμ, donde Uμ es la raíz cuadrática media de la velocidad instantánea expresada
como:
Uμ(z)=1N∑i=1Nu(ti,z)2+w(ti,z)21/2
(6)
La intensidad de cada componente de las fluctuaciones turbulentas (u'rms y w'rms) se estimó a partir de Su'u'(f) y Sw'w'(f) mediante la relación de Parseval. Los resultados de Uμ(z) presentaron valores (entre 10 y 60 veces) mayores que u'rms y w'rms, con lo que se sugiere considerar la existencia de turbulencia
congelada en nuestros experimentos.
En atención a la turbulencia congelada y mediante la relación 2πf=k1Uμ, se realizó la conversión de f a k1 en los sub-rangos inerciales identificados en los Su'u'(f) y Sw'w'(f). Los espectros de potencia Su'u'(f) y Sw'w'(f) también se transformaron al dominio del número de onda, para estimar Su'u'(k1) y Sw'w'(k1), respectivamente y posteriormente utilizarse en el análisis.
3.2. Tasa de disipación de la energía cinética turbulenta
La tasa de disipación de energía cinética turbulenta ε, incluida en la expresión del sub-rango inercial del espectro de
potencia de la velocidad (ver Ec. 3), es una característica de la cantidad de
turbulencia en un fluido y de la cantidad de mezcla generada por esa
turbulencia, especialmente al tratar un caso estacionario cuando existe un
equilibrio entre la generación y la disipación de esa energía cinética
turbulenta. La tasa de disipación ε, asociada a cada componente de las fluctuaciones turbulentas de la
velocidad, se puede estimar a partir de las expresiones del sub-rango inercial
de los espectros de potencia unidimensionales en función de la frecuencia (en
unidades de densidad de energía espectral) correspondientes a cada una de las
componentes de la velocidad turbulenta u' y w' mediante:
εu'(z)=C2πUμ(z)-1f5/2Su'u'(f,z)3/2
(7)
y
εw'(z)=C2πUμ(z)-1f5/2Sw'w'(f,z)3/2
(8)
en donde C corresponde a una constante del orden de launidad, y en este trabajo
se considera como C
=1. Para una mayor certeza en la estimación de ε, se realizó un promedio en frecuencia en (7) y (8).
De acuerdo con la teoría de Kolmogorov, la ley de k1-5/3 es apreciable dentro del intervalo 2π/L≪k1-5/3≪2π/nk, donde L representa la dimensión longitudinal de la macro-escala de la
turbulencia (escala integral), y 2π/L corresponde con el menor número de onda en ese intervalo y el que
contiene la mayor energía en el espectro. En el otro extremo de ese intervalo,
la micro-escala de la turbulencia (micro-escala de Kolmogorov) se define como nk=(ν3/ε)1/4, donde ν es la viscosidad cinemática del agua y puede estimarse a partir de
los valores de ε que se obtienen de los sub-rangos inerciales identificados en Su'u'(f) y Sw'w'(f). La micro-escala de Kolmogorov representa el tamaño de los remolinos
más pequeños en el campo turbulento, es en dicha escala que los efectos de la
disipación viscosa son de los más intensos.
4. Resultados
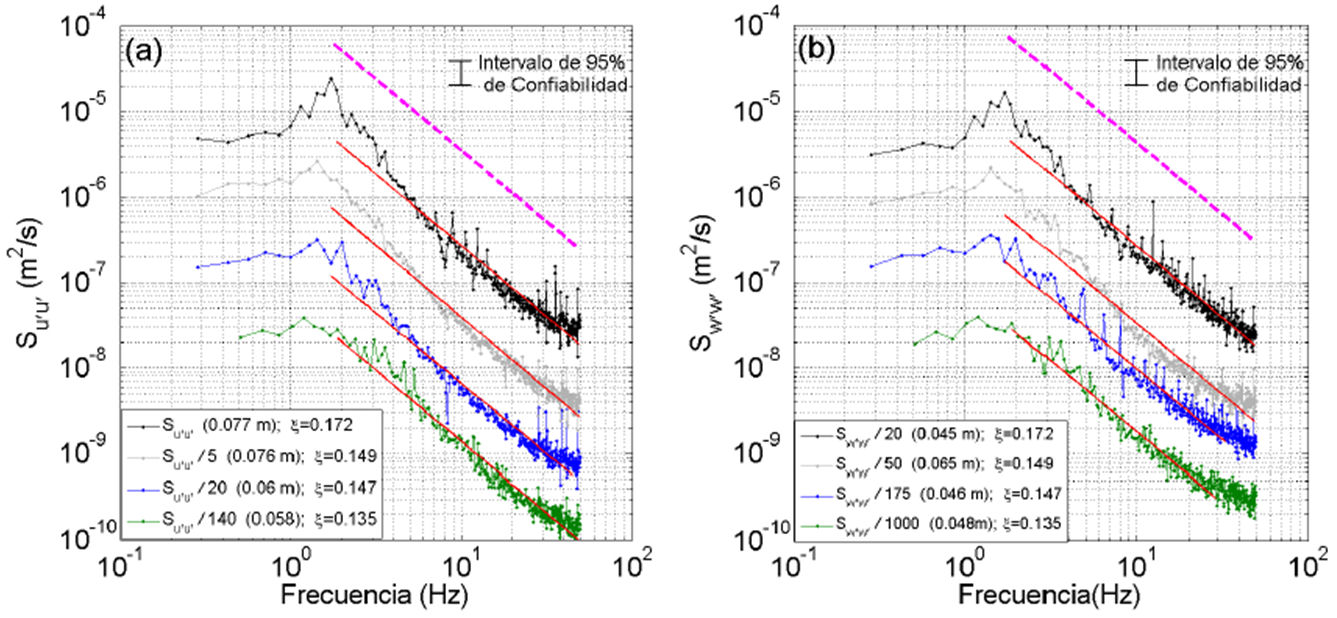
En las Figs. 1a y 1b se presentan ejemplos de los espectros Su'u'(f) y Sw'w'(f), respectivamente, obtenidos a partir de 4 experimentos con pendiente de
las olas entre 0.135 y 0.172. El conjunto de espectros de un color corresponde a un
experimento en particular y a una determinada profundidad.
En color negro los resultados del experimento n∘ 101, con ξ=0.172; en color gris, del experimento n∘ 91, con ξ=0.149; en azul, del experimento n∘ 105, con ξ=0.147 y en verde, los resultados del experimento n∘ 40, con ξ=0.135.
La línea segmentada magenta indica S∼f-5/3 que corresponde a la ley de Kolmogorov. La línea roja en cada conjunto
de espectros representa el ajuste de la energía espectral de un caso en particular
como ejemplo, en donde se identifica el sub-rango inercial con m=-5/3±0.04.
La Fig. 2, presenta el porcentaje del total (184
experimentos) de los espectros Su'u'(k1,z) (una vez transformados al dominio de k1 bajo la consideración de una turbulencia congelada), en donde se
identificó la presencia del sub-rango inercial. Los resultados se describen también
en función de la pendiente de las olas (𝜉) y de los intervalos verticales que
corresponden con profundidad: a) entre 0.028 y 0.039 m, b), entre 0.039 y 0.051 m,
c) entre 0.051 y 0.063 m, d) entre 0.063 y 0.074 m y e) entre 0.063 y 0.086 m, y en
el perfil completo que corresponde con profundidades f) entre 0.028 y 0.086 m. Un
valor de 100% indica que en ese experimento en particular se identificó la presencia
de sub-rango inercial en todos y cada uno de los espectros en todas las
profundidades en las que se realizaron las mediciones. El patrón de colores
especifica el promedio (del total de los experimentos) del número de onda
correspondiente al límite superior del sub-rango inercial (en el dominio de k1) identificado en cada intervalo y rango de profundidad indicados. Se
identificó la presencia del sub-rango inercial en los espectros Su'u'(k1) con una cierta variabilidad en el número de onda límite superior,
dependiendo de los diferentes intervalos de profundidad dentro de la gama completa
de valores de ξ(0.012-0.273). El mayor número de experimentos cuyos Su'u'(k1) presentaron sub-rangos inerciales, se observó en profundidades entre
0.051 y 0.074 m. Particularmente, el 46% de los experimentos presentó sub-rangos
inerciales en Su'u'(k1) en profundidades entre 0.051 y 0.063 m (Fig. 2c) y entre 0.067 y 0.074 m (Fig.
2d). En profundidades entre 0.028 y 0.039 m (Fig. 2a) y entre 0.067 y 0.086 m (Fig. 2e), se presentó la menor cantidad de experimentos con ocurrencia
de sub-rangos inerciales en los Su'u'(k1) (7% y 19% respectivamente), sugiriendo una relativa ausencia de
turbulencia. El 53% de los experimentos presentó sub-rangos inerciales en los Su'u'(k1) en profundidades entre 0.028 y 0.086 m (Fig. 2f).
En las Figs. 3a, b, c, d y e, se presenta el porcentaje de
ocurrencia de sub-rangos inerciales en los espectros de las componentes verticales
de las velocidades turbulentas Sw'w'(k1), en función de 𝜉, y se indica también el número de onda límite superior
de ese sub-rango. Se muestran los resultados obtenidos dentro de los intervalos de
profundidad indicados, en el rango 0.028-0.086 m de la columna en donde se realizaron las mediciones. En profundidades
entre 0.039 y 0.063 m se encontró la mayor cantidad de experimentos cuyos Sw'w'(k1) presentaron sub-rangos inerciales. Particularmente, 55% de los
experimentos presentaron sub-rangos inerciales en profundidades entre 0.039 y 0.051
m (Fig. 3b) y el 47% de los experimentos entre
0.051 y 0.063 m (Fig. 3c). En los intervalos de
profundidad entre 0.028 y 0.039 m (Fig. 3a) y
entre 0.067 y 0.086 m (Fig. 3e) se presentó la
menor cantidad de experimentos con ocurrencia de sub-rango inercial en Sw'w'(k1) (26% y 18% respectivamente) lo que sugiere menor presencia de
turbulencia. Dentro del rango completo de profundidades 0.028-0.086 m (Fig. 3f), el 61% de los
experimentos presentó sub-rangos inerciales en Sw'w'(k1).
5. Discusión y comentarios finales
En los espectros de potencia Su'u'(f) y Sw'w'(f) estimados a partir de las mediciones en el laboratorio, se identificaron
sub-rangos inerciales en 53% y 61% del total de experimentos respectivamente. En
ninguno de los intervalos de profundidad en el rango de las mediciones se encontró
relación entre el ancho en frecuencia de los sub-rangos inerciales identificados y
los valores de 𝜉. Sin embargo, en los sub-rangos inerciales en función de k1, el ancho que se observa corresponde a números de onda que disminuyen al
aumentar los valores de 𝜉 (ver Figs. 2c-f y 3a-c, f). Esto
sugiere que el proceso de cascada de energía en Su'u'(k1) y Sw'w'(k1), ocurre en remolinos turbulentos de mayor tamaño en las olas con
mayor𝜉. Además, se identificó que la variabilidad del ancho del sub-rango inercial
en el dominio de k1 en función de 𝜉 puede ser predominante en ciertos intervalos de
profundidad (ver Figs. 2a, b y 3d, e), con lo que se enmascara de manera
intermitente la presencia de la cascada de energía ya mencionada. En términos
generales, el proceso de cascada de energía se extiende hasta remolinos con menores
(mayores) escalas al disminuir (aumentar) ξ.
El número de onda límite superior del sub-rango inercial identificado en Su'u'(k1) y Sw'w'(k1) es menor que 2π/nk, en particular en 70% de Su'u'(k1) y 66% de Sw'w'(k1) donde se identificó el sub-rango inercial, el valor de su límite
superior resultó ser de un orden de magnitud menor que 2π/nk cumpliendo con la hipótesis de Kolmogorov, los valores de k1≥2π/nk definen el dominio en Su'u'(k1) y Sw'w'(k1) donde los efectos de la disipación viscosa son dominantes (rango de
disipación).
La presencia del sub-rango inercial en los espectros analizados es independiente de
la pendiente de las olas, sin embargo en Su'u'(k1) se identificaron sub-rangos inerciales con una mayor frecuencia de
ocurrencia en mediciones con profundidades entre 0.051 y 0.074 m, mientras que en Sw'w'(k1) la mayor ocurrencia se identificó en las mediciones con profundidades
entre 0.039 y 0.063 m. Babanin y Hauss [11],
presentaron resultados del sub-rango inercial identificado en espectros de potencia
de la componente u de la velocidad en función del número de onda. El sub-rango inercial fué
identificado en tres ocasiones a partir de las mediciones de cada experimento con
una duración de aproximadamente 15 periodos de las olas (10 segundos). La pendiente
de las olas en sus experimentos fue de 0.13≤ξ≤0.25. En los resultados del presente trabajo, el análisis llevado a cabo
corresponde con la duración de cada experimento en el que se incluyen entre 315 y
525 periodos de olas aproximadamente, en una columna de agua de 3.5 cm en un rango
de profundidad entre 2.8 y 8.6 cm. En 43% de los experimentos se identificó el
sub-rango inercial tanto en Su'u'(k1) como en Sw'w'(k1) mientras que el carácter natural de la turbulencia, induce la ausencia
intermitente del sub-rango inercial en el espectro de una o ambas componentes de la
velocidades fluctuantes.
Babanin y Hauss [11], identificaron sub-rangos
inerciales en el intervalo 800<k<2600 rad/m, siendo 2600 rad/m la máxima escala resuelta en los espectros. El
ancho del sub-rango inercial que encontraron presentó un orden de magnitud de 103 rad/m. En nuestros resultados, el sub-rango inercial en Su'u'(k1) y Sw'w'(k1) se identificó en el intervalo 753±588<k1<2300±1600 rad/m, con un ancho promedio de 1500 rad/m. En términos generales, el
sub-rango inercial en Su'u'(k1) y Sw'w'(k1) se identificó en un intervalo similar al de los resultados de Babanin y
Hauss [11], y con un ancho del mismo orden de
magnitud (generalmente cuando ξ>0.1).
A partir del sub-rango inercial en sus espectros de potencia de la velocidad, Babanin
y Hauss [11], estimaron valores de ε con órdenes de magnitud entre 10-4 y 10-3 m2/s3. En nuestros experimentos, los valores de ε obtenidos a partir del sub-rango inercial identificado en Su'u'(k1) y Sw'w'(k1), presentaron órdenes de magnitud de 10-4 m2/s3, y únicamente 20% y 8% de dichos valores respectivamente, presentaron
órdenes de magnitud de 10-3 m2/s3 especialmente en las menores profundidades, las que corresponden a la
parte superior y más cercana a la superficie del agua. Nuestra estimación de 𝜉
puede considerarse como un límite inferior con respecto a los valores calculados por
Babanin y Hauss [11].
Se establece que los espectros de potencia Su'u'(k1) y Sw'w'(k1) corresponden a un movimiento turbulento de las partículas de fluido,
apreciándose sub-rangos inerciales de forma intermitente, con lo que se infiere que
el movimiento inducido por olas que aún no rompen puede generar turbulencia
isotrópica desarrollada independientemente del valor de la pendiente de las olas en
las distintas profundidades en donde se realizaron las mediciones. Con los
resultados de Su'u'(k1) y Sw'w'(k1) se demuestra que el tamaño de los remolinos cuya energía se transfiere a
remolinos de menores escalas, es mayor al aumentar la pendiente de las olas.
Agradecimientos
Este trabajo representa una contribución del proyecto RugDiSMar (CONACYT
CB-2010-01-155793). Se agradece el apoyo por parte del Posgrado en Oceanografía
Física del CICESE, así como el apoyo económico para estudios de Posgrado por parte
del CONACYT. A la Facultad de Ciencias Marinas (FCM), al Dr. Rafael Hernández Wall y
M.C. Patricia Alvarado Graef, de la Universidad Autónoma de Baja California por
facilitar el desarrollo de los experimentos en el laboratorio de olas de la FCM. Se
agradece especialmente a L.A. Julieta Castro por su apoyo en procedimientos de
logística y administración durante las actividades propias de esta investigación.
Esta investigación ha sido financiada por el proyecto 201441
SENER-CONACYT-Hidrocarburos, y el proyecto 249795 CONACYT-SENER Sustentabilidad
Energética. La versión final de este trabajo se completó durante el programa
Planetary Boundary Layers in Atmospheres, Oceans, and Ice on Earth and Moons
(KIPT-UCSB 2018, NSF PHY17-48958).
References
1 D. Peregrine and L. Svendsen, Proc. 16th ICCE. 1
(1978) 540-550.
[ Links ]
2 O. Reynolds, Phil. Trans. Roy. Soc. London. 174
(1883) 935-982.
[ Links ]
3 R. J. Rapp, W. K. Melville, Philos. Trans. R. Soc. Lond.
A 331 (1990) 735-80.
[ Links ]
4 L. H. Kantha, and C. A. Clayson, Ocean Modell. 6
(2004) 101-124.
[ Links ]
5 Y. Noh, H. Min, and S. Raasch, J. Phys. Oceanogr.
34 (2004) 720-735.
[ Links ]
6 J. Gemmrich, J. Phys. Oceanogr. 40 (2010)
583-595.
[ Links ]
7 O. M. Phillips, J. Geophys. Res. 66 (1962)
2889-2893.
[ Links ]
8 V. V. Yefimov, and G. N. Khristoforov, Izv. Acad. Sci.
USSR Atmos. Oceanic Phys., Engl. Transl. 7 (1971)
1290-1310.
[ Links ]
9 L. Cavaleri, and S. Zecchetto, J. Geophys. Res.
92 (1987) 3894-3904.
[ Links ]
10 A. V. Babanin, Geophys. Res. Lett. 33 (2006)
L20605.
[ Links ]
11 A. V. Babanin , and B. K. Haus, J. Phys.
Oceanogr. 39 (2009) 2675-2679.
[ Links ]
12 D. Dai, F. Qiao, W. Sulisz, L. Han, and A. Babanin, J.
Phys. Oceanogr. 40 (2010) 2180-2188.
[ Links ]
13 I. B. Savelyev, E. Maxeiner, and D. Chalikov, J. Geophys.
Res. 117 (2012) C00J13.
[ Links ]
14 F. Veron, F., W. Melville, and L. Lenain, J. Atmos.
Oceanic Technol. 25 (2008) 307-326.
[ Links ]
15 J. Beyá, W. Peirson, and M. Banner, Exp. Fluids.
52 (2012) 1319-1330.
[ Links ]
16 B. Kinsman, Wind Waves: Their generation and propagation
on the ocean surface. (Prentice-Hall, Englewood Cliffs, N.J.
1965).
[ Links ]
17 Y. Goda, and Y. Suzuki, Proc. 15th ICCE, ASCE,
Hawaii. (1976) 628-650.
[ Links ]
18 E. P. D. Mansard, and E. R. Funke, Proc. 17th ICCE, ASCE,
Syndey, Australia. (1980) 154-172.
[ Links ]
19 F. Veron , andW. K. Melville , J. Atmos. Ocean.
Tech. 16 (1999) 1580-1597.
[ Links ]
20 N. Hashimoto, T. Nagai, and T. Asai, Coast. Eng.
Chapter 18 (1994) 223-246.
[ Links ]
21 C.-Y. Lin, and C.-J. Huang, Coast. Eng. 51
(2004) 395-406.
[ Links ]
22 A. N. Kolmogorov, Dokl. Akad. Nauk SSSR. 30
(1941) 9-13.
[ Links ]
23 A. S. Monin, and R. V. Ozmidov, Turbulence in the
ocean (D. Reidel Publ. Co. Dordrecht 1985) pp.
458.
[ Links ]
24 J. O. Hinze, Turbulence (McGraw-Hill, 1975)
790pp.
[ Links ]
25 G. I. Taylor, Proc. 5th Int. Congress App.
Mech., Cambridge Mass. (edited by J.P. Den Hartog and H. Peters, John
Wiley, New York. 1983) 294-310.
[ Links ]
26 S. R. Green, PHOENICS. J. CFD & Appl. 5
(1992) 294-312.
[ Links ]
27 A. Y. Benilov, and B. N. Filyushkin, Izv. Acad. Sci. USSR
Atmos. Oceanic Phys., Engl. Transl. 6 (1970)
477-482.
[ Links ]
28 E. B. Thornton, J. Geophys. Res. 84 (1979)
4931-4938.
[ Links ]
29 J. L. Lumley, and E. A. Terray, J. Phys.
Oceanogr. 13 (1983) 2000-2007.
[ Links ]













 nova página do texto(beta)
nova página do texto(beta)


