1. Introduction
The importance of the exact solutions of the non-relativistic wave equations in quantum mechanics cannot be over-emphasized. As such, non-relativistic spinless particles can be described using Schrödinger wave equation [1]. Most of the exactly solvable potentials are either exponential in nature. Some of these potentials that have been investigated include the Hulthen potential [2], Manning-Rosen potential [3], Eckart potential [4], Six-Parameter Exponential-Type Potential [5], Hylleraas potential [6], Eckart plus Modified Hylleraas potential [7] and other combined potentials [8]. The exact solutions of these equations with the potentials mentioned above are only possible in the s-wave where the angular momentum is zero. In a situation where the angular momentum is not zero, an approximate solution is obtained.
Different methods employed over the years in obtaining these solutions include Nikiforov-Uvarov (NU) method [9-12], Supersymmetry quantum mechanics (SUSYQM) [13-16], Asymptotic iteration methos (AIM) [17], Proper and exact quantization rule [18-19], Factorization method [20], Functional Analysis Approach FAA (also known here as Modified Factorization Method) [21], etc. The modified factorization method is usually used to transform a second-order homogeneous linear differential equation into a hypergeometric equation, with the help of a transformation scheme[22]. The uniqueness, simplicity and clarity of this method makes it preferable over other methods mentioned above. Recently, different authors have used this method in calculation of interaction potential energy curve and vibrational levels for Lithium molecule with the improved expression of the Manning-Rosen empirical potential energy model[23]; molecular energies of the improved Rosen-Morse potential energy model [24]; diatomic molecule energies of the Rosen-Morse potential energy model [25]; etc.
The Quadratic exponential-type potential (QEP) model of our interest can be used in the description of molecular dynamics [26-27]. It can also be used to study the vibrational energy of diatomic molecules [28]. This potential as earlier studied [29] has various applications in Physics and Chemistry.
The thermodynamic properties for the quadratic exponential-type potential are also studied in this research. These include vibrational partition function, vibrational mean energy, vibrational mean free energy, vibrational entropy, etc. Before now, different authors have investigated the thermodynamic properties for some physical systems [30-36]. The priority of this work is fact that the thermodynamic properties of this potential have not been considered to the best of our knowledge.
The organization of this work is in different folds. Firstly, we consider the
Schrödinger equation for a spherically symmetric potential in D-dimensions and solve
the Schrödinger equation for its
2. Solutions of the Schrödinger Equation in D-Dimensions
The radial part of the Schrödinger equation in D-dimensions [37] is given by:
where
where,
In solving Eq. (3), we invoke an approximation scheme[38] to deal with the centrifugal term since
Substituting Eq. (4) into Eq. (3) and employing a coordinate transformation of the
form
Where
From the asymptotic behaviour of Eq. (5), (i.e.,
Substituting Eq. (10) into Eq. (5), we obtain the following equation:
Equation (11) will become a Gauss hypergeometric equation if and only the following equations vanish:
Thus, Eq. (8) now reduced to:
From the Gauss hypergeometric function, the solution of Eq. (11) can be obtained as:
where the unknown parameters are expressed as:
Substituting Eqs. (15-18) into Eq. (10), we obtain the solution of the wave function
The hypergeometric function
Combining Eqs. (16), (19) and (20), we have:
Employing Eqs. (10) and (22) respectively, results in the following expressions:
Substituting Eq. (26) into Eq. (27) gives:
Combining Eqs. (24) and (25) appropriately, we have the following expressions given below:
Eq. (27) above can also be written as:
Where
Evaluating Eq. (12) and (13) results in the expression:
Substituting Eqs. (6), (7) and (28) into Eq. (30) gives the non-relativistic energy eigenvalues of the Quadratic Exponential-Type Potential as:
Also, the corresponding total wave function in a Gauss hypergeometric form is given as:
Using Eqs. (16), (14), (15) and (17), Eq. (29) can be expressed as:
3. Partition Function and Thermodynamic Properties
First of all, we write Eq. (31) in a closed form as:
where
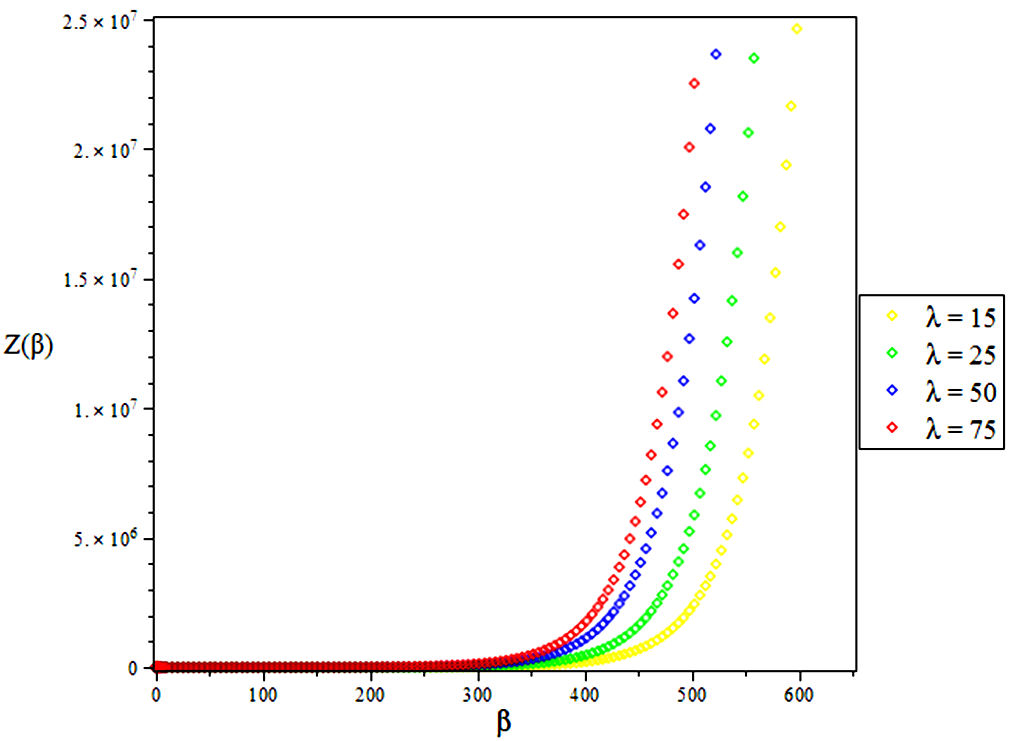
The partition function of the bound state system at a given temperature
Where
Replacing the sum by an integral in the classical limit, we have:
Due to the complicated nature of the integral contained in Eq. (39) above, we employ a Maple software to evaluate the partition function as given below [39]
Where
The imaginary error function given in Eq. (40) is defined as [39]:
Different numerical calculations can also be carried out using the imaginary error function given in Eq. (42), with the help of Maple software [40].
Using the vibrational partition function given in Eq. (40), other thermodynamic properties of the QEP model can be determined as follows:
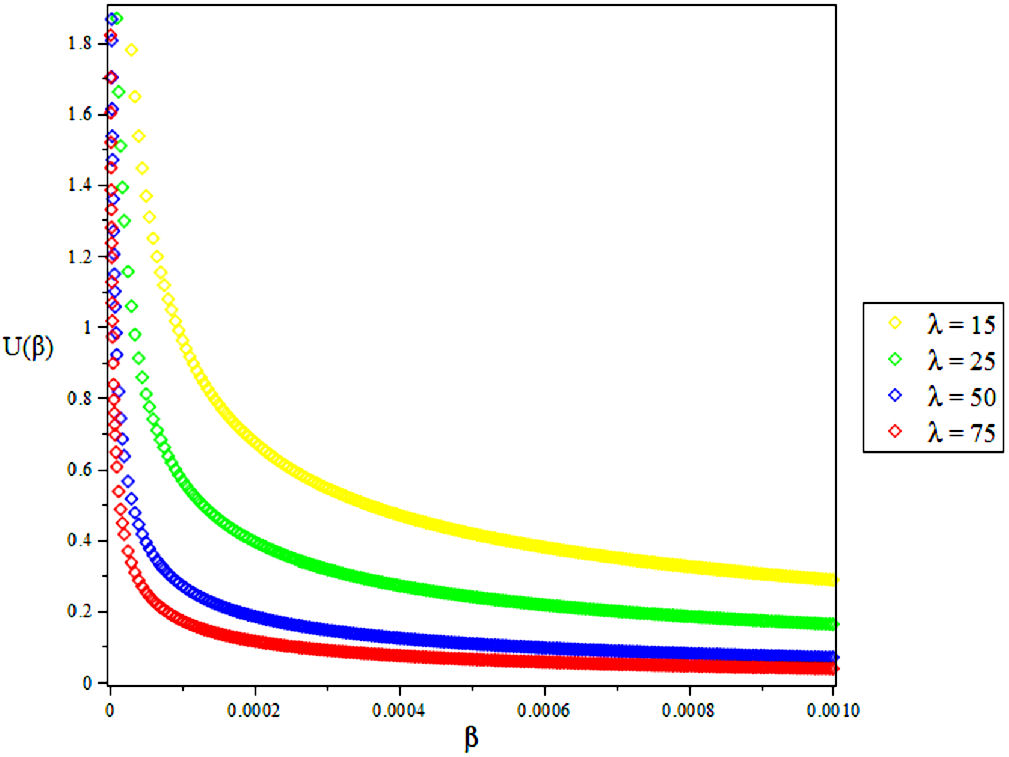
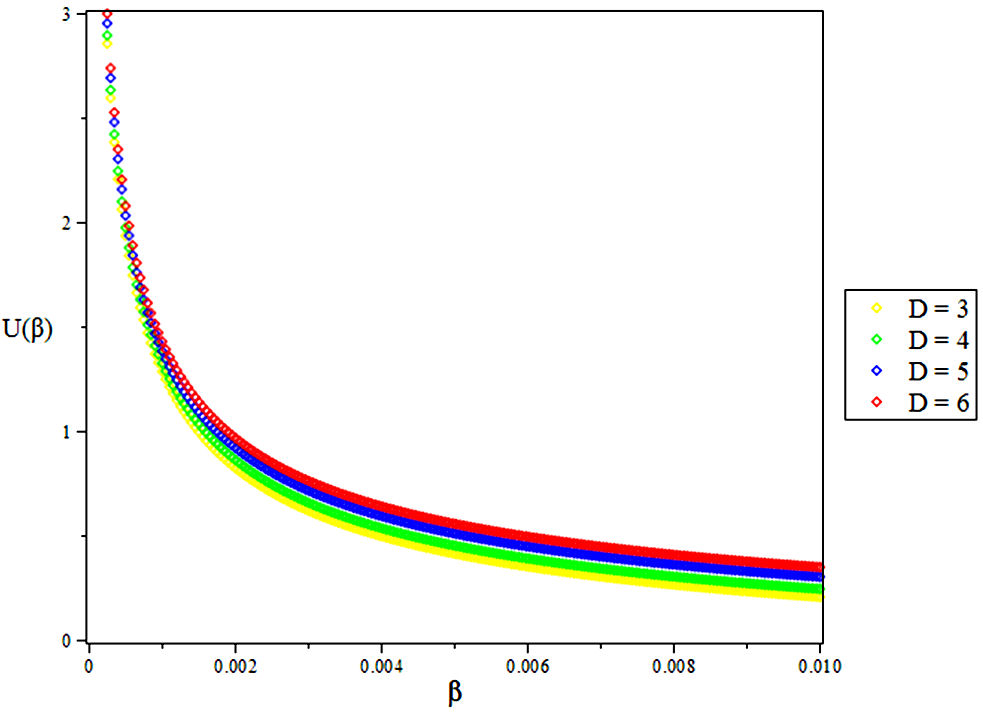
3.1. The Vibrational Mean Energy U
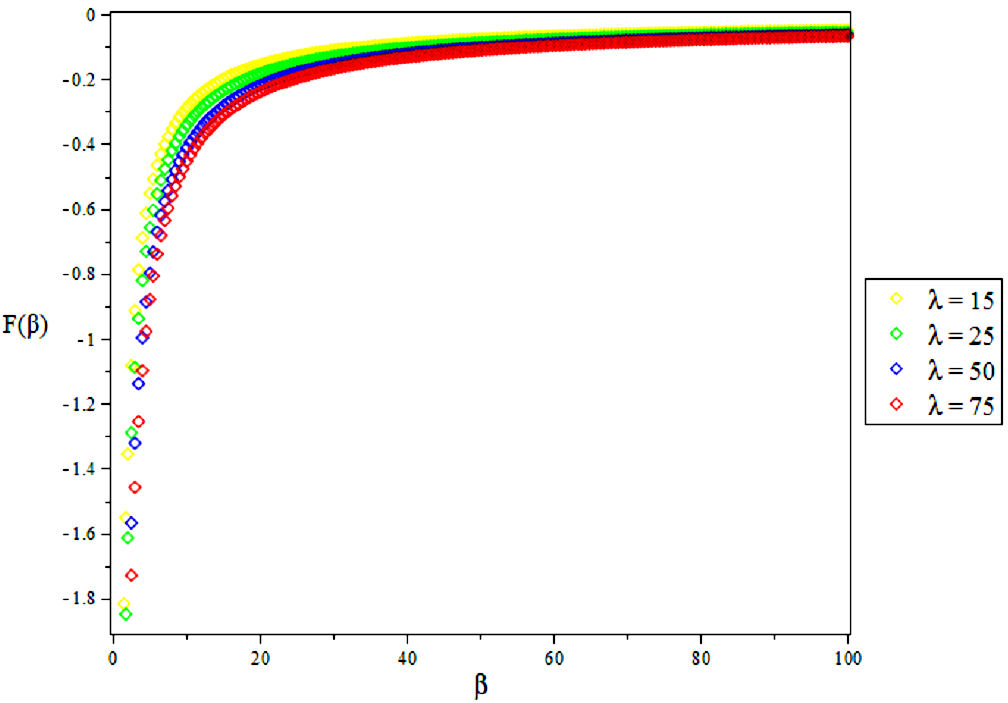
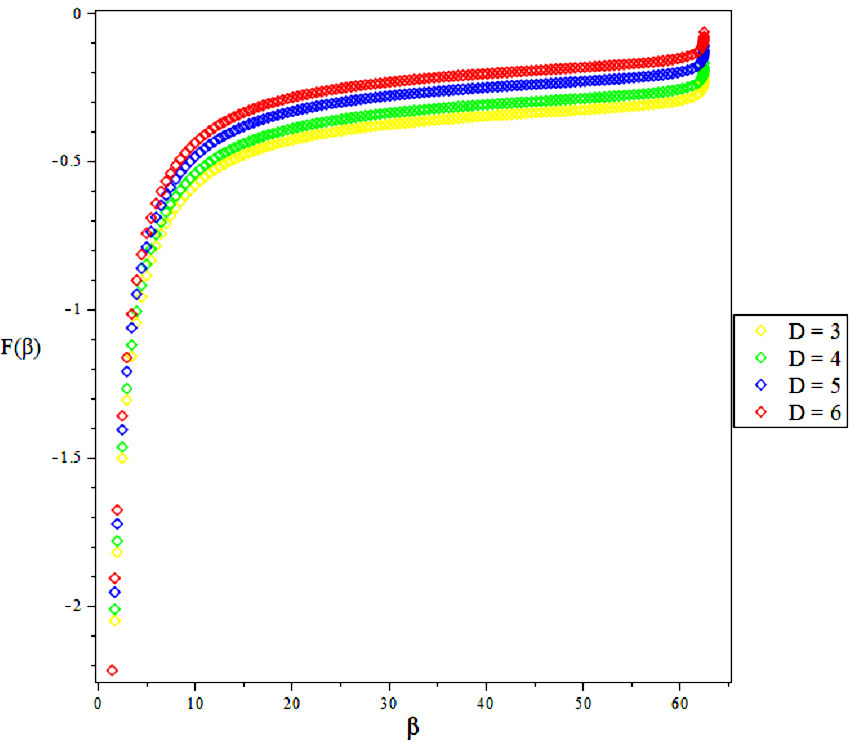
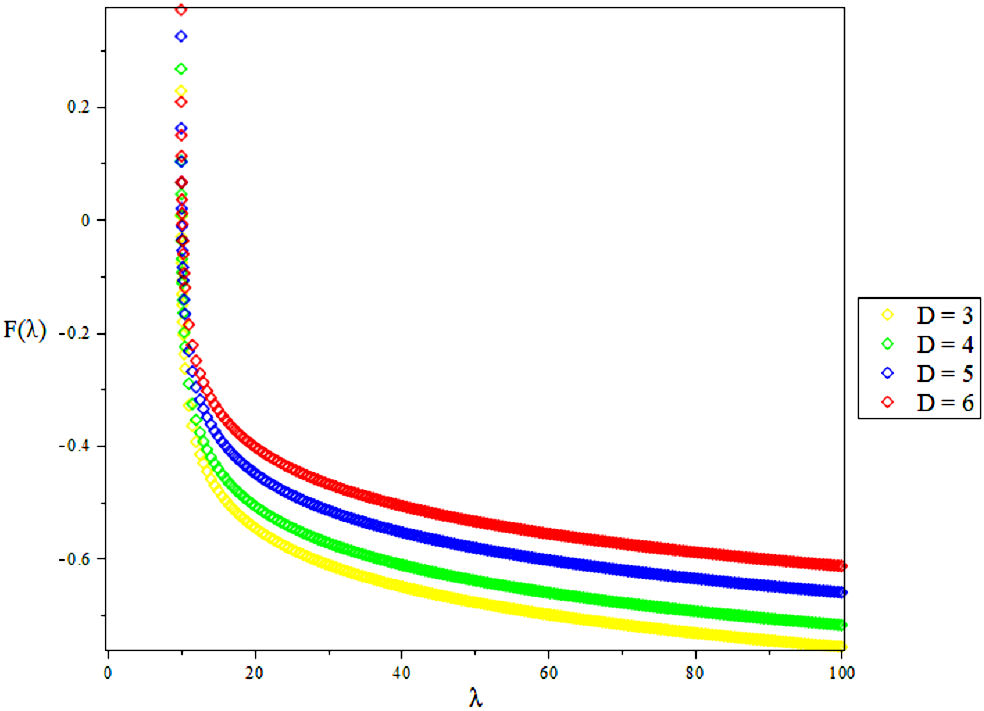
3.2. Vibratioal Mean Free Energy, F
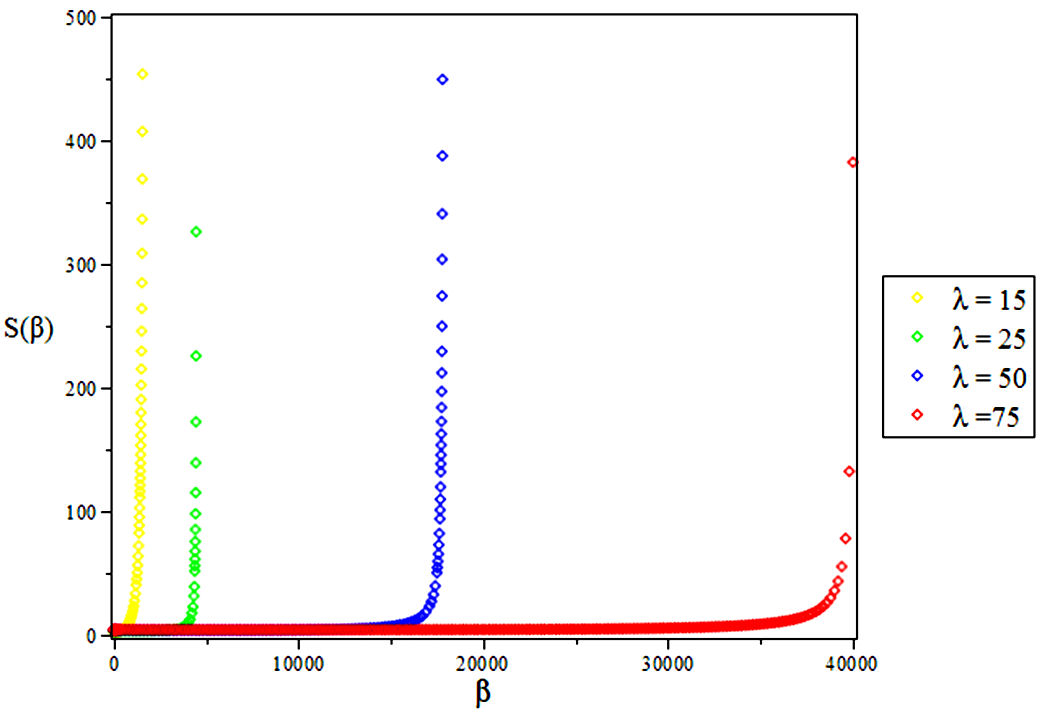
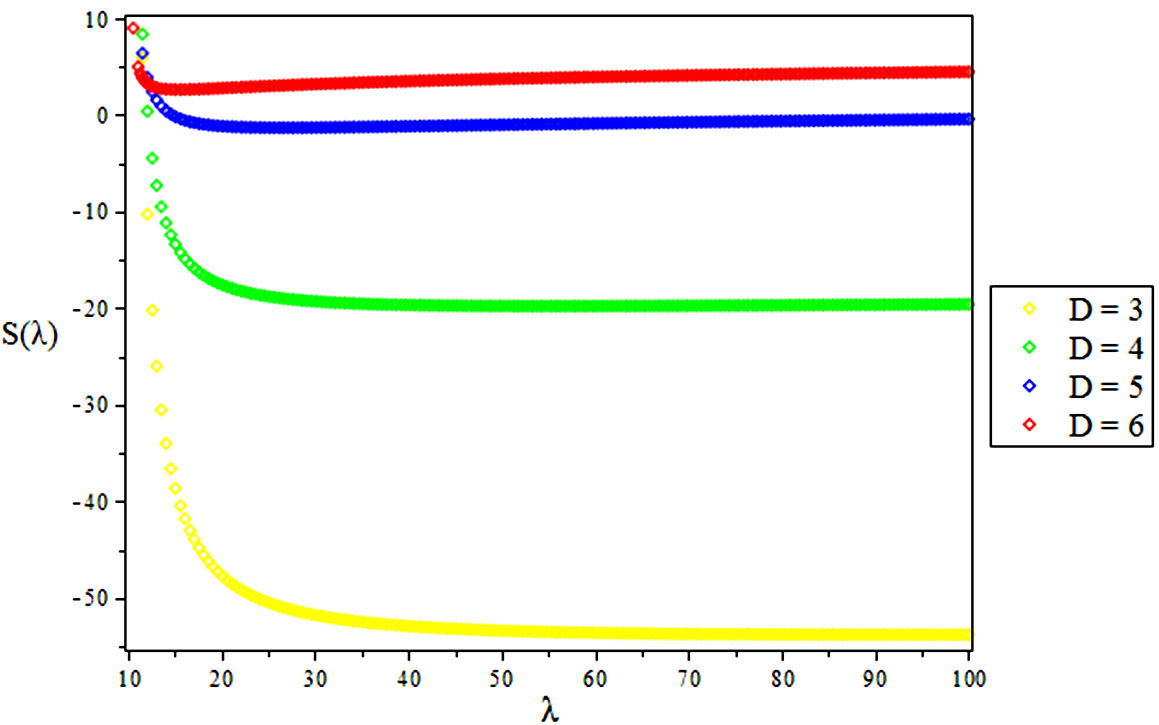
3.3. Vibrational Entropy, S
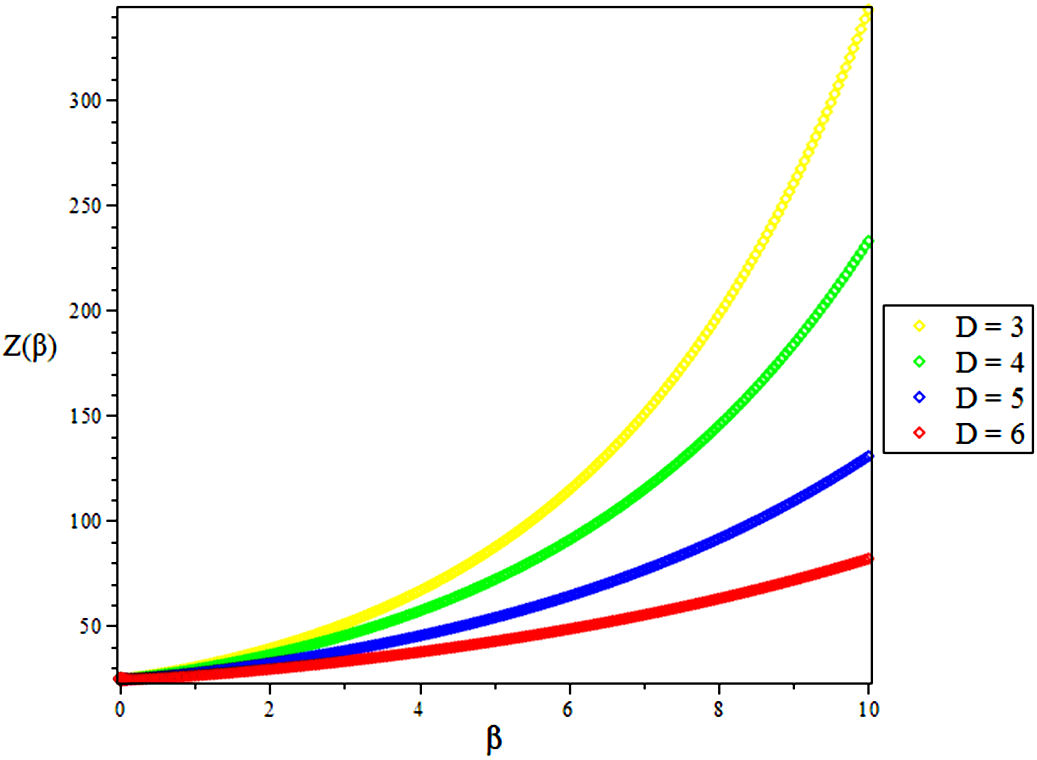
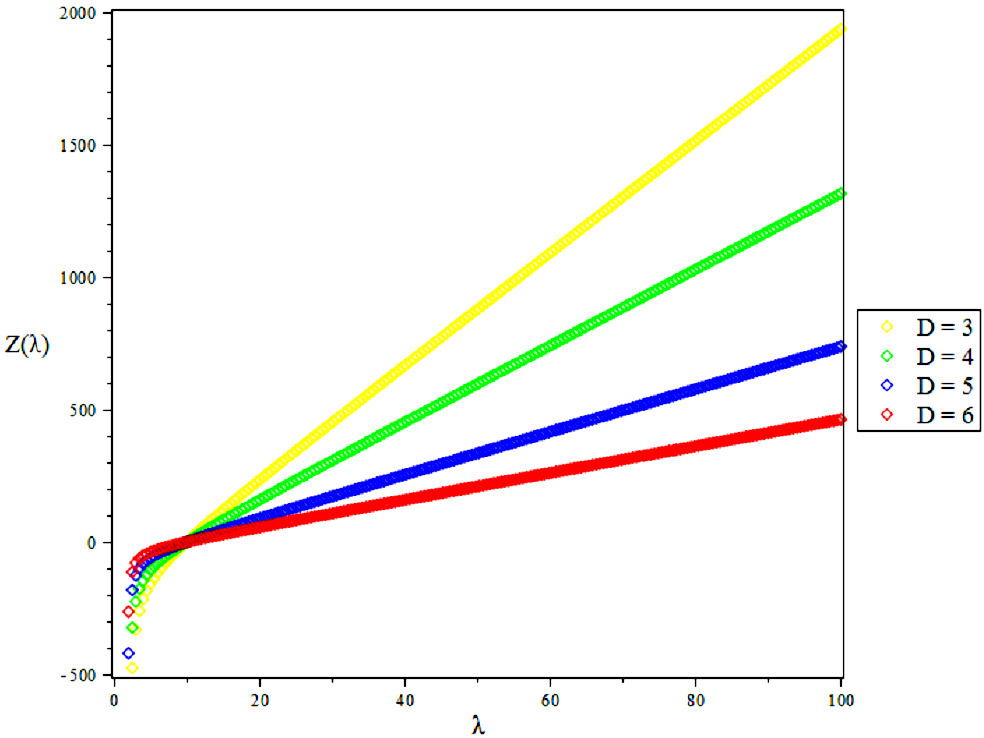
4. Results and Discussions
In this research, the electronic state of Rubidium dimer
5. Conclusion
In the present study, the Schrödinger equation has been solved in D-dimension with
QEP using the modified Factorization method and the energy eigenvalues and total
wave-functions obtained in terms of hypergeometric function. We have also calculated
the partition function and other thermodynamic properties of vibrational mean
energy. Vibrational mean free energy and vibrational entropy, for the electronic
state of











 nova página do texto(beta)
nova página do texto(beta)