1. Introducction
Thin folded matter configurations are present in nature. Some natural physical systems have a minimal state energy incrumpled configuration. Proteins are an example, and their properties have been studied 1-3. Other systems like polymerized membranes 4-7, graphene nanosheets 8-13 and crumpled paper balls 14,15,17,19-27 have been well studied and they are reported in literature. Authors of 17,18,21,23-27 had made remarkable findings working with thin folded matter, particularly randomly crumpled paper. A complete study of mechanical and dynamical properties of crumpled paper balls and many different measurements of fractals quantities has been reported in 26. In this sense the experimental and theoretical studies in crumpling phenomena is nowadays a very fertile area in science. Analytical relationships and numerical scaling exponents (fractal dimensionalities) have been stablished in relation to the morphological transformation of a flat sheet into a crumpled ball, and intensive studies over the recent decades had been made, fractal dimensionalities as chemical, random walk, shortest path, spectral, and others can be easily found 14,15,17,20-27. As a practical model, paper crumpled by hand offers an attractive way to explore the nature of complexity, and also represents a good option to emulate some natural systems to extrapolate and correlate their properties. In the present work we will focus principally in just one fractal dimension of this set of universality class scaling exponents, this is the shortest path fractal dimension defined by the scaling relation 26,28,29 (the present case: crumpled elastoplastic paper balls)
where l
min represents the chemical distance or shortest path and l
e
the Pythagorean or Euclidean distance. The shortest path l
min is clearly defined between two vertices randomly chosen on the crumpling network. Initially this quantity was studied extensively by authors of 18,28 for percolation cluster in 2D and 3D and re-write for the case of crumpling phenomena 25,26. Authors of 26 working with digitized images of stamped crumpling networks of paper balls got experimentally the d min value, finding that over 500 realizations
2. Experimental details and results
We started the experiment crushing by hand square sheets of copy paper type into quasi-spherical balls of diameter R, original sheet sizes edges were L = 12, 15, 22 y 30 cm. After we have turned a flat sheet into a ball we randomly assigned a collection of points on its surface and then a complete strain relaxation was permitted during 9 to10 days 21,23. To identify each randomly assigned point, a color code was needed. 30 balls of each size were measured. In the crumpled state, a digital Vernier caliper was used to get the Euclidean distances, and in flat state measurements were made using the ruler tool of Foxit Reader free software 30 after digitalizing the corresponding images of each different size sheet. The original form, crumpled and flat states of paper sheets, are shown in Fig. 1. Measuring the minimum distance between two points located in the same face of a sheet was an easy work, but in order to get measurements of distances of a pair of points in opposite sides of the flat sheet we devised the topological transformation presented in Fig. 2. For this case four distances data were obtained, the smallest one was chosen.

Figure 1 Copy paper type employed in the experiment. (a) Relaxed strain crumpled configuration and (b) Digitized sheet after being unfolded and flattened. The black corners were a guide to de eye.
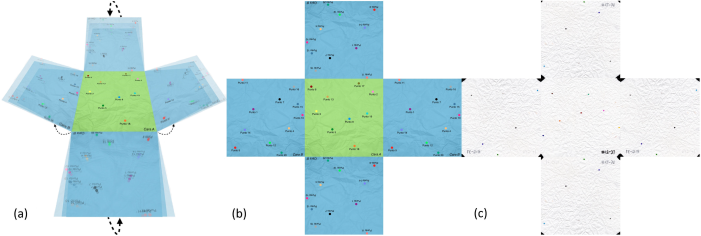
Figure 2 (a) and (b) images correspond to the topological transformation made on a virtual sheet just to show the process we followed, color points schematize the randomly assigned points on the surface of the crumpled ball, (c) image show a real one transformed digitized flatted sheet.
Once final data were collected a statistic analysis procedure was started for each of the four sizes, we first began realizing a probability distributions tests in order to choose those ones that best fit to our length data 17,20,21,23,26,29. We found that Gamma and Log-Normal distributions fitted very well in analogy with results of the study of length of crumpled creases reported in 20,21,29. Figure 3 is an example of the procedure we followed. Here, we show this test data for the Euclidean distances, the cases of 12 cm size sheet and all sizes together are presented.
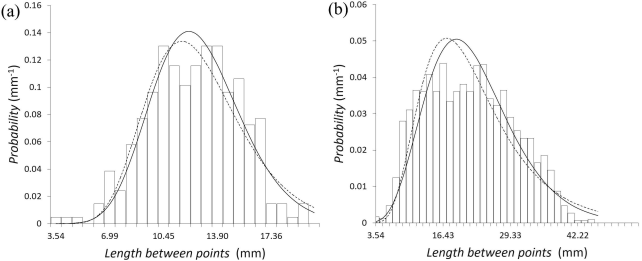
Figure 3 Statistical distributions of lengths between points randomly assignment on the surface of the hand crushed paper are shown. Curves: (a) 12 cm size paper; solid curve correspond to gamma distribution with α = 19:326 and ß = 0:6581, dashed curve corresponds to Log-Normal distribution with μ = 2:5143 and σ = 0:24918, (b) all the sizes of paper balls used in this work; solid curve correspond to gamma distribution with α = 6:9167 and ß = 3:2021, dashed curve corresponds to Log-Normal distribution with μ = 3:0165 and σ = 0:4202.
For this work we took the Gamma probability distribution of this X 2 tests for goodness of fit (following authors of [29]) to get the same-probability intervals to build graphs shown in Fig. 4 17,20,21,23,26,29.

Figure 4 Log-log plots of chemical distances versus Euclidean distances between two any points are shown, data came from the randomly set of points on the cuasi-spheres surfaces averaged over 30 balls each. Fitting curves are lmin = 4:8091l1 e:296 ; R2 = 0:8342, lmin = 1:9342 l e 1:3123 ; R2 = 0:7302, lmin = 8:2132 l e 1:314 ; R2 = 0:8114 and lmin = 1:2592 l e 1:2592 ; R2 = 0:7636; for (a) 30 cm, (b) 22 cm, (c) 15 cm and (d) 10 cm respectively. Uniquely solid circles are considered, empty circles are excluded from fitting in all cases.
A resume of the referred quantities is shown in Table I.
Table I Shortest path fractal dimensions per each size of paper sheet.
| Side sheet size (cm) | 30 | 22 | 15 | 10 |
| Shortest Path fractal dimension | 1.296 | 1.3123 | 1.314 | 1.2592 |
Global mean value can be written as
It is interesting to point out that, by definition, the chemical fractals dimensions in flat an crumpled configurations are both equal (
Is important to note that (3) is just valid for elastoplastic sheets, and correspond to a fractal property of crumpling network in the folded configuration. In that sense we postulate that (2) could also be universal, because for elastoplastic paper sheets it has been shown 21,23 that D l is universal only after a complete relaxation of the elastic tensions due to self-avoiding interactions.
In Fig. 4 we can see the log-log plot made for each size sheet, in total more than 5500 measurements were realized and graphs exhibit that
3. Discussion
Notwithstanding we did not smooth or neglect points except empty circles in last two cases (we are presenting the original set of resulting points), percentage error between expressions (2) and (3) is almost 3 percent. We believe that numerical result described by (2) for the shortest path fractal dimension may have a different meaning than just a coincidental value when compared with (3). But more interesting is the fact that (2) is also closely near up to one decimal to results of Monte Carlo simulations, reported by Zongzheng et al. in 18 as
4. Conclusions
In conclusion, we determined the shortest path fractal dimension











 nueva página del texto (beta)
nueva página del texto (beta)


