1. Introduction
Eighty years ago, Michels et al. 1 used the confined hydrogen atom (CHA) as a model to study the change in the polarizability of a hydrogen atom subjected to high external pressure. In this model, the nucleus of the hydrogen atom was clamped at the center of an impenetrable sphere of radius R c , while the electron could move within the included volume. In this system, ionization is not possible. The way to account for ionization is to allow the walls to be penetrable. This penetrable model was successfully used by Ley-Koo and Rubinstein2 to explain the ionization of a hydrogen atom trapped in alpha-quartz3-4.
Many applications have been developed from these models and they have been generalized to cavities with different geometries. This model has subsequently been applied to a wide range of physical problems 1-13. Observable properties of the systems such the energy spectrum, transition frequencies and probabilities, polarizability and the behavior of atoms trapped in fullerenes, etc., are changed by spatial confinement. Reviews and books on those topics are available 5. Recent experimental studies show that the electron capture nuclear decay rate is increased under compression 14-16. A partial explanation of this effect was given using the model of many-electron atoms confined in an impenetrable spherical cavity 17. With the advent of technology to construct atomic scale confinements, the study of confined systems has become increasingly relevant.
In most of the works on the properties of atoms and molecules, either free of any confinement or confined in cavities, it is assumed that the nuclei are points with charge and mass but without extent. The inclusion of a nucleus of finite size in the free hydrogen atom is accompanied by a shift in the electron energy 20-26. The magnitude of this shift is very small compared to the energy of the hydrogen atom with a point nucleus. Until now, no one has studied how this energy shift changes for the hydrogen atom, confined in spherical penetrable cavities, when a nucleus of finite size is considered.
Pyarelal and Bhatnagar 20 proposed a model of the hydrogen atom with an impenetrable nucleus of finite size. In that model, the wave functions must vanish at the surface of the nucleus. The reduction in the volume available for movement of the electron produces an increase in the energy of the electronic states. This problem has an exact solution, but the model is unrealistic.
A more realistic model consists of a spherical nucleus of radius r 0 , with an uniform distribution of charge. For hydrogen-like atoms with a small nuclear charge, Z, it is well-known that the Schrödinger equation adequately describes those systems 19. An exact solution to this problem was found by Ley-Koo et al. 19, in which they studied the muonic atoms, free of any confinement, with Z up to 90. In this work, we will adopt the model of a spherical nucleus with an uniform charge distribution, and we will use first-order perturbation theory to calculate the correction to the ground-state energy of the hydrogen atom confined in spherical penetrable and impenetrable cavities, as a function of the radius of confinement R c .
The objectives of this work are twofold: the former is to establish benchmark values for the energy of the ground state of the hydrogen atom confined in a spherical penetrable cavity, the second is to calculate the energy shift of this system when considering a spherical nucleus of finite volume with an uniform distribution of charge.
The organization of this work is as follows: in Sec. 2, we solve CHA with a point nucleus in a spherical, padded cavity. In Sec. 3 we use first-order perturbation theory to compute the energy correction due to inclusion of a nucleus of finite size. In Sec. 4 we show the results of the calculation of the energy correction due to a finite size nucleus, obtained for both penetrable and impenetrable confinements. Finally, in Sec. 5 we give our conclusions.
2. The CHA in a spherical padded cavity
In this section we give a brief description of the solution of the hydrogen atom confined in a spherical padded cavity. A detailed explanation can be found in Refs. 2, 7 and 9.
In atomic units (
where the potential is
Equation (1) can be solved using separation of variables
where
The Schrödinger equation for the inner region
whose solution is given by 8-9:
where
The external region,
which can be written as
where
and whose solution is given by 2
Hereafter, we restrict our attention to states with
The eigenvalues are determined by the requirement that the total wavefunction must be continuous with continuous first derivatives at
The normalization constants A and B are found from the requirements that
and the normalization condition
As mentioned above, the zeroes of the logarithmic derivative equation are the eigenvalues of the problem. The first zero corresponds to the ground state energy. With this value, we construct the wave function in each region. To find the zeroes of the equation we used Mathematica 9 with the command FindRoot with 50-digit precision variables. The eigenvalues obtained through this procedure are shown in Tables I, II, III, V as a function of the box radius R c and the potential height V 0 . These results are in complete agreement with previous calculations 2,7,9. The results are shown with 15 digits after the decimal point.
TABLE I CHA ground state energy E10 (1) , and first-order correction due to the finite nucleus, E10 (1) (Rc), as a function of the confinement radius Rc for V0 = 0. Also shown is the ratio between the energy correction of the confined system, E10 (1) (Rc), and the correction of the free hydrogen atom E10. Energies are in hartrees and distances are in bohrs.
| R c | E 10 | E101 (10-10) | E101(Rc) E101 |
| 0.75 | 0.002551608753406 | 0.342781939506244 | 0.345 |
| 0.8 | -.017424391031037 | 0.808141286815622 | 0.814 |
| 0.9 | -0.067406311452319 | 1.325196851197549 | 1.335 |
| 1.0 | -.125000000000000 | 1.544741614031751 | 1.556 |
| 1.1 | -.180067083549980 | 1.621160850903080 | 1.633 |
| 1.2 | -0.229179151514072 | 1.627437259807232 | 1.639 |
| 1.5 | -0.338167417956141 | 1.507712255705773 | 1.519 |
| 2.0 | -0.431218889241793 | 1.287458459987721 | 1.297 |
| 2.5 | -0.470393522970229 | 1.151246460119175 | 1.160 |
| 3.0 | -0.487223082818398 | 1.075285232620169 | 1.083 |
| 3.5 | -0.494519692585279 | 1.034355146835889 | 1.042 |
| 4.0 | -0.497674689400819 | 1.012980250520460 | 1.020 |
| 4.5 | -0.499025598864902 | 1.002187518743767 | 1.009 |
| 5.0 | -0.499596671366575 | 0.996918364180960 | 1.004 |
TABLE II CHA ground state energy
| R c | E 10 | ||
| 0.4 | 4.827691517791768 | 6.456668836007435 | 6.506 |
| 0.5 | 3.907609648085746 | 10.240494963124124 | 10.319 |
| 0.6 | 2.982382648801240 | 9.598999388792230 | 9.672 |
| 0.8 | 1.666642892127310 | 6.980485974979947 | 7.034 |
| 0.9 | 1.229573168163173 | 5.926377707785826 | 5.972 |
| 1.0 | 0.893377387585463 | 5.081081669583943 | 5.120 |
| 1.5 | 0.028688218476904 | 2.781656875168397 | 2.803 |
| 2.0 | -0.273954162644265 | 1.889596355389960 | 1.904 |
| 2.5 | -0.397386813501905 | 1.473407522212738 | 1.484 |
| 3.0 | -0.452163079706601 | 1.256864293020748 | 1.266 |
| 3.5 | -0.477542879189045 | 1.137865941478808 | 1.146 |
| 4.0 | -0.489507801753420 | 1.071253920964084 | 1.079 |
| 4.5 | -0.495153894267392 | 1.034166451405600 | 1.042 |
| 5.0 | -0.497794417047201 | 1.013927192430064 | 1.021 |
TABLE III CHA ground state energy E10 (1), and first-order correction due to the finite nucleus, E10 (1)(Rc), as a function of the confinement radius Rc for V0 = 10. Also shown is the ratio between the energy correction of the confined system, E10 (1)(Rc), and the correction of the free hydrogen atom E10. Energies are in hartrees and distances are in bohrs.
| R c | E 10 | E101 (10-10) | E101 (Rc)E101 |
| 0.3 | 9.846148432090808 | 9.930542047590157 | 10.007 |
| 0.5 | 5.639829938566619 | 17.491618217286550 | 17.626 |
| 0.6 | 4.097374126091258 | 13.822727567461880 | 13.929 |
| 0.7 | 2.995752750577570 | 10.917393851422899 | 11.001 |
| 0.9 | 1.620350180030345 | 7.179161687379589 | 7.234 |
| 1.0 | 1.185777102316168 | 5.992750426662855 | 6.038 |
| 1.5 | 0.116618456909048 | 3.048420555184699 | 3.071 |
| 2.0 | -0.240385375166330 | 1.999717840968987 | 2.015 |
| 2.5 | -0.382937517117798 | 1.527421154803173 | 1.539 |
| 3.0 | -0.445545908145495 | 1.285799849400771 | 1.295 |
| 3.5 | -0.474425028203553 | 1.080287038138810 | 1.162 |
| 4.0 | -0.488027526391939 | 1.080287038138810 | 1.088 |
| 4.5 | -0.494454829661503 | 1.039165583170746 | 1.047 |
| 5.0 | -0.497468459482318 | 1.016626789889568 | 1.024 |
TABLE IV CHA ground state energy E10 (1), and first-order correction due to the finite nucleus, E10 (1)(Rc), as a function of the confinement radius Rc for V0 = 10. Also shown is the ratio between the energy correction of the confined system, E10 (1)(Rc), and the correction of the free hydrogen atom E10. Energies are in hartrees and distances are in bohrs.
| R c | E 10 | E101 (10-10) | E101 (Rc)E101 |
| 0.5 | 14.747970030350280 | 54.536609722874516 | 54.956 |
| 0.6 | 9.527707806146348 | 33.740936784485875 | 34.000 |
| 0.7 | 6.469926127251262 | 22.720335291772468 | 22.895 |
| 0.8 | 4.543380181009424 | 16.278628704347120 | 16.403 |
| 0.9 | 3.262189536240119 | 12.229690823293298 | 12.323 |
| 1.0 | 2.373990866103664 | 9.538267646127938 | 9.611 |
| 1.5 | 0.437018065247256 | 3.969102513288022 | 3.999 |
| 2.0 | -0.125000000000000 | 2.355893659642013 | 2.374 |
| 2.5 | -0.334910185427921 | 1.695773616320432 | 1.708 |
| 3.0 | -0.423967287733454 | 1.374211998517624 | 1.384 |
| 3.5 | -0.464357128440197 | 1.202793634385484 | 1.212 |
| 4.0 | -0.483265302078022 | 1.107644656981758 | 1.116 |
| 4.5 | -0.492205427798878 | 1.054376061163177 | 1.062 |
| 5.0 | -0.496417006591452 | 1.024902478009865 | 1.032 |
3. Finite nucleus size correction
The Hamiltonian of the hydrogen atom with a finite nucleus confined by a spherical penetrable wall is given by
where
The first two terms in Eq. (15) are the usual terms of a free hydrogen atom with a finite size nucleus 6,19,21-23, and 𝑟 0 is the radius of the hydrogen atom, a proton. The third term is introduced to confine the hydrogen atom in a spherical cavity of radiusR c .
We define the potential
Adding and subtracting
This Hamiltonian can be written in the more familiar form
From Eq. (17) we immediately identify the first two terms as the Hamiltonian of a hydrogen atom confined in a penetrable spherical cavity, as analyzed in previous section. We note that forH
0
, the unperturbed Hamiltonian, the eigenfunctions
The perturbation is given by (6, 21-23)
As mentioned above, we are only interested in states with
A straightforward calculation gives the following expression. The eigenfunctions
Substituting (21) in (20) we obtain
In the region
Equation (22) then becomes
In this work we will use the most recent measured proton radius
4. Shannon entropy
Claude E. Shannon in 1948 introduced the so called Shannon entropy in his paper “A Mathematical Theory of Communication” 27. The quantum version of Shannon entropy 𝑆 𝑟 , in configuration space is defined as
where
The Shannon entropy in quantum computation means the absolute limit of the best possible lossless compression of any communication, under some particular constraints 33. On the other hand, the Shannon entropy has a wide variety of applications in Physics and Chemistry 34. Usually, it is interpreted as the uncertainty associated with the particle position, which is related with the degree of localization (delocalization) of the particle. In chemistry, the Shannon entropy is associated with the delocalization of an electron in aromatic compounds 35.
Panos et al. 36, computed and plotted S
r
as a function of the atomic number, Z, for many-electron atoms. They found that the curve
5. Results
In Tables I, II, III, we show the corrections to the ground-state energy of CHA, taking into account a nucleus with finite size. The correction to the energy is small compared with the energy of the unperturbed confined atom. As the confinement radius R
c
grows,
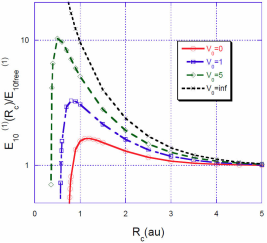
FIGURE 1 Ratio
where
For a spherical cavity with impenetrable walls, the correction to the energy grows rapidly as R
c
tends to zero because by reducing R
c
the electron is closer to the nucleus without the possibility to escape. In Fig. 1 we can see that for a value of
This value is in complete agreement with that calculated by Goldman and Joslin 6. They found that for very small values of 𝑅 𝑐 and very excited states, the correction of the energy,
For a fixed value of the barrier heightV
0
, the situation is quite different. The energy correction
Intuitively, one expects that the energy correction
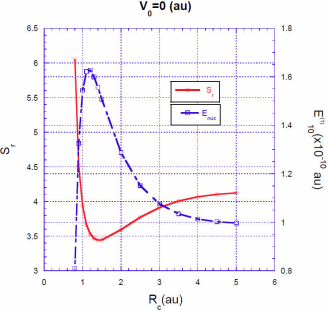
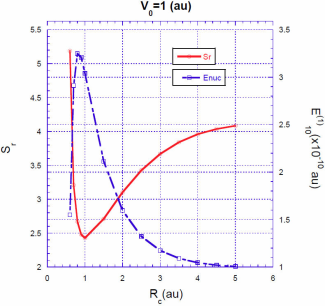
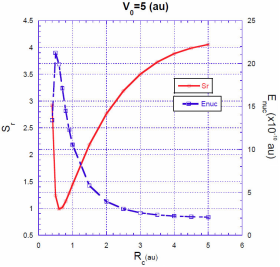
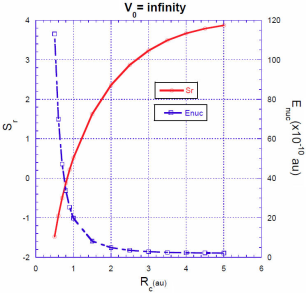
In Figs. 3, 4, 5 we show the energy correction
6. Conclusions
In this work we calculated the energies and wave functions, with high numerical precision, for the ground state of the hydrogen atom confined in a penetrable spherical cavity. We also calculated the energy correction due to a nucleus of finite size for the CHA as a function of R
c
and V
0
. For finite barriers, the curves of the energy correction reach a maximum value, while the curves of the Shannon entropy as a function of











 nueva página del texto (beta)
nueva página del texto (beta)