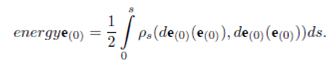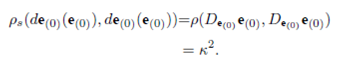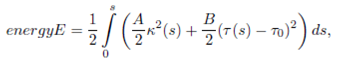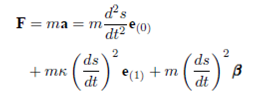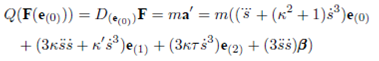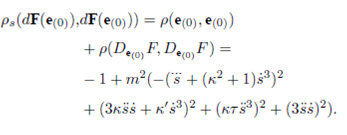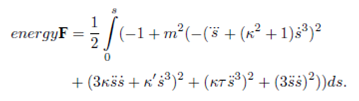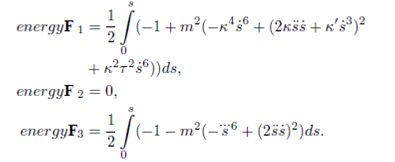1. Introduction
It is well known that there exists two different space forms having a constant sectional curvature, which are Lorentzian space form and Riemannian space form. The Lorentzian space form with the positive constant curvature is called De- Sitter space, which is the analogue in Minkowski spacetime of a sphere in ordinary Euclidean space.
Constant curvature space times have attracted much notice from observational and theoretical viewpoint of modern cosmology and physics. The major interest in De-Sitter spacetime is guided by current cosmological observations, which show that our universe is asymptotic. In other words solution of the equations of Einstein with positive cosmological constant is found in De-Sitter metric, which models an expanding universe1. To obtain this consequence focusing on kinematics and dynamical aspect of the corresponding spacetime is crucial.
A search of the literature indicates that there is almost no concrete computations on the entropy, laws of horizon dynamics and energy in De-Sitter spacetime. Various attempts are being made to describe the concept of energy by using quasi-local or local approach. However, these definitions of energy do not agree with each other all the time and they are not applicable to the universes of De-Sitter type2-4. Therefore, we choose to start with using local approach to make progress on the notion of energy in this spacetime. Thus, we consider that one of the most effective way is to use intrinsic geometric features of the moving particle in the De-Sitter spacetime.
Motion of a particle in space is important due to wide range of applications. Motion of the particle in absolute space and time was defined firstly by Newtonian dynamics5,6. Then, geometric generalization of the action, which includes terms belonging to the curvature of the trajectory of the moving particle, in different space times is given in7.
The equations of a moving particle in particular vector fields are obtained by considering its
generalized acceleration, velocity, and coordinate. Guided by this, energy of the
unit vector fields on a Riemannian manifold M is described to be
equal to the energy of the mapping
Recently, this subject has expanded to more up-to-date application fields as a parallel of the improvement in the field of relativity16. For example,17 defined the equations of motion in terms of the principal curvature of the worldline to model a relativistic particle. Then,18 considered an auxiliary variables method as an alternative of the standard theory of deformations for curves to construct the dynamics of relativistic particles. Further,19 used curvature functions to express both the Euler-Lagrange equations and the physical invariants of the motion associated with the Poincare symmetry of Minkowski space, the spin and the mass.
In this study, we mainly focus on the energy on the moving timelike particle in particular force fields in De-Sitter spacetime. Thus, we aim to obtain some consequences on Lorentzian space form.
The brief description of the organization of the paper is as follows. In Sec. 2, we firstly review some basic notions of the wordline Frenet-Serret geometry by describing trajectory of the particle. Then, we give some definitions, which are significant in order to compute energy on the moving timelike particle in unit vector fields. In Sec. 3, we obtain equations of motion and second law of Newton depending on the Frenet-Serret frame elements for De-Sitter spacetime. In Sec. 4, Sec. 5, and Sec. 6, we compute energy on the moving timelike particle in different force fields in De-Sitter space-time using its geometrical description, which is obtained by Frenet-Serret frame equations. We also compare energy on the moving timelike particle in distinct force fields and energy on the same particle in Frenet vector fields. In Sec. 7, we draw some conclusion and brief discuss the result.
2. Preliminaries
2.1. Kinematics of the Timelike Particle in De-Sitter Space
Let Γ be a particle moving in a space such that the precise location of the particle is specified by Γ = Γ(t) where t is a time parameter. Changing the time parameter determines the worldline of the motion of the particle. Hence, the worldline corresponds to a curve β in the space for the moving particle Γ. It is also convenient to remind that the arc-length parameter is used to compute the distance traveled by particle along its worldline. It is defined by
where
For non-negative coefficients κ, τ and
2.2. Energy of Unit Vector Fields in Space
We firstly give fundamental definitions and propositions, which are used to compute energy on the curve in the unit vector fields.
Definition 1. Let (M; ρ) and (N; h) be two Riemannian manifolds, then energy of a differentiable map f : (M; ρ ) → (N; h) is defined by
where {a} is a local basis of the tangent space and v is the canonical volume form in M,8.
Proposition 2. Let Q : T(T 1 M) →T 1 M be the connection map. Then following two conditions hold:
i)
ii) for
where D is the Levi-Civita covariant derivative8,21.
Definition 3. Let
This yields a Riemannian metric on TM. As is known ρs is called
the Sasaki metric. It also makes the projection
Now, let us turn our focus on how to imagine the motion of the particle in De-Sitter spacetime and how to compute energy on the particle by using aforementioned definitions. Particles left trajectories in space as they move. These trajectories correspond to particular type of curves. Since De- Sitter spacetime is a four dimensional structure and it is the analogue of a sphere in ordinary Euclidean space, we have following sample sketch for the trajectory of the timelike particle in space.
Now, we are able to compute energy on the moving timelike particle in De-Sitter spacetime in terms of the curvature and the torsion of the timelike curve. Here, we use Frenet equations and non-flat Lorentzian geometry.
Theorem 4. Let β be a unit speed timelike curve defined on the De-Sitter space. Then, energy on the moving timelike particle in the tangent, normal, binormal vector fields and energy on its own vector field are given by
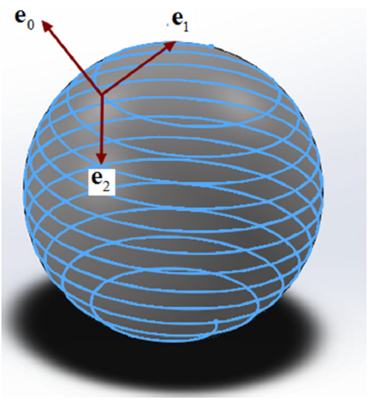
Figure 1 Particle trajectory together with Frenet-Serret vectors in 4-dimensional De-Sitter spacetime.
Proof. Here, we only prove energy on the moving timelike particle in the tangent vector field. Other statements can be proved by using similar approach. From (2) and (3) we know that
Moreover, we obtain from (4)
Since e(0) is a section, we get
We also have
Thus, we find that
So we can easily obtain
Following sketch illustrates energy variation on the moving timelike particle in tangent vector filed in De-Sitter spacetime. Here, we suppose that moving particle corresponds to a parameterized unit speed timelike curve in De-Sitter spacetime. We compute its curvature and torsion for the calculation of the energy. Hence, we get the following illustration for energy on the moving timelike particle with respect to time.
Elastica known as the solution of a variational problem, which deal with minimizing the bending energy of deformable materials. Bending energy of a space curve is defined by using curvature squared energy functional over a curve.
where s is the arc-length. On the appropriate length scale, bending energy provides a significant physical description of a bounding a soap film, thin wire with circular cross section, or the elastic properties of a stiff polymer. However, stiff polymers are the most interesting of them. It is used to investigate some other physical phenomena such as superconductors, vortices in fluids, mechanical properties of DNA, etc. Assuming that the curvature of space curve does not vanish, energy cost for being bent for stiff polymers is defined as

Figure 2 Energy distribution on the moving timelike particle in tangent vector field with respect to time.
where A, B, and
Corollary 5. Let β be a unit speed timelike curve defined on De-Sitter space. Then, energy on the moving timelike particle in the tangent, normal, binormal vector fields and energy on its own vector field can be expressed by bending energy of stiff polymers as follows, respectively.
i. If A = 1, and B = 0, then energyE = energy e(1). Here, we can also deduce that energyE =energy e(0).
ii.
If A = 1, B = 1,
iii.
If A = 0, B = 1, and
iv.
If A = 0, B = -1,
Proof. If we use Theorem 4 together with Eq. (5), and Eq. (6) for each case separately, then it is evident.
3. Classical Mechanics on a Particle with Dynamics
Arc-length parameter is also significant to define acceleration of the particle. Here we attain equations of motion for the timelike particle in De-Sitter spacetime. Equations of motion and second law of Newton are obtained thanks to Frenet- Serret frame, which is adapted to the worldline of the timelike particle. It includes geometric features of the timelike curve in De-Sitter spacetime.
Let the moving particle ¡ has a unit timelike tangent vector e(0) . Then, we have
And
According to second law of Newton the resultant force acting on the particle, which has a mass is defined by
For the set of Frenet vectors
Where,
Using this result we have following notations;
4. Energy on the Timelike Particle in a Resultant Force Field
Now, we reach to the point, where we define the work done by the force during the motion of the particle Γ along its trajectory. Kinetic energy of the moving particle Γ, which has a mass m is defined by
Assuming the kinetic energy of the particle varies from some initial and final value, total work done on that particle is given by
By the work-energy theorem we also have following relation between variation on the kinetic energy and resultant force F.
where
Now, we compute energy on the moving timelike particle, which is acting under a resultant force, in terms of the curvature and torsion of the particle in De-Sitter spacetime. Further, the relation between energy on the moving timelike particle and work done by forces can be investigated easily from (15) and (16).
Theorem 6. Let Γ be a moving timelike particle in De- Sitter spacetime. Then, energy on the timelike particle in the resultant force field F is stated by
where superposed dot denotes the time derivative of the function.
Proof. From (2) and (3) we get
By using Eq. (4), we have
Since e(0) is a section, we also get
Moreover, it is clear that
Thus, we find from (1) and (10)

Figure 3 Energy on the moving timelike particle in resultant force field and Frenet-Serret vector fields.
Finally, we have
Corollary 7. Let Γ be a moving timelike particle in De-Sitter space. Then, energy on the timelike particle in the resultant force field F can be written in terms of the energy on the same particle in tangent, normal, binormal, and its own vector field as the following.
Proof. It is obvious from Theorem 4 and Theorem 6.
Corlloray 8. Let w be a moving timelike particle in De-Sitter space. Then, energy on the timelike particle in the tangential, normal and binormal resultant force field F in De- Sitter spacetime is given by
Proof. Using Eq. (12) and Eq. (13) together with the Sasaki metric given in Eq. (4), we can easily reach the result for each case.
What we found so far is that the general formulation for the energy of the moving timelike
particle with a mass
5. Energy on the Timelike Particle in Dynamical Force Fields
In this section, we apply our findings to a well-known physical problem to show its originality and usefulness. We suppose that under the action of gravity on a downward concave surface there is a point particle sliding to the downward such that it follows a trajectory of a fixed curve in De-Sitter spacetime. Let assume that motion of the particle corresponds to a timelike curve and it has a Frenet characterization given by (1) in De-Sitter spacetime. Then, there are three distinct force affecting action of the particle. These forces are friction (f), weight of the particle (W), and normal force (N). They are defined geometrically as the following.
where
Theorem 9. Let Γ be a moving timelike particle such that it is under the action of (f), (W), (N) in De-Sitter spacetime. Then, energy on the timelike particle in the resultant force field F is stated by
Proof. We can verify this result similarly as in Theorem 6 bearing in mind the fact that
Main Result 10. We have following result of the energy on the moving timelike particle in the resultant force field in De-Sitter spacetime.
Proof. We reach the result by considering Theorem 6 and Theorem 9.

FIGURE 4 a) Trajectories of the curvature of the moving timelike particle in De-Sitter spacetime. b) Values of the curvature for particular input of the arc-length of the moving timelike particle in De-Sitter spacetime.

Figure 5 a)Trajectories of the torsion of the moving timelike particle in De-Sitter spacetime. b)Values of the torsion for particular input of the arc-length of the moving timelike particle in De-Sitter spacetime.
Thus, we obtain a sample solution family of third order non-linear ordinary differential
equation system. It gives the following illustrations for particular values of the
curvature and the torsion of the wordline of the timelike particle in De- Sitter
space together with the particular values of
Corollary 11. Let ¡ be a moving timelike particle in De- Sitter space. Then, energy on the particle in the resultant force field (F = f + N + W) can be written in terms of the energy on the same particle in tangent, normal, binormal, and its own vector field as the following.
Proof. It is obvious from Theorem 4 and Theorem 9. We can also compute energy on the moving timelike particle in each individual force field in De-Sitter spacetime. By this way, we might have an idea regarding energy variation and distribution on the resultant force fields by considering how much energy does the particle store on each force field.
Corollary 12. Let Γ be a moving timelike particle such that it is under the action of (f), (W), (N) in De-Sitter spacetime. Then, energy on the particle in the friction force field weight force field (W), and normal force field (N) are stated by using Sasaki metric as the following.

Figure 6 Energy on the timelike particle in resultant force field together with normal, weight, and frictional force field.
Proof. Let we consider each equality given in (17) separately. If we apply the argument in (2), (3), (4) to the Eq. (17), then the proof is obvious.
Corollary 13. Let Γ be a moving timelike particle in De-Sitter spacetime. Then, energy on the moving timelike particle in the friction force field (f), weight force field (W), normal force field (N) can be expressed by the energy on the particle in each Frenet vector field as the following.
6. Energy on the Timelike Particle in Electrodynamical Force Fields
Now, we investigate some consequences on another famous physical phenomena under the light of our findings. Let assume that we have a moving timelike charged particle, whose mass is denoted by m. We also assume that it is under the action of an electric force only in the electromagnetic field. The Lorentz force equation is described by
for the charged particle of velocity v, mass m, and electric charge q under the magnetic field B and electric field E,23. By the assumption the magnetic force vanishes, thus we have
Hence, we obtain
Corollary 14. Let ¡ be a moving timelike charged particle in De-Sitter space. Then, energy on the timelike charged particle in the electric force field (E) is stated by
Proof. It is obvious, if we consider (18) and (2), (3), (4).
Main Result 15. We have following result of the energy on the timelike particle in the resultant force field if there exists only an electric force acting on the particle in the electrodynamical field.

Figure 7 a)Trajectories of the curvature of the moving timelike charged particle under the action of electric force in De- Sitter spacetime. b)Values of the curvature of the moving timelike charged particle under the action of electric force in De-Sitter spacetime.

Figure 8 a)Trajectories of the torsion of the moving timelike charged particle under the action of electric force in De-Sitter spacetime. b)Values of the torsion of the moving timelike charged particle under the action of electric force in De-Sitter spacetime.
Proof. We reach the result by considering Theorem 6 and Corollary 14.
Thus, we obtain a sample solution family of third order non-linear ordinary differential equation system. It gives the following illustrations for particular values of the curvature and the torsion of the wordline of the timelike particle in De-Sitter space together with the particular values of electric charge q.
7. Conclusion
Computing the energy on the moving particle has a wide range of application in the theoretical and applied physics. As was stated aforementioned, this computation is deeply interested on dynamics of the particle including work done, force, and energy related concepts. It has also deep connection on mass-equivalence relation in special relativity theory.
In this study, we have studied motion of the timelike particle and energy on the timelike particle in the different force fields in De-Sitter space. Firstly, we set a connection between energy on the timelike particle in these force fields and energy on the particle in Frenet vector fields. This is important for our future work since a simple characterization on the energy of a vector field can be described as it is up to constants, in other words, it is square L2 norm of the vector field’s covariant derivative. Thanks to this definition, we will correlate the concept of the energy on the moving particle in different force fields with the concept of total bending functional and volume in these force fields in that space.
Furthermore, we apply our findings to compute the energy on the moving timelike particle in the existence of electromanetic force in De-Sitter space. We have examined energy on the charged particle while it is under the action of electric force. In the future studies, we turn our focus to Loretnz force of the particular magnetic fields in three dimension since they are quite important for some reasons. First of all, vector fields and 2-forms are in correspondence. Also, magnetic fields on three dimensional Riemannain manifolds come from vector fields of divergence free. Further, uniform magnetic fields and parallel vector fields correspond to each other.
This study will also lead up to further research on the relativistic dynamics of the particle in terms of computing energy on the relativistic particle in different spacetimes by considering mainly its geometric descriptions.











 nueva página del texto (beta)
nueva página del texto (beta)