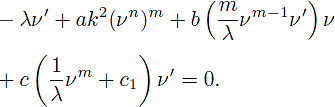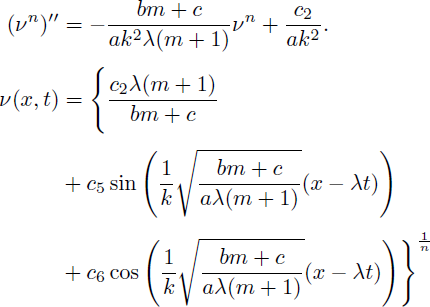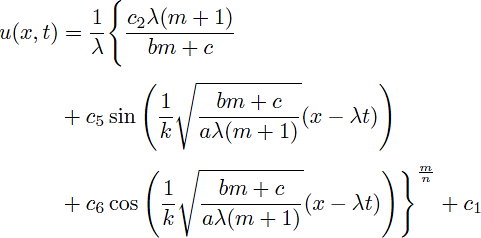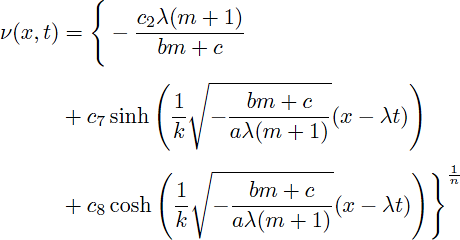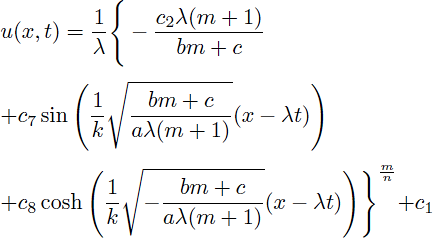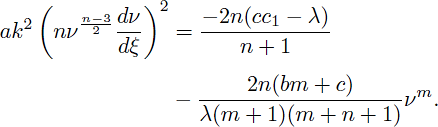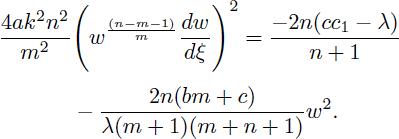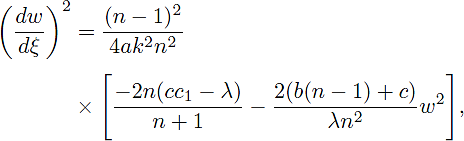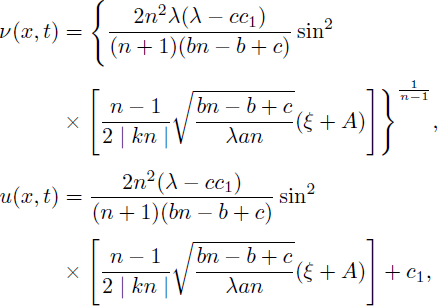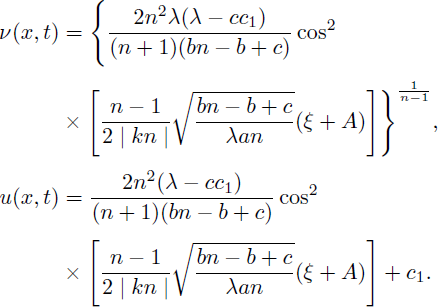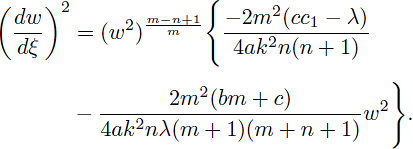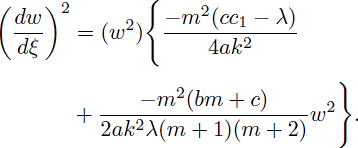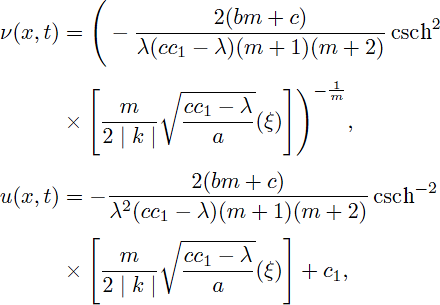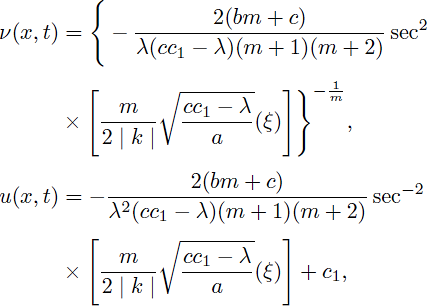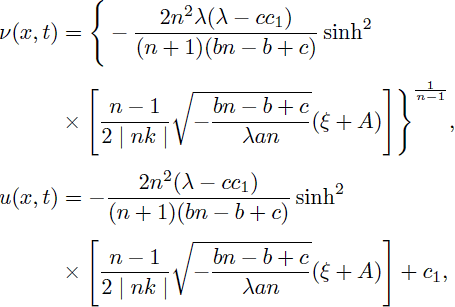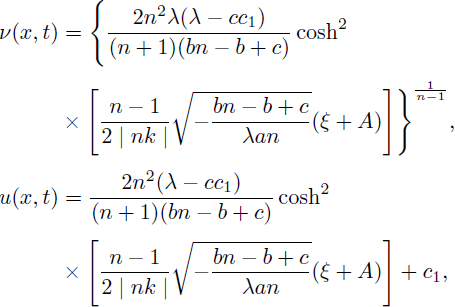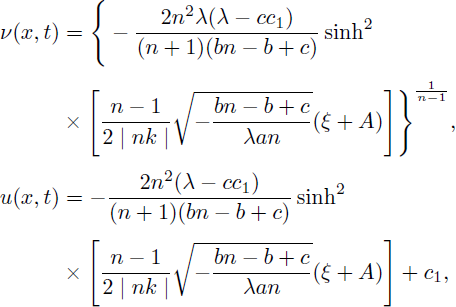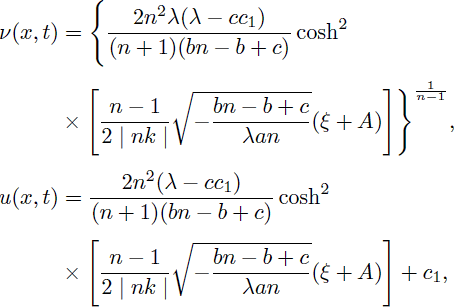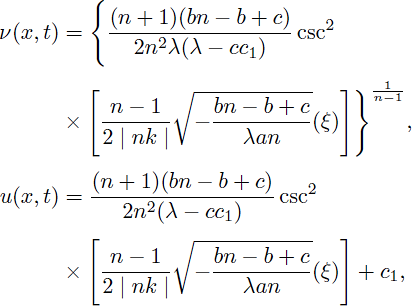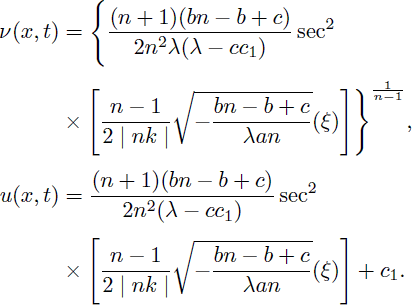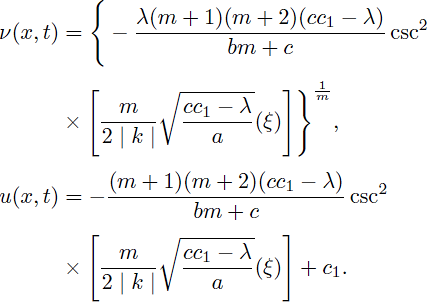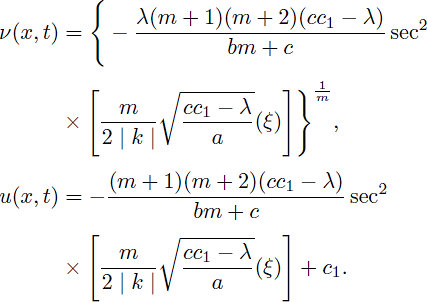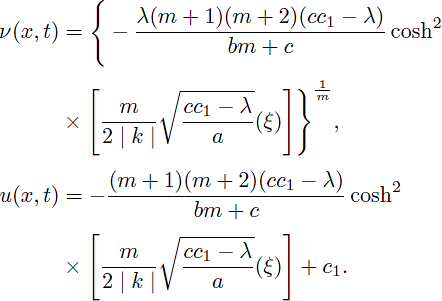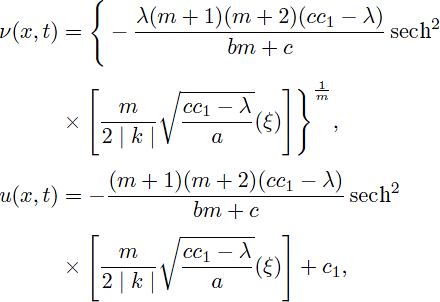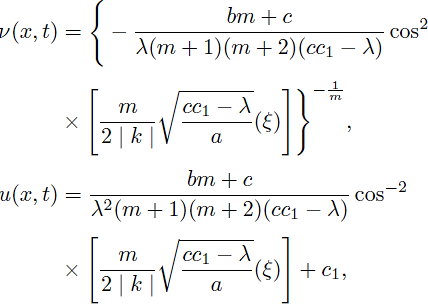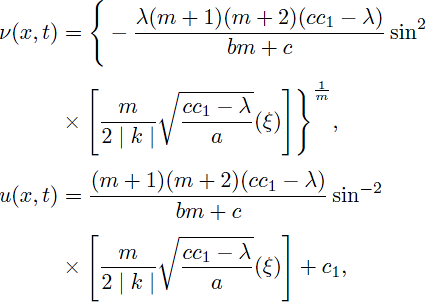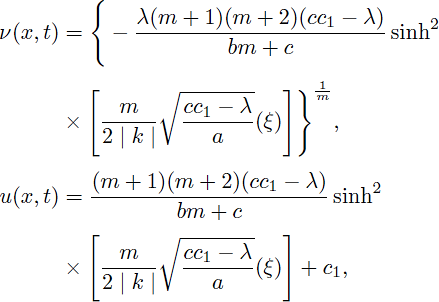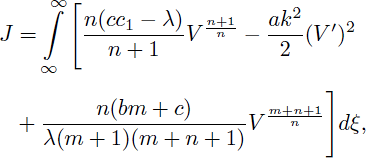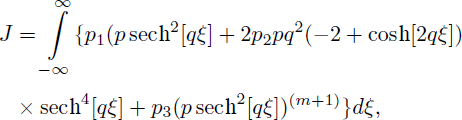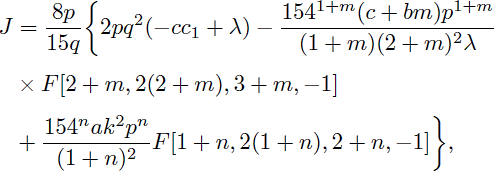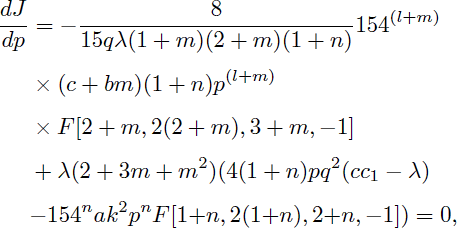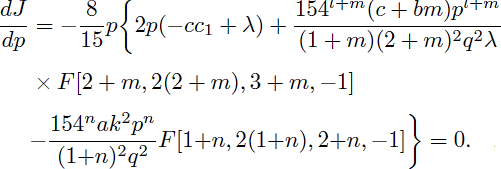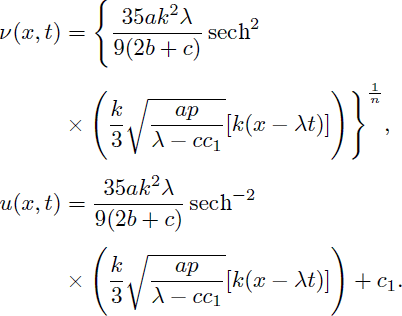PACS: 02.30.Jr; 02.30.Ik
1. Introduction
Nonlinear partial differential equations (NPDE) have been analyzed by different type of mathematical approach, among which include the Darboux transformation, the inverse scattering method, the Hirota method, the Backlund transformation, the tanh method, the sine-cosine method, the exp-function method, the variational iteration method, the homogenous balance method and among others 1-41.
In this article, the D(m, n) system 1 are considered:
For m = 2 and n = 1, the system (1) is called “The normal Drinfel’d-Sokolov system”
where a, b, c are unchanged. The system (2) is considered as an example of a system of nonlinear equations possessing Lax pairs of a special form 13. Wang obtained its Hamiltonian, recursion, symplectric and cosymplectric operators and roots of its symmetries and scaling symmetry of the system (2) 14.
For n = 1 the system (1) changes to “The generalized Drinfel’d-Sokolov system” as:
Wazwaz obtained some exact traveling wave solutions of the D(m, n) system with compact and noncompact structures by applying the tanh method and the sine-cosine method 15.
We firstly apply the ansatz method 16,17,18,19,20 to obtain the exact special solutions to the D(m, n) system. Then, we use the He’s variational approach 21 to obtain unknown traveling wave solution to the subsidiaries of the D(m, n) system. We give a comparison between the obtained solutions and those exist in the literature.
2. Ansatz method
We start by considering the solution of the equation
where a0 ≠ 0 and b0 ≠ 0 are constants. When b0 > 0, Eq. (4) admits two solutions as:
where A is an arbitrary unchanged. If b0 < 0, recognizing that cosh2 z + sinh2 z = 1 we know that Eq. (4) has two solutions of the form as:
Secondly, we make a consideration of the solutions of the equation of the form
where c0 ≠ 0 and d0 ≠ 0 are constants. If c0 < 0, Eq. (7) confesses two solutions
If c0 > 0 in Eq. (7), then the equation offers two solutions of the form
2.1. Nonlinear Dispersion D(m, n) System
We assume that the traveling wave solution has the form u(x, t) = u(ξ) with wave variable ξ = k(x - λt), (k, λ ≠ 0). Then, we get the following ordinary differential equation:
We get
by (11), where c1 is arbitrary constant. Substituting (12) into (11) we obtain
By integrating Eq. (13), we get
where c2 is integration constant.
Case 1. When c = -bm = λ/c1, the nonlinear ODE (14) becomes
Therefore, we get the rational solution of Eq. (15),
and
where c3 and c4 are arbitrary constants.
Case 2. If we take m = n - 1 and c = λ/c1 in Eq. (14), the following traveling wave solutions are obtained
and
where c5 and c6 arbitrary constants. In view of (18) and (19), we clearly see that these solutions exist provided that (bm + c)/(aλ(m + 1)) > 0
and
where c7 and c8 arbitrary constants. In view of (20) and (21), we clearly see that these solutions exist provided that (bm + c)/(aλ(m + 1)) < 0.
Case 3. c + bm ≠ 0, cc1 - λ ≠ 0 and specially c2 = 0.
Let
Substituting (22) into (14) leads to the following equation
Letting ν = w2/m, we have
which changes Eq. (23) to
If we take n = 2m + 1 in Eq. (25), we get the algebraic traveling wave solution of the form:
and
where
and
Case 4. If m = n - 1, we know that Eq. (25) becomes
where n ≠ 1 and a, k, n, λ ≠ 0.
If we take anλ(c + bn - b) > 0, then we acquire from Eqs. (5) and (28)
and
Theorem 1. The D(m, n) system has solutions in Eq. (28) described as follows:
1. When anλ(c + bn - b) > 0,
is a solitary wave solution with compact support.
2. When anλ(c + bn - b) > 0,
is a compacton solution for Eq. (1) and
3. Equation (25) can be written as following
If n = 1in Eq. (33) that yields as
When a(cc1 - λ) < 0,
which is a singular soliton solution for the D(m, n) equation for
4. When a(cc1 - λ) > 0 and m < 0,
is a traveling wave solution for the D(m, n) equation for
Remark 1. If (bn - b - c)/(λan) < 0, it follows from (6) and (28) that
and
Theorem 2. The D(m, n) equation with when m = n equation has the following solutions:
1. When (c + bn - b) < 0, anλ > 0, (λ - cc1)(n + 1) < 0 and n ≠ 1
is a solitary solution of Eq. (1).
2. When (c + bn - b) < 0, anλ > 0, (λ - cc1)(n + 1) > 0 and n ≠ 1
is a solitary solution of Eq. (1). If we take n < 1, then Eq. (40) is a bounded solution.
3. m = n < 1solutions (39) and (40) turns to solitary wave solutions
and
Case 5. a(cc1 - λ) > 0 and m > 0,
Thus, by using (8) and (34), the periodic solutions of Eq. (1) are obtained as:
and
Case 6. a(cc1 - λ) > 0 and m > 0,
Therefore, by considering (9) and (34), solitary pattern and bell-shaped solitary wave solutions of (1) are obtained as:
and
Case 7. a(cc1 - λ) > 0 and m ≠ 0,
Using the solutions of (43) and (44), gives the following compacton solutions as:
for
and u = 0, otherwise.
for
and u = 0, otherwise.
Case 8. a(cc1 - λ) > 0; m < 0 and m ≠ 1.
Using cosh(x) = cos(ix) and sinh(x) = -sin(ix) we have the following solitary pattern solutions of Eq. (1):
and
Remark 2. When m = n < 1, the obtained solution (42) agrees with the outcomes (2.13a), (2.13b) in 36 and (25) in 37. The solution (42) changes to the compacton solution (2.12a) and the periodic solution (2.12b) in 36,37.
If m > 0, the obtained solution (46) is consented with the outcomes (3.18a) and (3.18b) described in 36 and (26) in 37. The solution (46) changes to the solitary pattern solution (3.17a) and solitary wave solution (3.17b) in 36.
Remark 3. If a(cc1 - λ) < 0, the obtained solution (35) agrees with the outcomes (3.9a) and (3.9b) in 36 and (32) in 37. The solution (35) changes to the singular solitary wave solution.
Remark 4. If we take (c + bn - b) < 0, anλ > 0, (λ - cc1)(n + 1) < 0 then the obtained solution (39) similar to the solitary pattern solutions (3.7a) and (3.7b) in 36 and (46) in 37.
3. Variational principle
In this Section, He’s variational principle will be applied to the system (1). This technique was first proposed by He21 and it is popularly known as He’s semi-inverse variational principle. Some years back, it was applied mainly to extract soliton solutions of nonlinear PDEs and systems by many authors 16,17,18,19,20,21,22,23,24. Biswas and co-workers 17,18,19,20 obtained optical solitons and soliton solutions with higher order dispersion by applying the He’s variational principle. Xu and Zhang’s25 used a variational principle to construct catalytic reactions in short monoliths by He’s semi-inverse approach. He’s variational method was used to the effective nonlinear oscillators with high nonlinearity by Liu 26. Zheng et al. 27 established a class of generalized variational principles for the initial-boundary value problem of micromorphic magneto electrodynamics by He’s semi-inverse technique. In order to seek traveling wave solutions of the system (1). We consider
Let νn = V
the 1-soliton solution ansatz, given by
is substituted into (51). Here, in (53), the parameters p and q represent the amplitude and inverse width of the soliton, respectively.
where p1 = cc1 - λ, p2 = ak2 and
From the above equation it is obtained as
where F is Gauss’ hypergeometric function defined as
and Re[(2 + m)q] > 0, Re[(1 + n)q] > 0, Re[q] > 0.
Making J stationary with respect to p and q results in
Solving Eqs. (57) and (58) for m = n = 2 simultaneously, we get
Therefore, by substituting p and q in (52) we have the following a new solitary wave solution for the system (1) as:
So, the solitary wave solution (60) will exist for ap(λ - cc1) > 0.
4. Results and Discussions
In this article, we investigated the nonlinear dispersion D(m, n) system and obtained some traveling wave solutions by applying the ansatz technique and the He’s variational principle. Several forms of solutions including topological, non-topological, compacton, solitary pattern, singular soliton, algebraic and periodic wave solutions were acquired. The approaches can be used to a lot of other nonlinear differential equations and coupled systems. Some new obtained exact solutions were previously unknown by other methods. We proved the existence of these solutions for a generalized form of the D(m, n) system under specific conditions. In general, the outcome expose that the ansatz approach and the He’s variational principle are important mathematical techniques for solving nonlinear partial differential equations in terms of correctness and ability to avoid errors.











 nueva página del texto (beta)
nueva página del texto (beta)