1. Introducción
El ciclo hidrológico es la base fundamental de la hidrología, debido a que estudia la distribución del agua en la superficie terrestre. Para efectos prácticos, el componente denominado precipitación se constituye como la variable de entrada a dicho ciclo debido a la facilidad de poder registrar su magnitud, así como la relevancia que posee en la evaluación del cambio climático.
La precipitación es una variable aleatoria que evoluciona en el tiempo y en el espacio1,6, por lo tanto puede ser analizada de manera espacial y/o temporal utilizando estudios de series temporales, el cual consiste en el análisis de la precipitación para lograr comprender la evolución que presenta en el tiempo7; para lo cual se han aplicado métodos estocásticos y métodos fundamentados en la geometría fractal. Los métodos estocásticos permiten realizar predicciones y obtener la relación existente con otras variables climáticas, tales como temperatura y presión atmosférica8-10; sin embargo, presentan la desventaja que una variable aleatoria, en este caso la precipitación, no puede ser analizada a diferentes escalas11,12; por lo tanto, se han aplicado los fundamentos de la teoría fractal para el análisis de las series de precipitación a múltiples escalas y dimensiones6,13-22. La teoría fractal se basa en el concepto de fractal definido por Mandelbrot23, el cual establece que los fractales son objetos que poseen una apariencia similar cuando se observan en diferentes escalas y que poseen detalles que no pueden ser estudiados por la geometría Euclidiana. El estudio de los fractales está caracterizado por la prevalencia de variables aleatorias tales como la precipitación16,24 y, la determinación de sus características de autosimilitud y fluctuaciones espacio-temporales en múltiples escalas; para lo cual se han utilizado diversas metodologías, entre las cuales se encuentran el método de rango rescalado (R/S)(24.26), conteo de caja13,27, análisis multifractal de fluctuación sin tendencia (MF-DFA)28, método de Wavelet29, espectro de potencia30, método de Higuchi31, análisis de fluctuación sin tendencia (DFA)32, fractal-multifractal11, Hurst-Kolmogorov33, flujo integrado fraccional (FIF)34, superficie fractal Browniana35 y dimensión de correlación (D2)36. Debido a la aplicación de los métodos anteriores, se ha determinado que la precipitación posee características fractales21,37-44; sin embargo, la distribución de las gotas de la misma en el espacio no posee esta característica dentro del cuerpo nuboso45-50. También se ha encontrado que el comportamiento fractal de la precipitación, tiene relación con las características fisiográficas del entorno, debido a que la precipitación observada en zonas con mayor altitud, presenta una tendencia antipersistente más fuerte que las registradas en altitudes bajas29; así mismo, se estableció que la alta frecuencia de ceros en el análisis de series de tiempo es un factor importante a considerar, debido a que puede influenciar la estimación de los parámetros fractales y multifractales de la precipitación34,51,52.
Además de la precipitación, la temperatura se ha tomado como parámetro de referencia en el estudio del cambio climático, justificado como una consecuencia del efecto invernadero que provoca la emisión de gases; razón por la cual es una variable ampliamente estudiada53-62. Al igual que la precipitación, la temperatura es una variable que no presenta un comportamiento lineal en el tiempo ni en el espacio63, y también en la determinación de características de autosimilitud y fluctuaciones, se utilizan los fundamentos de la geometría fractal24,64,65. Las investigaciones desarrolladas al respecto revelan que la temperatura muestra comportamiento no estacionario para periodos de corto plazo que es posible expresar en función de una ley de potencia66-67 y puede cuantificarse con la función de autocorrelación ; además, a mayor distancia del Ecuador se encuentre la zona de estudio, menor será su exponente de correlación70. Así mismo la memoria de las series de temperatura disminuye en función de la altitud71,72, y existe una relación entre la temperatura del aire y la dimensión fractal estimada73. De acuerdo a lo anterior, la teoría fractal permite describir la estructura de las series, por lo que podría utilizarse la teoría multifractal para completar la descripción de series temporales de precipitación y temperatura74-96.
A continuación se presenta una revisión de la literatura enfocada a series de precipitación y temperatura, en donde se consideran dos secciones principales, una teórica y otra de aplicaciones. La sección teórica comprende la descripción de los métodos fractales que han sido utilizados para el análisis de la estructura y comportamiento persistente o antipersistente en series de precipitación y temperatura en distintas regiones del planeta, así como la fundamentación teórica de los mismos. La sección de aplicaciones, está constituida por la compilación de resultados obtenidos para valores del exponente de Hurst y dimensión fractal estimados en las investigaciones consultadas.
Es importante resaltar, que las investigaciones que han utilizado métodos fractales para el estudio de series de precipitación y temperatura a partir del exponente de Hurst y de la dimensión fractal han sido muy numerosas, de manera que el objetivo de este documento es compilar los métodos empleados, ventajas y desventajas; así como los resultados obtenidos en diversas condiciones climáticas.
2. Teoría de métodos fractales
Mandelbrot97 describió un fractal como un conjunto para el cual su dimensión de Hausdorff es mayor a su dimensión topológica. Así mismo definió la dimensión fractal como un valor no entero, que permite describir la geometría fractal, así como la heterogeneidad de figuras irregulares; permitiendo capturar la información perdida al utilizar representaciones de geometría tradicional. La dimensión fractal se relaciona con el exponente de Hurst, mediante la siguiente ecuación desarrollada por Voss98:
Despejando la ecuación anterior se obtiene una relación directa entre la dimensión fractal (D) y el exponente de Hurst (𝐻), por lo tanto:
Donde 𝐷 es la dimensión fractal y 𝐻 es el exponente de Hurst.
A continuación se presenta una descripción de las metodologías más utilizadas en el análisis fractal de series de precipitación y temperatura.
2.1 Rango Rescalado de Hurst (R/S)
Este método fue desarrollado por Hurst25,26, y permite obtener el valor del exponente de Hurst mediante el cociente entre la suma de rangos parciales de las desviaciones de las medias de una serie de tiempo y la desviación estándar.
El exponente de Hurst permite clasificar la serie de acuerdo a la correlación a largo plazo de sus incrementos. De acuerdo a Karner99, al estudiar la dependencia a largo plazo se deben tener en cuenta las siguientes consideraciones: a) Al analizar series de tiempo cortas, la correlación a corto plazo se considera importante y b) Es necesario detectar la trayectoria de interés antes de realizar cualquier análisis.
Debido a su sencillez, el método de rango rescalado ha sido utilizado de manera satisfactoria al momento de analizar las propiedades escalares de tiempo, estadísticos y el comportamiento antipersistente, persistente y aleatorio para series de precipitación, temperatura, nivel del mar, manchas solares, entre otras100. De acuerdo a Hurst25,26 el método consiste en los siguientes pasos:
Los datos de entrada son obtenidos de la diferencia entre registros de dos puntos consecutivos:
donde 𝐼 𝑖 es el registro para el tiempo 𝑖. El promedio de diferencias en un periodo 𝜏 está dado por:
Si 𝑋(𝑖,𝜏) es la diferencia entre 𝐼 ′ 𝑖 y ⟨𝐼′ ⟩ 𝜏 , definida como:
Finalmente, la variable 𝑅 y la desviación estándar 𝑆 están dadas por:
De donde se obtiene, para cada valor de escala 𝜏, un valor de 𝑅/𝑆 que obedece a una ley de potencia. Aplicando logaritmos a ambos términos de la igualdad, se obtiene el valor de 𝐻 igual al valor de la pendiente:
donde 𝐻 es el exponente de Hurst. Este generalmente toma valores entre 0 y 1. Este análisis es robusto debido a que el comportamiento está influenciado solamente por la persistencia a largo plazo, detecta ciclos no periódicos aúun cuando estos tengan longitud mayor o igual al periodo de muestreo en estudio y además es un método sensible para detectar correlaciones a largo plazo en procesos aleatorios.
2.2 Conteo de caja
Es uno de los métodos más utilizados, el cual consiste en generar una cobertura del sistema y medir la densidad de dicha cobertura27.
Al cubrir una señal binaria, con cajas de tamaño definido 𝛿, se procede a determinar la dimensión fractal, considerando el número de cajas que se requieren para cubrir la señal; es decir, se coloca una malla de cuadros de tamaño 𝛿 sobre la señal, este proceso se puede repetir para diversos tamaños de caja; posteriormente se grafica el número de cajas con datos, contra el tamaño de cajas (𝛿) de forma log-log. Si la gráfica se comporta de manera lineal, la pendiente de la curva se relaciona con la dimensión fractal101.
Siguiendo a Falconer102 y a Breslin y Belward27, el método se puede aplicar a conjuntos en cualquier dimensión, por ejemplo, ha sido utilizado para el análisis de imágenes que involucran desde agrupamientos menores hasta galaxias. Una curva fractal es aquella que posee detalle infinito debido a su autosimilitud, incrementando su resolución de acuerdo a la exactitud del método de medición. La dimensión fractal determina el incremento de resolución y por lo tanto la longitud de la misma. Para un fractal, la longitud 𝐿 como función de la resolución de la medida 𝛿 es dada por:
donde 𝐷 es un exponente conocido como la dimensión fractal. En el método de conteo de caja, se determina la medición de 𝐿(𝛿) para un 𝛿 variable, a partir del conteo del número de cajas que no se sobreponen de tamaño requerido para cubrir la curva mencionada anteriormente. Estas mediciones se basan en la Ec. (9) para obtener un estimado de la dimensión fractal, la cual se conoce como dimensión de caja.
Una dimensión fractal, puede ser asignada a un conjunto de datos de una serie de tiempo al graficarlos como función del tiempo y calcular la dimensión de caja. La Ec. (9) tendrá un rango finito de tamaños de caja. Las cajas más pequeñas tendrán un ancho de ventana de 𝜏, donde 𝜏 es la resolución en el tiempo y una altura 𝛼, donde 𝛼 es la resolución de los datos.
2.3 Análisis Multifractal de fluctuación sin tendencia (MF-DFA)
El método se basa en la identificación de los momentos de qésimo orden que dependen de la longitud de la señal con la generalización de 𝑞=2. Posteriormente se obtiene un promedio de todos los segmentos para determinar la función de fluctuación, el comportamiento escalar de la función se obtiene mediante gráficos log-log y finalmente se establece una ley en potencia, donde 𝑞(2)=𝐻 28.
Según Gómez y Poveda103 es posible identificar diversos órdenes de MF-DFA, los cuales se caracterizan por la forma en la cual se remueven las tendencias de los datos. En el orden más bajo (MF-DFA1) se determina, para cada segmento, el mejor ajuste lineal del perfil, y se identifican las fluctuaciones por medio de la varianza del perfil respecto a la línea recta. De esta forma, se elimina la posible influencia de tendencias lineales a escalas mayores a la del segmento. Es importante mencionar que al eliminar las tendencias del perfil, también se están eliminando en los datos.
El método permite generar una caracterización multifractal de una serie de tiempo multifractal no estacionaria, además permite determinar correlaciones de largo alcance contenidas en series temporales aparentemente no estacionarias, enfocándose en eliminar las tendencias que se puedan presentar en la señal analizada y que no están relacionadas con sus propiedades de correlación1.
De acuerdo a Movahed et al28 en el análisis multifractal de fluctuaciones sin tendencia (MF-DFA), se supone que 𝑥 𝑘 es una serie de longitud 𝑁 y que esta serie no posee valores de cero en un conjunto cerrado, es decir, 𝑥 𝑘 =0 para una insignificante fracción de valores. A continuación, se presenta el desarrollo de la metodología a seguir en el análisis de una serie de tiempo:
Paso 1.- Se determina el perfil:
La sustracción de la media ⟨𝑥⟩ no es obligatoria ya que será eliminada en el análisis de tendencia que se desarrolla en el paso 3.
Paso 2.- Se divide el perfil 𝑌(𝑖) en 𝑁 𝑠 =int(𝑁/𝑠) segmentos que no se sobrepongan de igual longitud 𝑠, ya que la longitud 𝑁 de la serie no es usualmente un múltiplo de la escala de tiempo 𝑠 considerada, una pequeña parte al final del perfil puede ser residual. Para eliminar la parte residual de la serie, se realiza el mismo procedimiento anterior, comenzando desde el extremo opuesto de la serie; por lo tanto se obtienen 2 𝑁 𝑠 segmentos.
Paso 3.- Se calcula la tendencia local para cada uno de los 2 𝑁 𝑠 segmentos por medio de un ajuste de mínimos cuadrados aplicados a la serie. Posteriormente se determina la varianza de la siguiente manera:
Para cada segmento 𝜈, 𝜈=1,…, 𝑁 𝑆 , y:
Para 𝜈= 𝑁 𝑠 +1,…,2 𝑁 𝑠 . En este punto 𝑦 𝜈 (𝑖) es el polinomio de ajuste en el segmento 𝜈. En el procedimiento de ajuste también se pueden emplear polinomios lineales, cuadráticos, cúbicos o de mayor orden. Dado que la eliminación de tendencia de la serie de tiempo se realiza por la sustracción del polinomio de ajuste al perfil; los análisis de fluctuaciones sin tendencia (DFA) de diferente orden, difieren en su capacidad de eliminar tendencias en la serie.
Paso 4.- Se promedia sobre todos los segmentos para obtener la función de fluctuación o fluctuación media de 𝑞-ésimo orden, definida como:
Donde, generalmente, la variable de índice 𝑞 puede tomar cualquier valor real excepto cero. Para 𝑞=2, se utiliza el procedimiento estándar del DFA.
Paso 5.- Se determina el comportamiento escalar de la función de fluctuación analizando los gráficos logaritmo-logaritmo de 𝐹 𝑞 (𝑠) contra 𝑠 para cada valor de 𝑞. Si la serie de tiempo 𝑥 𝑖 presenta correlaciones con una ley de potencia, entonces se tiene que:
En general, el exponente ℎ(𝑞) puede depender de 𝑞. Para series de tiempo estacionarias tales como fGn (Ruido Gaussiano fraccionario), 𝑌(𝑖) de la Ec. (10) será una señal fBm (movimiento Browniano fraccionario), por lo que, 0<ℎ(𝑞=2)<1. El exponente ℎ(2) es idéntico al conocido exponente de Hurst 𝐻 [104].
Por tal motivo se propone este método al considerar investigaciones que estiman la dimensión fractal de series de precipitación y temperatura.
2.4 Espectro de Potencia
Es un método que describe la variación de potencia de una señal respecto a la frecuencia [105]. Usualmente los fractales con autoafinidad son analizados con métodos espectrales.
2.4.1 Espectro de potencia de Wavelet
Método desarrollado por Grossmann y Morlet108, el cual de acuerdo a Malamud y Turcotte69, brinda información de la dependencia espacio-temporal de una serie de tiempo, posee una base fractal y usualmente se aplica a series de tiempo no periódicas.
De acuerdo a Torrence y Compo148 la transformada Wavelet permite descomponer una serie de tiempo en el dominio tiempo-frecuencia, y por lo tanto es posible determinar los modos dominantes de variablidad, y cómo varían tales modos con el tiempo. La función de tal trasnformada se define mediante:
donde 𝜆 es el parámetro de escala (dilatación), 𝑡 es el parámetro de localización (traslación) y 𝜓(𝑡) es la Wavelet madre. Se escoge la constante de normalización 1/ 𝜆 , de tal manera que
para todas las escalas. En este caso se toma la Wavelet madre de Morlet, definida mediante 𝜓 0 (𝜂)= 𝜋 −1/4 𝑒 𝑖 𝜔 0 𝜂 𝑒 − 𝜂 2 /2 . Siguiendo a Torrence y Compo148, la transformada Wavelet continua de una secuencia discreta, 𝑋 𝑛 , se define como la convolución de 𝑋 𝑛 con una versión de la función Wavelet 𝜓 0 (𝜂) escalada en el espacio y transladada en el tiempo:
donde (∗) indica la complejidad conjugada. Variando la escala Wavelet y trasladándola a lo largo de un índice 𝑛 de la serie temporal, se puede construir una imagen de la amplitud o cualquier otra variable que muestre cómo cambia ésta frente a la escala de tiempo.
Debido a que la función Wavelet escalada en el espacio y transladado en el tiempo en general es una función compleja, la transformada 𝑊 𝑛 (𝑠) también es compleja. Entonces la transformada puede ser divivida en una parte real, ℜ{ 𝑊 𝑛 (𝑠)}, y una parte imaginaria ℑ{ 𝑊 𝑛 (𝑠)}, con amplitud, | 𝑊 𝑛 (𝑠)|, y fase, tan −1 [ℑ{ 𝑊 𝑛 (𝑠)}/ℜ{ 𝑊 𝑛 (𝑠)}]. Finalmente se define el espectro de Wavelet como | 𝑊 𝑛 (𝑠) | 2 .
Según Velásquez et al [29], si la serie de tiempo posee autoafinidad, la varianza de
será afectada por un parámetro de escala de manera asintótica:
El exponente 𝛿 se encuentra entre -1 y 3, −1≤𝛿≤3; de tal manera que el exponente de Hurst quedará definido como:
donde FGN es un ruido Gaussiano fractal, mientras que FBM es un movimiento Browniano fraccionario.
2.4.2 Espectro de potencia de Fourier
Por analogía con el análisis de Fourier, se puede definir el espectro de potencia Wavelet como el cuadrado de la transformada Wavelet. Si la función fuese compleja, su espectro de potencia Wavelet será el cuadrado de la parte real de la transformada Wavelet.
La frecuencia expresada en Fourier y la escala de la Wavelet no son cantidades recíprocas, por lo tanto es necesario realizar un re-escalamiento con un factor que dependerá de la Wavelet madre, para la Wavelet de Morlet esta conversión es dada por 4𝜋𝑠/( 𝜔 0 + 2+ 𝜔 0 2 ). Para comparar espectros de Wavelet de señales distintas, el espectro de potencia Wavelet se normaliza con un factor ó valor de expectación 𝜎 2 /𝑁, donde 𝜎 2 corresponde a la varianza y 𝑁 es el número de puntos de la serie temporal148.
Por otra parte, los fractales con autoafinidad generalmente son analizados usando técnicas de espectro. La variación del espectro de potencia con frecuencia 𝑓 sigue la ley de potencia 𝑓 −𝛽 , permitiendo obtener una relación entre el exponente espectral 𝛽 y la dimensión fractal 𝐷30, de tal forma que se llega a la relación:
el exponente 𝛽 de la ecuación anterior, puede ser un indicativo de la ausencia de una escala de tiempo característica en el rango de la ley de potencias y por lo tanto se puede asumir la presencia de un comportamiento multifractal89,103. Así mismo, el exponente 𝛽 será mayor a 1 si la serie presenta persistencia fuerte y no es estacionaria; para valores entre 0 y 1 indicará una serie estacionaria con persistencia débil; un valor igual a 0, significará una serie estacionaria sin correlación; y un valor menor a 0, implicará una serie estacionaria antipersistente69.
La dimensión fractal se obtiene de la pendiente del espectro106, y se estable que:
donde 𝐷 denota la dimensión fractal estimada a partir del espectro de potencia.
Según Sivakumar107 y, Gómez y Poveda103, para un proceso aleatorio, el espectro de potencia oscila aleatoriamente alrededor de un valor constante, indicando que una frecuencia no explica más de la varianza de la secuencia que otra. Para secuencias periódicas o casi periódicas, solo existen picos a ciertas frecuencias, el ruido medido le agrega un piso continuo al espectro. De esta manera, en el espectro, la señal y el ruido son fácilmente diferenciados. Señales caóticas pueden tener líneas espectrales muy notorias, pero siempre en la ausencia de ruido ellas serán parte continua del espectro107.
2.5 Análisis de fluctuaciones sin tendencia (DFA)
Es un método introducido por Peng et al104. De acuerdo a Yuval y Broday32, el DFA permite detectar correlaciones de largo alcance contenidas en series temporales aparentemente no estacionarias; así mismo, el método a partir de un análisis de invariancia de escala es capaz de eliminar tendencias de diferentes órdenes que se puedan presentar en la señal analizada y que no están relacionadas con sus propiedades de correlación109.
Siguiendo a Yuval y Broday32, un conjunto de datos 𝑦 𝑖 es integrado de la siguiente forma:
A continuación la serie integrada se divide en segmentos que no se sobrepongan de igual longitud 𝑚 y un polinomio de ajuste 𝑋 se utiliza para cada segmento. La fluctuación sin tendencia en cada segmento es dada por:
Posteriormente para series de tiempo con autoafinidad, la fluctuación media de los segmentos está relacionada con su escala de longitud mediante la siguiente ley de potencia:
donde 𝐻 se puede encontrar mediante una regresión de log( 𝐹 (𝑚)) contra log(𝑚) usando un número de divisiones con longitud de segmento 𝑚.
2.6 Modelo Fractal-Multifractal
De acuerdo a Huai-Hsien et al11 el método fractal-multifractal utiliza funciones de interpolación fractal para transformar medidas multifractales a proyecciones derivadas, con el objetivo de representar la complejidad de patrones naturales más allá de las características estadísticas. A partir de los parámetros 𝑎 𝑛 , 𝑐 𝑛 , 𝑑 𝑛 , 𝑒 𝑛 , 𝑓 𝑛 genera de manera determinística una serie de patrones aparentemente aleatorios, en una o más dimensiones, preservando las características del conjunto de datos.
La gráfica 𝐺={𝑥,𝑓(𝑥)|𝑥∈[0,1]|} de la función de interpolación fractal 𝑓:𝑥→𝑦 que pasa por 𝑁+1 puntos ordenados a lo largo de 𝑥, {( 𝑥 𝑛 , 𝑦 𝑛 )| 𝑥 0 <…< 𝑥 𝑁 ,𝑛=0,1,…,𝑁} se define como un atractor determinístico único de 𝑁 mapas afines 𝑊 𝑛 110:
donde los parámetros de escala verticales 𝑑 𝑛 satisfacen | 𝑑 𝑛 |<1, y los otros parámetros se definen por medio de las condiciones iniciales:
De acuerdo a Cortis et al77, las condiciones iniciales anteriores, conllevan a un conjunto de ecuaciones lineales simultáneas que permiten encontrar los valores de los parámetros 𝑎 𝑛 , 𝑐 𝑛 , 𝑒 𝑛 , 𝑓 𝑛 , de forma que:
La gráfica de función fractal 𝑓, y con dimensión fractal entre 1≤𝐷<2, se obtiene mediante el procedimiento conocido como juego del caos110.
2.7 Dinámica de Hurst-Kolmogorov
El método se basa en un proceso estocástico, caracterizado por propiedades invariantes de la distribución de probabilidad multifractal33. Este modelo disgrega un ruido fraccional Gaussiano mediante un proceso de cascada aditiva diádica, el cual es posteriormente transformado de manera exponencial para obtener la serie de tiempo. Esta serie de tiempo obtenida, se supone que tendrá una distribución log-normal50,111.
De acuerdo a Koutsoyiannis et al33 Si Z es una variable aleatoria de interés, y se asume que está definida en un espacio bidimensional (2D) denotado por variables continuas (𝑥,𝑦) o discretas (𝑖,𝑗) que definen un espacio del campo estocástico ${\scriptsize \underrightharpdown{Z}(x,y)} $ o ${\scriptsize \underrightharpdown{Z}_{i,j}}$, éstas se pueden relacionar mediante:
donde 𝛥 se expresa como un intervalo fijo que representa una unidad de escala, utilizada en la conversión de representación continua a discreta de la variable de interés.
Debido a su simplicidad, se asume que el campo Z es estacionario e isotrópico, denotando su media como 𝜇=𝐸[ 𝑍 𝑖𝑗 ], su autocovarianza como 𝛾 𝑘,𝑙 =𝐶𝑜𝑣[ 𝑍 𝑖𝑗 , 𝑍 𝑖+𝑘𝑗+𝑙 ] y su correlación como 𝜌 𝑘,𝑙 =𝐶𝑜𝑟𝑟[ 𝑍 𝑖𝑗 , 𝑍 𝑖+𝑘𝑗+𝑙 ]= 𝛾 𝑘,𝑙 / 𝛾 0 , donde 𝛾 0 es la varianza. Además, se define el proceso promedio a escala espacial con un entero (𝑘=1,2,…) múltiplo de 𝛥, de manera que:
denotando su autocovarianza como 𝛾 𝑙,𝑚 (𝑘) , su varianza como 𝛾 0 𝑘 y su autocorrelación como 𝜌 𝑙,𝑚 𝑘 . Esta forma de representación implica que el superíndice 1 puede omitirse Z.
Un proceso de Hurst-Kolmogorov en 2D, puede definirse como un proceso estocástico, el cual para los índices 𝑖,𝑗,𝑚,𝑛 y cualquier escala 𝑘 y 𝑙, posee la siguiente propiedad:
donde = 𝑑 significa que las dos variables aleatorias poseen la misma función de distribución conjunta de orden finito. El exponente 𝐻 se conoce como el exponente de Hurst y toma valores entre 0 y 1. Este comportamiento Hurst-Kolmogorov es una representación de la evolución de los procesos naturales.
2.8 Flujo Integrado fraccional de 3 parámetros (basado en el Modelo Multifractal Universal)
La integración fraccional de orden 𝐻 de un modelo multifractal universal, se conoce como el método de flujo integrado fraccional de tres parámetros (FIF)34,112.
El modelo FIF se basa en el concepto de cascadas multiplicativas en el contexto de turbulencia, el cual fue desarrollado por Kolmogorov113 y Mandelbrot114. De acuerdo a este modelo, la energía cinética proporcionada a un sistema a gran escala, es transferida por un proceso multiplicativo conservador a escalas cada vez más pequeñas y finalmente es disipada en forma de calor. Este tipo de proceso se puede modelar al (i) distribuir uniformemente una cantidad dada en un intervalo definido; (ii) dividir el intervalo en subintervalos; (iii) asignar a los subintervalos la cantidad original dada, multiplicada por una variable aleatoria que no dependa de la escala115.
Cuando 𝐻 es diferente de cero, el campo resultante, denominado como 𝑅 𝜆 , no es estacionario; siendo 𝐻 denominado como el parámetro de no estacionariedad. 𝐻 es un tipo de exponente de Hurst que representa el grado de suavidad del proceso, la cual se incrementa con el valor de 𝐻34. Para los incrementos de campo se tiene que:
donde 𝛥 𝑅 𝜆 ( 𝑥 )= 𝑅 𝜆 ( 𝑥 +𝛥 𝑥 )− 𝑅 𝜆 ( 𝑥 ) y |𝛥 𝑥 |=𝐿/𝜆, siendo 𝜆 la resolución del modelo.
Si los términos de la Ec. (34) se elevan a la potencia 𝑞, se obtiene la función de estructura de 𝑅 para un orden 𝑞 y se tiene que:
donde 𝜉(𝑞)=𝑞𝐻−𝑘(𝑞), es llamado el exponente de la función de estructura.
2.9 Modelo de Higuchi
El método de Higuchi [116] determina la dimensión fractal de una serie de tiempo. De acuerdo a Kalauzi et al31, la señal observada consiste en una secuencia de tiempo 𝑥(𝑙),𝑥(2),…,𝑥(𝑁), y un número 𝑘 de nuevas series autosimilares 𝑋 𝑘 𝑚 se construyen de la siguiente manera:
donde 𝑚 es el tiempo inicial, para un 𝑚=1,2,…,𝑘; 𝑘 es el intervalo de tiempo, para un 𝑘=2,…, 𝑘 max y int(𝑟) es la parte entera del número real 𝑟.
La longitud de las series 𝑋 𝑘 𝑚 es definida como:
Finalmente se obtiene un conjunto de valores medios 𝐿(𝑘) y la dimensión fractal se estima como la pendiente del mejor ajuste lineal de mínimos cuadrados correspondiente al gráfico ln(𝐿(𝑘))𝑣𝑠ln(𝑙/𝑘), por lo tanto:
donde 𝐷 es la dimensión fractal obtenida mediante el método de Higuchi.
2.10 Dimensión de correlación fractal (FCD)
El método permite obtener una medida de las características de dimensionalidad del espacio ocupado por un conjunto de puntos aleatorios96; además se hace la consideración que la dimensión de correlación 𝐷 𝑐 se asemeja a la dimensión fractal 𝐷36.
Para un conjunto de datos:
Se considera la integral de correlación 𝐶(𝑅) que cuenta el número de pares { 𝑋 𝑖 , 𝑋 𝑗 } tales que ∥ ?? 𝑖 − 𝑋 𝑗 ∥ sea más pequeño que un umbral 𝑅>0, con ∥𝑔∥ siendo la distancia euclidiana estándar en 𝑅 𝑛 . La integral de correlación 𝐶(𝑅) se expresa de la siguiente manera:
donde 𝛩 es la función de Heaviside y 2/(𝑁(𝑁−1)) es el factor de normalización, de manera que 𝐶(𝑅) tienda a 1 cuando 𝑅 tiende a infinito. Esto hace que si el conjunto es fractal,𝐶(𝑅) se comporte como una ley en potencia de la forma:
esto es:
De donde se podrá obtener la dimensión de correlación fractal 𝐷 𝑐 mediante el coeficiente de regresión de la Ec. (43).
2.11 Estimación de la dimensión fractal a partir de diferencias consecutivas
De acuerdo a Kalauzi et al31, se utiliza este método para calcular la dimensión fractal de una señal unidimensional, considerando los valores medios absolutos de orden 𝑛 de diferencias consecutivas finitas para una señal 𝑦(𝑡) con 𝑚 𝑦 (𝑛) = media (abs( 𝑦 (𝑛) (𝑡))), se observa que los logaritmos para 𝑚 𝑦 (𝑛) , 𝑛=2,3,…, 𝑛 max son linealmente dependientes para 𝑛, con las pendientes estables y con 𝑌 intercepciones proporcionales a la dimensión fractal de la señal, entonces:
Para establecer una relación entre 𝑌 𝑖𝑛𝑡 y la dimensión fractal de la señal, se utiliza la familia de funciones Weierstrass, con parámetros de 𝐻(0<𝐻<1) y 𝛾(𝛾>1)(𝑛!)/(𝑟!(𝑛−𝑟)!) de la siguiente manera:
Estas funciones tienen una dimensión fractal definida teóricamente, 𝐷=2−𝐻. Ya que la dimensión fractal 𝐷 es linealmente dependiente de 𝑌 𝑖𝑛𝑡 , se establece:
Los parámetros de regresión 𝐴( 𝑛 max ) y 𝐵( 𝑛 max ) se calculan para 𝑛 max . El planteamiento anterior solo es aplicable para series monofractales.
2.12 Modelo de Superficie de interpolación Fractal Browniana
Mandelbrot23 estableció que la dimensión fractal de un método fractal Browniano es invariante cuando se aplican transformaciones.
De acuerdo a Tao y Barros35, para procesos que presentan autoafinidad, el exponente espectral 𝛽, la dimensión fractal 𝐷, y el exponente de Hurst 𝐻, son tres características intercambiables; 𝐷 y 𝐻 pueden ser obtenidas a partir del exponente espectral 𝛽 para un campo de tres dimensiones, de la siguiente forma:
El exponente espectral, definido como la pendiente del espectro de potencia de Fourier en un gráfico log-log en 2D, describe la variabilidad de la serie como una función de longitud de onda y/o escala espacial; donde la amplitud de rugosidad y la potencia en la longitud de onda más corta, miden la varianza de la serie a la escala espacial correspondiente. El exponente de Hurst, el cual también se conoce como el índice de autoafinidad, mide la correlación de largo alcance. Si el conjunto de interés presenta características de autoafinidad, entonces se puede igualar la pendiente espectral con el factor de rugosidad del conjunto. El modelo de superficie fractal Browniana, es dado por:
donde 𝑍(𝑢,𝑣), 𝑍(𝑢,𝑣 ) 𝑏 , 𝛽, 𝛽 𝑏 son las transformadas de Fourier de las superficies de interpolación y del movimiento Browniano, así como las exponentes del espectro de potencia referenciados y Brownianos respectivamente; 𝑘 𝑟 es el número de onda radial; 𝑆 𝑟,1 y 𝑆 𝑟,2 son los factores de rugosidad de superficie original y del ruido Browniano.
2.13 Modelo de variación
De acuerdo a Dubuc et al117, Breslin y Belward27, el método de variación utiliza una cobertura de intervalos, en lugar de ventanas. Es decir, se calcula la oscilación para un conjunto de puntos que se encuentran a lo largo de la curva 𝑋(𝑡). La oscilación en un punto 𝑋( 𝑡 0 ) será:
La ecuación anterior corresponde al espesor de cobertura; ∈ representa la escala de medición de la oscilación, similar al tamaño de caja en el método de conteo de caja. Al disminuir este valor, también disminuye la cobertura. El área de cobertura se encuentra integrando 𝑣, se conoce como la variación de 𝑋 y se denota como 𝑉(∈). Para encontrar la dimensión fractal se calcula el rango al cual el área 𝑉(∈) tiende a 0, mientras que ∈ tiende a 0. La pendiente del gráfico log-log de 𝑉(∈)/ ∈ 2 vs 1/ ∈ 2 es la dimensión fractal de la serie.
2.14 Ventajas y desventajas de los métodos fractales
A partir de la revisión de literatura realizada es evidente que existe una gran variedad de modelos que permiten estimar el exponente de Hurst y/o la dimensión fractal de una serie de tiempo. Sin embargo, existen métodos que presentan ventajas sobre otros; un factor importante al definir el método a utilizar, corresponde al número de parámetros de entrada; por lo tanto, entre mayor sea el número de parámetros, el modelo será más complejo.
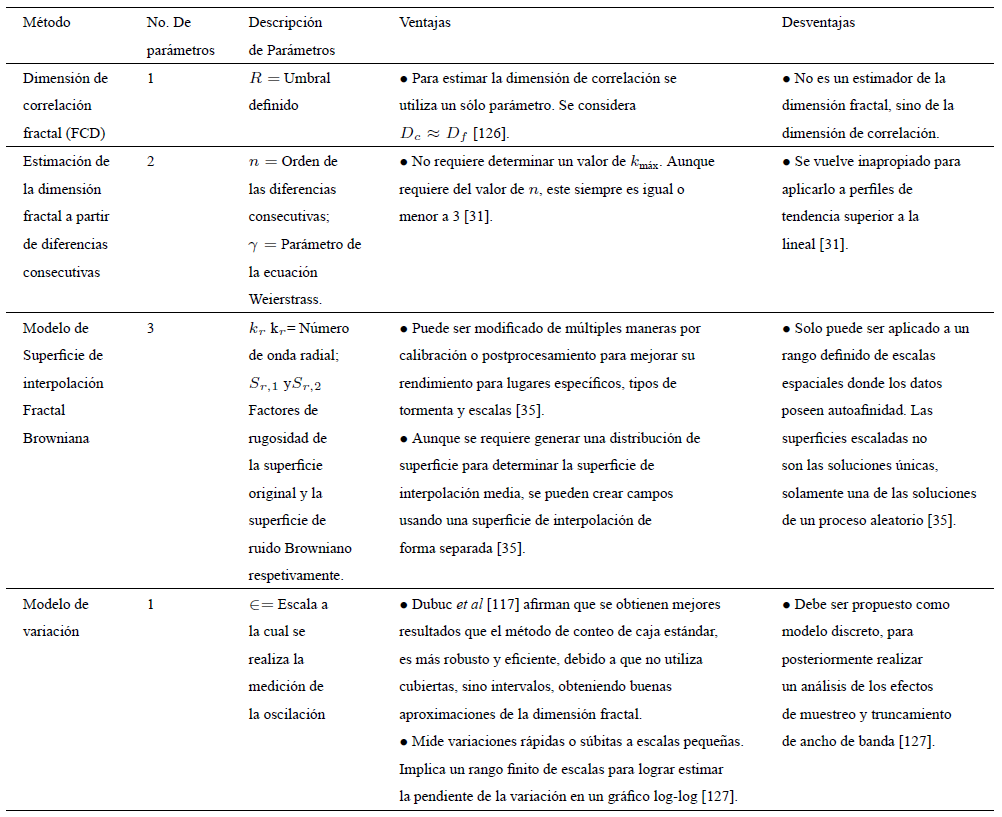
Debido a que se requiere evaluar detalladamente características como las anteriormente mencionadas para seleccionar el método más adecuado a desarrollar; a continuación se presentan las ventajas, desventajas y parámetros de entrada para los métodos revisados previamente (Tabla 1).
Basándose en la información presentada en la Tabla I, se han clasificado los métodos de acuerdo a su complejidad con base al número de parámetros de entrada que requieren en dos grupos:
Tabla 1 Ventajas, desventajas y parámetros correspondientes a los modelos fractales que permiten estimar el exponente de Hurst y/o la dimensión fractal de una serie de precipitación y temperatura.
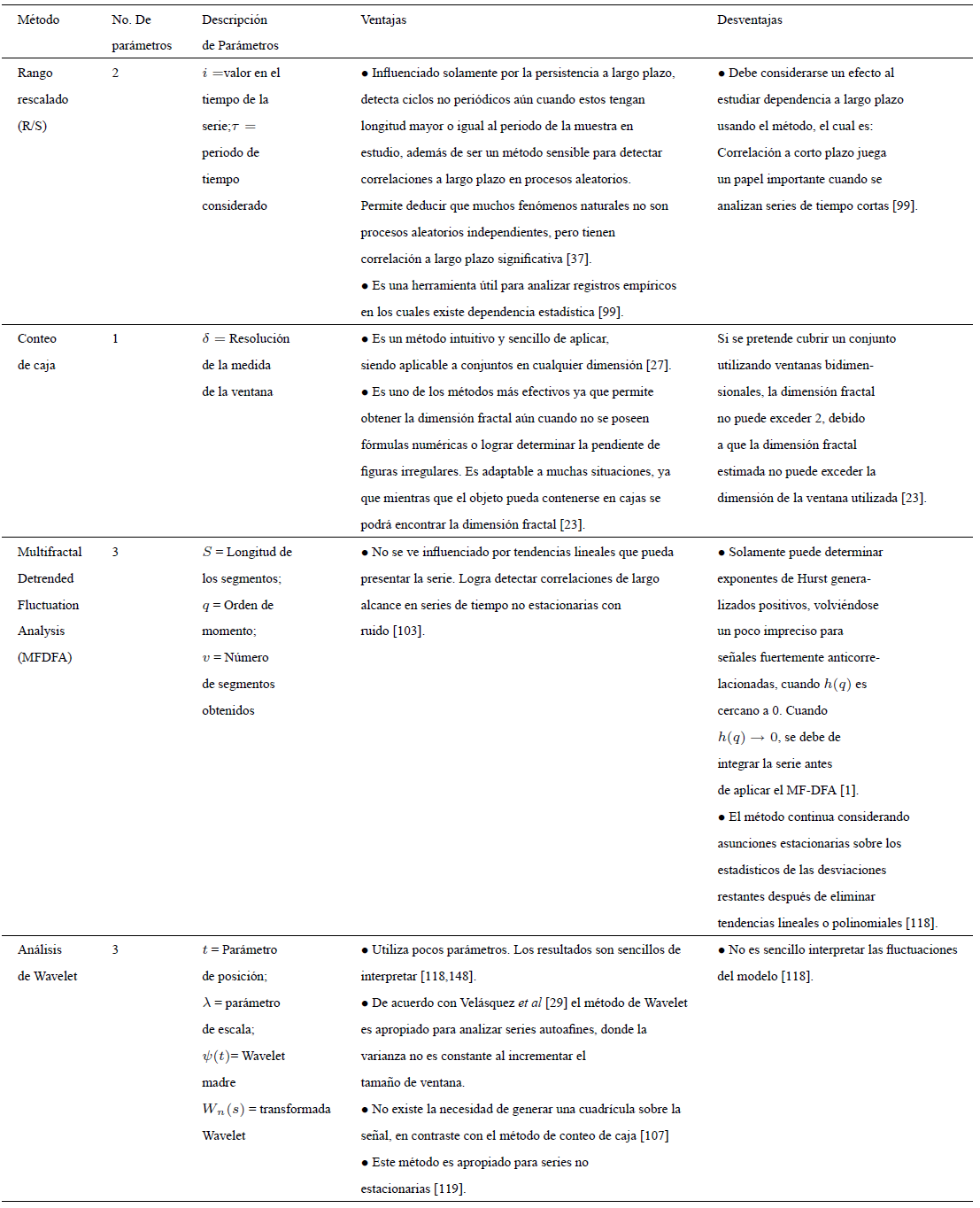
Métodos con baja complejidad: Se incluyen aquellos métodos que requieren de un número relativamente bajo de parámetros de entrada (menor a 3) y por ende son sencillos de desarrollar. Sin embargo, algunos de los métodos presentan desventajas significativas (solo puede aplicarse a series con ciertas características (Estimación de la dimensión fractal a partir de diferencias consecutivas), sólo es un estimador de la dimensión fractal (dimensión de correlación fractal), debe ser propuesto como modelo discreto (Modelo de variación), etc.) lo cual limita su aplicación. Métodos que pueden asignarse a esta clasificación son: Rango rescalado, conteo de caja, análisis de fluctuación sin tendencia, método de Higuchi, dimensión de correlación fractal, estimación de la dimensión fractal a partir de diferencias consecutivas y modelo de variación.
Métodos con alta complejidad: Se incluyen aquellos métodos que requieren un número considerable de parámetros de entrada (mayor o igual a 3). A pesar de ser más complejos de desarrollar que métodos con menor número de parámetros, presentan ventajas significativas (no se ve influenciado por tendencias lineales (método de análisis multifractal de fluctuaciones sin tendencia), son los más adecuados para series de tiempo con características específicas (análisis de Wavelet, espectro de potencia), determina el atractor de la serie (método fractal-multifractal), etc.). Métodos que se pueden asignar a esta clasificación son: análisis multifractal de fluctuaciones sin tendencia, análisis de Wavelet, espectro de potencia, método fractal-multifractal, dinámica de Hurst-Kolmogorov, flujo integrado fraccional de 3 parámetros y modelo de superficie de interpolación fractal Browniana.
Al desarrollar la clasificación anterior, se puede ampliar el panorama de los métodos que estiman la dimensión fractal. De acuerdo a las investigaciones consultadas, usualmente se utilizan métodos que presentan baja complejidad. El método más utilizado es el rango rescalado (R/S) a pesar de que presenta el inconveniente de tener que considerar los efectos de la correlación a corto plazo cuando se analizan series de tiempo cortas (Tabla I); lo cual es factible debido a que es sencillo desarrollarlo y estimar la dimensión fractal de un determinado conjunto o serie.
Referente a métodos con alta complejidad, el más utilizado es el análisis multifractal de fluctuaciones sin tendencia (MF-DFA), ya que aunque requiere de 3 parámetros (menor a métodos como la dinámica de Hurst-Kolmogorov y método fractal-multifractal), minimiza los efectos de tendencias lineales, característica que métodos de baja complejidad no poseen y que puede influenciar los valores estimados de dimensión fractal o exponente de Hurst. Se puede decir que es el más recomendable por la capacidad que presenta al considerar un análisis multifractal.
En el caso de ambas clasificaciones, se presentan métodos que sólo fueron registrados una vez en las investigaciones consultadas. Esto puede deberse a que métodos tales como espectro de potencia, método fractal-multifractal y dinámica de Hurst-Kolmogorov no fueron desarrollados para ser empleados a series de precipitación y temperatura.
En cuanto a las similitudes, una de las más evidentes es que métodos como rango rescalado, conteo de caja, MF-DFA, DFA y método de Higuchi, requieren segmentar la serie considerada en intervalos o ventanas para estimar el exponente de Hurst. Esta característica puede generar cierta incertidumbre al momento de estimar el exponente de Hurst con varios métodos; ya que valores del exponente de Hurst obtenidos a partir de un menor número de intervalos o ventanas pueden ser menos precisos. Se recomienda obtener un valor de exponente de Hurst promedio cuando se consideren varios métodos en un análisis.
Así mismo, se presentan diferencias entre los métodos; algunos se desarrollan con base a una imagen o gráfico de la serie (conteo de caja, análisis de Wavelet, espectro de potencia, método de Higuchi, Modelo de Superficie de interpolación Fractal Browniana y modelo de variación), mientras que otros métodos únicamente requieren la serie de datos para estimar el exponente de Hurst (rango rescalado, MF-DFA, DFA, fractal-multifractal, dinámica de Hurst-Kolmogorov, FIF, FCD) y estimación de la dimensión fractal a partir de diferencias consecutivas. De manera que la selección del método depende del enfoque que desee desarrollarse.
Como puede observarse en la Tabla I, existe una gran variedad de métodos que permiten estimar el exponente de Hurst (y por ende la dimensión fractal); sin embargo, la elección del más adecuado para evaluar una serie de determinada variable es fundamental. Se recomienda realizar comparaciones entre los métodos, previo a la elección de alguno de ellos.
3. Aplicaciones
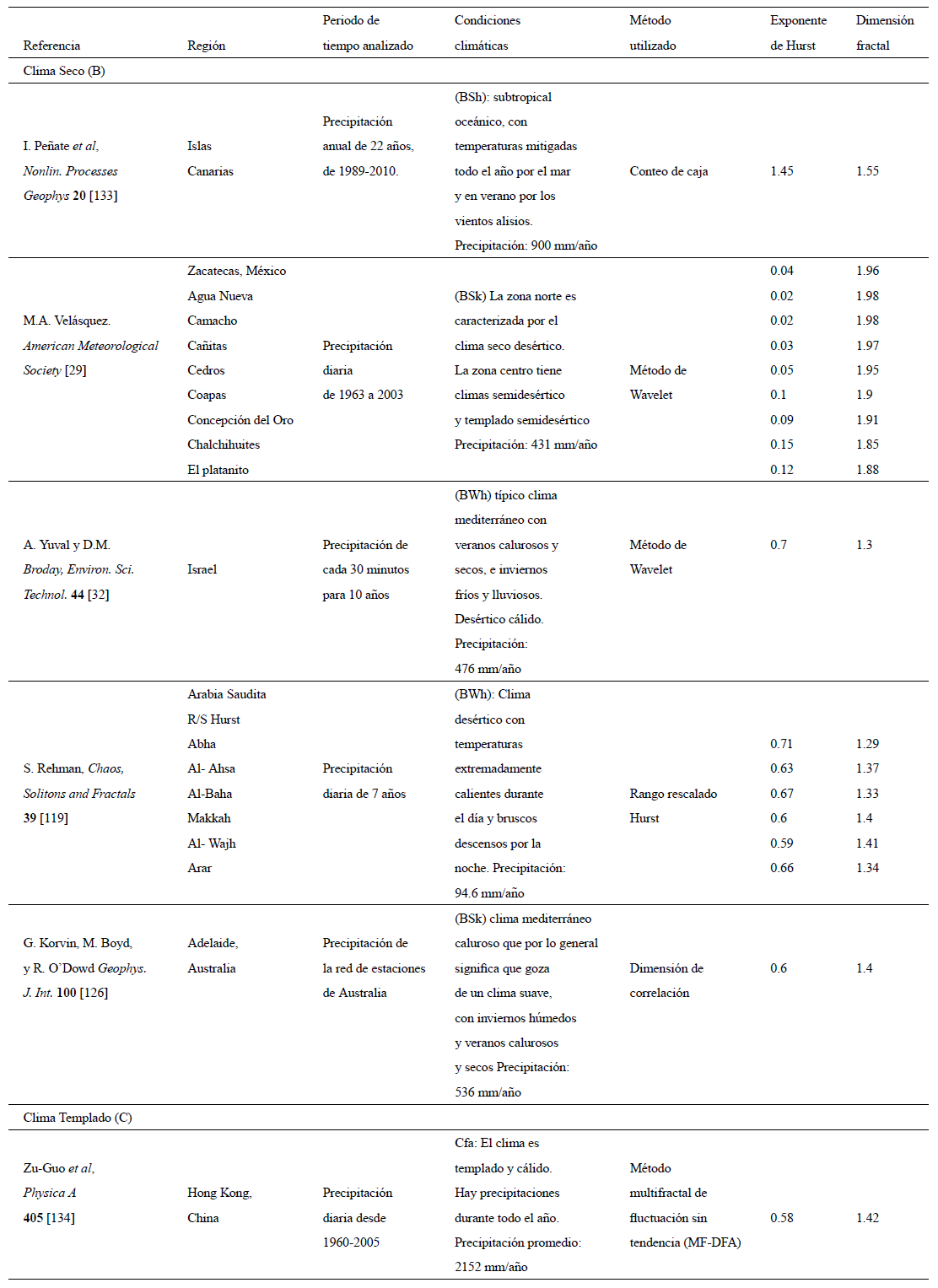
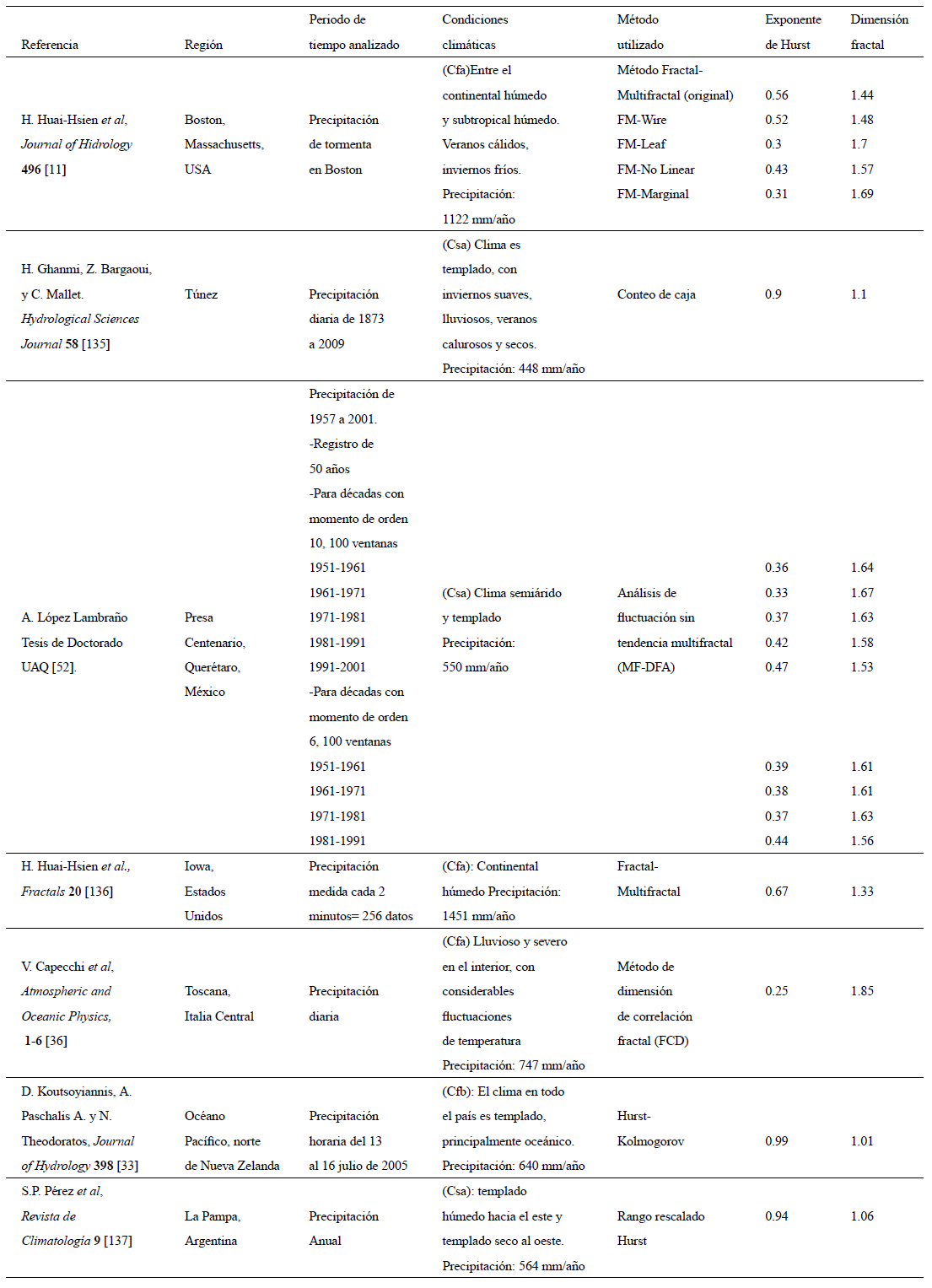
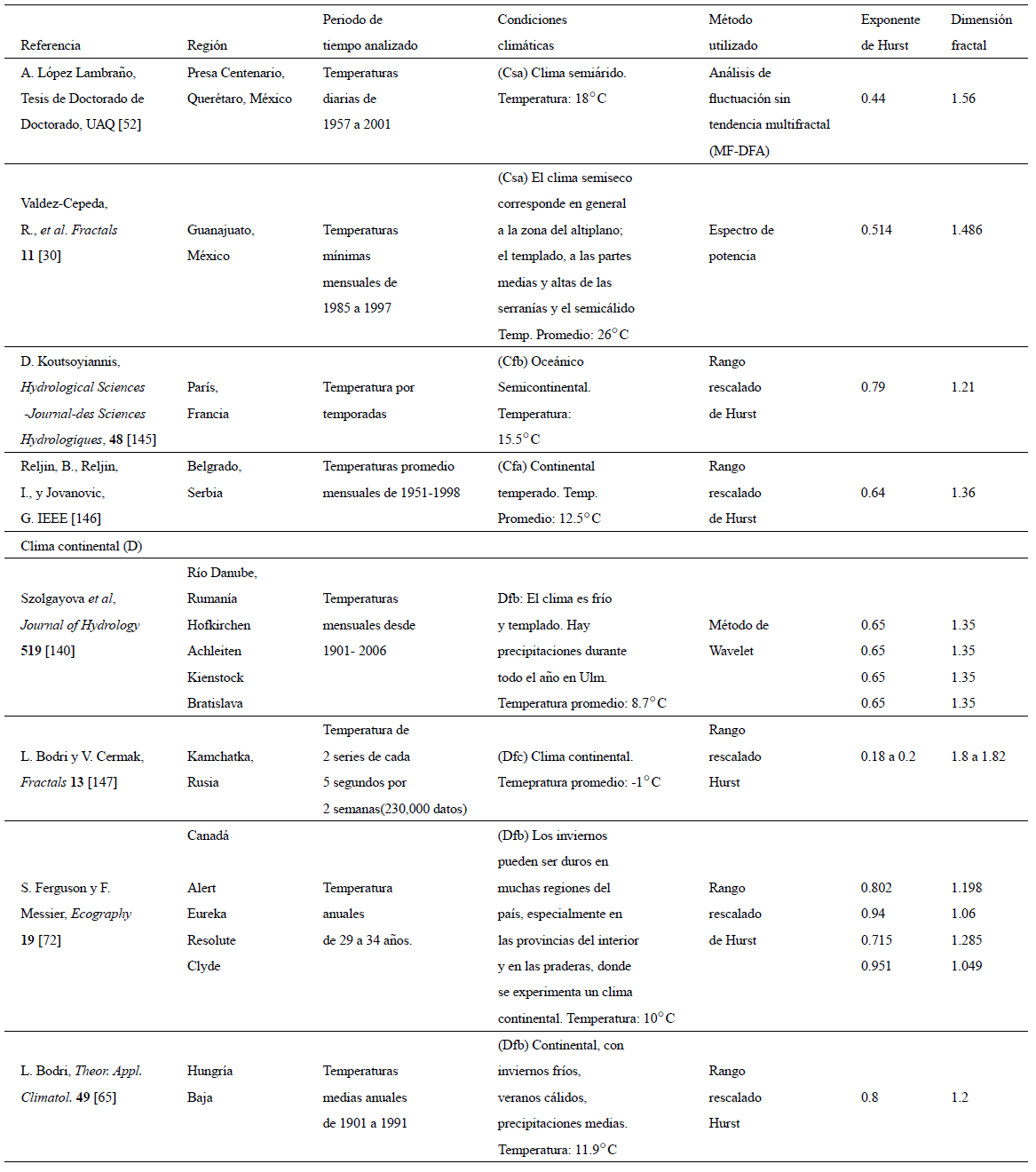
Los métodos basados en los fundamentos de la geometría fractal han sido aplicados al análisis de series de tiempo de precipitación y temperatura en diversas regiones del mundo. En esta sección se hace un inventario de las investigaciones que reportan la determinación del exponente de Hurst para series de precipitación y temperatura, así como un análisis de los resultados. Se ha utilizado la clasificación climática de Köppen128 para establecer una posible relación entre los valores estimados de exponente de Hurst con las condiciones climáticas de cada una de las regiones analizadas. En las Tablas II y III, se reportan las características de las series estudiadas, métodos de análisis y valores estimados del exponente de Hurst y dimensión fractal.
A partir de las Tablas II y III, se procede a analizar el comportamiento del exponente de Hurst de series de precipitación y temperatura con respecto a la clasificación climática de Köppen. Las investigaciones de series de precipitación desarrolladas en regiones con clima tropical (A), tales como Tamil Nadu, India129; Benín34; Pastaza, Ecuador31; regiones de Etiopía130; Australia131, Venezuela37, Brasil132; y Queensland, Australia27; muestran que las series de precipitación tienden a presentar valores del exponente de Hurst entre 0.075 y 0.45, es decir son antipersistentes en el tiempo. De acuerdo a Malamud y Turcotte69, esto significa que las series de precipitación que se registran en este tipo de clima, tienen alta probabilidad a presentar un incremento, seguido de un decremento y viceversa; además, una serie de tiempo antipersistente tendrá un comportamiento estacionario en el tiempo, debido a que los incrementos y decrementos se compensan entre sí, manteniendo los momentos estadísticos constantes e independientes del tiempo. De acuerdo a Rehman119 esto indica una memoria a corto plazo, dado que se presenta poca dependencia de los valores con los anteriormente registrados. Sin embargo, no todas las investigaciones reportadas en condiciones climáticas de tipo tropical (A) para series de precipitación, estiman valores del exponente de Hurst menores a 0.5; tal es el caso de Venezuela37, cuyo análisis reporta valores máximos de 0.7, lo que corresponde a series de precipitación persistentes. Lo anterior indica que la serie en análisis no es estacionaria en el tiempo, dado que un comportamiento de cambio (incremento o decremento) será seguido por un análogo, de manera que no se mantienen los momentos estadísticos en el tiempo. Además, existe un alto grado de ocurrencia de un evento registrado sobre los que se presenten en eventos futuros o presenta comportamientos con memoria a largo plazo69. También se puede establecer que se presenta una relación inversa entre el exponente de Hurst de las series y el valor de precipitación promedio anual (Tabla 2). Por ejemplo; series con precipitaciones promedio anual entre 2300 a 3500 mm/año corresponden a valores del exponente de Hurst de 0.4 y 0.075 respectivamente; mientras que una serie con precipitación promedio anual de 644 mm/año, corresponde a un valor de exponente de Hurst de 0.7; por lo tanto se tiene que la precipitación promedio anual se constituye en un parámetro que define la persistencia y estacionariedad de la serie de tiempo en condiciones climáticas tropicales, de manera que a menor precipitación promedio anual, la serie tendrá más fuerza de persistencia y no será estacionaria en el tiempo. Las diferencias entre los valores del exponentes de Hurst en regiones climáticas similares puede ser atribuida a dos situaciones: i) los diversos métodos empleados en los análisis desarrollados, y, ii) las características de las series de precipitación analizadas. Por ejemplo, el análisis desarrollado en Venezuela37, contempló series anuales, mientras que el resto de los análisis, se realizaron, a partir de series de
Tabla 2 Compilado de investigaciones sobre el análisis de series de precipitación aplicando geometría fractal.
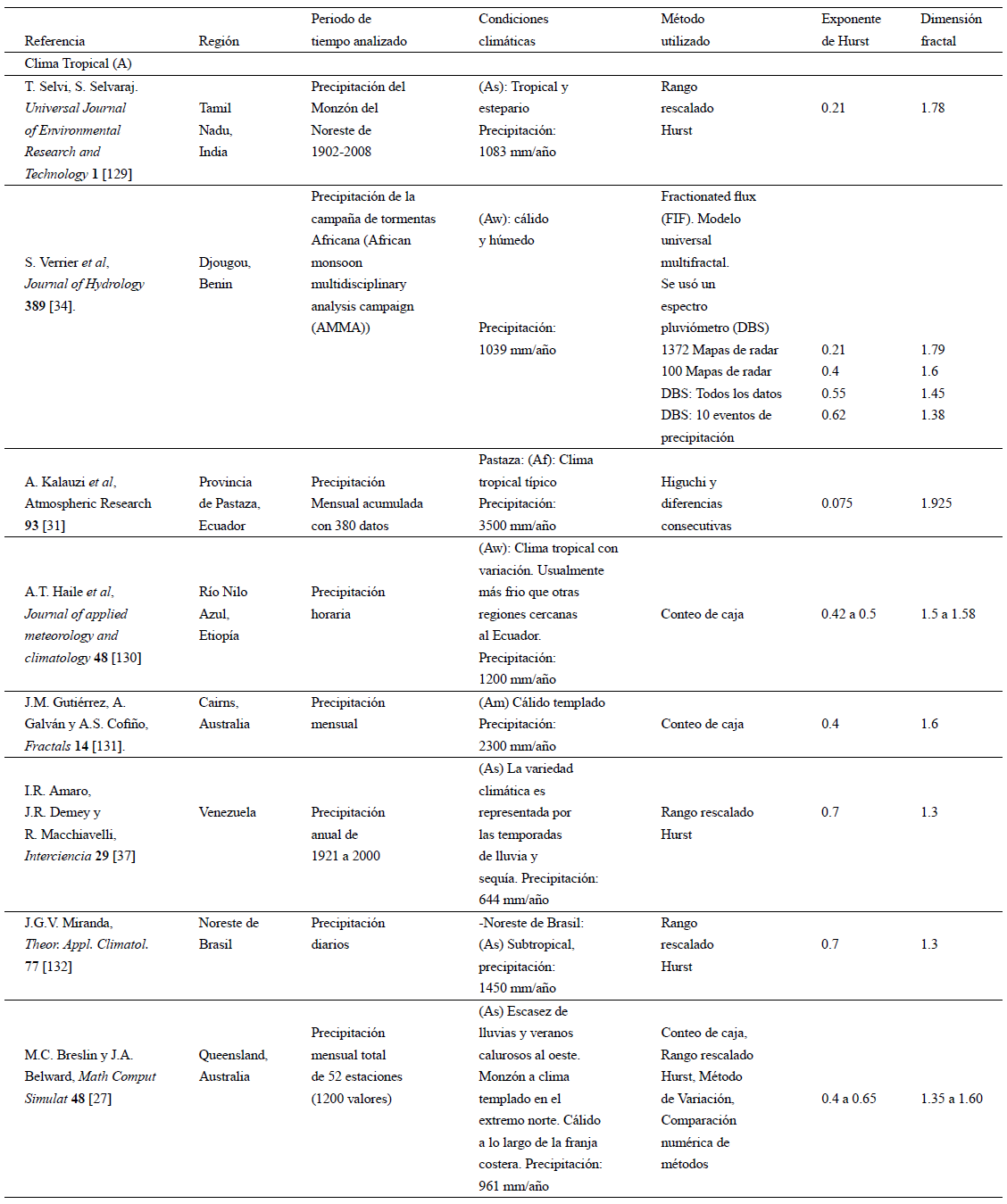
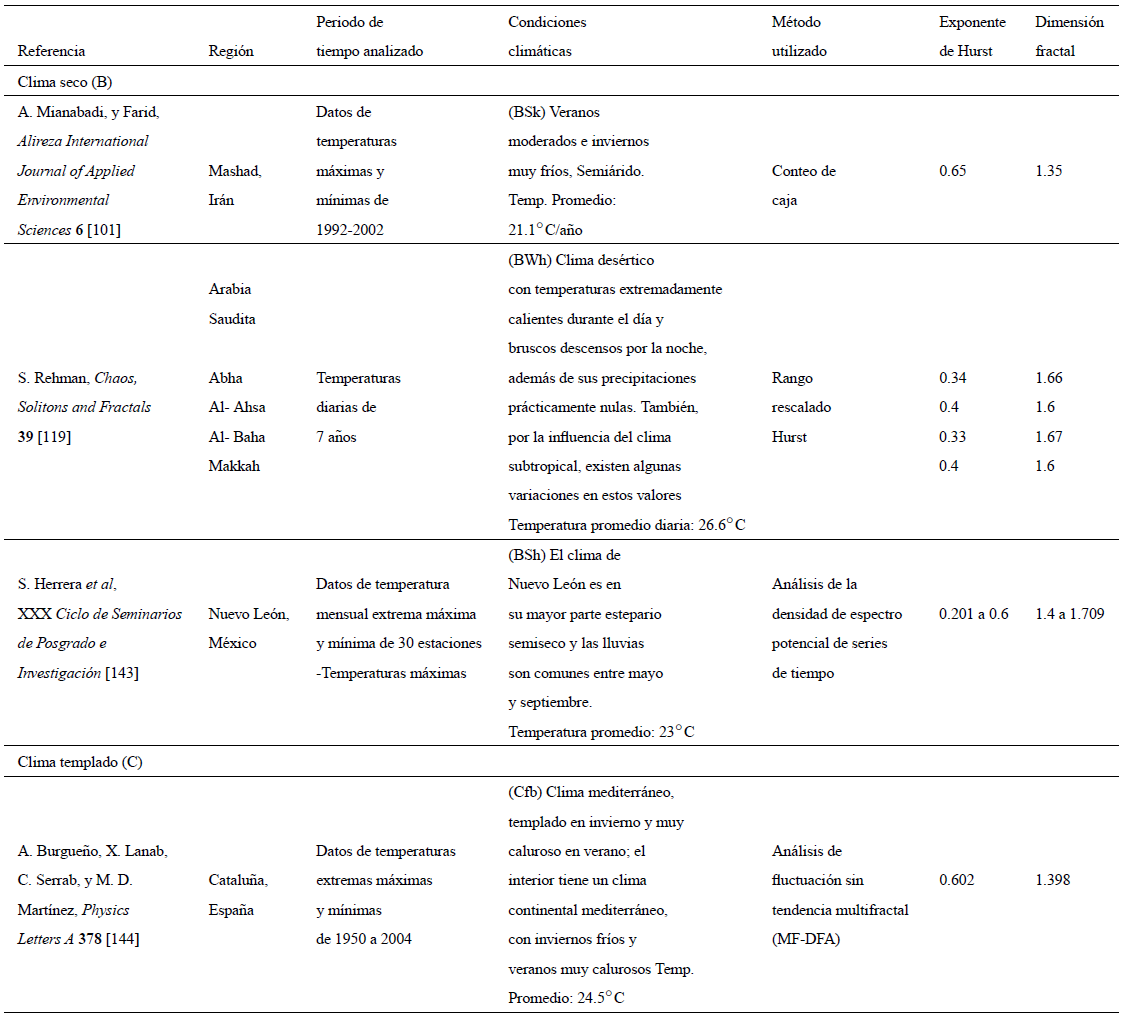
Tabla 3 Compilado de investigaciones sobre el análisis de series de temperatura aplicando geometría fractal.
tiempo mensuales y diarias; ésto implica que los valores de exponente de Hurst de series pueden verse influenciados por el método y la resolución temporal considerada.
De acuerdo a la Tabla 3, las series de precipitación que se registran en clima seco (B), tales como: (Islas Canarias133, Zacatecas, México29; regiones de Israel32 y Arabia Saudita119, tienden a ser antipersistentes, debido a que los valores del exponente de Hurst oscilan entre 0.02 y 0.45, como en el caso de las Islas Canarias y Zacatecas, México. Sin embargo, también se presentan series que tie-
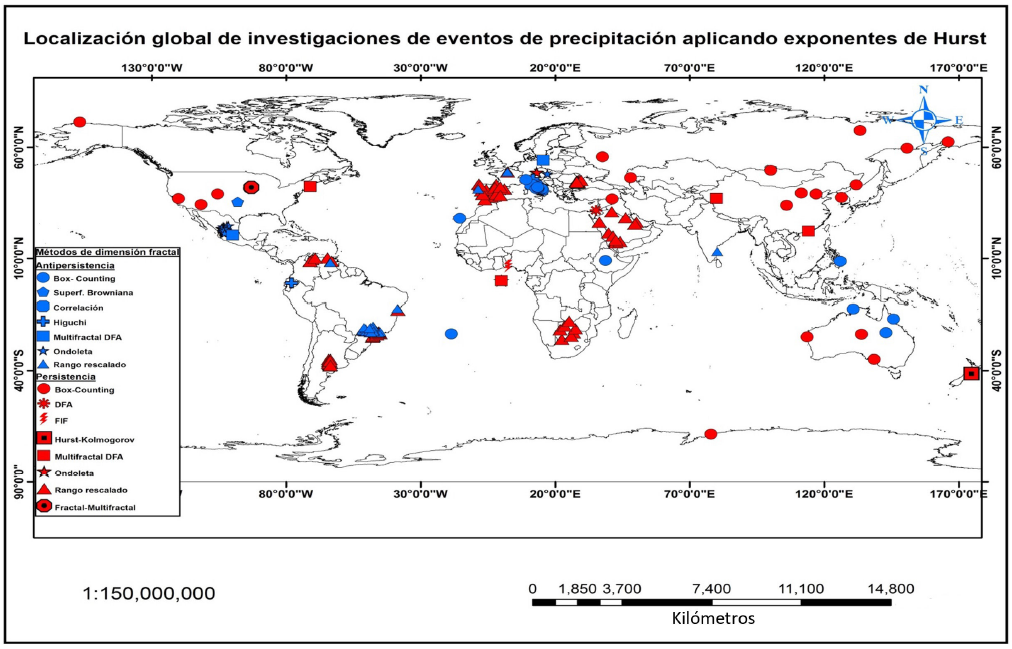
Figura 1 Localización global de investigaciones que estiman el exponente de Hurt en series de precipitación mediante la aplicación de diversos métodos.
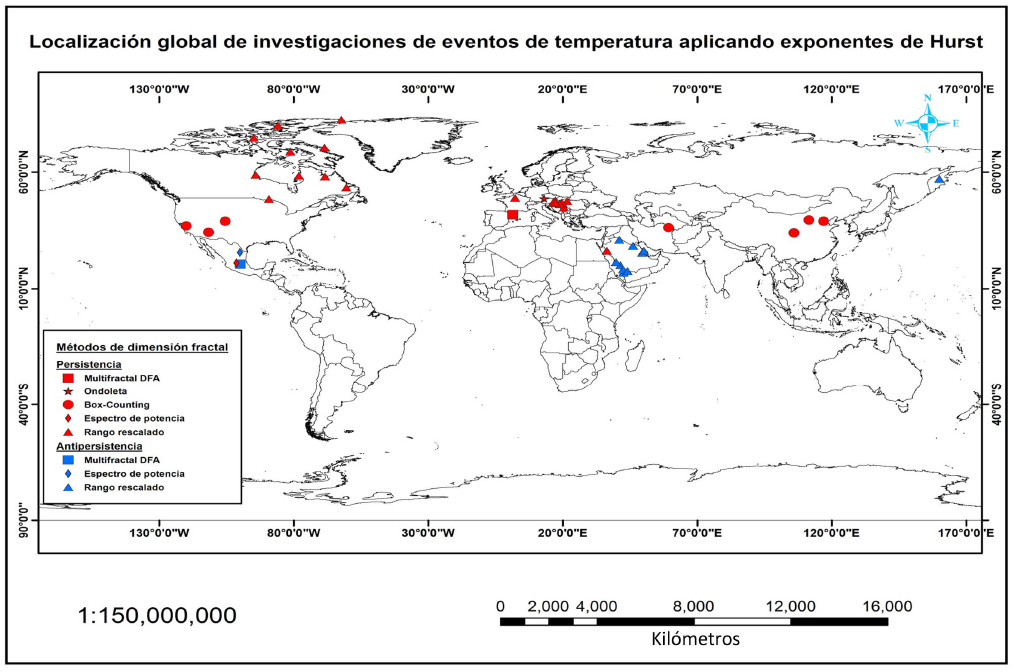
Figura 2 Localización global de investigaciones que estiman el exponente de Hurt en series de temperatura mediante la aplicación de diversos métodos.
nen un comportamiento persistente con valores del exponente de Hurst entre 0.6 y 0.7 (Israel, Arabia Saudita y Australia). Continuando el análisis en condiciones climáticas secas (B), se observa que a medida que disminuye la precipitación promedio anual, se incrementa el valor del exponente de Hurst de las series; por ejemplo, una serie de precipitación promedio anual de 94.6 mm, corresponde a un valor del exponente de Hurst de 0.71, mientras que una región con una precipitación promedio anual de 900 mm, presenta un valor de 0.45. También, se ha encontrado que la longitud del registro parece tener influencia en la estimación del exponente de Hurst; en series de tiempo con longitudes de registro menores, los valores que se estiman del exponente de Hurts aumentan.
En el caso de los estudios reportados en regiones con condiciones climáticas templadas (C), como en el caso de: Hong Kong, China134, Massachusetts, Estados Unidos11; Túnez, Túnez135; Querétaro, México52; La Pampa, Argentina137; París, Francia115; Sao Paulo, Brasil100; Drobudja, Rumanía138; Madrid, España131; Nápoles, Italia90; regiones de Botsuana139 y Montreal, España16, registran comportamientos antipersistentes y persistentes; lo anterior puede estar relacionado con la precipitación promedio anual registrada, es decir, se presenta una relación inversa entre los valores del exponente de Hurst y la precipitación promedio anual de la región correspondiente. Por ejemplo, en Hong Kong, China se registra una precipitación promedio anual de 2152 mm y se tiene un valor del Hurst correspondiente a 0.58; así mismo en Túnez se registran 448 mm/año y se tiene un valor del exponente de Hurst correspondiente a 0.9, lo anterior podría considerarse como un indicador al momento de caracterizar la precipitación promedio anual de una región. Al tomar en consideración otros factores tales como el método utilizado y las características de la serie analizada, se ha encontrado que en las regiones con clima templado, el método más empleado en la estimación del exponente de Hurst, corresponde al rango rescalado; éste método arroja valores más elevados del exponente de Hurst al compararse con los valores estimados al emplearse otras metodologías, entre ellas, el fractal-multifractal o el MF-DFA. También, se presenta la tendencia a que la longitud del registro parece tener influencia en el valor estimado del exponente de Hurst.
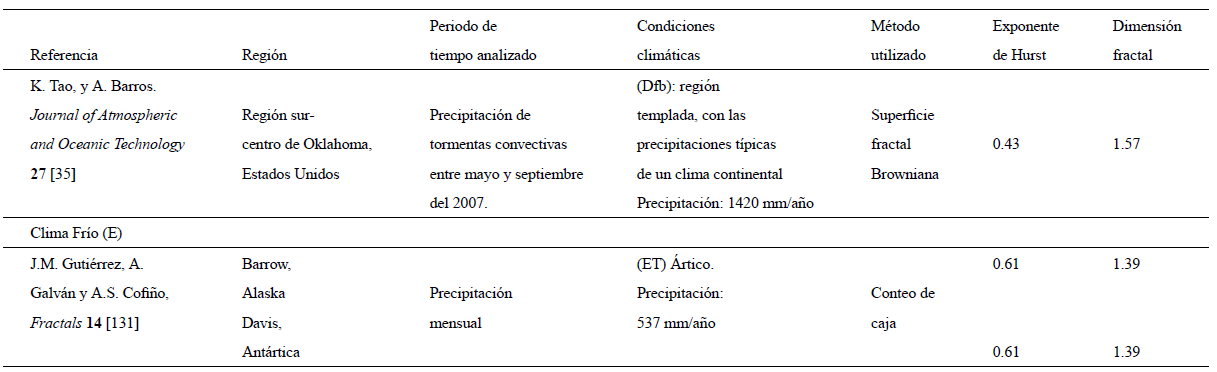
Cuando se analizan las series de precipitación registradas en condiciones de clima continental (D), los valores estimados correspondientes al exponente de Hurst, demuestran que la precipitación tiene una tendencia persistente y se han empleado diversos métodos para el desarrollo de los análisis. Para la condición climática fría (E), también se reporta un comportamiento persistente con un valor del exponente de Hurst de 0.61; la escasez de datos, limita los análisis para dicha condición de clima y se recomienda continuar desarrollando este tipo de estudios.
Al analizar el comportamiento las series de precipitación a partir de la clasificación climática de Köppen128, se realiza un análisis similar contemplando los reportes de las investigaciones que han empleado métodos fractales para el análisis de series de temperatura (Tabla 3).
De acuerdo a la Tabla III, las series de temperatura analizadas en climas secos (B) (Mashad, Irán101; y Nuevo León, México143), presentan valores del exponente de Hurst entre 0.2 y 0.4, indicando antipersistencia y estacionariedad69. Además, al considerar la temperatura promedio anual, se presenta una relación inversa con respecto a los valores del exponente de Hurst. Con respecto a las características de las series analizadas, se consideran series diarias o mensuales; en este caso los valores del exponente de Hurst no difieren significativamente al considerarse distintas resoluciones temporales en el análisis, caso contrario al de la variable precipitación. En las regiones con clima templado (C), (Cataluña, España144; Querétaro, México52; Guanajuato, México30; París, Francia145 y Belgrado, Serbia146) las series de temperatura presentan un comportamiento persistente y no estacionario en el tiempo, debido a que el valor del exponente de Hurst oscila entre 0.6 y 0.7; además no se define una relación entre la temperatura promedio anual y los valores del Hurst. En este tipo de clima las series con resolución temporal diaria, presentan los valores más bajos del exponente de Hurst (0.44) en comparación a los análisis que contemplan series mensuales, cuyos valores se encuentran en el rango de 0.6 a 0.8.
Con respecto a las series de temperatura registradas en la clasificación climática de tipo continental (D), y que comprende lugares tales como: Río Danube, Rumanía140; regiones de Canadá72 y regiones de Hungría65; las series tienden a presentar comportamiento persistente y no estacionario en el tiempo, debido a que el valor del exponente de Hurst se encuentra entre 0.65 y 0.95, es decir, presentan memoria a largo plazo. En el caso de las series analizadas en la región de Kamchatka, Rusia53, se obtiene un comportamieto antipersistente con valores del exponente de Hurt entre 0.18 y 0.20. Las series analizadas a partir de resoluciones temporales registradas cada 5 segundos, arrojaron los valores más bajos del exponente en estudio.
A partir de la información contenida en las Tablas 2 y 3, se ha realizado una espacialización de las investigaciones que reportan análisis fractal para series de precipitación y temperatura (Fig. 1 y 2); así mismo se puede visualizar el método empleado para la estimación del exponente de Hurt y la tendencia en el comportamiento de la serie, lo anterior permite identificar las regiones que poseen información y las que no cuentan con ningún tipo de análisis.
De acuerdo a la Fig. 1, la mayoría de las investigaciones referentes a series de precipitación se concentran en Europa Central y Medio Oriente, seguidas por el sur de África y Sudamérica. La concentración de investigaciones en dichas regiones proporciona información relevante para evaluar el comportamiento de las series de precipitación a una escala global o planetaria, sin embargo desarrollar un análisis detallado se ve limitado por la escasez de información en otras regiones del mundo, principalmente en climas continentales y fríos; se recomienda desarrollar este tipo de análisis en las regiones, tales como Groenlandia, Canadá, Rusia, Antártida, Norte de África, India y Centroamérica. En la Fig. 1, los símbolos rojos indican series de precipitación con persistencia en el tiempo (y no estacionariedad) y los azules indican antipersistencia (y estacionariedad); se puede notar que las series antipersistentes tienden a concentrarse en las zonas cercanas al Ecuador; que a su vez es la región en la que predominan las condiciones climatológicas de tipo tropicales (A). Al alejarse del Ecuador, comienzan a predominar las series de precipitación con tendencia persistente en el tiempo. Ahora bien, al inicio se planteó que existen indicios para afirmar que la precipitacion promedio anual mantiene una relación con la fuerza de persistencia, sin embargo las tendencias en el comportamiento fractal de la serie pueden depender de la variabilidad climática producto de fluctuaciones como la oscilación decadal del Pacifico (PDO) y la oscilación del sur (ENSO).
Al analizar la Fig. 2, es evidente que se tiene una situación aún más crítica debido a la escasez y falta de información en el análisis fractal de series de temperatura a partir del exponente de Hurst; las investigaciones referenciadas, se localizan en Canadá, México, Medio Oriente y Europa Central. Las series antipersistentes tienden a predominar en regiones cercanas al Ecuador (símbolos azules). No se reportan resultados en las condiciones climáticas tipo (A) y (B).
4. Conclusiones
El análisis de series de tiempo empleando los fundamentados de la geometría fractal, permiten caracterizar la estructura temporal y la ocurrencia de eventos de precipitación y temperatura; además, posee la ventaja que las variables aleatorias en mención, se pueden analizar en múltiples escalas y dimensiones. Los exponentes de Hurst representan una medición del grado de dependencia de las series en mención y pueden explicar el comportamiento espacio-temporal de dichas variables.
Los valores que se estiman del exponente de Hurst, y que permiten evaluar el comportamiento persistente o antipersitente de variables aleatorias como es el caso de la precipitación y temperatura, se encuentran correlacionados a las condiciones climáticas del área en estudio; la resolución temporal y longitud del registro también constituyen factores determinantes al momento de realizar un análisis de series temporales a partir del exponente de Hurst.
Se recomienda complementar al análisis de series de precipitación y temperatura, empleando la teoría multifractal, para así conceptualizar los posibles cambios de los momentos de la precipitación y temperatura con el tiempo.
Finalmente, el cambio climático y sus posibles consecuencias deben ser el origen minucioso de estudios, reflexiones y consideraciones de cambio de modelos de desarrollo; dado lo anterior, los resultados y las apreciaciones reportadas en el presente trabajo pueden ser relevantes para el análisis y comprensión de la dinámica del cambio climático, tomando como punto de partida la caracterización de la estructura temporal y la ocurrencia de la precipitación y la temperatura en diferentes escalas.











 text new page (beta)
text new page (beta)