Eigenestados exactos y estados entrelazados de un ión atrapado oscilando en dos dimensiones

Ramos Prieto, I.; Moya-Cessa, H.M.; Ramos Prieto, I.; Moya-Cessa, H.M.

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista mexicana de física

versión impresa ISSN 0035-001X

Rev. mex. fis. vol.63 no.2 México mar./abr. 2017

Research

Eigenestados exactos y estados entrelazados de un ión atrapado oscilando en dos dimensiones

I. Ramos Prieto^a^*

H.M. Moya-Cessa^a^**

^{^a}Instituto Nacional de Astrofísica, Óptica y Electrónica, Calle Luis Enrique Erro No. 1, Sta. Ma. Tonantzintla, Pue. 72840, México.

Resumen

Demostramos que es posible encontrar eigenestados exactos de la interacción de un ión atrapado oscilando en dos dimensiones y que cada uno de los eigenestados exactos son estados entrelazados. También demostramos que el hamiltoniano que describe dicha interacción puede ser mapeado a un escenario tipo Rabi cuántico (un átomo de dos niveles y dos campos electromagnéticos cuantizados) mediante una transformación unitaria.

Palabras clave: Iones atrapados; estados entrelazados

Abstract

We show that it is possible to find exact eigenstates in the interaction between a trapped ion oscillating in two dimensions and they will be entangled states. We also show that the Hamiltonian that describes this interaction may be mapped to a quantum Rabi interaction Hamiltonian (for a two-level atom and two quantized fields) by means of a unitary transformation.

Keywords: Trapped ions; entangled states

PACS: 03.65.-w; 42.50.Dv

1. Introducción

Uno de los candidatos más viables para la realización de procesamiento de información cuántica son los iones atrapados. Debido a que éstos pueden ser manipulados individualmente, los hace excelentes candidatos para un sin número de fenómenos que van desde la generación de estados vibracionales no-clásicos ¹, pasando por el modelado de efectos relativistas ²^,³, hasta la ingeniería de hamiltonianos de interacción específicos ⁴.

La utilización de estos efectos cuánticos genera una variedad de herramientas infinitamente superiores a sus predecesoras clásicas. Uno de tales efectos cuánticos de mayor análisis es sin duda alguna el entrelazamiento cuántico. Varias implicaciones tanto teóricas como prácticas generan este tipo de efectos. La generación de estados entrelazados puede encontrarse en los estados propios de un ión atrapado interactuando con haces láser, lo cual estudiamos a detalle en el presente manuscrito.

En el siglo pasado surgieron muchas propuestas para la realización de computadoras cuánticas, Feynman propuso la utilización de sistemas cuánticos controlables como instrumentos para producir o simular la dinámica de otros sistemas más tradicionales ⁵. La idea de utilizar a la mecánica cuántica como punto de partida para la realización de procesos demasiado complejos como algoritmos de factorización y búsqueda ⁶^,⁷, dio paso al nacimiento de la información cuántica, que incluye el análisis de diversos protocolos, como la distribución cuántica de claves secretas ⁸, y de aspectos fundamentales de la mecánica cuántica, como el entrelazamiento cuántico ⁹.

De hecho, ya en 1995, Cirac y Zoller hicieron una propuesta de una computadora cuántica basada en iones atrapados ¹⁰, que consiste en un arreglo lineal de iones atrapados enfriados a un estado de movimiento fundamental. Usando haces de luz láser enfocados, los estados individuales del ión en la cadena pueden ser rotados, y la interacción entre dos iones individuales de la cadena podrían ser implementados mediante el acoplamiento de los estados internos de los iones individuales con el movimiento colectivo de un modo particular. Además, recientemente se ha mostrado que es posible generar compuertas cuánticas estables ¹¹ y rápidas ¹², en este tipo de sistemas.

El estudio de iones atrapados interactuando con haces de luz láser ¹³^,¹⁴, produjo una serie de avances no solamente en el intento de elaboración de computadoras cuánticas, sino que trajo consigo investigación de física fundamental. El tratamiento teórico que se realiza en iones atrapados no es nada trivial, en general es demasiado complejo, incluso tratándose de un único ión atrapado, las aproximaciones requeridas para poder dar una solución físicamente aceptable no son del todo generosas. La aproximación de Lamb-Dicke ¹⁵^,¹⁶ es una de las primeras que se tienen que utilizar para poder simplificar el problema, donde dicha aproximación considera regiones espaciales más pequeñas que la longitud de onda del láser. Otro tipo de aproximaciones también delatan la complejidad del tratamiento general de un ión atrapado, por ejemplo, un acoplamiento débil del ión-láser puede simplificar el problema sin pérdida de generalidad. Debido a la complejidad para resolver este tipo de problemas, análisis perturbativos han sido realizados para intentar obtener mejores resultados analíticos ¹⁷. También el uso de transformaciones unitarias conduce a un escenario donde parece simplificarse el problema, y ésto ayuda a obtener una solución e interpretación de sistemas tan complejos como los iones atrapados interactuando con haces láser.

En trabajos realizados por Moya-Cessa y colaboradores ¹⁸^,¹⁹, utilizan una transformación unitaria que ayuda a linealizar el hamiltoniano ión-láser. La transformación unitaria lleva el hamiltoniano ión-láser a un hamiltoniano tipo Rabi que incluye los términos contra-rotantes, esta equivalencia genera interpretaciones que enlazan a un ión atrapado interactuando con haces láser y un átomo de dos niveles interactuando con un sólo modo de un campo electromagnético cuantizado.

Por otro lado, recientemente ha habido interés en la generación de modelos de Rabi cuánticos ²⁰^,²¹^,²². Debido a que, mediante una transformación unitaria se puede mostrar que los hamiltonianos de Rabi y de ión-láser son análogos, por lo que comparten el mismo espectro de energía y así modelar hamiltonianos tipo Rabi (cuánticos) es directo de realizar en la interacción ión-láser. Esta correspondencia es extremadamente útil ya que nos permite mapear propiedades interesantes de un modelo al otro.

En este trabajo enfocamos nuestra atención al estudio de un ión atrapado, vibrando en dos dimensiones e interactuando con haces láser (por simplicidad, consideramos el caso en resonancia), y utilizamos una transformación unitaria aplicada al hamiltoniano ión-láser para encontrar una correspondencia con el hamiltoniano de la interacción entre un átomo de dos niveles y un campo cuantizado. También obtenemos eigenestados exactos del hamiltoniano ión-láser utilizando el método descrito en ¹⁹, pero en este caso vemos que la vibración en dos dimensiones genera un rompimiento de la degeneración en el espectro de energías del sistema, además, la combinación de los parámetros que gobiernan la interacción ión-láser puede generar un rompimiento parcial de la degeneración.

Por último, encontramos estados entrelazados del hamiltoniano que caracteriza la interacción de ión atrapado y dos haces ortogonales, estos estados entrelazados son integrantes de una familia de eigenestados exactos de dicho hamiltoniano.

Una vertiente que también analizamos es la generación del modelo de Rabi para la interacción de un átomo de dos niveles y dos campos electromagnéticos cuantizados.

2. Hamiltoniano del sistema

En esta sección describimos someramente las diferentes trampas que se utilizan para poder atrapar iones y hablaremos de una en específico que es la trampa de Paul. También abordaremos uno de los puntos esenciales del trabajo, ya que, recurrimos al hamiltoniano que describe la interacción de un ión atrapado con dos haces de luz láser, y cómo aplicando una transformación unitaria a este hamiltoniano podemos obtener un hamiltoniano tipo Rabi.

2.1. Trampa de Paul

La posibilidad de atrapar partículas individuales abrió un abanico de estudios con menor incertidumbre ya que anteriormente se contaba únicamente con valores promedio, suponiendo un comportamiento similar estadístico en cada átomo del ensamble, así que, la necesidad de un conjunto de herramientas que pudieran atrapar y manipular partículas individuales se hace necesaria para poder estudiar a detalle el comportamiento de un átomo o iones individuales.

Diferentes trampas como la de Kingdon ²³ y Penning ²⁴ fueron desarrolladas para poder atrapar iones o cadenas de iones utilizando campos electromagnéticos, sin embargo, los cortos tiempos de almacenamiento y potenciales no armónicos hicieron que una trampa adicional fuera requerida. La trampa de Paul ²⁵ puede confinar partículas cargadas (iones por ejemplo) a una región en el espacio utilizando campos eléctricos oscilantes para formar así un potencial adecuado para que esto pueda ocurrir.

La trampa de Paul puede atrapar partículas cargadas utilizando campos electromagnéticos constantes, sin embargo, las partículas se desenfocarán y producirán choques con algunos componentes de la trampa y al tener potenciales parabólicos atractivos y repulsivos en direcciones radial y en el eje z respectivamente, se imposibilita el atrapamiento de partículas en 3 tres dimensiones. Por eso, en la trampa de Paul se utilizan campos eléctricos que oscilan armónicamente y que producen situaciones en las cuales las partículas cargadas pueden ser confinadas debido al cambio armónico de la fuerza que ejerce el campo eléctrico sobre la partícula cargada, ya que se puede llegar a alternar el enfocamiento y el desenfocamiento para así atrapar a las partículas cargadas. Para un tratamiento detallado de la trampa de Paul puede consultarse la referencia ²⁶.

2.2. Hamiltoniano tipo Rabi

En la sub-sección anterior hablamos de la trampa que hace posible atrapar átomos o iones individuales, y como el movimiento debe ser un movimiento armónico, por lo que pensar en un oscilador armónico cuántico para representar el movimiento de un único ión es necesario. Así que el hamiltoniano de un ión atrapado interactuando con un láser contempla la energía vibracional del centro de masa del ión, la energía interna del mismo y la energía de interacción entre el láser y el ión, por lo tanto:

H^ion=H^vibra+H^inter+H^I. (1)

El momento vibracional pude ser modelado como un oscilador armónico cuántico y la energía interna pude considerarse como la energía de transición entre dos niveles de todo su espectro, mientras que la parte de la interacción es una interacción dipolar eléctrica -er⃗⋅E⃗, donde er⃗ es el momento dipolar del ión y E⃗ es el campo eléctrico generado por el láser (onda plana). Así que el hamiltoniano puede escribirse explícitamente de la siguiente forma

H^ion=νa^†a^+ω2,12σz+λE0(σ+ei(kx-ωt)+σ-e-i(kx-ωt)), (2)

con ℏ=1 y masa del ión igual a 1. Al trasladarnos a un escenario rotante aplicando una transformación como la siguiente:

T^=eiω2σzt, (3)

el hamiltoniano se transforma en

H^=νa^†a^+δ2σz+λE0(σ+eiη(a^+a^†)+σ-e-iη(a^+a^†)), (4)

donde δ=ω2,1-ω es la desintonía entre la frecuencia del láser y la frecuencia de transisición del ión, y además hemos considerado las definiciones,

a^=ν2x^+i2νp^x, a^†=ν2x^-i2νp^x, (5)

η=k1/2ν (6)

para poder expresar el argumento de cada función exponencial en términos de los operadores de creación y aniquilación del oscilador armónico.

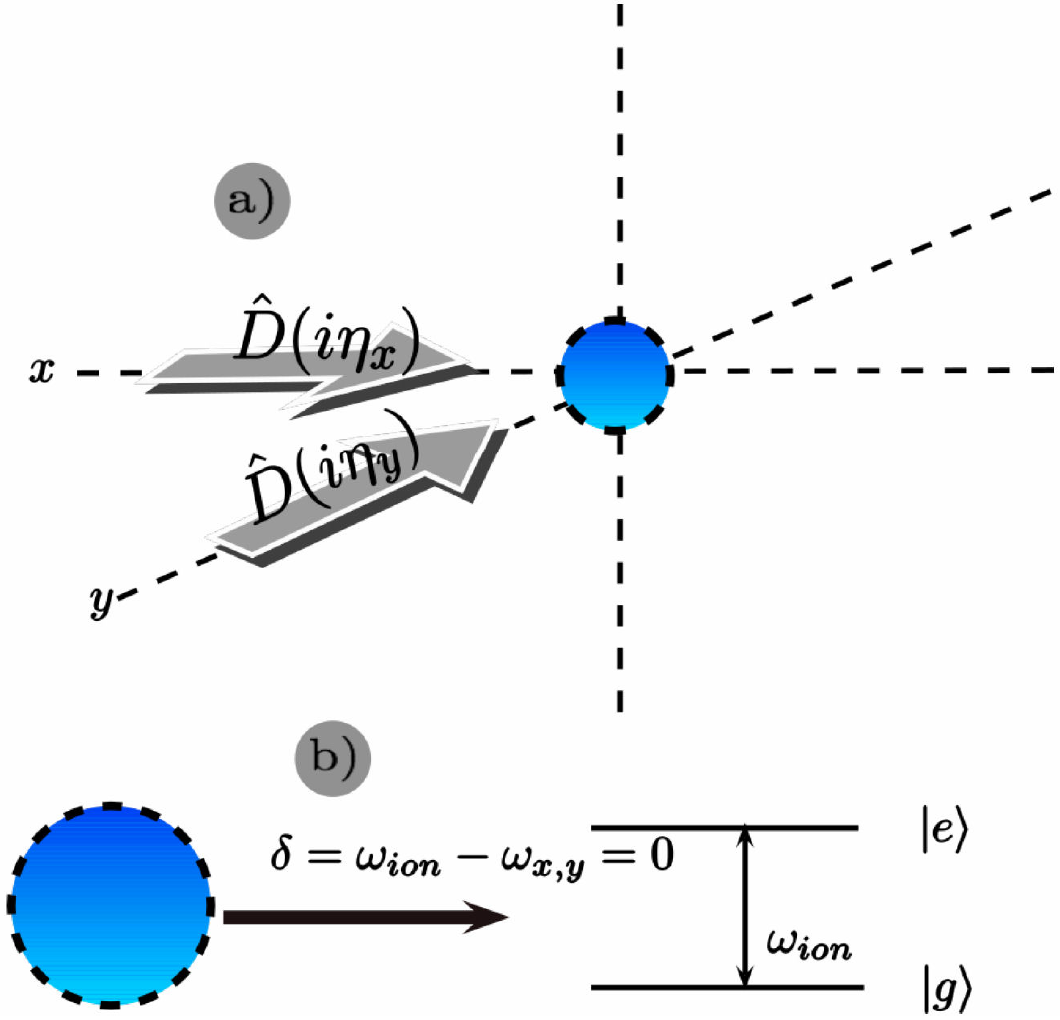
El hamiltoniano de un ión atrapado interactuando con un haz láser cerca de resonancia, teniendo en cuenta sólo dos niveles internos |g y |e, y un modo de oscilación (digamos orientado en dirección x) ha sido estudiado en ⁴^,¹⁸^,²⁷^,²⁸^,²⁹. En este artículo concentramos nuestra atención en hamiltonianos de este tipo, donde el ión atrapado interactúa con dos haces de luz ortogonales (orientados en direcciones x y y respectivamente). En la Fig. 1 presentamos un esquema donde el ión atrapado interactúa con dos haces ortogonales y estos dos haces láser ortogonales pueden ser interpretados como dos ondas planas ortogonales en direcciones x y y respectivamente, y las frecuencias de los dos haces ortogonales están sintonizadas a la frecuencia de transición del estado interno del ión.

Figura 1. Diferentes trampas existen hoy en día para poder atrapar iones, pero en nuestro caso estamos pensando en una trampa de Paul. En a) El ión se encuentra atrapado y está interactuando con dos haces láser de luz ortogonales en direcciones x y y respectivamente. b) La frecuencia de transición interna del ión coincide con la frecuencia conjunta de los dos haces ortogonales.

El modelo descrito por (4) indica un movimiento únicamente en una dirección (dirección x), por lo que podemos utilizar el mismo razonamiento y considerar una dirección ortogonal adicional para el movimiento del ión (dirección y) y una interacción con un haz láser en esa misma dirección. Esto puede ser representado por operadores que indican un modo adicional de movimiento, los cuales están definidos como sigue:

b^=ν2y^+i2νp^y y b^†=ν2y^-i2νp^y. (7)

Por lo tanto, el hamiltoniano que describe la interacción de un ión atrapado con dos haces ortogonales de luz siguiendo la Ec. (4) puede escribirse como

H^=ν(a^†a+b^†b)+Ω(σ^+D^(iηx)D^(iηy)+σ^-D^†(iηx)D^†(iηy)), (8)

donde D^(iηx)D^(iηy)=eiηx(a^†+a^)eiηy(b^†+b^) es el operador de desplazamiento representando a dos ondas planas ortogonales en dirección x y y respectivamente, σ+ y σ- las matrices de Pauli, v es la frecuencia inherente de la trampa, Ω es la frecuencia de Rabi del acoplamiento ión-láser, ηj con j={x,y} el parámetro de Lamb-Dicke respectivamente, y consideramos la desintonía del ión-láser δ=0. Reescribiendo explícitamente las matrices de Pauli el hamiltoniano (8) toma la forma

H^=ν(A^†A^+B^†B^)Ωeiη(A^†+A^)Ωe-iη(A^†+A^)ν(A^†A^+B^†B^), (9)

donde hemos definido a

ηx=ηcosθ, ηy=ηsinθ, η=ηx2+ηy2, (10)

y un par de nuevos operadores como:

A^=a^cosθ+b^sinθ (11)

=a^sinθ-b^cosθ. (12)

En lo que resta de este artículo haremos referencia a los hamiltonianos (8) o (9) como el hamiltoniano ión-láser.

La transformación unitaria que encuentran en la referencia ¹⁸ después de aplicarla a un hamiltoniano similar a (9) genera un nuevo hamiltoniano tipo Rabi ³⁰, tal transformación unitaria tiene una representación matricial de la siguiente forma,

T^=12D^†(iη/2)D^(iη/2)-D^†(iη/2)D^(iη/2), (13)

donde D^(iη/2)=eiη/2(A^†+A^) es el operador de desplazamiento. Utilizando esta idea, podemos aplicar la transformación unitaria definida por (13) al hamiltoniano ión-láser (9), pero antes debemos recordar que los nuevos operadores A^ y B^ son generadores de un álgebra Heisenberg-Weyl respectivamente, y además aprovechar que los operadores A^ y B^ conmutan. Bajo estas consideraciones podemos definir a H^=T^H^T^†, que al aplicar el lema de Hadamard sobre los operadores A^†A^ y B^†B^ respectivamente, se llega fácilmente a la siguiente expresión:

H^=νN^+Ω+νη24iην2(A^-A^†)iην2(A^-A^†)νN^-Ω+νη24, (14)

donde N^=A^†A^+B^†B^. Regresando a la notación implícita de matrices de 2×2, la última ecuación puede escribirse como:

H^=νN^+Ωσ^z+iην2(σ^++σ^-)(A^-A^†)+νη24. (15)

donde el último término (cuadrático) solamente agrega un corrimiento en los niveles de energía y se cancela cuando se calculan valores promedio.

Por otro lado el hamiltoniano que modela a un átomo de dos niveles interactuando con un campo cuantizado, es el hamiltoniano de Rabi, dado por la siguiente expresión:

HR=ωn^+ω02σ^z+iλ(σ^++σ^-)(a^-a^†). (16)

El modelo de Rabi descrito por la la ecuación (16) a primera vista se encuentra desligado del comportamiento de un ión atrapado interactuando con ondas planas definido por la ecuación (8), pero al utilizar la transformación unitaria (13) podemos llegar a un hamiltoniano tipo Rabi (15), donde evidentemente por un lado tenemos el hamiltoniano de Rabi y por el otro lado tenemos un hamiltoniano que modela situaciones física distintas, pero que podemos considerar como equivalente. Haciendo una comparación de estos dos hamiltonianos entendemos que el último término del hamiltoniano H^ corresponde a una energía constante, ν se convierte en la frecuencia de la cavidad ω, 2Ω es la frecuencia de transición atómica ω0 y η la razón entre la frecuencia de Rabi 2λ y la frecuencia de la cavidad ω.

Es importante decir que la transformación unitaria T^ mapea propiedades de un modelo al otro, i.e., los eigenestados de la interacción ión-láser y por supuesto la correspondencia uno a uno que se establece mediante una transformación unitaria como la vista anteriormente, traslada las propiedades de H^ a H^. Naturalmente, si |ψ es un eigenestado de H^ entonces T^|ψ será un eigenestado de H^. En este sentido es importante mencionar que, a pesar de que H^ y H^ describen sistemas que consisten de un átomo de dos niveles interactuando con dos modos bosónicos, no debemos identificar cada uno de estos subsistemas con su contraparte después de que la transformación haya sido aplicada. Esto es debido a que T^ además de ser una transformación unitaria también es una transformación de entrelazamiento, es decir: antes de aplicar la transformación unitaria los estados de movimiento internos del ión pueden ser estados separables, pero al aplicar la transformación unitaria estos estados son mapeados a estados entrelazados de un átomo de dos niveles en una cavidad y este sistema corresponde a una cavidad QED.

3. Eigenestados exactos

El tratado que haremos en la sección que comienza aquí, es la parte fundamental del trabajo realizado, ya que encontramos eigenestados exactos del hamiltoniano (8), es decir, estados que diagonalizan el hamiltoniano ión-láser. Ya en un trabajo realizado en ¹⁹, encuentran una familia de eigenestados pero cuando el ión atrapado únicamente interactúa con un haz láser (una onda plana), y aquí encontraremos una familia que la incluye. Un tratado numérico fijando los parámetros que gobiernan la interacción ión-láser es necesario para poder encontrar a toda la familia de eigenestados exactos. Y finalmente explicaremos como la elección de un valor en particular de alguno de los dos parámetros de Lamb-Dicke (ηx o ηy), hará que parte de la degeneración en los eigenestados exactos disminuya.

3.1. Familia de eigenestados de un ión atrapado interactuando con dos haces de luz

Los eigenestados y los eigenvalores de cualquier hamiltoniano juegan un papel fundamental para establecer la evolución del sistema, sin embargo, encontrarlos no es una tarea fácil en la mayoría de los casos y el hamiltoniano de la interacción ión-láser no es la excepción.

El hamiltoniano ión-láser puede escribirse como la suma de dos hamiltonianos donde H^A,H^B=0, así que

H^=H^A+H^B, (17)

donde

H^A=νA^†A^Ωeiη(A^†+A^)Ωe-iη(A^†+A^)νA^†A^, (18)

H^B=νB^†B^00νB^†B^. (19)

Para poder encontrar uno o más eigenestados exactos del hamiltoniano ión-láser es necesario imponer una serie de condiciones para que ésto se pueda cumplir. En ¹⁹ una familia de eigenestados es encontrada para un hamiltoniano similar al hamiltoniano H^A, por lo que la idea fundamental es la siguiente: expresar los operadores bosónicos involucrados en el hamiltoniano (8 o 9), de tal manera que, al expresar estos operadores, el hamiltoniano resultante sea un hamiltoniano ya conocido, que es el caso del hamiltoniano H^A. Aquí utilizaremos esta idea para poder encontrar uno o más eigenestados del hamiltoniano ión-láser. Los eigenestados del hamiltoniano H^B son inmediatos ya que es una matriz diagonal, por lo que siguiendo la idea de Moya-Cessa y colaboradores proponemos una familia de eigenestados de la forma:

|ψ=|Γn, me|e+|Γn, mg |g, (20)

donde hemos definido a

|Γn,me=Ων∑k=0n+1Ck |kA|mB, (21)

|Γn, mg=∑k=0ndk|-iη, kA |mB, (22)

con |kA y |mB estados de Fock (número) y también donde los estados |-iη, kA= D^†iη |kA, son reconocidos como estados de Fock desplazados ³¹. Es importante mencionar, que, para cada valor de n y m encontraremos un integrante de la familia de eigenestados exactos del hamiltoniano ión-láser.

Para que la relación (20) pueda considerarse como eigenestado del hamiltoniano ión-láser, debemos de exigir que

H^|ψ=(EnA+EmB)|ψ. (23)

Dicha exigencia se traslada a los coeficientes c _k y d _k , y por lo tanto, encontrar las relaciones que deben de cumplir cada uno de los coeficientes es de vital importancia para poder sostener dicha propuesta. El valor de EmB se encuentra inmediatamente ya que H^B es una matriz diagonal, mientras que para poder encontrar el valor de EnA, debemos aplicar el hamiltoniano ión-láser al eigenestado (20) e imponer (23), así que bajo estas consideraciones se puede encontrar fácilmente que

EnA+EmB=ν(n+m+1). (24)

Recordemos que definimos un par de nuevos operadores A^ y B^, que hicieron posible separar el hamiltoniano ión-láser en dos hamiltonianos ( H^A y H^B), sin embargo, después de proponer a la familia de eigenestados exactos (20), debemos de regresar a la base de Fock donde los operadores a^, a^†, b^ y b^† viven. La conexión entre una base y otra se encuentra en el inicio de las bases de Fock correspondientes, donde

|0A |0B = |0a |0b (25)

Para poder reproducir la familia de eigenestados ya reportada como caso particular de la familia que aquí encontramos, necesitamos hacer naturalmente m = 0 en (20), es decir, dejamos de iluminar el ión atrapado con una de las ondas planas y sólo nos quedamos con el vació. Pero también para poder encontrar una expresión matemática de este hecho, es necesario tomar en cuenta las definiciones de los operadores A^, B^ dadas por (11) y (12), para así poder regresar a los operadores iniciales a^ y b^, además de tomar en cuenta (25) y

(A^†)kk!(B^†)mm! |0A |0B = |kA |mB (26)

por lo que con m = 0, y todas estas consideraciones podemos pasar de las relaciones (21) y (22) a las relaciones,

donde ks es el coeficiente binomial. Y finalmente obtener la familia de eigenestados con m = 0 dada por

|ψ= |γn, 0e |e + |γn, 0g |g (29)

Sin embargo debemos recalcar que (29), unicamente será una familia de eigenestados del hamiltoniano ión-láser si los coeficientes y lo parámetros que gobiernan la interacción cumplen con las siguientes relaciones:

ck=dkn+1-k, 0≤k≤niην2Ω2n+1dn, k=n+1, (30)

además las condiciones en general que deben de cumplir los parámetros que gobiernan la interacción ión-láser son:

(εn-iη-iηεn-1iη2-iη2⋱⋱⋱ε1iηn-iηnε0)(d0d1d2⋮dn)=0, (31)

donde hemos definido

εn=Ω2ν2(n+1)+η2-(n+1). (32)

El determinante de la matriz tridiagonal que aparece en (31) proporciona el valor de alguno de los tres parámetros (η,Ω o v) donde cada integrante de la familia de eigenestados exactos pude ocurrir, con m = 0.

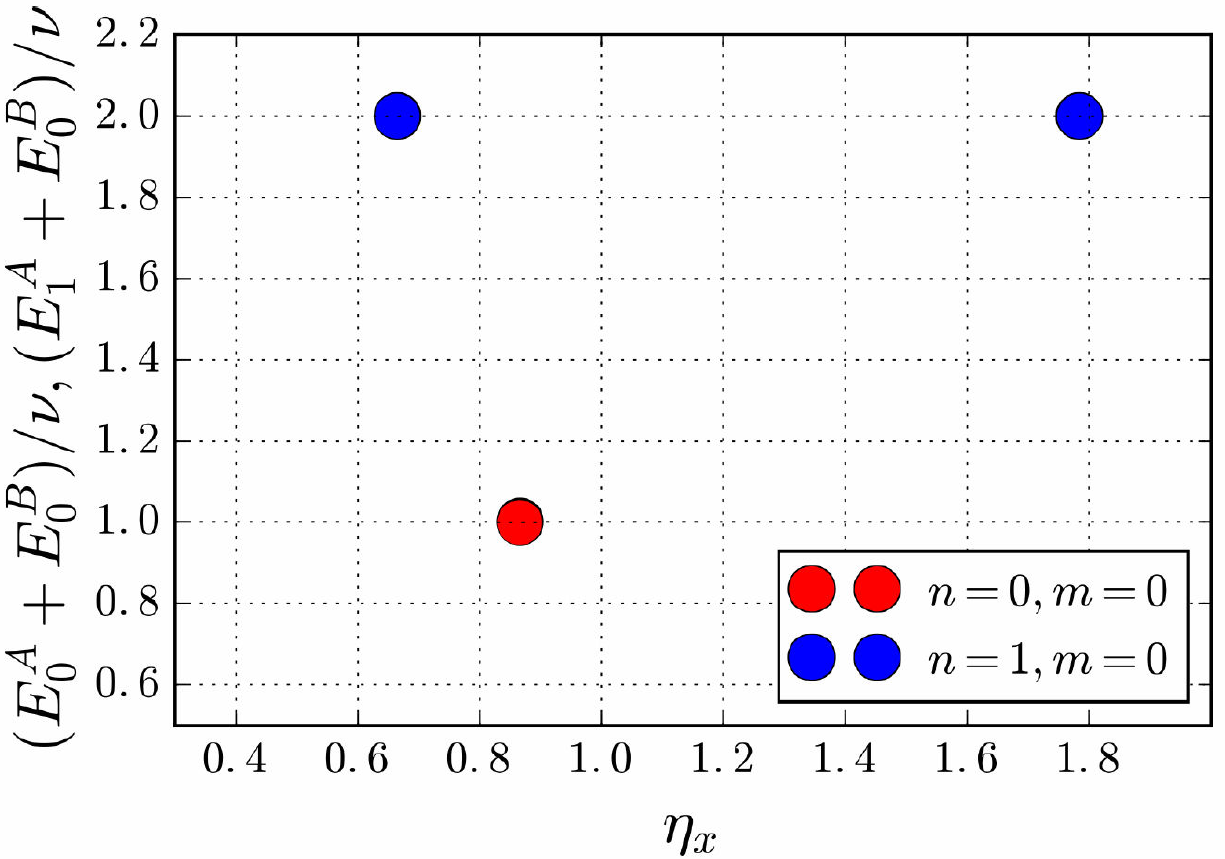
La condiciones que los coeficientes c _k y d _k deben de cumplir se encuentran de manera inmediata de la misma forma que las condiciones que se imponen sobre los parámetros que gobiernan la interacción ión-láser para m = 0. Sin embargo encontrar uno de los parámetros (η,Ω o v) fijando el resto se vuelve una tarea complicada y el grado de complejidad aumenta de la misma forma que aumentamos el valor de n, ya que el determinante de la matriz que aparece en (31) dará ecuaciones de ordenes cada vez grandes en η2. La solución analítica para el parámetro de Lamb-Dicke η donde ocurren los eigenestados exactos solamente puede encontrarse en un rango de 0≤n≤3, y esto hace que para valores cada vez mas grandes de n una solución numérica sea necesaria.

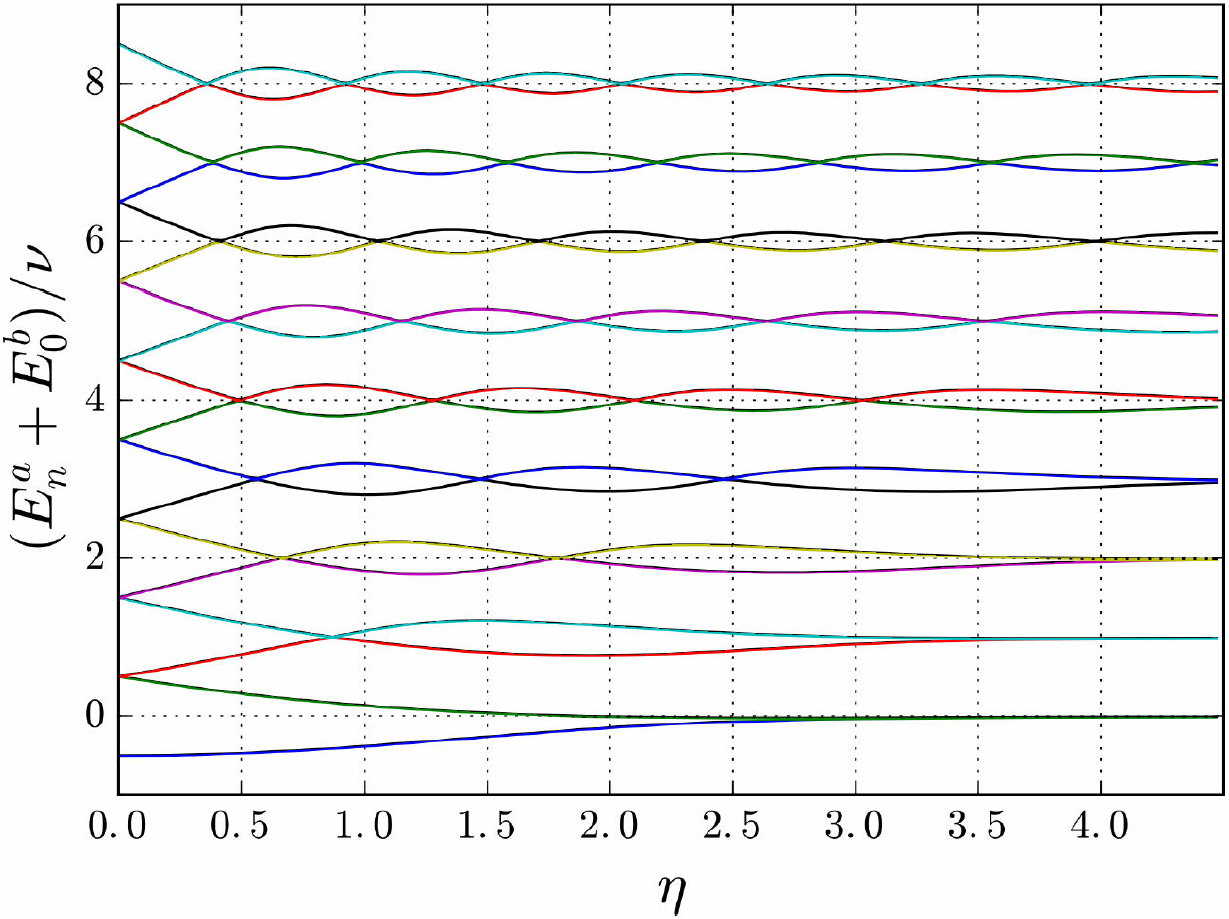
Encontrar numéricamente el valor del parámetro de Lamb-Dicke con Ω=ν/2 para cada uno de los eigenestados exactos se hace posible al utilizar Python y una paquetería llamada QuTip ³². En la Fig. 2 mostramos los primeros 8 niveles de energía (en unidades de 1/ν) en función del parámetro de Lamb-Dicke, donde podemos observar que la primer curva de color rojo (de abajo hacia arriba) parece juntarse con la siguiente curva que es de color cian, para después separarse y juntarse asintóticamente. Antes de juntarse asintóticamente cada curva en dicha gráfica, las curvas se juntan y se separan, esto indica la localización de cada uno de los integrantes de la familia de eigenestados exactos para m = 0 (para más detalles, ver apéndice).

Figura 2. Mostramos los primeros 8 niveles de energía (en unidades de ħ) de un ión atrapado interactuando con un haz láser como función del parámetro de Lamb-Dicke ƞ, donde Ω = v/2 y m = 0. El valor de E0b es igual a cero ya que m = 0 y el grado de degeneración es directamente proporcional al valor entero de n.

Hasta este punto nos hemos limitado al caso donde m = 0 y n toma cualquier valor, y hemos podido encontrar una familia de eigenestados como ya se sabía de ¹⁹, ahora estudiaremos el caso general, donde m≠0, es decir, el ión atrapado interactúa con dos ondas planas.

Para poder obtener una expresión matemática de la familia de eigenestados exactos para cualquier valor de m y n del hamiltoniano ión-láser, necesitamos regresar a los operadores a^ y b^ como ya lo hicimos para el caso de m = 0. Entonces tomando en cuenta (26) y (25) podemos pasar a las bases de Fock donde los operadores bosónicos iniciales viven, donde tenemos que hacer uso de una expansión binomial sobre los operadores A^ y B^ para llegar a la relación siguiente:

|kA|mB=∑j=0m∑j'=0kΛk,j'Θm,j×|k+m-j+j'a| j+j'b, (33)

donde los coeficientes Θm,j y Λk,j' están definidos por

Θm,j=(-1)jm!j!(m-j)!sinmθcotjθ, (34)

Λk,j'=cosk⁡θtanj'⁡θj'!(k-j')!×k!m+k-(j+j')!(j+j')!j!(m-j)!. (35)

Así que sustituyendo (33) en (21) y (22) respectivamente, obtenemos que

lo cual nos permite encontrar la familia de eigenestados exactos para un ión atrapado interactuando con dos haces de luz ortogonales (dos ondas planas), y que se puede escribir como:

|ψ= |γn, me |e + |γn, mg |g (38)

Es importante decir que la familia encontrada en ¹⁹ y descrita en esta sección por (29) es un subconjunto de la familia descrita por (38), es natural este resultado ya que, en el caso general tenemos un ión atrapado que interacciona con dos haces luz ortogonales, y al hacer m = 0, en realidad, estamos unicamente haciendo que el ión atrapado interactúe con un único haz de luz.

Las expresión (38) representa en general una familia de eigenestados exactos del hamiltoniano ión-láser, cada integrante de la familia puede ser encontrado tomando valores particulares de n y m respectivamente. Una familia ya reportada es encontrada tomando el valor de m = 0. En el caso general, también se necesita un tratamiento numérico para poder encontrar el valor del parámetro de Lamb-Dicke, donde cada integrante de la familia puede ser encontrado. Las condiciones que se imponen sobre los parámetros que gobiernan la interacción ión-láser se vuelven más complejas de encontrar y pasa lo mismo al intentar hallar expresiones generales que deben seguir los coeficientes de la familia de eigenestados exactos.

Por último, como hemos dicho necesitamos un tratamiento numérico para poder hallar el valor del parámetro de Lamb-Dicke donde cada integrante de la familia de eigenestados exactos puede ocurrir. En el caso, donde m y n pueden tomar cualquier valor entero positivo, es necesario fijar un parámetro extra, que sería ηx o ηy, y en nuestro caso fijamos ηy, y así poder encontrar los valores del parámetro de Lamb-Dicke (ηx), donde cada uno de los eigenestados exactos puede ser encontrado (pasaría lo mismo si ahora fijamos ηx y encontramos los valores de ηy donde los otros integrantes de la familia pueden encontrarse).

En la Fig. 3 fijamos ηy y además tomamos los dos primeros valores de m. Es claro que el grado de degeneración aumenta, mientras que en el caso m = 0, la degeneración aumenta de la misma forma que n aumenta, en este caso, la degeneración es directamente proporcional al valor de n + m + 1, i.e., si vemos en la la sub-Fig. 3a), la degeneración aumenta a partir del nivel de energía 2. Esto quiere decir que existen eigenestados exactos que se están agregando conforme el valor de m aumenta, en la familia ya encontrada (en este artículo la llamamos, una sub-familia de la que nosotros encontramos) también existe un grado de degeneración que es directamente proporcional al nivel de energía, pero en este caso, la aparición de un nuevo eigenestado exacto para cada valor de m en los diferentes niveles de energía aumenta el grado de degeneración. Es decir, cuando m≠0 el ión atrapado ahora puede oscilar en dos direcciones, por lo tanto, un grado de libertad es agregado y esto comienza a generar un aumento en el grado de degeneración.

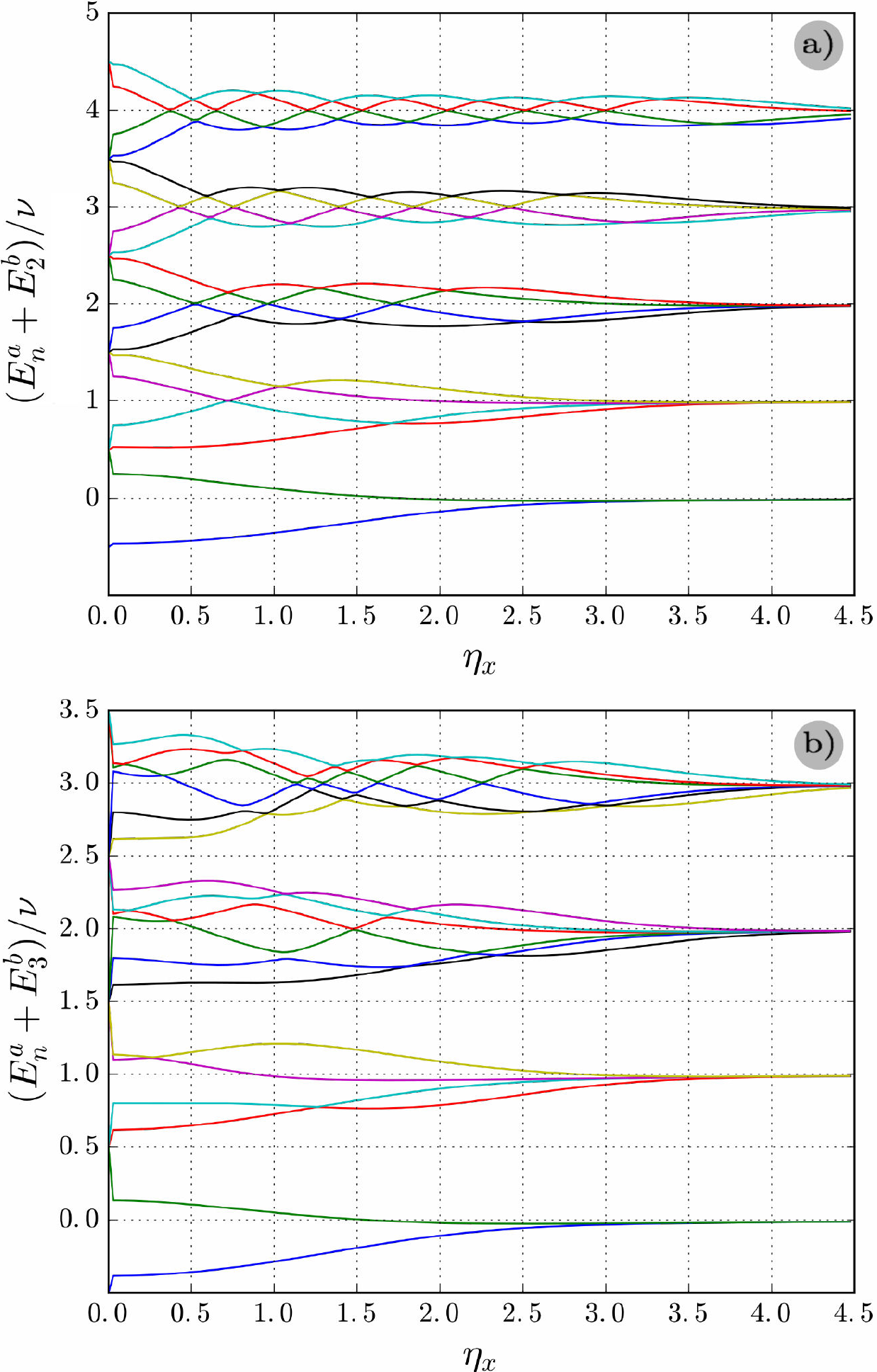
Figura 3. a) Niveles de energía en función del parámetro de Lamb-Dicke fijando ƞ _y = 0.5 y m = 2. b) Rompimiento de la degeneración ya que ƞ _y = 1 y m = 3, pero además existe rompimiento de degeneración debido a la presencia de dos ondas planas caracterizadas por D^inx y D^iny.

Finalizamos diciendo que alguno de los eigenestados exactos del hamiltoniano ión-láser desaparecen. La condición que se rompe para que alguno de los eigenestados exactos desaparezca de cada nivel de energía, Fig. 3b), muestra como la elección del parámetro de Lamb-Dicke que hemos fijado hace que la condición impuesta sobre el otro de los dos parámetros de Lamb-Dicke no se cumpla. Como podemos notar de la Fig. 3b) el grado de degeneración disminuye, ya que las condiciones impuestas sobre el parámetro de Lamb-DIcke libre, hace que la degeneración pueda romperse en cierto grado, sin embargo, el rompimiento de degeneración no es total como lo muestra la figura (para más detalles, ver apéndice).

4. Estados entrelazados

El entrelazamiento cuántico desempeña un rol fundamental desde el comienzo de la mecánica cuántica y actualmente es un recurso clave en la información cuántica y computación cuántica ³³. Si dos sub-sistemas están entrelazados (enredados), el vector de estado del sistema completo no puede escribirse como el producto de dos vectores de estado de cada uno de los sub-sistemas. La generación de estados entrelazados por dos o más partículas, es fundamental para demostrar la no localidad cuántica ³⁴.

Los iones atrapados en diferentes trabajos como ¹⁰^,¹³^,³⁵ muestran la posibilidad de encontrar estados entrelazados en los estados propios un ión atrapado interactuando con haces láser. Inclusive en la Sec. 2 de el presente trabajo ya hemos hablado de estados entrelazados, donde, después de la transformación unitaria T^ el vector de estado evoluciona a estados entrelazados, donde a ciertos tiempos específicos podemos encontrar estados gato de Schrödinger y a otros tiempos prácticamente los dos sub-sistemas (el sistema de dos niveles y el campo) logran separarse ³⁶. Aquí mostramos como la parte excitada de la familia de eigenestados exactos que encontramos en la sección anterior es un estado entrelazado.

4.1. Eigenestados exactos como estados entrelazados

En la sección anterior hallamos eigenestados exactos que pertenecen a una familia de eigenestados exactos descrita por la Ec. (38). Como ya sabemos, para cada valor de n y m, cada integrante de la familia es encontrado y si tomamos la parte excitada de cada integrante, siguiendo la Ec. (36) para n = 0 y m = 0, entonces

|γ0, 0e=Ων|0a |0b+iνΩ(ηx|1a|0b+ηy|0a|1b), (39)

donde ηx=ηcosθ y ηy=ηsinθ. Es importante mencionar que la anterior relación no se puede escribir como el producto de dos vectores que representan a los dos sub-sistemas respectivamente, lo cual podrá notarse en una representación gráfica de la matriz de densidad de |γ0, 0e.

En la Fig. 4 mostramos la matriz de densidad, definida como:

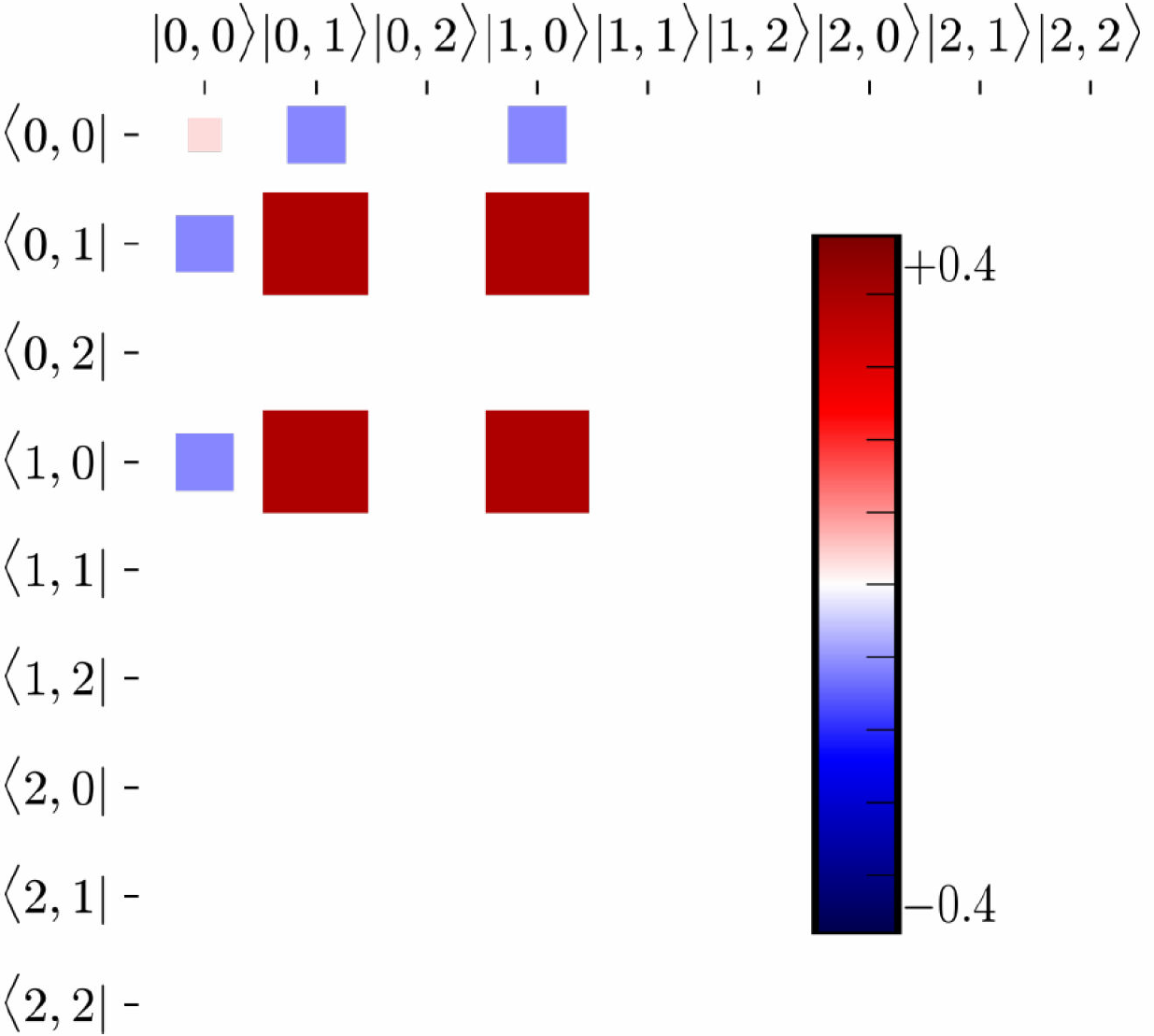
Figura 4. Matriz de densidad ρ^0,0e, con Ω = v/2y ƞ _x = ƞ _y = 34. Los estados |1, 0 = |1a |0b y |0, 1 = |0a |1b tiene una mayor probabilidad de ocurrencia, sin embargo las demás combinaciones restantes pueden también ocurrir y el estado se encuentra entrelazado.

ρ^0,0e=1G0,0|γ0, 0e γ0, 0e|, (40)

Donde G _0,0 es una constante de normalización. En dicha figura mostramos el valor de cada uno de los elementos de la matriz de densidad ya que cuando el estado es completamente separable, la simetría en la figura desaparecería y tendríamos un estado no entrelazado. Existen diferentes medidas de entrelazamiento, sin embargo, no estamos interesado en este momento en calcular grados de entrelazamiento y únicamente nos quedamos con una representación de los elementos de una matriz de densidad que representa un estado entrelazado, en la cual es notorio que el estado no puede escribirse como el producto de dos vectores. Así que la componente excitada del primer eigenestado exacto de la familia es un estado entrelazado.

Como último ejemplo representativo de un estado entrelazado tomaremos el segundo integrante de la familia de eigenestados exactos que obedece la expresión (38) que al tomar la parte excitada definida por (36), con los valores de n = 0 y m = 1 tiene la forma,

|γ0, 1e=Ων(sin⁡θ |1a |0b-cos⁡θ |0a |1b)+iνΩη(sin2⁡θ-cos2⁡θ |1a |1b+2cos⁡θsin⁡θ|2a |0b-|0a|2b). (41)

Tanto la relación (39) y (41) deben tomar los valores del del parámetro de Lamb-Dicke correspondiente que cumplen con las condiciones para que el eigenestado pueda existir (puede haber rompimiento de degeneración para algunos valores de uno de los dos parámetros de Lamb-Dicke y el eigenestado no existe), por lo tanto, en ambas expresiones hacemos uso de los valores de ηx y ηy, que cumplen con las condiciones necesarios (ver apéndice).

Podemos nuevamente construir la matriz de densidad de la parte excitada que corresponde a los valores de n = 0 y m = 1, lo cual de (41) fácilmente obtenemos que

ρ^0,1e=1G0,1 |γ0, 1e γ0, 1e|, (42)

Donde G _0,1 es una constante de normalización.

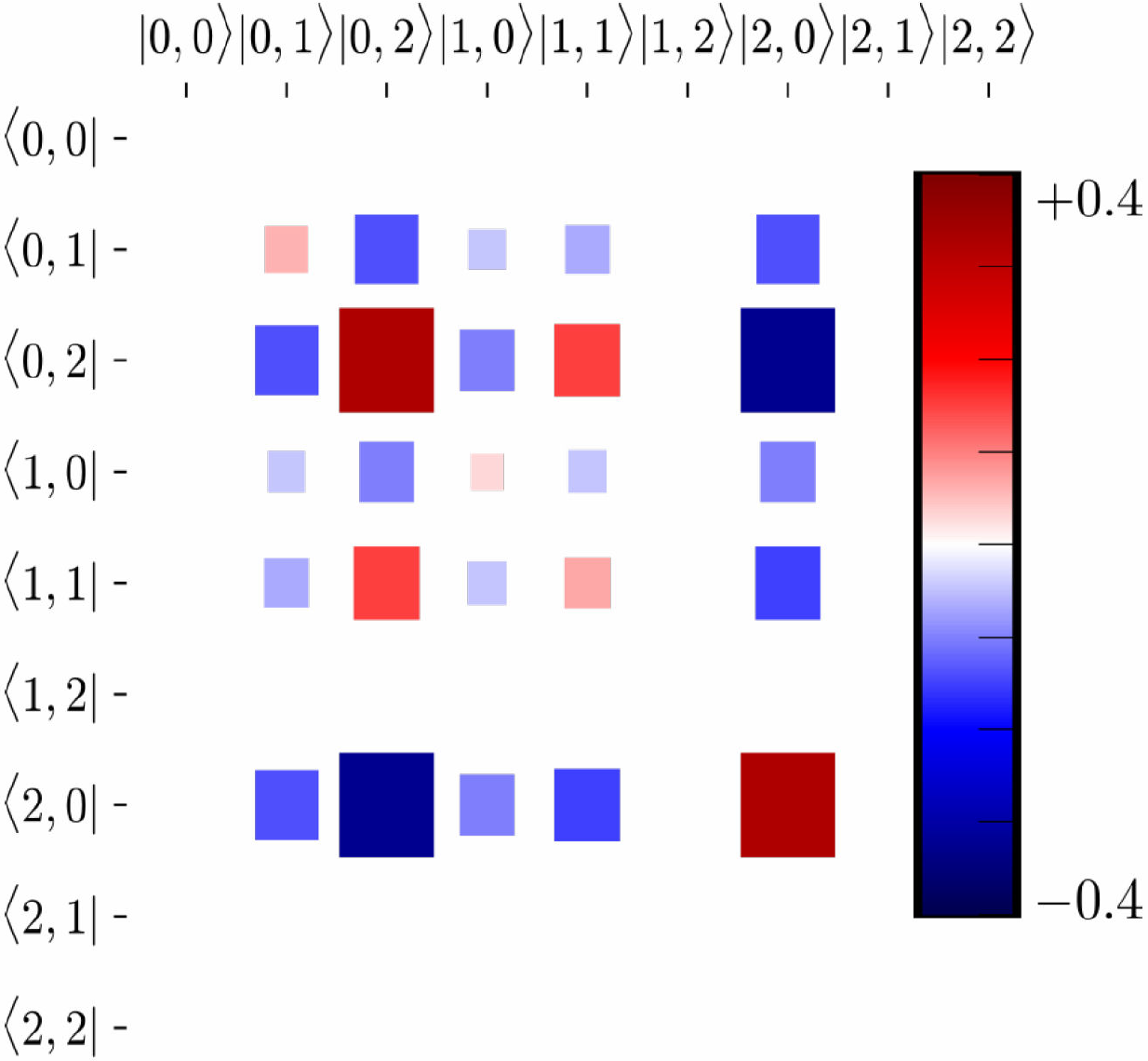
En la Fig. 5 mostramos la matriz de densidad ρ^0,1e, donde nuevamente cada elemento de la matriz es mostrado, y como cada elemento es proyectado en diferentes vectores ( j',k'ρ^0,1ej, k), con j,j',k,k'=0,1,2), y como es de esperarse encontramos un estado entrelazado ya que si fuera un estado separable, todas las posibles combinaciones para proyectar la matriz de densidad en un elemento que no sea propio de la misma, sería cero. Ésta representación gráfica de la matriz de densidad ayuda a entender la cantidad de información que existe en cada termino del estado entrelazado, sin embargo, la fragilidad en el grado de coherencia hace que por ejemplo la construcción de ordenadores cuánticos se encuentre en un horizonte lejano ¹⁰.

Figura 5. Matriz de densidad ρ^0,1e, con Ω = v/2, ƞ ≈ 0.7 y θ = π/5. Los estados |2, 0 = |2a |0b y |0, 2 = |0a |2b tiene una mayor probabilidad de ocurrencia, sin embargo las demás combinaciones restantes pueden ser no-nulas y el estado se encuentra entrelazado, pero en este caso existe un mayor número de combinaciones.

En general cada integrante de la familia de eigenestados hace posible un estado entrelazado, es decir, tomando la parte excitada de cada uno de los eigenestados exactos podemos encontrar estados entrelazados con las debidas condiciones sobre los coeficientes y los parámetros que gobiernan la interacción ión-láser.

5. Conclusiones

Demostramos que es posible mapear el hamiltoniano que describe la interacción de un ión atrapado y dos haces ortogonales, a un espacio donde vive un hamiltoniano tipo Rabi utilizando una transformación unitaria por lo que es posible modelar un hamiltoniano de Rabi cuántico para un átomo de dos niveles y dos campos electromagnéticos cuantizados. Por otro lado, re-encontramos una familia de eigenestados exactos y ésta familia de eigenestados exactos resulta ser un subconjunto de la familia de eigenestados exactos aquí expuesta y, además, mostramos como las condiciones impuestas sobre los parámetros que gobiernan la interacción ión-láser pueden romper un cierto grado de degeneración. Finalmente, los eigenestados exactos del hamiltoniano ión-láser generan estados entrelazados ya que al tomar la parte excitada de cada uno de ellos, podemos encontrar y reconocer estados entrelazados en cada eigenestado exacto de la familia.

Agradecimientos

I. Ramos-Prieto agradece a A. Zuñiga-Segundo y A. Urzúa-Pineda, por sus valiosos comentarios-sugerencias y a CONACYT por la beca doctoral otorgada.

Referencias

1. S. Wallentowitz and W. Vogel, Phys. Rev. A 58 (1998) 679. [ Links ]

2. R. Gerritsma et al., Nature 463 (2010) 68. [ Links ]

3. R. Gerritsma et al., Phys. Rev. Lett. 106 (2011). [ Links ]

4. R.L. de Matos Filho and W. Vogel, Phys. Rev. A 58 (1998) 661. [ Links ]

5. R.P. Feynman, International Journal of Theoretical Physics 21 (1982) 467. [ Links ]

6. P.W. Shor, In Proceedings of the 35 th Annual Symposium on Foundations of Computer Science 94 (1994) 124. [ Links ]

7. L.K. Grover, Phys. Rev. Lett. 79 (1997) 325. [ Links ]

8. Ch.H. Bennett and G. Brassard. Springer Berlin Heidelberg, Berlin, Heidelberg (1985) 475. [ Links ]

9. A. Einstein, B. Podolsky, and N. Rosen. Phys. Rev., 47 (1935) 777. [ Links ]

10. J.I. Cirac and P. Zoller, Phys. Rev. Lett. 74 (1995) 4091. [ Links ]

11. C.D.B. Bentley, R.L. Taylor, A.R.R. Carvalho, and J.J. Hope, Phys. Rev. A 93 (2016) 042342. [ Links ]

12. C.D.B. Bentley , A.R.R. Carvalho , and J.J. Hope , New Journal of Physics, 17 (2015) 103025. [ Links ]

13. B. E. King et al., Phys. Rev. Lett. 81 (1998) 1525. [ Links ]

14. C.E. Wieman, D.E. Pritchard, and D.J. Wineland. Rev. Mod. Phys. 71 (1999) S253. [ Links ]

15. R.H. Dicke, Phys. Rev. 89 (1953) 472. [ Links ]

16. W.E. Lamb, Phys. Rev. 51 (1937) 187. [ Links ]

17. V. Penna and F.A. Raffa, Journal of Physics B: Atomic, Molecular and Optical Physics 47 (2014) 075501. [ Links ]

18. H. Moya-Cessa, A. Vidiella-Barranco, J.A. Roversi, D.S. Freitas, and S.M. Dutra, Phys. Rev. A 59 (1999) 2518. [ Links ]

19. H. Moya-Cessa , D. Jonathan, and P.L. Knight, Journal of Modern Optics 50 (2003) (2003) 265. [ Links ]

20. D. Braak, Phys. Rev. Lett. 107 (2011) 100401. [ Links ]

21. J. Casanova, R. Puebla and M.B. Plenio, arXiv:1608.07434. [ Links ]

22. H. M. Moya-Cessa, Sci. Rep. 5 (2016) 17339. [ Links ]

23. K. H. Kingdon, Phys. Rev. 21 (1923) 408. [ Links ]

24. F.M. Penning, Physica 4 (1937) 71. [ Links ]

25. Wolfgang Paul. Rev. Mod. Phys. 62 (1990) 53. [ Links ]

26. J.M. Vargas-Martínez, E.A. Martí-Panameño, and H. Moya-Cessa , Revista Mexicana de Física E 55 (2009) 176. [ Links ]

27. D.J. Wineland , J.J. Bollinger, W.M. Itano, F.L. Moore, and D.J. Heinzen, Phys. Rev. A 46 (1992) R6797. [ Links ]

28. H. Moya-Cessa et al., Physics Reports 513 (2012) 229. [ Links ]

29. H. Moya-Cessa and P. Tombesi, Phys. Rev. A 61 (2000) 025401. [ Links ]

30. E.T. Jaynes and F.W. Cummings, Proceedings of the IEEE 51 (1963) 89. [ Links ]

31. H. Moya-Cessa , Journal of Modern Optics 42 (1995) 1741. [ Links ]

32. J.R. Johansson, P.D. Nation, and F. Nori, Computer Physics Communications 184 (2013) 1234. [ Links ]

33. M.A. Nielsen and I.L. Chuang, Quantum computation and quantum information. Cambridge university press, 2010. [ Links ]

34. J.S. Bellt, Physics (Long Island City, N.Y.) 1 (1964) 195. [ Links ]

35. R. Blatt and D. Wineland. Nature 453 (2008) 1008. [ Links ]

36. V. Bužek, H. Moya-Cessa , P.L. Knight , and S.J.D. Phoenix, Phys. Rev. A 45 (1992) 8190. [ Links ]

Apéndice

Como ya lo hemos dicho, para cada valor particular de n y m obtenemos un integrante de la familia de eigenestados del hamiltoniano ión-láser. Si n = 0 y m = 0, entonces de la Ec.(20) tenemos que

|ψ= |Γ0, 0e |e + |Γ0, 0g |g (A.1)

donde

|Γ0, 0e =Ωνc0|0A|0B+c1|1A|0B, (A.2)|Γ0, 0g =d0 |-iηA|0B. (A.3)

Para poder regresar a la base de Fock inicial, debemos tomar en cuenta las relaciones (25) y (26), además de las definiciones (11) y (12), y así poder pasar de las anteriores relaciones a las siguientes:

|γ0, 0e=Ων(c0|0a|0b+c1cos⁡θ|1a|0b+sin⁡θ|0a|0b),|γ0, 0g=d0 |-iηxa |-iηxb, (A.4) (A.5)

por lo tanto (A.1) se escribe ahora como:

|ψ= |γ0, 0e |e + |γ0, 0g |g (A.6)

El valor de la eigenenergía es

E0a+E0b=ν. (A.7)

pero la Ec. (A.6) representará un eigenestado exacto del hamiltoniano ión-láser, sí los coeficientes c _k y d _k , cumplen con las siguientes condiciones:

c0=d0=1,c1=iηx2+ηy2Ω2ν2, (A.8)

sin embargo también existe una condición sobre los parámetros que gobiernan la interacción ión-láser, la cual es

Ω2ν2+ηx2+ηy2-1=0. (A.9)

Es importante decir que si fijamos ηy=1 y tomando Ω=ν/2 el valor de ηx es complejo, por lo que el eigenestado exacto para estos valores no existe, y así para diferentes valores de n y m, como lo muestra la sub-Fig. 3b) se rompe parte de la degeneración.

Ahora para n = 1 y m = 1 siguiendo el mismo procedimiento anterior, tenemos de la relación (20) que

|ψ= |Γ1, 0g |g + |Γ1, 0e |e (A.10)

y de la relación (21) se tiene que

|Γ1, 0e=Ων(c0|0A|0B+c1|1A|0B+c2|2A|0B) (A.11)

mientras que de la relación (22) tenemos que

|Γ1, 0g= d0 |-iηA |0B +d1 |-iη, 1A |0B (A.12)

que al utilizar las relaciones (25) y (26), el eigenestado exacto es

|ψ= |γ1, 0e |e + |γ1, 0g |g (A.13)

con

|γ1, 0e=Ων(c0|0a|0b+c1cos⁡θ|1a|0b+sin⁡θ|0a|1b+c222cos2⁡θ|2a|0b+2cos⁡θsin⁡θ|1a|1b+2sin2⁡θ|0a|2b), (A.14)

pero ahora los coeficientes deben cumplir con

c0=d02,c1=d1, yc2=iηx2+η2ν2Ω22d1, (A.16)

mientras que

E1a+E0b=2ν. (A.17)

Sin embargo en este caso, al aplicar el hamiltoniano ión-láser al estado (A.13)) e imponer que éste último pueda considerarse como un eigenestado del hamiltoniano ión-láser, ésta operación generará un sistema de dos ecuaciones donde aparecen los parámetros que gobiernan la interacción y los coeficientes d ₀ y d ₁, por lo que es posible expresar tal sistema de ecuaciones en forma matricial. En este caso ésta matriz tiene la siguiente forma:

(Ω2ν2+ηx2+ηy2-2i(ηx2+ηy2)-i(ηx2+ηy2)Ω2ν2+ηx2+ηy2-1)×(d0d1)=(00). (A.18)

Es importante decir que, las condiciones que se imponen sobre los parámetros que gobiernan la interacción ión-láser son de suma importancia para poder encontrar el valor de alguno de los parámetros fijando el resto, en estos dos primeros casos, las Ecs. (A.9) y (A.18) proporcionan el valor o los valores del parámetro de Lamb-Dicke donde el primer y segundo eigenestado puede ocurrir. Por ejemplo, si deseamos establecer una representación gráfica de estos dos primeros casos donde n = 0, 1 y m = 0, debemos fijar los parámetros que aparecen en las diferentes condiciones y dejar libre alguno. Si tomamos Ω=ν/2 y como ηx2+ηy2=η2 en (A.9), entonces, el valor del parámetro de Lamb-Dicke donde ocurre el primer eigenestado exacto (A.6) del hamiltoniano ión-láser es

η=34, (A.19)

con (Ea0+Eb0)/ν=1. Mientras que el valor donde ocurre el segundo eigenestado exacto (A.13)) puede encontrarse calculando el determinante de la matriz de 2×2 que aparece en (A.18), y así obtener que

η=2916±48116. (A.20)

Pero en este caso, existen dos valores del parámetro de Lamb-Dicke donde el eigenestado exacto puede encontrarse, ya que, el determinante de la matriz genera un ecuación de segundo grado en η2, y éste, tiene la misma eigenenergía, es decir, tiene un grado de degeneración 2.

En la Fig. 6 mostramos estos dos valores del parámetro de Lamb-Dicke donde se encuentra los eigenestados exactos del hamiltoniano ión-láser. El primero donde n = 0 y m = 0, proporciona la ubicación donde el eigenestado exacto (A.6) del hamiltoniano ión-láser ocurre, mientras que el caso donde n = 1 y m = 0 muestra dos puntos donde el eigenestado exacto (A.13) se encuentra y existe degeneración, ya que el determinante de la matriz 2×2 que aparece en (A.18) da una ecuación de segundo grado en η2.

Figura 6. Cuando n = 0, m = 0 y Ω = v/2 el valor de (Ena+ Emb)/v= 1, mientras que para n = 1 y m = 0 el valor de (Ena+ Emb)/v= 2 con Ω = v/2. El punto rojo muestra el valor del parámetro de Lamb-Dicke donde ocurre el primer eigenestado exacto y los puntos azules muestran los dos valores donde ocurre el siguiente eigenestado exacto del hamiltoniano ión-láser.

La matriz (31) es una generalización de la matriz (A.18) para cada valor n y m = 0, y mientras estemos evaluando la Ec. (38) para estos valores encontraremos matrices tridiagonales de dimensión n×n, y por lo tanto, debemos calcular determinantes de la misma dimensión, pero esto hará que obtengamos ecuaciones de orden superiores en η y una solución numérica sea necesaria. Para el caso donde m comienza a tomar valores diferentes de 0, hallar una matriz de condiciones se vuelve una tarea aún más difícil de realizar.

Recibido: 26 de Agosto de 2016; Aprobado: 26 de Enero de 2017

^*e-mail: iran@inaoep.mx

^**e-mail: hmmc@inaoep.mx

Este es un artículo publicado en acceso abierto bajo una licencia Creative Commons