PACS: 34.80.Bm
1. Introduction
The collision between a charged particle and a gas atom may cause a number of different effects. If incident charged particle losses some kinetic energy in exciting internal motion in the atom, the collision is said to be inelastic. According to the situation of internal motion excitation, the inelastic may be further classified. The knowledge of good estimate of cross sections will play very significant role in the field of astrophysics, plasma physics and upper atmospheric physics 1. In an recent work Kim 2 proposed a method called BE f-scaling to calculate integral cross sections (ICS) of neutral atoms. This work 2 was based on classical collision theory as the first Born approximation (FBA). The BE f-scaling provided not only a simple way to calculate excitation cross sections of many atoms, but also to accurately estimate the excitation-autoionisation contributions in many open-shell atoms 2. The simply BE f-scaling approximation is applicable for excitations processes, and use atomic properties as, energy of incident particle (E o ), ionization energy (B), excitation energy (E), and the f dipole value that can be obtained, in principle, from accurate wave functions (free of adjustable parameters)2. The BE f-scaling proposed by Kim 2 also combine a simpler version, the called C-scaling and this version reproduces the experimental data better than BEf-scaling for some targets 2. Kim 2 obtain a compact, analytic expression for the C-scaling and has shown that the method in principle cannot be used to predict unknown cross sections, because the C-scaling is used to quantify the degree of disagreement between the BEf-scaling and the measurements, i.e, is used to “fit the experimental data”. Theoretically, the most questionable aspect of the C-scaling lies in the use at low energies and we will see here that the method provides good results when polarization effects are available in closed form, i.e., the C-scaling can be treated as a independent method and more efficient that the BE f-scaling. In this sense, the present approach retains much of the utility of the original BE f-scaling and requires a relatively small amount of computing effort. The C-scaling can be more important at low energies and more accurate that the BE f-scaling for several atoms. Numerical calculations of He, Na, K, and Hg by electron impact using C-scaling demonstrate the applicability of the model and well suitable as a benchmark for our model.
This paper is organized as follows: in Sec. 2 we describe the scaling Born method with the corrections proposed and in Sec. 3 we show our results for the electronic excitation of He, Na, K, and Hg by electron impact. Finally, present our conclusions in Sec. 4.
2. Theory
The scaled plane wave Born cross sections is described in detail by Kim 2, so only the more important points are mentioned here.
The f-scaled Born cross section,
where E
o
is the incident electron energy,
where “B” is the binding energy of the electron being excited, and E is the excitation energy. The BE-scaling corrects the deficiency of the Born approximation at low E
o
, without losing its well-known validity at high E
o
. If an unscaled Born is obtained from poor quality wavefunctions while an accurate f value is known, the both f scaling and BE-scaling can be applied to obtain a BE f-scaling Born cross section,
The essence of the BE f-scaling is adding a constant to the “E o ” in the denominator of Eq. (2) and this can be interpreted as polarizability of the target. Although this type of scaling has been used in several studies, its success remains to be explained. We now test the BE f-scaling as proposed by Kim 2, in which B + E is replaced by a constant C as proposed (2),
where C= (B + E) 2 and the fact that is necessary to introduce C for better agreement with experimental data. This considerations 2 requires a better description of the method and this has not been carried out. A hint to the meaning of adding B + E to E may be found in FBA cross section for the elastic scattering from the Yukawa potential. The potential is a screened Coulomb potential
where r is the radial coordinate, Z is the atomic number, and
where k is the momentum of the incident electron in atomic units. After writing
which has the E in the denominator shifted by a constant with the dimension of energy. Although this analogy is not rigorous, the similarity between the Eq. (2) and Eq. (6) suggests that the constant “C” can be seen as the scaling factor to represent the correlation between the electron and the target (the combination B + E should not be taken literally as a rigid rule, but only as an indicator of the order of magnitude for the cross section). As observed by Kim 2 the Eq. (4) indicates that C may be related to the polarizability of the target and is sensitive to the treatment of the target. The C-scaling corrects the deficiencies of the Born approximation at low Eo energy without losing its well-known validity at high E
o
. The term 1/(E
o
+ C) was included with the argument that effective kinetic energy of the electron seen by the target is E
o
plus the energy of the bound electron. The constant C represent a approximation to the polarizability of the target and a “loose” connection between the constant C and the polarizability ?d of the target can be consistent with the called closure approximation used for the second Born approximations-SBA 3. As cited by Walters 3 the intermediate states of the target are used as a average energy “
where “
The second Born term must contain polarization effect, and may be identified with the FBA using the optical theorem,
where physical intuition suggests that “C” can be used as a factor associated the polarization of the target using Eq. (6) and also normalize the FBA. We may assume that C should have the form proposed by Eq. (6) and in order to investigate the range of applicability of the Eq. (6), we have applied the C-scaling to the same He, Na, K, and Hg targets tested by Kim 2 using the BE f-scaling.
3. Results and Discussion
We present the calculated integral cross sections (ICS) for He, Na, K, and Hg atoms by electron scattering and the cross sections are compared to other theories and experiments. For all targets we used the theoretical f, and B value deduced by Kim 2 and the wave functions for the excited electronic states were all generated with the improved virtual orbital (IVO) 4.
He Atom
The BEf-scaling and our C-scaling are compared in Fig. 1 for He atom (1s2p1P state). Selected experimental data 5,6, and close coupling approximation-CC7 also are shown. As noted, the C-scaling generally agree well with experimental data 5,6, and CC7 for He atom (1s2p1P state).
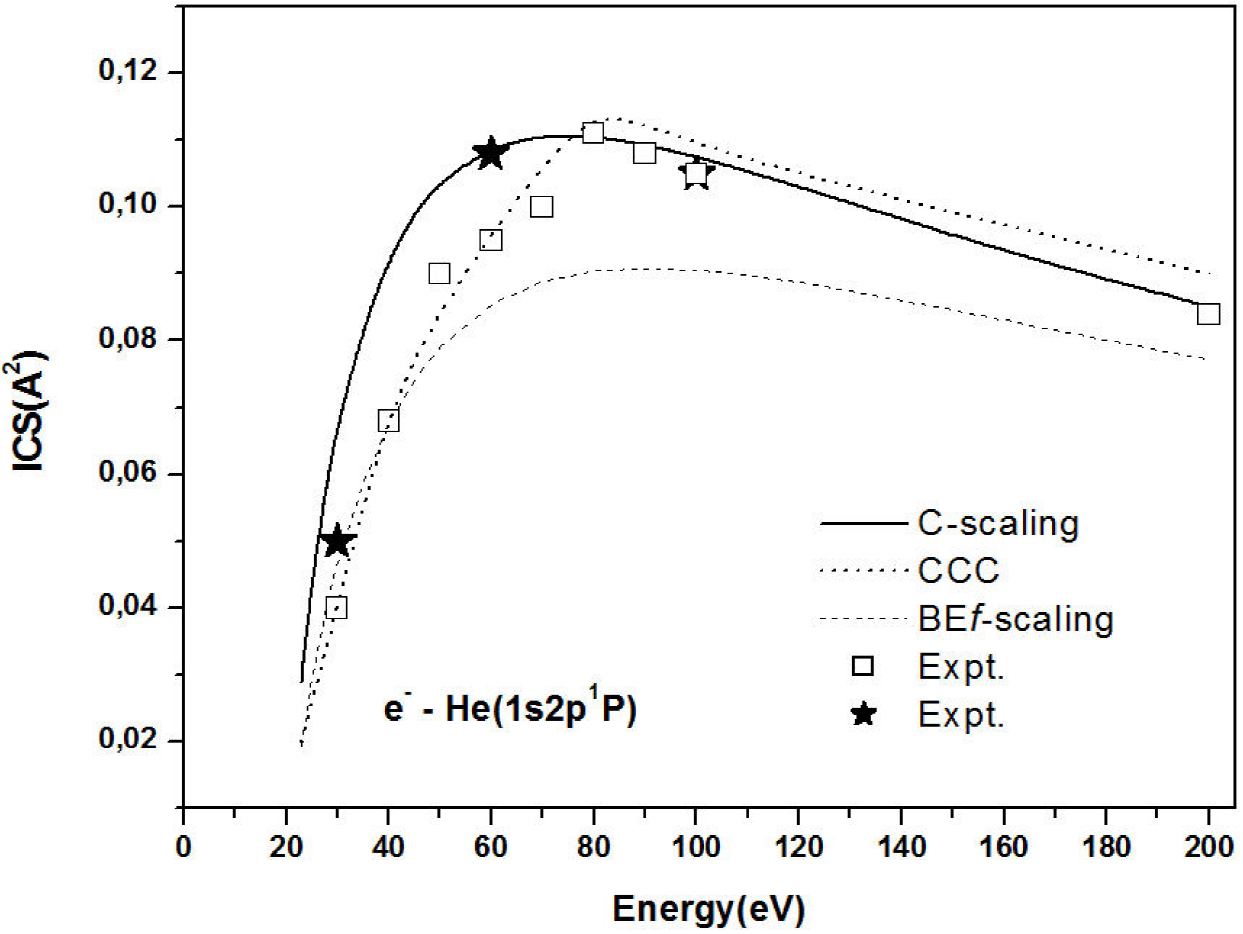
Figure 1. Integral cross sections (ICS) for electron impact excitation of the 1s2p1P states of He. Line solid, our C-scaling; dashed line, BEf-scaling of Kim 2; dott line, CC 7; square, experimental data 5, star black, experimental data 6.
Figure 2 show our C-scaling compared with experimental data 5,6 and again the BEf-scaling 2 for He atom(1s3p1P state). The comparison between our results and experimental data 5,6 is in general quite satisfactory.
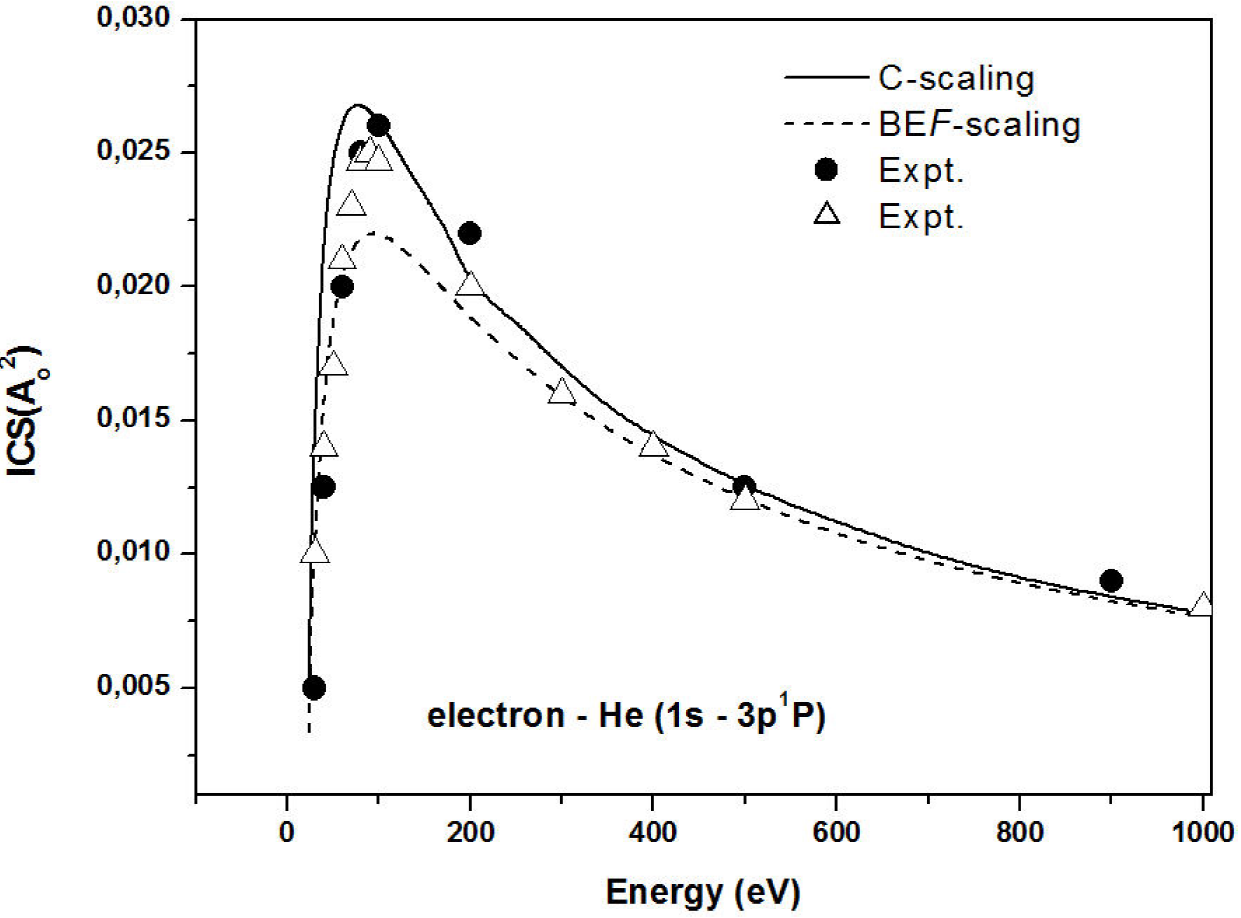
Figure 2. Integral cross sections for electron impact excitation of the 1s3p1P states of He. Line solid, our C-scaling; dashed line, BEf-scaling 2; black circle, experimental data 5, triangule, experimental data 6.
Figure 3 shows our C-scaling also compared with Bef-scaling 2, and experimental data 5 for He atom (1s4p state). As observed the C-scaling results are reasonably close to the experimental data 6. For the He atom the C-scaling clearly demonstrate great utility.
Na Atom
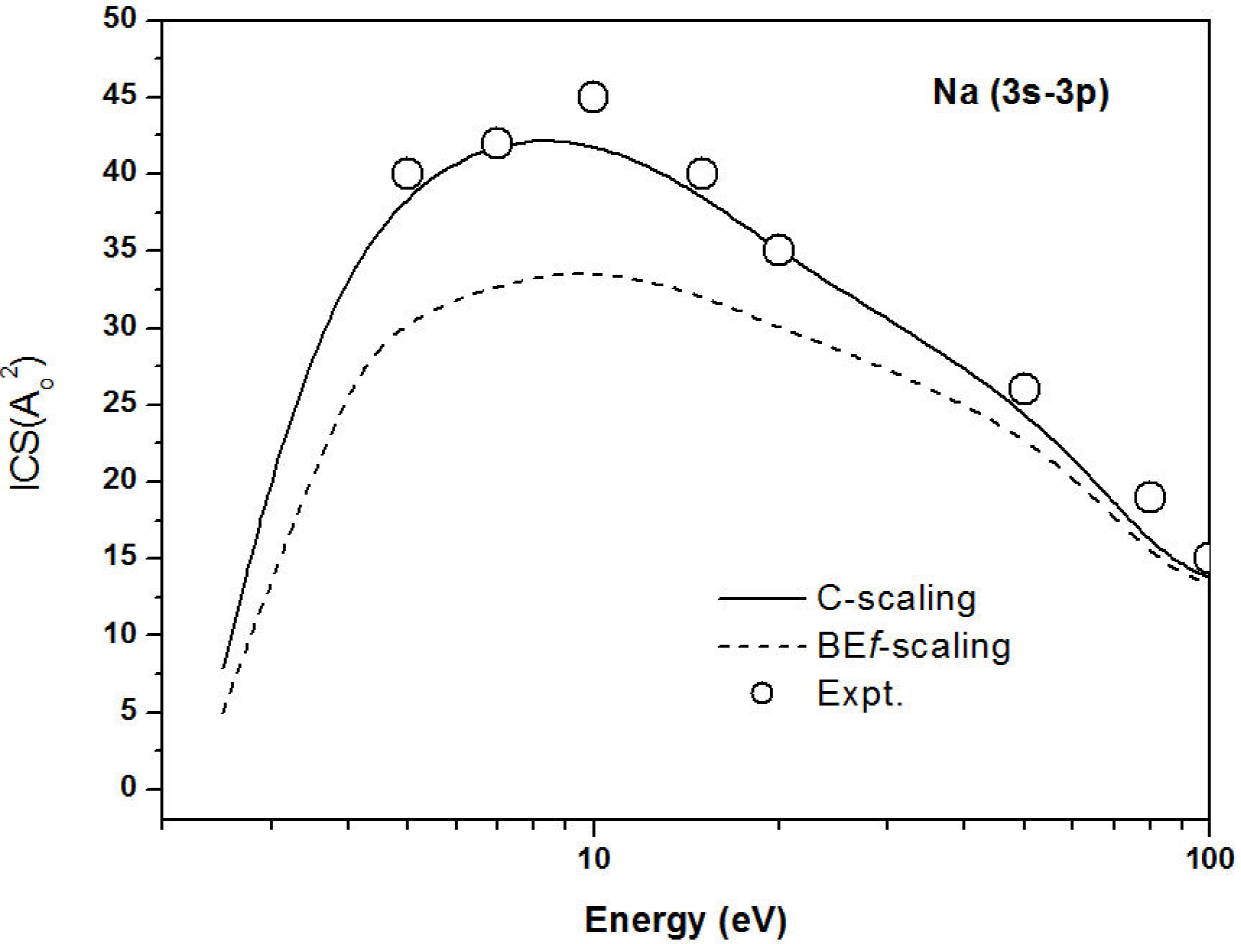
Figure 4 show the C-scaling for Na atom (3s-3p1P states) compared with experimental data 8, and the traditional BEf-scaling 2. As noted, C-scaling is reasonably close to the experimental data 8.
K Atom
Figure 5, show C-scaling for K atom (4s5p states) compared with experimental data 9 and BE f-scaling 2. As noted again, C-scaling is reasonably close to the experimental data 9.
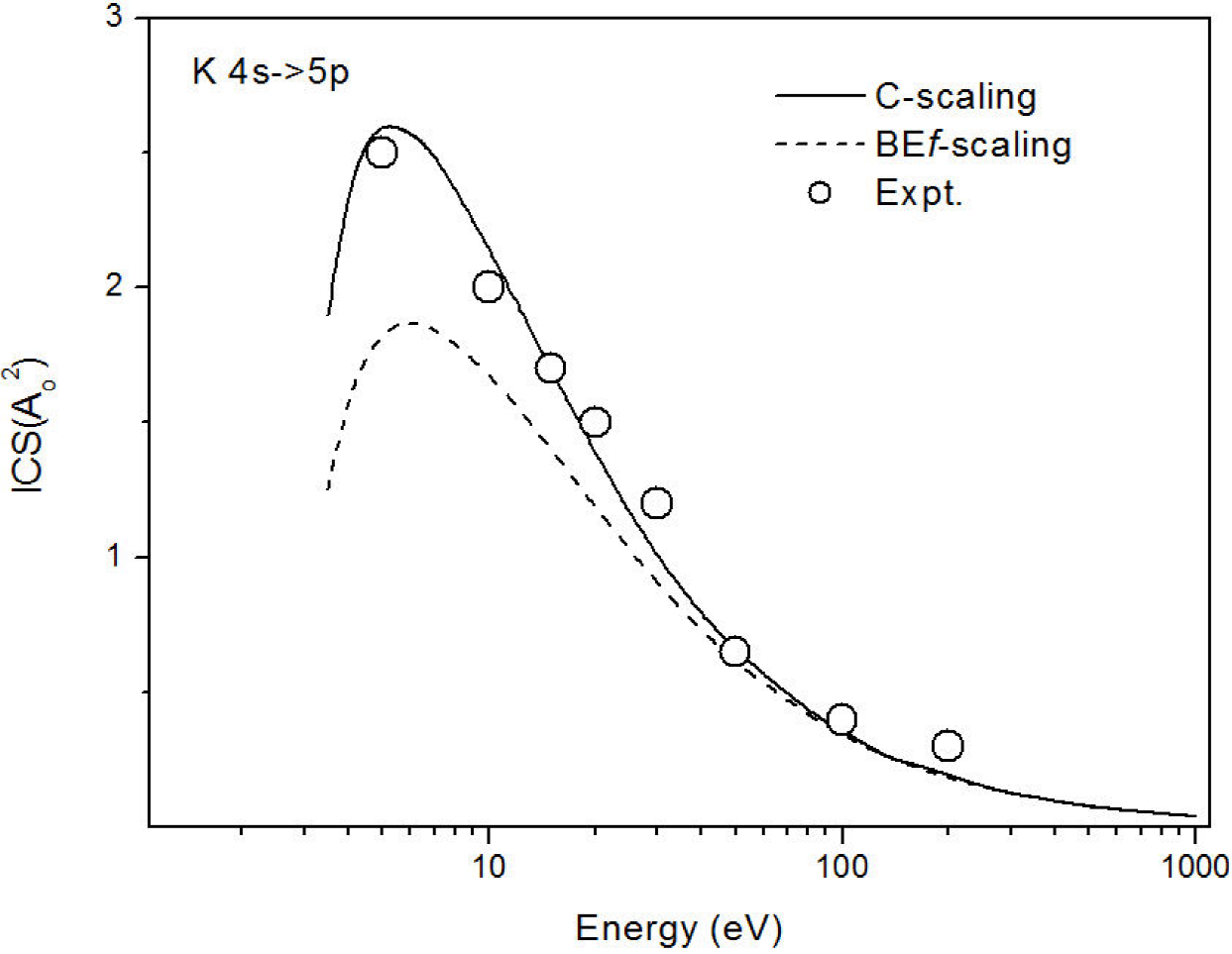
Figure 5. Integral cross sections for electron impact excitation of the 4s->5p states of K. Line solid, C-scaling; dashed line, BEf- scaling 2; open circle, experimental data 9.
Figure 6, show C-scaling for K atom (4s6p states) compared with experimental data9 and Be f-scaling 2. As observed the C-scaling is adequate when compared with BE f-scaling.
Hg Atom
Figure 7 show the C-scaling for electron impact excitation of the 6s6p states of Hg. As noted, our results also agree quite well with experimental data (10). For all targets here tested we can see that our Eq. (4) is consistent and significant tool for the study of electron-atoms collision process.
4. Conclusions
The approximate C-scaling derived here, based on BE f-scaling demonstre the utility this model as a simple way to obtain reliable electron-impact cross sections for dipole allowed excitations of neutral atoms. The C-scaling which represent a version this method qualitatively may be related to the polarizability of the target and represent a method sufficient to convert the BE f-scaling cross sections into excellent agreement with experimental data. The C-scaling here proposed clearly agree much better with experimental data which shown that the representation of polarization effect is imperative and that this implementation can be readily applied to the electron scattering problem. This suggest that the C-scaling represent a viable method to analyze electron-impact excitation cross sections for atoms and is relatively simple when compared to state-of-the-art ab initio theories.











 text new page (beta)
text new page (beta)