Research
Precise analytic approximation for the modified Bessel function I 1 (x)
P. Martina
*
J. Olivaresb
A. Sotomayorb
aDepartamento de Física, Universidad de Antofagasta, Chile.
bDepartamento de Matemáticas, Universidad de Antofagasta, Chile. jorge.olivares@uantof.cl; adrian.sotomayor@uantof.cl
Abstract
Precise analytic approximations have been found for the modified Bessel function I
1 (x) of order one. The approximant is simple and with good accuracy for every positive value of the variable x. The method to obtain the approximant is an improvement of the multipoint quasi-rational approximation technique, MPQA. This is obtained combining rational functions with elementary auxiliary functions as a bridge function between the power series and asymptotic expansion.
Keywords: Approximations and expansions; special functions
PACS: 02.30.Mv; 02.38.Gp
1. Introduction
The modified Bessel functions appear very often in Mathematics and Physics 1,2,3,4,5. There are some approximations for these Bessel functions using polynomials, but each approximation is limited to a narrow interval of the variable 1 (p. 378). Here we are interested in the modified Bessel function I
1 (x) of the first kind and order one. This is an entire function with a power series of infinite radius of convergence, but a lot of terms of this series are usually needed to get good accuracy for large values of x. The asymptotic expansion is also well known, but good only for high values of the independent variable x. A precise analytic approximation for the modified Bessel functions is needed, valid for all positive values of the variable x and simple to calculate. This can be obtained using rational functions combined with elementary auxiliary functions in the so called MPQA, multi-point quasi-rational approximants 6,7. The procedure requires the simultaneous use of power and asymptotic expansions, in such a way that the approximant constitutes a bridge between both expansions. This technique is here applied to find a precise analytic approximant for the modified Bessel function I
1 (x). Some improvements to the method have been introduced to determine the approximants to I
1 (x). In particular we are selecting the auxiliary functions in such a way that the power series of the approximants have only odd-powers as in the case of the original power series of I
1 (x). This is one of the improvements on the form of previous approximants for Bessel functions J (x) published in the past 8,9. This way to obtain new approximations is more efficient and produce the same accuracy with less parameters. Keeping this idea in mind, several approximants have been obtained, and here we are presenting the one with the best accuracy for a given number of parameters.
The form of the approximant is determined in Sec. 2, showing the criterion to select the auxiliary functions. The determination of the parameters is done in Sec. 3, and a discussion of the relative error is also performed. Finally the last Section is devoted to the Conclusion.
2. Approximant structure
The power series of I
1 (x) is
I1(x)=x2∑k=0∞1k!(k+1)!(x24)k=x2(1+x28+x4192+⋯)
(1)
and the asymptotic expansion is
I1(x)∼ex2πx1-38x-15128x2-⋯.
(2)
Now an analytic function must be created in such a way that it is a bridge between both series. Clearly this function should contain the exponential function, as well as rational functions as in Pade’s method. However now there is the important fact that the power series of I
1 (x) contains only odd powers, which means that the auxiliary function should also contain only odd powers, thus there are two possibilities x(e
x
+ e
-x
) or (e
x
- e
-x
). Both possibilities have been considered here, but the best results are obtained for the second alternative. The second consideration is in relation with the fractional power x
-1/2 in the asymptotic expansions. An auxiliary function must be introduced in the approximant in such a way that this fractional power should appear at infinity, but not in the region of approximation, which in our case is the positive real axis x > 0. Furthermore, this auxiliary function should have only even powers in the power series around zero. All of these conditions are accomplished by the function 1+λ2x23/4, where λ2 is chosen as a positive number. All of these previous considerations are satisfied by the approximant
I1~x=x cosh x1+λ2x23∕4 - ∑i=0npix2i1+∑i=1nqix2i
(3)
This approximant at infinity should be as 2πx-(1/2)ex and therefore pn and qn must be related as
pn=2πλ3∕2qn
(4)
Now the parameters pi and qi are determined by imposing the condition of the equality between terms of the power series of I
1 (x) and I1˜(x). The number of terms in the power series of I
1 (x) must be 2n, if we leave free the choice of λ. This is convenient, because in this way only algebraic linear equations are obtained, and the parameters of the approximation can be determined analytically.
3. Determination of parameters
Here the approximant
I1~x=x cosh x1+λ2x23∕4 ∙ p0+2πλ3∕2q1x21+q1x2
(5)
will be considered.
To obtain only linear equations to determine the parameters p0 and q1, it is better to rationalize Eq. (5), and after that to proceed to equate the coefficients of the series. Thus
(1+q1x2)(1+λ2x2)3/4I1(x)≃xcoshx(p0+2πλ3/2q1x2).
(6)
Now we have to get the two first terms of the series for I
1 (x), 1+λ2x23/4 and cosh x, and to equate coefficients, that is
(1+q1x2)(1+λ2x2)3/4x2(1+x28)≃x(1+x22)(p0+2πλ3/2q1x2)+O(x4).
(7)
In this way the parameters p0 and q1 are determined by the algebraic equations
12=p0; 34λ2+18+q1=12+4λ3∕22πq1
(8)
The value of q1 is determined by Eq.(7) giving
q1=34λ2-3842πλ3∕2-1
(9)
Since we are interested in an approximant to I
1 (x) for positive values of x, then q
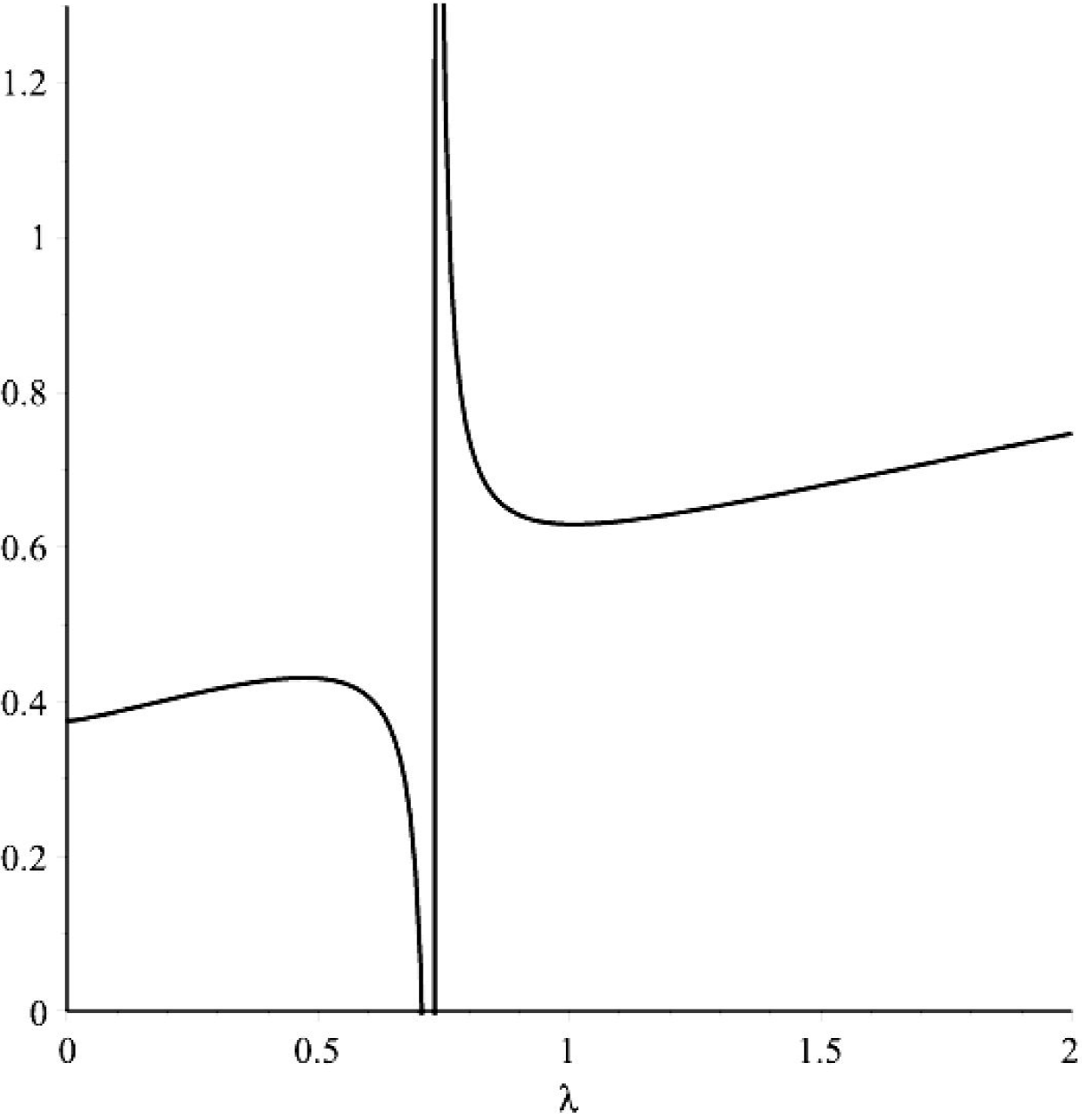
1 must be positive, and λ should be chosen in such a way that this condition is verified. The critical values for λ are for the zeros of the numerator and the denominator of q
1 is zero, therefore λ must be chosen such that
0<λ<0.5; π813<λ<∞
(10)
A graph of q
1 as a function of λ is shown in Fig. 1.
From this graph, it is clear that λ should be in one of the intervals in Eq. (10). The lowest relative error has been found for λ=0.2, giving for I1˜(x)
I1~(x)=xcoshx21+(0.2)2x23/4⋅1+342π(0.2)3/2⋅1-2(0.2)21-22π(0.2)3/2⋅x21+381-2(0.2)21-22π(0.2)3/2⋅x2
(11)
I1~(x)=x coshx21+(0.2)2x23/4⋅1+0.05744x21+0.40244x2,
(12)
where in the equation the smallest number of decimals have been chosen such that the relative error is not modified. The relative errors ε(x) are calculated by the equation
ε(x)=|I(x)-I1˜(x)||I(x)|.
(13)
The accuracy of this approximant is high, as it can be also seen in Fig. 1.
The maximum relative error of this approximant is about 1%, but it is important to point out that the errors for small and large values of x are much lower.
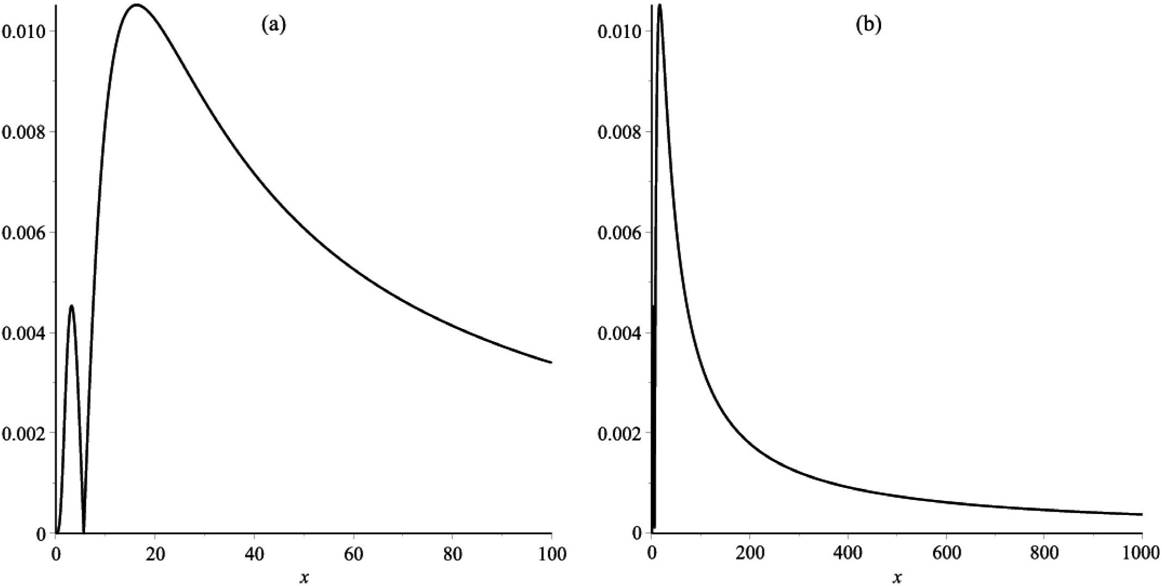
In Fig. 2, the relative errors are shown for different values of λ. The selection of λ=0.2 is because for this value there is a minimum relative error.
It is interesting to point out that there is a second way to obtain the parameters p
0, p
1 and q
1, which consist in leaving p
0 and p
1 as unknown, giving q
1 as a function of p
1. In this way, after equating coefficients in the power series the value for q
1 as a function of λ is
q1=π2λ-32p1
(14)
which is little different from our previous value. This way to obtain the coefficients of the approximant lead to a slightly different approximant, and the smallest relative error is for λ2=0.54, which is a little larger than that determined using the main method previously described.
In order to clarify the method, in Fig. 3 we have shown three plots: one for the best value λ=0.2 (the smallest relative error); the case of λ=0.4 which is the curve which is an approximant with any value in the right intervals and finally the third curve with the method using Eq. (14). In this case the maximum relative error is larger than the other two curves.
4. Conclusion
A simple and precise approximant has been found for the modified Bessel function I1(x) of the first kind and order one. The approximation found here is very simple and valid for all positive values of the independent variable x. The method used here is based in the so called multi-point quasi-rational approximation (MPQA), which combines series powers and asymptotic expansions simultaneously, in such a way that the approximant is like a bridge between both expansions. In this way, as in Pade’s method, rational functions are used, but now combined with auxiliary elementary functions as exponentials, trigonometric and fractional powers. Here the calculation has been carried out for simple approximants with only three parameters, but approximations with more parameters can also be determined. Here, the modified Bessel function of order one has also been considered, but this technique could be also applied to other Bessel functions of integer order.
Although essentially the MPQA method has been used here, some improvements have been introduced comparing with previous papers, in order to improve efficiency in the approximants by using only auxiliary functions with a convenient form as, for instance, power series with only odd-powers. In this way, a good accuracy has been obtained with only a low number of parameters.
An analysis is also performed of the best way to choose the parameter λ which essentially is done by analyzing the sign of the coefficient of the largest power of the denominator of the approximant.
Acknowledgments
A.S. is partially supported by Project Fondecyt 1161192, Chile.
References
1. M. Abramowitz and I.A. Stegun, Handbook of Mathematical Functions, Ninth Printing, Dover Publications Inc., (New York, 1970) pp. 374-379.
[ Links ]
2. G.N. Watson, A treatise on the theory of Bessel functions, 2nd. ed., Cambridge, England: Cambridge University Press (1966).
[ Links ]
3. J.D. Jackson, Classical Electrodynamics, 2nd. ed., John Wiley and Sons, Inc., Ch. 3 (1975).
[ Links ]
4. G. Arfken, Mathematical Methods for Physicists, 3rd. ed., Academic Press, Orlando Fl., USA, (1985) pp. 573-596.
[ Links ]
5. D. Kh. Morozov and V.V. Voitsekhovich, Rev. Mex. Fis. 44 (1998) 231.
[ Links ]
6. P. Martin, E. Castro, J.L. Paz and A. De Freitas, “Multipoint quasi-rational approximants in Quantum Chemistry", Ch. 3 of New Developments in Quantum Chemistry, Transworld Research Network, Kerala, India, (2009) pp. 55-78.
[ Links ]
7. P. Martin, E. Castro and J.L. Paz, Rev. Mex. Fis. 58 (2012) 301.
[ Links ]
8. P. Martin and L. Guerrero, J. Math. Phys. 26 (1985) 705.
[ Links ]
9. P. Martin and L. Guerrero, J. Comp. Phys. 85 (1989) 487.
[ Links ]











 nueva página del texto (beta)
nueva página del texto (beta)



