Research
Nanosecond laser pulse propagating through turbid media: a numerical analysis
B. Morales-Cruzadob
*
E. Sarmiento-Gómezc
S. Camacho-Lópezd
F.G. Pérez-Gutiérreza
aFacultad de Ingeniería, Universidad Autónoma de San Luis Potosí, Álvaro Obregón 64, San Luis Potosí, S.L.P., México.
bCONACYT - Universidad Autónoma de San Luis Potosí, Álvaro Obregón 64, San Luis Potosí, S.L.P., México.
cInstituto de Física “Manuel Sandoval Vallarta”, Universidad Autónoma de San Luis Potosí, Álvaro Obregón 64, San Luis Potosí, S.L.P. , México.
dDepartamento de Óptica, Centro de Investigación Científica y de Educación Superior de Ensenada, Carretera Ensenada-Tijuana 3918, Zona Playitas, Ensenada, B.C. 22860, México.
Abstract
A short pulse transmitted by a turbid medium is both distorted in shape and shifted temporally as its passes through. If the incident pulse is short enough an analytical expression of the deformed pulse can be calculated using the diffusion approximation of the radiative transport equation (RTE), and the optical properties of the medium can be recovered from the transmitted pulse. In this work, the effect of a homogeneous turbid medium on the transmitted temporal profile of nanosecond laser pulses was studied both experimentally and numerically for samples with different optical properties and various laser pulse widths. The numerical results showed a dependence of the pulse distortion on the variables tested, finding that this dependence dramatically changes upon varying pulse width. This work contributes to the field by showing that the interaction between turbid media phantoms and nanosecond laser pulses can also be analyzed, as it is the case for ultrashort laser pulses, by using the diffusion approximation of the RTE in certain regimes. This finding is significant and useful for applications when a laser pulse must attain to certain duration and shape after propagation through a turbid medium or when at a certain time an intensity threshold is required.
Keywords: Wave propagation in random media; propagation, transmission, attenuation, and radiative transfer
PACS: 42.25.Dd; 42.68.Ay
1. Introduction
The interaction between pulsed lasers and matter is well understood to depend on both the laser pulse intensity and the optical properties. On the one hand, advances in laser technology have allowed to deliver ultrashort laser pulses in the range of tens of femtoseconds and a few nanojoules of energy which focused down to a spot of a few micrometers of diameter, produce peak intensities in the range of GW/cm2 to TW/cm2. Longer laser pulses (from picosecond to millisecond duration) with the same energy and under similar focusing parameters lead to much lower peak intensities. On the other hand, it is also known that when a laser pulse propagates through a turbid medium, the transmitted and reflected laser pulses are significantly different from the incident pulse, its temporal profile is distorted, mainly influenced by the scattering events1 but also by linear and nonlinear absorption. Such a distortion in the laser pulse temporal profile modifies the laser pulse intensity, and therefore it affects the expected laser-matter interaction as compared to what it would occur with the undistorted pulse.
Various fields of modern science and technology have been benefited from applications of the interaction between pulsed lasers and turbid media. In medicine, for instance, windows to the brain (WttB) applications are being developed using femtosecond and picosecond laser pulses to write buried waveguides within polycrystalline Zirconia (YSZ) implants that allow delivery of laser light to treat brain lesions2,3. Longer laser pulses have been used either as a tool for laser-induced plasma formation (intraocular microsurgery, dental drilling, neurosurgery, angioplasty and other4,5,6) or lighting (photodynamic therapy4, blood coagulation, tattoo removal7, etc.). Using the diffusion model for light propagation has become another very useful tool for monitoring biological processes8. Another interesting application is photoacoustic tomography, where images are reconstructed from optically excited photoacoustic waves9. In this technique the target object is immersed in a semitransparent medium, which also possess scattering, through which a laser pulse propagates; therefore the technique faces the limitations given by the optical properties of the medium, which change the shape of the initial pulse and likewise the pulse profile is temporarily shifted during propagation due to the turbid medium.
A good estimation of the deformation of the pulse propagating through a turbid media, proves very relevant when the laser-matter interaction is sensible to either time shift or stretching of the pulse that might occur during beam propagation. A clear example of this is the above mentioned photoacoustic tomography (biotissue, opaque solids, gels, etc.) technique, where the generated acoustic signals must be well timed and synchronized to achieve accurate images9. Another field where a precise knowledge of the time profile of the pulse, and its possible distortion, becomes of high relevance is materials processing. Laser-matter interactions in general can be allocated by well-defined characteristic times, which relate to specific physical domains. For instance, when the interaction is driven by the conduction electrons, these electrons are excited within the first few femtoseconds, later (in the order of 100 femtoseconds) these electrons thermalize to the lattice and phonons are excited heating up the bulk within a few tens of picoseconds, the bulk temperature rises and it can melt and evaporate a few tens or hundreds on nanoseconds later10. If a laser pulse propagates through a turbid medium and becomes both shape distorted and time shifted it will affect how the interaction takes place within the above-described physical domains. Therefore, it becomes highly relevant to have a manner of determining the shape distortion and time shifting for laser-matter interactions occurring through turbid media; a modern and typical example of such a scenario would be the pulsed laser irradiation of metallic nanoparticles in biological tissue for the purpose of localized tissue damage.
A phenomenological description of light propagation through turbid media lies in the so called radiative transfer equation (RTE)11. It is expected that the temporal profile of the transmitted laser pulse depends on the temporal width of the original pulse. Approximations of the RTE, such as the diffusion approximation12, can be useful for the evaluation of the effect of a turbid medium on the transmitted temporal profile, giving a tool for determining the optical properties from the deformation of a short pulse propagating through. This technique is called time-of-flight spectroscopy (TOF)12, and examples of the use of this technique are widely found in the literature (see 12,13,14,15 for examples of the recovery of optical properties using TOF). In TOF, the diffusion approximation for the radiative transfer equation is set with a delta initial condition, predicting the temporal profile of the transmitted pulse, thus, in all cases analytical solutions are limited to simple geometries or short temporal profiles of the incident pulse, of the order of picoseconds or even shorter, and it is useful only in a limited range of optical thicknesses. In addition, the diffusion approximation technique has its own limitations: 1) the radiance is nearly isotropic, 2) the photon current is temporally broadened relative to the transport mean free time11. Thus, it is required samples with a high albedo (μ's≫μa). Another alternative is to use Monte Carlo simulations to compute the transmitted pulse, and thus to compare it with experimental results14,16,17,18. However a comprehensive study of pulse deformation for longer incident pulses in media with a wide range of optical properties is still missing.
In this paper, the behavior of nanosecond laser pulses with different pulse widths propagating through a turbid medium was studied. The temporal intensity profile time shift Δt, as well as the pulse stretching Δσ, were both found to be related to the scattering properties of the medium; a strong dependence of Δt and Δσ on the incident pulse width was also found. Finally, a relationship of the time shift relative to the pulse width for varying optical properties was identified. Such a relationship is based on basic assumptions coming from the diffusion approximation for light propagation and it depends on the incident pulse width, showing that even when it is not possible to analytically solve the diffusion equation for this initial condition, the diffusion approximation can still be used to predict pulse deformation. In particular, our results show that the interaction between turbid media phantoms and nanosecond laser pulses, within the pulse width range and the optical properties tested, is described by two regimes. In the first one, both the pulse time shift Δt and the pulse stretching Δσ, are consistent with what it is predicted by the diffusion approximation of the radiative transport equation for pulse durations σ<10 ns and a scattering coefficient μs
> 30 cm-1; while in the second regime, Δt and Δσ cannot be described by the same means for pulse durations σ≥ 10 ns and μs
≤ 30 cm-1.
2. Materials and methods
2.1. Preparation of phantoms
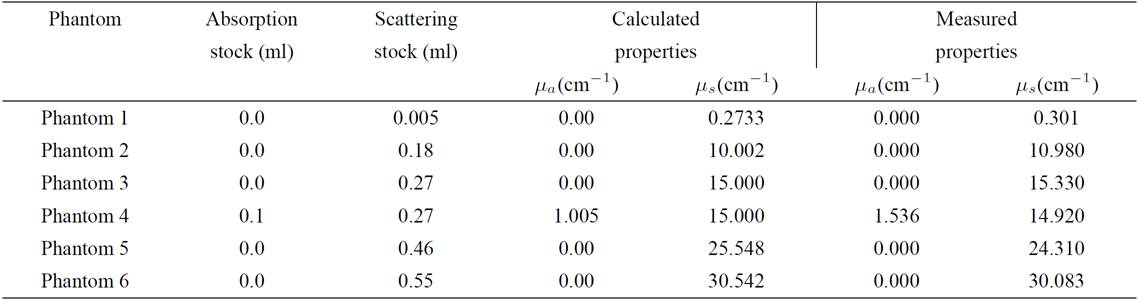
Six turbid media phantoms with different scattering and absorption properties were prepared using polyurethane (BJB part A and B, refractive index 1.5) as a polymer matrix, zirconium dioxide particles (ZIROX K, 1.3 μm diameter and 2.3 refractive index) as scattering agent, and Indian ink as absorptive agent. A concentrated stock solution, 4 mg of zirconium dioxide in 10 ml of ethanol, was mixed with different amounts of polyurethane to reach the desired scattering coefficient. The phantoms were 6 cm in diameter and 1.0 cm thick, approximately. In order to determine its optical properties, a small sample of the absorption stock was measured using integrating spheres and the IAD program was used to retrieve its optical properties19. The absorption coefficient (μa) was estimated from the absorption coefficient of the stock added to the pre-polymerized mixture, and the scattering coefficient (μs) was calculated using Mie’s theory11. The optical density of the sample ranged from 0.3 to 30 and it was calculated as τ=(μa+μs)d, where d is the physical thickness. Table I shows the content of the main components of each phantom along with the values of the resulting optical properties.
Table I. Composition and optical properties of the phantoms.
2.2 Experimental Setup
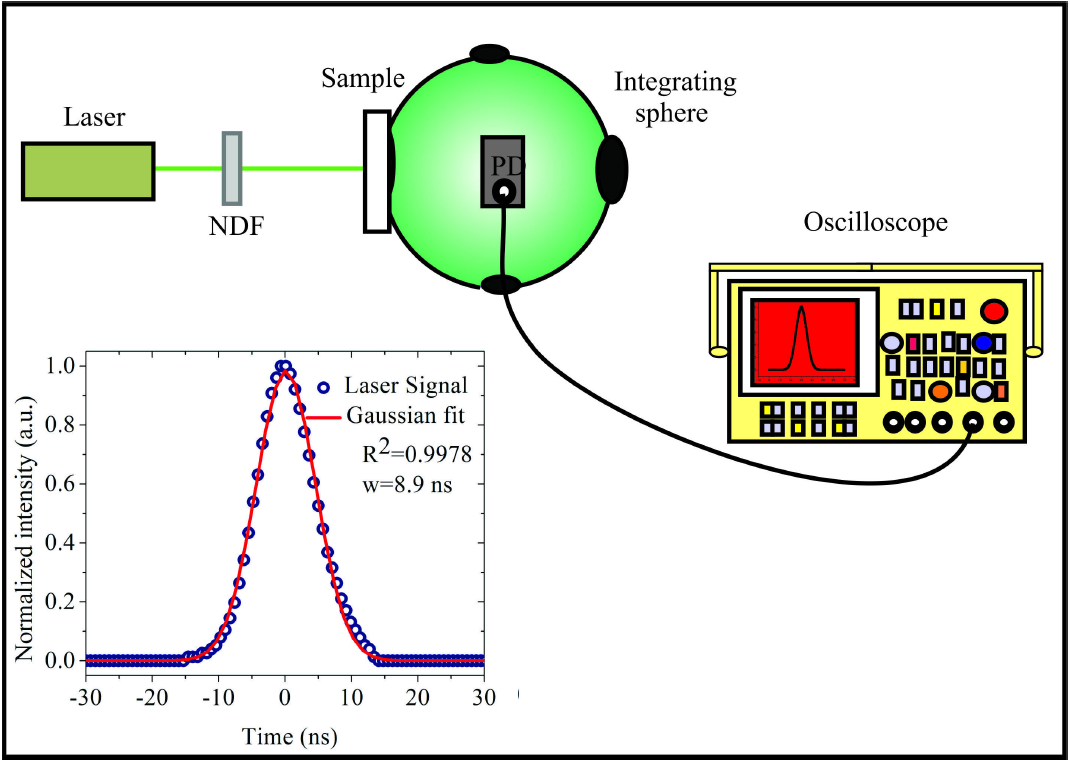
The temporal profile of the laser pulses transmitted through each sample was acquired using the experimental set up shown in Fig. 1. It consists of an integrating sphere (819C-SF-6, Newport) with the sample positioned at the entrance port, and a 600 ps rise time biased photodetector (818-BB-20, Newport) attached to an oscilloscope (Tektronix DPO 4104B). The used source was a Q-switched, frequency doubled (λ=532 nm), Nd:YAG laser, which emits 8.9 ns long laser pulses as experimentally determined by placing the photodetector directly in the optical axis, without intervening sample or integrating sphere. The temporal profile fits to a Gaussian curve with a 1/e full-width of 8.9 ns, as it is shown in the inset of Fig. 1. This pulse duration was used for the computation throughout this work. A series of neutral density filters (NDF) were used to attenuate the laser pulse energy to prevent saturation of the photodiode (PD).
As it has been reported before19 an experimental measurement, using integrating spheres, of the temporal profile of a laser pulse propagating through a turbid medium, produces a distortion associated with the integrating sphere itself. This effect can be modeled by considering the sphere as a linear system, thus the measured signal can be calculated as the convolution of the incident pulse with a characteristic transfer function of the system. In this case, the transfer function can be written as:
f(t)= 0fort<0A1t1+t2+t3exp(-tt1+t2+t3)fort≥0
(1)
where t
1 = 10.66 ns which depends on optical and geometrical parameters of the integrating sphere only, t
2 and t
3 are associated with the optical properties of the sample. Thus, the measured signal includes this linear effect, and it was taken into account for the further analysis regarding the deformation of the pulse caused by the sample.
2.3. Monte Carlo simulations
As we will show below, the deformation of the temporal profile of the laser pulse due to the optical properties of the material strongly depends on the temporal width of the incident pulse. In our case, due to the impossibility to experimentally analyze pulses of different durations, Monte Carlo simulations were carried out to study a selection of pulse widths. The known Monte Carlo Multi-Layered program (MCML), regularly used to simulate light transport through a turbid medium20, was modified to simulate the propagation of an initially Gaussian laser pulse temporal profile through a turbid medium, given that its initial pulse duration is known. The MCML method allows obtaining the temporal intensity profile for the transmitted pulse given an incident Gaussian pulse with an easily modifiable duration19. The Monte Carlo simulations included 10 different pulse widths ranging from 0.01 to 100 ns. In all cases the program launches two million photons into the media which is characterized by the following features: physical thickness d = 1.0 cm, refractive index n = 1.5, anisotropy factor g=0 and 0.74, absorption coefficient μa ranging from 0 to 5 cm-1 and scattering coefficient μs ranging from 0 to 100 cm-1. Monte Carlo simulations with g=μs=μa=0 were used as a time-reference to locate the maximum of the pulse profile in the case of a completely transparent medium.
3. Results and discussion
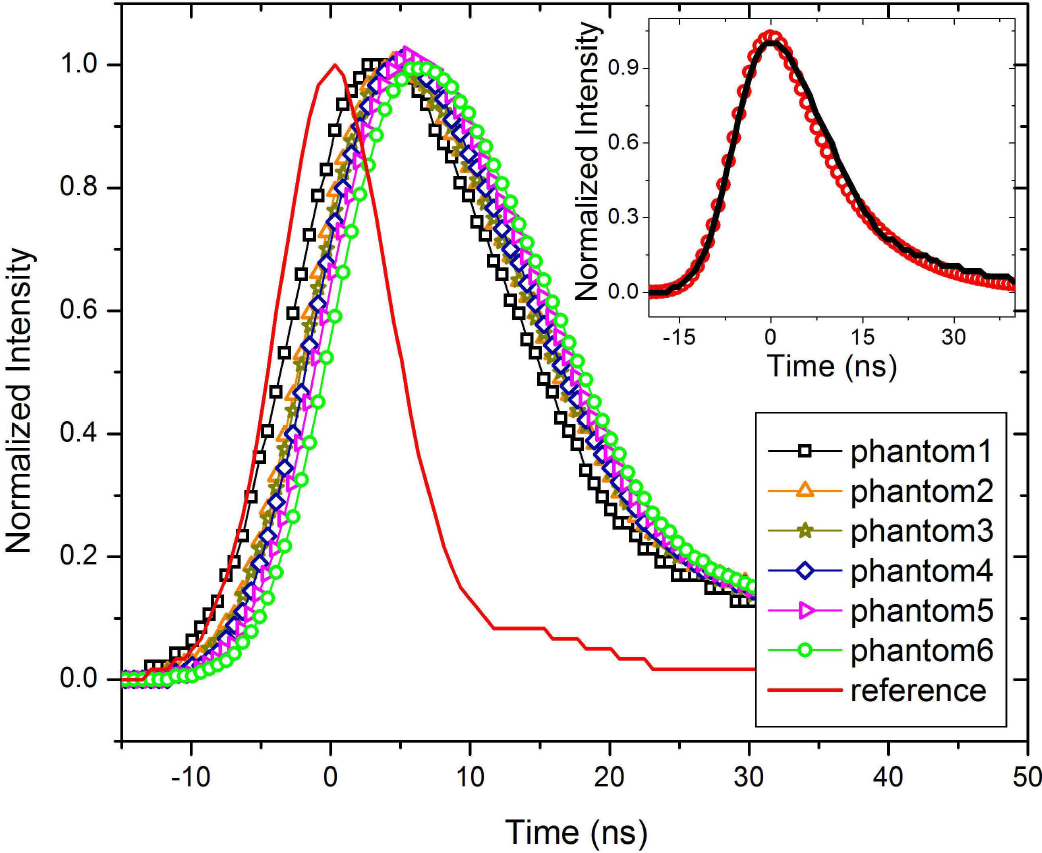
Figure 2 shows the experimentally obtained oscilloscope trace of a laser pulse that propagates through the experimental set up and different samples as previously described. For comparison purposes, the incident pulse (continuous line) was set at t = 0; all the pulse traces measured throughout the experimental set up appear shifted. It has been shown in a previous work19 that the integrating sphere introduces stretching of the laser pulse; this is due to both multiple reflections within the internal Lambertian surface, and to the light reflected back to the sphere by the sample. To show this effect, inset in Fig. 2 shows a comparison between the experimental data and a simulation results using MCML affected by the integrating sphere, showing a good agreement between them19. As it can be seen in Fig. 2, the experimentally measured pulses are not just stretched but also shifted to the right as compared to the incident pulse. This shift is directly related to the scattering properties of the sample, as cannot be explained by the integrating sphere’s effects, also finding that larger the scattering coefficient the larger the pulse shift. For further investigation of the effects of a turbid medium on the pulse deformation, and being unable to experimentally change pulse width, we simulated the propagation of laser pulses with different durations using MCML.
The inset in Fig. 3 shows the temporal profile of a laser pulse whose initial duration is 0.5 ns, this incident pulse is transmitted through a non-scattering (μs=0) but absorbing material with an absorption coefficient μa ranging from 0 up to 5 cm-1, the transmitted pulse profile was computed using our modified MCML program. As expected, the laser pulse intensity is simply attenuated due to linear optical absorption and no further deformation of the pulse, either stretching or shifting, was found. Thus, in the following results only scattering media were considered. Figure 3 shows the result for the simulation of the same incident laser pulse (0.5 ns duration) transmitted through a non-absorbing (μa=0) but scattering material with a scattering coefficient μs of 0 and 20 cm-1. It is quite clear how the pulse intensity peak falls off sharply as the scattering coefficient increases; notice that the area under the curve also decreases for increasing scattering coefficient, which is directly related to the total transmittance of the sample. It must be pointed out that for the scattering features tested here the laser pulses maintain its Gaussian profile. This Gaussian shape is completely different from the typical deformation found in TOF experiments12, which can be expected because of the longer pulse durations used in the present study. The computed laser pulse profile for the transmitted pulse agrees well with results obtained for 500 ps incident pulses, using Monte Carlo pulses in a similar range of optical properties19. The time shift between the incident laser pulse and the modified pulse is denoted by Δt.
To better appreciate these effects, Fig. 4 shows the normalized intensity profiles resulting from the Monte Carlo simulations for a 0.5 ns incident laser pulse propagating through media with μs ranging from 1 to 100 cm-1. Values of μs larger than 100 cm-1 were tried, but we got a poor signal to noise ratio because of the lower amount of photons transmitted through the sample; therefore those results were not included in this report. As indicated above, increasing scattering coefficient produces a shift of the pulse peak to the right, and on top of that a distortion of the pulse profile was obtained in the form of a long tail at the late end of the pulse19. The reference pulse peak corresponding to propagation in a medium without scattering was centered to time zero and all other pulses appear shifted.
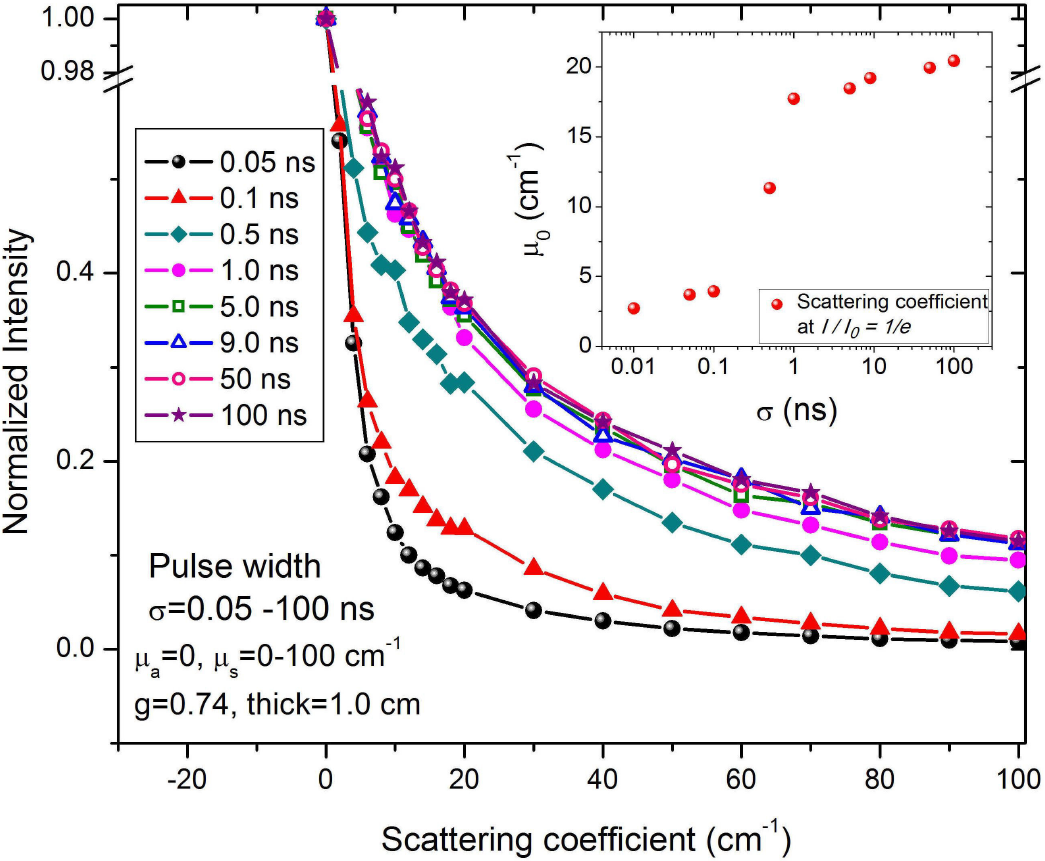
Figure 5 shows the decay of the intensity of the transmitted light as a function of the scattering coefficient for several pulse durations from 0.01 ns and up to 100 ns, such decay is nearly exponential regardless of the pulse duration used for the simulation. This intensity loss is due to photons leaving through the edges of the sample and also because there is light backscattered from the sample. Shorter pulse durations (0.01 - 0.1 ns) present a more sensitive scattering transmittance dependence, with a faster drop than it occurs for longer pulses. The inset in Fig. 5 shows the scattering coefficient μ0 at which the transmitted intensity falls to a value of 1/e of the incident intensity, this μ0 is plotted for all the pulse durations considered in the present study. μ0 increases as the pulse duration σ increases; it shows an abrupt increment between σ=0.1 ns and σ=1 ns. Within this range, μ0 increases from 4 to 16 cm-1, while μ0 increases slowly elsewhere.
As it is shown in Fig. 4, there is a direct relationship between the pulse peak time shift Δt and the optical properties of the sample. It was found that the initial pulse duration plays a very important role in the later pulse deformation, as it has been clearly shown in Fig. 5. Moreover, Fig. 6A shows the dependence of Δt with the scattering coefficient μs ranging from 0 to 100 cm-1, for pulse durations from a few picoseconds and up to tens of nanoseconds (0.01 to 100 ns). Larger scattering coefficients produce longer time shifts of the transmitted pulse due to the higher number of scattering events that light suffers along the sample, thus increasing the time of flight that the photons require to reach the detector. In a similar way, the longer the initial pulse duration, the larger the pulse time profile stretching due to the increment in the interaction time between photons and the medium. Figures 6A and 6B show the relationship between Δt with both the scattering coefficient and the incident pulse duration, respectively. Two regimes are clearly identified in Fig. 6: In the first regime, increasing the incident pulse duration σ from 0.01 to 5 ns produces a slight increment of Δt, following a nearly linear relationship with the scattering coefficient, as it can be seen in Fig. 6A. In the second regime, incident pulse durations σ longer than 5 ns result in a more significant Δt increment (following a nonlinear relationship) with the scattering coefficient. These two regimes can be also appreciated in the inset of Fig. 6B. Figure 6B is analogous to Fig. 6A, in this case Δt is plotted as a function of the pulse duration for different scattering coefficients. A σ0 value was determined from the intersection point between the linear fit to the curves in Fig. 6B for σ≤5 ns and the linear fit to the same curves for σ>5 ns. The inset shows such σ0 value as a function of the scattering coefficient, which decreases with increasing μs, with a sharp drop off for scattering coefficient values from 30 to 40 cm-1.
Several theoretical descriptions of the propagation of light in a turbid media are available21,22,23,24, however because of the limited range in which they apply for both pulse duration and optical properties, we still do not have an analytical theoretical description for the case of nanosecond pulse propagation in turbid media for a wide range of optical parameters. In particular, an approach similar to the work by Patterson et al12 is not possible here, due to the impossibility of analytically solving the diffusion approximation case using the correct initial condition. Nevertheless, a qualitative analysis is possible indeed by using the diffusion approximation, which treats light propagation through a turbid media at scales larger than the diffusive free path as a random walk, with a description similar to the random motion of Brownian particles in a viscous fluid11,12. Under such description, a photon diffuses inside the sample with some defined probabilistic rules. In particular, the mean squared free path of a photon is proportional to the diffusion coefficient and it is linear in time25. Thus, the mean time Δt required for a photon to travel a distance L, is proportional to L
2/6D, considering an infinitesimal source. For an extended source, Δt is expected to be also proportional to L
2/6D, but with a constant that depends on the duration of the short pulse and thus we propose a linear relationship between the temporal displacement Δt and the scattering coefficient as follows
Δt=αL26D
(2)
where α is a proportionality factor that depends on the time duration of the incident pulse, L is the physical thickness of the sample, D is the diffusion coefficient D=v/3(μa+μ's), and v is the speed of light in the medium. The relation (2) is based on the diffusion approximation of light propagation in a turbid medium, and it can be seen as the average time required for the energy density to propagate a distance L. Figure 7A shows the time shift of the laser pulses as a function of L2/6D for incident pulse durations ranging from 0.01 to 100 ns. As it can be seen in Fig. 7A, the linear relationship between Δt and L2/6D as given by (2) holds within small deviations for incident pulse durations shorter than 10 ns; however for 10 ns pulses and longer, the time shift increases following a different behavior than the expected linear one. This indicates that diffusion approximation holds for short enough pulses in scattering media, but it breaks up for long incident pulse durations. Another possibility is that pulse deformation is not linear for longer pulses giving an error in the estimation of Δt. A more detailed analysis of this effect is required to understand its nature, but this analysis is beyond the scope of this work. Figure 7B shows a plot to determine the value of α which is obtained from the slop of the curve.
Figure 8 shows the dependence of α on the incident pulse duration. In general, by increasing the incident pulse duration produces α to grow. It is noticeable how it increases slowly for incident pulse durations below 10 ns to increase much faster for longer incident pulses. The error bars for α are significant for long incident pulse durations, as it might be expected from Fig. 7A. This error bars, as indicated before, are related to the failure of the diffusion approximation for light propagation in turbid media.
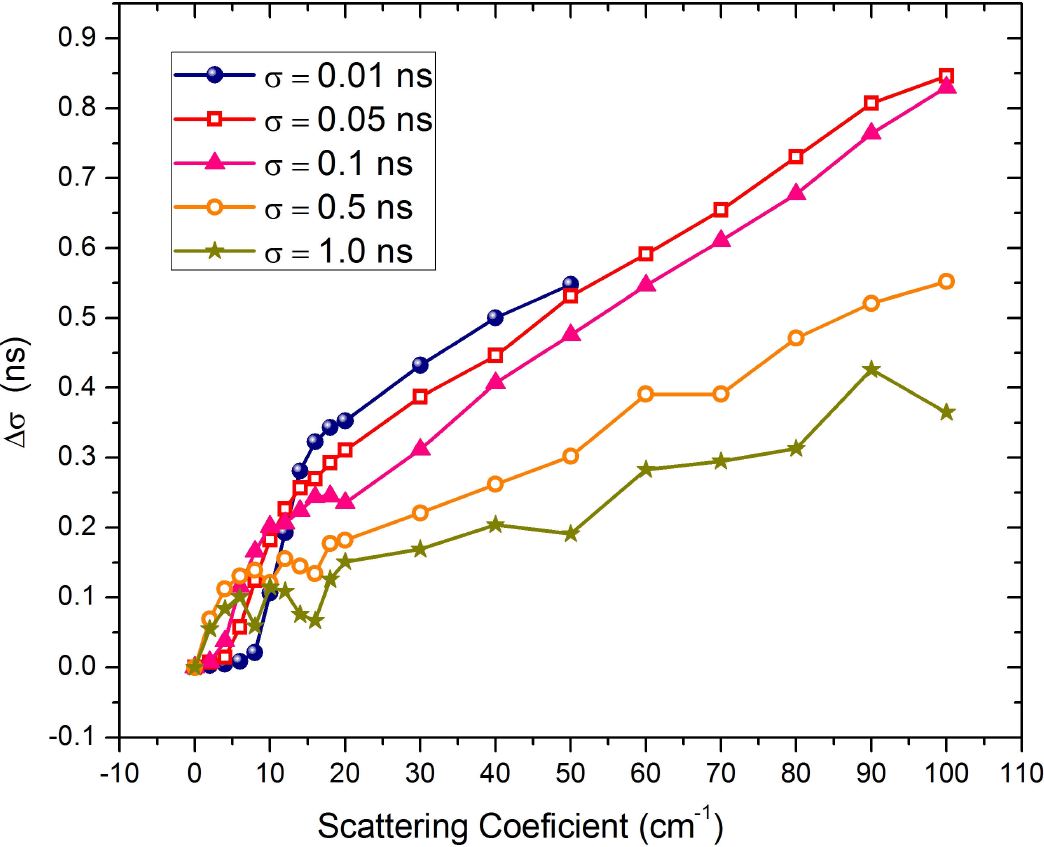
Figure 9 shows the pulse stretching Δσ as a function of μs, for pulse durations shorter than 10 ns, once the laser pulse has fully propagated through the turbid medium. We also included information from a 10 ps pulse, even though is expected that diffusion approximation cannot describe the phenomena with accuracy, as found by Patterson et al.12. As expected, we observe that the pulses stretch more for larger scattering coefficient (Δσ was measured at 1/e of the peak intensity). Along with this effect, a deformation of the pulse was also found; the transmitted pulses show a long tail at the end of the pulse, as it has already been seen in Fig. 3. It holds, in general, that an increase in the μs is related to a larger stretching of the pulse. For μs up to 20 cm-1, Δσ increases with the scattering coefficient with a fast slope; in contrast, for μs larger than 20 cm-1, the slope slows down and Δσ increases linearly. Note that the latter is close to the regime in which the diffusion approximation holds as it was pointed out above. Curve for 10 ps laser pulse, even though is following same trend, shows some differences with other pulses, being this evidence of the breakdown of diffusion approximation for such small times. Results are not shown here for pulses longer than 10 ns because those results did not show any useful trend with the scattering coefficient, which means that the phenomenon cannot be described by the diffusion approximation.
4. Conclusions
We successfully proposed a methodology to study the time shift and stretching that occurs to an incident nanosecond laser pulse, with a Gaussian profile, as it passes throughout a turbid medium. The understanding of the shifted and stretched pulses is important, so that these effects can be taken into account when the light matter interaction relays in both the pulse peak position and pulse duration.
We found that the distortion of the transmitted pulse, cannot be well described by using the standard mathematical relations coming from the diffusion approximation theory of light propagation, which are used in time-of-flight spectroscopy. Instead, by using Monte Carlo simulations, we were able to describe both the pulse peak time shift Δt and the pulse stretching Δσ, that take place when a laser pulse is transmitted through a turbid medium. It was found that Δt as well as Δσ both increase as the incident pulse becomes longer, but these increase more importantly for incident pulse duration around 10 ns and scattering coefficient values greater than 20 cm-1. We proposed a linear relationship between the time shift Δt of a pulse and the scattering coefficient of the sample through the light diffusion coefficient D, all based on basic assumptions from the diffusion approximation of RTE. The proportionality factor α of this linear relationship depends on the incident pulse duration following a linear function. The experimental results presented in this paper in Fig. 2 were contrasted to the results obtained through the Monte Carlo simulation for an incident pulse of 8.9 ns duration, and a limited range for the scattering coefficient of the prepared samples, the results are qualitatively consistent.
References
1. Z. Guo, S. Kumar, and K-C San, Journal of Thermophysics and Heat Transfer, 14 (2000) 504-511.
[ Links ]
2. Y. Damestani et al., Nanomedicine: Nanothecnology, Biology and Medicine 9 (2013) 1135-1138.
[ Links ]
3. G.R. Castillo-Vega, E.H. Penilla, S. Camacho-Lopez, G. Aguilar and J.E. Garay, Optical Materials Express 2 (2012) 1416-1424.
[ Links ]
4. M.H. Niemz, Laser-Tissue Interactions: Fundamentals and Applications, 3rd. ed., (Springer 2007).
[ Links ]
5. D.X. Hammer et al., Appl. Opt. 36 (1997) 5630-5640.
[ Links ]
6. A. Vogel and V. Venugopalan, Chem. Rev. 103 (2003) 577-644.
[ Links ]
7. S. Choudhary, M.L. Elsaie, A. Leiva and K. Noury, Lasers Med 25 (2010) 619-627.
[ Links ]
8. T. Durduran, R. Choe, W.B. Baker and A.G. Yodh, Rep. Prog. Phys. 73 (2010) 076701.
[ Links ]
9. R. Nuster, G. Zangerl, M. Haltmeier and G. Paltauf, Opt. Express 18 (2010) 6288-6299.
[ Links ]
10. John Dowden, The theory of laser materials processing, (Springer 2009).
[ Links ]
11. L.V. Wang and H. Wu, Biomedical Optics, (John Wiley & Sons 2007).
[ Links ]
12. M.S. Patterson, B. Chance, and B.C. Wilson, Appl. Opt. 28 (1989) 2331-2336.
[ Links ]
13. D.T. Delphy, M. Cope, P.van der Zee, S. Arridge, S. Wray and J. Wyatt, Med. Biol. 33 (1988) 1433-1442.
[ Links ]
14. E. Alerstam, S. Andersson-Engels, S. Svensson, J. Biomed. Opt. 13 (2008) 060504.
[ Links ]
15. A. Liebert, H. Wabnitz, D. Grosenick, M. Möller, R. Macdonald and H. Rinneberg, Appl. Opt. 42 (2003) 5785-5792.
[ Links ]
16. Z. Guo, J. Aber, B.A. Garetz and S. Kumar, J. Quant. Spectrosc. Radiat. Transf. 73 (2002) 159-168.
[ Links ]
17. S. Jacques, IEEE Trans Biomed Eng. 36 (1989) 1155-1161.
[ Links ]
18. M. Bondani, et al., J. Opt. Soc. Am. B 20 (2003) 2383-2388.
[ Links ]
19. B. Morales-Cruzado, F.G. Pérez Gutiérrez, D.F de Lange. and R. Romero-Méndez, Appl. Opt. 54 (2015) 2383-2390.
[ Links ]
20. L. Wang, S. Jacques and L. Zheng, Comput. Meth. Prog. Biomed. 47 (1995) 131-146.
[ Links ]
21. P. Kubelka J. Opt. Soc. Am. 38 (1948) 448-457.
[ Links ]
22. P. Kubelka, J. Opt. Soc. Am. 44 (1954) 330-335.
[ Links ]
23. B.C Wilson, M.S. Patterson and S.T. Flock, Photochem. Photobiol. 46 (1987) 601-608.
[ Links ]
24. G. Yoon, S.A. Prahl and A.J. Welch, Appl. Opt. 28 (1989) 2250-2255.
[ Links ]
25. R. Landauer and M. Büttiker Phys. Rev. B 36 (1987) 6255-6260.
[ Links ]
















 text new page (beta)
text new page (beta)