PACS: 74.20.De; 74.70.Rp; 74.70.Pq
1. Introduction
In a triplet superconductor the electrons in the Cooper pairs are bound with spins parallel rather than antiparallel to one another, i.e. they are bound in spin triplets5,7,13. For this kind of superconductors, the spins are lying on the basal plane, while the pair orbital momentum is directed along the z-direction and their order parameter Ψ is represented by a three-dimensional vector d(k). If Ψ is of the type kx ± i ky, there is a Cooper pair residual orbital magnetism, which gives place to an state of broken time reversal symmetry, edge currents in the surface of the superconductor, and a tiny magnetic field around non-magnetic impurities.
Based on the results of the Knight shift experiment performed through the superconducting transition temperature Tc8,9, it has been proposed that Sr2RuO4 is a triplet superconductor. These experiments showed that Pauli spin susceptibility of the conduction electrons in the superconducting state remains unchanged respect to its value in the normal state. Moreover, it has been reported10 that Ψ breaks time reversal symmetry, which constitutes another key feature of unconventionality.
The Sr2RuO4 elastic constants Cij have been measured as the temperature T is lowered through Tc. The results show a discontinuity in one of the elastic constants2 . This implies that Ψ has two different components with the time reversal symmetry broken. Similar conclusions from a muon spin relaxation (μSR) experiment were reported by Luke et al.10 . Recently, experiments on the effects of uniaxial stress σi, as a symmetry-breaking field were performed by Clifford and collaborators3 , reporting that for Sr2RuO4 the symmetry-breaking field can be controlled experimentally. Additionally, experiments by Lupien et al.2 showed the existence of small step in the transverse sound mode T[100].
This body of results evidences the need of extending or developing theoretical models to explain the changes occurring in Cij at Tc, which, as far as we know, has not been carried out even in quite recent works3 . Thus, the aim of our work is to extend an elasticity property phenomenological theory to show that Sr2RuO4 is an unconventional superconductor with a two-component Ψ 4,11. Here, let us mention that a different theory of Sr2RuO4 elastic properties was presented by Sigrist12 . However, unlike this paper, Sigrist work does not take into account the splitting of Tc due to σi, and directly calculates the jumps at zero stress, where the derivative of T with respect to σi doesn’t exist.
In this work, we first perform an analysis based on a Ψ that transforms as one of the two dimensional irreducible representations of the Sr2RuO4 point group4,13. Subsequently, we construct the Sr2RuO4 superconducting phase diagram under an external σi . This phase diagram is employed to develop a complete theory of the elastic behavior of Sr2RuO4, based on a two component Ginzburg-Landau (GL) model. This allows to properly calculate the jumps in the components of the elastic compliances Sij. Finally, we propose that there are significant advantages for using Sr2RuO4 as a material for a detailed study of symmetry-breaking effects in superconductivity described by a two-component Ψ.
2.Ehrenfest relations for a uniaxial stress σi
Provided that σi does not split the phase transition , for applied σi, Ehrenfest relations can be derived in analogous manner to the case of applied hydrostatic pressure 11,14, under the condition that Tc is known as a function of σi. In order to simplify the calculations, we make use of the Voigt notation i = xx, yy, zz, yz, zx, xy.15
For a second order phase transition, the Gibbs free energy G derivatives
respect to T, the entropy S =
-(∂G/∂T)σ, and
respect to σi, the elastic strain
ei =
By using the definitions of the thermal expansion
From the first expression in Eq. (2), the relation for αi is found to be
likewise, from the second expression of Eq. (2), the relation for Sij is obtained to be,
It is important to distinguish that the print letter S denotes the entropy, while the symbol Sij means the elastic compliances. In similar manner, the print letter C stands for the specific heat and the symbol Cij for the elastic stiffness. Let us also point out that in deriving these expressions, we used the fact that for a given thermodynamic quantity Q, its discontinuity along the transition line points is obtained from ΔQ = Q(Tc + 0+)-Q(Tc - 0+), where 0+ is a positive infinitesimal quantity. Finally, by combining Eqs. (3) and (4), the variation in Sij is found to be:
Before continuing, it is interesting to mention that besides of our previous works4,11, we are not aware of any other works that have derived Ehrenfest relations for the case where applied σi produces a phase transition splitting.
3. Ginzburg-Landau model
In this section, a phenomenological model which takes into account the Sr2RuO4 crystallographic point group D4h is derived and employed. As we show, the analysis of G, using an order parameter which belongs to any of the one dimensional representations of D4h is not able to describe the splitting of Tc under an external stress field. In order to account properly for the splitting, superconductivity in must be described by a Ψ, transforming as one of the D4h two dimensional irreducible representations, E2g or E2u, which at this level of theoretical description render identical results4,11.
3.1. Superconducting free energy
In order to derive a suitable GL free energy GΓ, we first will suppose that the Sr2RuO4 superconductivity is described by an order parameter ψΓ, which transforms according to one of the eight one-dimensional representations of D4h: Γ = A1g, A2g, B1g, B2g, A1u, A2u, B1u, or B2u. Let us notice that an analysis employing the D4 point group renders similar results. Here we will analyze the terms in GΓ linear in σi and quadratic in ψΓ:
The terms proportional to σxx, σyy and σzz in Eq. (6) give rise to discontinuities in the elastic constants, evidenced from sound speed measurements17 . On the other hand, discontinuities in the elastic compliance S66 and in the elastic constant C66i arise from the linear coupling with σxy . However, due to symmetry, the later linear coupling does not exist for any Γ; therefore, S66 and C66 are expected to be continuous at Tc for any of the one-dimensional irreducible representation that assumes a one-dimensional ψΓ,. Nevertheless, the results of Lupien et al. experiments2 showed a discontinuity in C66. Hence, based exclusively on sound speed measurements, we conclude that none of the one-dimensional irreducible representations can provide an appropriate description of superconductivity in Sr2RuO4. As far as we know, this conclusion has not been previously established in the literature3 . Let us mention that for any one-dimensional Γ, a detailed analysis of the calculation of the jumps in C66 is presented in Ref. 11.
Due to the absence of discontinuity in S66 for any of the
one-dimensional Γ, the superconductivity in
Sr2RuO4 must be described by an order parameter
ψE transforming as one of the two-dimensional
representations
For the zero σi case, the expansion of G gives place to:
where α = α'(T - Tc0) and the coefficients b1, b2, and b3 are material-dependent real constants 20,21. These coefficients have to satisfy special conditions in order to maintain the free energy stability. The analysis of G is accomplished by considering two component (ψx, ψy) with the form:
where ηx and ηy are both real and larger than zero. After substitution of ψx and ψy in Eq. (7), G becomes:
For fixed values of the coefficients b1 and b2, if b3 > 0, G will reach a minimal value if the last term vanishes, i.e. if φ = 0. Moreover, if ηx and ηy have the form ηx = ηsin χ and ηx = ηcos χ, G becomes
where
At this point it is important to understand why the state (ψx, ψy) ∼ (1, ± iϵ) has been chosen for the analysis of σ6 and why it gives rise to the discontinuity in S6611. Minimization of Eq. (7) with respect to φ and χ, and employing Eq. (8) renders a set of solutions for the two-component order parameter which depend on the relation between the coefficients b1, b2, and b3 and also on the value of the phases φ and χ. Thus, for the E representation, solutions of the form,
are obtained, which are very similar to those found for the D4 one-dimensional irreducible representation. Therefore, these solutions are not able to account for the jump in C66. However, solutions with both components different than zero are also attained:
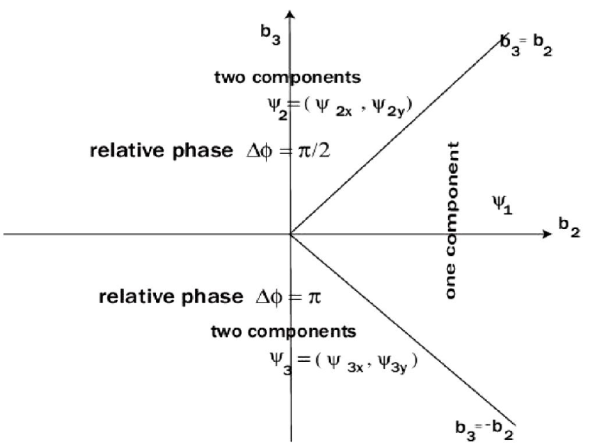
Each of these solutions corresponds to different relations for the bi. This is illustrated by Fig. 1, which shows the phase diagram, displaying the domains of ψ1, ψ2 and ψ3 as a function of b1, b2, and b3. Now, if the jump in C66 corresponds to a G minimum, the coupling term with σ6 must be taken to be different from zero. If the solution ψ2 is considered, the term containing σ6 becomes zero; therefore it is not acceptable. On the other hand, this requirement is satisfied by Ψ3, with the form (1, i)η. Hence, the GL analysis renders Ψ3 as the solution that breaks time reversal symmetry.
3.2. Coupling of the order parameter to an external stress
The transition to an unconventional superconducting state shows manifestations as the breakdown of symmetries, such as the crystal point group or the time reversal symmetry20,21. This loss of symmetry has measurable manifestations in observable phenomena, as the splitting of Tc under an elastic deformation. The coupling between the crystal lattice and the superconducting state is described Refs. 20 and 21. As explained there, close to Tc, a new term is added to G, which couples in second order Ψ with eij and in first order Ψ with σij. These couplings give place to discontinuities in Sijkl at Tc.
3.3 Analysis of the phase diagram
An expression for G accounting for a phenomenological coupling to C66 in the basal plane is given by
Here, Λi are the temperature-dependent
αi,
dij are the coupling terms between Ψ and
Sij and
Ej are the invariant
elastic compliance tensor components, defined below. In order to determine these
invariants describing the coupling of the order parameter to the stress tensor,
we construct the tensor Ej with
Voigt components E1 =
|ψx|2,
E2 =
|ψy|2 and
Now, let us consider the case of uniaxial compression along the a axis (only with σ1< 0). If in Eq. (13), only quadratic terms in Ψ are kept, this equation can be written as
here Tc+ (σ1) and Tcy (σ1) are given by
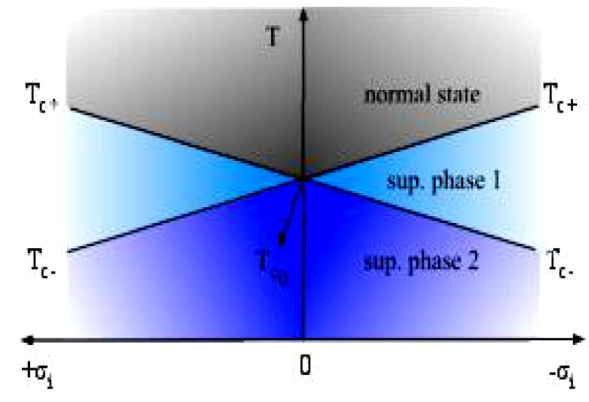
In what follows, we assume that d11 −d12> 0, such that T c+> Tcy . Notice that this does not imply any lost in generality, assuming d11 − d12< 0, would render an identical model, simply by exchanging the x and y indices. Here, Tc+ is the higher of the two critical temperatures at which the initial transition occurs. As should be expected, just below Tc+, only ψ x is non zero. As T is further lowered, another phase transition happens at Tc-, which is different than Tcy. Below Tc-, the ψy is also different from zero (see Fig. (2)). Thus, in the presence of a non zero compressible σ1, Ψ has the form (ψx, ψy) ≈ ψ(1, ± I ϵ) where ϵ is real and equal to zero between Tc+ and Tc- (phase 1), and increases from ϵ = 0 to ϵ ≈ 1 as T becomes smaller than Tc- (phase 2), as illustrated in Figs. (1) and (2).

Figure 2 Temperature behavior of the two component order parameter (ψx, ψy) for the case of a nonzero uniaxial stress below Tc. Notice that only the BCS component ψx (Tc+) ecomes non zero for temperatures between Tc+ and Tc-. The second unconventional component ψyTc-) only appears below Tc-.
The next step is finding Tc-. To achieve this goal, the equilibrium value of the non zero component of ψx,
To obtain Eq. (16), it is assumed that
4. Calculation of the discontinuities
As discussed before, an external uniaxial stress acting on the Sr2RuO4
basal plane breaks the tetragonal symmetry of the crystal. As a consequence of this,
when a second order transition to the superconducting state occurs, it splits into
two transitions. For the case of applied σ1, the
analysis of the behavior of the sound speed at
Tc requires a systematic study
of these second-order phase transitions. Moreover, thermodynamic quantities, such as
dTc/dσi,
Cσ, and
ασ, which are needed in order
to calculate the components
As depicted in Fig. (3), for a given σ1 ≠ 0 as T is lowered below Tc+, a first discontinuity for a thermodynamical quantity Q is observed at the first line of transition temperatures. This discontinuity along the transition line, corresponding to the higher transition temperatures, T = Tc+ (σi) is given by ∆Q+ = Q(Tc+ + 0+) − Q(T c+ − 0+), where 0+ is a positive infinitesimal number. If T is further dropped below T c-, a second discontinuity arises, and the lower line of transition temperatures appears. The discontinuity along this line, a T = Tc- (σi), is defined by ∆Q− = Q(Tc− + 0+) − Q(Tc− − 0+)18. The sum of these two discontinuities
gives the correct expressions for the discontinuities at Tc0, for the case with σi = 0, where the Ehrenfest relations do not hold directly 4. As an example of these discontinuities, the two jumps in Cσ under an external σi are sketched in Fig. (4).
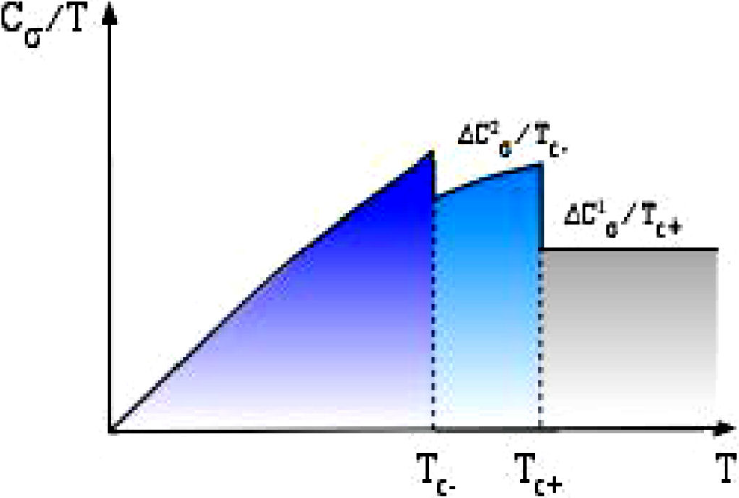
Figure 4 Schematic dependence of the specific heat on the temperature, for the case of an uniaxial stress splitting the Sr2RuO4 transition Temperature. Notice the two jumps in the heat capacity near the transition temperatures Tc+ and Tc-.
4.1. Jumps due to a uniaxial stress σ1
The free energy, Eq. (13), for the cases where both σ1 and σ6 are nonzero is:
Here αx = α'(T −Tc0 )+σ1d11 and αy = α'(T −Tc0 )+ σ1d12. If only σ1 is applied, this equation becomes:
Where ∆G = G − G0(T). The nature of the superconducting state that follows from Eq. (19), depends on the values of the coefficients b1, b2, and b3. The analysis from Eq. (19) of the superconducting part of G is performed by using, as was done previously, an expression for Ψ given by Eq. (8).
At Tc+ and in the presence of σ1, the second order terms in Eq. (19) dominate and Ψ has a single component ψx; whereas at Tc- a second component ψy appears. Thus, at very low T, the fourth order terms dominate the Eq. (19) behavior. Each of these two-component domains has the form of ψ2 given by Eq. (12). In this case, G can be written in terms of ηx and ηy as
The analysis of Eq. (20) depends on the relation between the coefficients b1, b2, and b3. Assuming that b3 > 0, and ηx and η y are both different from zero, and following the procedure described after Eq. (9) one arrives to
where ϵ is real and grows from ϵ = 0 to ϵ ≈ 1 as T is reduced below Tc-, while Eq. (20) becomes
To calculate the jumps at Tc+, we use
αx =
α'(T
−Tc+) and
αy =
α'(T −
Tcy), and assume that
Tc+>
Tcy . For the interval
Tc+> T >
Tc−, the equilibrium value for
Ψ satisfies αx
> 0 and αy = 0,
i.e. ηx
> 0 and ηy = 0,
with
The specific heat discontinuity at Tc+, relative to its normal state value, is calculated by using:
and renders the result
A schematic depiction of the Cσ discontinuities below this transition temperature is exhibited in Fig. (4). At Tc+, the discontinuity in ασ is calculated by applying the Ehrenfest relation of Eq. (3), yielding:
The discontinuities in Sij are obtained by using Eqs. (4) and (5), rendering the result,
In the previous expression a prime on an index (as in i' or j') indicates a Voigt index taking only the values 1,2, or 3. Thus, from Eq. (27) the change in S11 at Tc+ can be calculated to be
To find the discontinuities at Tc-, the invariant
In this expression, the second order term in ηy
is renormalized by the square of
ηx. The second transition
temperature is determined from the zero of the total prefactor of
Below Tc- the superconducting free energy, Eq. (28) has to be minimized respect to both components of Ψ. After doing so, ηx and ηy for this temperature range are found to be
This analysis shows that the second superconducting phase is different in symmetry, and that time reversal symmetry is broken. The change in
which results in
The size of these jumps is complicated to infer, because it depends on the material parameters b1, b2, and b3, and on the coupling constants d11 and d12.
With the help of the Ehrenfest relation, Eq. (3), the discontinuity in αi at Tc- is obtained to be
and after employing Eqs. (4) and (5), the discontinuity in
Here
Before continuing, it is important to emphasize that at at zero stress, the derivative of Tc with respect to σi is not defined; therefore, there is no reason to expect any of the Ehrenfest relations to hold 4,11.
4.2Jumps due to a shear stress σ6
When a shear stress σ6 is applied to the basal plane of Sr2RuO4, the crystal tetragonal symmetry is broken, and a second transition to a superconducting state occurs. Accordingly, for this case the analysis of the sound speed behavior at Tc also requires a systematic study of the two successive second order phase transitions. Very important to mention that the C66 discontinuity observed by Lupien 2 at Tc, can be explained in this context.
If there is a double transition, the derivative of Tc with
respect to σ6
i.e.
dTc/dσ6
is different for each of the two transition lines. At each of these transitions,
The Tc −σ6 phase diagram will be similar to that obtained for σ1; therefore, the diagram in Fig. (3) also qualitatively holds here. In the case of an applied σ6, ΔG is given by
Here α = α'(T − Tc0), and the minimization of ΔG is performed as in the σ1 case, i.e. by substituting the general expression for Ψ given in Eq. (8). After doing so, ΔG becomes
In the presence of σ6, the second order term determines the phase
below Tc+, which is characterized
by ψx and by
ψy = 0. As the temperature
is lowered below Tc- , depending of
the value of b3 a second component
ψ
y may appear. If at
Tc- a second component
occurs, the fourth order terms in Eq.
(37) will be the dominant one. Thus for very low T’s, or for
σ6 → 0, a time-reversal symmetry-breaking
superconducting state emerges. The analysis of Eq. (37) depends on the relation between the coefficients
b2 and b
3. It also depends on the values of the quantities η
x and
ηy, and of the phase
φ. If b3<
0, and ηx and
ηy are both nonzero, the
state with minimum energy has a phase φ = π/2. The transition
temperature is obtained from Eq.
(37), by performing the canonical transformations:
If, as was done before, ηξ = η sinχ and ηµ = η cosχ, Eq. (38) takes the form
ΔG is minimized if cos2χ = 1, this is, if χ = 0. Also, in order for the phase transition to be of second order, b', defined as b' ≡ b1 + b2 + b3, must be larger than zero. Therefore, if σ6 is non zero, the state with the lowest free energy corresponds to b3< 0, phase φ equal to π/2, and Ψ of the form:
In phase 1 of Fig. (3), φ = 0, and as T is lowered below Tc-, phase 2, φ grows from 0 to approximately π/2. Again, following an analysis similar to that carried out for σ1, the two transition temperatures Tc+ and Tc- are obtained to be:
The derivative of Tc+ with respect to σ6, and the discontinuity in
After applying the Ehrenfest relations, Eqs. (4) and (5), the results for
For Tc-, the derivative of this transition temperature with respect to σ6, and the discontinuities in the specific heat, thermal expansion and elastic stiffness respectively are:
Since for the case of σ6, the derivative of Tc with respect to σ6 is not defined at zero stress point, the Ehrenfest relations do not hold at Tc0. Thus, the discontinuities occurring at Tc0, in the absence of σ6, are calculated by adding the expressions obtained for the discontinuities at Tc+ and Tc-,
Notice that in this case, there is no discontinuity for
Since the phase diagram was determined as a function of σ6,
rather than as a function of the strain, (see Fig.
(3)), in this work, as in Refs. 4 and 11, we make use of the 6 × 6
elastic compliance matrix S, whose matrix elements are
Sij. However, the sound speed
measurements are best interpreted in terms of the elastic stiffness matrix
C, with matrix elements
Cij, which is the inverse
of S
23. Therefore, it is important
to be able to obtain the discontinuities in the elastic stiffness matrix in
terms of the elastic compliance matrix. Thus, close to the transition line,
C(Tc
+0+) =
C(Tc −
0+) + ∆ C and
S(Tc + 0+) =
S(Tc −
0+) + ∆S, where 0+ is positive and
infinitesimal. By making use of the fact that
5. Final remarks
Since for Sr2RuO4, the symmetry-breaking field, due to
σi, is under experimental control,
states of zero symmetry-breaking stress and of
σi single direction can be a-
chieved1,2,3. Hence, it has significant advantages the use of as
a material in detailed studies of superconductivity symmetry-breaking effects,
described by a two-component order parameter. Nevertheless, determining from
experimental measurements the magnitude of the parameters in the Ginzburg-Landau
model is complicated, because the number of independent parameters occurring for the
case of tetragonal symmetry is greater than for the case of hexagonal symmetry
(i.e. UPt3) 24,25,26. Thus for Sr2RuO4, three
linearly independent parameters b1,
b2, and b3, are required
to specify the fourth order terms in Ψ occurring in Eq. (1); whereas only two independent parameters,
b1 and b2, are required
for UPt3. For Sr2RuO4, two
independent ratios can be formed from the three independent
bi parameters, and these two
independent ratios could be determined, for example, by experimentally determining
the ratios
Measurements results for the Sr2RuO4 elastic constants below Tc are presented in Ref. 2. There, it is concluded that the quantities C44 and C11 − C12 follow the same behavior as those of the BCS superconducting transition, which is evidenced by a change in slope below T c0. On the other hand, a discontinuity is observed for C66 below Tc0, without a significant change in the sound speed slope as T goes below 1 Kelvin. It has been previously stated 2,11 that this kind of C66 changes can be understood as a signature of an unconventional transition to a superconducting phase. Thus, this set of results and others, as those of Clifford et al. 3, lead to consider Sr2RuO4 as an excellent candidate for a detailed experimental investigation of the effects of a symmetry-breaking field in unconventional superconductors.











 nueva página del texto (beta)
nueva página del texto (beta)