1.- Introduction

The stagnation point encounters highest pressure, enhancement of heat transfer and rate of mass deposition. Some practical examples are cooling of electronic devices by fans, cooling of nuclear reactors during emergency shutdown, heat exchangers placed in a low velocity environment, solar central receivers exposed to wind current and many others ¹. Due to these aspects, the study of stagnation point flow and heat transfer has attracted many researchers and engineers. Hiemenz ² initiated the study of two dimensional stagnation point flow over a stationary flat plate. He transformed the Navier-Stokes equations into ordinary differential equations by using similarity transformations and provided the exact solution of the nonlinear differential equations. Homann ³ extended this work to three dimensional problem of axisymmetric stagnation-point flow. Schlichting and Bussmann ⁴ provided numerical solution of Hiemenz problem and Eckert ⁵ also extended the work of Heimenz ² by incorporating heat transfer rate in the stagnation point flow. Ariel ⁶ obtained the analytical solution by introducing suction in flow field. Stagnation point flow over moving surfaces is also significant in practical purposes including paper production, the spinning of fibres, glass blowing, continuous metal casting ⁷, manufacturing of sheeting material through extrusion process especially in the polymer extrusion in a melt spinning process, aerodynamic extrusion of plastic sheets ⁸ etc. Chiam ⁹ investigated two-dimensional stagnation point flow of a viscous fluid over a linear stretching surface. He considered the situation where stretching velocity is equal to straining (free stream) velocity and concluded that no boundary layer exist in this case. Contrary to the Chiam ⁹, Mahapatra and Gupta in ^10,11, analysed the effects of magnetohydrodynamics and heat transfer respectively, in the region of stagnation point flow towards a stretching surface. They showed that the boundary layer is formed when a/c > 1 (ratio of straining to stretching velocity) and inverted boundary layer is emerge when a/c < 1. Unsteady analysis of flow over a stretching sheet is reported by Nazar et al., ¹². Recently, Mustafa et al. ¹³ Bhattacharyya et al., ¹⁴, Sharma and Singh ¹⁵, Bhattacharyya et al., ¹⁶, and Javed et al.,¹⁷ reported the investigations on the stagnation point flow over linear and non-linear stretching/shrinking sheets in different aspects. Wang ¹⁸ did the pioneering work and investigated the fluid flow due to stretching cylinder. Ishak et al. ^19,20 extended the work of Wang ¹⁸ by including the heat transfer effects due to impermeable stretching cylinder by considering suction and injection cases. They produced numerical and perturbation solutions of the flow problem. Inspired by previous work, many researchers performed their analysis over stretching cylinder with Newtonian and non-Newtonian fluids ^21-27 and incorporating innumerable physical configurations. In all aforementioned studies, the investigations carried out with temporally constant surface condition and the transient development of flow and heat transfer over stretching cylinder is not extensively studied. Merkin²⁸ stated that the value of surface temperature does not remains constant, it often fluctuate about some mean value. The influence of time dependent oscillations in surface conditions has received very little attention to date.

The aim of this paper is to study the unsteady mixed convection stagnation point flow over a cylinder with sinusoidal time dependent wall temperature. Graphs for velocity and temperature profiles, skin friction coefficient, Nusselt number and isotherms are plotted for various governing parameters.

2.- Problem formulation

We consider two dimensional unsteady laminar boundary layer fluid flow near the stagnation point over a cylinder as shown in Fig. 1. The cylinder is of radius r is permeable and continuously stretching with velocity V_w (z) along its own axis. To investigate the analysis, a cylindrical coordinate system is considered as such that the z-axis is taken along the axis of the cylinder and the r-axis is in the radial direction. It is assumed that the stretching (V_w ) and straining (V_e ) velocities are proportional to distance z from the stagnation point i.e., Vw=cz/l and Ve=az/l. The temperature at the surface of cylinder (T_w ) is considered to be sinusoidal and the ambient fluid temperature is T _∞ such that (T_w > T _∞). The unsteady boundary layer equations with Boussinesq approximation and viscous dissipation for continuity, momentum and energy equations are given by

FIGURE 1 Physical Model of the problem. 

(1)

The boundary conditions of the assumed flow are

where u and v are the velocity components along r and z directions, respectively, T is the temperature of the fluid within the boundary layer, v is the kinematic viscosity, g is the acceleration due to gravity, β_t is the thermal expansion coefficient, α is the thermal diffusivity, μ is the dynamic viscosity of fluid, ρ is the fluid density, c_p is the specific heat constant, U ₀ is the mass flux velocity, T ₀ is some temperature scale, t is the time, ϵ is the amplitude of surface temperature oscillation and ω is the frequency of the oscillation. Introducing the following non-dimensional variables

In which, η is the similarity variable, ψ is the stream function defined as u=r-1∂ψ/∂r and v=-r-1∂ψ/∂z which identically satisfies Eq. (1), ƒ(η, τ) is the dimensionless function and θ (η, τ) is the dimensionless temperature field. From relation (5), we obtain

Substituting Eqs. (5) and (6) into Eqs. (2) and (3), we get the following dimensionless system of partial differential equations

(7)

The boundary conditions in Eq. (4) become

(9)

(10)

where γ=νl/cR2 is curvature parameter, a/c is the ratio of straining (free stream) to stretching velocities, λ=Grz/Rez2 is the mixed convection parameter (Grz=gβtT0z4/lν2) and (Rez=cz2/lν). It is important to note that λ=0 corresponds to forced convection flow, λ>0 (T0>0) corresponds to assisting flow (i.e., the buoyancy forces acts parallel to free stream velocity), λ<0 (T0<0) corresponds to opposing flow (i.e., the buoyancy forces acts opposite to free stream velocity), β=lω/c is unsteady parameter (arises due to temperature oscillations), =ν/α is Prandtl number, S is the suction/injection parameter with S>0 represents suction case and S<0 is for injection case. The quantities of physical interest are the skin friction coefficient Cf and the local Nusselt number Nuz which are defined as:

in which the wall skin friction (τw) and the wall heat flux ( qw) are

Using the transformation (5) the skin friction coefficient and the local Nusselt number can be written as

3.- Numerical solution procedure

The nonlinear partial differential Eqs. (7) and (8) subject to the boundary conditions (9) are solved by using an implicit finite difference second order accurate scheme known as Keller Box method. The detailed method has explained in the book by Cebeci and Bradshaw ²⁹. The main steps are follows:

Step I: Eqs. (8) and (9) are reduced into first order differential after letting

as follows

with boundary conditions

Step II: The derivatives in η and τ-direction are replaced by central differences at j-1/2 and n-1/2 positions respectively as follows

However, the values of the functions are replaced by its mean value like

and as a result, the nonlinear system of algebraic equations is obtained.

Step III: To handle the non-linearity of resulting system of algebraic equations, Newton’s linearization process is implemented. For (i+1)th iterations, we write for every unknown function fji+1=fji+δfji, we obtained the system of linear equations.

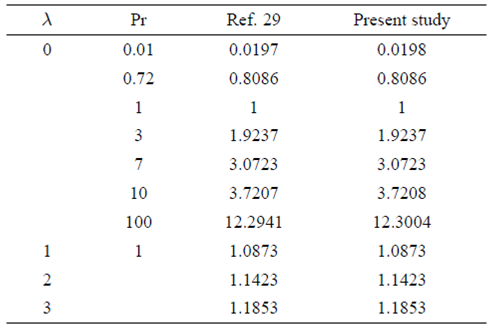
Step IV: The obtained system of linear equations is solved by block tri-diagonal technique. The edge of boundary layer thickness η∞ is chosen according to the values of the parameters. The iteration is continued for refinement in the solution until we achieved the difference between two consecutive iterations is less than 106. The employed technique is validated after comparing the numerical values of fηη(0,τ) with Mahapatra and Gupta ¹¹ and Nazar et al. ¹² as shown in Table I as a limiting case. Table II gives the comparison of -θη(0,τ) with Ishak et al. ²⁸ for limited cases. These results are in good agreement that gives us a confidence in accuracy of the employed numerical technique.

TABLE I Numerical values of fηη (0, τ ) for various values of a/c when γ = λ = S = β = τ = 0 with Mahapatra and Gupta ¹¹ and Nazar et al. ¹². 

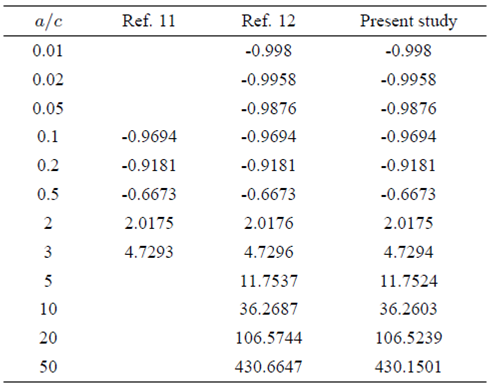
TABLE II Comparsion of −θη (0, τ ) for various values of λ and Pr when γ = a/c = S = β = € = 0 with Ishak et al.²⁹. 

4.- Results and Discussion

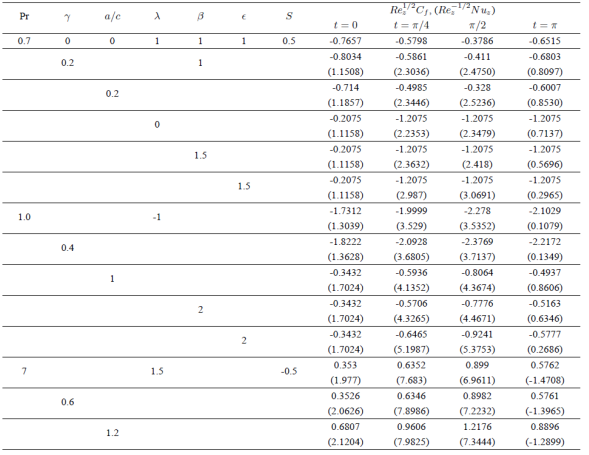
The non-linear partial differential Eqs. (7-8) subject to the boundary conditions (9) are solved numerically using very efficient implicit scheme known as Keller Box method for various values of emerging dimensionless parameters namely, curvature parameter (γ), velocity ratio parameter (a/c), mixed convection parameter (λ), suction/injection parameter (S), unsteadiness parameter (β), Prandtl number (Pr) and amplitude of oscillation in temperature (ϵ). The numerical results are computed in terms of velocity and temperature profiles, skin friction coefficient and Nusselt number. Figure 2 exhibits the velocity profile for different values of a/c for assisting case (λ=1) and opposing case (λ=1) at different time steps levels (τ= 0, π/4, π/2). It is observed that velocity increases for increasing values of time (τ) in assisting flow case (λ=1) and opposite behavior is observed in opposing flow case (λ=-1). This is due to the reason that in assisting flow, buoyant force assist the flow and in opposing flow, buoyant force delays the flow. Figures 3 and 4 show the velocity and temperature profiles for various values of curvature parameter (γ) and suction/injection parameter (S). In Fig. 3, it is noted that the velocity profile decreases near the surface of cylinder and increases far away from the surface with increase in curvature parameter (γ) for both suction (S=0.5) and injection (S=-0.5) parameter. It is also observed that in case of injection (S=-0.5), the velocity and momentum boundary layer thickness become higher as compare to suction (S=0.5). This is because injection enhances the flow near the surface. In Fig. 4 for both values of suction/injection parameter (S), the temperature profile increases with increase in curvature of the cylinder. It is further noted that, thermal boundary layer thickness can be increased with increase in curvature parameter (γ) both for injection/suction cases. Figure 5 demonstrates the effects on temperature profiles for various values of velocity ratio parameter (a/c) at different time step levels τ=0 and π/2. The temperature profile increase with the increasing value of time (τ) for all values of a/c. It is further important to note that the temperature profile decreases due to velocity ratio parameter (a/c) and hence thermal boundary layer thickness become smaller for large values of velocity ratio parameter (a/c). In Fig. 6, the temperature profile increases within the boundary layer for increasing time steps levels in both assisting and opposing flow cases. In opposing flow case the thermal boundary layer thickness is larger as compared to assisting flow case for all time steps levels (τ= 0, π/4, π/2). Influence of curvature parameter (γ) on velocity and temperature profile for (assisting flow) and (opposing flow) is shown in Figs. 7 and 8, respectively. As curvature parameter (γ) increases the surface of cylinder squeezes due to which surface area reduces. As a result velocity of the fluid increases with increase in curvature parameter (γ). Similarly temperature of the fluid also enhances within the boundary layer region due to increase in curvature parameter (γ). In addition, momentum boundary layer augments in case of λ= 0.5 (assisting flow) in comparison with λ= -0.5 (opposing flow) but very little change is observed in momentum boundary layer for λ= 0.5 (assisting flow) and λ= -0.5 (opposing flow) cases. Figures 9 and 10 illustrate the variations in skin friction coefficient and Nusselt number against time (τ) for different values of unsteadiness parameter (β). Due to sinusoidal nature of temperature, the amplitude of skin friction enhanced with backward phase shift against time (τ) with increase in unsteadiness parameter (β). Figures 11 and 12 show the values of skin friction and Nusselt number against (τ) for different values of (ϵ). It is noted that amplitude of oscillations in the values of skin friction and Nusselt number increases with increase in (ϵ). It is also perceived that as the values of (ϵ) drop, the amplitude of oscillations in skin friction and Nusselt number also diminish for (ϵ=0), the case of constant surface temperature is recovered. The effect of Prandtl number (Pr) on heat transfer rate is observed in Fig. 13. The heat transfer rate enhances due to increase in Prandtl number (Pr) and amplitude of oscillation become larger for large values of Prandtl number (Pr) against time (τ). Figures 14 and 15 demonstrate the isotherms for curvature parameter (γ) and amplitude of temperature oscillations (ϵ). Due to increase in curvature parameter (γ) and amplitude of temperature oscillations (ϵ), a pattern of increasing behavior in sinusoidal nature of isotherms is clearly visible. Table III is constructed to exhibit the behavior of sundry parameters on skin friction coefficient (Rez1/2Cf) and local Nusselt number (Rez-1/2Nuz). It is important to mention that negative values of local Nusselt number represent that heat is transferred from surface of cylinder to the fluid.

FIGURE 2 Velocity profile for λ = 1 (assisting flow) and λ = −1 (opposing flow). 

FIGURE 3 Velocity profile for different values of γ at S = 0.5 (suction) and S = −0.5 (injection). 

FIGURE 4 Temperature profile for various values of γ at S = 0.5 (suction) and S = −0.5 (injection). 

FIGURE 5 Temperature profile for various value of a/c at time τ = 0 and τ = π/2. 

FIGURE 6 Temperature profile for various values of τ. 

FIGURE 7 Velocity profile for various values of γ. 

FIGURE 8 Temperature profile for various values of γ. 

FIGURE 9 Variation of skin friction coefficient against time for different values of β. 

FIGURE 10 Variation of local Nusselt number against time for different values of β. 

FIGURE 11 Variation of skin friction coefficient against time for different values of ϵ. 

FIGURE 12 Variation of local Nusselt number against time for different values of ϵ. 

FIGURE 13 Variation of local Nusselt number against time for different values of Pr. 

FIGURE 14 Isotherms for different values of curvature parameter γ. 

FIGURE 15 Isotherms for different values of amplitude of temperature oscillations ϵ  

TABLE III Values of Re1/2 Cƒ and (Rez−1/2 Nuz) for various parameter a/c, γ, λ, ϵ, β, S and Pr. 

5.- Conclusion

In this paper, unsteady mixed convection stagnation point flow due to stretching cylinder with sinusoidal wall temperature is reported. The governing partial differential equations are transformed into dimensionless form. The obtained partial differential equations are solved by an efficient and accurate finite difference scheme known as Keller box method. It is noted that the assisting buoyant flow increases the velocity profile and opposing buoyant flow decreases the velocity profile. It is apparent that as the amplitude of temperature oscillation drop, the amplitude of oscillations in skin friction and Nusselt number also diminish. The heat transfer rate increases due to increase in Prandtl number and amplitude of oscillation also increases with passage of time. Most importantly, this phenomenon of maximizing heat transfer near the stagnation point flow over a stretching cylinder can be enhanced by introducing the sinusoidal heat at the surface of the cylinder.

Nomenclature

a, c Dimensionless constant

R Radius of cylinder

Cf Skin friction coefficient

cp specific heat at constant pressure

ƒ Dimensionless stream function

k Thermal conductivity of fluid

l reference length

Nuz Nusselt number

p Pressure

Pr Prandtl number

cp specific heat at constant pressure

qw Surface heat flux

Rez Local Reynolds number

r Radial coordinate

T Fluid temperature

Tw Temperature at the surface of cylinder

T∞ Ambient fluid temperature

u Radial velocity component

Ve Free stream velocity

Vw Stretching velocity of cylinder

v Axial velocity component

z Axial coordinate

Greek symbols

β Unsteady parameter

βt Thermal expansion coefficient

γ Transverse curvature

ϵ Amplitude of temperature oscillation

η Similarity variable

θ Dimensionless temperature

ν Kinematic viscosity

µ Dynamic viscosity

τ Time

τ_w Surface shear stress

ρ Density

ψ Stream function

Subscripts

w Conditions at the surface

∞ Conditions at infinity