Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Geofísica internacional
versión On-line ISSN 2954-436Xversión impresa ISSN 0016-7169
Geofís. Intl vol.50 no.4 Ciudad de México oct./dic. 2011
Review paper
Seismic waves and surface waves: past and present
Peter G. Malischewsky*
Friedrich–Schiller–Universitat Jena Institut für Geowissenschaften Jena, Germany. *Corresponding author: p.mali@uni–jena.de
Received: September 22, 2011.
Accepted: September 26, 2011.
Published on line: September 30, 2011.
Resumen
La presente disertación fue presentada por el autor a raíz de una estancia de un año en la Universidad Nacional Autónoma de México. La fértil relación entre las ciencias de la tierra de América Latina con Alemania se remonta a Alejandro von Humboldt. Se analizan algunos aspectos de la evolución de la sismología en general, y en Jena en particular, que tocan el desarrollo de la teoría de ondas y específicamente, de las ondas superficiales. El trabajo fue presentado en el Gran Auditorio de la Universidad Federico Schiller en Jena, Alemania, como una conferencia invitada en ocasión de la celebración del Centésimo Aniversario de la Investigación Sismológica en Jena.
Palabras clave: historia de la sismología, teoría de ondas, ondas superficiales.
Abstract
The author presented this lecture after a one–year stay at UNAM, in Mexico. The link between Latin American and German Earth scientists is invoked by citing the example of Alexander von Humboldt. Some aspects of the evolution of seismology in general and particularly in Jena are discussed. Special attention is paid to developments in wave theory and the theory of surface waves. This presentation was given on June 16, 2000 in the great hall of the Friedrich–Schiller University Jena on the celebration of "Hundred Years of Earthquake Research at Jena."
Key words: history of seismology, wave theory, surface waves.
Introduction
In a letter to Schiller (1800), Johann Wolfgang von Goethe called the city of Jena a "mainspring of knowledge." Farsighted scientists such as Heinrich v. Eggeling, Rudolf Straubel and Adolf Winkelmann pioneered seismological research in Jena. While the subject may have seemed rather exotic at the time —and still is, at least in some parts of Europe— it fitted the universality of Goethe's genius. A celebration of hundred years of seismology in Jena is most timely as it allows me to express our indebtedness to the great naturalist Alexander von Humboldt (17691859, see Ertel, 1953). We owe Humboldt an early monographic treatment of some specific earthquakes, and geologist Leopold von Buch (1774–1853) the earliest scientific earthquake theory based on the assumption of a causal connection with volcanism.
The concept of volcanism was then broader than it is today, as tectonic processes were included. The association of earthquake science with Jena becomes clear when one considers Humboldt's interest in the classics. In a letter of 1806 addressed to Karoline von Wolzogen he reminisces:
"Whether deep in the Amazon forests or on the high peaks of the Andes I could perceive, from pole to pole, the same pulse of life in rocks, plants and animals that animates the human spirit. Everywhere I felt transported by the powerful feelings born of my Jena experience: as Goethe's profound insights on nature had raised me to a state where I felt as if endowed with new sensory organs".
Humboldt was quite active in the developmental stage of geophysics at a time when seismology and other geophysical disciplines were emerging as independent fields. Unfortunately he was prevented from making more substantial contributions to the field because he died before seismology had fully emerged as a science.
Emil Wiechert (1861–1928) formulated in 1902 the purpose of seismological research as follows: "A tremor in rock yields signals from afar: let us decipher the message!". In order to fully achieve this lofty objective we must first understand the behavior of seismic waves and the theory of these phenomena. Independent contributions in this area were achieved in Jena somewhat late: thus I feel justified in pointing out some milestones achieved elsewhere, though without any claim to completeness. The foundation of the theory of seismic waves is undoubtedly the theory of elastic waves. Elastic–wave theory began to stagnate toward the end of the 19th century, after the 1887 Michelson experiment had discarded the existence of elastic ether as a carrier of electromagnetic wave phenomena. Speaking of Jena, it is worth mentioning that this experiment, crucial as it was to the development of physics, was duplicated in Jena by Georg Joos (1894–1959) with narrower error margins.
Broadly speaking, we may understand waves as propagation phenomena in space and time which satisfy the general differential equation of total hyperbolic type
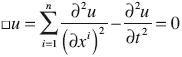
where □ is the d'Alembert operator.
Periodic waves, an important particular case, are represented by the monochromatic ansatz
u = A(x,y,z)eiωt
where the amplitude A satisfies the Helmholtz equation
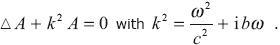
It is often represented by the expression for plane waves
A(x,y,z) = A0 exp [i k (n1 x + n2+y+n3 z]
with n12 + n22 + n32 = 1,
which contains all the major properties of seismic waves. In terms of the behaviour of the wave number k and the components of the unit vector  in the direction of propagation we may classify waves as follows:
in the direction of propagation we may classify waves as follows:
• longitudinally damped, when damped in the direction of propagation,
• obliquely damped, when damped at an angle to the direction of propagation, and
• transversely damped, when damped normally to the direction of propagation.
The surface wave phenomenon may also be explained by transversely damped waves. While progressive waves are always in the form

vibrations are changes of state of a quantity that is a periodic time function, such as φ(t) = A sin (ωt + ψ). It should be clear that seismograms of every kind are always recordings of vibrations, as they are obtained at a fixed station while waves are more complicated processes in space and time. The theory of vibrations is an independent field of physics with important applications in engineering seismology. A former member and director of the Jena institute, Hans Martin (1899–1991), dealt intensely with vibrations in his thesis and returned later to this subject. His outstanding chapter on "Mechanical vibrations" in the popular manual of experimental physics by Wien and Harms (1934) deserves an important place among the relevant literature.
The first recorded teleseism was a Japanese earthquake record obtained by v. Rebeur–Paschwitz in Potsdam somewhat coincidentally on 17 April, 1889 (Figure 1). Around the turn of the century there was already continuous recording in Jena. An example is the N–S record of the horizontal Wiechert pendulum of an earthquake in Jan Mayen at 2500 km distance (Figure 2). The arrivals of body waves and surface waves are clearly seen. Both wave types are predicted by the equations of motion in an elastic halfspace. They represent the response of the Earth to an excitation at the source.
A separate treatment of these wave types is historically conditioned: it is also done for practical reasons. The Earth is excited by an earthquake and it yields normal oscillations as those caused when striking a bell. This concept is not new, but the theoretical analysis took a long period of time and is still continuing (Dahlen and Tromp, 1998). Normal oscillations of the Earth are represented as complicated spherical harmonics such as those shown in Figure 3 for the 6th degree and the first order.

Such standing oscillations may be used to synthesize propagating seismic waves as observed in the Earth. Conversely, surface waves which have completed at least one path around the Earth may be used to synthesize the normal modes by superposition. In his thesis "Velocity of propagation and absorption of earthquake waves", W. Pechau discussed the propagation of such waves in 1912 in Jena.
The extremely complicated processes which occur after an earthquake may be illustrated by the computer program SeisWave by Alan J. Jones. Figure 4 shows a snapshot of an earthquake in New Zealand in 1994. Some seismograms from stations around the Pacific are shown on top. The surface waves are seen as thin concentric circles around New Zealand, and the phases SS, S and PP are shown as bold circles (below, left). The figure at the lower right represents the paths of different body waves in a section through the Earth.
All surface wave phenomena may be understood as special cases of waveguide phenomena. When discussing surface waves, the pioneering work of Lord Rayleigh (18421919) should not be omitted. As early as 1885 he predicted the existence of guided waves on the free surface (now known as Rayleigh waves) and he brilliantly recognized their importance in earthquakes from first principles. Other types of surface waves were discovered by Augustus E. H. Love (1863–1940), Horace Lamb (1849–1934) and others, and are known by their discoverers (Figure 5).
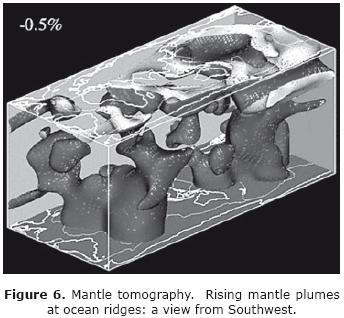
Seismic tomography followed upon the success of medical tomography. It has produced impressive advances over the past twenty years for the exploration of the interior of the Earth. Figure 6 shows an application of mantle tomography by Wei–jia Su of the Harvard seismological laboratory, using P and S waves. Plate tectonics is driven by convection, and the figure shows how the lighter material rises into the spreading centers of oceanic rises.
The current trend in tomography is toward the analysis of the whole seismogram ("waveform tomography"), rather than of single wave types. Despite the single out the following, among many others. Snieder and Trampert (1999) point out the importance of nonlinearity in tomography. In Figure 7, the ray paths in a tomographic experiment are shown with uniform velocity (left), with a low–velocity inclusion (center), and with a high–velocity inclusion (right). In the second case the paths are bent around the inclusion while in the third case there is a shadow zone at the central station. Both cases present problems of interpretation.
Wielandt (1992) pointed out the surprising fact that little thought has been given to the interpretation of non–uniform wave fields. What is the meaning of phase velocity in this case? It turns out that one must carefully distinguish between a dynamic and a structural wave number. It is important to recall that every reflection of waves ahead of the reflector generates a complicated time–dependent interference pattern. Figure 8 shows an example for oblique incidence ( j=10°), where transformed waves are not shown.

Even for the simple case of vertical incidence the superposition of direct and reflected waves generates a wave field of non–uniform phase velocity, where one might speak of "accelerated" waves. Waves of time–dependent phase velocity and amplitude may be described by the following expressions not previously published:
cos (k x – ωt)+r cos(k x+ωt)=A(t)cos[k x –d(t)]
where r is the reflection coefficient, A is the amplitude
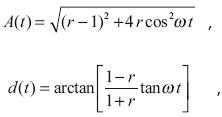
and the variable phase velocity is
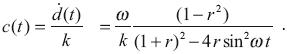
Such effects must be considered in more accurate investigations.
The preceding observations are of a general nature. As a complementary information we present some early work done in Germany and Switzerland on the theory and observation of surface waves. K. Uller (1914, 1918, 1928) provided new and unconventional contributions to the theory of surface waves, some of which were misunderstood or discredited. A final evaluation from a modern point of view is still pending. There are contributions to the theory of Love waves by E. Meissner (1921, 1922, 1927). Both G. Angenheister (1906) and O. Meissner (1913) discussed the extinction of seismic surface waves as a result of anelasticity. They also contributed observations of surface waves along oceanic and continental paths [O. Meissner (1915), G. Angenheister (1921)]. Furthermore, O. Meissner (1929) investigated the problem of the distance dependence of the period.
Let us now describe the development of surface wave research in Jena. Early systematic studies of surface waves centered on group velocity determinations using the "peak and trough" method for Eurasian earthquakes (Figure 9) by D. Güth (1962).
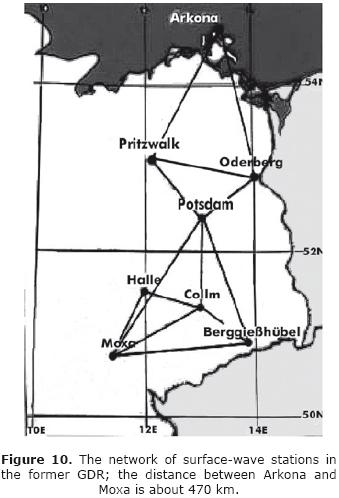
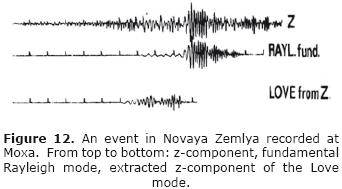
Later, research on surface waves expanded significantly and a network of standard seismic stations was built up in 1969 (Figure 10). It operated for about 15 years and produced many results, some of which should be mentioned here. Neunhöfer (1985) obtained mean dispersion curves of phase velocities (Figure 11) for the Variscan south and the pre–Variscan north of the former German Democratic Republic. He found some significant differences originating in the crust and upper mantle. A different line of research concerned the behavior of surface waves in anisotropic media. Anisotropy perturbs the splitting of surface waves into Rayleigh and Love waves thus producing generalized families of surface waves. Neunhöfer and Malischewsky (1981) studied an event in Novaya Zemlya and succeeded in extracting an abnormal z–component of Love waves (Figure 12). Another event from Kyushu, Japan, showed a similar effect. It was tempting to assume that the cause of these anomalies was anisotropy in the northern part of the Eurasian continent.

Considerable research on the reflection of surface waves at discontinuities has been done at Jena. Figure 13 presents an example by Neunhöfer (1985), who extracted the reflected wave groups from an earthquake in South America. He also attempted to localize the reflecting elements for these wave groups, which should be collocated on an ellipse for geometrical reasons.
After about 1970 there was considerable research on surface wave theory in Jena, because the available theory had failed to explain all effects of propagation of surface waves in perturbed waveguides. The following are some key results of this research:
• Combination of Rayleigh and Love waves into an homogenous eigenfunction system
• Orthogonality and completeness
• Research on reflected and transmitted surface waves
• Formulation by singular integral equations with consideration of body waves
• Treatment of complicated waveguide structures
• Investigation of critical Poisson ratios
• Problems of surface waves on curved surfaces.
The results obtained up to 1986 are outlined in a monograph by Malischewsky (1987). The applications include coal–seam seismics and optical waveguides. Subsequently, the research on reflected wave groups was significantly extended by Meier, who succeeded in producing a more solid theoretical and experimental foundation for tomography by reflected and dispersed surface waves using ultrasound experiments (Meier et al., 1997). GRSN data were used extensively, and experimental reflection coefficients were obtained for a region in Central Europe. Figure 14 illustrates how important geological structures and new insights can be gained in this way.
Recently Meier and Malischewsky (2000) studied surface wave mode conversion at a passive continental margin on a curved Earth. Finally, Malischewsky (2000) revised the old familiar formulas for the reflection of body waves at a free surface in terms of their relationship with Rayleigh waves. New results were obtained.
In conclusion may I quote William Blake (1757–1827): Every thing possible to be believ'd is an image of truth. With a bow to Blake I submit that not everything offered as truth by 3–D seismic tomography is possible to be believed— unless the fine structure of wave theory has been considered.
Acknowledgements
A word of thanks goes to Dr. Cinna Lomnitz at UNAM, who translated this oral presentation into English. I thank Dr. H. Neunhöfer, Jena, for numerous comments and discussions, Mrs. K. Rehm, University of Jena, for supplying historical seismograms, and Dr. J. Schweitzer, NORSAR, Norway, for his extensive literature search. The following bibliography contains some references that appear as secondary references in works by B. Gutenberg (1936) and Güth, Germann and Stelzner (1974).
I wish to dedicate this article to Dr. Ismael Herrera, honored academic teacher and friend whose 80th birthday we are celebrating these days. He paved my way to Mexico, a remarkable and wonderful country, and I will never forget this.
Bibliography
Dahlen F.A., Tromp J., 1998, Theoretical Global Seismology. Princeton University Press, Princeton, 944 pp. [ Links ]
Ertel H., 1953, Entwicklungsphasen der Geophysik, Deutsche Akademie der Wissenschaften zu Berlin, Vorträge und Schriften, Heft 52, Akademie–Verlag, Berlin. [ Links ]
Goethe J.W. von, 1887–1919, Goethes Werke in 133 Bänden, 4. Abteilung, Briefe, Bd. 15, Weimar, p. 91. [ Links ]
Grossmann E., Martin H., Schmidt H., 1934, Schwingungs– und Wellenlehre, In: Handbuch der Experimentalphysik Bd. 17,1 von W. Wien und F. Harms (Herausg.), Akad. Verl.–Ges., Leipzig, pp.1–38. [ Links ]
Gutenberg B. (Ed.), 1936, Handbuch der Geophysik Bd. IV. Verlag Gebrüder Bornträger, Berlin. [ Links ]
Güth D.,1962, Gruppengeschwindigkeitsdispersion kurzperiodischer Oberflächenwellen von Eurasischen Erdbeben, in Proceedings of the 8th Assembly of the ESC, Jena, Germany, September. [ Links ]
Güth D., Germann D., Stelzner J., 1974. Zur Geschichte der Forschungseinrichtungen für Seismologie in Jena von 1899–1969, AdW der DDR, Zentralinstitut für Physik der Erde, printed as manuscript, Potsdam. [ Links ]
Malischewsky P., 1987, Surface waves and Discontinuities. Elsevier, Amsterdam, 229 pp. [ Links ]
Malischewsky P.G., 2000, Some special solutions of Rayleigh's equation and the reflection of body waves at a free surface. Geofísica Internacional, 39, 155–160. [ Links ]
Meier T., Malischewsky P.G., Neunhöfer H., 1997, Reflection and transmission of surface waves at a vertical discontinuity and imaging of lateral heterogeneity using reflected fundamental Rayleigh waves. Bull. Seis. Soc. Am., 87, 1648–1661. [ Links ]
Meier T., Malischewsky P.G., 2000, Approximation of surface wave mode conversion at a passive continental margin by a mode–matching technique. Geophys. J. Int., 141, 12–24. [ Links ]
Neunhöfer H., Malischewsky P.G., 1981, Anomalous polarization of Love waves indicating anisotropy along paths in Eurasia. Gerl. Beitr. Geophysik, 90, 179–186. [ Links ]
Neunhöfer H., 1985, Primär– und Sekundäreffekte bei der Ausbreitung seismischer Oberflächenwellen und ihre geophysikalischen Ursachen. Veróffentl. des Zentralinstituts für Physik der Erde, No. 85, Potsdam. [ Links ]
Snieder R., Trampert J., 1999, Inverse Problems in Geophysics, in: Wavefield Inversion (ed. by A. Wirgin). Springer–Verlag, New York, pp. 119–190. [ Links ]
Wielandt E., 1993, Propagation and structural interpretation of non–plane waves. Geophys. J. Int., 113, 45–53. [ Links ]














