Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Geofísica internacional
versão On-line ISSN 2954-436Xversão impressa ISSN 0016-7169
Geofís. Intl vol.50 no.4 Ciudad de México Out./Dez. 2011
Review paper
A brief overview of non–overlapping domain decomposition methods
Ismael Herrera*, Antonio Carrillo–Ledesma and Alberto Rosas–Medina
Instituto de Geofísica, Universidad Nacional Autónoma de México, Ciudad Universitaria, Delegación Coyoacán 04510, México D.F. *Corresponding author: iherrera@geofisica.unam.mx
Received: July 1, 2011.
Accepted: July 7, 2011.
Published on line: September 30, 2011.
Resumen
Se presenta una visión general de los métodos de descomposición de dominio con dominios ajenos. Los métodos más eficientes que existen en la actualidad, el BDDC y el FETI–DP, se ubican en un marco 'primal' (el 'espacio de vectores derivados (DVS, por sus siglas en inglés)'), el cual permite una presentación sintética y efectiva tanto de las formulaciones primales como de las 'duales'. El marco conceptual del espacio de los vectores derivados tiene alguna similitud con el que usa BDDC, pero una diferencia importante es que en el marco DVS el problema tratado se transforma en otro definido en el espacio vectorial producto, mientras que en el BDDC no se hace tal cosa. Esto simplifica los algoritmos, los cual se sintetizan en un breve conjunto de fórmulas matriciales muy generales que son aplicables a matrices simétricas, no simétricas e indefinidas, cuando ellas provienen de la discretización de ecuaciones diferenciales parciales o sistemas de tales ecuaciones. Las fórmulas matriciales de este conjunto, son explícitas y pueden ser usadas directamente para desarrollar códigos computacionales. Hasta donde sabemos, dos de los algoritmos precondicionados del conjunto mencionado, son totalmente diferentes a cualquiera de los reportados en la literatura y deben ser motivo de investigaciones futuras.
Palabras clave: subestructuración iterativa, métodos de descomposición en dominios ajenos; BDD, BDDC; FETI, FETI–DP; pre condicionadores; espacio producto; multiplicadores de Lagrange.
Abstract
An overview of non–overlapping domain decomposition methods is presented. The most efficient methods that exist at present, BDDC and FETI–DP, are placed in a 'primal' framework (the 'derived–vectors space (DVS)') which permits a synthetic and effective presentation of both: primal and 'dual' formulations. The derived–vectors space is similar to the setting used in BDDC. A significant difference is that, in the DVS framework, the problem considered is transformed into one that is defined in a product vector space while in BDDC that is not done. This simplifies the algorithmic formulations, which are summarized in a set of matrix–formulas applicable to symmetric, non–symmetric and indefinite matrices generated when treating numerically partial differential equations or systems of such equations. They can directly be used for code development. Two preconditioned algorithms of the mentioned set had not been reported previously in the DDM literature, as far as we know, and are suitable for being researched.
Key words: iterative substructuring, non–overlapping domain decomposition, BDD, BDDC, FETI, FETI–DP, preconditioned, product space, Lagrange multipliers.
Introduction
In this paper we present a synthetic and brief overview of some of the most important algebraic formulas of non–overlapping domain decomposition methods (DDM). We will use a framework that is very convenient for this purpose, which will be called the 'derived–vector space (DVS)' framework [Herrera and Yates 2010; Herrera and Yates 2009 ].
Among the frameworks that are used in non–overlapping DDM formulations two categories are distinguished: dual frameworks, which as in the case of FETI and its variants use Lagrange multipliers, and primal frameworks, which as in the case of BDD and its variants tackle the problems directly without resource to Lagrange multipliers [Dohrmann 2003; Mandel and Dohrmann 2003; Mandel et al, 2005; Toselli and Widlund 2005]. The derived–vector space (DVS) framework used here is a primal framework similar to that of the BDDC formulations. A significant difference between the DVS framework and that of BDDC formulations is that in the DVS–framework the problem is transformed into one defined in the derived–vectors space, which is a product space containing the discontinuous functions, and thereafter all the work is carried out in it. In BDDC formulations, on the other hand, the original space of continuous functions is never completely abandoned; indeed, one frequently goes back and forth from the degrees of freedom associated with the original space of continuous functions to the degrees of freedom associated with the substructures, which in such formulations play the role of the product space (see Section 15 for a more detailed discussion).
Although the DVS framework is a primal framework, dual formulations can also be accommodated in it; this feature permits unifying in its realm both dual and primal formulations; in particular, BDDC and FETI–DP. Also, the derived–vectors space constitutes a Hilbert–space with respect to a suitable inner product –the Euclidean inner–product– and, while using the DVS formulation, we will profit from its Hilbert–space structure achieving in this manner great simplicity for the algorithm formulations. Furthermore, the theory of partial differential equations in discontinuous piecewise defined functions [Herrera 2007] is used for establishing clear correspondences between the problems at the continuous level and those obtained after discretization (see, Section 9 of [Herrera and Yates 2010] and Appendix "B" of the present article). In particular, in this paper using the DVS–framework we present simple explicit matrix formulas that can be applied to simplify code development of models governed by a single differential equation or systems of such equations; they have a wide range of applications to practical problems which includes non–symmetric and indefinite matrices. We also remark that all our developments are carried out in vector spaces subjected to constraints and therefore all the DVS algorithms here presented are algorithms with constraints.
In this paper, a survey of the non–overlapping DDM algorithms that can be developed in the DVS framework is carried out, which yields a synthetic and brief overview of some of the most important algebraic formulas of non–overlapping domain decomposition methods (DDM). In particular, FETI–DP [Farhat and Roux 1991; Mandel and Tezaur 1996; Farhat et al., 2001; Toselli and Widlund 2005] and the BDDC [Dohrmann 2003; Mandel and Dohrmann 2003; Mandel et al., 2005; Mandel 1993; Mandel and Brezina 1993; Mandel and Tezaur 2001], which are the most successful nonoverlapping DDM, are incorporated producing in this manner DVS–versions of them. In recent years a number of papers have discussed connections between BDDC and FETI–DP [Mandel et al., 2005; Li and Widlund 2006; Klawonn and Widlund 2001], and similar connections encountered using the DVS–framework are here discussed. Also, by now in the literature the developments on DMM for non–symmetric and indefinite matrices have been significant (see for example [Da Conceição 2006; Farhat and Li 2005; Li and Tu 2009; Toselli 2000; Tu and Li; Tu and Li]). As said before, the DVS–framework for non–overlapping DDM is applicable to such kind of matrices; indeed, [Herrera and Yates 2009] was devoted to extend the DVS framework to non–symmetric and indefinite matrices. The assumptions under which such extension is possible were spelled out with precision and detail in Section 9 of [Herrera and Yates 2009]. When such results are complemented with those presented in Sections 7 to 14 of this paper, they permit establishing with certainty and precision in each case when such algorithms can be applied. Thus far, we have not seen discussed this topic with this generality elsewhere, in spite of its obvious importance.
In conclusion, our results can be effectively summarized in eight matrix–formulas; of them, those with greater practical interest are of course the preconditioned formulations. The non–preconditioned ones are included because they are important for understanding properly the theoretical developments. Of the four preconditioned matrix formulas contained in that summary, as said before, two correspond to the BDDC and FETI–DP algorithms, while for the other two we have not been able to find suitable counterparts in the DDM literature already published, although the effectiveness of their performance can be expected to be of the same order as BDDC or FETI–DP.
The paper is organized as follows. Section 2 is devoted to present an overview of the DVS framework. The problem to be dealt with (the original problem) is stated in Section3, while Sections 4 and 5 introduce the notions of the derived–vectors space. The general problem with constraints defined in the derived–vector space, equivalent to the original–problem, is formulated in Section 6. The guidelines for the manner in which Sections 7 to 14 were organized is supplied by the results of Appendix "B". Only two basic non–preconditioned algorithms were considered: the Dirichlet–Dirichlet and the Neumann–Neumann algorithms; a primal and a dual formulation is supplied for each one of them. In turn, each one of the four non–preconditioned formulations so obtained is preconditioned. This yields, in total, the eight algorithms mentioned before. Sections 7 to 10 are devoted to the four non–preconditioned algorithms, while Sections 11 to 14 are devoted to the preconditioned algorithms. The DVS versions of BDDC and FETI–DP are obtained when the primal and dual formulations of the non–preconditioned Dirichlet–Dirichlet algorithms are pre–conditioned, respectively. Some comparisons and comments about FETI–DP and BDDC as seen from the DVS framework are made in Section 15, while the Conclusions are presented in Section 16. Three Appendices are included in which some complementary technical details are given.
Section 2
Overview of the DVS framework
In previous papers [Herrera and Yates 2010; Herrera and Yates 2009] a general framework for domain decomposition methods, here called the 'derived vector space framework (DVS–framework)', has been developed. Its formulation starts with the system of linear equations that is obtained after the partial differential equation, or system of such equations, has been discretized. We shall call, this system of linear equations, the 'original problem'. Independently of the discretization method used, it is assumed that a set of nodes and a domain–partition have been defined and that both the nodes and the partition–subdomains have been numbered. Generally, some nodes belong to more than one partition–subdomain (Figure 1). For the formulation of non–overlapping domain decomposition methods, this is an inconvenient feature. To overcome this problem, the DVS framework introduces a new set of nodes, the 'derived nodes'; a derived node is a pair of natural numbers: a node–index followed by a subdomain–index, which may be any that fulfills the condition that the node involved belongs to the corresponding partition–subdomain. As for the node–indices, they are referred to as the 'original–nodes'.


Furthermore, with each partition–subdomain we associate a 'local subset of derived–nodes', which is constituted by the derived–nodes whose subdomain–index corresponds to that partition–subdomain. The family of local subsets of derived–nodes so obtained, one for each partition–subdomain, constitutes a truly disjoint (i.e., non–overlapping) partition of the whole set of derived–nodes (Figure 2). Therefore, it is adequate for overcoming the difficulty mentioned above. Thereafter, the developments are relatively straightforward. A 'derived–vector' is defined to be a real–valued function1 defined in the whole set of derived–nodes; the set of all derived–vectors constitutes a linear space: the 'derived–vector space (DVS)'. This latter vector–space must be distinguished from that constituted by the real–valued functions defined in the original–nodes, which is referred to as the 'original–vector space'. A new problem, which is equivalent to the original problem, is defined in the derived–vector space. Of course, the of this new problem is different to the original–matrix, which is not defined in the derived–vector space, and the theory supplies a formula for deriving it; the procedure for constructing it is similar to substructuring (see, Appendix "A"). From there on, in the DVS framework, all the work is done in the derived–vector space and one never goes back to the original vector–space.
The derived–vector space is a kind of product–space; namely, the product of the family of local subsets of derived–nodes mentioned above. Fur–thermore, it constitutes a Hilbert–space (finite–dimensional) with respect to a suitable inner–product, called the Euclidean inner product, and it is handled as such throughout. Although the DVS framework was originally developed having in mind applications to symmetric and definite matrices, in [Herrera and Yates 2009 it was extended to nonsymmetric and indefinite matrices. The assumptions under which such extensions are possible were spelled out in detail there (see Section 9 of [Herrera and Yates 2009]). In this paper, we carry out a survey, as exhaustive as possible, of the DDM algorithms that can be developed in the DVS framework, both preconditioned and non–preconditioned. Thereby, DVS versions of both the BDDC and FETI–DP algorithms are produced.
At the continuous level, the most studied procedures are the Neumann–Neuman and the Dirichlet–Dirichlet algorithms [Toselli and Widlund 2005; Quarteroni and Valli 1999]. During the development of the DVS framework, very precise and clear correspondences between the processes at the continuous level, before discretization, and the processes at the discrete level, after discretization, were established [Herrera and Rubio 2011]. Using such correspondences the results of our survey can be summarized in a brief and effective manner. They are:
I) Non–Preconditioned Algorithms
a) The primal Dirichlet–Dirichlet problem (Schur–complement algorithm)
b) The dual formulation of the Neumann–Neumann problem
c) The primal formulation of the Neumann–Neumann problem
d) The second dual formulation of the Neumann–Neumann problem
II) Preconditioned Algorithms
a) Preconditioned Dirichlet–Dirichlet (The DVS–version of BDDC)
b) Preconditioned dual formulation of the Neumann–Neumann problem (The DVS–version of FETI–DP)
c) Preconditioned primal formulation of the Neumann–Neumann problem
d) Preconditioned second dual formulation of Neumann–Neumann problem
All these algorithms are formulated in vector spaces subjected to constraints, so the algorithms are constrained algorithms.
Section 3
The original problem
The DVS–framework applies to the system–matrix that is obtained after discretization. Its procedures are independent of the discretization method used; it could be, FEM, finite–differences, or any other. It requires, however, that some assumptions (or axioms) be fulfilled, as it is explained in what follows. Such axioms are stated in terms of the system–matrix and two additional concepts: the original nodes and a family of subsets of such nodes, which is associated with a domain partition (or, domain decomposition). To illustrate how such concepts are introduced, consider a variational formulation of the discretized version of a general boundary value problem. It consists in finding 
 V, such that
V, such that

Here, V is a finite dimensional linear space of real–valued2 functions defined in certain spatial domain Ω, while g V is a given function.
V is a given function.
Let  ={1, ..., n} be the set of indices, which number the nodes used in the discretization, and {φ1, ..., φn}
={1, ..., n} be the set of indices, which number the nodes used in the discretization, and {φ1, ..., φn} V be a basis of V, such that for each i
V be a basis of V, such that for each i
 , φ1= 1 at node i and zero at every other node. Then, since
, φ1= 1 at node i and zero at every other node. Then, since 
 V, we have:
V, we have:

Here,  i is the value of
i is the value of  at node i. Let
at node i. Let  and
and  be the vectors
be the vectors  ≡ (
≡ ( 1,...,
1,...,  n) and
n) and  ≡ (
≡ ( 1, ...,
1, ...,  n)3, with
n)3, with

The variational formulation of Eq. (3.1) is equivalent to:

The matrix  , which will be referred to as the 'original matrix', is given by
, which will be referred to as the 'original matrix', is given by

After the problem has been discretized, a partition of W into a set of non–overlapping subdomains, {Ω1, ... ΩE}, is introduced; more precisely, for each α = 1, ..., E, Ωα, is open and:
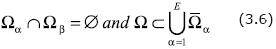
Where  α stands for the closure of Ωα. The set of 'subdomain–indices' will be
α stands for the closure of Ωα. The set of 'subdomain–indices' will be

 α, α = 1, E, will be used for the subset of original–nodes that correspond to nodes pertaining to
α, α = 1, E, will be used for the subset of original–nodes that correspond to nodes pertaining to  α. As usual, nodes will be classified into 'internal' and 'interface–nodes': a node is internal if it belongs to only one partition–subdomain closure and it is an interface–node, when it belongs to more than one. For the application of dual–primal methods, interface–nodes are classified into 'primal' and 'dual' nodes. We define:
α. As usual, nodes will be classified into 'internal' and 'interface–nodes': a node is internal if it belongs to only one partition–subdomain closure and it is an interface–node, when it belongs to more than one. For the application of dual–primal methods, interface–nodes are classified into 'primal' and 'dual' nodes. We define:
 1
1 
 as the set of internal–nodes;
as the set of internal–nodes;
 Γ
Γ 
 as the set of interface–nodes;
as the set of interface–nodes;
 π
π 
 as the set of primal–nodes4; and
as the set of primal–nodes4; and
 Δ
Δ 
 as the set of dual–nodes.
as the set of dual–nodes.
The set  π
π 
 Γ is chosen arbitrarily and then
Γ is chosen arbitrarily and then  Δ is defined as
Δ is defined as  Δ ≡
Δ ≡  Γ –
Γ –  π. Each one of the following two families of node–subsets is disjoint:{
π. Each one of the following two families of node–subsets is disjoint:{ 1,
1,  Γ} and {
Γ} and { 1,
1,  π,
π,  Δ}. Furthermore, these node subsets fulfill the relations:
Δ}. Furthermore, these node subsets fulfill the relations:

The real–valued functions defined in  = {1, ..., n} constitute a linear vector space that will be denoted by
= {1, ..., n} constitute a linear vector space that will be denoted by  and referred to as the 'original vector–space'. Vectors
and referred to as the 'original vector–space'. Vectors 

 will be written as
will be written as  = (
= ( 1,...,
1,...,  n), where
n), where  i for i =1, n, are the components of the vector
i for i =1, n, are the components of the vector  . Then, by the 'original–problem' consists in: "Given
. Then, by the 'original–problem' consists in: "Given 

 , find a
, find a 

 such that Eq. (3.4) is fulfilled". Throughout our developments the original matrix
such that Eq. (3.4) is fulfilled". Throughout our developments the original matrix  is assumed to be non–singular (i.e., it defines a bijection of
is assumed to be non–singular (i.e., it defines a bijection of  into itself).
into itself).
Conditions under which the DVS–framework is applicable to indefinite or/and non–symmetric were given in [Herrera and Yates 2009]; in particular, the following assumption ('axiom') is adopted here: "Let the indices i
 α and j
α and j
 β be internal original–nodes, then:
β be internal original–nodes, then:

Section 4
Derived–Nodes
As said before, when a non–overlapping partition is introduced some of the nodes used in the discretization belong to more than one partition–subdomain. To overcome this inconvenient feature in the DVS–framework, besides the original–nodes, another set of nodes is introduced, called the 'derived nodes'. The general developments are better understood, through a simple example that we explain first.
Consider the set of twenty five nodes of a "non–overlapping" domain decomposition, which consists of four subdomains, as shown in Figure 1. Thus, we have a set of nodes and a set of subdomains, which are numbered using of the index–sets:  ≡{1, ..., 25} and
≡{1, ..., 25} and  = {1, 2, 3, 4}, respectively. Then, the sets of nodes corresponding to such a non–overlapping domain decomposition is actually overlapping, since the four subsets
= {1, 2, 3, 4}, respectively. Then, the sets of nodes corresponding to such a non–overlapping domain decomposition is actually overlapping, since the four subsets

are not disjoint (see, Figure 1). Indeed, for example:

In order to obtain a "truly" non–overlapping decomposition, we replace the set of 'original nodes' by another set: the set of 'derived nodes'; a 'derived node' is defined to be a pair of numbers: (p, α), where p corresponds a node that belongs to  α. In symbols: a 'derived node' is a pair of numbers (p, α) such that p
α. In symbols: a 'derived node' is a pair of numbers (p, α) such that p
 α. We denote by X the set of derived nodes; we observe that the total number of derived–nodes is 36 while that of original–nodes is 25. Then, we define Xα as the set of derived nodes that can be written as (p, α), where a is kept fixed. Taking α successively as 1, 2, 3 and 4, we obtain the family of four subsets, {X1, X2, X3, X4}, which is a truly disjoint decomposition of X, in the sense that (see, Figure 2):
α. We denote by X the set of derived nodes; we observe that the total number of derived–nodes is 36 while that of original–nodes is 25. Then, we define Xα as the set of derived nodes that can be written as (p, α), where a is kept fixed. Taking α successively as 1, 2, 3 and 4, we obtain the family of four subsets, {X1, X2, X3, X4}, which is a truly disjoint decomposition of X, in the sense that (see, Figure 2):

Of course, the cardinality (i.e., the number of members) of each one of these subsets is 36/4 equal to 9.
The above discussion had the sole purpose of motivating the more general and formal developments that follow. So, now we go back to the general case introduced in Section 3, in which the sets of node–indexes and subdomain–indexes are  = {1, ..., n} and
= {1, ..., n} and  = {1, ..., E}, respectively, and define a 'derived–node' to be any pair of numbers, (p, α), such that p
= {1, ..., E}, respectively, and define a 'derived–node' to be any pair of numbers, (p, α), such that p
 α. Then, the total set of derived–nodes, fulfills:
α. Then, the total set of derived–nodes, fulfills:

In order to avoid unnecessary repetitions, in the developments that follow where we deal extensively with derived nodes, the notation (p, α) is reserved for pairs such that (p, α) X. Some subsets of X are defined next:
X. Some subsets of X are defined next:

With each α = 1, ..., E, we associate a unique 'local subset of derived–nodes':

The family of subsets {X1, ..., XE}, is a truly disjoint decomposition of the whole set of derived–nodes, in the sense that:

Section 5
The "Derived Vector–Space (DVS)"
Firstly, we recall from Section 3 the definition of the vector space  . Then, for each α = 1, ..., E, we define the vector–subspace
. Then, for each α = 1, ..., E, we define the vector–subspace  α
α 
 , which is constituted by the vectors that have the property that, for each i
, which is constituted by the vectors that have the property that, for each i
 α, its i–component vanishes. With this notation, the 'product–space' W, is defined by
α, its i–component vanishes. With this notation, the 'product–space' W, is defined by

As explained in Section 3, the 'original problem' of Eq.(3.4) is a problem formulated in the original vector–space  and in the developments that follow we transform this problem into one that is formulated in the product–space W, which is a space of discontinuous functions.
and in the developments that follow we transform this problem into one that is formulated in the product–space W, which is a space of discontinuous functions.
By a 'derived–vector' we mean a real–valued function5 defined in the set X, of derived–nodes. The set of derived–vectors constitute a linear space, which will be referred to as the 'derived–vector space'. Corresponding to each local subset of derived–nodes, Xα, there is a 'local subspace of derived–vectors', Wα, which is defined by the condition that vectors of Wa vanish at every derived–node that does not belong to Xα. A formal manner of stating this definition is
• u Wα
Wα W, if and only if, u(p, β) = 0 whenever β≠α
W, if and only if, u(p, β) = 0 whenever β≠α
An important difference between the subspaces Wα and  α that should be observed is that Wα
α that should be observed is that Wα W, while
W, while  α
α W. In particular,
W. In particular,

In words: the space W is the product of the family of subspaces { 1, ...,
1, ...,  E}, but at the same time it is the direct–sum of the family {W1, ..., WE}. In view of Eq. (5.2), it is straightforwa rd to establish a bijection (actually, an isomorphism) between the derived–vector space and the product–space. Thus, in what follows we identify both.
E}, but at the same time it is the direct–sum of the family {W1, ..., WE}. In view of Eq. (5.2), it is straightforwa rd to establish a bijection (actually, an isomorphism) between the derived–vector space and the product–space. Thus, in what follows we identify both.
For every pair of vectors, u W and w
W and w W, the 'Euclidean inner product' is defined to be
W, the 'Euclidean inner product' is defined to be
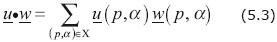
In applications of the theory to systems of equations, when u(p, α) itself is a vector, Eq. (5.3) is replaced by

Here, u w. means the inner product of the vectors involved. An important property is that the derived–vector space, W, constitutes a finite dimensional Hilbert–space with respect to the Euclidean inner product. We observe the Euclidean inner product independently of the nature of the original matrix
w. means the inner product of the vectors involved. An important property is that the derived–vector space, W, constitutes a finite dimensional Hilbert–space with respect to the Euclidean inner product. We observe the Euclidean inner product independently of the nature of the original matrix  ; in particular it may non–symmetric or indefinite.
; in particular it may non–symmetric or indefinite.
The natural injection, R: 
 W, of
W, of  into W, is defined by the condition that, for every û
into W, is defined by the condition that, for every û
 , one has
, one has

The 'multiplicity', m(p), of any original–node p
 is characterized by the property [Herrera and Yates 2010, Herrera and Yates 2009]:
is characterized by the property [Herrera and Yates 2010, Herrera and Yates 2009]:

The space W will be decomposed into two orthogonal complementary subspaces W11 W and W12
W and W12 W, so that
W, so that

Here, the subspace W12 W is the natural injection of
W is the natural injection of  into W; i.e.,
into W; i.e.,

and W11 W its orthogonal complement with respect to the Euclidean inner product. For later use, we point out that the inverse of R:
W its orthogonal complement with respect to the Euclidean inner product. For later use, we point out that the inverse of R: 
 W, when restrictedjto W12
W, when restrictedjto W12 W, exists and will denoted by R1: W12
W, exists and will denoted by R1: W12 
 . Here, we recall that it is customary to use the direct–sum notation:
. Here, we recall that it is customary to use the direct–sum notation:

when the pair of equalities of Eq. (5.7), holds. The 'subspace of continuous vectors' is defined to be W12 W, while the 'subspace of zero–average vectors' is defined to be W11
W, while the 'subspace of zero–average vectors' is defined to be W11 W. Two matrices
W. Two matrices  : W
: W W and
W and  : W
: W W are here introduced; they are the projections operators, with respect to the Euclidean inner–product, on W12 and W11, respectively. The first one will be referred to as the 'average operator' and the second one will be the 'jump operator', respectively. We observe that in view of Eq. (5.7), every vector, u
W are here introduced; they are the projections operators, with respect to the Euclidean inner–product, on W12 and W11, respectively. The first one will be referred to as the 'average operator' and the second one will be the 'jump operator', respectively. We observe that in view of Eq. (5.7), every vector, u W, can be uniquely written as the sum of a zero–average vector plus a continuous vector (we could say: a zero–jump vector); indeed:
W, can be uniquely written as the sum of a zero–average vector plus a continuous vector (we could say: a zero–jump vector); indeed:

The vectors  u and
u and  u are said to be the 'jump' and the 'average' of uu, respectively.
u are said to be the 'jump' and the 'average' of uu, respectively.
The linear subspaces that are defined next are chosen to mimic those used by other authors [Mandel and Dohrmann 2003; Mandel et al., 2005]. In particular, WI WΓ, Wπ, and WΔ are defined by imposing the restrictions that follow to their members. Vectors of:
• WI vanish at every derived–node that is not an internal node;
• WΓ vanish at every derived–node that is not an interface node;
• Wπ vanish at every derived–node that is not a primal node; and
• WΔ vanish at every derived–node that is not a dual node.
Furthermore,
We observe that each one of the following families of subspaces are linearly independent:
{WI , WΓ}, {WI ,Wπ,WΔ }, {WΠ, WΔ}
And also that
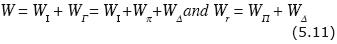
The above definition of Wr is appropriate when considering dual–primal formulations; other kinds of restrictions require changing the term  Wπ by
Wπ by  rWπ, where
rWπ, where  r is a projection on the restricted subspace.
r is a projection on the restricted subspace.
Section 6
The general problem with constraints
The following result is similar to results shown in [Herrera and Yates 2010; Herrera and Yates 2009]; its proof, as well as the definition of the matrix  : Wr
: Wr  Wr that is used in it, is given in Appendix "A":
Wr that is used in it, is given in Appendix "A":
"A vector 

 is solution of the original problem, if and only if, u' = R
is solution of the original problem, if and only if, u' = R 
 Wr
Wr W fulfills the equalities:
W fulfills the equalities:

The vector  = (R
= (R )
)  W12
W12  Wr , will be written as
Wr , will be written as  ≡
≡  Π +
Π +  Δ, with
Δ, with  Π
Π WΠ and
WΠ and  Δ
Δ WΔ."
WΔ."
This is the 'dual–primal problem formulated in the derived–vector space'; or, simply, the DVS–dual–primal problem. We remark that this problem is formulated in the subspace Wr of the derived–vector space W, in which the restrictions have been incorporated. Thus, all the algorithms to be discussed include such restrictions; in particular, those imposed by means of primal
nodes. In what follows, the matrix A:  r
r 
 r is assumed to be invertible. In many cases this can be granted when a sufficiently large number of primal nodes, adequately located, are taken. Let u'
r is assumed to be invertible. In many cases this can be granted when a sufficiently large number of primal nodes, adequately located, are taken. Let u'  Wr be solution of it, then u'
Wr be solution of it, then u'  W12
W12 W necessarily, since
W necessarily, since  u' = 0, and one can apply the inverse of the natural injection to obtain
u' = 0, and one can apply the inverse of the natural injection to obtain

Since this problem is formulated in the derived–vectors space, in the algorithms to be presented all the operations are carried out in such a space; in particular, we will never return to the original vector space,  , except at the end when we apply Eq. (6.2).
, except at the end when we apply Eq. (6.2).
Section 7
The schur complement algorithm
The matrix  of Eq. (6.1), can be written as (here, we draw from Appendix "A"):
of Eq. (6.1), can be written as (here, we draw from Appendix "A"):

Using this notation, we define the 'dual–primal Schur–complement matrix' by

Let be u≡u' – 
 Π, then Eq. (6.1) is equivalent to: "Given
Π, then Eq. (6.1) is equivalent to: "Given  =
=  Δ
Δ 
 WΔ, find a uΔ
WΔ, find a uΔ WΔ such that
WΔ such that

Here, u = uΠ+ uΔ and

We observe that the Schur complement matrix,  :WΔ
:WΔ  WΔ, is invertible when so is
WΔ, is invertible when so is  :Wr
:Wr  Wr [Herrera and Yates 2010; Herrera and Yates 2009].
Wr [Herrera and Yates 2010; Herrera and Yates 2009].
In Appendix "B" it is shown that Eq. (7.3) is the discrete version of a non–preconditioned Dirichlet–Dirichlet problem. Thus, this algorithm could be called the 'non–preconditioned Dirichlet–Dirichletalgorithm'. However, in what follows, the algorithm that corresponds to Eq. (7.3) will be referred to as the Schur–complement algorithm', since it is a variant of one of the simplest forms of substructuring methods described, for example, in [Smith et al., 1996].
Section 8
The dual Neumann–Neumann problem
In this paper we present three alternative procedures for obtaining the algorithm we are about to derive. One is as a Neumann–Neumann formulation, discussed in Appendix "B" using an operator, which is the counter–part of the Steklov–Poincaré operator; one more is in what could be called the classical manner that consists in using a Lagrange multipliers treatment of the problem of Section 7 [Toselli and Widlund 2005] (the DVS version of this approach is presented in Appendix "C"); and the third one –used in this Section– stems from the identity

This latter equation is clear since  +
+ =
=  .
.
Eqs.(7.3) and (8.1), together, imply that

when the vector  is defined to be
is defined to be

Therefore, 

 WΔ. Thus, the problem of finding uΔ has been transformed into that of finding the 'Lagrange multiplier'
WΔ. Thus, the problem of finding uΔ has been transformed into that of finding the 'Lagrange multiplier'  6, since once
6, since once  is known one can apply
is known one can apply  –1 to Eq. (8.2), to obtain
–1 to Eq. (8.2), to obtain

Furthermore, in Eq. (8.4), uΔ
 WΔ, so that
WΔ, so that

Hence, 
 WΔ fulfills
WΔ fulfills

Thereby, we mention that 
 uΔ is discretized version of the of the average of the normal derivative [Herrera and Yates 2010; Herrera and Yates 2009].
uΔ is discretized version of the of the average of the normal derivative [Herrera and Yates 2010; Herrera and Yates 2009].
Section 9
The primal Neumann–Neumann problem
In Appendix "B", it was shown that there is a second and more direct manner of formulating the non–preconditioned Neumann–Neumann problem, which is given by Eq.(18.28). Here, we derive it for the general problem we are considering. Our starting point will be Eq.(7.3).
We multiply the first equality in Eq. (7.3) by  –1, observing that
–1, observing that 
 Δ, to obtain
Δ, to obtain

Thus, Eq. (7.3) can be transformed into

or

If we define:

Eq. (9.3) is transformed into:

The iterative form of this algorithm is obtained multiplying by  –1:
–1:

If the solution of Eq. (7.3) is known, then vΔ WΔ defined by Eq. (9.4) fulfills Eq. (9.6); conversely, if vΔ
WΔ defined by Eq. (9.4) fulfills Eq. (9.6); conversely, if vΔ WΔ satisfies Eq. (9.6), then
WΔ satisfies Eq. (9.6), then

is solution of Eq. (7.3). We shall refer to the iterative algorithm defined by Eq. (9.6) as the 'multipliers–free formulation of the non–preconditioned Neumann–Neuman problem'.
Section 10
The second dual Neumann–Neumann problem
Our starting point will be Eq. (8.6). Firstly, we observe the following identity:

Then, we multiply the first equality in Eq. (8.6) by  to obtain
to obtain

Or

If we multiply the first of these equalities by  –1 and define:
–1 and define:

Eq. (10.3) is transformed into:

We observe that this latter equation is equivalent to Eq. (10.3) because  –1 is non–singular. If the solution of Eq. (8.6) is known, then
–1 is non–singular. If the solution of Eq. (8.6) is known, then 
 WΔdefined by Eq. (10.4) fulfills Eq. (10.5). Conversely, if
WΔdefined by Eq. (10.4) fulfills Eq. (10.5). Conversely, if 
 WΔ satisfies Eq. (10.5), then
WΔ satisfies Eq. (10.5), then

is solution of Eq. (8.6).
We notice that Eq. (10.5) does not define an iterative algorithm. However, multiplying Eq. (10.5) by  an iterative algorithm is obtained:
an iterative algorithm is obtained:

Eq. (10.7) supplies an alternative manner of applying the Lagrange–multipliers approach.
The equality 
 –1
–1  = 0 may be interpreted as a restriction; indeed, It can be shown that it is equivalent to
= 0 may be interpreted as a restriction; indeed, It can be shown that it is equivalent to 


 WΔ.
WΔ.
Section 11
The DVS version of the BDDC algorithm
The DVS version of the BDDC is obtained when the Schur–complement algorithm, of Section 7, is preconditioned by means of the matrix 
 –1. It is: "Given
–1. It is: "Given  Δ
Δ WΔ, find uΔ
WΔ, find uΔ WΔ such that
WΔ such that

The following properties should be noticed:
a) This is an iterative algorithm;
b) The iterated matrix is
–1
;
c) The iteration is carried"outm the subspace
WΔ
WΔ;
d) This algorithm is applicable whenever the Schur complement matrix
is such that the logical implication is fulfilled, for any w
WΔ
e) In particular, it is applicable when
is definite.
Properties a) to c) are interrelated. The condition  uΔ = 0 is equivalent to uΔ
uΔ = 0 is equivalent to uΔ
 WΔ; thus the search is carried out in
WΔ; thus the search is carried out in  WΔ. When the matrix
WΔ. When the matrix 
 –1
–1
 is applied repeatedly, one remains in
is applied repeatedly, one remains in  WΔ, because for every w
WΔ, because for every w WΔone has
WΔone has  (
(
 –1
–1
 w) = 0. As for property d), it means that when the implication of Eq. (11.2) holds, Eq. (11.1) implies Eq. (7.3). To prove this, observe that
w) = 0. As for property d), it means that when the implication of Eq. (11.2) holds, Eq. (11.1) implies Eq. (7.3). To prove this, observe that

and also that Eq. (11.1) implies

When the implication of Eq. (11.2) holds, Eqs. (11.3) and (11.4) together imply

As desired, this proves that Eqs. (11.1) implies Eq. (7.3), when Eq. (11.2) holds.
The condition of Eq. (11.2), is weaker than that of (or generalizes that of) requiring that the Schur complement matrix  be definite, since the implication of Eq. (11.2) is_always satisfied when
be definite, since the implication of Eq. (11.2) is_always satisfied when  is definite. Assume that
is definite. Assume that  is definite, then for any vector w
is definite, then for any vector w WΔ such that
WΔ such that 
 –1w = 0 and
–1w = 0 and  w = 0, one has
w = 0, one has

This implies w= 0, because  –1 is definite when so is
–1 is definite when so is  . Thereby, Property e) is clear.
. Thereby, Property e) is clear.
Section 12
The DVS version of FETI–DP algorithm
The DVS version of the FETI–DP algorithm is obtained when the 'Lagrange–Multipliers formulation of the non–preconditioned Neumann–Neuman problem', of Section 8, Eq. (8.6), is preconditioned by means of the matrix _S. It is: "Given  Δ
Δ
 WΔ, find
WΔ, find 
 WΔ such that
WΔ such that

For this algorithm the following properties should be noticed:
i. This is an iterative algorithm;
ii. The iterated matrix is
–1;
iii. The iteration is carried out in the subspace
WΔ
WΔ;
iv. The algorithm is applicable whenever the Schur complement matrix
is such that the logical implication is fulfilled, for any w
WΔ:
v. In particular, it is applicable when
is positive definite.
Properties i) to ii) are interrelated. The condition 
 = 0 is equivalent to
= 0 is equivalent to 

 WΔ; thus the search is carried out in
WΔ; thus the search is carried out in  WΔ. When the matrix
WΔ. When the matrix 


 –1 is applied repeatedly one remains in
–1 is applied repeatedly one remains in  WΔ, because for every
WΔ, because for every 
 WΔ, one has
WΔ, one has  (
(


 –1
–1 ) = 0. As for property iv), it means that when the implication of Eq. (12.2) holds, Eq. (12.1) implies Eq. (8.6). To prove this, assume Eq. (12.1) and observe that
) = 0. As for property iv), it means that when the implication of Eq. (12.2) holds, Eq. (12.1) implies Eq. (8.6). To prove this, assume Eq. (12.1) and observe that

and also that Eq. (12.1) implies

When the implication of Eq. (12.2) holds, Eqs. (12.3) and (12.4) together imply

As desired, this proves that Eqs. (12.1) implies Eq. (8.6), when Eq. (12.2) holds.
The condition of Eq. (12.2), is weaker than that of (or generalizes that of) requiring that the Schur complement matrix  be definite, since the implication of Eq. (12.2) is always satisfied when
be definite, since the implication of Eq. (12.2) is always satisfied when  is definite. Indeed, assume that
is definite. Indeed, assume that  is definite, then for any vector
is definite, then for any vector 
 WΔ such that
WΔ such that 

 = 0 and
= 0 and 
 = 0 , one has
= 0 , one has

This implies  = 0, because
= 0, because  is definite. Thereby, Property v) is clear.
is definite. Thereby, Property v) is clear.
Section 13
Preconditioned primal Neumann–Neumann algorithm
This algorithm is a preconditioned version of the multipliers–free formulation of the non–preconditioned Neumann–Neumann problem. It can be derived multiplying the first equality in Eq. (9.5) by the preconditioner  –1
–1
 . Thus, such an algorithm consists in searching for a function vΔ
. Thus, such an algorithm consists in searching for a function vΔ WΔ, which fulfills
WΔ, which fulfills

For this algorithm the following properties should be noticed:
A. This is an iterative algorithm;
B. The iterated matrix is
–1
;
C. The iteration is carried out Tn the subspace
–1
WΔ
WΔ;
D. The algorithm is applicable whenever the Schur complement matrix
is such that the logical implication is fulfilled, for any w
WΔ:
E. In particular, it is applicable when
is positive definite.
Properties A) to C) are interrelated. The condition 
 vΔ= 0 is equivalent to v
vΔ= 0 is equivalent to v

 –1WΔ; thus the search is carried out in the subspace
–1WΔ; thus the search is carried out in the subspace 
 –1WΔ. When the matrix
–1WΔ. When the matrix  –1
–1

 is applied repeatedly one remains in
is applied repeatedly one remains in 
 –1WΔ, because for every vΔ
–1WΔ, because for every vΔ WΔ, one has
WΔ, one has 
 (
( –1
–1

 vΔ) = 0. As for property D), it means that when the implication of Eq. (13.2) holds, Eq. (13.1) implies Eq. (9.5). To prove this, assume Eq. (13.1) and define
vΔ) = 0. As for property D), it means that when the implication of Eq. (13.2) holds, Eq. (13.1) implies Eq. (9.5). To prove this, assume Eq. (13.1) and define

Furthermore, in view of Eq. (13.1)

Using Eq. (13.2), it is seen that Eqs. (13.3) and (13.4) together imply

Now Eq. (9.5) is clear and the proof is complete.
The condition of Eq. (13.2), is weaker than (or generalizes that of) requiring that the Schur complement matrix  be definite, since the implication of Eq. (13.2) is always satisfied when
be definite, since the implication of Eq. (13.2) is always satisfied when  is definite. Indeed, assume that
is definite. Indeed, assume that  is definite, then for any vector w
is definite, then for any vector w WΔ such that
WΔ such that 
 w = 0 and
w = 0 and  w = 0, one has
w = 0, one has
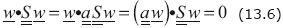
This implies w = 0, because  is definite. Thereby, Property E) is clear.
is definite. Thereby, Property E) is clear.
Section 14
Preconditioned second dual Neumann–Neumann algorithm
This algorithm is a preconditioned version of the 'second form of the Lagrange–Multipliers formulation of the non–preconditioned Neumann–Neuman problem', of Section 10. Multiplying Eq. (10.5) by the matrix 

 –1, we obtain:
–1, we obtain:

The iterative non–overlapping algorithm that is obtained by the use of Eq. (14.1) is similar to FETI–DP. The following properties should be noticed:
I. Firstly, this is an iterative algorithm;
II. The iterated matrix is
–1
;
III. The iteration is carried out in the subspace
WΔ
WΔ;
IV. This algorithm is applicable whenever the Schur complement matrix
is such that the logical implication is fulfilled, for any w
WΔ:
V. In particular, it is applicable when
is positive definite in WΔ.
Properties I) to III) are interrelated. The condition 
 –1
–1 = 0 is equivalent to
= 0 is equivalent to 


 WΔ; thus the search is carried out in the subspace
WΔ; thus the search is carried out in the subspace 
 WΔ. When the matrix
WΔ. When the matrix 

 –1
–1 is applied repeatedly one remains in
is applied repeatedly one remains in 
 WΔ, because for every
WΔ, because for every 
 WΔ, one has
WΔ, one has 
 (
( –1
–1


 ) = 0. As for property IV), it means that when the implication of Eq. (14.2) holds, Eq. (14.1) implies Eq. (10.5). To prove this, assume Eq. (14.1) and define
) = 0. As for property IV), it means that when the implication of Eq. (14.2) holds, Eq. (14.1) implies Eq. (10.5). To prove this, assume Eq. (14.1) and define

Furthermore, in view of Eq. (14.1)

Eqs. (14.3) and (14.4), together, imply

Now Eq. (10.5) is clear and, as desired, it has been shown that Eq. (14.1) implies Eq. (10.5), when the condition of Eq. (14.2) holds.
The condition of Eq. (14.2), is weaker than (or generalizes that of) requiring that the Schur complement matrix  be definite, in the sense that any positive definite matrix fulfills it. Indeed, assume that
be definite, in the sense that any positive definite matrix fulfills it. Indeed, assume that  is definite, then for any vector w
is definite, then for any vector w WΔ such that
WΔ such that 
 –1w = 0 and
–1w = 0 and  w = 0, one has
w = 0, one has

This implies w = 0, because  –1 is definite when so is
–1 is definite when so is  . Thereby, Property V) is clear.
. Thereby, Property V) is clear.
Section 15
FETI–DP and BDDC from the DVS perspective
As said in the Introduction, both the FETI–DP and BDDC can be accommodated in the DVS–framework. In this Section, we show that the DVS version of FETI–DP presented in Section 12, is obtained when suitable choices are made in the general expressions of FETI–DP. As for BDDC, its relation with the algorithm presented in Section 9 is a little more complicated.
FETI–DP
The FETI preconditioner is given by

and we now have to solve the preconditioned system

were Fr = BrS†BrTand dr = BrS† f (see, page 157, Eq. (6.51) and (6.52) of [Toselli and Widlund 2005]). Developing the expression and replacing  r–1 we get
r–1 we get

We take Pr =  . So, we have
. So, we have

replacing  = DrBr, get
= DrBr, get

simplifying

Now, we choose Br ≡  and Dr ≡
and Dr ≡  , so that BrT =
, so that BrT =  , to obtain
, to obtain

One advantage of introducing  is its very convenient algebraic properties; for example, it is idempotent. In particular, here we have used the fact that
is its very convenient algebraic properties; for example, it is idempotent. In particular, here we have used the fact that 
 r =
r =  r, since
r, since 
 r = 0. Except for slight changes of notation this is the same as Eq. (12.1).
r = 0. Except for slight changes of notation this is the same as Eq. (12.1).
BDDC
In the standard notation used in BDDC [Dohrmann 2003; Mandel and Dohrmann 2003; Mandel et al., 2005; Da Conceição 2006]

where S and the preconditioner M––1 are

respectively. Furthermore, N is the number of subdomains and for each i = 1, ..., N

Ri = Γ Γi is the restriction operator from Γ into Γi; when applied to a functiondefined in Γ, it yields its restriction to Γi. As for
Γi is the restriction operator from Γ into Γi; when applied to a functiondefined in Γ, it yields its restriction to Γi. As for  i,
i,  i : Γ
i : Γ Γi is given by
Γi is given by  i = DiRi. Here, Di =diag{δi} is a diagonal matrix defining a partition of unity. Substituting S and M–1 in Eq. (15.8), we obtain
i = DiRi. Here, Di =diag{δi} is a diagonal matrix defining a partition of unity. Substituting S and M–1 in Eq. (15.8), we obtain

This equation is to be compared with our Eq. (9.1). For the purpose of comparison, the vectors u and f of Eq. (15.11) can be identified with vectors u and  of our original space,
of our original space,  . Furthermore, we apply our natural injection, R :
. Furthermore, we apply our natural injection, R : 
 W, defined by Eq.(5.5), to Eq.(9.1) and pre–multiply the resulting equation also by the natural injection, with u and
W, defined by Eq.(5.5), to Eq.(9.1) and pre–multiply the resulting equation also by the natural injection, with u and  Δ replaced by Ru and R
Δ replaced by Ru and R , respectively. In this manner we obtain.
, respectively. In this manner we obtain.

We have verified that indeed Eqs. (15.11) and (15.12) are equivalent.
Comparisons
The DVS approach, and therefore also the DVS–versions of FETI–DP and BDDC here presented, starts with the matrix that is obtained after the problem has been discretized and for its application does not require any information about the system of partial differential equations from which it originated. Generally, all the non–preconditioned DVS–algorithms that have been presented throughout this paper are equally applicable to symmetric, indefinite and non–symmetric matrices. The specific conditions required for its applicability are spelled out in detail in [Herré ra an d Yates 2009] (Section 9). Throughout all the developments it is assumed that the dual–primal Schur–complement matrix  , defined in Section 7, Eq.(7.2), is non–singular.
, defined in Section 7, Eq.(7.2), is non–singular.
As said before, for FETI we show that the DVS–version of FETI–DP can be obtained when suitable choices are made in the general expressions of FETI–DP. Although, these choices represent particular case of the general FETI–DP algorithm, in some sense the choices made are optimal because both  and
and  are complementary orthogonal projections, as it has been verified numerically in [Herrera and Yates 2010; Herrera and Yates 2009] and other more recent numerical implementations. When carrying out the incorporation of BDDC in the DVS–framework we encountered more substantial differences. For example, when the inverses of the local Schur–complements exist, in the DVS framework the inverse of
are complementary orthogonal projections, as it has been verified numerically in [Herrera and Yates 2010; Herrera and Yates 2009] and other more recent numerical implementations. When carrying out the incorporation of BDDC in the DVS–framework we encountered more substantial differences. For example, when the inverses of the local Schur–complements exist, in the DVS framework the inverse of  t is given by (see Appendix "A"):
t is given by (see Appendix "A"):

A similar relation does not hold for the BDDC algorithm. Indeed, in this latter approach in that case we have instead:

and

even when the inverses of the local Schur–complements exist and no restrictions are used.
The origin of this problem, encountered in the BDDC formulation, may be traced back to the fact that the BDDC approach does not work directly in the product space. Indeed, one frequently goes back to degrees of freedom associated with the original nodes. This is done by means of the restriction operators Ri : Γ Γi which can be interpreted as transformations of the original vector–space into the product vector–space (or, derived vector–space). If the algorithm of Eq. (15.11) is analyzed from this point of view, it is seen that it repeatedly goes from the original vector–space to the product–space (or derived vector–space) and back. For example, consider the expression:
Γi which can be interpreted as transformations of the original vector–space into the product vector–space (or, derived vector–space). If the algorithm of Eq. (15.11) is analyzed from this point of view, it is seen that it repeatedly goes from the original vector–space to the product–space (or derived vector–space) and back. For example, consider the expression:

occurring in Eq. (15.11). After starting with the vector u in the original vector–space, we go to the derived–vector space with  iu and remain there when we apply Si. However,we go back to the original vector–space when
iu and remain there when we apply Si. However,we go back to the original vector–space when  it is applied. A similar analysis can be made of the term
it is applied. A similar analysis can be made of the term

Summarizing, in the operations indicated in Eq. (15.16) four trips between the original vector space and the derived–vector space were made, two one way and the other two in the way back. In the DVS–framework, on the other hand, from the start the original problem is transformed into one defined in derived–vector space, where all the work is done afterwards, and that permits avoiding all those unnecessary trips. Thereby, the matrix formulas are simplified and so is code development. The unification and simplification achieved in this manner, permits producing more effective and robust software.
Section 16
Conclusions and discusions
1. A primal framework for the formulation of non–overlapping domain decomposition methods has been proposed, which is referred to as 'the derived–vector space (DVS) framework';
2. Dual and primal formulations have been derived in a unified manner. Symmetric, non–symmetric and indefinite matrices are also included. Furthermore, detailed conditions that such matrices need to satisfy in order for the general algorithms to be applicable to them have been given in Section 9 of [Herrera and Yates 2009] and in Sections 7 to 14 of the present paper;
3. A brief and effective summary of non–overlapping domain decomposition methods has been obtained. It consists of eight matrix–formulas: four are primal formulations and the other four are dual formulations;
4. The non–preconditioned formulas are:

5. The preconditioned formulas are:

6. The most commonly used methods, BDDC and FETI–DP, have been incorporated in this framework, producing in this manner DVS–versions of such methods. Eq. (16.1), is the primal formulation of a Dirichlet–Dirichlet problem; when this is preconditioned the DVS–BDDC is obtained. The formulation of a Neumann–Neumann problem using the counter–part of the Steklov–Poincaré operator, given in Appendix "B", yields a dual formulation, which is stated in the second equality of Eq. (16.2). The DVS version of FETI–DP, of Eq. (16.4), is the preconditioned form of this formulation;
7. For the other matrix–formulas, two preconditioned and two more non–preconditioned, we have not been able to find suitable counterparts in the DDM literature already published;
8. Using the detailed definitions given in [Herrera and Yates 2010; Herrera and Yates 2009], the above DVS formulas can be used directly for code development. They are somewhat simpler than those of the BDDC framework and have permitted us to simplify code–development and also to develop very robust computational codes for the examples considered in [Herrera and Yates 2010; Herrera and Yates 2009].
FETI– DP and BDDC are optimal in the sense that the condition number κ of its interface problem grows asymptotically as [Dohrmann 2003; Klawonn and Widlund 2001; Tezaur 1998]:

Furthermore, they perform quite similarly when the same set of primal constraints is used. Therefore, to be competitive the last two preconditioned Dirichlet–Dirichlet algorithms of Eq. (16.5) should have a similar behavior, but at present that is an open question.
Acknowledgement
We thank Dr. Norberto Vera–Guzmán for his valuable assistance in several aspects of the research reported in this article.
Bibliography
Da Conceição D.T. Jr., 2006, Balancing domain decomposition preconditioners for non–symmetric problems, Instituto Nacional de Matemática Pura e Aplicada, Agencia Nacional do Petróleo PRH–32, Rio de Janeiro, May. 9. [ Links ]
Dohrmann C.R., 2003, A preconditioner for substructuring based on constrained energy minimization. SIAM J. Sci. Comput. 25(1):246–258. [ Links ]
Farhat Ch., Roux F., 1991, A method of finite element tearing and interconnecting and its parallel solution algorithm. Internat. J. Numer. Methods Engrg. 32:1205–1227. [ Links ]
Farhat C., Lesoinne M., LeTallec P., Pierson K., Rixen D., 2001, FETI –DP a dual–primal unified FETI method, Part1: A faster alternative to the two–level FETI method, Int. J. Numer. Methods Engrg., 50, 1523–1544. [ Links ]
Farhat C., Li J., 2005, An iterative domain decomposition method for the solution of a class of indefinite problems in computational structural dynamics. ELSEVIER Science Direct Applied Numerical Math. 54 pp 150–166. [ Links ]
Herrera I., 2007, Theory of Differential Equations in Discontinuous Piecewise–Defined–Functions, NUMER METH PART D E, 23(3), pp 597–639, DOI 10.1002 NO. 20182. [ Links ]
Herrera I., Rubio E., 2011, Unified theory of Differential Operators Acting on Discontinuous Functions and of Matrices Acting on Discontinuous Vectors 19th International Conference on Domain Decomposition Methods, Zhangjiajie, China 2009. (Oral presentation). Internal report #5, GMMC– UNAM. [ Links ]
Herrera I., Yates R.A., 2009, The Multipliers–free Domain Decomposition Methods NUMER.METH. PART D. E. 26: 874–905 July 2010, DOI 10.1002/num. 20462. (Published on line Jan 28). [ Links ]
Herrera I., Yates R.A., 2010, The Multipliers–Free Dual Primal Domain Decomposition Methods for Nonsymmetric Matrices NUMER. METH. PART D. E. 2009, DOI 10.1002/Num. 20581, (Published on line April 28). [ Links ]
Klawonn A., Widlund O.B., 2001 FETI and Neumann–Neumann iterative substructuring methods: connections and new results. Comm. Pure and Appl. Math. 54(1):57–90. [ Links ]
Li J., Tu X., 2009, Convergence analysis of a Balancing Domain Decomposition method for solving a class of indefinite linear systems. Numer. Linear Algebra Appl. 2009; 16:745–773. [ Links ]
Li J., Widlund O.B., 2006, FETI–DP, BDDC, and block Cholesky methods. Int. J. Numer. Methods, Engng. 250–271. [ Links ]
Mandel J., 1993, Balancing domain decomposition. Comm. Numer. Meth. Engrg., 9:233–241. [ Links ]
Mandel J., Brezina M., 1993, Balancing Domain Decomposition: Theory and performance in two and three dimensions. UCD/CCM report 2. [ Links ]
Mandel J., Dohrmann C.R., 2003, Convergence of a balancing domain decomposition by constraints and energy minimization, Numer. Linear Algebra Appl, 10(7):639–659. [ Links ]
Mandel J., Dohrmann C.R., Tezaur R., 2005, An algebraic theory for primal and dual substructuring methods by constraints, Appl. Numer. Math., 54: 167–193. [ Links ]
Mandel J., Tezaur R., 1996, Convergence of a substructuring method with Lagrange multipliers. Numer. Math 73(4): 473–487. [ Links ]
Mandel J., Tezaur R., 2001, On the convergence of a dual–primal substructuring method, Numer. Math 88:543–558. [ Links ]
Quarteroni A., Valli A., 1999, Domain decomposition methods for partial differential equations, Numerical Mathematics and Scientific Computation, Oxford Science Publications, Clarendon Press–Oxford. [ Links ]
Smith B., Bjorstad P., De Gropp W., 1996, Domain Decomposition, Cambridge University Press, New York. [ Links ]
Tezaur R., 1998, Analysis of Lagrange multipliers based domain decomposition. Ph.D. Thesis, University of Colorado, Denver. [ Links ]
Toselli A., 2000, FETI domain decomposition methods for scalar advection–diffusion problem. Technical Report TR2000–800, Courant Institute of Mathematical Sciences, Department of Computer Science, New. York University. [ Links ]
Toselli A., Widlund O.B., 2005, Domain decomposition methods– Algorithms and Theory, Springer Series in Computational Mathematics, Springer–Verlag, Berlin, 450p. [ Links ]
Tu X., Li J., A Balancing Domain Decomposition method by constraints for advection–diffusion problems. www.ddm.org/DD18/ [ Links ]
Tu X., Li J., BDDC for Nonsymmetric positive definite and symmetric indefinite problems. www.ddm.org/DD18/ [ Links ]
1 For the treatment of systems of equations, vector–valued functions are considered, instead
2 The theory to be presented, with slight modifications, works as well in the case that the functions of V are vector–valued.
3 Strictly, these should be column–vectors. However, when they are incorporated in the middle of the text, we write them as row–vectors to save space.
4 In order to mimic standard notations, as we try to do in most of this paper, we should use Π instead of the low–case π. However, we have found convenient to reserve the letter Π for another use.
5 For the treatment of systems of equations, such as those of linear elasticity, such functions are vector–valued.
6 In the Appendix C, it is shown that X is indeed the Lagrange multiplier when such an approach is adopted.



















