Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Geofísica internacional
versión On-line ISSN 2954-436Xversión impresa ISSN 0016-7169
Geofís. Intl vol.49 no.4 Ciudad de México oct./dic. 2010
Articles
Comparison of regional elevation heights in the Aguascalientes basin using DGPS technique with INEGI's digital terrain model
M. Ortiz1*, J. A. Reyna2, M. Balcazar2, A. Hernández Espriu3,4, L. E. Marín5
1 Posgrado en Ciencias de la Tierra, Universidad Nacional Autónoma de México, Ciudad Universitaria, Del. Coyoacán, 04510, Mexico City, Mexico. * Corresponding author: mortiz@geofísica.unam.mx
2 Grupo Ha', Moctezuma 97–A, Col. Toriello Guerra, Del. Tlalpan, 14050, Mexico City, Mexico.
3 Grupo de Hidrogeología de la Facultad de Ingeniería, Universidad Nacional Autónoma de México, Ciudad Universitaria, Del. Coyoacán, 04510, Mexico City, Mexico.
4 Facultad de Ciencias Geológicas, Universidad Complutense de Madrid, Madrid, Spain.
5 Departamento de Recursos Naturales, Instituto de Geofísica, Universidad Nacional Autónoma de México,Ciudad Universitaria, Del. Coyoacán, 04510, Mexico City, Mexico.
Received: January 2, 2009
Accepted: August 19, 2010
Resumen
Las alturas de ochenta y un puntos fueron medidas usando receptores DGPS en bancos de nivel de INEGI y una estación geodética. Cincuenta y ocho puntos se midieron utilizando dos receptores y veintitrés puntos utilizando tres receptores. El análisis de sensibilidad de las alturas obtenidas utilizando dos y tres receptores mostró un rango en las mediciones entre 0.1 y 4.1 cm con una desviación estándar de 1.1 cm. Las alturas obtenidas fueron comparadas con las del Modelo Digital de Elevaciones (MDE) escala 1:50,000 publicado por INEGI (2000). Cuatro áreas fueron identificadas: una con diferencias menores a un metro (Zona I), una con diferencias entre 1.01 y cinco metros (Zona II), una con diferencias entre 5.01 y diez metros (Zona III) y una con diferencias mayores a diez metros. Los resultados muestran que el empleo de mediciones con DGPS proveen una forma útil y práctica de validar MDE regionales y podría ayudar a incrementar la resolución de proyectos o investigaciones específicas.
Palabras clave: DGPS, Aguascalientes, DTM.
Abstract
The elevations of eighty–one points were measured using DGPS receivers at local INEGI benchmarks and at a geodetic station. Fifty–eight points were measured using two receivers and twenty–three points using three receivers. A sensitivity analysis on the heights obtained using the three and two receivers showed a range in measurements between 0.1 and 4.1 cm with a standard deviation of 1.1 cm. The heights obtained were compared to those of the regional Digital Terrain Model (DTM) published by INEGI (2000). Four areas were identified: those with differences less than one meter (Zone I), those with differences between 1.01 and five meters (Zone II), those with differences between 5.01 and ten meters (Zone III), and those with differences greater than ten meters. The results show that the DGPS technique provides a useful way to validate regional terrain models (DTM), and may help in increasing the resolution for special surveys or projects.
Key words: DGPS, Aguascalientes, DTM.
Introduction
The Instituto Nacional de Estadística, Geografía e Informática of México maintains a first–order network of geodetic benchmarks (INEGI, 2000). Their digital terrain model for Mexico contains errors that can be as high as tens of meters (S. Peña, oral com.). Vertical control is essential for the geosciences, including hydrogeology. Marín and others (1998) found that the vertical errors using a hand–held Global Position System (GPS) are greater than 100 meters. Marín and others (2005) conducted a study to determine the precision on the vertical axis using a Differential Global Positioning System (DGPS) and found that using two receivers, the error could be as high as 60 cm. The GPS has been used extensively in geodesic issues, such as crustal deformation, and plate tectonics (Cabral–Cano, et al., 2008). Geodetic surveys typically call for permanent stations, or use long occupation times. Engineering studies, on the other hand, typically use very short occupation times.
In order to be able to map groundwater flow directions, one must first calculate the groundwater flow velocity which is given by Darcy's Law (Freeze and Cherry, 1979). Equation 1 gives the equation used to calculate these velocities.
V = Ki (1)
where
V = Groundwater flow velocity, m/s K = Hydraulic conductivity, m/s
i = Hydraulic gradient, dimensionless
In México, the national mapping agency, INEGI, has established over the years a series of first order benchmarks throughout the country. However, often these first order benchmarks have been destroyed, or are unavailable. Thus, although the best technique to measure the hydraulic gradient is using a total station, it is not possible to do so, if there are no first–order benchmarks available in the vicinity of the proposed study area. In this situation, using the DGPS technique may be the only available solution, particularly, when the study area is large.
Marín and others (1998) compared different techniques for estimating the hydraulic gradient (Equation 1). Knowledge of the hydraulic gradient is important in order to be able to determine the direction and velocity of groundwater. Marin and others (2005) have concluded that using the DGPS technique one can conduct surveying with an error bar in the vertical direction on the order of less than one meter. The hydraulic gradient in the coastal aquifer of Northwest Yucatan is on the order of seven to ten millimeters per kilometer. In a setting such as the Yucatan, an error on the order of tens of centimeters, is not acceptable. Marín and others (2008) used three simultaneous receivers (i.e. three receivers that were recording the data at the same time), and were able to obtain a difference on the vertical axis of less than five cm using simultaneous occupation times on the order of 30 minutes per station.
The purpose of this paper is to compare DGPS surveys using both two and three receivers, and to determine the error bar between the DTM (Digital Terrain Model) and the DGPS technique using as an example the city of Aguascalientes and surroundings.
Methodology
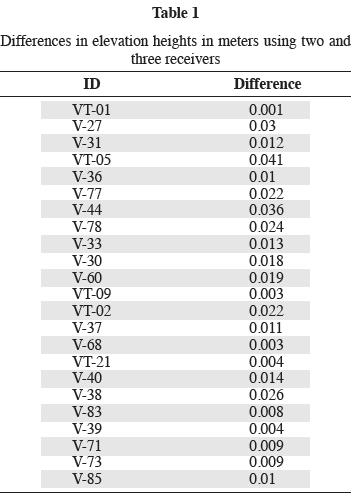
A total of 23 points were measured using three receivers, and 58 points were measured using two receivers in the greater Aguascalientes Valley (Fig. 1, 2a and 2b). Two base receivers (Trimble 5700), and one portable receiver (Trimble 5800) were used. The survey was conducted between October and November, 2004, along a north–south line with a length of 120 km using four base stations (Cosio, San Francisco de los Romos, Aguascalientes, and Peñuelas). The Aguascalientes benchmark was tied into INEGI's benchmarks located at INEGI's headquarters in Aguascalientes City, Aguascalientes. From this control point, elevations of the other benchmarks were determined using the TGO software. Once an initial elevation is given, the TGO software calculates the difference in elevation, and gives the new elevation to each one of the other benchmarks and wells that were surveyed. Each one of the receivers logs the data received from the available satellites automatically. Data logged in the receivers were downloaded to a computer for post–processing after every measurement period. The software used for postprocessing was the Trimble Geomatic's Office Software (TGO, 1999). When using the TGO software, the user may use the predicted orbits that are broadcast by each one of the satellites, or one may download the real orbits. Marín (unpublished) has found differences less than two centimeters between predicted and real orbits. Thus, predicted orbits were used for this experiment. All tripods were preset to an elevation of 1.80 meters. Occupation times were 20 minutes at each station. Baselines ranged between 1.5 to 46 kilometers. The DGPS baselines were processed using the TGO software and results show that they passed the quality control imposed by TGO software. The TGO software has three different quality control filters. Only the baselines that passed all three controls were used. Fig. 1 shows the location of the study area. Fig. 2a and 2b shows the location of the measurements as well as the location of the base receivers. The datum used was the WGS84. A sensitivity analysis was performed on 23 points that were measured using both two and three receivers in the following manner: when two receivers are used (one base receiver and one rover or portable receiver), one baseline is obtained. When three receivers are used (two base receivers and one rover), three baselines are obtained. For all 23 points with the three receivers, one receiver was eliminated (reducing the baselines from three to one), and the vector was re–calculated. The resulting elevation was then compared with the elevation obtained using the three receivers (Table 1).
Results and discussion
Table 1 shows the difference in elevations using two and three receivers. Differences are in the range between 0.1 to 4.1cm. The standard deviation was 1.1 cm.
The results presented in this study are very different than those presented by Marín and others (2005). This paper presents a maximum error of less than 5 cm, whereas Marín and others report an error as high as 60 cm. The explanation may be mainly due to the following. Experiments were carried out in different areas. The experiment that is reported in this paper was carried out in Aguascalientes, which is less than 800 km from the continental U.S. The satellite coverage for the continental United States is very good. As the distance from the continental US increases, the GPS coverage diminishes significantly. This research paid special attention to satellite geometry, and the surveys were conducted while there was a maximum satellite cover in his study region.
The results from this survey were used to estimate the error bar on the DTM for the Aguascalientes Valley. Fig. 3 shows four distinct areas where the difference between both models (The DTM and the DGPS models) is less than one meter (zone I), between one and five meters (zone II), between five and ten meters (zone III), and greater than ten meters (zone IV). It is not surprising that zone I is placed along the valley, and is where most of the population is established itself. INEGI has given priority to having better DTM's in urban areas in contrast to rural areas. The highest error is found in the higher areas where there is probably less topographical control.
Conclusions
The research presented here shows that provided an adequate satellite coverage, two DGPS receivers generate an acceptable DTM model for the area under study. Three receivers give redundant information and allow the user to close the polygons offering increased confidence on the measured values.
DTM models are an approximation and may be used as an initial value. Based on the results presented here, we suggest that DTM's may only be used for regional studies, and can not be used to estimate the hydraulic gradient in aquifers in Mexico.
Acknowledgements
Ortiz acknowledges a fellowship from the Consejo de Ciencia y Tecnología del Estado de Aguascalientes; Marín acknowledges support from the Dirección General de Asuntos del Personal Académico of the Universidad Nacional Autónoma de México. This is contribution 01 from Grupo Ha'.
Bibliography
Cabral–Cano, E., T. H. Dixon, F. Millares Wilheim, O. Díaz Molina, O. Sánchez and R. E. Carande, 2008. Space Geodetic Imaging of rapid subsidence in Mexico City, GSA, Geological Society of American Bulletin, 120, 1556–1566. [ Links ]
Freeze, A. J. C. Cherry, 1979. Groundwater, Prentice–Hall, New Jersey, USA, 679 p. [ Links ]
INEGI, 2000. La Nueva Red Geodésica Nacional, una visión hacia el futuro, Aguascalientes, Aguascalientes, México, 29 p. [ Links ]
INEGI, 2000. www.inegi.gob.mx [ Links ]
Marín, L. E., X. Pérez and E. Rangel, 1998. Comparison of three surveying techniques and its applications to hydrogeological studies: level, barometer, and GPS, Geofísica Internacional, 37, 127–129. [ Links ]
Marín, L. E., B. Steinich, O. A. Escolero F.,2005. Precision Estimates for Ellipsoidal Height Determinations for Short Baselines using a DGPS System, Geofísica Internacional, 44, 4, 391–394. [ Links ]
Marín, L. E., M. Balcazar, M. Ortiz, B. Steinich, J. A. Hernandez–Espriu, 2008. Comparison of elevation heights using a Differential Global Positioning System (DGPS) and a Total Station, Geofísica Internacional, 47, 1, 81–83. [ Links ]














