Artículos

 

Future Contingents and Aristotle's Fantasy

 

Los futuros contingentes y la fantasía de Aristóteles

 

Andrea Iacona

 

Università dell'Aquila. E–mail: ai@cc.univaq.it

 

Received: March 3, 2007
Revised: September 28, 2007
Accepted: November 6, 2007

 

ABSTRACT

This paper deals with the problem of future contingents, and focuses on two classical logical principles, excluded middle and bivalence. One may think that different attitudes are to be adopted towards these two principles in order to solve the problem. According to what seems to be a widely held hypothesis, excluded middle must be accepted while bivalence must be rejected. The paper goes against that line of thought. In the first place, it shows how the rejection of bivalence leads to implausible consequences if excluded middle is accepted. In the second place, it addresses the question of why one should reject bivalence, and finds no satisfactory answer.

KEY WORDS: future contingents, excluded middle, bivalence, fatalism.

 

RESUMEN

Este artículo trata el problema de los futuros contingentes, y se enfoca en dos principios lógicos clásicos: el tercero excluido y la bivalencia. Se podría pensar que una solución del problema requiere actitudes diferentes hacia estos dos principios. Según una hipótesis que parece ampliamente compartida, el tercero excluido debe ser aceptado, mientras que la bivalencia debe ser rechazada. Este artículo argumenta en contra de esta línea de pensamiento. En primer lugar, se aborda cómo el rechazo de la bivalencia lleva a consecuencias poco plausibles si el tercero excluido es aceptado. En segundo lugar, se enfrenta la cuestión de por qué se debería rechazar la bivalencia, sin encontrar una respuesta satisfactoria.

PALABRAS CLAVE: futuros contingentes, tercero excluido, bivalencia, fatalismo.

 

1. One of the things Aristotle seems to claim in De interpretatione IX is that bivalence entails fatalism. Bivalence is the principle according to which truth and falsity are mutually exclusive and jointly exhaustive values. Fatalism is the doctrine according to which if something happens, it is necessary that it happens, and if something does not happen, it is impossible that it happens. The claim is phrased in terms of the sea battle example. If the sentence

(1)  There will be a sea battle tomorrow

is either true or false, then either it is necessary or it is impossible that there will be a sea battle tomorrow. The argument goes as follows, for any sentence 'p' such as (1):

BF

(2)  Either 'p' is true or 'p' is false

(3)  If 'p' is true then it is necessary that p

(4)  If 'p' is false then it is impossible that p

________________________________________________

(5)  Either it is necessary that p or it is impossible that p

As fatalism is highly controversial, in that events such as sea battles seem contingent, this may be regarded as a reason to think that bivalence does not hold for future contingents, that is, for sentences about such events. So thought Lukasiewicz when he constructed his system of three–valued logic (Lukasiewicz 1920).

Another thing Aristotle seems to claim in De interpretatione IX is that excluded middle does hold for future contingents. Excluded middle is the principle according to which any disjunction of a sentence and its negation is true. So the following disjunction is true:

(6)  Either there will be a sea battle tomorrow or there will not be a sea battle tomorrow

The plausibility (6) is hardly deniable. Either a sea battle will take place or it will not. What else could happen? Perhaps Lukasiewicz was not so impressed by this principle, as his system leaves no room for it. But few after him have been willing to follow that route. Several attempts have been made to provide an account of future contingents that rejects bivalence but preserves excluded middle, either by amending Lukasiewicz's system or by constructing a different formal apparatus. Accounts of the first kind are the revisions of three–valued logic proposed by Tooley and Bourne.¹ Accounts of the second kind are Thomason's supervaluationism and MacFarlane's relativism.²

The problem, however, is that bivalence seems derivable from excluded middle:

EB

(7)  Either p or not–p

(8)  If p then 'p' is true

(9)  If not–p then 'p' is false

__________________________

(2) Either 'p' is true or 'p' is false

According to EB, from (6) it follows that either (1) is true or (1) is false.³ This means that if bivalence entails fatalism, so does excluded middle. Therefore, it is natural to think that there may be something wrong with claiming both that excluded middle holds and that bivalence does not hold. Quine attributed to Aristotle the "fantasy" that the truth of a disjunction does not entail the truth of one of its disjuncts.⁴ This paper is about the fantasy that an account of future contingents must save excluded middle but sacrifice bivalence. Sections 2—4 show how the separation of the two principles leads to undesirable consequences. Each of the accounts mentioned is bound to reject other principles that are no less plausible than excluded middle. Sections 5—6 explain why the fantasy is unfounded. Bivalence does not entail fatalism, and has little to do with it. What Aristotle really says in De interpretatione IX is quite a different story.

2. In Lukasiewicz's system, the trouble with excluded middle originates from the semantic treatment of the connectives. As in two–valued logic, the connectives are assumed to be truth–functional, and their meaning is given by truth tables:

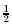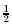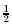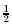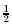Here 1 stands for 'true', 0 for 'false', and for 'indeterminate'. Inde–terminateness is conceived as a third status that obtains when it is not settled whether truth or falsity obtains. Thus, (1) is indeterminate, and the same goes for its negation 'There will not be a sea battle tomorrow', as the table for ~ says that ~ p = if p = . Since the table for V says that p V q= if p=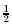 and q = 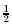, (6) is indeterminate. That is, a sentence of the form p V ~ p can fail to be true, hence excluded middle does not hold.⁵

This unpalatable result clearly depends on the assumption that V is truth–functional, so that every disjunction with indeterminate disjuncts is indeterminate. The assumption causes no trouble when we consider sentences such as 'Either there will be a sea battle tomorrow or it will rain tomorrow'. But in the case of sentences of the form p V ~ p things are different, as we feel entitled to assert the disjunction even if we don't know what to say about the truth value of its disjuncts. Accordingly, one way to preserve excluded middle within a three–valued framework is to drop the assumption that V is truth–functional. Once this is done, it may be claimed that some disjunctions with indeterminate disjuncts are indeterminate, such as 'Either there will be a sea battle tomorrow or it will rain tomorrow', whereas others are true, such as (6). Tooley adopts this strategy, and argues that the truth of a disjunction of the second kind is not to be explained in terms of truth–functionality.⁶

The strategy provides a reason to doubt EB, for it provides a reason to doubt its validity. EB is an argument of the form p V q, p r, q s ; r V s. On a standard understanding of the connectives this is a valid form, in the obvious sense that all its instances are valid arguments. But it is part of the standard understanding of the connectives that p V q is true if and only if either p is true or q is true. If not so, it is possible that the premises of an argument of this form are true even though its conclusion isn't true. Let q be ~ p, and suppose that p = 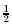, r = 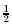, and s = 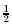. Then, p V q = 1, being one of those disjunctions that are true when both disjuncts are indeterminate. Besides, p r = 1 and q s = 1, given the table for . However, it may happen that r V s = 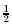, for r V s may not be one of those disjunctions that are true when both disjuncts are indeterminate. This turns out clear in the case in which r and s are replaced by p, for p V p must have the same value as p. Therefore, the form in question is not valid, hence it does not guarantee the validity of EB.

Tooley's strategy is not very attractive, in that it blocks an apparently correct generalization. The following argument seems valid: either it snows or it doesn't, if it snows, then I go out, if it doesn't, then I watch a movie; therefore, either I go out or I watch a movie. The same goes for the following: either the Earth is round or it is flat, if it is round, then Columbus was right, if it is flat, then Columbus was wrong; therefore, either Columbus was right or he was wrong. It is easy to see that these two arguments have the same form. And it is also easy to see that any other argument of that form seems valid. But if one accepts Tooley's account, one is entitled to say neither that all arguments that have the same form as these two are valid, nor that either of them is valid in that it has that form. This is implausible. Moreover, since BF has the same form, the strategy seems at odds with the very idea that motivates three–valued logic, namely, that BF justifies the rejection of bivalence. For it turns out that, just as in the case of EB, the validity of BF is not guaranteed by the fact that it has that form.

Another way to preserve excluded middle within a three–valued framework is to change the truth tables. This is the strategy adopted by Bourne. According to him, it is the definition of negation that causes the trouble. Instead of being as above, the table for ~ should be

 

That is, instead of implying that ~ p =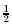 if p = 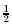, the definition of negation should imply that ~ p = 1 if p = 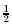. The motivation provided is that if p is indeterminate, "to say that it is not the case that p is clearly to say something true". As for the other tables, the proposal is to leave those for A and V as above, but to change that for in order to preserve the equivalence between p q and ~ ( p ~ q ):

This system preserves excluded middle without losing truth–functionality. For p V ~ p turns out true for any assignment of truth values to p. At the same time, it accounts for the difference between an instance of excluded middle and a disjunction such as 'Either there will be a sea battle tomorrow or it will rain tomorrow'. For a disjunction of the latter kind does not involve negation of one of the disjuncts, so nothing prevents it from being indeterminate.⁷

The strategy adopted by Bourne provides a reason to doubt EB. For it provides a reason to doubt one of its premises, namely (9). Let F be a predicate that stands for 'false', and [p] be a name of p. It seems correct to stipulate that F[p] = 1 only if p = 0. This way (9) can be rephrased as ~ pF[p]. Now suppose that the connectives are defined as Bourne recommends, and that p = 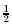. It follows from the table for ~ that ~ p = 1. But our stipulation about F entails that the value of F[p] cannot be 1, for p = 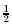. This means that either F[p] =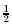or F[p] = 0. In both cases, the table for tells us that ~ p F[p] = 0. Therefore, (9) can't be true.

The reason so provided to doubt EB, however, counts as a reason to doubt the plausibility of the system itself. Taken at face value, (9) expresses a platitude, namely, that if it is not the case that things are a certain way, it is false to say that they are that way. If someone says that it is raining, and it is not the case that it is raining, it is natural to think that what he or she says is false. For it is false to say that it is raining when it is not. (9), together with (8), seems central to our ordinary understanding of truth and falsity. Tarski regarded (8) and (9) as part of the "classical" conception of truth, which he illustrated by quoting the famous passage from Aristotle's Metaphysics: "to say of what is that it is not, or of what is not that it is, is false, while to say of what is that it is, or of what is not that it is not, is true".⁸

It might certainly be contended that 'It is not the case that it is raining' is not quite the same thing as 'It is not raining', in that the first expression, but not the second, allows for the possible indeterminacy of 'It is raining'. In this case the denial of (9) would not entail denial of the platitude that it is false to say that it is raining when it is not. But then it would no longer be clear that ~ expresses negation as we ordinarily understand it, hence that the system preserves excluded middle as we ordinarily understand it. For excluded middle as we ordinarily understand it does not imply that the truth of 'Either it is raining or it is not raining' depends on the second disjunct meaning that either it is indeterminate whether it is raining or it is not raining. What the second disjunct means is simply that it is not raining. In substance, either ~ expresses negation as we ordinarily understand it, and so the implausible consequence follows, or it doesn't express it, and so it is not clear how excluded middle can be preserved.

3. Another account that gives up bivalence but saves excluded middle is supervaluationism. This account rests on the idea that the evaluation of future contingents must take into account all the possible histories that are compatible with the present. The metaphor is that of time as a line branching from the present into a range of possible futures each of which branches again and again. Thomason shows how semantics can be framed in terms of this metaphor: a tree is a world, a line along the tree is a history, that is, a way the world might have gone or might go, and a point along the line is a moment. Sentences can be evaluated in the classical fashion as true or false at moments relative to histories. This holds in particular for sentences of the form p, where is the future tense operator 'it will be the case that'. At a moment m, p = 1 on a history h if for some m' along h such that m' > m, p = 1 at m' on h, otherwise p = 0 on h. Truth at m is defined as truth on all histories passing through m. That is, p is true at m if p = 1 on all histories passing through m, false if p = 0 on all histories passing through m, and neither true nor false otherwise. The definition entails that bivalence does not hold for future contingents, while excluded middle does. For if p is a future contingent, there are histories passing through m on which p = 1 and histories on which p = 0. Therefore, p is neither true nor false at m. However, p V ~ p is true at m, as p V ~ p = 1 on all histories passing through m.⁹

This obviously does not squares well with EB. It is reasonable to assume that the language whose semantics is given in terms of the supervaluational apparatus can include two predicates T and F that stand for 'true' and 'false'. Otherwise, its expressive limits would seriously affect the credibility of the theory. But if such predicates are in the language, then it seems that bivalence can be derived in accordance with EB. That is, from p V ~ p, p T[p] and ~ p F[p], it follows that T[p] V F[p]. Therefore, supervaluationism must have something to say about EB.

The options available are basically two. One is to define T and F in such a way that their application to [p] relative to a given history depends on the truth value of p relative to that history. That is, at any m, T[p] = 1 on h if p = 1 on h, otherwise T[p] = 0 on h. Similarly, at any m, F[p] = 1 on h if p = 0 on h, otherwise F[p] = 0 on h. In this case EB goes through. For it turns out that p T[p] = 1 and ~ p F[p] = 1 at any m on any history, hence that p T[p] and ~p F[p] are true at any m. This entails that T[p] V F[p] is true at any m. Therefore, what can be said is at most that T and F do not express truth and falsity as they are understood in terms of the supervaluational apparatus, in that bivalence holds for them.¹⁰ The outcome of this option is evident. If T and F are so defined, it must be assumed that the definition is correct in some important sense. Otherwise, it is hard to see why it should be adopted. But then it must be granted that bivalence is correct in some important sense. That is, the view can't be that there is one thing, truth, and the supervaluational apparatus captures it. Rather, it must be that different facts about truth are captured by two different predicates: one is a metalinguistic predicate, the other is a predicate in the object language. According to the latter, it is correct to say that (1) is either true or false.¹¹

The other option is to define T and F in terms of the supervaluational apparatus, so that their application to [p] at a moment on a history depends on the truth value of p at that moment relative to all histories passing through that moment. That is, T[p] = 1 at m on h if p = 1 on all histories passing through m, otherwise T[p] = 0 at m on h. Similarly, F[p] = 1 at m on h if p = 0 on all histories passing through m, otherwise F[p] = 0 at m on h. In other words, T[p] is true relative to a given history at a given moment when p is non–relatively true at that moment, and F[p] is true relative to a given history at a given moment when p is non–relatively false at that moment. In this case the definition provides a reason to reject EB, as it provides a reason to reject (8) and (9). In order for p T[p] to be true at a moment m, there must be no history passing through m on which p = 1 and T[p] = 0. But consider two histories h1 and h2 passing through m such that p = 1 on h₁ and p = 0 on h₂. At m T[p] = 0 on both h₁ and h₂, as p = 0 on h₂. It follows that there is a history, h₁, on which p = 1 and T[p] = 0 at m. The same goes for ~p F[p]. As p = 1 at m on h₁, F[p] = 0 at m on both h₁ and h₂. It follows that there is a history, h₂, on which ~p = 1 and F[p] = 0 at m. The rejection of (8) and (9), however, can be seen as an implausible consequence of this option. As noted in section 2, (8) and (9) seem to express platitudes about truth and falsity. But something can't be a platitude if it is not true.¹²

4. The relativist account advocated by MacFarlane is intended to vindicate two intuitions. One is the "indeterminacy intuition", according to which today we are inclined to say that (1) is neither true nor false. The other is the "determinacy intuition", according to which tomorrow we will be inclined to assign truth or falsity to it. MacFarlane's point is that these two intuitions turn out to be incompatible on the assumption that the truth value of the sentence is "absolute", i.e., that it does not change with the "context of assessment". Therefore, he claims that truth must be relativized both to the context of utterance and to the context of assessment, and shows how this relativization can be handled in a formal semantics. As a first step, he defines truth at a point m/h, where h is a history and m is a moment that belongs to h. In particular, if is 'it will be the case that', then p = 1 at m/h if for some m' such that m' > m, p = 1 at m'/ h. Then, he defines truth relative to a context of utterance u and context of assessment a as follows: p is true at u and a if and only if p = 1 at every m/h such that m is the moment of u, and that h passes through m and (if the moment of a > m) through the moment of a as well. The definition of falsity is analogous. This gives us the desired result. Suppose that there are only two histories h₁ and h₂ passing through a moment m₀, and that p = 1 at m₀/ h₁ while p = 0 at m₀/h₂. If both u and a are at m₀ we get that p is neither true nor false at u and a. That is, (1), uttered today, is neither true nor false as assessed today. Now suppose that m₁ and m₂ are moments later than m₀ that belong to h₁ and h₂ respectively, and that p = 1 at m₁ / h₁ while p = 0 at m₂/h₂. If u is at m₀ and a is at m₁ we get that p is true at u and a, because only h1 passes through m₀ and m₁. That is, (1), uttered today, is true as assessed tomorrow if there is a sea battle tomorrow. Similarly, if u is at m₀ and a is at m₂ we get that p is false at u and a, because only h₂ passes through m₀ and m₂. That is, (1), uttered today, is false as assessed tomorrow if there is no sea battle tomorrow.¹³

MacFarlane's account differs from supervaluationism in that it entails that (1) is true or false as assessed tomorrow. But as far as today is concerned it is exactly like supervaluationism. That is, (1) is neither true nor false, and it is so because it is true relative to some histories and false relative to others. Similarly, excluded middle holds, as (6) is true relative to all histories. Therefore, as far as today is concerned, MacFarlane's account runs into the same dilemma as supervaluationism, assuming that ascription of truth and falsity can be expressed in the language. One option is to define T and F as follows: T[p] = 1 at m/h if p = 1 at m/h, otherwise T[p] = 0 at m/h, and F[p] = 1 at m/h if p = 0 at m/h, otherwise F[p] = 0 at m/h. If T and F are so defined then EB goes through. For its premises are true at u and a when both u and a are at m0, hence its conclusion is also true at u and a.¹⁴

The other option is to define two predicates Tua and Fua that express relative truth and relative falsity, where u and a stand for the moment of utterance and the moment of assessment. Presumably, the definition must imply that Tua[p] = 1 at any point if p is true at u and a, otherwise Tua[p] = 0 at any point. Similarly, Fua[p] = 1 at any point if p is false at u and a, otherwise Fua[p] = 0 at any point. This means that, in the situation described above, Tm₀m₀[p] and Fm₀m₀[p] are false at any point. For p = 1 at m₀ /h₁ and p = 0 at m₀/h₂. It follows that p Tm₀m₀[p] = 0 at m₀/h₁ and ~ p Fm₀m₀[p] ⁼ 0 at m₀/h₂. However, it is not clear what rationale can lie behind this result. It is plausible to say that, if there will be a sea battle tomorrow, then (1) is true as uttered today and assessed today. Similarly, it is plausible to say that, if there will not be a sea battle tomorrow, then (1) false as uttered today and assessed today. The relativization of truth to a context of utterance and a context of assessment does not deprive (8) and (9) of their apparent correctness.¹⁵

5. The implausible consequences of the accounts considered are no worse than fatalism. Therefore, if rejecting bivalence were the only alternative to fatalism, they could be accepted as a reasonable price to pay. This means that the credibility of those accounts ultimately depends on the soundness of BF. For if bivalence does not entail fatalism, there is no price to pay. And given that BF is no less valid than EB, the question turns on (3) and (4). Why should one think that if (1) is true then it is necessary that there will be a sea battle tomorrow? Or that if (1) is false then it is impossible that there will be a sea battle tomorrow? Note that here necessity and impossibility are to be understood in such a way that (3) and (4) turn out to be sentences of the form p ℘ q. Otherwise, BF wouldn't be valid. Therefore, (3) and (4) cannot be justified by appeal to the fact that the truth of (1) necessarily entails that there will be a sea battle tomorrow, and that its falsity necessarily entails that there will not be a sea battle tomorrow. For this can count at most as a reason to think that two sentences of the form ℘ (p q are true, and it is a straightforward modal fallacy to infer p ℘ q from ℘ (p q).¹⁶

The best way to make sense of (3) and (4) seems to be the following. To say that (1) is true today is to say that the way things are today is sufficient to determine that tomorrow there will be a sea battle, hence that the sea battle is inevitable. Therefore, if (1) is true, then it is necessary that there will be a sea battle tomorrow. The same reasoning applies to the case in which (1) is false. In other words, the truth or falsity of (1) entails that today there is some fact or event that determines what is going to happen tomorrow. This is why it is often noted that BF rests on the assumption that truth is correspondence with reality. That is, if (1) is true, there must be some fact or event to which it corresponds. Conversely, if there is no such fact or event, (1) can't be true.¹⁷

What is often not noted, however, is that the correspondence assumption does not suffice by itself to justify (3) and (4). A stronger condition is needed, namely, that in order for a sentence uttered at a certain time to be true, there must be at that time a fact or event to which it corresponds. This condition is essential to the justification, as what happens tomorrow can be necessary only if it is determined by some fact or event that exists today. But it also makes the justification dubious, as there seems to be no independent reason to accept it. Take the sentence 'Brutus killed Caesar' as it is uttered today. Given its truth, the correspondence assumption entails that it is made true by something. This is plausible enough. However, there seems to be no reason to think that the something in question must exist today. As the sentence is about an event that occurred in 44 b.C., it is quite natural to think that what makes it true is that very event. The same goes for the future. It is plausible to assume that if (1) is true, then its truth is due to something. But there seems to be no reason to think that this something must exist today.¹⁸

The assumption that truth is correspondence with reality is perfectly compatible with the possibility that what makes a sentence uttered at a certain time true is something that exists at a different time. Certainly, such a possibility entails that correspondence is a relation that can obtain even if its terms are entities that exist at different times. But this is not a problem, as nothing in the notion of a relation rules it out. In fact, some of the relations we are familiar with are naturally understood this way. For example, when one says that x is an ancestor of y one does not imply that x and y exist at the same time. What usually happens is that x exists when y does not exist, and vice versa. In substance, even assuming that truth is correspondence with reality, there seems to be no reason to think that the truth or falsity of (1) entails the existence of some fact or event today. Accordingly, there seems to be no reason to think that (3) and (4) are true. As far as BF is concerned, bivalence does not entail fatalism.¹⁹

6. So far it has been said that the combination of excluded middle with the denial of bivalence has implausible consequences, and that an argument that traditionally has inspired the denial of bivalence is a bad argument. This leads us to think that bivalence is like excluded middle in at least two important respects. One is that it does hold for future contingents. The other is that it holds independently of the metaphysical question of whether fatalism is right or wrong. This last section is intended to substantiate that thought, by showing how one can make sense of excluded middle and bivalence without presupposing this or that way of settling the metaphysical question. The two principles can be justified in purely epistemic terms.

For any n, let t_n be a time and w_n be a possible world that represents the way things are at t_n. Thus t₀ is the present time, and w₀ is the actual world as it is now. As far as we know at t₀, given any n > 0, different possible worlds are equally good candidates for being w_n. Only at t_n we will know which of them will be "successful", that is, which of them will turn out to be w_n. Let p be a sentence uttered at t₀ that involves reference to a later time t₁, i.e. a sentence of the form 'at t₁, p'. Suppose that the truth or falsity of p depends on a property of w₁ in the following way: p = 1 in w₀ if p = 1 in w₁, and p = 0 in w₀ if p = 0 in w₁. Suppose also that the set of candidates can ideally be divided into two non–empty sets α nd β such that for every w in it, w belongs to α if and only if p = 1 in w and w belongs to β if and only if ~ p = 1 in w. Given that at t0 we are not in a position to know which of the candidates will be successful, we are not in a position to know whether p = 1 in w₁. Therefore, at t₀ we are not in a position to know whether p = 1. The expression 'in a position to know' is to be understood in the following way. To be in a position to know x at t is not quite the same thing as to know x at t. One may be in a position to know x at t without knowing x at t. But if one is in a position to know x at t, and one does what one is in a position to do at t to get to know x, then one gets to know x at t. If we call a sentence definitely true when it is true and we are in a position to know that it is true, then at t₀ p is not definitely true. The same goes for ~p. This accounts for the fact that today we are not able to tell whether (1) is true or false. Only tomorrow we will.²⁰

There are, however, properties of possible worlds that belong to all candidates, so that at t₀ we are in a position to know that they belong to w₁. For even if at t₀ we are not in a position to know which of the candidates will be successful, we are in a position to know that the successful candidate will have them. One such property is that of being a possible world such that either p = 1 in it or ~p = 1 in it. Each candidate w has this property, in that either w belongs to α or w belongs to β. This means that there are only two options open for

(a)  p = 1 in w₁

(b)  ~p = 1 in w₁

Therefore, the following holds for any q:

(c) if (a) entails that q = 1 in w₀ and (b) entails that q= 1 in w₀, then q = 1 in w₀

Now suppose (a). It follows that p = 1 in w₀, hence that p V ~p = 1 in w₀. Suppose instead (b). It follows that ~p = 1 in w₀, hence that p V ~p = 1 in w₀. Therefore, both (a) and (b) entail that p V ~ p = 1 in w₀. Given (c), we may conclude that p V ~p = 1 in w₀. This accounts for the fact that today we are able to say that (6) is true. That is, excluded middle holds for future contingents.²¹

Bivalence straightforwardly follows from the same property of w1 and the definition of the usual predicates T and F. Let T be such that for every w, T[p] = 1 in w if p = 1 in w and T[p] = 0 in w if p = 0 in w. Similarly, let F be such that F[p] = 1 in w if p = 0 in w and F[p] = 0 in w if p = 1 in w. Suppose (a). It follows that p = 1 in w₀, hence that T[p] = 1 in w₀ . Therefore, T[p] V F[p] = 1 in w₀. Suppose instead (b). In this case p = 0 in w₁. It follows that p = 0 in w0, hence that F[p] = 1 in w₀. Therefore, T[p] V F[p] = 1 in w₀. Given (c), we may conclude that T[p] V F[p] = 1 in w₀. This means that T[p] V F[p] is definitely true at t₀.

An analogy may help. Candidate for possible worlds and their properties are like candidates for the presidency of the United States and their properties. The day before the elections we are not in a position to know whether the future president will be Republican. For the property of being Republican is possessed by one candidate but not by the other, and the day before the elections we are not in a position to know who will win. Accordingly, 'The future president will be Republican' is neither definitely true nor definitely false. However, there are properties that both candidates share, such as being either Republican or not Republican. Even if the day before the elections we are not in a position to know who will win, we are in a position to know that the winner will be either Republican or not Republican. Accordingly, 'The future president will be either Republican or not Republican' is definitely true, and the same goes for 'Either "The future president will be Republican" is true or it is false'. In other words, we can say something true about the winner before knowing who the winner will be.

The epistemic justification outlined does not settle the metaphysical question of whether fatalism is right or wrong. If fatalism is right then given any n > 0, w₀ determines a unique possible world for t_n. This means that at t₀ it is already decided which of the candidates will turn out to be w_n, although we are not in a position to know which. In the same way, if the result of the elections is decided by some fact existing the day before, then one of the two candidates is bound to win. By contrast, if fatalism is wrong then different possible worlds are compatible with w₀. This means that at t₀ it is not yet determined which of them will turn out to be w_n. If the result of the elections is not decided the day before, neither of the two candidates is bound to win. In the first case the future is like the past, in that, given any n < 0, there is a unique possible world corresponding to t_n. In the second case they differ: the past is already decided, the future is still open.

The justification entails the metaphysically neutral claim that a disjunction can be definitely true even though neither of its disjuncts is definitely true. (6) is definitely true, yet neither (1) nor its negation is definitely true. The same goes for 'Either (1) is true or (1) is false'. At t₀ we are in a position to know that T[p] V F[p] = 1. But we are not in a position to know whether T [p] = 1, as we are not in a position to know whether p = 1. Similarly, we are not in a position to know whether F[p] = 1, as we are not in a position to know whether p = 0. In other words, definite truth does not distribute over disjunction. This seems correct. Or at least, it is not a fantasy.

 

REFERENCES

Andjelkovic, M. and T. Williamson, 2000, "Truth, Falsity and Borderline Cases", Philosophical Topics, vol. 28, pp. 211–244.         [ Links ]

Ackrill, J.L., 1963, Aristotle's De interpretatione, Clarendon Press, Oxford.         [ Links ]

Bourne, C., 2004, "Future Contingents, Non–Contradiction, and the Law of Excluded Middle Muddle", Analysis, vol. 64, pp. 122–128.         [ Links ]

Conee, E. and T. Sider, 2005, Riddles of Existence, Oxford University Press, Oxford.         [ Links ]

Haack, S., 1974, Deviant Logic, Cambridge University Press, Cambridge.         [ Links ]

Horwich, P., 1987, Asymmetries in Time, MIT Press, Cambridge, Mass.         [ Links ]

Kneale, W. and M. Kneale, 1962, The Development of Logic, Clarendon Press, Oxford.         [ Links ]

Lukasiewicz, J., 1922, "On Determinism", in Selected Works, ed. L. Borkowski, North–Holland, Amsterdam, 1970, pp. 110–128.         [ Links ]

––––––––––, 1920, "On Three–Valued Logic", in Selected Works, ed. L. Borkowski, North–Holland, Amsterdam, 1970, pp. 87–88.         [ Links ]

MacFarlane, J., 2008, "Truth in the Garden of Forking Paths", in M. García–Carpintero and M. Kölbel. (eds.), Relative Truth, Oxford University Press, Oxford, pp. 00–00.         [ Links ]

––––––––––, 2003, "Future Contingents and Relative Truth", Philosophical Quarterly, vol. 53, pp. 321–336.         [ Links ]

McGee, V. and B. McLaughlin, 1995, "Distinctions without a Difference", The Southern Journal of Philosophy, vol. 33 (Supplement), pp. 203–251.         [ Links ]

Prior, A.N., 1953, "Three–Valued Logic and Future Contingents", Philosophical Quarterly, vol. 3, pp. 317–326.         [ Links ]

Quine, W.V.O., 1953, "On a So–Called Paradox", Mind, vol. 62, pp. 65–67.         [ Links ]

Rice, H., 2002, "Fatalism", in Stanford Encyclopedia of Philosophy: http://plato.stanford.edu/search/searcher.py?query=fatalism.         [ Links ]

Tarski, A., 1944, "The Semantic Conception of Truth and the Foundations of Semantics", Philosophy and Phenomenological Research, vol. 4, pp. 341–375.         [ Links ]

Thomason, R.H., 1970, "Indeterminist Time and Truth–Value Gaps", Theoria, vol. 36, pp. 264–281.         [ Links ]

Tooley, M., 1997, Time, Tense, and Causation, Clarendon Press, Oxford.         [ Links ]

Tweedale, M.M., 2004, "Future Contingents and Deflated Truth–Value Gaps", Noûs, vol. 38, pp. 233–265.         [ Links ]

Van Fraassen, B.C., 1966, "Singular Terms, Truth–Value Gaps, and Free Logic", Journal of Philosophy, vol. 63, pp. 481–495.         [ Links ]

 

NOTES

¹ See Tooley 1997; Bourne 2004.

² See Thomason 1970; MacFarlane 2003.

³ Kneale and Kneale 1962, p. 47, and Rice 2002, §1, draw attention to the derivability of bivalence from excluded middle and its relevance to the problem of future contingents. A broader treatment of the derivability issue is given in Andjelkovic and Williamson 2000, whose focus is vagueness. The affinities between the two problems and the purported solutions to them are evident, so there is no need to highlight them in the rest of the paper.

⁴ Quine 1953, p. 65.

⁵ Lukasiewicz 1920; Prior 1953.

⁶ Tooley 1997, pp. 135–146.

⁷ Bourne 2004.

⁸ Aristotle, Metaphysics IV, 7, 1011b 26–27; Tarski 1944, p. 343.

⁹ Van Fraassen 1966; Thomason 1970.

¹⁰ In Thomason 1970, p. 278, a truth operator is defined along these lines.

¹¹ This is a problem only so long as supervaluationism is framed as an attempt to provide an account of future contingents that preserves excluded middle but rejects bivalence. But it is not necessary that it is framed that way. For example, the supervaluationist view advocated, for different purposes, in McGee and McLaughlin 1995 admits two truth predicates, one of which conforms to bivalence.

¹² The considerations in van Fraassen 1966, pp. 494–495, do not affect this point.

¹³ MacFarlane 2003.

¹⁴ Again, this is a problem only so long as the view is framed as an attempt to provide an account that preserves excluded middle but rejects bivalence. As in the case of supervaluationism, it is not necessary that relativism is framed that way. In MacFarlane 2008, less emphasis is placed on the rejection of bivalence, and a disquotational predicate is defined for propositional truth.

¹⁵ This second option does not exclude the first. The relativist could have two predicates, as in MacFarlane 2008, and take them to capture different facts about truth. But the question would still arise of which of them is to be employed to express EB.

¹⁶ Haack 1974, pp. 74–78, attributes the modal fallacy to Aristotle himself.

¹⁷ Ackrill 1963, pp. 140–141, Lukasiewicz 1922, pp. 122–123, Prior 1953, pp. 322–323.

¹⁸ As recognized in Horwich 1987, p. 30, Rice 2002, §1, Conee and Sider 2005, p. 28. One might deny that (1) can be made true by a future event on the basis of a conception of temporal reality according to which future events, unlike past and present events, are not "real", hence not actual (in some sense of 'actual' that matters to truth–making). But in this case the justification of (3) and (4) would depend on that conception. So the point remains that correspondence alone does not suffice.

¹⁹ This means that there is no need to endorse a deflationist conception of truth in order to avoid fatalist implications, as suggested in Tweedale 2004.

²⁰ This is the only fact to be accounted for. There is no "intuition" that the sentence is neither true nor false, as MacFarlane seems to assume. If there were, no argument would be needed to justify the denial of bivalence.

²¹ Obviously, here the assumption is that 'There will not be a sea battle tomorrow' is adequately formalized as ~p. An alternative formalization would be ~p. Note, however, that the two formulas have the same truth conditions. That is, ~ p = ~p = 1 in w₀ if p = 0 in w₁, and ~ p = ~p = 0 in w₀ if p = 1 in w₁.