Artículos

 

La teoría de la explicación causal de Salmon y la mecánica cuántica

 

Salmon's Theory of Causal Explanation and Quantum Mechanics

 

José Luis Rolleri

 

Facultad de Filosofía, Universidad Autónoma de Querétaro. jlrolleri@yahoo.com

 

Recibido el 20 de junio de 2006
Revisado el 24 de abril de 2007
Aceptado el 7 de mayo de 2007

 

RESUMEN

Salmon ha afirmado que su teoría de la explicación causal no es enteramente adecuada para el dominio cuántico debido a ciertas anomalías causales como el dualismo onda/partícula y, especialmente, a las correlaciones estadísticas que surgen de experimentos tipo EPR. En este escrito se analizan las nociones causales de Salmon, en las cuales se basa su teoría probabilista de la explicación, con el fin de delimitar su alcance en ese dominio mostrando que sólo abarca procesos de transición pero no procesos de transmutación. Además, se propone, a muy grandes rasgos, una noción alternativa de causalidad indeterminista que pretende ser adecuada para ciertos procesos cuánticos como procesos estocásticos. Por último se arguye que si bien la explicación de las correlaciones cuánticas es un problema abierto, sería erróneo considerar que una teoría de la explicación causal, como la de Salmon, concebida y elaborada primordialmente para procesos físicos individuales, pueda y deba dar cuenta de tales correlaciones.

PALABRAS CLAVE: proceso causal, proceso estocástico, causalidad indeterminista, correlaciones cuánticas.

 

ABSTRACT

Salmon has said that his theory of causal explanation is not fully adequate for the quantum domain because of certain causal anomalies such as the wave/particle dualism and, in particular, the statistical correlations which arise from EPR–type experiments. This paper analyzes Salmon's causal notions, on which his probabilistic theory of explanation is based, in order to delimit its scope within that domain by showing that it covers only transition processes but not processes of transmutation. Beside, I propose, very roughly, an alternative notion of indeterministic causality, intended to be adequate for certain quantum processes as stochastic processes. Finally, I also argue that, while the explanation of the quantum correlations is an open problem, is would be a mistake to think that a theory of causal explanation, like Salmon's, conceived and worked out primarily for individual physical processes, could and should account for such correlations.

KEY WORDS: causal process, stochastic process, indeterministic causality, quantum correlations.

 

1. Introducción

Durante varios lustros Wesley C. Salmon elaboró algunas teorías de la explicación científica; su última propuesta consiste en una teoría de la explicación causal que se basa en una concepción de la estructura causal del mundo físico (Salmon 1984). La idea básica de explicación de Salmon consiste, a grandes rasgos, en que un suceso o proceso físico es explicado en la medida en que pueda ser insertado en una red causal constituida por procesos e interacciones causales; la fuerza explicativa proviene de exhibir la red causal de la que forma parte el suceso o proceso que se pretende explicar.

Desde el inicio de sus trabajos sobre el tema, Salmon se ocupó de ofrecer una noción de explicación estadística adecuada para sucesos y procesos físicos que, de acuerdo con las teorías científicas disponibles, no están gobernados por leyes de forma universal, sino por leyes de forma probabilista. En sus investigaciones, Salmon parte, principalmente, del rechazo del requisito de alta probabilidad del modelo estadístico–inductivo de Hempel. Ese principio estipula que un suceso tiene que ser altamente probable para que pueda ser explicado, con la consecuencia obvia de que los sucesos cuya probabilidad de acontecer es media o baja quedan del todo inexplicables. Como se sabe, los sucesos con probabilidades medias o bajas abundan en el mundo cuántico, por ello, la mecánica cuántica cobra un interés especial en los escritos de Salmon.

Salmon considera que las restricciones impuestas por ese requisito de alta probabilidad son una razón convincente para abandonar ese modelo de explicación de Hempel e intentar construir un modelo alternativo que permita explicar también sucesos con probabilidades medianas y sucesos muy poco probables, como sucede en el ámbito cuántico; así, a este respecto, él arguye: "Si una y la misma distribución de probabilidad [.. . ] provee la explicación de dos sucesos separados —uno con una probabilidad alta y otro con una probabilidad baja— las dos explicaciones son igualmente valiosas" (1984, p. 89).

No obstante, en varios de sus ensayos, Salmon afirma que su propia teoría no es del todo aplicable al mundo cuántico —donde acontece un sinnúmero de sucesos con probabilidades bajas— debido a que ciertos fenómenos cuánticos, como el comportamiento dual de los fotones, parecen no admitir una explicación causal; por ello, la mecánica cuántica constituye, según él, el mayor desafío a cualquier teoría de la explicación en términos causales. De hecho, Salmon parece hacer afirmaciones opuestas al respecto. En la sección "La explicación en mecánica cuántica" de ese libro suyo, escribe:

De acuerdo con la versión explícitamente probabilista de la causalidad desarrollada en los capítulos precedentes, es posible ofrecer explicaciones causales de sucesos ineluctablemente estocásticos. Incluso si adoptamos la interpretación estadística generalmente aceptada de la mecánica cuántica, su carácter indeterminista no plantea ningún obstáculo a la versión causal de la explicación que he estado propugnando. (1984, p. 243)

Más adelante, sin embargo, cuando se refiere a las descripciones en términos de ondas y de partículas, mutuamente incompatibles, del experimento de las dos ranuras, y a la tesis de Bohr de que ambas descripciones son complementarias, dice:

Esto implica que no puede haber una única descripción consistente que explique qué acontece en términos de procesos causales espacio–temporalmente continuos e interacciones causales locales. Consideraciones de este género parecen sugerir que la teoría de la explicación causal que he intentado desarrollar en capítulos precedentes simplemente no puede ser extendida al dominio cuántico. (1984, p. 245)

En este escrito no analizaré críticamente la teoría sobre la estructura causal del mundo físico de Salmon, lo cual ya ha sido hecho satisfactoriamente por Phil Dowe;¹ en su lugar sólo discutiré su alcance en el dominio cuántico y la cuestión de si los procesos cuánticos podrían encajar en alguna noción no clásica de causalidad apropiada —que capture su carácter estocástico— que abriera la posibilidad de que esos procesos admitan una explicación adecuada. Pienso que Salmon no está del todo en lo correcto al creer que su teoría de la explicación debe aplicarse a ciertos "fenómenos" como las correlaciones cuánticas asociadas a experimentos tipo Einstein, Podolosky y Rosen (EPR, en adelante), puesto que expresamente es una teoría concebida y elaborada para explicar sucesos individuales y no correlaciones entre secuencias aleatorias de sucesos individuales. Por ello creo que Salmon es un tanto severo con su propia teoría: le exige demasiado.

Nuestro objetivo aquí es doble. Primero, intentar mostrar que la teoría causal de Salmon no captura explícitamente el carácter estocástico de los procesos cuánticos y que si bien podría aplicarse a algunos procesos cuánticos, no es adecuada para aquellos que entrañan una transformación del sistema físico (procesos como la fusión y la fisión nucleares y la desintegración radiactiva) —los cuales pueden ser considerados procesos ineluctablemente estocásticos—; junto con ello, delinear a grandes trazos, una noción alternativa de causalidad indeterminista que pretende modelar ciertos procesos cuánticos en cuanto procesos estocásticos. Segundo, tratar de hacer ver que una teoría de la explicación causal como la de Salmon —elaborada y propuesta para sucesos o procesos individuales— ni puede ni tiene que explicar las correlaciones cuánticas que surgen al comparar secuencias aleatorias de resultados individuales de experimentos tipo EPR. El género de explicación que requerirían esas correlaciones no puede ser el mismo que el tipo de explicación causal de sucesos individuales, como el propuesto por Salmon; por esto, el hecho de que su teoría no pueda dar cuenta de ellas no representa una objeción a ésta.

 

2 . El modelo mecánico–causal–estadístico

Una vez que Salmon deja a un lado el requisito de alta probabilidad, elabora un patrón de explicación estadística basado en la idea de que los factores que tienen relevancia estadística, aquellos que delimitan las subclases de referencia objetivamente homogéneas para calcular las distribuciones de probabilidad condicional, ofrecen las razones relevantes para las explicaciones. Un ensamblaje de tales factores relevantes, junto con un conjunto adecuado de valores de probabilidad, constituye una explicación estadística de sucesos singulares, sin importar que las probabilidades asignadas sean altas o bajas. Esto, a primera vista, permite ofrecer explicaciones de sucesos azarosos, como Salmon anota:

En circunstancias de un tipo específico C, un suceso de un tipo dado E algunas veces ocurre y algunas veces no. No hay, en principio, una manera de explicar por qué, en una ocasión dada, E ocurre en lugar de no E. Lo que es más, si en una ocasión C explica por qué E ocurre, entonces en otra ocasión el mismo género de circunstancias explica por qué E deja de ocurrir. (1984, p. 318)

Aunque, para Salmon, esta consecuencia es fuertemente contraintuitiva, no la encuentra intolerable.

Si bien el rechazo del requisito de alta probabilidad le permite a Salmon abordar el problema crucial de la explicación de sucesos azarosos, como lo muestra el planteamiento anterior, su modelo R–E no es satisfactorio, porque, como él mismo lo señala, no es suficiente que se dé una correlación estadística, ni siquiera una al cien por ciento, entre dos tipos de sucesos, para poder explicar sucesos de uno de los tipos en referencia a la ocurrencia de sucesos del otro tipo. El caso del barómetro y la vecindad de tormentas lo muestran. Aunque se tenga que en todos los casos, y sólo en ellos, cuando el barómetro desciende se precipita una tormenta, la baja en el barómetro no explica la ocurrencia de la tormenta, solamente la indica. Hay, más bien, una circunstancia que podría explicar ambos sucesos, las condiciones atmosféricas en el entorno, que es la causa común de ellos.

La relevancia estadística, entonces, carece de fuerza explicativa. Ésa es la razón por la que Salmon modifica su modelo de explicación estadística, agregando a la condición de relevancia estadística una condición de relevancia causal, porque las causas son los factores que otorgan valor explicativo; en este sentido, él arguye que "hay que poner las 'causas' después del 'porque' en las respuestas a las preguntas '¿por qué?' " (1984, pp. 315 y ss.).

El nuevo modelo de Salmon, llamado el modelo mecánico causal (estadístico), M–C–E, es dual:

En el nivel más básico, es necesario, para los propósitos de la explicación, subsumir el suceso a explicar bajo un conjunto apropiado de relaciones estadísticas relevantes. En el segundo nivel, me parece, las relaciones estadísticas relevantes que se invocan en el primer nivel deben ser explicadas en términos de relaciones causales. La explicación, en esta concepción, no es completa hasta que se provean los componentes causales del segundo nivel. (1984, p. 22)

Por un lado, los factores estadísticamente relevantes son necesarios para la explicación de sucesos singulares, pues nos brindan el conocimiento de la probabilidad de que ocurran y sirven de evidencia de una correlación genuina, no accidental, entre pares de tipos de sucesos; por el otro, las conexiones causales entre sucesos estadísticamente correlacionados ofrecen las razones suficientes para las explicaciones estadísticas.

De hecho, Salmon elabora una teoría de la causalidad, con el propósito de obtener un patrón general de explicación científica, diseñada desde la perspectiva de que la causalidad es primariamente una propiedad de procesos individuales. Esa teoría pretende lograr varios desiderata, entre ellos, concebir la causalidad como un rasgo objetivo y contingente del mundo físico, que sea a la vez consistente con el indeterminismo cuántico.

Salmon opta por una ontología de procesos, entendiendo por un proceso cualquier entidad que pueda exhibir persistencia de estructura en un intervalo espacio–temporal,² entidades como ondas, partículas elementales, cuerpos materiales clásicos; aunque no estén sometidas a alguna transformación, porque incluso un objeto material en reposo cuenta como un proceso (cfr. 1981, p. 286). Dentro de ellos, Salmon distingue los procesos causales de los pseudoprocesos. Los primeros son los procesos capaces de transmitir a otro proceso una marca o señal local, en concordancia con el principio señal de la teoría de la relatividad, el cual establece que ninguna información o mensaje puede viajar a una velocidad mayor que la de la luz. Los pseudoprocesos son incapaces de marcar o ser marcados por otro proceso, como las sombras.

Los procesos causales propagan, de una región del espacio–tiempo a otra, su propia estructura y, por ello, son capaces de transmitir influencia causal, es decir, son capaces de influir causalmente en otros procesos. Si un par de tales procesos se intersecan en un punto espacio–temporal, cada uno es marcado e imprime una marca al otro; esto es, ambos sufren una modificación en su estructura, lo cual constituye una interacción causal. En general, lo que transmiten los procesos causales son magnitudes físicas como el momentum, la energía o la carga, las cuales definen su "estructura".

Salmon formula la noción central de transmisión de una marca, TM, con la siguiente definición:

Sea P un proceso que, en ausencia de interacción con otros procesos, podría permanecer uniforme con respecto a una característica Q, la cual podría manifestarse consistentemente sobre un intervalo que incluye ambos puntos A y B (A ≠ B). Entonces una marca (que consiste en una modificación de Q en Q'), que ha sido introducida en el proceso P por medio de una interacción local singular en el punto A, es transmitida al punto B, si P manifiesta la modificación Q' en B y en todos los estadios del proceso entre A y B sin interacciones adicionales. (1984, p. 148)

Mas los procesos causales no producen influencias causales, sólo las transmiten. La producción de influencias causales está a cargo de lo que Salmon llama bifurcaciones interactivas. En este tipo de bifurcaciones, dos procesos causales se intersecan en un punto espacio–temporal produciendo una modificación mutua o, mejor, un intercambio de, al menos, una magnitud en cada uno. Esos intercambios, que modifican la estructura de ambos procesos, están regidos, principal pero no exclusivamente, por leyes físicas de conservación. Como ejemplos de ellas podríamos pensar en el choque de dos bolas de billar y en la fisión de un par de átomos.

La idea clave de interacción causal, IC, Salmon la define en referencia a la noción de transmisión de marca o modificación de una característica, de la siguiente manera:

Sean P₁ y P₂ dos procesos que se intersecan en el espacio–tiempo S, el cual pertenece a la historia de ambos. Sea Q una característica que el proceso P₁ podría exhibir a través de un intervalo (que incluye subintervalos en ambos lados de S en la historia de P₁si la intersección con P2 no ocurre; sea R una característica que el proceso P₂ podría exhibir a través de un intervalo (que incluye subintervalos en ambos lados de S en la historia de P₂ si la intersección con P1 no ocurre. Entonces, la intersección de P₁ y P₂ en S constituye una interacción causal si (1) P₁ exhibe la característica Q antes de S, pero exhibe una característica modificada Q' a través de un intervalo inmediatamente posterior a S; y (2) P₂ exhibe R antes de S pero exhibe una característica modificada R en un intervalo inmediatamente después de S. (1984, p. 171)

El ejemplo favorito de Salmon de las anteriores nociones causales lo constituye el efecto de dispersión Compton. Cuando un fotón de rayo–X con energía E = hv colisiona con un electrón en reposo, el fotón emerge con energía E₁ = hv' y el electrón se pone en movimiento adquiriendo una energía cinética E₂ igual a la diferencia de energía hv del fotón incidente y la energía h del fotón dispersado; i.e., igual a h (v — v'). En esta situación, E = E₁+E₂, lo que satisface la ley de conservación de energía. Salmon explica la aplicación de sus nociones causales al efecto Compton como sigue:

El fotón y el electrón son procesos causales. Cuando el fotón y el electrón colisionan, ambos son modificados. La frecuencia, la energía y el momentum del fotón cambian, así como la energía y el momentum del electrón (en esta interacción, la energía y el momentum se conservan). Además, esos cambios persisten más allá de la colisión. Esta persistencia es esencial para una interacción causal; la dispersión Compton es un excelente ejemplo. (1990, pp. 202 y 203)

El siguiente gráfico representa lo anterior, donde P₁ es el fotón, P₂ es el electrón, S es el punto espacio–temporal de la colisión, Q' es E₁ y R' es E₂:

 

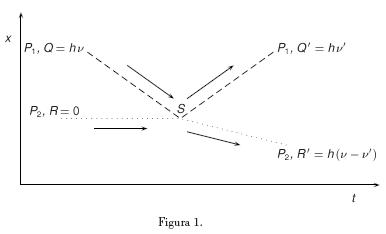
Formalmente, la noción de bifurcación interactiva se caracteriza por cuatro desigualdades. Primero, que el suceso o "causa común" C sea una causa positiva de dos sucesos, A y B; i.e., que la probabilidad de cada uno de ellos sea mayor en la presencia de C que en su ausencia:

Segundo, que los efectos A y B estén estadísticamente correlacionados:

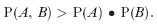
Tercero, que se dé una correlación estadística positiva entre A y B, dado C, i.e., que la probabilidad de que acontezcan conjuntamente A y B sea mayor al producto de las probabilidades de su ocurrencia separada, es decir:

que expresa la falta de independencia estadística de A y B, condicionada a que acontezca C.

La conexión de esta definición con las anteriores nociones de proceso causal e interacción causal puede explicitarse considerando que la causa común C representa la interacción causal en S de dos procesos causales P₁ y P₂, mientras que los sucesos A y B representan estados modificados, Q' y R' respectivamente, de esos dos procesos causales, producidos por la causa común C.³

En la teoría causal de Salmon, básicamente, esos dos tipos de mecanismos, procesos e interacciones causales, son los mecanismos causales del mundo físico que conforman la estructura causal de ese mundo; parafraseando a Salmon, por medio de los procesos causales se propagan o transmiten estructuras, mientras que las interacciones causales producen las modificaciones en estructura (cfr. 1981, p. 298).

Como anotamos, el mayor reto para esta teoría, en cuanto teoría de la explicación de sucesos azarosos, lo constituyen las correlaciones cuánticas que surgen en los experimentos tipo EPR, porque, según Salmon, la mecánica cuántica actualmente no ofrece una compresión del mecanismo físico que las genera (cfr. 1984, pp. 245—252).

 

3 . La adecuación de la teoría de Salmon al dominio cuántico

Como Salmon afirma, su teoría de la causalidad física es compatible con el indeterminismo cuántico. Sin embargo, es adecuada, como veremos, sólo para ciertos procesos atómicos, aquellos que involucran la transición del sistema físico de un estado actual a otro estado posterior producida por una interacción de sus elementos (como en el efecto de dispersión Compton), pero no lo es, en cambio, para otros procesos atómicos que entrañan una transformación del sistema físico mismo por la transmutación de sus elementos, sea ésta producida por una acción mutua entre ellos (como en los procesos de fusión y fisión nucleares) o de manera espontánea (como en el proceso de desintegración radiactiva).

Respecto a lo primero, podemos considerar cierto ajuste de la teoría de Salmon para hacer explícita su adecuación a procesos no deterministas, que sean irreductiblemente probabilistas. Tomemos su ejemplo favorito, la dispersión Compton.

En la teoría de la causalidad basada en procesos causales e interacciones causales, las relaciones causales no tienen que ser deterministas. Por ejemplo, cuando hay una interacción entre dos procesos causales, varios resultados diferentes pueden ser posibles, cada uno de ellos tiene su propia probabilidad. En una colisión entre un fotón energético y un electrón, como fue investigado por Arthur Compton, hay un rango de posibles ángulos para la trayectoria del electrón y un rango de posibles energías; no obstante, esto constituye una interacción causal. (Salmon 1998, p. 24)⁴

En cada interacción individual, el electrón y el fotón adoptan una energía especifica dentro de rangos respectivos de posibles energías. Esto puede representarse así. Sea {R'₁,. .., R'_n} el rango de los n posibles valores de energía con los que puede emerger el electrón, proceso causal P₂, después de haber impactado con el fotón. Entonces en cada interacción física individual, P₂ exhibe una característica R, que ha sido modificada por el impacto y que persiste por un intervalo posterior a ella, tal y como lo requiere la noción de interacción causal. Mutatis mutandis para los posibles m valores de energía, característica Q'_i, del fotón, proceso causal P₁, después de la colisión.

A grandes rasgos, el ajuste requerido, sugerido por el ejemplo anterior, consiste en asumir que a un mismo tipo de interacción causal C, de dos procesos P₁ y P₂, es probable que el proceso P₁ adopte una característica Q'_i (dentro de un número m de características, excluyentes y exhaustivas), mientras que el proceso P₂ adquiera una característica R'_j (dentro de un número n de características, excluyentes y exhaustivas).

Ahora bien, si C es la interacción entre los procesos P₁ y P₂, A_i representa que P₁ exhibe la característica Q'_i, B_j que P₂ exhibe la característica R'_j, entonces podemos formular, para toda A_i y toda B_j, las cuatro siguientes desigualdades:

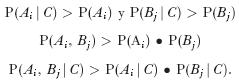
En el efecto de dispersión Compton, la terna A_i, B_j y C cumple esas cuatro condiciones, correspondientes al arreglo anterior de la noción de bifurcación interactiva, como una interacción causal no determinista.

Lo anterior muestra que la teoría de Salmon deja abierta la posibilidad de considerar como interacciones causales no sólo las interacciones físicas clásicas, deterministas, como la colisión de un par de bolas de billar, sino también ciertas interacciones físicas atómicas, indeterministas. Los tipos de procesos físicos, tanto clásicos como cuánticos, a los que parece aplicarse esa teoría, entrañan la idea de la modificación de algunas magnitudes producida por la interacción de partículas (clásicas o elementales), que conforman un sistema físico. Esto involucra solamente, para decirlo en otras palabras, la transición, sea determinista o aleatoria, del sistema físico en cuestión de un estado anterior a un estado posterior, producida por la interacción de sus elementos.

Sin embargo, de acuerdo con la mecánica cuántica, existen procesos naturales en los que ciertos sistemas físicos sufren una transformación que no puede capturarse en los anteriores términos, porque no se da una transición del sistema de un estado anterior a otro posterior —una modificación de algunas de las magnitudes que definen el estado del sistema—, sino una transmutación de los elementos que conforman el sistema. Casos típicos de estos procesos son la fusión y la fisión nucleares. Esos tipos de procesos cuánticos acotan el ámbito de aplicación de la teoría causal de Salmon, porque en esos procesos la "modificación" de los elementos del sistema ("procesos causales" en la terminología de Salmon) no consiste en un mero cambio en el valor de unas magnitudes que definen el estado del sistema, sino en una transmutación de los elementos mismos. Por ello falla la noción de interacción causal, ya que las modificaciones que sufren los "procesos causales" que se intersecan no consisten en cambios de alguna de sus características conservando sus "estructuras" sino, para decirlo en los términos de Salmon, en cambios de las estructuras mismas.

En los procesos de fisión puede verse lo anterior. Si se bombardea con un neutrón un átomo de uranio 235, típicamente se desdobla en un átomo de bario 142 y en uno de criptón 91 (expulsando a la vez tres neutrones), aunque es probable que se produzcan muchas combinaciones distintas de núcleos más pequeños. Esto se expresa en la siguiente fórmula que dice que es probable la transformación del sistema al lado izquierdo de la flecha en el sistema al lado derecho:

Como puede apreciarse claramente, la "estructura" de los procesos causales (neutrón y uranio) que se intersecan espacio–temporalmente no persiste después de la interacción, sino, más bien, ésta genera otros elementos o "procesos causales" (bario y criptón) distintos de los que inciden, los cuales se definen de manera diferente. En otras palabras, las modificaciones que sufren los elementos como producto de la interacción consisten en cambios de sus masas y números atómicos y esos cambios significan una transmutación de los elementos incidentes a otros elementos con masas y números atómicos diferentes, con distintas identidades. Como el número atómico define los elementos, no podemos decir, en este caso, que los "procesos causales" incidentes conservan sus "estructuras" después de la interacción física. De esta manera, pues, este tipo de procesos atómicos demarca el ámbito de aplicación de la teoría causal de Salmon.

En los tres casos de procesos físicos que hemos mencionado —la colisión de dos bolas de billar, el efecto Compton y la fisión nuclear—, se encuentra involucrada la idea de que acontece una interacción entre partículas, sean clásicas o elementales y, con ello, la idea de que los efectos (modificación de características o transmutación de partículas) o, en la terminología de Salmon, los "procesos causales" emergentes, son producidos por la interacción física. Al adoptar una noción de interacción causal, la teoría causal de Salmon cobra poder explicativo, porque permite atribuir a las interacciones físicas la producción de los efectos, sean determinados o aleatorios.

Sin embargo, de acuerdo con la teoría cuántica, existen ciertos procesos físicos de desintegración de elementos radiactivos, en los que no se da interacción alguna con otras partículas, a las que pudiéramos atribuir la producción del decaimiento. Un ejemplo típico de esto es la desintegración, sin intervención externa, de una partícula inestable de plomo 210, que puede adoptar dos rutas posibles: una desintegración alfa que conduce a una partícula de mercurio 206, o una desintegración beta que conduce a una partícula de bismuto 210.⁶

Claramente las nociones causales de la teoría de Salmon no son adecuadas a este tipo de proceso de desintegración. La condición CI, interacción causal, falla puesto que no acontece interacción alguna. La condición TM, transmisión de marca, no se cumple debido a que el sistema mismo transmuta a otro, sin que persista estructura alguna. Así, de nuevo, encontramos delimitada la aplicación de esa teoría al dominio cuántico.

Con todo, el anterior tipo de proceso atómico representa una dificultad mayor no sólo para la teoría de Salmon sino para cualquier teoría causal que pretenda atribuir a las condiciones causales la producción de los efectos, porque en ese tipo de procesos aquéllas tan sólo ocasionan que éstos tengan lugar. Se encuentra una tensión entre la idea de producción involucrada en la noción de causa, por un lado, y la espontaneidad con la que acontecen de manera natural los procesos de desintegración, por el otro, de tal suerte que si asociamos indisolublemente la producción de los efectos por parte de las causas, obtenemos que los elementos resultantes de los procesos de desintegración espontánea son acausados.

 

4. Esbozo de una noción de causalidad indeterminista

Los procesos naturales de transmutación de elementos, sea por acción mutua entre partículas (fusión y fisión) o de manera espontánea (desintegración), motivan a adoptar una ontología de sistemas físicos, en lugar de una ontología de procesos, porque es preciso tener en cuenta que lo que acontece en esos tipos de procesos es una conversión del sistema mismo y no meramente una modificación de algunas de las características de sus elementos. A la vez sugieren elaborar una noción general de transformación de un sistema físico que comprenda tanto procesos de transición como de transmutación.

Debemos distinguir dos tipos de transformaciones de sistemas cuánticos. Primero, una transformación de transición que consiste en la modificación del estado del sistema o, en la manera formal de hablar, en un cambio en la descripción de estado, en los valores que se asignan probabilistamente a las magnitudes pertinentes, prescrito por una ecuación o ley específica de evolución del sistema. Segundo, una transformación de transmutación consistente en una conversión del sistema mismo o, en la manera formal de decirlo, en un cambio en la especificación de las partículas P que conforman el sistema, prescrito por una ecuación o ley específica de transmutación. En toda transformación de un sistema cuántico, como han señalado varios autores,⁷ se cumplen las leyes de conservación de energía, momentum y carga.

Mas la satisfacción de esas leyes universales de conservación no es lo que caracteriza el peculiar comportamiento aleatorio de algunos sistemas cuánticos. La cuestión en discusión es si podemos analizar o modelar a los procesos cuánticos con unas nociones causales que capturen adecuadamente su carácter estocástico.⁸ El rasgo peculiar de ciertos sistemas cuánticos reside en que las transformaciones, los procesos físicos, que sufren no están causalmente determinadas; más bien acontece que, en ciertas condiciones causales específicas (p. ej., una interacción física), pueden transitar aleatoriamente a diferentes estados posibles alternativos y excluyentes o pueden transmutar, de manera aleatoria, a distintos sistemas posibles alternativos y excluyentes; precisamente en eso radica su carácter estocástico. Los tipos de procesos físicos que hemos mencionado anteriormente de dispersión Compton, físión nuclear y desintegración radiactiva despliegan un comportamiento aleatorio, manifestando su carácter estocástico, no determinista.

El carácter estocástico de esos procesos cuánticos nos conduce, pues, a intentar esbozar una noción no clásica de causalidad que sea apropiada para modelarlos como tales, como procesos estocásticos, en términos probabilistas, conforme a la estructura probabilista de la mecánica cuántica.

Ahora expondré unas cuantas nociones básicas, asumiendo una ontología de sistemas, i.e., una ontología de conjuntos de partículas elementales. Primero se precisa introducir el concepto de descripción de un sistema físico:

Sea S un sistema físico —una configuración de partículas físicamente no separables—. Entonces una descripción de S consiste en las reglas que asignan objetos matemáticos adecuados a los estados y a las magnitudes de S, junto con las prescripciones que permiten calcular la distribución de probabilidad de los valores posibles de las magnitudes físicas pertinentes una vez que el estado de S está especificado. (Beltrametti y Cassinelli 1981, p. 3)

En mecánica cuántica, las descripciones de los estados de los sistemas cuánticos se obtienen representándolos en espacios de Hilbert, mientras que las ecuaciones cuánticas son los medios para calcular las distribuciones de probabilidad de las magnitudes físicas involucradas.

A las descripciones de un sistema cuántico S, para un momento t, corresponden sucesos físicamente posibles en S, que denotaré por d(S)_t . Un proceso físico en un sistema S, durante un intervalo de t a t', consiste en una transformación del sistema de tal manera que la descripción de S en t es distinta a la descripción de S en t', i.e., d(S)_t ≠ d(S)_t' .

Un proceso estocástico en un sistema S es un conjunto < d₀(S)_t , {d₁(S)_t' ,...,d_n(S)_t'} tal que⁹

(1)  d₀(S)_t es la descripción inicial del sistema S, en el momento t, que corresponde al suceso que origina el proceso y{d₁(S)_t' ,...,d_n(S)_t'}es el rango de las posibles descripciones de S, en un momento posterior t, que corresponden a los posibles sucesos futuros, alternativos y mutuamente excluyentes, en S;

(2)  Para cada d_i(S)_t' en {d₁(S)_t' ,...,d_n(S)_t'}, P(d_i(S)_t' | d₀(S)_t es un número real positivo menor que 1 y, en el caso específico de que este conjunto sea exhaustivo: ∑ P(d_i(S)_t' ) = 1, con i = 1, 2,. . . , n;

(3)  Para cualquier suceso d(S)_t'' temporalmente anterior a d₀(S)_t , se cumple la siguiente igualdad:

Esta noción de proceso estocástico involucra que es probable que se dé, en cada caso individual, una transformación aleatoria del sistema S del suceso origen d₀(S)_t a uno, y sólo uno, de los posibles sucesos posteriores d_i(S)_t' . Los casos más simples, pero significativos, consisten en bifurcaciones aleatorias, cuando el rango de posibles resultados o estados finales de un proceso físico son dos sucesos, mutuamente excluyentes y conjuntamente exhaustivos; destacadamente esto es así en los procesos de medición de cantidades discretas con dos valores propios, como el espín o la polarización.

La primera cláusula especifica que la correspondencia entre la descripción inicial y los sucesos en la clase de estados finales posibles asociada es uno a muchos, mientras que la segunda significa que no es suficiente que el suceso origen acontezca para que el sistema físico se transforme a un estado posterior específico de manera unívoca, puesto que a ningún estado posterior se le asigna una probabilidad igual a la unidad, y expresa, en términos cuantitativos, el grado de posibilidad física de los sucesos d_i(S)_t' , dado d₀(S)_t , de acuerdo con una teoría de la física con estructura probabilista.¹⁰ Por último, la tercera cláusula estipula la propiedad markoviana para los procesos estocásticos, es decir, que si d₀(S)_t es el estado actual de un sistema S, entonces la transformación futura de S está definida sólo por d₀(S)_t , de tal suerte que es independiente de los estados anteriores a d₀(S)_t o, mejor, si la descripción del estado actual d₀(S)_t de S es completa, entonces la evolución de S o su conversión a otro tipo de sistema, es independiente de cómo S haya asumido el estado d₀(S)_t , lo que significa, pues, que las probabilidades que una teoría le asigne a d₀(S)_t y a cada d_i(S)_t' no depende de algún suceso d(S)_t'' anterior a d₀(S)_t , del cual el sistema S ha evolucionado o transmutado al estado actual d₀(S)_t .

La forma en que ciertos procesos cuánticos encajan con la noción anterior de proceso estocástico puede verse advirtiendo que cumplen con las tres cláusulas. Por ejemplo, en el proceso de medición del espín de electrones tenemos que a unas condiciones iniciales fijas, o preparación, dos resultados son físicamente posibles, a saber, +1/2 y –1/2, con probabilidades respectivas, digamos, 0.85 y 0.15. La primera cláusula se cumple puesto que ambos resultados son posteriores, en cada ensayo, al suceso de la emisión de electrones. El valor de probabilidad de cada uno de esos resultados es positivo, y su adición igual a la unidad, con lo que se satisface la segunda cláusula. Para ver que la tercera cláusula también se cumple debemos tener en cuenta que lo único que define las probabilidades de los dos resultados aleatorios es la descripción inicial d₀(S)_t del sistema en el momento de la emisión de los electrones hacia el aparato de medición del espín, y que esas probabilidades son independientes de cualquier suceso anterior a éste.

Como segundo ejemplo considérense los procesos de desintegración radiactiva, donde tenemos dos alternativas excluyentes y aleatorias: el decaimiento de una partícula de plomo, con un desdoble en una partícula de mercurio y una de bismuto o que no se dé decaimiento alguno. Esos dos resultados posibles, desdoble de la partícula inestable de plomo y no decaimiento, tienen probabilidades positivas y son posteriores a una descripción inicial d₀(S)_t en un momento determinado, con lo que se satisfacen las cláusulas (2) y (1). La satisfacción de la tercera cláusula puede verse considerando que lo único que es relevante para que estén definidas las probabilidades de esos dos estados posteriores al estado inestable de la partícula de plomo es que esté efectivamente en ese estado inicial d₀(S)_t y no cómo llegó a adoptar ese estado.

Por último, tomemos los procesos de fisión nuclear, los cuales son semejantes a los anteriores, salvo en que en éstos los estados aleatorios futuros, dado el bombardeo, son mayores en número; esta diferencia no afecta el cumplimiento de las cláusulas de la noción en cuestión.

Así, pues, las transformaciones de los sistemas cuánticos que satisfacen la noción anterior no corresponden a procesos deterministas sino estocásticos, que están prescritos por la mecánica cuántica como probables.

En las transformaciones de transición, donde el sistema evoluciona de un estado actual a un estado posterior distinto, las partículas del sistema no se modifican mientras que algunas de las magnitudes de ellas cambian, variando sus valores. El efecto Compton ejemplifica esto: el fotón y el electrón que sufren una colisión permanecen como tales después de ésta, a la vez que las magnitudes energía y momentum de ambos cambian variando sus respectivos valores, dentro de un rango de posibles valores. Si representamos un sistema por el conjunto de partículas P no separables que lo conforman y por las magnitudes mi que lo definen, y cuyos valores determinan sus estados, las transiciones adoptan la siguiente forma general:

donde las magnitudes m'_j y m'_k (digamos, energía y momemtum) han sufrido una modificación producida por cierta condición causal (una interacción física) de los elementos de P (fotón y electrón).

Las transformaciones de transmutación, en cambio, difieren debido a que en ellas, además del cambio de los valores de algunas de las magnitudes o variables de estado, son los elementos mismos del sistema los que se modifican, convirtiéndose en otros elementos. Los procesos de fisión ejemplifican esto: en el caso del bombardeo de una partícula de uranio 235 por un neutrón, es probable que el uranio se despliegue en una partícula de bario 142 y una de criptón 91 (emitiendo además tres neutrones); aquí el conjunto de partículas P (uranio más neutrón) se convierte en otro conjunto de partículas P' (bario y criptón más neutrones) como resultado del rompimiento del núcleo atómico producido por el impacto, transformándose el sistema original en otro tipo de sistema.

En ciertos tipos de transformaciones se pueden reconocer ciertos sucesos, interacciones físicas, que acontecen en los sistemas en cuestión y que podemos considerar las causas que producen la modificación del sistema. Una noción de interacción causal similar a la de Salmon, que no implique persistencia de estructura sino sólo continuidad espacio–temporal, podría ser adecuada para caracterizar, en términos causales, la relación entre el sistema original y el sistema modificado, sea que se trate de una transformación de transición o una de transmutación. Un par de condiciones necesarias podrían consistir en que, primero, se dé una intersección espacio–temporal de las partículas que conforman el sistema original y, segundo, que la descripción del sistema original sea distinta de la descripción del sistema resultante de la transformación.

Podemos considerar que tales procesos estocásticos, sean de transición o de transmutación, son procesos causales indeterministas en tanto que exista un suceso que origine el proceso en el sistema y éste se transforme de manera aleatoria, adoptando uno de los posibles resultados finales alternativos. El carácter indeterminista de los procesos cuánticos reside en que el suceso que origina el proceso no determina la transformación del sistema a un único resultado final físicamente necesario. Podríamos atribuir una naturaleza causal a tales procesos si reconocemos que el suceso origen produce la transformación del sistema. Esto no parece una cuestión problemática en los dos tipos de procesos que hemos mencionado (dispersión Compton y fisión), ya que podemos pensar que las interacciones físicas que se dan entre las partículas que conforman los respectivos sistemas, los sucesos que originan los procesos, producen el estado que el sistema posteriormente adopte o la conversión del sistema que acontezca. La naturaleza causal de los procesos de desintegración espontánea sí es, en cambio, problemática, debido a la ausencia de cualquier acción externa a la partícula que decae a la que pudiéramos atribuir la producción del proceso. Este tipo de procesos atómicos, creo, nos impide imponer una noción general de interacción causal como la de Salmon en el dominio cuántico. La dificultad es doble. Por un lado, no reconocemos el suceso origen, el suceso en que se origina la desintegración, como responsable de la producción de la misma y, por otro lado, el sistema no persiste sino que transmuta a otro tipo de sistema, dándose sólo una continuidad espacio–temporal.

Para que podamos concebir una noción de causa indeterminista, una noción de causa que sea apropiada a procesos estocásticos como los cuánticos, es necesario renunciar no sólo a la idea de que las condiciones causales provocan de manera suficiente sus efectos, sino incluso a la idea de que las condiciones causales producen, en todos los casos, dichos efectos. Los casos de desintegración nos exigen, creo, debilitar la idea de condiciones causales de tal suerte que sólo involucre que en determinadas condiciones físicas de ciertos sistemas cuánticos sea probable que se desencadene el proceso, sin que exista una acción externa que lo produzca. La condición inestable intrínseca de los elementos radiactivos, debida a su constitución atómica, ocasiona, mas no produce, que en un momento dado se desintegren, se inicie un proceso estocástico de desintegración; podríamos reconocer el suceso origen en este tipo de procesos como la condición causal de la conversión del sistema, si asentimos en una noción general de condición causal que no sea restrictiva a las interacciones causales.

Resumiendo, hemos encontrado tres tipos de procesos en sistemas cuánticos: en primer lugar, procesos que consisten en una transición de estado del sistema producida por una interacción de sus componentes; en segundo, procesos en que se da una transmutación del sistema mismo causada por una interacción de sus elementos; por último, procesos de transmutación del sistema a otro tipo de sistema de manera espontánea, sin que intervenga acción externa alguna. La noción de interacción causal de Salmon sólo es aplicable al primer tipo de esos procesos. Ni siquiera el tercer tipo contaría como proceso causal en el sentido de Salmon ya que, aunque se da continuidad espacio–temporal, no hay persistencia de la estructura del sistema. ¿Podemos concebir a esos tres tipos de procesos estocásticos como procesos causales indeterministas? La respuesta sería afirmativa si incorporamos una noción de condiciones causales que incluya tanto sucesos de interacción física que producen los alternativos efectos aleatorios como sucesos en que se originan los procesos de manera espontánea y que conducen de manera aleatoria a uno de los efectos alternativos físicamente posibles.

Tal vez una noción de condición causal adecuada, que abarque el espectro de procesos cuánticos que hemos estado considerando, pueda obtenerse diferenciando, en la noción de proceso estocástico que hemos propuesto, tres formas que pueden tomar tanto el suceso origen d₀(S)_t , como los posibles resultados posteriores asociados d_i(S)_t' . En el primer tipo de transformación, la transición de un mismo sistema de un estado origen a uno de los posibles estados alternativos posteriores (efecto Compton), d₀(S)_t consiste en una interacción que modifica el estado del sistema. En el segundo tipo de transformación, la transmutación de un sistema por acción externa (fisión y fusión), d₀(S)_t consiste también en una interacción que produce la conversión de los elementos del sistema original. Por último, en el tercer tipo de transformación, la transmutación de un sistema de manera espontánea (desintegración), d₀(S)_t es el suceso que ocasiona el inicio del proceso de conversión del elemento que integra el sistema. En estos tres tipos de transformación podríamos concebir al suceso origen d₀(S)_t representando las condiciones causales en las que se desenvuelven los procesos correspondientes. Tomando en cuenta el carácter estocástico de dichos procesos, podemos decir que esas condiciones causales son indeterministas y que los posibles sucesos posteriores d_i(S)_t' representan los efectos aleatorios alternativos.

Asumiendo el indeterminismo cuántico y la irreductibilidad de las probabilidades cuánticas, hemos concebido y elaborado la presente propuesta con el propósito de modelar, en términos causales, ciertos procesos cuánticos en tanto procesos estocásticos. Así, el desideratum central de nuestro análisis causal es que sea adecuado al dominio cuántico y sólo a ese dominio. El rasgo peculiar de nuestra noción de proceso causal reside, precisamente, en su carácter indeterminista, que intenta capturar conceptualmente la aleatoriedad de los sucesos cuánticos considerados como efectos alternativos provocados por condiciones causales insuficientes, u ocasionados en ellas.

Algunos filósofos que han desarrollado teorías causales no han hecho suyo ese propósito como uno de sus objetivos principales ni han explicitado el carácter estocástico de procesos físicos como los cuánticos. Hemos visto, respecto a la teoría de Salmon, que, por un lado, es preciso hacer una modificación a la formulación de la noción de bifurcación interactiva para que puedan encajar en esa teoría interacciones causales como el efecto de dispersión Compton y que, por otro lado, esa teoría encuentra contraejemplos en el ámbito cuántico con procesos como el de fisión nuclear. Aunque Salmon asume el indeterminismo cuántico y que la causalidad es un rasgo contingente del mundo físico, no explora las consecuencias de estas tesis.

Igualmente, otras destacadas teorías causales no son adecuadas porque encuentran contraejemplos en el ámbito cuántico. Con el fin de contrastarlas con nuestra noción de proceso estocástico, y así resaltar las diferencias, revisaremos, muy brevemente, las nociones básicas de un par de esas teorías: la teoría probabilista de la causalidad de Patrick Suppes (1970) y la teoría de las cantidades conservativas de Phil Dowe (2000). Al igual que Salmon, estos dos autores asumen el indeterminismo cuántico y reconocen la irreductibilidad de los enunciados probabilistas cuánticos, por ello resulta pertinente considerar sus teorías aquí.

Suppes parte de la idea básica de que la causa aumenta la probabilidad de los efectos y la formula con la estipulación de que la probabilidad condicional del efecto E_t dada la causa C_t es mayor que la probabilidad absoluta de E_t (donde los subescritos t y t refieren a instantes temporales, tal que t es anterior a t. Para asegurar que C_t sea una causa genuina, a diferencia de espuria, de E_t , Suppes agrega la condición de que no exista un suceso F_t'' temporalmente anterior al suceso C_t que anule éste como causa de E_t, debido a que la probabilidad condicional de E_t, dados conjuntamente C_t y F_t'' , sea igual a la probabilidad condicional de E_t dado sólo F_t. Una formulación sucinta de esa noción de causa genuina es la siguiente:

Sea que E_t, y C_t' son sucesos, con t' < t, y que P(C_t' y P(C_t' , F_t'' son positivas. Entonces C_t' es una causa genuina de E_t si y sólo si

(1)  P(E_t | C_t' ) > P(E_t);

(2)   No existe un suceso F_t'' , con t'' < t' , tal que P(E_t | C_t' , F_t'' = P (E_t | F_t'' )¹¹

El ejemplo cuántico contrario a la teoría de Suppes más claro se debe a Salmon:

Supongamos que tenemos un átomo en un estado excitado al cual me referiré como el cuarto nivel energético. [. .. ] Sea que P(m n) refiere a la probabilidad de que un átomo en el nivel m haga una transición directa al nivel n. Asumamos que las probabilidades tienen los siguientes valores:

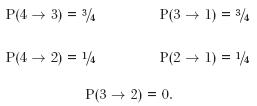
Se sigue que la probabilidad de que el átomo ocupe el primer nivel energético en el proceso de decaimiento hacia el estado base es 10/16; si, sin embargo, ocupa el segundo nivel en su camino abajo, entonces la probabilidad de que ocupe el primer nivel es ¼. Por lo tanto, ocupar el segundo nivel es negativamente relevante a ocupar el primer nivel. No obstante, si el átomo va del cuarto nivel al segundo y al primero, la secuencia constituye una cadena causal, a pesar de la relevancia estadística negativa de la etapa intermedia (1980, pp. 200–201).¹²

Esto es, si tomamos el suceso de ocupar el primer nivel como el efecto E y ocupar el segundo nivel como la causa C, entonces la probabilidad condicional de E dado C, P(E | C = ¼, no es mayor que la probabilidad absoluta de E, P(E = 10/16, sino menor, con lo que no se cumple la condición anterior (1).

De esta manera, la exigencia de que la causa aumente la probabilidad del efecto resulta fuerte en el dominio cuántico ya que excluye procesos cuánticos como el anterior de la clase de los procesos causales. Nuestra noción sólo requiere que la probabilidad del efecto, dada la causa, sea positiva (menor que la unidad), por lo que resulta débil con respecto a la noción de Suppes y a salvo del ejemplo anterior. Para apreciar esto último, considérese lo siguiente. En la situación física que supone Salmon tenemos que, de acuerdo con nuestra noción de proceso estocástico, no se sigue el par < 4, 1> de los pares < 4, 2 > y < 2, 1 > porque la condición markoviana implica la no transitividad entre procesos causales indeterministas; por ello, no se da ninguna cadena causal en esa secuencia.

Dowe no formula una relación probabilista entre causa y efecto, sino, más bien, parte de la idea general de que lo que hace causal una interacción física es que se dé un (inter)cambio de una cantidad conservativa entre los procesos u objetos involucrados. Una cantidad conservativa, nos dice Dowe, es cualquier cantidad gobernada por una ley conservativa de acuerdo con las teorías físicas disponibles (cfr. 2000, p. 91). Así, las cantidades físicas masa/energía, momentum y carga son conservativas.

El núcleo de la teoría de Dowe se expresa por estas dos condiciones:

CC1. Un proceso causal es una línea de mundo de un objeto que posee una cantidad conservativa.

CC2. Una interacción causal es una intersección de líneas de mundo que involucra un intercambio de una cantidad conservativa (2000, p. 90).

Las nociones primitivas de la condición definitoria CC2 son las de línea de mundo, intersección e intercambio de una cantidad conservativa. Dowe las explica en estos términos: "Una línea de mundo es la colección de puntos en un diagrama espacio–tiempo (Minkows–ki) que representa la historia de un objeto"; "una intersección es simplemente la superposición (overlapping) en el espacio–tiempo de dos o más procesos" mientras que "un intercambio ocurre cuando al menos un proceso incidente y un proceso resultante sufren un cambio en el valor de una cantidad conservativa" (2000, pp. 90, 91 y 92, respectivamente).

La noción de interacción causal antes presentada no está exenta de contraejemplos cuánticos. Para poder exponer uno, es preciso primero plantear un ejemplo contrario a la teoría de Salmon debido al propio Dowe.

[Q]uisiéramos ser capaces de incluir en cualquier definición de interacción causal tipos de interacciones distintas de aquellas que producen modificaciones en dos procesos. [. . . ] Un ejemplo genuino de una interacción tipo–Y es la desintegración de radio 226 a radón:

Salmon mismo expresa un deseo de incorporar interacciones tipo–λ y tipo–Y (1984, p. 182). Desafortunadamente, las interacciones causales de Salmon son definidas en términos de dos y sólo dos procesos. (2000, p. 83)¹³

De esta manera, arguye Dowe, la razón por la que ese proceso de desintegración no contaría como una interacción causal en el sentido de Salmon consiste en la restricción impuesta en la formulación de esa noción a dos y sólo dos procesos tanto incidentes como resultantes. Esto es correcto, pero lo que resulta sorprendente es que precisamente este ejemplo de proceso de desintegración tampoco cumple con la condición CC2 de Dowe y justamente por la misma razón, es decir, porque es necesario para que se dé una interacción causal que dos o más procesos se intersequen, i.e., se traslapen en una región constituida por todos los puntos que son comunes a ambos (o todos los) procesos (cfr. 2000, p. 92). Resulta desconcertante que Dowe use ese mismo tipo de proceso de desintegración para ejemplificar sus nociones causales. Más adelante, después de reproducir el ejemplo, arguye: "Esto califica como una interacción causal por CC2, porque hay un intercambio de energía, donde la carga del proceso incidente es dividida entre los dos procesos resultantes" (2000, p. 93). Si bien Dowe limita su noción de interacción causal a que al menos uno de los procesos incidentes y al menos uno de los procesos resultantes sufran una modificación en una cantidad conservativa, lo cual sí se cumple en el ejemplo anterior, él exige, para que se dé una interacción, al menos dos procesos incidentes.

Como hemos visto, los procesos de desintegración espontánea, en los que no se da interacción alguna, representan un reto a las teorías de la causalidad en el ámbito cuántico y la de Dowe no es una excepción. Mas no creo que la objeción anterior sea definitiva porque no dudo que las ideas básicas de Dowe puedan re–formularse de tal suerte que se evite este tipo de contraejemplos; en todo caso, la cuestión es que, por su generalidad, las nociones causales de Dowe no capturan la peculiaridad de los procesos e interacciones cuánticos de exhibir un comportamiento aleatorio, por el siguiente par de razones. Primero, esa teoría no distingue entre una interacción clásica, determinista, tipo–X, como la colisión de dos bolas de billar, y una interacción cuántica, indeterminista, del mismo tipo, como el efecto de dispersión Compton. Segundo, no modela que en las mismas condiciones causales, en diferentes ensayos individuales, sistemas cuánticos del mismo tipo se transformen de maneras distintas, alternativas y excluyentes; no modela que, por ejemplo, cuando dos deuterones se fusionan 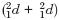, es físicamente posible que se transformen en dos rutas: o bien producen un núcleo de helio–3 más un neutrón o bien uno de tritio–3 más un protón; ambas rutas son igualmente probables con resultados alternativos y excluyentes. Ninguno de los tres tipos X, Y y λ con los que Salmon y Dowe pretenden modelar las interacciones causales corresponde a la forma de ese tipo de proceso de fusión, porque no se trata de una interacción conjuntiva sino más bien de una interacción disyuntiva, con efectos mutuamente excluyentes.

De nuevo, el rasgo peculiar de nuestra propuesta reside en modelar, básicamente con la noción de proceso estocástico o causal indeterminista, el comportamiento aleatorio de ciertos sistemas cuánticos, como los considerados aquí.

 

5 . Las correlaciones cuánticas

A primera vista, cada uno de los ensayos en una serie de un experimento tipo EPR, como procesos individuales, constituye una bifurcación aleatoria. Referidos a propiedades físicas con valores propios, como la polarización de fotones o el espín de electrones, para partículas individuales que previamente han interactuado, los posibles valores propios que se miden del par de partículas involucradas son efectos aleatorios excluyentes. Si el par de partículas, en cada ensayo, constituye un solo sistema físico no separable, entonces el estado inicial del sistema, en el momento de la interacción, es la causa indeterminista del efecto aleatorio que se observa. En estos casos, el carácter aleatorio del proceso físico involucrado reside en que las partículas adoptan azarosamente uno de los dos valores propios. Si de la teoría cuántica se deriva la ecuación nómica aplicable a los procesos físicos de la polarización de fotones o del espín de electrones y se especifican como casos particulares cada uno de esos ensayos individuales, se puede establecer el valor de probabilidad de cada uno de los resultados aleatorios observados, en los procesos de medición, de manera análoga a los procesos de fusión y fisión. El problema surge del hecho de que las secuencias aleatorias de los resultados de las mediciones en ese tipo de experimentos generan correlaciones de las que se pide también una explicación.

Antes de intentar ver dónde radica el problema, distingamos someramente tres niveles de situaciones físicas relacionados: el nivel de los ensayos individuales, el de una secuencia de esos ensayos y el de la relación entre dos, o más, secuencias de ensayos. Para el primero, pensemos en un experimento en el que se mide la polarización de fotones que son emitidos individualmente, uno por uno, a 45° sobre un polarizador HV (horizontal/vertical). El resultado de cada uno de los ensayos es aleatorio, pues cada fotón, que logra traspasar el polarizador, puede emerger bien con una dirección horizontal o bien con una vertical. Éste es el nivel básico de análisis, donde encontramos el carácter estocástico del proceso de medición de la polarización de fotones individuales. Si reconocemos el indeterminismo en esos procesos físicos, no hay problema en que los resultados observados sean aleatorios. Para el segundo nivel, consideremos las secuencias de resultados que se forman con la repetición de ensayos individuales; tenemos que aproximadamente la mitad de los fotones emergen horizontalmente polarizados y la otra mitad verticalmente polarizados. De ello obtenemos una probabilidad de 0.5 para cada uno de los dos resultados alternativos. Esto tampoco representa problema alguno, puesto que la probabilidad de los resultados alternativos no es, en algún sentido, sino un desenlace de la acumulación de los resultados individuales. Si comparamos dos secuencias, o más, de la misma extensión, de resultados del experimento anterior, en el tercer nivel, tampoco se presenta ningún problema, porque observaríamos que la proporción de los resultados de fotones horizontal y verticalmente polarizados se mantiene estable y regular; la diferencia sólo se encontraría en la posición que ocupan en las secuencias los resultados particulares H o V, como un producto del carácter aleatorio de los ensayos individuales.

Los experimentos tipo EPR son un tanto distintos del anterior. Una descripción sucinta de un experimento tal iría como sigue. Tenemos un dispositivo formado por dos alas en posiciones opuestas y a la misma distancia respecto de una fuente emisora de fotones (átomos de calcio excitados por rayos láser en los experimentos efectivos llevados a cabo por Aspect y colaboradores). En cada ala, izquierda y derecha, están, de manera idéntica, un conmutador ultrasónico, dos polarizadores orientados y dos detectores de polarización; además, las dos alas están conectadas a un monitor electrónico que registra los resultados de las detecciones. En la ala izquierda se mide la polarización de fotones individuales en un detector en los estados horizontal o vertical y en el otro en los ángulos ± θ (45° en los experimentos efectivos), mientras que en el ala de la derecha se mide la dirección de la polarización en los ángulos en un detector y en los ángulos ± φ en el otro (67.5° y 22.5°, respectivamente, en los experimentos de Aspect y colegas).

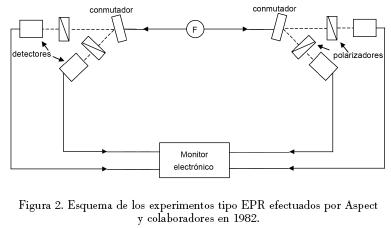
En cada ensayo individual, la fuente emite dos fotones, que previamente han interactuado, cada uno dirigido a una de las alas izquierda o derecha. A mitad del camino hacia los polarizadores respecto de la fuente, cada conmutador dirige a cada fotón hacia uno de los dos polarizadores ubicados en cada ala, de manera azarosa e independiente, después se mide la polarización de cada fotón individual por los detectores y se registran los resultados en el monitor. Esto constituye un ensayo individual en el experimento. Una vez decidido un polarizador en cada una de las alas (p. ej., ala izquierda: θ ala derecha: φ, los resultados que se obtienen son aleatorios y con una probabilidad, igual para cada estado de polarización, de aproximadamente 0.5, i.e., en el ala izquierda tenemos P(+ θ) = P(– θ) = 0.5, mientras que en la derecha P(+ φ) = P(–φ) = 0.5. Éste es el nivel básico, donde se encuentra, como en el ejemplo anterior, el carácter estocástico del proceso de medición de la polarización de fotones individuales. También tenemos que, como en el caso anterior, las secuencias de ensayos repetidos en la medición de la polarización de fotones individuales en cada uno de los cuatro polarizadores, tomadas separadamente, son estables y regulares.

Cada serie de repeticiones de ensayos específicos constituye una secuencia aleatoria con cuatro posibles resultados alternativos. Por ejemplo, cuando se deciden por los conmutadores los anteriores estados ± θ y ± φ, se obtiene un grupo de cuatro posibles resultados excluyentes, a saber: {< + θ , + φ> , <+ θ , – φ> , – θ, + φ>, < – θ , – φ>}. Como las secuencias de ensayos repetidos en la medición de la polarización de fotones individuales en cualquiera de las alas, tomadas separadamente, son estables y regulares, con un valor de probabilidad de 0.5 para cada valor propio, cabría esperar que la probabilidad de cada uno de esos cuatro pares de resultados conjuntos sea igual a 0.25, simplemente el producto de sus probabilidades separadas. Esto es, si suponemos que los resultados individuales son independientes, se obtendría que P(+ θ, + φ) = P(+ θ) • P(+ φ) = 0.5 • 0.5 = 0.25, y lo mismo para las otras tres combinaciones, lo que sumaría la unidad.

Pero de esta última estimación probabilista es de donde surge el problema de las correlaciones, porque los datos que arroja el monitor electrónico que registra los resultados medidos en las dos alas son: 40 % para cada coincidencia en estados positivos y negativos —primer y cuarto pares— y 10 % para cada divergencia de estados positivos y negativos —los pares segundo y tercero—, en lugar de 25 % para cada una de las cuatro combinaciones. En cierto sentido, lo anterior no debería representar ningún problema, porque precisamente esos coeficientes de correlación que se obtienen experimentalmente son los que prescribe la física cuántica para ese tipo de experimentos.

Lo que resulta sorprendente y un tanto desconcertante es ese patrón probabilista que emerge de correlacionar las secuencias aleatorias de ensayos individuales de los experimentos tipo EPR. En estas correlaciones encontramos que tomando dos secuencias de longitud n de tales resultados individuales, por ejemplo,

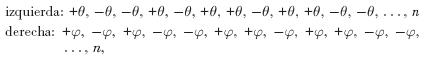
se obtendría, en cada hilera, aproximadamente el mismo porcentaje de estados positivos y negativos; sin embargo, el patrón probabilista correspondiente a la correlación de ambas hileras, en las columnas, es de 0.4 para coincidencia de dos estados positivos, 0.4 para coincidencia de dos estados negativos y 0.1 para cada una de las divergencias de un estado positivo y un estado negativo.

Las nociones causales de bifurcación conjuntiva e interactiva no logran modelar esos procesos estocásticos cuánticos. Por un lado, no se cumple la condición definitoria de las bifurcaciones conjuntivas, a saber: P(A, B | C) = P(A | C) • P(B | C), porque claramente en los cuatro grupos de combinaciones anteriores, los valores de P(± θ , ± φ | C) y de P(± θ | C) • P(± φ | C) son desiguales. Por otro lado, la noción de bifurcación interactiva no encaja con ese tipo de procesos cuánticos, porque si bien la condición de definición de esa noción P(A, B | C) > P(A | C) • P(B | C) se cumple para los casos de coincidencia de estados positivos y estados negativos, falla en los dos casos de divergencia de estados ya que, como hemos visto, P(+ θ, – φ) = 0.1 mientras que P(+ θ) • P(– φ) = 0.25; igualmente para el par < – θ, + φ>.

Ahora bien, ¿qué es lo que se tendría que explicar respecto de las correlaciones cuánticas? No es claro, porque como arguye Fine:

Si tratamos a los sucesos individuales como indeterminados y retiramos la carga de explicar por qué surge un patrón para cada una de las dos secuencias, ¿por qué no adoptar la misma actitud hacia los patrones que emergen entre pares de resultados, el patrón que constituye la correlación? ¿Por qué, desde una perspectiva indeterminista, el hecho de que hay un patrón entre secuencias aleatorias debe requerir una mayor explicación que el hecho de que hay un patrón interno a las secuencias mismas? (1989, pp. 191 y 192)¹⁴

Sin pretender sugerir que las correlaciones cuánticas no representan un serio problema, quiero aquí sólo reseñar algunas hipótesis que se han elaborado para dar cuenta de ellas. Se han propuesto un par de hipótesis de vena determinista para explicar las correlaciones cuánticas con base en factores causales que darían cuenta de las proporciones de coincidencia entre las polarizaciones en estados positivos y negativos y la proporción de divergencia en estados positivo y negativo.

Una consiste en sostener que, de alguna manera, las mediciones entre las dos alas del dispositivo experimental se influyen entre sí de tal suerte que determinan tanto los resultados coincidentes como los divergentes de acuerdo con alguna ley aún no descubierta. Esas influencias causales explicarían las correlaciones observadas en la medida en que mostraran que el patrón probabilista correspondiente obedece a un orden determinista subyacente. Esta hipótesis equivale a postular acciones causales a distancia, superluminales, porque, dado el diseño del dispositivo experimental, está bloqueada la posibilidad de señales entre las dos alas que se propaguen con una velocidad, a lo sumo, igual a la velocidad de la luz. La distancia entre las alas (cerca de nueve metros en los experimentos efectivos de 1982) y el hecho de que los sucesos de detección de la polarización de los fotones son simultáneos aseguran esto; simplemente no hay tiempo suficiente para señales entre las dos alas. Esta hipótesis explicativa que postula acciones a distancia va en contra del principio señal de la teoría de la relatividad que sustenta la localidad de las influencias causales acotándolas a influencias que viajen a una velocidad a lo sumo igual a la de la luz; por ello es, como afirma Fine, enteramente ad hoc y a priori (cfr. 1989, p. 183).

Otra hipótesis explicativa de las correlaciones cuánticas consiste en postular la intervención de ciertas variables ocultas no locales. La acción de tales variables se ubicaría en el estado común en el que los pares de fotones se producen. Esta hipótesis sería explicativa en tanto que la intervención de las variables ocultas daría cuenta del patrón probabilista extraído de esas correlaciones con base en mostrar que las condiciones iniciales de ese estado común no son iguales en todos los ensayos del experimento; a diferentes estados iniciales del sistema corresponderían diversos efectos, es decir, distintas proporciones en los posibles estados finales. La intervención de factores causales presentes en el estado común de la producción de cada par de fotones, debida a magnitudes hasta ahora desconocidas, que determinaran sus estados de polarización está obstruida en el diseño del dispositivo experimental por los conmutadores ultrasónicos que deciden azarosamente, a la mitad del viaje de los fotones, a cuáles polarizadores son dirigidos. Esto significa que, si por los factores ocultos en el estado común que produce los pares de fotones, las polarizaciones están determinadas de modo que arrojaran las correlacionadas registradas, el súbito cambio aleatorio y simultáneo que esos conmutadores efectúan en la dirección de los fotones anula esa supuesta determinación de origen. Si bien es cierto que por el carácter no local de las variables ocultas que se postula, lo anterior no es concluyente para eliminarlas, dado el estado actual de conocimiento sobre esos procesos cuánticos, esa hipótesis se antoja del todo implausible.

Desde un enfoque que asuma el indeterminismo cuántico, podría intentarse una vía de explicación de esas correlaciones, asumiendo tendencias de los sistemas cuánticos a exhibir regularidades estadísticas estables, llamadas propensiones. Según la interpretación propensista de la probabilidad, tanto las probabilidades de las secuencias aleatorias como el patrón probabilista de las correlaciones cuánticas serían, de algún modo, una consecuencia de las propensiones inherentes del dispositivo experimental a comportarse de ciertas maneras regulares y estables. Es evidente que esta hipótesis atribuye poderes explicativos a las propensiones, pero la principal dificultad en ella consiste, como lo anota Fine, en que esas entidades físicas hipostasiadas no han sido objeto de teorización física ni, a pesar de que Popper sostenga que son medibles por frecuencias relativas, de investigación experimental (cfr. 1989, p. 191). Más bien se antojan como entidades ocultas que, aunque son responsables de regularidades estadísticas y patrones probabilistas, no admiten un escrutinio empírico.

Sin pretender explicar las correlaciones cuánticas sino más bien con la intención de despojarlas de su ropaje enigmático, señalamos que los pares de fotones emitidos en cada ensayo han interactuado previamente conformando un sistema no separable. Esto significa, en parte, que los dos fotones que se producen de una interacción, aunque se distancien espacialmente, constituyen un solo sistema físicamente no separable, que los fotones no tienen estados propios ajenos entre sí, sino que, como un todo, son un sistema físico cuyo estado no es igual a la suma de los estados de los fotones individuales. Tal vez el problema de las correlaciones cuánticas únicamente se presenta bajo la concepción de los fotones individuales como sistemas físicos separables.

 

6. Conclusión

Con todo, no podemos extraer, de las probabilidades de las secuencias aleatorias de los resultados en los ensayos de experimentos tipo EPR, el patrón probabilista de las correlaciones cuánticas, sino más bien, como hemos visto, entre ambos niveles de situaciones —el de las secuencias aleatorias mismas y el de la relación entre esas secuencias—, se da una especie de incongruencia o falta de conformidad, que es el origen del problema. En el nivel básico, el nivel de los ensayos individuales del experimento, no se presenta el problema. Los ensayos individuales, con sus excluyentes resultados aleatorios, constituyen procesos estocásticos que tienen en común un mismo estado inicial, la producción idéntica de pares de fotones. Ésta es la característica peculiar de los procesos estocásticos, que a una misma situación física, a un mismo estado inicial del sistema, estén asociados distintos efectos, estados finales, de manera aleatoria, donde esa situación física invariante, el estado inicial común, representa a las condiciones causales indeterministas.

La noción de causalidad indeterminista propuesta aquí pretende aplicarse a sucesos aleatorios o procesos estocásticos individuales, como los procesos cuánticos, y los procesos de medición en los experimentos tipo EPR, los ensayos individuales, no representan ninguna excepción. Considerando en cada ensayo individual a un único sistema físico, compuesto por dos partículas no separables, el complejo proceso involucrado está formado por un par de bifurcaciones aleatorias, que similarmente a los procesos simples de medición de la polarización de un solo fotón individual, constituyen procesos estocásticos que generan secuencias aleatorias regulares y estables con probabilidades definidas. El alcance pretendido de las nociones causales propuestas aquí son ciertos procesos estocásticos, y las explicaciones que pudieran extraerse de ellas se agotarían en procesos cuánticos individuales. No pretendo que esas nociones sean aplicables de manera general a cualquier tipo de fenómeno físico que represente una anomalía o problema que surge respecto de patrones probabilistas entre secuencias aleatorias, sino sólo a la cuestión de si los sucesos singulares que acontecen aleatoriamente admiten o no algún género de explicación. Si se pide explicar las correlaciones cuánticas, la explicación que se precisaría sería de un género muy diferente que no puedo indicar.

Salmon tiene toda la razón al considerar que su teoría de la explicación no da cuenta de las correlaciones cuánticas que emergen entre secuencias aleatorias de los resultados individuales de experimentos tipo EPR, pero, como dije al inicio, creo que una teoría como la suya, concebida para procesos físicos individuales, no puede ni tiene que explicar esas correlaciones. Quizá la creencia de Salmon de que una teoría de la explicación científica debe dar cuenta de ese tipo de correlaciones cuánticas provenga del carácter dual de su modelo M–C–E, de acuerdo con el cual, en un primer nivel, se requiere subsumir el suceso que se pretende explicar bajo un conjunto de relaciones estadísticas relevantes y, en un segundo nivel, estas relaciones deben ser explicadas en términos de conexiones causales. En lo que falla la teoría de Salmon es en cumplir este segundo requisito de su modelo.¹⁵

 

BIBLIOGRAFÍA

Beltrametti, E.G. y G. Cassinelli, 1981, The Logic of Quantum Mechanics, Addison–Wesley, Reading, Mass.         [ Links ]

Dowe, P., 2000, Physical Causation, Cambridge University Press, Cambridge.         [ Links ]

Fair, D., 1979, "Causation and the Flow of Energy", Erkenntnis, vol. 14, pp. 219–250.         [ Links ]

Feller, W., 1950 (1973), Introducción a la teoría de las probabilidades y sus aplicaciones, trad. Salvador Morales Vaca, vol. I, Limusa, México.         [ Links ]

Fine, A., 1989, "Do Correlations Need to Be Explained?", en J.T. Cushing y E. McMullin (comps.), Philosophical Consequences of Quantum Theory, University of Notre Dame Press, Notre Dame, pp. 175–194.         [ Links ]

Martínez, S., 1993, "La probabilidad y la causalidad", en C. Ulises Moulines (comp.), La ciencia: estructura y desarrollo, Enciclopedia Iberoamericana de Filosofía, no. 4, Trotta, Madrid, pp. 111–125.         [ Links ]

Mellor, D., 1988, "On Raising the Chances of Effects", en J. Fetzer (comp.), Probability and Causality: Essays in Honor of Wesley C. Salmon, Reidel, Dordrecht, pp. 229–239.         [ Links ]

Rolleri, J.L., 2002, "La probabilidad como grado de posibilidad", Crítica, vol. 34, no. 101, pp. 3–26.         [ Links ]

Russell, B., 1948 (1977), El conocimiento humano, trad. Néstor Miguez, Taurus, Madrid.         [ Links ]

Salmon, W.C., 1998, Causality and Explanation, Oxford University Press, Nueva York/Oxford.         [ Links ]

––––––––––, 1994, "Causality without Counterfactuals", en Salmon 1998, pp. 248–260.         [ Links ]

––––––––––, 1990, "Causal Propensities: Statistical Causality versus Aleatory Causality", en Salmon 1998, pp. 200–207.         [ Links ]

––––––––––, 1984, Scientific Explanation and the Causal Structure of the World, Princeton University Press, Princeton.         [ Links ]

––––––––––, 1981, "Causality: Production and Propagation", en Salmon 1998, pp. 285–301.         [ Links ]

––––––––––, 1980, "Probabilistic Causality", en Salmon 1984, pp. 184–205.         [ Links ]

Suppes, P., 1970, A Probabilistic Theory of Causality, North–Holland, Amsterdam.         [ Links ]

Van Fraassen, B., 1980, La imagen científica, trad. Sergio Martínez, Paidós/Instituto de Investigaciones Filosóficas–UNAM, México, 1996.         [ Links ]

 

NOTAS

¹ Véase Dowe 2000, cap. 4. Dos de las principales objeciones, de índole conceptual, a esa teoría que Dowe señala son, por un lado, que no logra distinguir correctamente los procesos causales de los pseudoprocesos y, por otro, que las nociones centrales de proceso causal e interacción causal involucran una doble circularidad. Véanse también Van Fraassen 1980, cap. 5; Mellor 1988 y Martínez 1993.

² Esta noción tiene su antecesora en la de línea de mundo de un objeto propuesta por Bertrand Russell; véase, Russell 1948, parte VI, cap. 5.

³ En el ejemplo anterior del efecto Compton, C es la colisión entre el fotón y el electrón, A es la energía modificada E₁ (= hv' ) del fotón y B = es la energía modificada E₂ (= h (v – v' )) del electrón.

⁴ El ejemplo de la dispersión Compton tiene la ventaja de ser irreductiblemente estadístico y, así, no analizable, ni siquiera en principio, como una bifurcación perfecta", Salmon 1984, p. 170, n. 11.

⁵ Donde el supraíndice indica el valor de la masa atómica y el subíndice el número atómico.

⁶ Dowe señala que las probabilidades cuánticas referentes a estos procesos son irreductibles. Véase Dowe 2000, p. 25.

⁷ Fair 1979, Dowe 2000 y Salmon 1990 y 1994.

⁸ Exploramos aquí esta cuestión únicamente en sistemas cuánticos —y no en otros sistemas físicos presuntamente estocásticos como los mecánicos estadísticos— no sólo porque son los sistemas relevantes en la discusión con la teoría de la explicación de Salmon sino, principalmente, porque son los sistemas físicos que presumiblemente podemos concebir como irreductiblemente indeterministas.

⁹ Esta noción intenta capturar la idea básica de los procesos cuyo desarrollo futuro no está determinado de manera única. Preferimos el término "proceso estocástico" en vez del de "proceso aleatorio" porque introducimos un orden temporal, lo cual se apega al uso general. Véase al respecto Feller 1950, pp. 415 y 416.

¹⁰ Esto según la interpretación de la probabilidad que proponemos en términos de posibilidades físicas en Rolleri 2002.

¹¹ Véase Suppes 1970, pp. 12, 21 y 22.

¹² Salmon aclara que aunque este ejemplo es ficticio es similar a esquemas reales de átomos.

¹³ Nótese que las interacciones causales de Salmon son de tipo–X.

¹⁴ En líneas generales, sigo a este autor en el planteamiento del problema; en ese artículo se encuentran una extensa discusión del problema en relación con las desigualdades de Bell, y varios argumentos escépticos acerca de la necesidad de explicar las correlaciones cuánticas.

¹⁵ Agradezco las valiosas observaciones críticas de los árbitros a una versión previa de este escrito, las cuales me resultaron de gran utilidad; por supuesto, ellos no tienen responsabilidad alguna de esta nueva versión.