Introducción
Cuando se habla de las dificultades de impartir cálculo diferencial e integral, se habla, en parte, de vencer la mecanización de procesos algebraicos. El límite y la derivada son conceptos primordiales que el alumno debe de comprender para desarrollar la habilidad de calcular e interpretar y, del mismo modo, para incorporar conocimiento posterior dentro de ciencias como la física y las matemáticas. El aprender matemáticas no solo requiere de la habilidad para realizar ejercicios, sino también de plasmar ideas y representaciones a través de símbolos, los cuales representan un movimiento, un estado, una variación o una incógnita. A esa idea plasmada en la forma de una ecuación u operación, si no se conoce su significado, es imposible añadirle mayor conocimiento, lo cual incide en la resolución de un problema. Como lo señalan White y Mitchelmore (1996), la resolución de problemas de aplicación debe acompañarse de un conocimiento conceptual y no de una “comprensión instrumental”.
En una investigación relacionada con el proceso/objeto para el caso del límite, Cottrill et al. (1996) subrayan que la dificultad de comprender el concepto de límite radica en que para ello se requiere la reconstrucción de dos procesos coordinados. Más tarde, Sierra, González y López (2000) señalan la dificultad de la compresión de los conceptos de límite y continuidad incluso después del proceso de enseñanza. Mientras que Ferrini-Mundy y Graham (1994) documentaron la dificultad del estudiante de conectar la representación simbólica de una derivada con cualquier tipo de comprensión geométrica. Y una investigación posterior, de Habre y Abboud (2006), señala que, a partir de una enseñanza con énfasis en la visualización, los alumnos entienden a la derivada como un cambio instantáneo o como la pendiente de una curva en un punto. Martínez, López, Gras y Torregrosa (2002), por su parte, describen las aportaciones e insuficiencias de las concepciones históricas de Leibnitz y Cauchy.
En esa línea trazada por los ejemplos arriba citados, en esta investigación se ha comprobado la escasa interpretación de conceptos fundamentales en el cálculo y una habilidad insuficiente en el manejo algebraico en el cálculo de límites e integrales. Ferrini-Mundy y Gaudard (1992) también muestran que una enseñanza basada en procesos algorítmicos es inadecuada para lograr la interpretación correcta de conceptos dentro del cálculo diferencial. Asimismo, Rojas (2015) documenta secuencias didácticas que buscan favorecer la comprensión del concepto de límite de una función, las cuales descansan sobre una adecuada comprensión del concepto, lo cual no era así a principios del siglo XIX con Cauchy.
Con base en ello y sabiendo de la importancia del manejo algebraico y la resolución de límites y derivadas, se hace una propuesta a través del dibujo y la animación digital para buscar incidir en la comprensión del concepto de derivada con ayuda de Desmos, una calculadora gráfica de libre acceso y disponible para varios sistemas operativos y dispositivos.
En Rojas (2019), Thomas (2015), Montijo (2017) y Almarshedi, Wanick, Wills y Ranchhod (2017) se señala la importancia del dibujo a través de la calculadora gráfica Desmos y de la transición actitudinal del alumno para aprender a través de la gamificación. Sin embargo, el dibujo por sí mismo no incide en una respuesta, sino más bien en un orden de ideas o pasos para desarrollar, o bien, para plasmar un fenómeno ya sea físico o químico, por mencionar un par de ejemplos.
Sin embargo, el hecho de derivar una función no implica el entendimiento del uso de esta; cuando se habla de derivada se habla de cambios, de variaciones, y quizá no es de interés saber los resultados de esos cambios, sino cómo se originaron y a lo que conllevan; quizá acontecieron en un lapso muy pequeño, lo cual puede pasar desapercibido para el “ojo humano”. Así que es necesario redefinir el fenómeno y acotarlo en un cierto intervalo. No obstante, la derivación por incrementos nos permite definir formalmente a la derivada. A este método también se le conoce como la regla de los cuatro pasos, la cual tiene la particularidad de que es necesario involucrar límites; además, permite interiorizar el aprendizaje a diferencia de la derivación por fórmulas; o bien, como diferencial, que provino de un proceso “tormentoso” para Newton y Leibnitz y que vio la luz con la llegada de Cauchy.
El incremento de cualquier función continua obedece a la definición formal de infinitesimal, no tiene sentido utilizar el término diferencial para referirse al incremento (infinitesimal) de una función. Si a esto se añade la sospecha acumulada a lo largo de los años sobre la diferencial y los infinitesimales de servir de base a tratamientos matemáticos poco rigurosos, el terreno resultaba claramente abonado para que la diferencial quedase relegada a un papel marginal en el nuevo marco teórico del cálculo (Martínez et al., 2002, p. 275).
Una vez que el cimiento de la derivada se encuentra fuerte, es posible evolucionar a la instrucción del cálculo de esta a través de procesos algorítmicos.
La importancia de conocer la derivación por incrementos radica en la matematización y modelación matemática (Rojas, 2018; Martínez, Cobos y Torres, 2015; Arrieta y Díaz, 2015) para la apropiación del lenguaje y de la síntesis de una conceptualización ya posterior. Además, la recuperación de saberes a priori es importante para crear un andamiaje matemático.
Todo lo anterior constituye un cúmulo de motivos suficientes para realizar una investigación donde se programe con ayuda de la calculadora gráfica Desmos el método de derivación por incrementos y analizar su contribución en la comprensión de la derivada en un curso de cálculo.
Método
El presente trabajo está moldeado por la forma de investigación-acción, pues la intervención y el análisis de esta es lo que nos hace mejorar la comprensión de la realidad educativa y transformarla de acuerdo con la modalidad técnica y práctica que la caracteriza (Colmenares y Piñero, 2008). Se contó con la participación de 20 alumnos inscritos en la asignatura Cálculo Diferencial e Integral de 2.° semestre de la licenciatura en Biotecnología de la Universidad Michoacana de San Nicolás de Hidalgo. Los participantes tienen una edad de entre 17 a 19 años. Se siguió la práctica “trae tu propio dispositivo” (BYOD, por sus siglas en inglés): los alumnos trabajaron con su smartphone y, desde ahí y a través de una conexión a Internet, programaron y accedieron a la calculadora gráfica Desmos para desarrollar la actividad. Después de experimentar con la app, se recogieron los datos a través de Kahoot!, plataforma que permite, a manera de juego, realizar un quiz y verificar las respuestas de manera instantánea; en este momento el uso de la app Desmos no se permitía. Durante toda intervención se tomaron observaciones de empatía, manejo y dificultades que se presentaron durante el experimento.
Desarrollo
La regla de los cuatro pasos o derivación por el método de incrementos, de acuerdo con Cauchy, consiste por definición en lo siguiente:
Sea una función y = f (x)
Este proceso lo trasladamos a código; después, lo programamos en la calculadora gráfica de Desmos, definiendo, por ejemplo, a la función
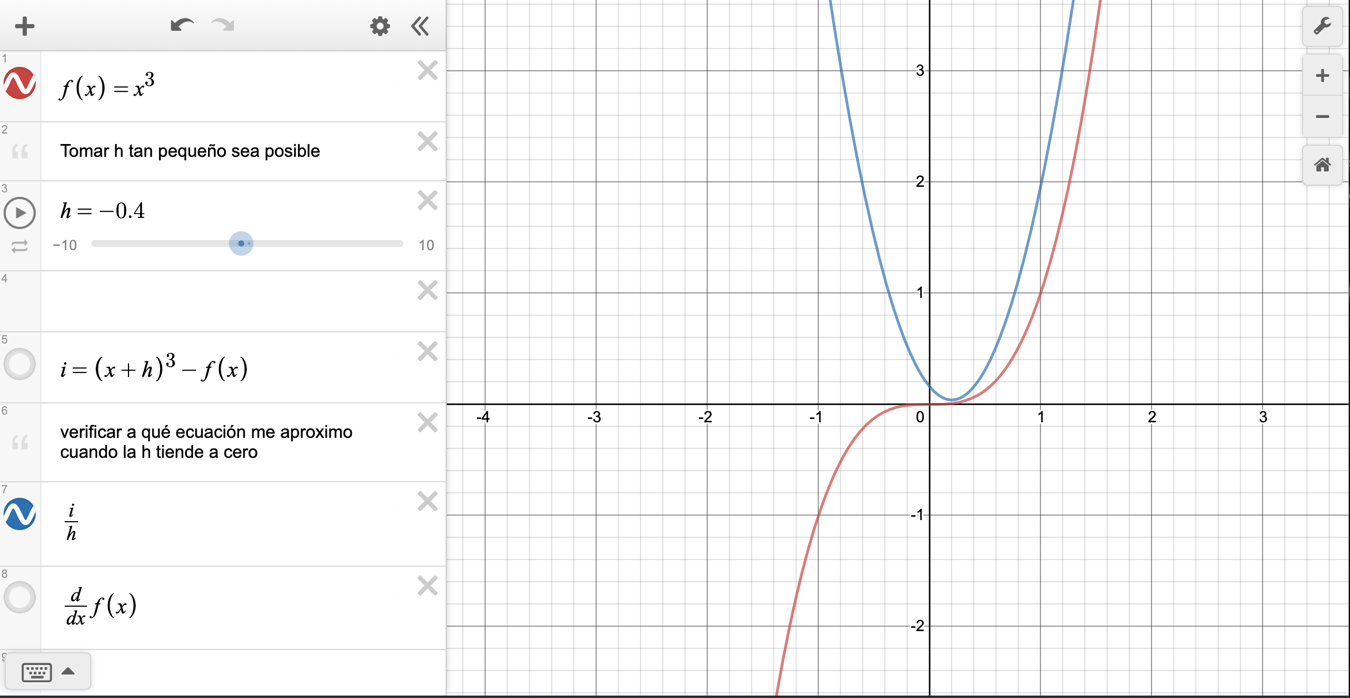
Asignamos un valor h tan pequeño como sea posible, y que recorra números negativos con un número de paso mayor a dos decimales, tal y como se observa en la Figura 1.
Es conveniente graficar en Desmos el renglón número ocho para hacer la comparación de los valores antes emitidos y permitir comparar la función derivada.
Asimismo, se recomienda inhabilitar el renglón cinco y ocho, como queda patente en la Figura 2.
Una vez realizado lo anterior, solo basta mover el deslizador de h lo más cercano a cero, pues se busca que
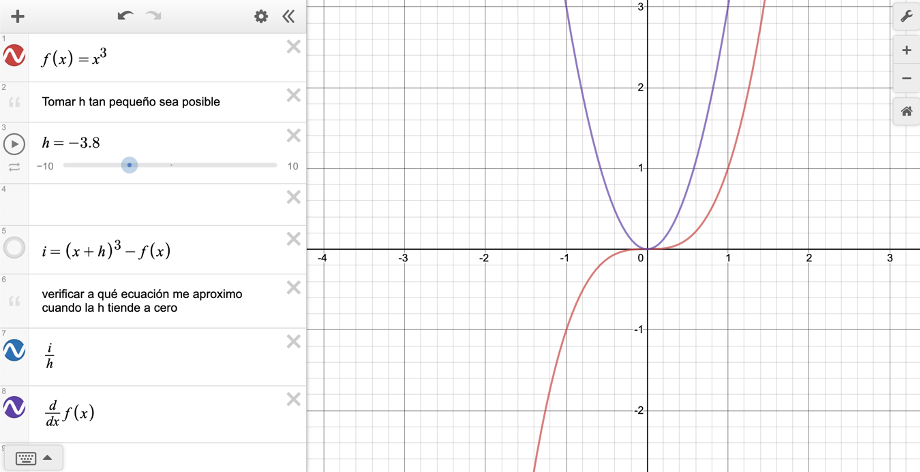
Fuente: Elaboración propia
Figura 3 La derivada en un punto versus el límite de la razón de los incrementos cuando la variable dependiente tiende a cero mediante Desmos
El docente cuestiona a los alumnos con lo siguiente:
Resultados
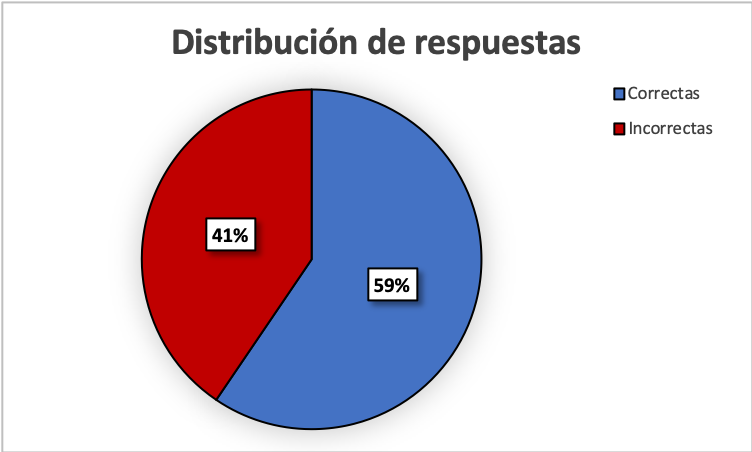
Después de la experimentación con la plataforma Desmos, se procede a realizar los cuestionamientos anteriormente señalados. Los resultados fueron capturados a través de cinco quizzes en la plataforma de Kahoot!, con un lapso de respuesta de hasta 60 segundos, excepto para el Quiz 5 (Q5), que fue hasta de 90 segundos por la complejidad que representa. Si el alumno contestaba fuera de ese intervalo de tiempo, la respuesta no se consideraba ni para puntaje del quiz ni para la estadística que se involucra en este trabajo.
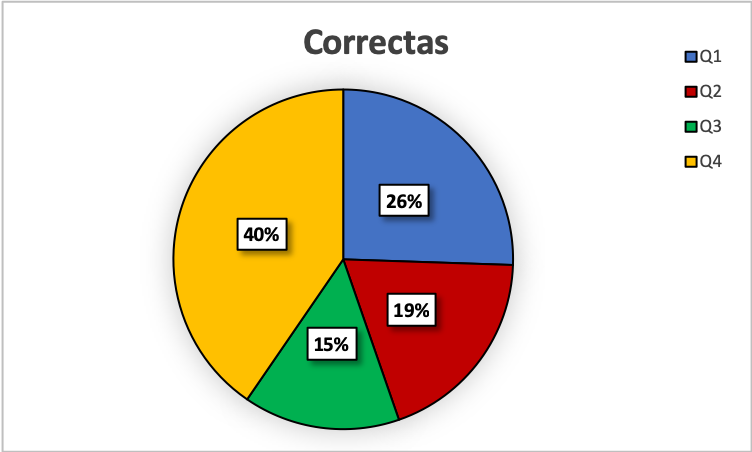
Los resultados encontrados se observan en la Figura 4 y en la Tabla 1.
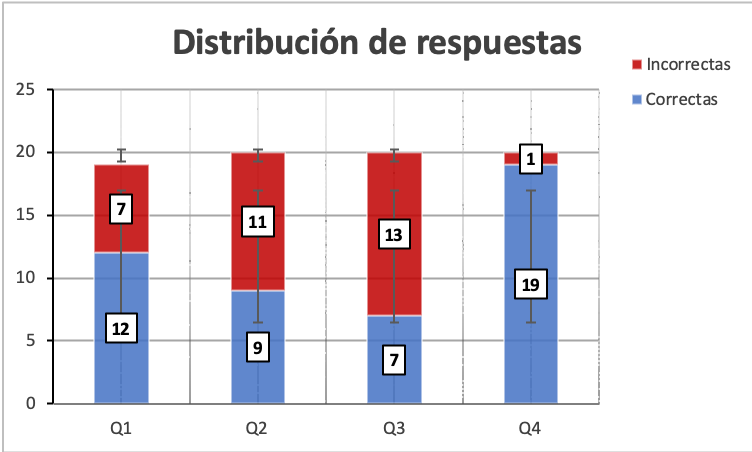
Tabla 1 Distribución de respuestas
| Quiz | Correctas | Incorrectas | |
| Válido | Q1 | 12 | 7 |
| Q2 | 9 | 11 | |
| Q3 | 7 | 13 | |
| Q4 | 19 | 1 | |
| Q5 | 1 | 18 | |
| Total | 98 |
Fuente: Elaboración propia
Dada la complejidad del Q5, se omite del análisis en las siguientes figuras, pues requiere una interpretación particular de sus resultados; además, no pertenece al objetivo del presente trabajo; resultaba inquietante, sin embargo, conocer hasta dónde podía llegar un análisis matemático.
Fuente: Elaboración propia
Figura 5 Desviación estándar de la distribución de respuestas por número de quiz
Discusión
Ha quedado en evidencia que el uso de Desmos en el aula favorece a la comprensión del concepto de derivada de una función (Q4). Sin embargo, existen áreas de oportunidad.
Durante las observaciones que se hicieron en el aula al momento de la intervención con la plataforma, los alumnos mostraron confusión para realizar la programación. Pues el crear un deslizador lo asumían como punto; otros definían la función como y, donde matemáticamente es correcto pero en el algoritmo no es conveniente escribir la función como tal, sino definirla como una función que depende de una variable x. Al momento de terminar la programación en la plataforma y de ejecutar la animación, la actitud no fue de empatía ni entusiasmo. Además, no se manifestó el reflejo de un aprendizaje, sino más bien la obediencia de seguir los pasos que el profesor les indicaba para realizar la tarea.
También quedó en evidencia que aún no logran comprender la definición de límite (Q3), de forma análoga a los suscitado en Sierra et al. (2000), pues, a pesar de haber sido tratada en una unidad temática previa, los alumnos no pudieron relacionarla: persiste la idea de que el límite se basa en una sustitución de la variable dependiente (matemáticamente hablando y no metodológicamente), sin importar que es imposible obtener su resultado. Por el contrario, la identificación de funciones (Q1) se vio muy favorecida al momento de graficar, pues lograron identificar, no de la manera exacta, sino más bien intuitiva, la función que se expresa matemáticamente.
El último quiz (Q5) tenía un grado de dificultad muy superior a los límites del objetivo en esta investigación trazado, pues para responderlo se requerían conocimientos superiores y de una asignatura avanzada, como lo es el análisis matemático; sin embargo, el desafiar a los alumnos puede resultar interesante, aunque es notorio que no respondieron de manera acertada, pero se crea el antecedente de que no siempre es posible que una función sea diferenciable en todo punto. Si bien un solo alumno acertó en la respuesta, no logró justificarla.
Limitaciones
Tamaño de la muestra
Las pruebas estadísticas normalmente requieren un tamaño de muestra más grande para asegurar una distribución representativa de la población y ser consideradas representativas de los grupos de personas estudiados. Aunque el tamaño de la muestra es menos relevante en la investigación cualitativa, es imperativo señalar que cuando hablamos de un proceso de enseñanza, y más en matemáticas, no debe abordarse ante un grupo masivo, a pesar de que algunos grupos en la realidad así estén estructurados, como en algunas escuelas o universidades. Por lo que si es un grupo más allá de 20 alumnos, la tecnología en el aula no es recomendada.
Conclusiones
Se concluye de manera general que Desmos es un auxiliar de utilidad para la tarea de esbozo de una función, pues simplifica el cómputo y el trazado de funciones, y señala los puntos discontinuos que operacionalmente pudieran pasarse por alto. Pero la habilidad y la detección de los puntos problema, así como la interpretación de los resultados, sigue siendo terreno humano, es decir, no hay comprensión si no hay un desarrollo cerebral, un trabajo que rete a ello, y es aquí donde las habilidades individuales se ven exteriorizadas. El uso de la tecnología en el aula permite modelar ciertas realidades y comprender definiciones que ciertamente pueden ser complicadas de entender, pero el uso de la tecnología en matemáticas no es una forma válida de demostrar teoremas. A pesar de que es posible encontrar la derivada de una función a través de incrementos, no es conveniente recurrir a ello como único procedimiento. Pues, a pesar de ser un método holístico que incluye un límite, el factor tiempo puede jugar un papel ponderante, especialmente si es una función que necesita mucha experiencia algebraica o trigonométrica para ser encontrada de manera sintetizada. Por lo que se recomienda que se dé el paso al cálculo de la derivada por fórmulas.











 nueva página del texto (beta)
nueva página del texto (beta)