Introducción
El estado de Quintana Roo (Q. Roo) ocupa el segundo lugar nacional en producción maderable de taxones latifoliados, con una cosecha aproximada de 47 139 m3 de madera en rollo (m3 mr) de especies comunes tropicales (12.10 % de la producción total) y de 4 807 m3 mr de especies preciosas (15.18 % de la producción nacional), con un valor de aproxímadamente $84 091 064 y $17 306 518, respectivamente, que lo ubica con una contribución al PIB por abajo de 0.2 % del registrado a nivel nacional (Semarnat, 2017). Bursera simaruba (L.) Sarg. (chakáh) y Metopium brownei (Jacq.) Urb. (chechem negro) son especies comunes tropicales de interés comercial para la industria forestal (Silva et al., 2011; Gallegos et al., 2012), se distribuyen ampliamente en la Península de Yucatán (Herbario CICY, 2010), son utilizadas en la agroforestería por su crecimiento y regeneración (Bursera simaruba); así como para la elaboración de muebles y artesanías (Metopium brownei) (Román et al., 2016; OIMT, 2020).
La estimación precisa del volumen fustal, del volumen total al incluir las ramas, y del volumen comercial a partir de las dimensiones que exige el mercado es importante para desarrollar las prácticas silvícolas propuestas en el plan de manejo forestal, de acuerdo con los datos de los inventarios forestales realizados (Corral-Rivas y Návar-Cháidez, 2009; Diéguez-Aranda et al., 2009; Gómez-García et al., 2016; Tamarit et al., 2017; Niño et al., 2018).
La modelación matemática es una herramienta de apoyo para los manejadores de los recursos forestales, por lo que el ajuste de modelos que estiman el volumen fustal, total y comercial; o modelen, con precisión, la proporción entre el volumen comercial y el fustal (Vc/Vf), así como su dinámica de disminución en el volumen acumulado de un árbol, con el incremento de la altura y la reducción del diámetro sobre el fuste, hasta llegar a la altura total (funciones de razón de volumen); además de que describan el ahusamiento de los árboles (diámetro a diferentes alturas) por especie contribuye a la realización de planes de manejo acordes a las condiciones específicas y actuales de los recursos (Burkhart, 1977; Tapia y Návar, 2011; Barrios et al., 2014; Özçelik y Göçeri, 2015; Hernández-Ramos et al., 2018a).
En México, durante años recientes, la modelación se ha realizado por medio de funciones que consideran los diámetros a distintas alturas sobre el fuste y sistemas compatibles de ahusamiento - volumen comercial para diferentes especies del género Pinus (Tapia y Návar, 2011; Quiñonez-Barraza et al., 2014; Tamarit et al., 2016; Silva et al., 2018); o por modelos de razón de volumen para especies como Eucalyptus urophylla Blake en Huimanguillo, Tabasco, Swietenia macrophylla King en Quintana Roo y P. pseudostrobus Lindl. en San Juan Nuevo Michoacán, entre otras (Hernández-Ramos et al., 2018a; García-Espinoza et al., 2018).
Los sistemas de volumen comercial compuestos por modelos de razón son una herramienta para calcular con precisión el volumen comercial y la distribución de productos maderables de árboles en pie (Prodan et al., 1997; Hernández-Ramos et al., 2018a; García-Espinoza et al., 2018). La estimación de estos volúmenes es fundamental en la proyección del aprovechamiento del recurso maderable y el rendimiento para la industria forestal, porque posibilitan la estimación del ingreso financiero del bosque a partir de datos de inventarios forestales, principalmente la distribución de los productos por unidad de superficie (Niño et al., 2018; Silva et al., 2018); y contribuyen, además, a evitar el sobre aprovechamiento, en general, de taxones con importancia comercial, no solo en bosques tropicales.
Para la zona de interés, Hernández-Ramos et al. (2018a y 2018b) ajustaron modelos de volumen total y generaron un sistema de volumen comercial a partir de modelos de razón, además de un sistema segmentado de ahusamiento (d) compatible con el volumen comercial (Vc) para Swietenia macrophylla (caoba) en bosques tropicales de Quintana Roo. López et al. (2019) ajustaron un sistema compatible de ecuaciones de volumen comercial que consta de fuste, ramas y tallo y ramas gruesas de árboles para 11 especies tropicales importantes en el sureste de México.
Tradicionalmente, las ecuaciones para diseñar esos sistemas de volumen comercial se han ajustado mediante modelos de regresión lineal y no lineal que asumen normalidad, igualdad de varianzas e independencia de los errores (Carrero et al., 2008).
Sin embargo, la obtención de ecuaciones confiables para algunas variables es compleja, debido a la variabilidad que existe en estas relaciones por efecto de las diferentes formas de los fustes y condiciones en que se desarrolla cada individuo (Quiñonez et al., 2012). En la actualidad, el ajuste bajo el enfoque de modelos de efectos mixtos (MEM) es una opción viable para dicho tipo de estudios (Corral-Rivas et al., 2014), ya que su incorporación permite agrupar las fuentes de variabilidad y reducir la varianza del error (Seoane, 2014). La técnica de MEM incluye en su formulación parámetros fijos comunes a toda la población y parámetros aleatorios específicos de cada nivel de agrupación (Seoane, 2014). De ello, resultan estimadores más eficientes, precisos y confiables que los parámetros fijos del modelo; y por lo tanto, se pueden hacer estimaciones con mayor certidumbre de la variable de interés (Carrero et al., 2008). Por todo lo anterior, el objetivo del presente estudio fue ajustar una función no-lineal con efectos aleatorios que estime el volumen comercial para Bursera simaruba y Metopium brownei en el centro y sur de Quintana Roo, México.
Materiales y Métodos
El estudio se realizó en distintas áreas forestales de Quintana Roo, México, que se ubican en zonas con topoformas de lomeríos bajos y llanura rocosa, a una altitud de 20-180 m. El clima predominante es de tipo cálido subhúmedo (Aw), con temperatura media anual de 22 °C y una precipitación media de 1 300 mm (Semarnat, 2014).
A partir de recorridos en las áreas forestales del estado, se seleccionaron árboles con diámetro normal superior a 7.5 cm, situados aleatoriamente en zonas no perturbadas del bosque tropical, donde se muestrearon 188 ejemplares de Bursera simaruba y 133 de Metopium brownei, los cuales abarcaron todas las categorías diamétricas presentes en estos ecosistemas forestales (10-50 y 10-60 cm, respectivamente). De cada uno de ellos, se obtuvo información del diámetro del tocón (dt), diámetro normal (d), altura total (H) y diámetros y alturas parciales sobre el fuste (d i y h i ). La muestra se eligió con árboles monopódicos, sin presencia de daños mecánicos ni de plagas o enfermeda≥des, además de estar por lo menos a 20 m de distancia de los caminos, claros o de lugares con desmontes para evitar efectos de borde. La estadística descriptiva de las variables analizadas se muestra en el Cuadro 1.
Cuadro 1 Estadística descriptiva de la muestra de árboles de Bursera simaruba (L.) Sarg. y Metopium brownei (Jacq.) Urb.
| Estadísticos | Especie | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bursera simaruba | Metopium brownei | |||||||||
| d | H | Vt | R | Vc | d | H | Vt | R | Vc | |
| Promedio | 23.82 | 13.97 | 0.4938 | 0.44 | 0.2143 | 30.00 | 15.45 | 0.6820 | 0.46 | 0.3174 |
| Error típico | 0.24 | 0.08 | 0.0110 | 0.01 | 0.0080 | 0.30 | 0.09 | 0.0140 | 0.01 | 0.0120 |
| Desviación estándar | 9.21 | 3.19 | 0.4360 | 0.38 | 0.3200 | 10.13 | 3.11 | 0.4840 | 0.37 | 0.3950 |
| Coeficiente de variación | 38.66 | 22.88 | 88.2900 | 87.05 | 149.2900 | 33.77 | 20.13 | 70.9600 | 81.52 | 124.4300 |
| Varianza | 84.79 | 10.22 | 0.1900 | 0.14 | 0.1020 | 102.64 | 9.67 | 0.2350 | 0.14 | 0.1560 |
| Curtosis | -0.50 | -0.60 | 1.5000 | -1.50 | 2.3000 | -0.60 | 0.50 | -0.1000 | -1.60 | 3.2000 |
| Coeficiente de asimetría | 0.60 | -0.10 | 1.4000 | 0.50 | 2.6000 | 0.20 | -0.50 | 0.8000 | 0.40 | 1.9000 |
| Mínimo | 7.00 | 5.57 | 0.0239 | 0.01 | 0.0013 | 9.40 | 4.63 | 0.0337 | 0.02 | 0.0028 |
| Máximo | 49.80 | 21.80 | 2.1000 | 1.00 | 2.1000 | 57.30 | 23.10 | 2.3000 | 1.00 | 2.3000 |
d = Diámetro normal (cm); H = Altura total (m); Vt = Volumen total (m3); R = Razón de volumen (m3); Vc = Volumen comercial (m3).
Las mediciones de los diámetros (di) a diferentes alturas sobre el fuste (h i ) de 0.3 m, 0.6 m, 0.9 m, 1.3 m y 2.5 m se realizaron de forma directa con una forcípula graduada al milímetro; mientras que el resto de hi y d i con un Telerelascopio de Bitterlich a lo largo del fuste, cuando fue posible desde los 2.5 m hasta la altura total (H) o diámetro cero (d 0 ). Para el cálculo del volumen fustal (Vf) se sumaron los volúmenes de las distintas secciones (trozas), mismas que se determinaron mediante la fórmula de Smalian y para el volumen de punta o última troza (Vp) con la fórmula del cono; la razón de volumen (R) resultó del cociente entre el volumen a distintas secciones sobre el fuste (Vi) y el Vf, para ello se utilizó la expresión: Vi/Vf (Balzarini et al., 2005; Hernández-Ramos et al., 2018a; García-Espinoza et al., 2018).
Como se señala en la Norma Oficial Mexicana NOM-152-SEMARNAT-2006, para cada especie se ajustó una función no-lineal (modelo general), la cual está conformada por dos componentes: el primero incluye una estructura matemática que corresponde a una ecuación de Vf (a 0 +a 1 (d 2 H/1000), y el segundo es una ecuación referida a la razón existente entre los volúmenes de la secciones y la R (e (-(a2)*((di/d)/1000) e (a3*(di/d)) ). Ecuaciones que al multiplicarse estiman el volumen comercial (Vc) (Schabenberger y Pierce, 2002; Balzarini et al., 2005) (Cuadro 2). Este último, se define por las dimensiones que demande la industria del aserrío o los productos maderables que se tenga interés de estimar: largas dimensiones o primarios, cortas o secundarios y desperdicio o leña. Para las dos especies se probó el modelo general y el efecto aleatorio aditivo a cada combinación de los parámetros fijos, y resultaron ocho expresiones a partir del modelo general.
Cuadro 2 Modelos de volumen comercial ajustado con efectos fijos y aleatorios para Bursera simaruba (L.) Sarg.y Metopium brownei (Jacq.) Urb.
| Identificador | Estructura de los modelos |
|---|---|
| General |
|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
d = Diámetro normal (cm); d
i
= Diámetro a distintas alturas sobre el fuste;
H = Altura total (m); Vc =
Volumen comercial;
El modelo general (Cuadro 2) se ajustó, en principio, por mínimos cuadrados ordinarios (MCO) y dos variantes de la ecuación de volumen fustal de Spurr (1952): una lineal de la forma y =a 0 +a 1 X, y la segunda de tipo exponencial de forma y = aX b . En ellas, y es la variable respuesta (Vf = volumen fustal), X representa la variable independiente incluida en el modelo (d 2 H), a y b corresponden a los parámetros por ser estimados.
La incorporación del efecto aleatorio a los parámetros fijos (a i + u) se hizo por árbol para explicar la variabilidad en su ahusamientos, al considerar el sentido biológico de cada uno; por ejemplo, al incluir el efecto aleatorio en el parámetro referente a la forma del árbol, la velocidad de cambio de cuerpo geométrico en el fuste, la razón de proporción entre el volumen fustal y el volumen comercial o en los tres de manera simultánea dentro de cada uno de los componentes en la función no-lineal propuesta, en la que el valor de probabilidad del efecto deberá ser significativo (P ≥ 0.05) (Cuadro 1, 1-16).
El ajuste se realizó en el programa SAS 9.3® mediante el procedimiento nlmixed y el método de primer orden FIRO, el cual define con mayor precisión la aproximación por verosimilitud de los valores en los parámetros estimados (Beal y Sheiner, 1982; SAS, 2011). La distribución tanto para las variables dependientes, como para los efectos aleatorios (a i + u) se especificó en la programación como NORMAL para ajustarlos por la técnica de optimización Dual Cuasi-Newton y el método de integración Cuadratura Gaussiana Adaptativa del Sistema de Análisis Estadísticos (SAS, 2011).
La selección de la mejor combinación, cuando se incorporan los efectos aleatorios dentro del modelo no-lineal, se hizo a través de la significancia de los parámetros estimados tanto en efectos fijos, como aleatorios a un valor de 95 % de confiabilidad (P ≥ 0.05), y los mejores valores de Verosimilitud-2Log y Criterio de Información de Akaike Corregido (CIAC) (García y Rapelli, 2011; Gómez-García et al., 2016); además, para la mejor expresión se verificó de forma gráfica la tendencia en las estimaciones al emplear por separado las estructuras del modelo en el volumen fustal (Vf = primera estructura matemática) y razón de volumen (R = segunda estructura matemática), y de manera conjunta para estimar el volumen comercial (Vc) de cada especie, o hasta un diámetro de 20 cm (Cuadro 1, modelo general).
En el modelo seleccionado se verificó la homocedasticidad de los residuos mediante la prueba de White, bajo las hipótesis de que los residuales se distribuyen de manera homogénea alrededor de cero (Hipótesis nula: Ho); mientras que, la hipótesis alternativa refiere una distribución heterocedástica de los residuos (Hipótesis alternativa: Ha) a un nivel de confiabilidad de 95 % (Martínez et al., 2006). La calidad de las estimaciones para las variables Vf, R y Vc se determinó a través del sesgo (E) (Quevedo et al., 2010) y el coeficiente de determinación (R 2 ) y con el análisis gráfico de los valores observados contra los valores estimados de cada variable (Pece, 1994).
Resultados
Al ajustar el modelo general y las variaciones en la inclusión de los efectos aleatorios, se observó que tanto la estructura general del modelo, como las expresiones 1, 2, 4 y 5 para Bursera simaruba; y 1, 2, 4 y 5 para Metopium brownei en algunos de sus parámetros fijos no fueron significativos a 95 % de confiabilidad (P ≥ 0.05). Mientras que, en las combinaciones de inclusión de los efectos aleatorios de las expresiones 6 y 8 en ambas especies, los parámetros relacionados a los afectos mixtos no pudieron estimarse, aun cuando se trató de ajustar por el método Gauss-Hermite (Pinheiro y Bates, 1995). Por lo cual, se descartaron para posteriores análisis y no se presentan en el Cuadro 3. Debido a esa situación, solo se muestran las combinaciones de inclusión de los parámetros aleatorios de las expresiones 3 y 7 para árboles de Bursera simaruba y Metopium brownei para los análisis posteriores, en los cuales todos fueron significativos (P ≥ 0.05) al ajustarlos con 1 476 y 1 130 pares de datos, respectivamente.
Cuadro 3 Parámetros estimados para las diferentes expresiones del modelo de volumen comercial ajustado para de Bursera simaruba (L.) Sarg.y Metopium brownei (Jacq.) Urb.
| Especie | Sistema | Parámetro | Estimador | Eea | Valor t | Pr>|t| | ICI | ICS |
|---|---|---|---|---|---|---|---|---|
| Bursera simaruba | 3 | a 0 | 0.01238 | 0.0059 | 2.09 | 0.0381 | 0.00068 | 0.02407 |
| a 1 | 0.04866 | 0.0011 | 42.69 | <0.0001 | 0.04642 | 0.05091 | ||
| a 2 | 9.15250 | 0.9572 | 9.56 | <0.0001 | 7.26420 | 11.04070 | ||
| a 3 | 5.32220 | 0.1084 | 49.09 | <0.0001 | 5.10840 | 5.53610 | ||
| se | -0.04927 | 0.0009 | -50.28 | <0.0001 | -0.05121 | -0.04734 | ||
| su 1 | 0.00861 | 0.0006 | 13.71 | <0.0001 | 0.00737 | 0.00985 | ||
| su 2 | 0.91109 | 0.1575 | 5.79 | <0.0001 | 0.60120 | 1.22250 | ||
| 7 | a 0 | 0.05710 | 0.0024 | 23.37 | <0.0001 | 0.05228 | 0.06192 | |
| a 1 | 0.94400 | 0.0200 | 47.09 | <0.000 1 | 0.90440 | 0.98350 | ||
| a 2 | 9.18550 | 0.9675 | 9.49 | <0.0001 | 7.27700 | 11.09400 | ||
| a 3 | 5.32100 | 0.1092 | 48.73 | <0.0001 | 5.10560 | 5.53640 | ||
| se | -0.04964 | 0.0009 | -50.26 | <0.0001 | -0.05158 | -0.04769 | ||
| su 1 | -0.07213 | 0.0062 | -11.45 | <0.0001 | -0.08456 | -0.05971 | ||
| su 2 | -0.93620 | 0.1633 | -5.73 | <0.0001 | -1.25830 | -0.61400 | ||
| Metopium brownei | 3 | a 0 | 0.00807 | 0.0118 | 0.68 | 0.4977 | -0.01541 | 0.03155 |
| a 1 | 0.04111 | 0.0013 | 29.79 | <0.0001 | 0.03838 | 0.04384 | ||
| a 2 | 3.08900 | 0.5345 | 5.78 | <0.0001 | 2.03160 | 4.14640 | ||
| a 3 | 6.30480 | 0.1792 | 35.18 | <0.0001 | 5.95030 | 6.65930 | ||
| se | -0.07122 | 0.0016 | -43.68 | <0.0001 | -0.07444 | -0.06799 | ||
| su 1 | -0.00954 | 0.0007 | -12.65 | <0.0001 | -0.01103 | -0.00805 | ||
| su 2 | 0.36620 | 0.0785 | 4.66 | <0.0001 | 0.21090 | 0.52150 | ||
| 7 | a 0 | 0.04722 | 0.0040 | 11.57 | <0.0001 | 0.03914 | 0.05529 | |
| a 1 | 0.95240 | 0.0333 | 28.58 | <0.0001 | 0.88650 | 1.01830 | ||
| a 2 | 3.09670 | 0.5375 | 5.76 | <0.0001 | 2.03330 | 4.16000 | ||
| a 3 | 6.30360 | 0.1798 | 35.06 | <0.0001 | 5.94800 | 6.65930 | ||
| se | -0.07144 | 0.0016 | -43.52 | <0.0001 | -0.07468 | -0.06819 | ||
| su 1 | -0.08848 | 0.0079 | -11.1 | <0.0001 | -0.10430 | -0.07271 | ||
| su 2 | 0.37550 | 0.0810 | 4.63 | <0.0001 | 0.21520 | 0.53580 |
a 0 , a 1, a 2 y a 3 = Parámetros de efectos fijos; su 1 y su 2 = Desviación estándar de los efectos aleatorios; Eea = Error estándar del estimador; se= Desviación estándar de los residuos en el sistema; ICI e ICS = Intervalos de confianza del estimados inferior y superior, respectivamente.
Para las dos especies, la combinación en la estructura matemática que contiene el modelo de volumen fustal de Spurr en su forma exponencial registró los mayores valores estadísticos en los indicadores de Verosimilitud -2Log y CIAC; por ello las estructuras del modelo 7 fueron las seleccionadas para Bursera simaruba y Metopium brownei, respectivamente. Al contrastar estos valores con los obtenidos al ajustar el modelo general por mínimos cuadrados ordinarios (MCO), se observó una ganancia estadística promedio al aplicar el enfoque de modelos de efectos mixtos de 5.6 % y 6.9 % para Bursera simaruba y Metopium brownei, respectivamente (Cuadro 4). Además, las pruebas de White para ambas especies resultaron no significativas (a < 0.05), lo cual indicó que los residuales de ambos modelos se distribuyen de manera homocedástica; por lo tanto, se acepta la hipótesis nula (Ho) y se rechaza Ha.
Cuadro 4 Indicadores de ajuste estadístico del modelo de volumen comercial ajustado para Bursera simaruba (L.) Sarg. y Metopium brownei (Jacq.) Urb.
| Especie | Bursera simaruba | Metopium brownei | ||||
|---|---|---|---|---|---|---|
| Modelo con
efectos aleatorios |
Modelo
general |
3 | 7 | Modelo
general |
11 | 15 |
| Verosimilitud -2 Log | -4 617 | -4 368 | -4 360 | -2 588 | -2 409 | -2 396 |
| CIAC | -4 601 | -4 354 | -4 346 | -2 543 | -2 395 | -2 382 |
CIAC = Criterio de Información de Akaike Corregido.
Los sesgos estimados para las dos especies evidenciaron buena precisión en las estimaciones al evaluarlos de forma individual para Vf y R, así como un modelo completo para estimar el Vc, ya que en todos los casos fueron menores a 0.03 m3 (Cuadro 5). Además, cuando se hizo la evaluación gráfica y mediante una regresión de los valores observados contra los predichos por variable de interés, no se observaron problemas evidentes en las estimaciones; situación que se reflejó en el valor del coeficiente de determinación (R 2 ), que en todos los casos fue mayor a 0.9 (Figura 1).
Cuadro 5 Sesgo estimado por variable independiente en el modelo de volumen comercial ajustado.
| Variable independiente | Vf (m 3 ) | R (V i /Vf) | Vc (m 3 ) |
|---|---|---|---|
| Modelo con la inclusión de efectos aleatorios | Sesgo (E) | ||
| 7. Bursera simaruba (L.) Sarg. | -0.012543 | 0.029831 | -0.001384 |
| (R 2 = 0.95) | (R 2 = 0.93) | (R 2 = 0.94) | |
| 7. Metopium brownie (Jacq.) Urb. | 0.014684 | 0.019924 | 0.008979 |
| (R 2 = 0.93) | (R 2 = 0.94) | (R 2 = 0.92) | |
Vf = Volumen fustal; R = Razón de volumen basado en el diámetro; Vi = Volumen a distintas secciones sobre el fuste; Vc = Volumen comercial; R 2 = Coeficiente de determinación de los valores observados contra los valores predichos.
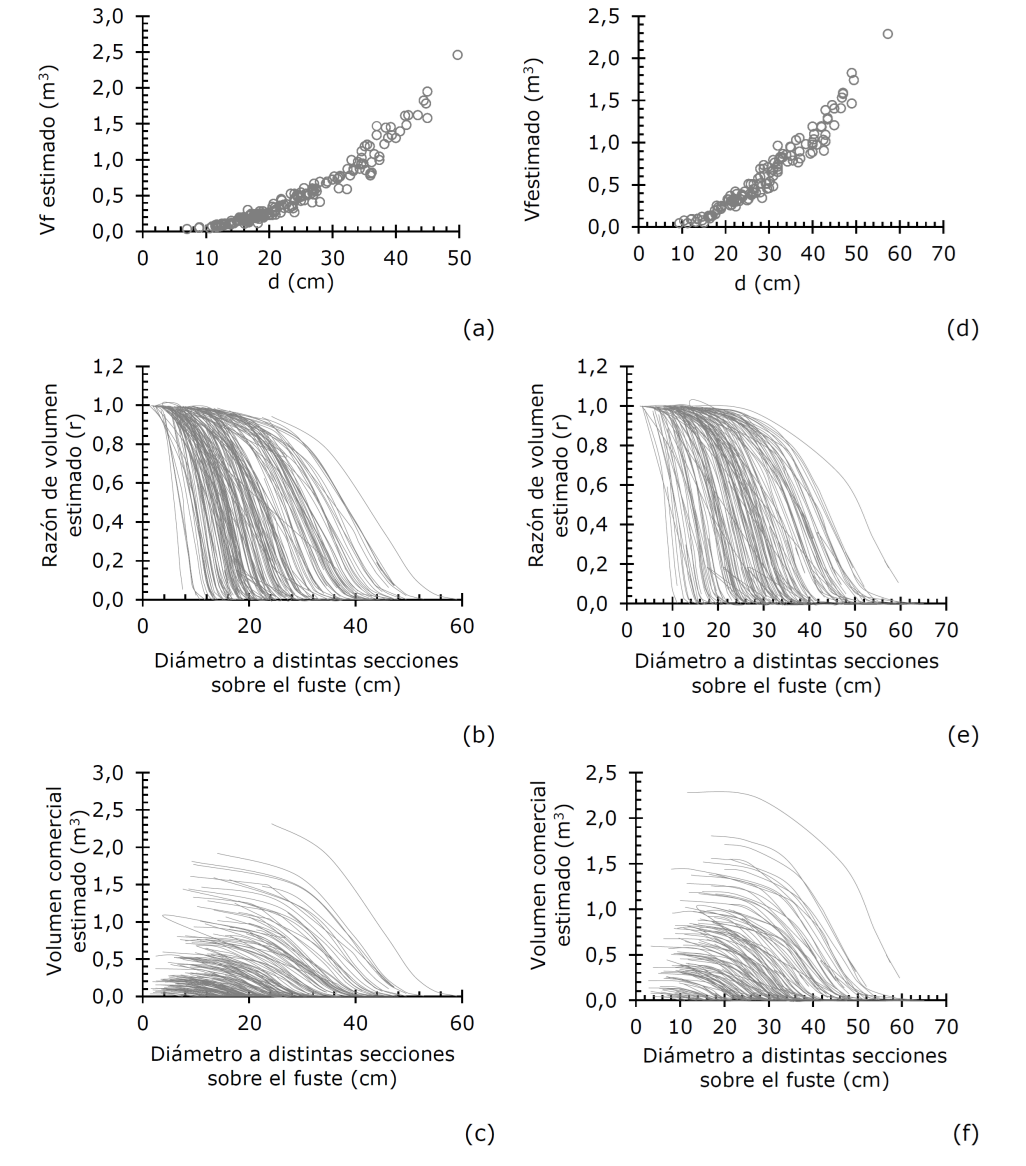
Figura 1 Tendencia de las estimaciones de volumen fustal, razón de volumen y volumen comercial para las especies de Bursera simaruba (L.) Sarg. (1a, 1b y 1c) y Metopium brownei (Jacq.) Urb. (1d, 1e y 1f).
Para ejemplificar el uso de la estructura que mejor se ajustó a los datos observados del modelo de volumen comercial, se consideraron como referencia los valores de diámetro normal (d) = 30 cm y altura total (H) = 15 m para Bursera simaruba, y d = 40 cm y H = 20 m para Metopium brownei, y se usó el modelo 7 con sus parámetros para cada especie para realizar la estimación de volumen fustal (Vf) y razón de volumen (R) al emplear por separado las dos secciones del modelo, y al aplicar el modelo completo ajustado para volumen comercial (Vc). De la expresión general del modelo se utiliza el primer componente correspondiente a Vf, el cual al sustituirlo se tiene para Bursera simaruba: Vf = 0.0571 ((30 2 · 15)/1000)0.9440 = 0.6663 m3, y para Metopium brownei: Vf = 0.0472 ((40 2 · 20)/1000)0.9524 = 1.5049 m3.
A continuación, se establece el diámetro mínimo para productos primarios, que en este caso fue 20 cm; enseguida se toma la segunda sección del modelo general y se sustituyen los valores, de lo que resulta para Bursera simaruba:
R =Exp(-9.1855·((20/30)/1000)·Exp(5.321*(20/30)))= 0.8085, y para Metopium brownei: R = Exp(-3.0967·((20/40)/1000)·Exp(6.3067*(20/30))) = 0.9644.
Finalmente, para obtener el Vc al diámetro mínimo de corta establecido se multiplican los valores de Vf y R; o bien, se aplica de forma directa el modelo propuesto para cada especie, de la forma siguiente para Bursera simaruba: Vc = [0.0571 ((30 2 · 15)/1000)0.9440]([ Exp(-9.1855·((20/30)/1000)·Exp(5.321*(20/30)))] = 0.5387 m3, y para M. brownei: Vc = [0.0472 ((40 2 · 20)/1000)0.9524] [Exp(-3.0967·((20/40)/1000)·Exp(6.3067*(20/30)))] = 1.4514 m3 .
Discusión
Los MEM permiten corregir la estructura de varianzas-covarianzas asociadas con las variables de clasificación de los árboles (Littell et al., 2006), ya que al agrupar la información en clase, bajo el enfoque de MEM, se reduce el error; puesto que, la variabilidad entre las clases se explica mediante la inclusión de parámetros aleatorios, que se estiman de forma simultánea a los parámetros fijos (Castedo et al., 2006; Corral et al. 2019). En esta técnica de análisis (MEM) se asume que la varianza es específica para cada nivel de clasificación (Seoane, 2014), por lo que se logra incrementar el R 2 y mejorar otros criterios de bondad de ajuste, tales como el AIC y BIC.
En los modelos evaluados, los efectos aleatorios se incluyeron para considerar en las ecuaciones el efecto de las covariables de clasificación durante el ajuste. En este caso, el efecto aleatorio fue específico a cada nivel del factor de clasificación, lo que de acuerdo con De los Santos et al. (2006), Tamarit-Urias et al. (2014) y García-Espinoza et al. (2019) permite la obtención de estimadores más eficientes, precisos y confiables de los parámetros fijos del modelo y la predicción de parámetros aleatorios específicos de cada unidad muestral, que reflejan el patrón de desviación con respecto de la media; pero posterior al ajuste, los valores que resultan para los parámetros aleatorios no se usan para construir las predicciones, por lo que la parsimonia de los modelos no se modifica.
En el caso de la estructura del modelo de volumen 3 para Bursera simaruba, y 7 para M. brownei, todos los parámetros fueron significativos (P ≥ 0.05) (Cuadro 3), similares a lo citado por Quevedo et al. (2010), dichos autores analizaron los modelos de volumen fustal bajo el enfoque de efectos mixtos para Tabebuia rosea Bertol. en Venezuela, donde se realizó una agrupación por categoría diamétrica y transformación de la variable dependiente. De igual forma al estudio realizado por Gómez-García et al. (2016), quienes desarrollaron una función de perfil mediante efectos mixtos para Pinus sylvestris L. en Turquía, la que se ajustó por el método FIRO (first-order), del programa R-project, que es el mismo método empleado en este trabajo.
Para la elección del modelo 3 y 7 del Cuadro 1 para Bursera simaruba y Metopium brownei, respectivamente se considera como referencia lo descrito por García y Rapelli (2011), quienes refirieron que los modelos con los valores más cercanos a cero en los indicadores de Verosimilitud -2Log y CIAC tienen una mayor verosimilitud en el ajuste. Además, dichos valores fueron congruentes con los criterios de evaluación utilizados por Gómez-García et al. (2016); y por Quiñonez-Barraza et al. (2014), autores que ajustaron sistemas compatibles de ahusamiento-volumen comercial para las principales especies de Pinus de Durango, México.
Los valores del sesgo en los modelos propuestos por especie y los coeficientes de determinación (R 2 ) que se obtuvieron al contrastar los datos observados, contra los predichos por variable de interés (Vf, R y Vc) coinciden con lo indicado por Pece (1994), quien usó un modelo de razón de volumen para estimar el volumen comercial en Eucalyptus pellita F. Muell. en Brasil, cuyos sesgos al realizar los cálculos por categoría diamétrica fueron entre 0.06 y 0.11. Además, es similar a lo determinado por Hernández-Ramos et al. (2017), autores que proponen sistemas de razón de volumen para Eucalyptus urophylla en Tabasco y obtienen estimaciones precisas con sesgos menores en las variables de Vt, R y Vc que los estimados en el presente trabajo (< 0.0077); y R 2 al contrastar los valores estimados versus observados mayores de 0.94.
De igual manera, la precisión de las estimaciones de este estudio para el volumen comercial (Vc) son semejantes a lo señalado por Hernández-Ramos et al. (2018b) mediante sistemas de razón de volumen en árboles de Swietenia macrophylla en Quintana Roo, cuyos sesgos para estructuras de razón de volumen basadas en el diámetro normal y en la altura total son de -0.0121 y 0.0053, respectivamente. Sin embargo, difieren con García-Espinoza et al. (2018) quienes proponen estructuras basadas en la razón de volumen para P. pseudostrobus en Michoacán, y registran buena precisión en las estimaciones y un sesgo menor en el Vc, en comparación con las determinadas en el trabajo que aquí se documenta (< 0.001 m3).
La evaluación gráfica de las tendencias en las estimaciones (Figura 1) concuerda con lo registrado por Tapia y Návar (2011) quienes ajustaron modelos de volumen fustal y ahusamiento para P. pseudostrobus en Nuevo León; Tamarit-Urias et al. (2016), al modelar el perfil fustal de nueve especies del género Pinus y obtener proyecciones acordes a las tendencias de los datos observados. También coincide con los resultados de Tamarit et al. (2017) en la construcción de un sistema de cubicación de árboles individuales para el género Quercus en Puebla y con los de Silva et al. (2018) referentes a las funciones compatibles de ahusamiento y volumen comercial para tres especies de Pinus en Chihuahua.
Las herramientas generadas en el presente trabajo pueden complementarse con las ecuaciones propuestas por García et al. (2017), quienes estiman el volumen fustal a partir de las dimensiones del diámetro de tocón en Bursera simaruba y Metopium brownei en los bosques tropicales de Quintana Roo, y pueden considerarse como una actualización de las ecuaciones propuestas por De los Santos (1976) y Patiño et al. (1994) para ambas especies.
Conclusiones
Los modelos de volumen propuestos basados en el diámetro a distintas alturas sobre el fuste son confiables para estimar el volumen fustal, ya que emplean la primera parte de la ecuación; la razón de volumen a partir de la segunda parte; y el volumen comercial cuando se utiliza de forma conjunta en las dos especies estudiadas. Lo anterior es una ventaja muy significativa, si se compara con las ecuaciones generadas hace más de 30 años para estimar el volumen de fuste limpio o volumen fuste total para árboles de grandes dimensiones, lo cual no corresponde a los diámetros que se aprovechan hoy en día. Con las estructuras matemáticas propuestas por taxón, es factible construir tablas de distribución de productos para proyectar los rendimientos maderables de áreas bajo aprovechamiento forestal, acorde a las condiciones actuales de Bursera simaruba (chakáh) y Metopium brownei (chechem negro) en bosques tropicales localizados en el centro y sur del estado de Quintana Roo, México.
Es necesario realizar este tipo de estudios en Quintana Roo para, al menos, las 30 especies más importantes desde el punto de vista comercial.











 texto en
texto en 



