Introduction
During the last century, water consumption has widely grown with increasing population growth. Around the world, a significant amount of wastewater is discharged daily into rivers, lakes, and oceans [1-3]. In the developed countries, the industries are the largest consumers of water, while in the developing countries, the agricultural sector is the largest consumer of water [4]. Industrial wastewater, leads to environmental problems and threatens the health of humans, due to its toxic nature, including organic compounds and heavy metals [5-7].
Car wash stations enter a large amount of contaminated wastewater into a municipal sewage cycle [8]. This wastewater contains pollutants such as detergents, grease, oils, heavy metals and organic matter which increase the amount of Biological Oxygen Demand (BOD) and Chemical Oxygen Demand (COD) in the wastewater [9]. Therefore, the treatment of this wastewater is necessary before entering urban sewage. Furthermore, the return of water from wastewater treatment to the consumption cycle reduces water consumption during the washing process at the car wash.
Various methods such as flocculation [9], membrane filtration [10], adsorption [10], biological treatment [9] and chemical oxidation [11] have been used for the treatment of car wash wastewaters(CW). The limitations in these processes and operations can be eliminated by the use of alternative methods. In the recent years, Advanced Oxidation Processes (AOP) have attracted the attention of researchers [12]. These AOPs operate on the basis of the production of oxidants such as hydroxyl radical. Hydroxyl radical is able to decompose organic pollutants during a short and non-selective contact [13-15]. In the end, organic matter decomposes into non-toxic compounds such as water and carbon dioxide when exposed to hydroxyl [16-18]. The most commonly used AOP is the Fenton process. In the Fenton reaction and in acidic conditions, electron transfer between ferrous ions (Fe2+) and H2O2 leads to hydroxyl radical production (Eq. 1) which plays a main role in reducing COD [19, 20]:
Electrochemical Advanced Oxidation Processes (EAOP) can use electricity to produce hydroxyl radical [21]. The most popular process among EAOPs is the electro-Fenton (EF) process because it uses electricity as an eco-friendly source of energy. Cost-effectiveness and simplicity of operation are the other advantages to make EF suitable for wastewater treatment [22,23]. The EF process which is a combination of Fenton and electro-coagulation processes has a high impact in treating hazardous and organic pollutants [24]. In this process with in situ production of hydroxyl radical as the second most powerful oxidizing species (E˚=2.8V) is able to oxidize organic pollutants to inorganic ones (Eqs. 2 and 3).
So, an EF process was employed for the treatment of a real CW. The effect of main independent variables [such as reaction time, current density, pH, H2O2/Fe2+ molar ratio and volume ratio of H2O2/CW (mL/L)] was studied on Chemical Oxygen Demand (COD), Biological Oxygen Demand (BOD5), Total Organic Carbon (TOC), Total Suspended Solids (TSS), heavy metals, Electrical Conductivity (EC), surfactants and hardness (as water quality parameters) removal from CW using iron electrodes. A statistical method was used to optimize these parameters [25]. In order to maximize COD and the other water quality parameters removal, Box-Behnken design (BBD) and response surface methodology (RSM) were used to design the experiments and optimize the operating conditions [26]. In fact, the electro-Fenton process can be applied when there are large amounts of COD in wastewater and BOD5/COD ratio is less than one [24]. Furthermore, a car wash wastewater is containing huge amounts of sands and suspended solids which assist the electro-Fenton process that is based on the flocculation and coagulation.
Experimental
Materials and methods Wastewater sampling and characteristics
The wastewater used in this study was collected from a local car wash station (Sadaf Car wash, Malayer, Iran). The samples were collected over a week (9-11 a.m. of every day). 20 L of the car wash station was prepared and stored in a plastic container. The container was transported to Arak University Chemical Engineering Research Lab and stored at 4 °C before further analysis. According to the analysis done by the Oil Industry Health Center on this wastewater, the initial quality characteristics of wastewater were reported in Table 1. The pH can be adjusted by 0.1 M H2SO4 and 0.1M NaOH (supplied by Merck Co., Quebec, Canada) for each experiment. Since the wastewater cannot pass the environmental protocol, it should be treated. Moreover, BOD5/COD ratio is less than 1 (≈0.34). Therefore, the EF process as a rapid, easy and efficient one is suggested [28].
Experimental set-up
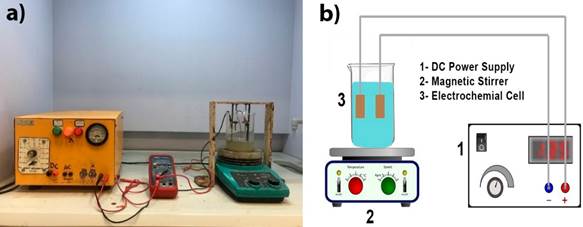
The experimental set-up main parts are DC power supply, digital magnetic mixer, 400 mL cell as the reactor and two parallel plate iron electrodes in a rectangular shape with total surface of 1cm2, where the spacing between them was 3 cm (Fig. 1). In each run, 150 cm3 of CW was taken and its pH was measured using a pH meter (METTLER-TOLEDO 320, Ohio, US). The pH meter was calibrated with the standard buffers kit (supplied by Merck Co.) at the room temperature (25 ± 2 °C) before each analysis. A desired amount of ferrous salt (FeSO4.H2O) and hydrogen peroxide (H2O2) were added to the cell before turning on the DC power supply.
Then, the electrodes were connected to a constant potential difference that was provided from a DC power supply (30 V and 10 A). The stirrer speed was fixed at 400 rpm (without observing vortex formation). All experiments were carried out at room temperature (25 ± 2 °C) and atmospheric pressure.
The power source was turned off when the reaction time was obtained. Then, the solution was left around 30 min for sedimentation of suspended solids. After each run, the electrodes were cleaned with distilled water to remove any sludge residues on the surfaces. Then, the sample was placed in a calibrated UV-Vis spectrophotometer (HACH, US) and analyzed in terms of COD at wavelength of 276 nm [28]. For the other water quality parameters, all samples were sent to Reliable Environmental Lab of Arak city and they were carefully analyzed (in terms of each water quality parameter) by special techniques and devices.
Design of experiments
The Design Expert software (version 10.0.0) was applied for the experiments design. As shown in Table 2 five independent variables including reaction time (X1), current density (X2), pH (X3), volume ratio of H2O2/CW mL/L (X4) and H2O2/Fe2+ molar ratio (X5) with three level full factorial Box-Behnken response surface experimental designs were used. Therefore, forty seven experiments were designed [27, 28]. The goal of this study was to find the optimized operating conditions for maximizing the COD removal percentage (Y%) as a main factor in the water quality consideration.
Table 2 Independent variables and their levels
| Variable | Factor | Coded factors | ||
|---|---|---|---|---|
| -1 | 0 | +1 | ||
| Reaction time (min) | X1 | 15 | 50 | 85 |
| Current density (mA/cm2) | X2 | 20 | 50 | 80 |
| pH | X3 | 2 | 3.5 | 5 |
| H2O2/wastewater (mL/L) | X4 | 0.3 | 1.4 | 2.5 |
| H2O2/Fe2+ | X5 | 0.5 | 2.75 | 5 |
Removal percentage calculated by the following equation:
where, Ci and C0 are initial and final concentrations, respectively. Table 3 shows experimental matrix design obtained by the software.
Table 3 Experimental matrix design and COD data
| Run | Reaction time (min) |
Current density (mA/cm2) |
pH | H2O2/wastewater (mL/L) |
H2O2/Fe2+ molar ratio |
COD Removal (%) | ||
|---|---|---|---|---|---|---|---|---|
| Predicted | Actual | |||||||
| 1 | -1 | +1 | -1 | -1 | -1 | 24.31 | 24.84 | |
| 2 | +1 | +1 | +1 | -1 | +1 | 36.09 | 36.10 | |
| 3 | +1 | -1 | -1 | -1 | +1 | 32.79 | 33.40 | |
| 4 | 0 | 0 | +1 | 0 | 0 | 52.66 | 53.16 | |
| 5 | -1 | +1 | +1 | -1 | +1 | 20.06 | 20.32 | |
| 6 | -1 | 0 | 0 | 0 | 0 | 51.0 | 50.23 | |
| 7 | +1 | +1 | -1 | -1 | +1 | 47.94 | 48.31 | |
| 8 | -1 | -1 | +1 | +1 | -1 | 17.28 | 17.83 | |
| 9 | -1 | +1 | +1 | +1 | -1 | 34.27 | 33.95 | |
| 10 | 0 | 0 | 0 | +1 | 0 | 59.41 | 59.25 | |
| 11 | -1 | -1 | +1 | +1 | +1 | 16.11 | 16.83 | |
| 12 | 0 | 0 | 0 | 0 | 0 | 63.26 | 63.15 | |
| 13 | +1 | +1 | -1 | +1 | +1 | 57.43 | 56.71 | |
| 14 | -1 | +1 | +1 | +1 | -1 | 22.00 | 22.31 | |
| 15 | -1 | +1 | +1 | +1 | +1 | 26.28 | 25.20 | |
| 16 | +1 | +1 | +1 | -1 | -1 | 27.96 | 27.70 | |
| 17 | 0 | 0 | 0 | 0 | 0 | 63.26 | 63.85 | |
| 18 | +1 | +1 | -1 | +1 | -1 | 43.35 | 43.98 | |
| 19 | -1 | -1 | -1 | +1 | -1 | 20.65 | 19.75 | |
| 20 | -1 | +1 | +1 | -1 | -1 | 18.12 | 18.25 | |
| 21 | 0 | +1 | 0 | 0 | 0 | 59.53 | 59.60 | |
| 22 | -1 | -1 | -1 | +1 | +1 | 23.10 | 23.53 | |
| 23 | +1 | -1 | +1 | -1 | +1 | 24.59 | 23.87 | |
| 24 | 0 | 0 | 0 | 0 | 0 | 63.26 | 63.98 | |
| 25 | 0 | 0 | -1 | 0 | 0 | 60.28 | 59.23 | |
| 26 | -1 | +1 | -1 | +1 | -1 | 29.03 | 28.93 | |
| 27 | +1 | -1 | +1 | +1 | -1 | 28.12 | 27.53 | |
| 28 | +1 | -1 | -1 | +1 | +1 | 42.18 | 41.98 | |
| 29 | 0 | 0 | 0 | 0 | -1 | 52.99 | 52.37 | |
| 30 | 0 | 0 | 0 | 0 | 0 | 63.26 | 64.05 | |
| 31 | 0 | 0 | 0 | -1 | 0 | 52.77 | 52.38 | |
| 32 | 0 | 0 | 0 | 0 | 0 | 63.26 | 63.48 | |
| 33 | 0 | -1 | 0 | 0 | 0 | 49.60 | 48.98 | |
| 34 | -1 | -1 | +1 | -1 | +1 | 10.00 | 10.28 | |
| 35 | +1 | 0 | 0 | 0 | 0 | 65.95 | 66.67 | |
| 36 | +1 | -1 | +1 | +1 | +1 | 33.14 | 32.71 | |
| 37 | +1 | +1 | -1 | -1 | -1 | 36.19 | 35.41 | |
| 38 | -1 | -1 | +1 | -1 | -1 | 13.50 | 12.59 | |
| 39 | +1 | -1 | -1 | +1 | -1 | 33.54 | 34.20 | |
| 40 | +1 | -1 | +1 | -1 | -1 | 21.91 | 22.93 | |
| 41 | -1 | -1 | -1 | -1 | -1 | 16.03 | 17.23 | |
| 42 | -1 | +1 | -1 | +1 | +1 | 36.93 | 37.58 | |
| 43 | -1 | -1 | -1 | -1 | +1 | 16.14 | 15.58 | |
| 44 | -1 | +1 | -1 | -1 | +1 | 29.87 | 29.63 | |
| 45 | +1 | +1 | +1 | +1 | +1 | 44.74 | 45.27 | |
| 46 | 0 | 0 | 0 | 0 | +1 | 58.28 | 58.35 | |
| 47 | +1 | -1 | -1 | -1 | -1 | 26.49 | 25.93 | |
Regression model based on ANOVA and testing
In this paper, correlations between the response function (Y) and the independent variables were obtained by the following second-order quadratic polynomial model [29]:
where, Y is the response. β0 is a constant coefficient. βj, βij and βjj are the coefficients for the linear, quadratic and interaction effects, respectively. Xi and Xj are the coded levels for the independent variables. K is the number of independent variables and ɛ is the random error.
The following equation presents the BBD model for COD removal percentage obtained from the software. In fact, it shows the relation between all responses and operating variables.
where, X1, X2, X3, X4 and X5 are reaction time (min), pH, current density (mA/cm2), H2O2/wastewater volume ratio and H2O2/Fe2+ molar ratio, respectively. The experimental and predicted data (obtained from Eq. 6) for COD are shown in Table 3, as well.
ANOVA analysis
Table 4 shows analysis of variance (ANOVA) for response surface quadratic model terms for COD removal. They will be significant when Prob > F values are less than 0.05. A model can properly predict the response when R2 is close to one. Therefore, X1, X2, X3, X4, X5, X1X2, X1X4, X2X3, X2X4, X2X5, X3X4, X4X5, X12, X22, X32, X42, X52 terms for COD removal were significant and non-negligible terms. There is a good agreement between the predicted data and the experimental ones since the R2 equals to 0.9987 for COD. As the R2, R2 adjusted, R2 predicted amounts are close to one, it can be concluded that regression model is appropriate for this research as illustrated in Table 5 [30].
Table 4 Analysis of variance for response surface quadratic model terms for COD removal.
| Source | Sum of Squares | DF | Mean Square | F-Value | Prob > F |
|---|---|---|---|---|---|
| Model | 13426.70 | 20 | 671.33 | 972.85 | < 0.0001 |
| A | 1776.12 | 1 | 1776.12 | 2573.83 | < 0.0001 |
| B | 839.43 | 1 | 839.43 | 1216.45 | < 0.0001 |
| C | 492.41 | 1 | 492.41 | 713.56 | < 0.0001 |
| D | 374.16 | 1 | 374.16 | 542.21 | < 0.0001 |
| E | 237.81 | 1 | 237.81 | 344.62 | < 0.0001 |
| AB | 4.09 | 1 | 4.09 | 5.93 | 0.0221 |
| AC | 8.41 | 1 | 8.41 | 12.18 | 0.0017 |
| AD | 11.81 | 1 | 11.81 | 17.11 | 0.0003 |
| AE | 76.57 | 1 | 76.57 | 110.96 | < 0.0001 |
| BC | 26.75 | 1 | 26.75 | 38.77 | < 0.0001 |
| BD | 0.021 | 1 | 0.021 | 0.030 | 0.8628 |
| BE | 59.30 | 1 | 59.30 | 85.93 | < 0.0001 |
| CD | 1.42 | 1 | 1.42 | 2.06 | 0.1634 |
| CE | 26.21 | 1 | 26.21 | 37.98 | < 0.0001 |
| DE | 10.95 | 1 | 10.95 | 15.87 | 0.0005 |
| A2 | 50.79 | 1 | 50.79 | 73.60 | < 0.0001 |
| B2 | 186.66 | 1 | 186.66 | 270.50 | < 0.0001 |
| C2 | 113.84 | 1 | 113.84 | 164.97 | < 0.0001 |
| D2 | 126.94 | 1 | 126.94 | 183.95 | < 0.0001 |
| E2 | 143.55 | 1 | 143.55 | 208.03 | < 0.0001 |
| Residual | 17.94 | 26 | 0.69 | ||
| Lack of Fit | 17.37 | 22 | 0.79 | 5.50 | 0.0546 |
| Pure Error | 0.57 | 4 | 0.14 | ||
| Cor Total | 13444.64 | 46 |
Table 5 Quadratic model ANOVA result for COD removal.
| COD Removal | Variable |
|---|---|
| 0.83 | Standard Deviation |
| 38.07 | Mean |
| 0.9987 | R2 |
| 0.9976 | R2 adjusted |
| 0.9952 | R2 predicted |
| 2.18 | Coefficient of variance (C.V) |
| 64.74 | Press |
| 100.773 | Adequate precision |
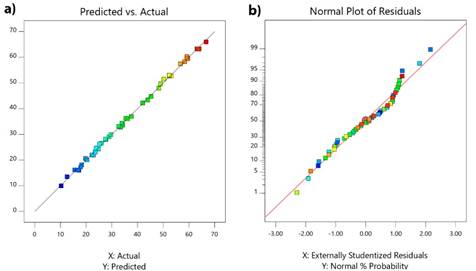
The ANOVA for COD showed that F-value is 972.85 for the quadratic model. Furthermore, the large F-value indicates that the most of variation in the response can be explained by the regression model [30]. The prob> F-value (<0.05) expresses that model terms are significant, as well [30, 31]. The coefficient of variance (CV) (as the ratio of the standard error of estimated data to the mean value of the observed response) is a normative of the model reproducibility [30, 32]. The adequate precision (AP) measures the signal to noise ratio (>4 is desirable) and AP was compared for the range of the predicted values at the design points to the average prediction error [30, 31]. For the present research, signal to noise ratios were around 100.773 for COD. The adequacy of developed mathematical models to the experiment was examined by the diagnostic plots such as predicted plot versus actual one (Fig. 2(a)) and normal percent probability graphs (Fig. 2b). According to Fig. 2 (a) and (b), the actual values are very close to the predicted ones because actual values were distributed near the straight line. These plots state that there is a very good agreement between the observed data and the correlated ones obtained from the models.
Three dimensional plots for the regression model
The effects of the independent variables on COD removal were graphically represented by three dimensional response surface plots (Fig. 3). The response surface plots are shown to visualize the effects of the experimental independent variables on the COD removal (as response). In fact, three dimensional plots show strong interaction between parameters and surfaces.
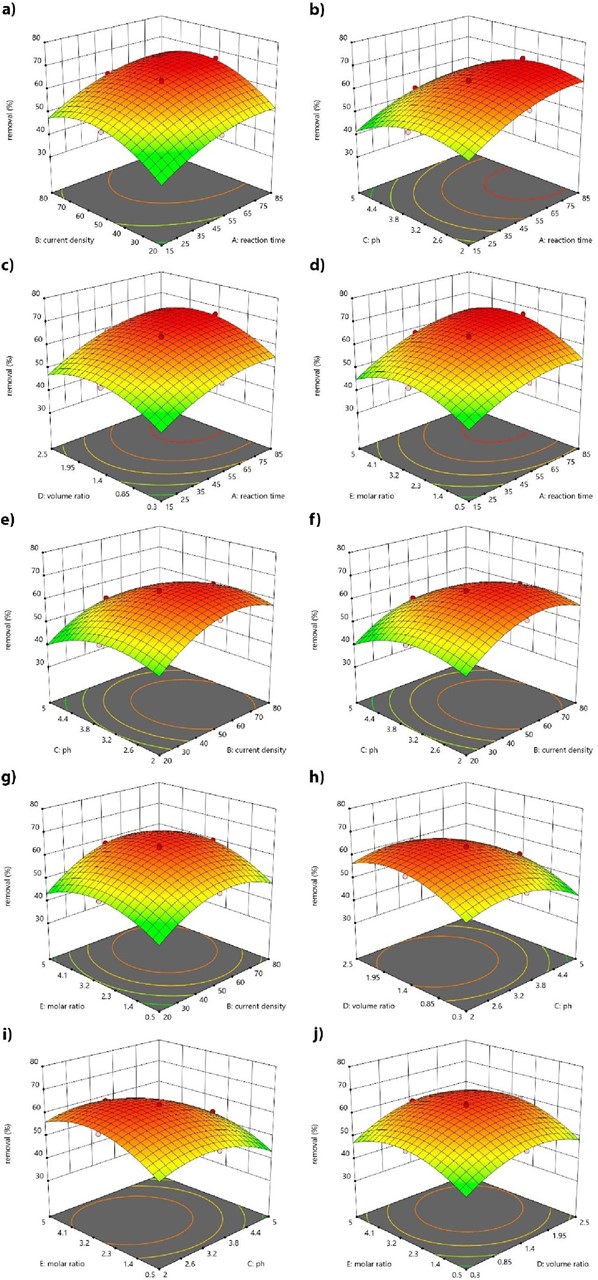
Fig. 3 Three-dimensional surface of COD removal (as a water quality sample) as a function: (a) reaction time and current density, (b) reaction time and pH, (c) reaction time and H2O2/CW (mL/L), (d) reaction time and H2O2/Fe2+, (e) current density and pH, (f) current density and H2O2/CW (mL/L), (g) current density and H2O2/Fe2+, (h) pH and H2O2/CW (mL/L), (i) pH and H2O2/Fe2+, (j) H2O2/CW (mL/L) and H2O2/Fe2+.
Effect of pH
The pH is one of the most important parameters for the EF process because it controls the hydroxyl radical formation [33]. In fact, hydroxyl radical formation can be expected to play a significant role during the EF reaction. The COD changes with pH are shown in Figs. 3(b), 3(e), 3(h) and 3(i). It affects the ferrous ions speciation and hydrogen peroxide decomposition. The ferrous ions precipitate when pH increases. In fact, it inhibits the ferrous ions regeneration. Therefore, the Fenton reaction rate decreases. Moreover, hydrogen peroxide cannot be decomposed to hydroxyl radical by Fe2+ when pH is less than two. It seems that hydrogen peroxide is changed to H3O2 + by capturing one proton. Since H3O2 + is an electrophilic compound, hydrogen peroxide and Fe2+ reaction rate will be decreased. The highest COD removal (66.67%) was obtained at pH of 3.5 [34-37]. The Fenton's reaction in the bulk of solution was promoted when the produced hydrogen peroxide reacted with Fe2+. Furthermore, the hydroxyl radicals generated at the reaction increase [34,38,39].
Effect of current density
The current density is directly related to COD removal. The effect of current density (20-80 A/m2) on COD removal are shown in Figs. 3(a), 3(e) 3(f) and 3(g) [30,40]. The COD removal increases with increasing the current density. In fact, this is due to increasing ferrous ions regeneration from ferric ions at cathode in high current densities. It then enhances the Fenton reaction and increases the hydroxyl radical generation at the anode surface [41]. Moreover, the removal will be decreased after a certain point of current density. This may due to the competitive reactions in the cell. The oxygen production on anode and the hydrogen production on cathode occur at high current densities.
Effect of reaction time
The effect of reaction time on COD removal is shown in Figs. 3(a), 3(b), 3(c) and 3(d). The COD removal increases, and it reaches a maximum value of 66.67% at reaction time of 85 min. It seems that the reaction time of 85 min is enough for the COD removal. This is due to large amount of hydrogen peroxide production which causes H2O2 decomposition to oxygen and water. Moreover, combination of hydroxyl radicals decreases their concentration in the solution [30].
Effects of H2O2/Fe2+ molar ratio and volume ratio of H2O2/CW
According to Figs. 3(c), 3(f), 3(h) and 3(j), COD removal increased with H2O2 amount increment. On the other side, the molar ratio is a significant factor in the EF process which directly affects on the economical aspects of the process. Effects of H2O2/Fe2+ molar ratio on the COD removal are shown in Figs. 3(d), 3(g), 3(i) and 3(j). It can be observed that increasing the H2O2/Fe2+ molar ratio increases the amount of COD removal, as well [42].
As shown in these figures, hydroxyl radicals are decomposed by excessive hydrogen peroxide. In this side reaction, hydrogen peroxide and hydroxyl radical react and a weaker oxidant (hydroperoxyl radical) is produced (Eq. 7) [28,40].
Optimization and validation
Numerical optimization was done to find the maximum value of COD and the other water quality parameters removal. The optimum conditions were statistically obtained at reaction time of 75.80 min, current density of 58.81 mA/cm2, pH of 3.02, volume fraction of H2O2/CW of 1.62(ml/ l) and H2O2/Fe2+ molar ratio of 3.66 for 65.26% COD removal (predicted one). The optimized operating condition values for all water quality parameters were reported in Table 6, as well. Furthermore, the experimental data for validation of the optimization procedure were illustrated in Table 7. For example, for COD removal, the experimental percentage was around 68.72% (observed one) that was close to the predicted value with an error of 5%. A very good agreement between experimental optimum data and statistical ones was observed. Moreover, the final treated wastewater pH was at 6.80.
Table 6 Optimized operating data obtained from the software for all water quality parameters.
| Water quality parameter |
Operating Parameters | ||||
|---|---|---|---|---|---|
| Reaction time (min) |
Current density (mA/cm2) |
pH | H2O2/wastewater (mL/L) |
H2O2/Fe2+ molar ratio |
|
| COD | 75.80 | 58.81 | 3.02 | 1.62 | 3.66 |
| BOD5 | 60.20 | 75.14 | 2.88 | 2.02 | 2.79 |
| TOC | 80.05 | 66.12 | 3.56 | 1.25 | 3.65 |
| TSS | 69.44 | 55.36 | 2.94 | 2.14 | 2.94 |
| Heavy metals | 74.36 | 76.80 | 2.69 | 1.07 | 3.26 |
| EC | 82.30 | 70.05 | 3.14 | 1.85 | 3.78 |
| Surfactants | 68.88 | 61.55 | 3.66 | 1.53 | 2.80 |
| Hardness | 78.66 | 44.14 | 3.00 | 1.66 | 3.60 |
Conclusion
The EF process as an efficient, simple and eco-friendly technique was proposed for the treatment of a real CW. However, the dissolved organic pollutants are mineralized in inorganic sludge during the electro-Fenton process and abundance of suspended solids facilitates the mineralization process but, formation of an impermeable film layer may reduce the reduction of Fe3+ on the cathode and reduce the process efficiency. ANOVA showed good coefficient of determination values (R2 > 0.99) for the correlation. According to the analysis, reaction time had a very significant effect on the COD removal. Since CW COD reduced to 143.88 mg/L (at the optimum conditions), a series of EF process or another supplementary treatment (applicable for lower COD values such as biological treatment) is requested for lower COD values than this however it properly satisfies the environmental standards.











 nueva página del texto (beta)
nueva página del texto (beta)