Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Journal of the Mexican Chemical Society
versión impresa ISSN 1870-249X
J. Mex. Chem. Soc vol.56 no.3 Ciudad de México jul./sep. 2012
Artículo
Rate Constants and Branching Ratios in the Oxidation of Aliphatic Aldehydes by OH Radicals under Atmospheric Conditions
Romina Castañeda,1 Cristina Iuga,2 J. Raúl Álvarez-Idaboy1 and Annik Vivier-Bunge3,*
1 Facultad de Química, Departamento de Física y Química Teórica, Universidad Nacional Autónoma de México, México DF 04510, México.
2 Departamento de Ciencias Básicas, Universidad Autónoma Metropolitana-Azcapotzalco.
3 Departamento de Química, Universidad Autónoma Metropolitana-Iztapalapa, 09340 México D. F., México.
Received January 06, 2012.
Accepted April 26, 2012.
Abstract
In this work, a theoretical study is presented on the mechanism of OH reactions with C1-C5 aliphatic aldehydes. We have shown that, starting from butanal, the Cβ H-abstraction channel becomes relatively important and it contributes moderately to the total rate constant. Calculated overall rate coefficients at the CCSD(T)/6-311++G**//BHandHLYP/6-311++G** level are in excellent agreement with experimental data, supporting the proposed mechanisms. Negative activation energies are found to be in agreement with the temperature dependence observed for aldehydes. The branching ratio between the aldehydic and Cβ hydrogen abstraction is not significantly modified as temperature increases from 230 to 330 K.
Key words: Radical-Molecule Reactions, Atmospheric Reactions, Reaction, Mechanism, Negative Activation Energy, Reactant Complexes.
Resumen
En este trabajo se presenta un estudio teórico del mecanismo de las reacciones de radicales OH con aldehídos alifáticos de uno a cinco carbonos. Mostramos que, a partir del butanal, el camino de abstracción del átomo de hidrógeno unido al Cβ se vuelve relativamente importante y contribuye moderadamente a la constante de velocidad total. Las constantes calculadas con el método CCSD(T)/6-311++G**//BHandHLYP/6-311++G** reproducen perfectamente los datos experimentales, respaldando así el mecanismo propuesto. Se obtienen energías de activación negativas, en acuerdo con la dependencia anti-Arrhenius observada experimentalmente. La proporción entre las constantes de velocidad para las abstracciones aldehídica y del Cβ no se modifica apreciablemente al aumentar la temperatura de 230 a 330 K.
Palabras clave: Reacciones radical-molécula, reacciones atmosféricas, mecanismos de reacción, energía de activación negativa, complejos pre-reactivos.
Introduction
Aliphatic aldehydes play an important role in atmospheric and environmental sciences due to their high reactivity and to their large concentration in the troposphere, especially in urban and industrial areas. These oxygenated compounds are important in the formation of photochemical smog and of secondary pollutants, such as peroxyacetyl nitrate (PAN) and tropospheric ozone [1]. Photodissociation of aldehydes may also represent an important source of free radicals in the lower atmosphere, and thus may significantly influence the atmospheric oxidation capacity [2].
The gas phase aldehyde + OH reaction has been widely studied by experimental techniques [3, 4] as well as by theoretical methods [5, 6]. According to the chemical kinetics database supported by the National Institute of Standards and Technology (NIST) (http://kinetics.nist.gov/index.php), there are many experimental measurements of the rate constant for the low molecular mass aldehydes + OH. They fall in a small range between 1 and 3 × 10-11 cm3 molecule-1 s-1 and increase slightly with the length of the alkyl group [7, 8, 9].
The rate constant for the OH reaction with formaldehyde is virtually independent of temperature in the region of atmospheric relevance, while higher aldehydes show a slightly negative temperature dependence [10]. Negative activation energies have been adequately explained in terms of a complex reaction mechanism involving the initial formation of a pre-reactive complex [6].
In principle, aliphatic aldehydes may react with an OH radical through any one of the following reaction paths:
(i) abstraction of the formyl hydrogen atom and subsequent formation of a water molecule and an acyl radical:
RCHO + •OH → RCO• + H2O
(ii) hydrogen atom abstraction from one of the alkyl chain C-H bonds:
RCHO + •OH → •RCHO + H2O
or (iii) addition of an OH radical to the C=O double bond, with formation of the corresponding hydroxyl-acyl adduct radical:
RCHO + •OH → R•CHO(OH)
The available kinetic and mechanistic data show that the reaction of OH radicals with small aldehydes proceeds predominantly by H-atom abstraction from the -CHO group (reaction path (i)). In general, hydrogen atom abstraction from the C-H bonds of the alkyl chain is considered to be of minor importance. Addition to the C=O bond (iii) does not occur.
Although it is clear that formaldehyde and acetaldehyde react exclusively by aldehydic hydrogen abstraction, as the alkyl chain size increases the possibility of hydrogen abstraction from other chain carbon atoms may become relevant. Knowledge of branching ratios for these alternative pathways is important, as they yield different products. Moreover, branching ratios depend on temperature. In the troposphere, one of the most significant meteorological impacts in modeling ozone concentrations is the temperature reduction with altitude, which alters chemical reaction rates. Thus, the use of overall rate coefficient expressions that take into account all possible pathways as a function of temperature permits simulations over a wide range of temperatures for urban, rural and remote regions, as well as for different seasons, and the evaluation of the impact of these aldehydes in PAN and ozone formation.
In this work, all abstraction pathways have been considered, and branching ratios have been evaluated in the 230-330 temperature range for C3 to C5 aldehydes. Corresponding data for formaldehyde and acetaldehyde have been obtained with the same methodology for comparison purposes.
Computational Methodology
Electronic structure calculations have been performed with the Gaussian 09 program package, within the density functional theory framework. We have used the BHandHLYP functional, which has previously been tested to model complex reactions, and which has been shown to provide [11-14] excellent geometries.
Unrestricted calculations were used for open shell systems. Frequency calculations were performed for all the stationary points at the same level of theory as the geometry optimization and local minima and transition states were identified by the number of imaginary frequencies. It was verified that the atomic motion along the reaction coordinate corresponds to the expected transition vector. Corrections for zero-point energy (ZPE) (residual vibrational energy at 0 K) were obtained from the force constant analysis and were added to the total energies. Intrinsic Reaction Coordinate (IRC) [15] calculations were also performed to confirm that the transition state structures properly connect reactants and products.
In this work, we have used a procedure that has become common in the study of the stationary points of chemical reactions of polyatomic systems because it is relatively inexpensive from a computational point of view and it usually reproduces correctly the main features of the reaction path. It is known as B//A approach, and it consists of geometry optimizations at a given level (A) followed by single point calculations, without optimization, at a higher level (B). Based on our previous experience [11-14], the use of a B//A approach at the CCSD(T)// BHandHLYP level of theory properly describes the energetic and kinetic features of VOCs + OH hydrogen abstraction reactions. It should be emphasized that a possible error of ~ 1 kcal/ mol on the computed critical energies implies an uncertainty in the predicted rates of a factor of ~ 10 at temperatures of interest in atmospheric chemistry. In addition, for this kind of reaction it has been proved [16] that the differences in geometries between several DFT methods compared to CCSD and QCISD are minimal for BHandHLYP. We have used it in combination with the 6-311++G(d,p) basis set [17] that is large enough to yield a good description of hydrogen-bonded complexes and transition structures involving hydrogen transfer, such as the ones considered in this work.
The calculated rate constants were obtained using conventional Transition State Theory (CTST) [18, 19]. Tunneling corrections were determined using the Eckart asymmetrical barrier as implemented in The Rate program at the Computational Science and Engineering Online website (www.cseo.net) [20].
Result and discussion
The mechanism for gas phase radical-molecule reactions is well established [6]. It involves the formation of a pre-reactive complex that is in equilibrium with the separated reactants, followed by the irreversible formation of the products:

In the pre-reactive complexes, (RC) the OH free radical approaches the aldehyde molecule guided mainly by the Coulomb interaction between the positively charged hydrogen atom of the OH radical and a lone electron pair on the aldehyde oxygen atom. Then, the oxygen of OH leans towards the hydrogen to be abstracted, as the energy increases to a maximum at the transition state (TS). A product-complex (PC) is obtained, which, in the next step, yields the final products, i. e., a water molecule and the corresponding free radical.
In principle, in aliphatic aldehydes, there are three important types of H-abstraction sites: the carbonylic and the α and β sites. Formaldehyde and acetaldehyde are special cases in the aliphatic aldehydes series. In the case of formaldehyde, only aldehydic hydrogen atoms are available while, in acetaldehyde, a H-methyl abstraction is also possible. In the larger aldehydes, all three channels may occur.
In the present work, all abstraction pathways in C1 to C5 aldehydes have been considered. The minimum energy path MEP was computed using the two-level theory approach CCSD(T)//BHandHLYP with the 6-311++G(d,p) basis set. Results have been grouped according to the type of H atom that is being abstracted.
Geometries and energies
Aldehydic H-abstraction
In the aldehydic H-abstraction reaction pathway, the pre-reactive complex structures are stabilized by two main interactions: (i) the OH radical hydrogen atom with the carbonyl oxygen, and (ii) the OH radical oxygen atom with the aldehydic H atom. The first one is a hydrogen bond, while the second one is a very weak interaction that occurs at more than 3.6 A. All pre-reactive complexes for this type of path have very similar shapes.
In the transition states, these interactions are inverted, the distance between the OH radical hydrogen atom and the car-bonyl oxygen is larger, while the OH radical oxygen atom approaches the aldehydic H atom at a hydrogen bond distance. A frequency analysis of the transitions state structures indicates that the vibration mode corresponding to the imaginary frequency is essentially the characteristic H atom motion between the Cald and Ooh atoms, and that there is little heavy atom motion as the system moves along the reaction path. Finally, a water molecule separates from the system and an organic radical is formed. In Figure 1, the BHandHLYP/6-311++G** optimized molecular structures for pre-reactive complexes and transition states in the C1-C5 aliphatic aldehydes are represented.
α and β H-abstraction
Starting from ethanal, an a hydrogen abstraction is also possible. In the ethanal minimum energy structure, one of the methyl hydrogens lies in the molecular plane. In principle, this hydrogen is slightly different than the other two methyl hydrogens, and thus, two types of reaction paths should be considered. We have calculated these reaction paths and found that, although abstraction of off-plane hydrogens is slightly favored in terms of Gibbs free energy, rotation of the methyl group is sufficiently free that all methyl hydrogen atoms are almost equivalent. The same argument can be used for α and β H-abstraction in propanal, butanal and pentanal. In Figure 2 we show the optimized structures of the pre-reactive complex and of both types of a transition structures in acetaldehyde. The TS al structure corresponds to the in-plane H-abstraction, while TS α2 corresponds to the two off-plane H-abstractions. In TS α1, the hydrogen atom of the OH radical interacts with the carbonylic oxygen of the acetaldehyde molecule. Even though, in TS α2, the hydrogen atom of the OH radical and the carbonylic oxygen of the acetaldehyde molecule do not interact, this is an early transition state structure that presents a lower barrier, in terms of Gibbs free energy, than TS α1. Thus TS α2 has been used in the rate constant calculation.

Also, the TS α2 transition structure resembles the corresponding α H-abstraction structures in propanal, butanal and pentanal. In Figure 3, transition structures in α H-abstraction reactions from C3-C5 aliphatic aldehydes by OH radicals are shown.

For aldehydes whose alkane chains have three or more carbon atoms, both α and β hydrogen abstractions are possible. In propanal, a pre-reactive complex structure is observed in which the OH radical oxygen atom is oriented towards a terminal methyl hydrogen, while in larger aldehydes (butanal and pentanal) the OH radical oxygen atom is oriented towards a β H atom of the aliphatic chain. The fully BHandHLYP/6-311++G** optimized geometries of the β pre-reactive complexes and the corresponding transition structures for C3-C5 aliphatic aldehydes are shown in Figure 4. The main bond distances are indicated.
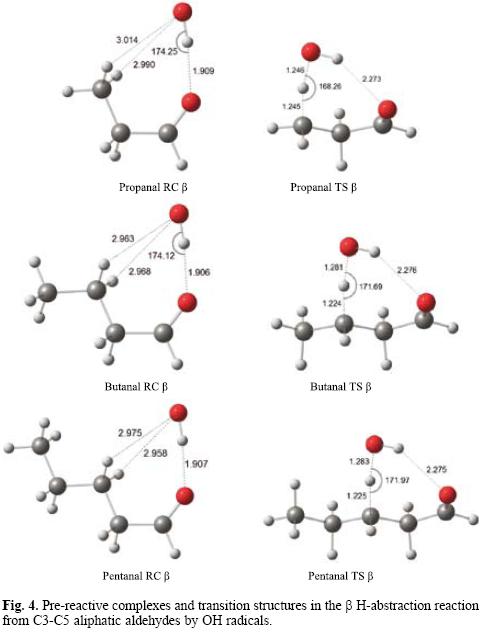
In butanal and pentanal, hydrogen atoms attached to C4 and C5 can also be abstracted in principle, but they will not be considered here, as it is well known that they are not relevant. From the geometries shown in Figure 3, it is clear that transition states involving carbon atoms that are too far from the aldehydic group should be much less favored.
Energies
Relative electronic energies (including ZPE corrections) and Gibbs free energies calculated for the stationary points involved in the hydrogen atom transfer (HAT) by •OH radicals are reported in Table 1. In this table, relative energies are calculated relative to the separated reactants. ΔE1 is the pre-reactive complex stabilization energy, which is calculated as ΔE1=ERC-ER; ΔE≠ is the transition state energy, ΔE≠ = ETS-ER; and ΔE is the reaction energy, ΔE = EP- ER. Analogously, ΔG1 = GRC-GR, ΔG≠ is the effective free energy of activation, ΔG≠ = GTS - GR, and ΔG is the reaction free energy ΔG = GP - GR.

The pre-reactive complexes stabilization energies E1 are very similar among themselves and quite independent of the type of reaction path, i. e, in all cases (except formaldehyde), these energies are about 4 kcal/mol. This is not surprising as all of them involve the same type of hydrogen bond and van der Waals interactions. Corresponding free energies are positive on account of the rather large decrease in entropy when the two molecules interact.
The results in Table 1 show that the largest energy barrier corresponds to formaldehyde. This is in agreement with experimental results. The inductive effect of the carbon chain on the carbonyl group tends to favor the aldehydic hydrogen abstraction in larger aldehydes.
The effective activation energies are negative, in all cases, for the aldehydic H-abstraction path. It is also negative for β H-abstraction in butanal and pentanal. Although the energy barriers are about 1 kcal/mol larger than for aldehydic H-adsorption, it is clear that this channel cannot be ruled out entirely for aldehydes with 4 or more carbon atoms. The branching ratios will be calculated in the next section in terms of the respective reaction rates.
Also, the energy barrier for α H-abstraction is consistently much larger than for β abstraction. In all cases, Ea decreases slightly with the chain length. However, the radicals formed after α H-abstraction are much more stable than those obtained after β H-abstraction, because, in the former, the unpaired electron can delocalize over the carbonyl double bond. This is valid for all α H-abstractions in aldehydes.
The aliphatic saturated chain is very stable, and remains linear in the reaction mechanism.
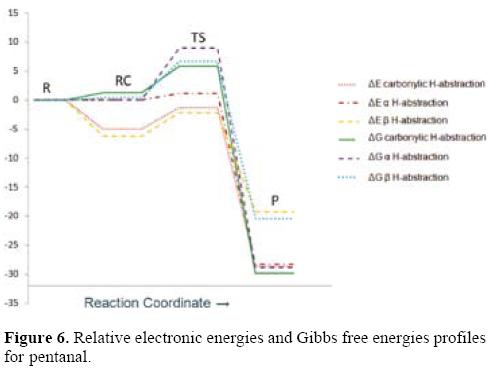
Energy profiles for pentanal are shown in Figure 6. For the aldehydic H-abstraction pathway, the energy profiles show that all the studied stationary points are lower in energy than the corresponding reactants.
Kinetics
Using the steady-state approximation the equation of the classical apparent rate constant is the same as the corresponding equation ignoring the pre-reactant complex, however, the tunneling correction depends on the actual height of the barrier, and it can be significantly larger if the pre-reactant complex is included in the mechanism. Thus, in this work, all abstraction reactions were assumed to be complex (for more details see ref. [6, 21-24]).
The steady state approximation can be used in this mechanism only if the reactant complex does not accumulate, i.e. if (k-1 + k2) > k1. In fact for most atmospheric reactions the enthalpy of complexation is smaller than the associated entropy loss, and the reactant complex has a higher Gibbs free energy than the isolated reactants (Figure 1). It means that KP = k1/k-1 is < 1, and k-1 > k1. Therefore, the steady state approximation applies, regardless of the k2 value.
According to the proposed mechanism, if k1 and k-1 are the forward and reverse rate constants for the first step and k2 corresponds to the second step, a steady-state analysis leads to a rate coefficient for each overall reaction path that can be written as:

Although the energy barrier for k-1 is in the same magnitude order that one for k2, the entropy change is much larger in the reverse reaction than in the formation of products. Hence, following the hypothesis proposed by Singleton and Cvetanovic [20] k2 is expected to be much smaller than k-1. Based on this assumption, k can be rewritten as:

where E1 and E-1 correspond to the energy barriers of the forward and reverse directions for the Step 1, respectively; E2 is the barrier for Step 2, and the A's are the partition functions. Since E1 is zero, the apparent energy barrier for the overall reaction channel is:

where ETS, ERC and ER are the total energies of the transition state, the reactant complex and the reactants, respectively. Considering basic statistical thermodynamic principles, the equilibrium constant (k1/k-1)of the fast pre-equilibrium between the reactants and the reactant complex may be obtained as:

where QRC and QR represent the partition functions of the reactant complex and the isolated reactants, respectively.
Under sufficiently high-pressure conditions, such as normal conditions in the troposphere, an equilibrium distribution of reactants is maintained and the CTST formula can be applied [25] to calculate k2:

where κ2 is the tunneling factor, kB and h are the Boltzmann and Planck constants, respectively, and QTS is the partition function of the transition state. The energy differences include the ZPE corrections. The effective rate coefficient of each channel is then obtained as:

where σ is the symmetry factor that is related to the reaction path degeneracy. The symmetry factor is obtained by imaging all identical atoms to be labeled and by counting the number of different but equivalent arrangements that can be made by rotating the molecule.
The rate constants for all the studied reactions have been determined using Transition State Theory. In all cases the complex mechanism, Eqs. 1 and 2, has been considered. The energy values, partition functions and thermodynamic data were taken from the quantum-mechanical calculations. The effective rate constant is obtained using the following equation:

The tunneling correction κ2 of the second step is calculated according to the Eckart model, with an asymmetric barrier [26]. Eckart transmission coefficients depend on the apparent reaction barrier, on the reaction energy, and especially on the magnitude of the imaginary frequency, υ*, of the vibration along the reaction coordinate. Rate constants were calculated using energies and partition functions based on CCSD(T)/6-311++g**//BHandHLYP/6-311++g** calculations.
The symmetry factor σ accounts for the possibility of more than one symmetry-related reaction path. In bimolecular reactions, the pre-reactive complex determines the path and the symmetry number, and is obtained by counting the number of different but equivalent arrangements that can be made by rotating the molecule. Thus, the symmetry number for the formaldehyde + OH reaction is 2. In the acetaldehyde α H-abstraction and in propanal β H-abstraction, the symmetry number is 3; because of the internal rotation of the -CH3 terminal group, there are three equivalent H atoms that can be abstracted. In butanal and pentanal β H-abstraction, the symmetry number is 2.
The calculated rate constants obtained with the methodology used in this work are reported in Table 2.

The first conclusion that can be drawn from the data of Table 2 is that, starting from butanal, the β H-abstraction becomes quite important and represents a non-negligible percent in the overall reaction rate constant. Thus, it is reasonable to suggest that, for aldehydes larger than pentanal, both abstraction pathways should be considered.
The overall rate constant is obtained by adding the partial rate constants corresponding to all channels. The results are presented in Table 3.


The calculated rate constants are in excellent agreement with the experimental ones, the ratio between experimental and calculated results being less than 2, i.e. the error in the activation free energies is less that 0.41 kcal/mol. Moreover, the trend to increase the rate constant as the number of carbons increases is adequately reproduced by the calculated rate constants.
Branching ratios are calculated according to the following expression:

The overall rate coefficients and branching ratios as a function of T for butanal and pentanal are displayed in Tables 4 and 5, respectively. It can be observed that branching ratios for the aldehydic H-abstraction do not change significantly as a function of the temperature in the range between 238-338 K and represent about 96% of the total reaction for butanal, and 93% for pentanal. As the carbon chain becomes longer it is possible that β H-abstraction become increasingly important.


Conclusions
In this work we have studied the OH radical hydrogen abstraction reaction on C1-C5 aliphatic aldehydes. The BHandH-LYP functional yields an excellent description of the reaction profiles and kinetics for the studied systems. The agreement between experiment and calculations validates the use of the chosen DFT method for kinetic calculations, especially for large systems.
On the basis of the calculated rate constants we conclude that, in the reaction of an OH free-radical with formaldehyde, acetaldehyde, propanal, butanal and pentanal, the rate constant increases with the chain length. For aldehydes with four and more carbon atoms, the chain β H-abstraction contributes between 4 and 6% to the total rate constant and it cannot be neglected, as the products that are formed are different than the ones obtained after an aldehydic H-abstraction. Branching ratios, however, do not change noticeably with temperature.
Negative activation energies are obtained in all aldehydic H-adsorptions and in butanal and pentanal β H-abstraction., meaning that the overall rate constant decreases as temperature increases, in agreement with experimental results. Negative activation energies are rationalized in terms of a complex mechanism that involves the initial formation of a pre-reactant complex which is more stable than the isolated reactants.
Acknowledgments
We dedicate this article to Professor José Luis Gázquez Mateos, distinguished mexican scholar and leader in the field of density functional theory. This work is a result of the FONCICYT Mexico-EU 'RMAYS' network, Project N° 94666. We gratefully acknowledge the Laboratorio de Visualización y Cómputo Paralelo at Universidad Autónoma Metropolitana-Iztapalapa and the Dirección General de Cómputo y de Tecnologías de Información y Comunicación (DGCTIC) at Universidad Nacional Autónoma de México for computer time.
References
1. Atkinson, R. and Arey, J.: Chem. Rev., 2003, 103, 4605-4638 [ Links ]
2. B. J. Finlayson-Pitts, J. N. Jr. Pitts, Chemistry of the Upper and Lower Atmosphere. Theory, Experiments, and Applications, 2000, Academic Press. [ Links ]
3. Atkinson, R.; Baulch, D.L.; Cox, R.A.; Crowley, J.N.; Hampson, R.F, Jr.; Kerr, J.A.; Rossi, M.J.; Troe, J., J. Phys. Chem. Ref. Data, 2000, 29, 167-266 [ Links ]
4. Butkovskaya, N. I.; Setser, D. W. J. Phys. Chem. A 2000, 104, 9428-9435 [ Links ]
5. Francisco, J. S. J. Chem. Phys. 1992, 96, 7597-7602. [ Links ]
6. Alvarez-Idaboy J. R., Mora-Diez N., Boyd R. J., Vivier-Bunge A., J. Am. Chem. Soc, 2001, 123, 2018-2024 [ Links ]
7. Atkinson, R.; Baulch, D.L.; Cox, R.A.; Crowley, J.N.; Hampson, R.F, Jr.; Kerr, J.A.; Rossi, M.J.; Troe, J., IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry Web Version December 2001,1-56, [ Links ]
8. W. B. DeMore, S. P. Sander, D. M. Golden, R. F. Hampson, M. J. Kurylo, C. J. Howard, A. R. Ravishankara, C. E. Kolb, M. J. Molina, Chemical kinetics and photochemical data for use in stratospheric modeling. Evaluation number 12 JPL Publication 1997, 97-4, [ Links ].
9. D'Anna, B.; Andresen, O.; Gefen, Z.; Nielsen, C.J. Phys. Chem. Chem. Phys., 2001 3, 3057-3063. [ Links ]
10. Tyndall G. S., Orlando J. J., Wallington T. J., Hurley M. D., Goto M., Kawasaki M., Phys. Chem. Chem. Phys. 4, 2002, 2189-2193. [ Links ]
11. Alvarez-Idaboy JR, Galano A, Bravo-Pérez G, Ruiz-Santoyo ME (2001) J. Am. Chem. Soc. 123:8387. [ Links ]
12. Galano A, Alvarez-Idaboy JR, Ruiz-Santoyo ME, Vivier-Bunge A (2004) Chem. Phys. Chem. S:1379. [ Links ]
13. Galano A, Alvarez-Idaboy JR, Ruiz-Santoyo ME, Vivier-Bunge A (2005) J. Phys. Chem. A 109:169. [ Links ]
14. Galano A, Cruz-Torres A, Alvarez-Idaboy JR (2006) J. Phys. Chem. A, 110:1917. [ Links ]
15. Gonzalez, C.; Schlegel, H. B. J. Phys. Chem. 1990, 94, 5523-5527 [ Links ]
16. Szori, M.; Csizmadia, I. G.; Fittschen, C.; Viskolcz, B, J. Chem. Theory Comput. 2006, 2, [ Links ]
17. McLean A. D. Chandler G. S., J. Chem. Phys., 72 (1980) S639 [ Links ]
18. Eyring, H., J. Chem. Phys. 1935, 3, 107-115. [ Links ]
19. Truhlar D. G., Hase W. L., Hynes J. T., J. Phys. Chem. 1983, S?, 2664 -2682. [ Links ]
20. Zhang S. Truong T. N., VKLab version 1.0, University of Utah, 2001. [ Links ]
21. Singleton D. L. Cvetanovic R. J., J. Am. Chem. Soc., 1976, 98, 6812- 6819. [ Links ]
22. Alvarez-Idaboy J. R, Mora-Diez N. Vivier-Bunge A., J. Am. Chem. Soc., 2000, 122, 3715-3720. [ Links ]
23. (a) Mora-Diez N., Alvarez-Idaboy J. R. Boyd, R. J. J. Phys. Chem. A, 2001, 105, 9034 -9039; [ Links ] (b) Alvarez-Idaboy J. R., Cruz-Torres A., Galano A. Ruiz-Santoyo M. E., J. Phys. Chem. A, 2004, 108, 2740-2749. [ Links ]
24. Galano A. Alvarez-Idaboy J. R., Atmospheric Reactions of Oxygenated Compounds + OH Radicals: Role of Hydrogen-Bonded Intermediates and Transition States. ch. 12 In Advances in Quantum Chemistry, in Applications of Quantum Chemistry to the Atmosphere, ed. M. E. Goodsite and M. S. Johnson, Elsevier, Amsterdam, 2008, 55, 245-274. [ Links ]
25. Pilling M. J., Seakins P. W., Reaction Kinetics; Oxford University Press: New York, 1996 [ Links ]
26. Truhlar, D. G.; Kuppermann, A., J. Am. Chem. Soc. 1971, 1840. [ Links ]
* The asterisk indicates the name of the author to whom inquires about the paper should be addressed.














