1. Introduction
Many techniques have been developed in order to detect gear faults through vibration analysis. Currently, the main researches are focused to detect gear faults under non stationary conditions (Feng, Chen, & Liang, 2015; Feng, Qin, & Liang, 2016; He, Ding, Li, & Jiao, 2016; Park, Kim, & Choi, 2018; Shao, Hu, Wang, & Qi, 2014; Xiang & Zhong, 2017; Yuan, Ji, Gao, Zhou, & Yuan, 2018), which is achieved by a group of algorithms through the application of some monocomponent signal decomposition technique.
Recently, a new technique, called TARSE (Ruiz Barrios, Hernández Montero, Gómez Mancilla, & Palomino Marín, 2019), has been developed as a choice for estimating the rotation speed of a rotating machine comprising gears. The instantaneous rotation speed is very useful for detecting gear faults under non stationary conditions. Algorithm TARSE applies a monocomponent signal decomposition technique (SSD (Bonizzi, Karel, Meste, & Peeters, 2014) is implemented) and performs the detection, for every delivered monocomponent signal, of the modulation corresponding to the first (or second) harmonic of the gear vibration. The effectiveness of TARSE, as for the rest of the techniques that applies some monocomponent signal decomposition technique, depends on the method chosen for the monocomponent signal decomposition.
Studies focused to determine which tool could be more suitable to be used, given an application, in order to decompose the monocomponent signals of the vibration produced by a mechanical system can’t be found. This work presents a research addressing the assessment of which monocomponent signal decomposition technique, given a group of them, could perform more effectively in the context of the algorithm TARSE. Since TARSE is based on the detection of the modulation in the vibration produced by a gear, this means to find out which monocomponent signal decomposition technique is more capable of delivering the monocomponent signal corresponding to such a modulation in the clearer form (higher modulation detection index).
2. The gear vibration signal
The influence of the gear vibration signal might be modeled by the following equation (Ruiz Barrios, Hernández Montero, Palomino Marín, & Gómez Mancilla, 2019):
where Xk and
The amplitude modulation function,
where Ai and A o are amplitudes related to the input gear and the output gear, respectively, and m v is the gear ratio.
3. Modulation detection index
The identification of the monocomponent signal corresponding to the amplitude modulation whose carrier frequency is the gear-mesh frequency, or its second harmonic, is performed through the normalization of the coefficient proposed in (Hernández Montero & Iturrospe Iregui, 2015), D 0 (f,α) 3 , designed to detect amplitude modulations, then called as Modulation Detection Index (MDI). This index is expressed as follows (Ruiz Barrios et al., 2019)
Notice that equation (3) is able to detect the phase-related spectral components corresponding to an amplitude modulation with carrier frequency at f
c
and spectral sidebands components at
Since the rotational speed can vary, the MDI cannot be determined by means of the Fourier transform. In this work, it is computed as performed in (Ruiz Barrios et al., 2019).
4. Method
As described in (Ruiz Barrios et al., 2019), TARSE is based on the application of some monocomponent signal decomposition technique and then, the identification of the monocomponent signal related to the first (or second) harmonic of the vibration produced by the gear through the synchronous detection of the corresponding modulation. In that context, this work is aimed to determine, given the vibration produced by a mechanical system, which monocomponent signal decomposition technique can deliver, more effectively, the first (or second) harmonic of the vibration produced by a gear. Here, the term “high effectiveness” can be interpreted as the clearer delivery of the characteristic modulation, performed by some monocomponent signal decomposition technique.
MDI is the parameter chosen in order to distinguish which monocomponent signal decomposition technique delivers, more effectively, the vibration signal produced by the gear: given a group of monocomponent signal decomposition techniques and their own deliveries of the first (or second) harmonic of the vibration produced by a gear, the higher value of the MDI of such signals, the more effective the monocomponent signal decomposition technique. Among the different monocomponent signals delivered by each signal decomposition technique, the one corresponding to the first (or second) harmonic of the vibration produced by a gear is chosen by using the MDI: the monocomponent signal with higher MDI is the selected one.
In this work, several monocomponent signal decomposition techniques were put under test: Empirical Mode Decomposition (EMD) (Qin & Zhong, 2006), ensemble EMD (EEMD) (Wu & Huang, 2009), Variational Mode Decomposition (VMD) (Dragomiretskiy & Zosso, 2014), Singular Spectrum Decomposition (SSD) (Bonizzi et al., 2014) and Complete EEMD with Adaptive Noise (CEEMDAN) (Xiao, Chen, Zatar, & Hulsey, 2019).
5. Working with simulation signals
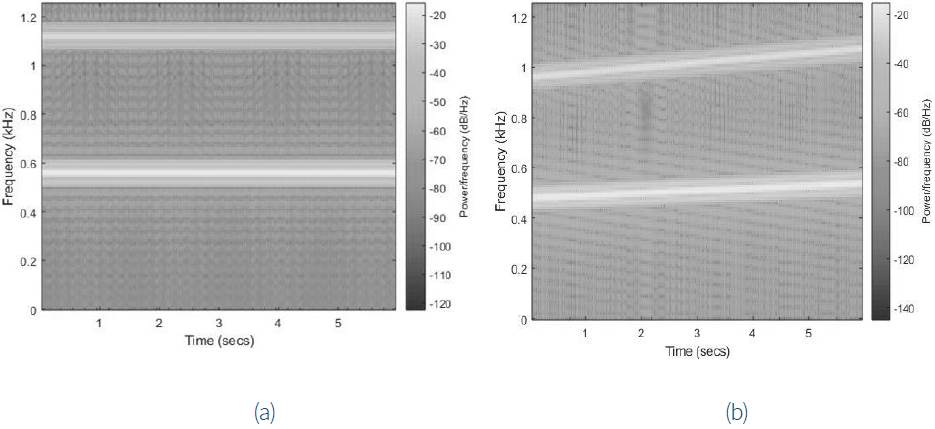
A first experimental work was accomplished by using simulation signals. Such signals were based on the vibration model expressed by equation (1). Two simulation signals were programmed: (1) a signal (S1) simulating the vibration produced by a 16 tooth gear, rotation speed equal to 30 Hz (thus, the meshing frequency is equal to 480 Hz) and modulation index equal to 0.4; and (2) a signal (S2) with the same characteristics, except by the rotation speed that is variable, leading the gear-mesh frequency to span linearly between 480 Hz to 536 Hz. The signals were sampled at 2.5 kHz. Spectrograms of both signals can be shown in figure 1, where the second harmonic of the meshing frequency can be also shown.
Normal distribution noise was added to these signals, in such a way that noisy signals with signal-to-noise rates ranging from - 10 dB to 14 dB, with a step equal to 2 dB, were obtained. Fifty realizations of noisy signals per SNR were generated.
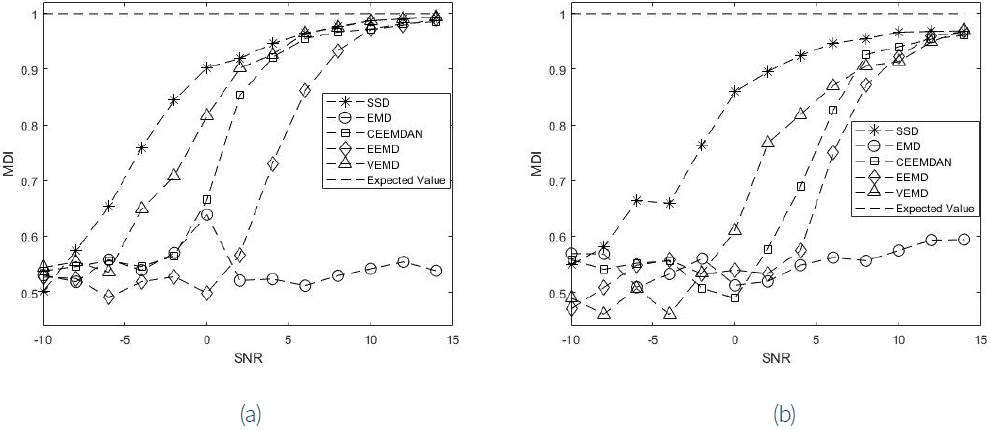
The monocomponent signal decomposition techniques under test, EMD, EEMD, VMD, SSD and CEEMDAN, were applied on simulation signals S1 and S2. For each realization of noisy signal and each group of monocomponent signals delivered by the decomposition techniques, the monocomponent signal that corresponds to the first (or second) harmonic of the vibration produced by the gear was selected by means of the MDI computation: the monocomponent signal with higher MDI was the selected one. Since 50 realizations of noisy signals were generated per SNR, the average of the selected 50 MDI values, per technique, was computed. The results can be shown in figures 2a and 2b.
Figure 2 reveals how the performance of the monocomponent signal decomposition techniques is degraded as the SNR diminishes. This figure also shows that technique SSD exhibits a less degradation and then can be considered as the technique with a more convenient performance.
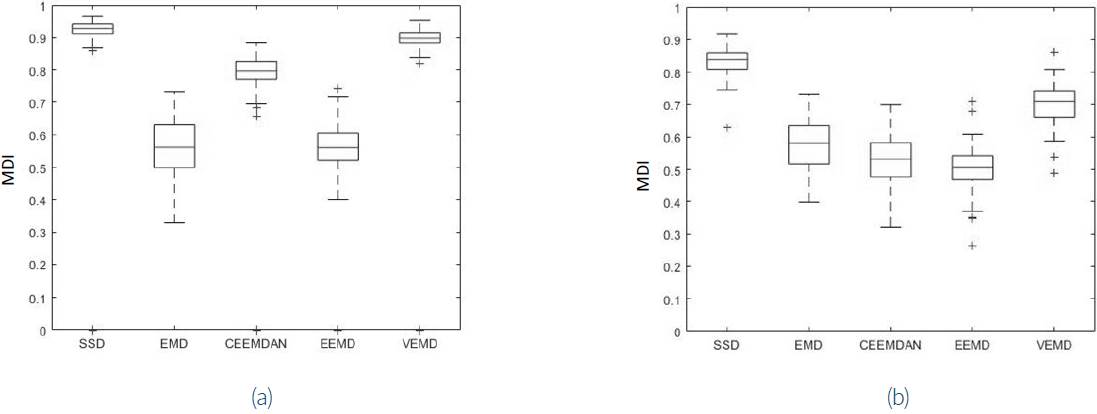
Boxplot of MDI values, for each monocomponent signal decomposition technique, simulation signal S1, and SNR = 2 dB and SNR = - 2 dB, can be shown in figures 3a and 3b, respectively. On each box of every boxplot of this research, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers, and the outliers are plotted individually using the“+” symbol. Figure 3 clearer reveals which techniques deliver with higher quality the modulation signal and which techniques degrade less the performance as the SNR reduces. In general, the technique SSD exhibits a better performance.
The MDI values and 50.% percentile, for each monocomponent signal decomposition technique, simulation signal S2, and SNR = 2 dB and SNR = - 2 dB, can be shown in figures 4a and 4b, respectively. Figure 4 shows a result very similar to that achieved by simulation signal S2. In addition, the emergence of SSD as the technique with best performance is confirmed too.
6. Working with true signals
In case of the experimentation with true signals, gear vibration signals emitted by 3 MW wind turbines, available in website data-acoustics.com, were used. Signals were gathered by an accelerometer for 6 s (sampling frequency is equal to 97656 Hz). A 32-teeth gear was monitored and the nominal speed was 30 Hz.
Two datasets were processed. A first dataset, comprising 12 different signals, was built up by signals coming from two wind turbines in good operation condition. The second dataset, comprising 6 different signals, was built up by signals coming from a wind turbine with a local fault in the gear. Since the mechanical system has a gearbox, it is expected that the modulation that characterizes the vibration produced by a gear is present in the acquired signals. Then, the work now is aimed to determine which monocomponent signal decomposition technique delivers more clearly the modulation corresponding to the gear vibration, that is, which technique delivers the monocomponent signal corresponding to the gear vibration with the highest value of MDI.
It is also expected that the modulation will be shown off more clearly in the signal gathered from the faulty gear, since this modulation is powered by the fault. In case of the modulation produced by a healthy gear, it can be considered as a low-level modulation.
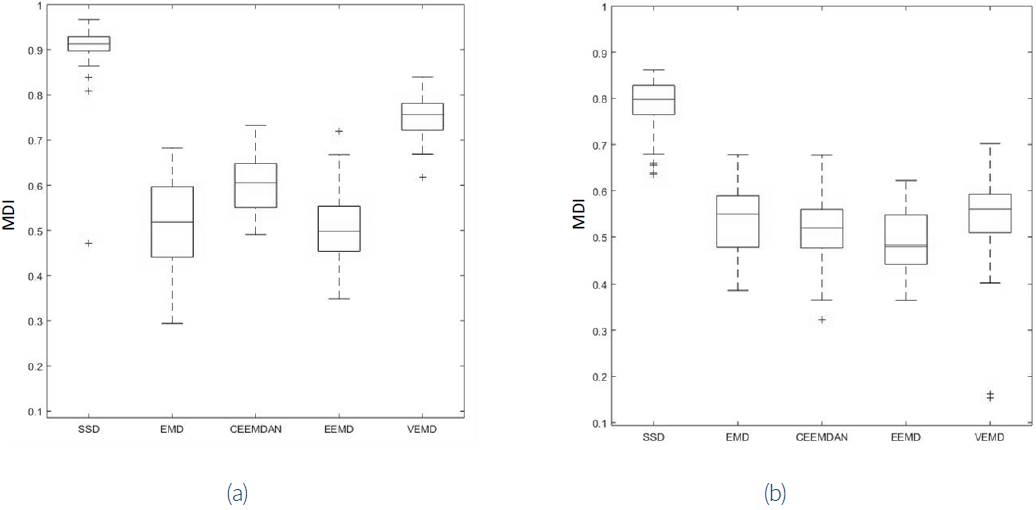
The monocomponent signal decomposition techniques were applied on signals gathered from the wind turbines. For each signal, each monocomponent signal decomposition technique delivered a group of monocomponent signals, from which the monocomponent signal corresponding to the first (or second) harmonic of the vibration produced by the gear was selected (the monocomponent signal that yielded the highest MDI). The boxplot of the highest values of MDI, achieved by each monocomponent signal decomposition technique, in case of signals registered from both the healthy and the faulty wind turbines are shown in figure 5a and 5b, respectively.
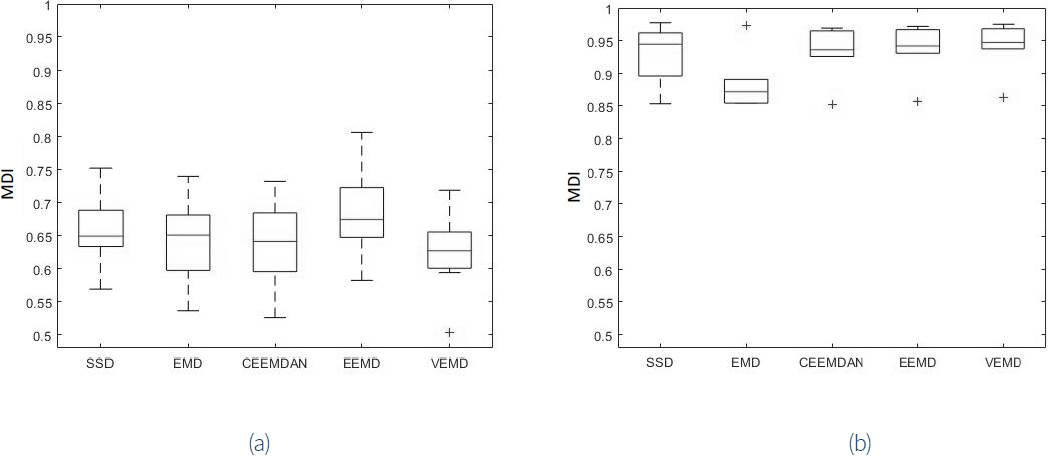
Figure 5 Boxplot of the top values achieved by the computation of the MDI of the signals delivered by the monocomponent signal decomposition techniques. a) Vibrations gathered from the healthy wind turbines. b) Vibrations gathered from the faulty wind turbine.
Figure 5 reveals how the modulation quality is improved when the gear is damaged. With regard to the question of which technique performs in a more suitable form, this figure shows that almost all techniques exhibit similar results. In table 1, statistical quantities of the achieved MDI are presented. It can be observed that in case of the low-level modulation, the best outcomes are achieved by the techniques EEMD and SSD (higher mean values and lower variances). In case of the high level modulation, the results achieved by the techniques were very similar, except by technique EMD, which exhibited the worst results.
7. Conclusions
In this work, several results were presented concerning the assessment, given a group of signal decomposition techniques, of the technique more convenient to be applied by algorithm TARSE. That is, which technique could be able to deliver, in a clearer form (higher Modulation Detection Index), the monocomponent signal corresponding to the first (or second) harmonic of the vibration produced by a gear.
As result of the work with simulation and true signals, it was confirmed that among the group of monocomponent signal decomposition techniques under test, the technique SSD exhibited a better performance: it was the more consistent technique since it exhibited good results when both simulation and true signals were used. This technique was able to yield higher values of MDI, but also, in case of low-level modulations, it was one of the techniques with better performance.











 nueva página del texto (beta)
nueva página del texto (beta)