1. Introduction
Critical thinking is a fundamental aspect to be developed in education (Facione (2007), European Commission (2015), Jaramillo et al. (2016) ...), and it must be encouraged in all individuals in any context: science, history, literature, politics, ethics, and in everyday life in general. The definition of critical thinking that we find in specialized literature contemplates a wide range of components and skills, which makes it difficult to provide a concrete definition. One aspect that is generally mentioned is the ability to make autonomous decisions based on reasoned and justified criteria. Therefore, it is inextricably linked to scientific education and, in particular, to the mathematical method, which relies on the exposition of principles or axioms, reflection, interrelation of concepts and rigor. In turn, it is closely related to creativity, imagination and innovation, characteristics that are increasingly essential for scientific and social progress.
Our research is based on the hypothesis that, except perhaps for mathematicians, engineers, computer scientists and physicists, it is common for most students in a first-year university course in social sciences to blindly trust the results of computers and to question the need to learn the steps in the algorithms and their properties, if problems can be solved using specialized and recognized mathematics software. Therefore, in this paper our aim is to reveal a poor critical attitude toward software in university social sciences students, to justify that software results cannot be relied upon blindly and to develop a critical attitude toward computer software in the context of mathematics education.
We understand the term critical attitude to mean the capacity or ability to detect, in some cases, erroneous or confusing results and, in others, the ability to justify, without a doubt, that a result is indeed correct. This disposition is undoubtedly necessary for self-learning in any context.
In the areas of economics, business, accounting and finance, as in many others, using software of all kinds is unavoidable: social media, computer software, verification and use of databases, which is growing exponentially due to the increased memory available in general-use platforms and computers, etc. Some authors have researched how the use of technology is changing even the way we act and make decisions (Rossi, 2017), and the role of university teachers in this new context (Rodrigo Cano et al., 2018).
From a quantitative point of view, the dimension of actual problems in terms of the volume of data available and the number of variables required makes solving them by hand untenable. The study we describe in this work involves first-year university students who are not yet familiar with large databases, but who are in the perfect position to become citizens trained in their chosen fields. Their education will require them to use both quantitative and qualitative data extensively, data that must be processed using advanced software. In particular, where big data is involved. At the same time, they must also interpret and contextualize these data and be critical of the algorithms used and conscious of the decisions, correct and incorrect, that said algorithms can output.
This context requires a methodological reflection of some depth in order to avoid the various types of errors that can be made. On the one hand, to avoid personal errors when using any software, it is recommended that manuals or user forums (usually created to provide mutual assistance) be consulted. However, to avoid interpretation errors require more solid, broader knowledge that is in no case provided by the software itself or its manual. On the other hand, all software contains programming errors, as these are algorithms designed by people. Although it is not in our power to correct this type of error, we can mitigate its consequences, and that is a primary focus of this paper.
We note below some of the papers that are most closely related to our study. For example, Ponce and Rivera (2011) involving high school students analyzes examples of calculating the primitives of a function using different software packages; Jehlicka and Rejsek (2018) provides a didactic proposal to illustrate the limitations of calculations made by computer due specifically to finite arithmetic. In a more scientific field and at the level of mathematics majors, Ciaurri and Varona (2006) considers if we can rely on calculations done by a computer, which was an important motivation behind our own research. The authors assume that errors in numerical results due to floating point arithmetic and problems of stability in numerical algorithms are well known by students because they are covered in the courses taken by mathematics majors. However, as they emphasize, the errors that can occur in symbolic computation, if finite arithmetic is not used, are less known. Some of the errors mentioned in Ciaurri and Varona (2006) using the Mathematica software have been corrected in later versions. However, as this type of software introduces new algorithms, in our work it is implicit that we can always find examples that will be affected by certain errors of varying importance.
As far as we could review the references consulted, we could not find any didactic proposals to achieve one of our objectives of assessing the critical attitude toward software of first-year economics and business majors, whose level of mathematics is more basic than that of, say, physics or engineering majors. Specifically, most of the books or papers recommended to the students of the subjects in our context, in which the use of various mathematical software packages is encouraged as a reasoning aid, do not warn of any potential errors in the software of the kind considered in this paper; rather, they focus on teaching different programs, depending on the author, to solve the exercises proposed and highlighting the increasing advantages of everything digital (González Pareja, 1997, 1999, Cahill and Kosicki, 2001, Barrios-García et al., 2005, 2006, Franco-Brañas, 2011, Hillier and Liberman, 2010, Taha, 2012, Cardeño and Córdoba, 2013).
As far as we know, critical thinking when using software in the social sciences context that we consider has not been properly investigated and is not being addressed, especially as it involves errors due to reasons other than those that result from the limitations of finite arithmetic. Thus, our approach of providing examples adapted to the level of economy, accounting and business majors is novel. Many readers will be surprised by the presence of programming errors in very basic problems. Therefore, one of our goals is to have university social sciences students ask for mathematical theory by having them recognize that software does not solve every problem. We also wish to make them aware of the fact that mathematical results obtained with a computer are not as infallible and accurate as they generally believe. As a consequence, we want them to appreciate even more the need to know the mathematical theory that underlies, for example, the models of mathematical economics. This theory is the only measure available to gauge the reliability of the results of such models. Therefore, when solving problems, even if they are using the best computer programs, they have to be mindful of employing critical thinking and creative reasoning at all times. Specifically, in keeping with Facione (2007), we believe that critical thinking skills (interpretation, analysis, evaluation, inference, explanation and self-regulation) can be acquired through mathematical training, provided that students are open to it by being inquisitive, judicious, systematic, analytical, truth-seeking, open-minded and confident in their reasoning. Also, as per Lithner (2008), our proposal would lead students to a necessarily creative attitude as it requires a process of reasoning and argumentation beyond the purely imitative. We cite the task provided in Olsson (2018) as an example of a learning activity that, through software interaction (in this case, Geogebra), encourages the same type of creative reasoning that is needed in our didactics, although its objective does not involve ensuring that there are no errors due to the software, but rather the need to discover the method that must be applied to arrive at a solution.
From the instructor’s point of view, our work exposes the need to enrich the literature with new didactic proposals that help students develop critical thinking and creative reasoning when using software at any level. To this end, we provide material, part of which we have used to identify and assess the deficiency mentioned, in two areas, one to complete our training as instructors and another to design exercises aimed at students. The objective of completing and updating the set of exercises with a variety of original activities that require the student to ensure, in several ways, the goodness of the results that may be obtained through software will always remain open.
We also believe that this work contributes to increasing the multidisciplinary interest in STEM (Science, Technology, Engineer, Mathematics) subjects. As observed in, for example, Kolstø (2001), Elías (2008), Jehlicka and Rejsek (2018), and several of their references, although secondary and university students throughout all the world often employ technological means, the interest in science and technology in depth has declined enormously. For the most part, students’ use of technology is very superficial, essentially at the level of end users who are fully reliant on the tool at their disposal. In this sense, references such as, for example, Bruton and Coll (2005), Lorenzo (2005), Carreras-Marin et al. (2013) try to encourage an interest in mathematics by creating links between theoretical and real problems and emphasizing multidisciplinarity. Increasingly, educators recognize the need to develop skills associated with the productive use of computing. Mathematics is thus undergoing a change in terms of the tools available to teachers and the possible ways to help students explore the potential of this discipline in various contexts (Pei et al., 2018).
In the next section, we explain the research methodology that we employed. In Section 3, we describe some of the materials that we as teachers have been gathering and that shaped the objective of critical thinking focused on teaching mathematics in economics and business, using computer software. The exercises selected involve matrix algebra and mathematical optimization, which are closely related to the applications in our area of interest. Section 4 describes the implementation of the classroom experiment, and includes the results obtained by the students and the group discussion. We finish with some conclusions and bibliographical references.
2. Research methodology
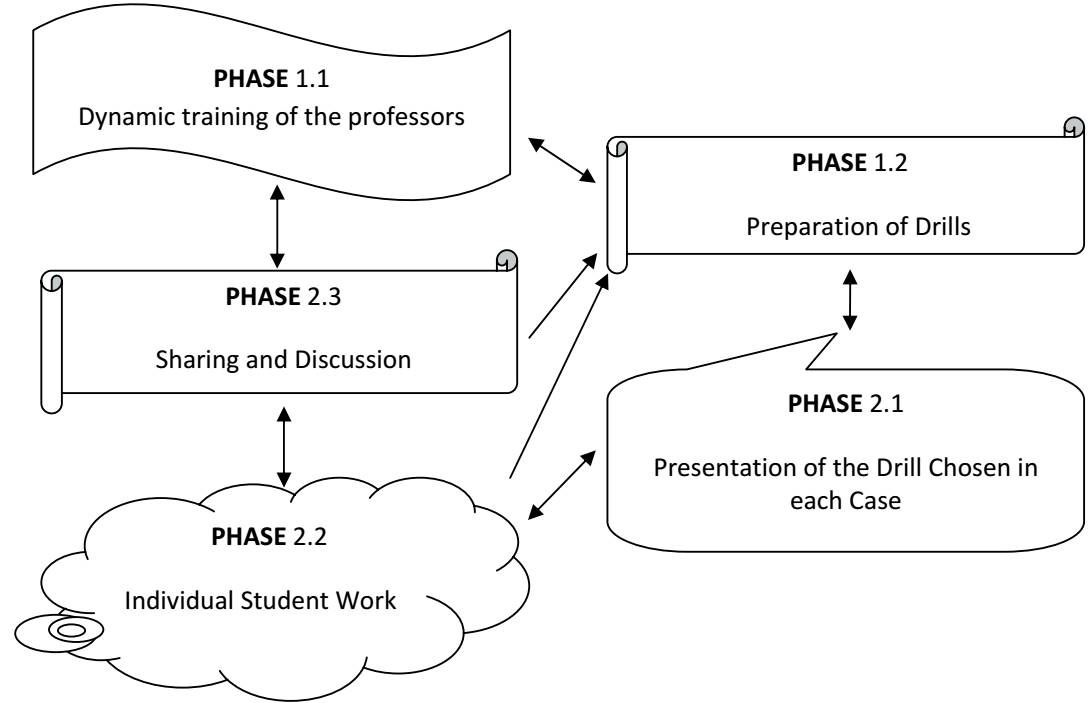
We followed the five interrelated phases shown in Figure 1.
The research methodology was constantly enhanced by the questions posed by our students regarding the convenience and limits of the use of theory and computation, and the reasons why one cannot be replaced by the other. This teacher-student relationship gives a circular character to this methodology, as indicated by the dual direction of some arrows, as appropriate. The border separating the work of the faculty and the students is very diffuse, although we can say that Phase 1.1 focuses on the faculty while Phase 2.2 corresponds exclusively to the students. Either one can mark the start point of the methodology. For the faculty, the methodology includes the five phases. Feedback is used to round out and update the teaching method. For the students, the practical exercises begin in Phase 2.1 and end in Phase 2.3.
2.1. Description of the phases
Phase 1.1- Dynamic training of the professors (and research question Q1)
The faculty has advanced mathematical training and routinely uses computer software as a problem-solving tool. However, this experience has taught us to be more critical in how we conduct our teaching by observing how students behave toward computer results. Therefore, we had to acknowledge the need for more dynamic training, if possible, if the goal is to use computer software to give students a critical and creative attitude. Therefore, in Phase 1.1, the professors must first find simple exercises suitable for a first-year social science course in which a specialized, powerful and prestigious mathematics software package (such as Mathematica, Matlab, Maxima, Geogebra or Derive) performs erroneously or confusingly. They also have to find a way to present them to students so that they not only learn to compute, but also acquire a critical attitude toward the use of software. It must be borne in mind that correcting the source codes is not within the reach of the user, and even if it were, it would be beyond the scope of this work.
Since the examples of errors that we have found in the mentioned references are not at the basic level required for our courses, and most of them were corrected in later versions, our first goal is to provide an answer to the following research question:
Q1: Is it possible to find interesting examples at the level of mathematics courses taught to first-year economics, business and finance majors that easily convince our students that they should not accept, without question, the results obtained through mathematical software (regardless of how well-regarded the software is and of how many improved versions have been marketed over the years)?
To this end, we started by computationally solving the Collection of Proposed Exercises that are presented in the course using theoretical mathematical methods. We chose the free online platform of Mathematica software, i.e., Wolfram Alpha (https://www.wolframalpha.com/), hereinafter WA. The specific results obtained depend on this choice, but the essence of the research remains valid regardless of the software selected, since all software is prone to similar weaknesses and will sometimes yield confusing or erroneous answers. Despite this platform’s limitations, we believe that this choice is suitable primarily because it is based on a powerful symbolic calculation program, Mathematica.
As we will see, the answer to question Q1 will be affirmative, and the faculty found the list of examples, which was broader than expected, to be highly enriching from the start, allowing us to advance to the following phase.
Phase 1.2 - Preparation of Drills (and research question Q2)
In this Phase, we focus on preparing Drills based on a Collection of Proposed Exercises for Computing. We choose those that would allow the student, on the one hand, to positively value the computational tool as a complement to the theory, inescapable in certain applications, and on the other, accept the fact that the results are not always infallible, even in very simple cases. Therefore, the students must be very attentive when employing these tools. Each drill contains exercises where the software performs well and others where the software behaves erroneously or incompletely, to see if the students identify the difference, or are at least mindful of it.
The exercises selected are not all those collected in Phase 1.1, since the goal is to have them be sufficiently direct for the students to be able to easily interpret the computed results. To ensure that students remain attentive and critical, the activities have been designed with no apparent difference between a problem that the software solves perfectly well and one that it solves erroneously or incompletely.
The exercises were selected in an effort to answer the following research question:
Q2: In general, do our students use the mathematical software mechanically and accept the results without questioning them?
Phase 2.1 - Presentation of the drill chosen in each case
This is the first phase that is carried out in the classroom, where the first part of the drill to be conducted is presented. In it, the students are informed that the goal is to have them solve the proposed exercises, theoretically and computationally, in order to compare the results. This work will be done individually at first (outside the classroom) and then, in the second part, it will be evaluated by way of a classroom test.
Previously, similar exercises will have been solved in class. They will have been told to be mindful of the results at all times due to potential mistakes that might be made and that can lead to confusing or incorrect findings, regardless of the method used. We note that students tend to rely more on the computer than on the results obtained by hand. They are encouraged to be critical of the computational results by offering them some very simple alternatives to self-discover potential errors, namely, theoretically solving the exercise and solving it computationally by using alternative commands, if they exist, or through other software. These alternatives should be available to students without additional explanations from the professor, who will be available if they need help. However, the goal is to have them identify their own mistakes and the limitations of the software.
So far the methodology has focused on developing the materials and presenting them in class so that students can, in some way, realize that there are always different alternatives to solve any mathematical exercise and that, sometimes, mistakes arise from blindly trusting the answer provided by the software. We can say that, this phase focused on achieving two objectives:
− To have the students learn mathematics and teach themselves to use computing software and discover its potential and need.
− To have the students run into limitations and be ready to be critical.
And as the course progresses, we will see if the students learn cautiously, with a critical attitude, or if the initial bias persists.
Phase 2.2 - Individual student work
In this Phase, the students do the first part of the drill individually outside the classroom, noting everything they deem appropriate both for and against the methods used, as well as any questions or suggestions for changing the proposed drill, any contradiction or confusion identified in the results and anything they believe to be of interest. In this step of the process, any questions or suggestions have to be presented directly to the professor and not to the group as a whole, as it could affect the findings of other students. The professor will determine if changes need to be made to the drill or if a previous phase has to be repeated.
While doing the drill outside the classroom, the students are asked to reflect on questions of the type: What new reasons am I identifying to determine whether or not to be critical of computations in my exercises? How can I validate, to the extent possible, the solutions obtained? How can I solve the problem creatively with alternative methods and/or with different computer programs? Should I investigate in the manual and online forums the specifics of each instruction and the limitations of the software? Am I aware of the need to continually acquire knowledge and experience in the subject at hand by asking someone with more experience, reading, etc.?
Phase 2.3 - Test and discussion
This individual work, by the teacher and students, culminates in a test and group discussion to highlight any problems encountered and to interpret the results. This phase is very important because it will reveal the scope and conclusions of the work carried out. This is the last phase for the students, but for the professors it is one more step in their dynamic training. We trust that a large majority of the students now accept the importance of being critical of their calculations, even if they are obtained using globally accepted computer programs. In addition, we will learn how each student suggests solving each problem, each error and discover new ways that we had not previously considered.
In this phase, both the faculty and students are asked a question of the type: What would you change in the drill done and what other type of exercise do you think can enhance the acquisition of a critical attitude toward computing?
And in the continuous answers, we discover that there are many other exercises to be done and that no software is free from potential errors, which feeds back our teaching and the training of all the agents. We trust that students will appreciate the acquisition of this critical attitude and will be motivated to extrapolate it to other subjects and circumstances in their daily life.
3. Search for materials to implement the study: answer to research question Q1
In this section we implement Phase 1.1 of the methodology and, for our training and to develop materials as instructors, we look for examples with results that are faulty, confusing or that could lead to errors. The errors that can result are due, on the one hand, to Mathematica’s poor programming of the theoretical methods used, which in turn can be limited and, on the other hand, to the specifics of a certain instruction that, even if they are detailed in the software documentation, will likely not be known to the users in question. Determining why a software error occurs relies on reviewing its source code, something that, as noted, is not within our reach. Our goal here is merely to describe the error and justify it by emphasizing that there is a contradiction in some sense.
It is important to note that software errors, in general, are not easy to detect, and given the level of our students, we have selected examples in which an error is evident or can be induced. Therefore, we must take the same precautions both when the software performs well and when its performance is wrong or confusing. We did not look directly for the examples presented in this section; rather, we found them over several years of teaching by being attentive, with a constructive critical attitude, to what might appear. It must be noted that some of the mistakes we found in the past have already been corrected in WA, and that we continue to find new ones, without looking for them, when solving new problems. It also happens that in the history of computing, updated versions of software have behaved worse in some specific aspect than the previous version (Ciaurri and Varona, 2006). It is thus necessary to note that the exercises that were solved using WA in this paper employed the version available in March 2019.
For this work, we decided to focus the search for examples and errors on two of the modules typically used in our courses: Matrix Algebra and Optimization. The former allows us to convey the usefulness of matrix language as a powerful symbolic tool for studying economic models formulated in terms of systems of linear equations (static, dynamic, multisector and other models) in the areas of consumer theory, production, cost and profitability analysis, etc. The latter provides an opportunity to train students on the mathematical tools needed to make efficient decisions in contexts where economic agents pursue multiple goals and the resources to obtain them are scarce or limited. In both, the examples we provide can constitute the preliminary, intermediate or final interpretive step in solving mathematical problems or in an applied economics context.
3.1. Some cases involving Matrices and Systems of Linear Equations
Example 1. Calculating the rank of a matrix with parameters.
Let us calculate, for example, the rank of the matrix (a2 1 1 1 a2 1 1 1 a2 2+a2 4−a3).
In WA, the instruction and the result are the following:
In this example, WA result leads to confusion or misinterpretation, as it does not warn that the rank is only 3 if a≠1 or a≠−1. It also does not mention that if a=1, the rank is 1 and if a=−1, the rank is 2, which is easily verified by substituting in these values.
To find out the reason for this mistake, the question we must ask is: When studying the rank with parameters, does WA never warn of the different cases? The first thing we must ask is if we are using the Rank instruction correctly. If we look into which Mathematica instruction WA uses to calculate the rank, we see that it is MatrixRank. We then look in Mathematica Documentation (https://reference.wolfram.com/language/ref/MatrixRank.html) and find that when working with parameters, Mathematica assumes that every symbol is independent. It outputs the maximum rank, which will obviously lead to confusion or error as in the previous example, since we do not expect WA not to indicate the parameters for which the result is valid when it has the capacity to do so.
Next, we illustrate the influence of the error described with a simple case from applied economics:
Example 2. A consulting firm has in its portfolio three types of projects (A, B and C). Each type of project has different needs in terms of analysts, programmers and terminals, as indicated:
To develop the projects, the company has 20 programmers and 30 analysts. The number of computer terminals that will be available is not yet known. For what number of terminals made available, denoted by M, does the proposed problem have some combination of projects to be carried out in which every analyst, programmer and terminal is used?
Letting x, y and z denote the number of
projects of type A, B and C, respectively, that the company can perform, the
mathematical approach to this exercise would symbolically be:
The results could lead us to conclude, erroneously, that the proposed system is inconsistent, meaning there is no solution to the problem presented. But the rank of the augmented matrix would in fact be 2 if M=40, and 3 if M≠40. Therefore, the correct answer is: it has a solution only if 40 computer terminals are made available.
Example 3. Misleading solution of linear systems
If we solve the linear system:
| Instruction | solve |
| WA Results |
|
Note that if we look at line 3 of WA Results, we could misinterpret that if a=1, then x=1−t, y=0, z=0, which is incorrect since if a=1, then y=0, z=1, x=−t is also a solution (among others), which is included in the first line. Therefore, the results of this example are misleading.
Example 4. Situation that seems to have been corrected by WA
With respect to the specific system 2x+ay=3 and 4x+8y=6, Ciaurri and Varona (2006) notes that Mathematica did not recognize the indeterminate consistent case. However, this has been corrected, as we observe in the current output of WA:
Therefore, one might think that Mathematica already provides in its output all possible consistent cases when studying a system with parameters. However, the following example shows that this is not the case.
Example 5. WA does not always consider all consistent cases
If we solve the linear system:
| Instruction | solve |
| WA Results |
|
Note that it does not warn of the case a=−1, which is obviously inconsistent (the first equation would be x+y+z=3 and the second equation x+y+z=5, which is absurd).
This might lead one to think that the WA Solve instruction informs of all the consistent systems, but not of the inconsistent ones. But this statement is not true because it also does not warn of the case a=1, for which the system is reduced to the equation x+y+z=3, which is obviously consistent and indeterminate, with 2 degrees of freedom.
As a consequence of this exercise, we note that the WA Solve instruction does not solve all the consistent systems and does not warn of what happens in cases of inconsistency.
The following example provides a simulated real context in which WA does not warn of cases in which the system is inconsistent.
Example 6. An economic example with incomplete information from WA
The equilibrium in the goods market in a simplified Keynesian model can be represented by the equation Y=a1+a2(1−t)Y+a3 r+G, while the equilibrium in the money market is given by M=b1+b2 Y+b3 r, where Y is income, t the marginal propensity to tax, r the interest rate, G the public expenditure and M the amount of money. Assume a specific economy in which a1=10, a2=0.8, t=0.2, b1=15, b2=1.5, b3=−1. What condition must a3 satisfy for there to exist an equilibrium solution for variables Y and r?
| Instruction: | solve |
| WA Results |
|
Note that there is no warning that in the remaining cases it is inconsistent, that is, if G≠6M/25-68/5 and a=6/25.
We now consider whether WA always deems consistent systems to be determinate. To address it, we provide the following example.
Example 7. On systems that are consistent and determinate
Consider the following linear system:
| Instruction | solve |
| WA Results |
|
Let us also calculate the determinant of the matrix associated with the system:
Note that the infinite cases in which this determinant is different from zero, and therefore the system is consistent and determinate, that is, if a≠b≠c and a≠c, are not considered in the WA results.
3.2. Some Optimization cases
Example 8. Wrong optimization results
If we try to calculate the maxima and minima of e x +e y subject to x+y=10 we find:
| Instruction | extrema |
| WA Results |
Global maxima: (no global maxima found) Global minimum: min{ e x +e y / x+y=10}=2e5 at (x,y)=(5,5) Local maximum: max{ e x +e y / x+y=10}≈296.826 at (x,y)=(5,5) |
The result is disconcerting since the same point is given as a local maximum and minimum. If we consider maximization and minimization separately, we get:
| Instruction | maximize e^x+e^y with x+y=10 | minimize e^x+e^y with x+y=10 |
| WA Results |
Global maxima: (no global maxima found) Local maximum: max{e x +e y /x+y=10}≈296.826 at (x,y)=(5,5) |
Global
minimum: min{e x +e y / x+y=10}=2e5 at (x,y)=(5,5) |
This is still confusing, since the same point is erroneously given as a local maximum and global minimum. We resort, therefore, to the theoretical method to dispel all doubts.
If we assume that y=10−x, then we solve the same problem using the substitution method, that is, Opt f(x)=e x +e 10-x . Given that the unique candidate for this function is the critical point, that is, x=5, and the second derivative is always positive for any value of x, we can state that the point (5,5) is an absolute minimum of the initial problem.
Example 9. Not all instructions lead to the same results
| Instruction | extrema xy with x^2+y^2=8 |
| WA Result |
Global
maxima: max{xy/x 2+y 2=8}=4 at (x,y)=(−2, −2) max{xy/x 2+y 2=8}=4 at (x,y)=(2,2) Global minima:min{xy/x 2+y 2=8}=−4 at (x,y)=(−2,2) min{xy/x 2+y 2=8}=−4 at (x,y)=(2, −2) Local minima:min{xy/x 2+y 2=8}=4 at (x,y)=(−2, −2) min{xy/x 2+y 2=8}=4 at (x,y)=(2,2) |
Notice how WA reports that the points (−2, 2) and (2,2) are global maxima, with the value of the objective function equal to 4 and, at the same time, local minima. This is obviously an error.
Unlike what happened in the previous example, this error does not occur in this example with the maximize or minimize instruction.
Example 10. Incomplete solution
| Instruction | extrema (x−y+2z+3)^2 | minimize (x−y+2z+3)^2 |
| WA Result |
Global maxima: (no global maxima found) Global minimum:min{(x−y+2z+3)2}=0 at (x,y, z)=(0,0, − |
Global
minima: min{(x−y+2z+3)2}=0 for y=x+2z+3 |
Given the output of extrema instruction, it may seem as if the function has a single global minimum. However, with the output provided by the minimize instruction, we see that there are infinite global minima. It is easy to verify that the latter is true given that the function is non-negative and is zero at all points where y = x + 2z + 3 is satisfied. Therefore, they are global minima.
Example 11. Minimize does not always work well
| Instruction | minimize (x−y)^2 on x^2+y^2<=− 0.1 |
| WA Results |
Global
minimum: min{(x−y)2 / x 2+y 2 < − 0.1}=0 at (x,y)=(0,0) |
It is obvious that the optimization problem has no solution since it is impossible to satisfy the restriction. The program not only does not detect this, but it proposes as a solution a point that obviously does not satisfy the restriction.
Although we could continue adding examples and more interesting “creative” comments, not only from these two modules but also from the other modules in our courses, what has been presented so far allows us to show that the answer to Q1, our first research question, is obviously affirmative.
4. Lack of critical attitude toward software: answer to research question Q2
The material compiled in the previous section, along with other exercises in the collection that did not exhibit problems with the software, allowed us to present various drills in the different modules in an effort to let the students work with the software on a regular basis and observe not only its benefits, but its limitations as well. The research we present herein is intended to assess if the students manifest a critical attitude toward the software used. So as not to unnecessarily prolong this paper, and since the philosophy followed in preparing the drills does not depend on the module in which they are employed, we will comment on only two of them in the Linear Algebra module. In this section, we call them Drill 1 and Drill 2, which include exercises in which the software gives a wrong or misleading result. The basic level chosen is necessary for two reasons:
So that students can do the drills even without having studied while allowing the professors to determine if they relied blindly on the software.
So that the professors can clearly identify how the students use the software without being unduly influenced by the level of knowledge.
Even so, we have to eliminate from the sample those students who are unable to interpret correct software results at a very basic level.
As noted, each drill consists of two parts, Part A and Part B. The student does Part A outside the classroom and then solves Part B in class by taking a test that is answered by taking Part A into account.
To help promote a critical attitude, when the drills are corrected in class, the students are warned not to accept the result output by software without thinking, and the mistakes made in this regard in the drill are highlighted.
4.1. Drills
In this section, by way of example, we show the two drills mentioned. We will denote by A1.i and A2.i the i-th exercises that the students did for homework from Drills 1 and 2, respectively, and by B1.i and B2.1 the questions in the tests given in class on the results from exercises A1.i and A2.i, respectively. We emphasize here the importance of Phase 2.2 of the methodology, to have students think in a relaxed setting outside the classroom. The student must justify all the answers chosen.
We note that the questions are asked in a way that implicitly aims to encourage the students to think creatively so they can identify mistakes in the software.
Drill 1
Exercise 1.1. Let
A1.1 Enter {{0, −1},{1,0}}{{2,6},{1,3}}+{{2, −1},{−1,2}} into WA, write down the result and anything you think is interesting.
B1.1 In A1.1, what were you asked to calculate?
Example of justification for the answer selected:
We see that WA, in the line it calls Input, believes that it has to calculate C(A+B). Since the order of matrices A and B does not alter the sum, it is the same as C(B+A), meaning the right answer is b). However, in keeping with the symbology learned in mathematics, since parentheses were not used, one might mistakenly think that WA solved option a).
The “creative way” of correctly answering B1.1 requires solving with WA, or by hand, each algebraic operation separately.
Exercise 1.2.
A1.2 Use WA to calculate the determinant of the matrix
B1.2 In Exercise A1.2:
a) The determinant of E is never zero
b) The determinant of E is zero if a=2 or a=−1
c) The determinant of E is zero if a=−2 or a=1
d) None of the above
Example of justification for the answer selected:
Replacing in the determinant given by WA, we see that c) is correct.
Exercise 1.3.
A1.3 Use WA to calculate the inverse matrix of E, write down the result and anything you think is interesting.
B1.3 In Exercise A1.3:
a) Since the determinant of E is not a2+a−2, the inverse of WA must be incorrectly calculated because the formula of the inverse is divided by the determinant of E, that is,
b) E always has an inverse and is the one given by WA.
c) E does not always have an inverse, but when it does, it is the one given by WA.
d) None of the above.
Example of justification for the answer selected:
Since, as noted in Exercise 1.2, the determinant of E is zero if a=1 or a=−2, these are the only two cases in which the inverse does not exist. When it exists, WA gives the correct simplified result. That is, the correct answer is c).
Drill 2
Exercise 2.1.
A2.1 Given the matrix
B2.1 If the matrix in Exercise A2.1 were the extended matrix of a linear system of three equations with three unknowns:
a) This system would be consistent and determinate since its rank would be 3, the same as the number of unknowns.
b) Such a system would be inconsistent since when triangulating the extended matrix, one row indicates inconsistency.
c) The system would be consistent and indeterminate.
d) None of the above
Example of justification for the answer selected:
When triangulating by hand, we find that it is only consistent (indeterminate) if M=40.
Note that WA does not indicate that the rank is not always 3. Therefore, the correct answer is d).
Exercise 2.2.
A2.2 In WA, write Solve(a^2x+y=3, x+a^2y=4−a), copy the result to test it.
| Instruction | solve (a^2x+y=3, x+a^2y=4−a) |
| WA Results |
y= 3−x and a=1 |
B2.2 The linear system in exercise A2.2:
a) Is always consistent because WA has given all the possible solutions.
b) Is always consistent and indeterminate because the solutions have degrees of freedom.
c) Is inconsistent if a=0.
d)None of the above
Example of justification for the answer selected:
Note that WA does not warn of the case a=−1, which is obviously inconsistent since the system we have in this case is: x+y=3, x+y=5. The correct answer is d).
Exercise 2.3.
B2.3 Provide a recommendation and warning to your classmates when working with WA that you have deduced from this drill.
We expect the students provide answers such as the following:
− In exercises with parameters, you have to be careful because sometimes WA does not offer all the possibilities:
− Consider whether the results are logical.
− When it solves it well, it is no doubt an invaluable aid.
− Do not blindly assume that any software will do everything correctly.
In the next section, we outline the results obtained from the students for these two drills.
3.3. Discussion of results: Answer to research question Q2
As indicated, in Drill 1 the correct answers are B1.1b, B1.2c and B1.3c. We decided to remove those who did not mark B1.2c from our study since they do not have enough of a baseline for us to interpret if their incorrect evaluation is independent of having used the software or not. Of the remaining students, those who marked B1.1a were deemed to be using the software incorrectly, and those who marked B1.1c, that they do not know how to work correctly with matrices. Regarding Drill 2, those who marked B2.1a or B2.1b and B2.2b or B2.2c have a very poor baseline and were removed from the study. Those that marked B2.1a and B2.2a were deemed to be using the software incorrectly.
The results from a Mathematics course for Accounting and Finance majors at the University of La Laguna, during the academic year 2017-18, for students who attended class on a regular basis, were as follows:
| Drill 1 | Drill 2 | |
|---|---|---|
| Students present | 124 | 89 |
| Sample with minimum level | 70 | 38 |
| Incorrect use of the software | 27 | 24 |
Comments on the Table:
Drill 1: 56% had the minimum level needed to do it, of whom 38% used the software incorrectly.
Drill 2: 43% had the minimum level needed to do it, of whom 63% used the software incorrectly.
We believe there were fewer students in the second drill because after the first two months, some dropped out of the course and focused on others that they had a better chance of passing.
We do not think that the absolute percentages are critically important. They vary depending on the test and the subjective interpretation that we give based on the answer that they mark. However, we can conclude, based on our objective, that the number of students who do not analyze the results provided by the computer is high. Even after being advised to do it, we did not detect an improvement in their use of the software. We can say that at least 38% used the software without questioning it, blindly, without analyzing the results.
Similar studies were conducted in other mathematics courses given to Economics and Business Management majors. As a summary of the results obtained in the three university degrees and their various first-year mathematics courses, we can say that in each drill, at least 30% of the students, and in most cases around 60%, used the software without questioning it and without checking the results for errors.
Therefore, in answer to research question Q2, we can confirm our perception that the software is used mechanically and that the results are accepted without reasoning.
Although the study provided a basis for developing a constructive critical attitude toward software, even more activities would be necessary in this area, and not only in our courses.
5. Conclusions
We hope that the wider use of this methodology can contribute in several aspects, such as:
− Awakening in the students a positive and prudent critical attitude toward any software.
− Creating a desire to learn more about mathematical methods, which provide the only safe option to review and reason in various ways the result obtained in any mathematical context.
− Encouraging teachers to create new materials to develop critical thinking and creative reasoning toward the results provided by any software.
− Positively assessing the acquisition of a critical and creative attitude to any matter and circumstance in life.
By way of summary, we can conclude that this work:
− Confirms, by using examples, that even in highly improved versions of specialized software, errors can still be found in exercises. The exercises do not have to be of such a high level that students cannot encounter them.
− Easily proves that they are indeed software errors, not attributable to us, by highlighting some contradiction in the results.
− Contributes another possible answer, of the many it has, to the question, “Why study the mathematical methods in depth if we have specialized software to do the calculations?” It is “Because no matter how powerful it is, we can’t rely blindly on software results, even for simple exercises of our courses.”
− Shows students that a large percentage of them accept, without question, the results provided by a computer, something that must not be done.
− Promotes multidisciplinarity since, although our exercises involved mathematics, the basic ideas can be extrapolated to any computer tool that is used without being aware of its benefits and limitations.
− Provides guidelines and recommendations to try to alleviate, and in some cases correct, the deficiency detected.
We finish by noting that, without a doubt, it is better to have software than not. Keeping a constructive critical attitude is what makes using it truly useful, rather than a mistake.
At the same time, we intend to recommend to software distributors that they provide online the list of errors found in each version and that are corrected in the next version. This, rather than making their software less reliable, will generate more confidence in their product.
As a final point, we propose a historical summary of the errors involving real cases and described in, among others, Ciaurri and Varona (2006), or on the website http://ta.twi.tudelft.nl/users/vuik/wi211/disasters.html, which contains a collection of disasters resulting from computer errors. Knowing the history behind certain software errors, some of which have caused deaths, rocket explosions, economic losses, etc., suggests that the problem will persist no matter how sophisticated the technology may become.
This study encourages us to continue with the idea by introducing different didactic proposals that contribute to the critical awakening of students, to a level that is adequate to our courses.











 nueva página del texto (beta)
nueva página del texto (beta)