Artículos

 

Conocimiento de futuros profesores sobre la idea de juego equitativo

 

Knowledge of future teachers in relation to the idea of fair games

 

Juan Jesús Ortiz*, Carmen Batanero**, José Miguel Contreras**

 

* Universidad de Granada, España. jortiz@ugr.es

** Universidad de Granada, España. batanero@ugr.es

*** Universidad de Granada, España. jmcontreras@ugr.es

 

Recepción: Abril 23, 2010
Aceptación: Septiembre 28, 2011.

 

RESUMEN

En este trabajo se evalúan los conocimientos de 167 futuros profesores de educación primaria en España respecto a un juego equitativo. Para valorar el conocimiento común del contenido, se analizaron las soluciones que dieron los docentes a dos problemas abiertos. También se estudiaron dos componentes del conocimiento didáctico, considerando el trabajo de los maestros en pequeños grupos: para evaluar el conocimiento especializado del contenido, se pidió a los participantes que identificaran los contenidos matemáticos en la tarea, mientras que para determinar el conocimiento del contenido y los estudiantes se les solicitó que distinguieran, entre un grupo de respuestas a la tarea hecha por alumnos de educación primaria, cuáles eran correctas e incorrectas. Los resultados de la investigación sugieren la necesidad de reforzar la formación de los futuros profesores, tanto en el conocimiento matemático como en el conocimiento didáctico.

PALABRAS CLAVE: Probabilidad, Juego equitativo, Formación de profesores.

 

ABSTRACT

In this paper we assess pre–service primary school teachers' knowledge in relation to fair games. Common knowledge of content is assessed through the responses given by 167 pre–service primary school teachers to two open–problems. In addition, two components of didactic knowledge are inferred trough the participants analyses, when working in small groups: (a) Specialized knowledge of content is assessed from their analyses of the tasks' mathematical content; and (b) knowledge of content and students is assessed from their assessment of responses provided by primary school students. Results suggest the need to reinforce the training of pre–service teachers both in the mathematical and the didactic knowledge.

KEY WORDS: Probability, Fair game, Teacher training.

 

RESUMO

Neste trabalho são avaliados os conhecimentos de 167 futuros professores de educação primária na Espanha em relação a um jogo equitativo. Para avaliar o conhecimento comum do conteúdo, foram analisadas as soluções dadas pelos docentes para dois problemas abertos. Também foram estudados dois componentes do conhecimento didático, considerando o trabalho dos mestres em pequenos grupos: para avaliar o conhecimento especializado do conteúdo, foi pedido aos participantes que identificassem os conteúdos matemáticos na tarefa, enquanto que para determinar o conhecimento do conteúdo e dos estudantes, foi solicitado que distinguissem entre um grupo de respostas na tarefa feita por alunos de educação primária, quais eram corretas e incorretas. Os resultados da pesquisa sugerem a necessidade de reforçar a formação dos futuros professores, tanto no conhecimento matemático como no conhecimento didático.

PALAVRAS CHAVE: Probabilidade Jogo equitativo Formação de professores.

 

RÉSUMÉ

Ce travail évalue les connaissances de 167 futurs professeurs de l'éducation primaire en Espagne en ce qui concerne un jeu équitable. Afin d'apprécier la << Common Content Knowledge >> (CCK; les connaissances générales du contenu), les solutions proposées par les futurs instituteurs pour résoudre deux problèmes ouverts ont été analysées. En examinant leur travail dans des petits groupes, deux composantes relevant des connaissances didactiques ont de même été étudiées : pour évaluer la << Specialized Content Knowledge >> (SCK; les connaissances spécialisées du contenu), on demanda aux participants d'identifier les contenus mathématiques du problème alors que pour déterminer la connaissance du contenu et les écoliers, on leur demanda, parmi un ensemble de réponses au problème apportées par les élèves de primaire, de faire la distinction entre celles qui étaient correctes et celles qui ne l'étaient pas. Les résultats de cette recherche suggèrent qu'il est nécessaire d'améliorer la formation des futurs professeurs, tant sur le plan de leurs connaissances mathématiques que sur celui de leurs connaissances didactiques.

MOTS CLÉS: Probabilité, Jeu équitable, Formation des professeurs.

 

1. INTRODUCCIÓN

En la actualidad observamos un interés en iniciar el estudio de los fenómenos aleatorios y la probabilidad desde la Educación Primaria. Por ejemplo, en los Decretos de Enseñanzas Mínimas en España (MEC, 2006) se incluyen los siguientes contenidos: "Fenómenos aleatorios y vocabulario relacionado"; "descripción y cuantificación de situaciones aleatorias"; "reconocimiento de fenómenos aleatorios en la vida cotidiana"; "planificación y realización de experimentos simples para estudiar el comportamiento de los fenómenos aleatorios". Otros programas recientes (NCTM, 2000; SEP, 2006) sugieren transmitir al niño un lenguaje elemental probabilístico mediante juegos, experimentos y observación de fenómenos naturales, para que aprenda a identificar las situaciones aleatorias y llegue al final de la etapa a asignar algunas probabilidades sencillas.

La consecución de estos objetivos requiere una formación adecuada del futuro profesor de Educación Primaria. Por ejemplo, en España, el Ministerio de Educación (MEC, 2007) ha establecido las siguientes competencias que deben adquirir los futuros profesores:

– Competencias matemáticas básicas (numéricas, geométricas, estimación y medida, organización e interpretación de la información).

– Capacidad para desarrollar y evaluar contenidos del currículo mediante recursos didácticos apropiados y para promover las competencias correspondientes en los estudiantes.

La investigación sobre formación de profesores es hoy día muy amplia (ver, por ejemplo, Llinares & Krainer, 2006; Ponte & Chapman, 2006; Wood, 2008), aunque pocos trabajos se han centrado en los conocimientos de los futuros profesores respecto a la estadística. Este olvido ha llevado a la International Commission on Mathematics Education (ICMI) y la International Association for Statistics Education (IASE) a organizar un estudio conjunto para promover la investigación sobre el tema (Batanero, Burrill & Reading, 2011).

En nuestro trabajo tendremos en cuenta, en primer lugar, la diferencia entre el conocimiento del contenido matemático y el conocimiento pedagógico del contenido, que Shulman (1986, p. 8–9) describe como "la forma particular del conocimiento del contenido que incorpora el aspecto del contenido que guarda más relación con la enseñanza" o bien "esa amalgama especial de contenido y pedagogía que es el campo propio de los profesores, su forma especial de comprensión profesional".

Ball, Lubienski y Mewborn (2001) denominan conocimiento matemático para la enseñanza a la unión del conocimiento del contenido matemático y el conocimiento pedagógico del contenido. Dicho conocimiento es descrito por Hill, Ball y Schilling (2008) como "el conocimiento matemático que utiliza el profesor en el aula para producir instrucción y crecimiento en el alumno" (p. 374). Dentro del conocimiento del contenido matemático distinguen varios componentes: El Conocimiento Común del Contenido es el puesto en juego para resolver problemas matemáticos por cualquier persona instruida en matemática, sin que necesariamente sea un profesor, el Conocimiento Especializado del Contenido es conocimiento matemático, pero incluye aspectos que no necesariamente tiene una persona ordinaria, por ejemplo, identificar las ideas matemáticas trabajadas en un problema o buscar un ejemplo adecuado para presentar una idea matemática. El Conocimiento en el Horizonte Matemático aporta perspectiva a los profesores para su trabajo, e incluye, por ejemplo, conocimiento de la relación con otras materias, o la historia de las matemáticas.

Para el conocimiento pedagógico del contenido Hill, Ball y Schilling (2008) proponen tener en cuenta tres componentes. El Conocimiento del Contenido y los Estudiantes es el "conocimiento de cómo los estudiantes piensan, saben, o aprenden este contenido particular" (p. 375). Incluye el conocimiento de los errores y dificultades, concepciones erróneas, estrategias utilizadas por el alumno y cómo evoluciona su razonamiento matemático. El Conocimiento del Contenido y la Enseñanza incluye saber construir, a partir del razonamiento de los estudiantes y las estrategias utilizadas por ellos, procesos pertinentes para promover su aprendizaje. El último componente es el Conocimiento del Currículo.

La finalidad de este trabajo es evaluar los conocimientos matemáticos para la enseñanza de los futuros profesores de Educación Primaria en relación con la idea de juego equitativo. Más concretamente, nos centraremos en el conocimiento común y especializado del contenido y en el conocimiento del contenido y los estudiantes, en la terminología de Hill, Ball y Schilling (2008). A continuación presentamos, en primer lugar, los antecedentes del trabajo y describimos su metodología. En segundo lugar, analizamos las soluciones dadas por 167 futuros profesores de Educación Primaria a dos problemas relacionados con la idea de juego equitativo, para evaluar su conocimiento común del contenido. Seguidamente se evalúan el conocimiento especializado del contenido, a partir de los contenidos matemáticos que los participantes, trabajando en grupo, identifican, en dichos problemas. El conocimiento del contenido y los estudiantes se deduce de las evaluaciones que los mismos grupos de participantes realizan de las respuestas a dichos problemas proporcionadas por algunos niños. Finalizamos con la discusión y conclusiones.

 

2. ANTECEDENTES

La investigación sobre la didáctica de la probabilidad es muy amplia (ver Jones, 2005 y Jones, Langrall, y Mooney, 2007), aunque es escasa la centrada en los conocimientos de los futuros profesores. Para este trabajo son relevantes tres tipos de investigaciones: (a) La relacionada con la comprensión del juego equitativo por parte de los niños, que permitirá seleccionar ítems y respuestas típicas de estudiantes utilizadas en la construcción del cuestionario propuesto a los futuros profesores, y para mostrar que algunas respuestas de los futuros profesores son similares a las de los niños; (b) Puesto que un paso para decidir si un juego es equitativo es comparar las probabilidades de los sucesos implicados, consideraremos también las estrategias descritas por Piaget e Inhelder (1955) en la comparación de probabilidades, que serán utilizadas para analizar las usadas por los futuros profesores participantes en el estudio al resolver los problemas propuestos; (c) Finalmente será necesario tener en cuenta las investigaciones previas sobre comprensión de la probabilidad por parte de futuros profesores. A continuación se hace un resumen de estos tres tipos de investigación.

2.1. Comprensión de la idea de juego equitativo en niños y adolescentes

Los juegos de azar son uno de los principales contextos en el que los niños pueden comprender las características de las situaciones aleatorias (Batanero, 2005). Por este motivo, varias investigaciones han analizado las concepciones que los niños tienen sobre el juego equitativo.

Watson y Collis (1994) estudiaron las estrategias que siguieron niños entre 8 y 10 años para decidir si juego es o no equitativo. Los autores encontraron que, al jugar con un dado, aproximadamente la mitad de los niños creían que algunos números tenían más probabilidad que otros de salir, incluso en dados no sesgados. Otros mostraron concepciones antropomórficas, pensando que un dado tenía su propio razonamiento, se guiaron por las características físicas de los dados o usaron otros aspectos irrelevantes para decidir si el juego era equitativo.

Lidster, Pereira–Mendoza, Watson y Collis (1995) analizaron la influencia de las experiencias extraescolares en el desarrollo de la idea de juego equitativo. Para ello realizaron entrevistas a niños de 12 a 14 años, utilizando juegos de azar, y deduciendo sus concepciones, a partir de la interpretación y predicción que hacen sobre datos obtenidos en dichos juegos. En Lidster, Watson, Collis y Pereira–Mendoza (1996) describen un estudio con alumnos de 8 a 14 años, a los que se preguntó cuáles, entre una serie de dados, eran o no sesgados. Los autores sugieren que las nociones de juego equitativo y sesgo se desarrollan antes del comienzo de la escuela e indican un desajuste entre el aprendizaje previsto por el profesor y el conocimiento construido por el alumno.

Scholttmann y Anderson (1994) estudiaron las intuiciones de los niños de 5 a 10 años sobre la esperanza matemática, utilizando para ello dos tipos de juegos con un solo jugador: (a) juegos con un solo premio, donde el niño puede obtener un premio en caso de resultar un cierto suceso de un experimento aleatorio; (b) juegos con dos premios, donde el niño siempre obtiene un premio, que tiene diferente valor, según el resultado del experimento. Los autores concluyen que los niños, incluso los más jóvenes, poseen una intuición correcta sobre la esperanza matemática, teniendo en cuenta para tomar sus decisiones, tanto la probabilidad como el valor del premio. Sin embargo, en la asignación de probabilidad siguen, con frecuencia, estrategias aditivas.

Vahey, Enyedy y Gifford (1997) examinaron el razonamiento de alumnos de secundaria dentro de un entorno de aprendizaje basado en la tecnología, que conceptualizaba e implicaba a los alumnos en el análisis de la equitatividad de los juegos de azar. Su investigación mostró que los alumnos empleaban el razonamiento probabilístico en forma productiva en esa tarea. Según estos autores hay dos situaciones posibles cuando se estudia la equitatividad de un juego: (a) si en cada partida todos los jugadores tienen la misma probabilidad de ganar, el juego es equitativo cuando cualquier jugador obtiene la misma cantidad en caso de salir premiado; (b) si las probabilidades de ganar los distintos jugadores son diferentes, el juego es equitativo sólo cuando la esperanza matemática (producto de la probabilidad de ganar por la cantidad que se obtiene como premio) es idéntica para todos los jugadores.

Cañizares, Batanero, Serrano y Ortiz (1999) analizaron las concepciones de alumnos entre 10 y 14 años, sobre el juego equitativo utilizando los dos tipos de situaciones propuestas por Vahey, Enyedy y Gifford (1997). Aunque la mayoría de los alumnos mostró una adecuada concepción del juego equitativo, hubo una gran variedad de respuestas, desde alumnos que no diferenciaron entre sucesos equiprobables y no equiprobables, hasta otros que fueron capaces de obtener el valor del premio para transformar un juego no equitativo en otro equitativo. En nuestra investigación se utilizarán dos ítems propuestos por Cañizares et al., y ejemplos de las respuestas más frecuentes proporcionadas por alumnos participantes en dicha investigación, para construir las tareas propuestas a los futuros profesores. También se comparará, ocasionalmente, las respuestas de los futuros profesores con las de los alumnos en la investigación de Cañizares et al., para mostrar la similitud de dichas respuestas, aunque la comparación entre los dos grupos no es un objetivo del trabajo.

2.2. Estrategias en la comparación de probabilidades

Para decidir si un juego es equitativo, el primer paso es compararlas probabilidades de ganar de los diferentes jugadores. Para analizar las estrategias utilizadas por los futuros profesores al realizar esta comparación, en nuestro estudio aplicaremos la clasificación que realizaron de dichas estrategias Piaget e Inhelder (1951), mostrando que, en algunos casos, los futuros profesores no alcanzan las consideradas por Piaget e Inhelder como adecuadas en los sujetos adultos.

En sus investigaciones, Piaget e Inhelder se centran en dar criterios para determinar en qué nivel de desarrollo intelectual se encuentra el niño a diversas edades, postulando que el conocimiento es construido activamente por el sujeto y no recibido pasivamente del entorno. El niño trata de adaptarse al mundo que le rodea. Cuando una idea nueva se le presenta, se crea un "conflicto cognitivo" si esta idea choca con las ya existentes, que se resuelve mediante un proceso de "equilibración", que consiste en los pasos de asimilación y acomodación. El desarrollo intelectual del sujeto sigue una serie de etapas, cada una de las cuáles tienen un modo de razonamiento similar y la progresión de una etapa a otra siempre sigue un cierto patrón. Para el estudio de la probabilidad son relevantes la etapa Preoperatoria, caracterizada por la necesidad de manipular objetos reales para el aprendizaje de un cierto concepto, Operaciones concretas, donde aparecen conceptos secundarios, que no necesitan ser abstraídos de la experiencia concreta y Operaciones abstractas, donde se pueden manipular relaciones entre representaciones simbólicas, y se comprende el significado de abstracciones, sin referirse a objetos particulares.

Piaget e Inhelder, indican que, cuando se propone a los niños comparar dos probabilidades, al comienzo de la etapa preoperatoria, tratan de comparar los casos posibles y posteriormente, centran su atención en la comparación de los casos favorables. Al final de esta etapa, si se propone comparar dos probabilidades, cuando hay el mismo número de casos favorables, los sujetos comparan el número de casos desfavorables. Una estrategia más avanzada es la estrategia de correspondencia, que consiste en establecer un criterio de proporcionalidad en una fracción (por ejemplo, comprobar que el número de casos favorables es el doble que el de desfavorables) y aplicarlo a la otra (comprobar si la razón entre casos favorables y desfavorables es mayor, igual o menor que en la primera). Esta estrategia aparece durante el período de operaciones concretas, aunque no se desarrolla en su totalidad hasta el periodo de operaciones formales, para ir transformándose en una estrategia multiplicativa, en que se comparan los cocientes entre casos favorables y los posibles en las dos probabilidades. Esta sería la estrategia adecuada en la edad adulta según los autores.

2.2. Formación de profesores para enseñar probabilidad

Como hemos indicado, el gran esfuerzo de investigación sobre formación de profesores realizado en los últimos años, apenas ha tenido en cuenta el caso específico de la formación de profesores para enseñar probabilidad y, mucho menos, en relación con el juego equitativo.

Las escasas investigaciones sobre razonamiento probabilístico señalan la existencia de concepciones erróneas y dificultades en los futuros profesores. Por ejemplo, Azcárate (1995) propone a 57 profesores de Educación Primaria un cuestionario donde se pide decidir si una serie de experimentos son o no aleatorios. La autora encontró que pocos mostraban una idea clara sobre las características de los fenómenos aleatorios. Algunos participantes explicaron la aleatoriedad mediante criterios de causalidad (por ejemplo, indicaron que un fenómeno es aleatorio únicamente si se desconocen sus causas). Otros tuvieron una fuerte influencia de los aspectos contextuales o consideraron que no es posible el estudio matemático de los fenómenos aleatorios. Se detectó también falta de esquemas combinatorios y escasa competencia de cálculo de probabilidades, cuantificando las probabilidades de un suceso desde criterios personales. Resultados similares fueron obtenidos por Serrano (1996) en un estudio exploratorio con 10 futuros profesores, utilizando entrevistas en las que propone realizar y evaluar experimentos aleatorios. Algunos de esto profesores también mostraron dificultades con el concepto de independencia y el sesgo de equiprobabilidad (Lecoutre, 1992), que consiste en creer que todos los sucesos asociados a cualquier experimento aleatorio, son equiprobables. Estas mimas concepciones incorrectas sobre la aleatoriedad e independencia fueron encontradas por Batanero, Arteaga, Ruiz y Roa (2010) en un estudio con 200 futuros profesores de Educación Primaria, donde se pide a los participantes evaluar sus propias concepciones sobre la aleatoriedad, a partir de un proyecto que incluye la realización de un experimento aleatorio.

Ortiz, Mohamed, Batanero, Serrano y Rodríguez (2006) analizaron las estrategias que 102 futuros profesores de Educación Primaria utilizaron en la resolución de problemas elementales de comparación de probabilidades. Observaron que, en general, hacían uso de estrategias correctas (multiplicativas y de correspondencia), que indicaba un buen nivel de razonamiento proporcional, aunque todavía había un grupo importante que utilizaron estrategias incorrectas o mostraron sesgos de razonamiento. Otros autores se han preocupado del diseño de acciones formativas para ayudar a los futuros profesores a mejorar su razonamiento probabilístico. Por ejemplo, Batanero, Godino y Cañizares (2005) proponen un cuestionario a 132 futuros profesores de educación primaria, observando sesgos en su razonamiento probabilístico, como la heurística de la representatividad (consistente en juzgar la probabilidad de una muestra en base a su similitud con la población de la que se toma) y la heurística de la equiprobabilidad. Estos sesgos se vieron notablemente reducidos después de un experimento de enseñanza basado en la simulación con dispositivos manipulativos y ordenadores.

Respecto a la idea de juego equitativo, el único antecedente que hemos encontrado es el trabajo de Azcárate (1995), quien, en la investigación ya citada propuso tres ítems basados en el lanzamiento de dos dados, preguntando a los 57 profesores participantes si sería equitativo apostar a producto par, suma par y suma 5 o 6. Los participantes mostraron mucha dificultad para diferenciar los juegos equitativos y basaron sus argumentos en la equiprobabilidad de los resultados, reglas aritméticas o argumentación combinatoria.

Son también escasos los trabajos centrados en el conocimiento didáctico de los profesores. Entre ellos encontramos el de Lopes (2006), que analizó la forma en que los profesores diseñan y llevan a cabo unidades didácticas para la enseñanza de la probabilidad, sobre todo en la escuela primaria, mostrando la gran dificultad de estos profesores al enfrentarse a conceptos nuevos para ellos. En el estudio de Stohl (2005) examina cómo 35 profesores de educación secundaria interpretaban las interacciones de los alumnos con una herramienta de simulación, encontrado que muchos de los profesores fallaron al implementar el enfoque experimental en la enseñanza de la probabilidad, porque las tareas que proponían a los estudiantes sólo utilizaban muestras pequeñas. Por este motivo, los estudiantes de estos profesores no pudieron apreciar la convergencia o el efecto del tamaño de la muestra sobre la misma, es decir no llegaron al punto central del enfoque frecuencial de la probabilidad.

En este trabajo completaremos las investigaciones anteriores, centrándonos específicamente en el concepto de juego equitativo que apenas ha sido considerado en los antecedentes y analizando tanto el conocimiento matemático, como el didáctico de los futuros profesores. A continuación describimos la metodología y los resultados obtenidos.

 

3. MÉTODO

3.1. Muestra

La muestra participante estuvo formada por 167 futuros profesores de Educación Primaria de la Universidad de Granada, España, de entre 19 y 20 años, en su primer año de estudios. Todos ellos habían estudiado probabilidad simple y condicional, durante la Educación Secundaria, dos años antes de ingresar en la universidad. Un 65% de estos estudiantes provenían del Bachillerato de Ciencias Sociales, en el que en el último año hay un cuatrimestre de Estadística, donde estudiaron la probabilidad condicional, distribuciones de probabilidad binomial y normal e introducción al muestreo e inferencia. El resto había cursado el Bachillerato de Ciencia y Tecnología o formación profesional, donde no se estudia estadística.

3.2. Cuestionario utilizado

Para la construcción del cuestionario se siguió la metodología propuesta por Godino (2009) para formular cuestiones de evaluación del conocimiento matemático para la enseñanza. Dicha metodología consta de dos pasos:

1. Elegir una tarea matemática cuya solución ponga en juego los principales aspectos del contenido, o competencias a desarrollar; en nuestro caso, la idea de juego equitativo;

2. Formular consignas que cubran los componentes del conocimiento del profesor. Para evaluar el conocimiento común del contenido, dicha consigna consistiría en resolver el problema; para evaluar el conocimiento especializado del contenido habría que identificar los objetos y procesos matemáticos puestos en juego en la solución; para evaluar el conocimiento del contenido y los estudiantes, una consigna posible sería describir los razonamientos que los alumnos han desarrollado al resolver la tarea propuesta o los principales errores en dicha solución.

En la Figura 1 se muestra el cuestionario utilizado en esta investigación, donde se han incluido las dos situaciones que, de acuerdo a Vahey, Enyedy y Gifford (1997), pueden presentarse al analizar la equitatividad de un juego:

(a) que los dos jugadores tengan la misma probabilidad de ganar (ítem 1), y

(b) que tengan distinta probabilidad (ítem 2). Como se ha indicado, los dos ítems fueron utilizados previamente en la investigación de Cañizares et al. (1999).

Las respuestas incluidas en la segunda parte de cada tarea son respuestas típicas que proporcionaron en cada uno de los ítems niños participantes en dicha investigación.

En el ítem 1, que Cañizares tomó de Fischbein y Gazit (1984), el número de casos favorables y posibles en las dos urnas guarda proporción, por lo cual las probabilidades de obtener una bola blanca en las dos urnas son iguales. Como ambos jugadores reciben el mismo premio, el juego es equitativo. El ítem incluye un distractor, que describe la creencia de algunos niños en que, a pesar de tener igual probabilidad, el número de casos favorables representa una ventaja. Para resolver el problema, primero se calculan las probabilidades de cada jugador, bien observando que la proporción entre casos favorables y posibles es la misma en las dos urnas o aplicando la regla de Laplace. A continuación se observa que la cantidad a ganar es la misma para los dos jugadores y, por tanto, el juego es equitativo. El contenido matemático (apartado b) incluye, en consecuencia, comparación de fracciones, experimento aleatorio, descripción del espacio muestral, casos favorables, desfavorables y posibles, juego equitativo y proporción, probabilidad y cálculo de probabilidades.

Las respuestas correctas (apartado c) son las de los alumnos A3, A6 y A7. Los alumnos A3 y A6 han comparado la razón entre casos desfavorables/favorables, han usado las ideas de probabilidad y la comparación de razones. El alumno A7 aplica la regla de Laplace (cociente entre casos favorables y posibles), utiliza las ideas de probabilidad, fracción, número decimal, comparación de fracciones y decimales. Respecto a las dificultades previstas en los estudiantes (apartado d), el alumno A1 razona sólo en base al número de bolas negras (casos desfavorables), y el estudiante A2 razona sólo en base al número de bolas blancas (casos favorables); mostrando ambos dificultad en la comparación de probabilidades y fracciones. El alumno A4 compara probabilidades mediante estrategias aditivas en vez de multiplicativas y el A5 manifiesta una concepción errónea de la aleatoriedad, suponiendo que todos los sucesos son equiprobables.

En el ítem 2, que Cañizares tomó de Green (1983), las probabilidades de ganar son diferentes, por lo que, para que el juego sea equitativo, las ganancias deberán ser inversamente proporcionales a la probabilidad de ganar de cada jugador. De este modo, sería igual la esperanza matemática de los jugadores. Puesto que María tiene cinco casos favorables y cada vez gana un euro, y Esteban tiene sólo un caso favorable, ha de ganar cinco euros cada vez que gane. Para resolver este problema, el alumno debe identificar los casos favorables y posibles, saber lo que es un juego equitativo y aplicar las ideas de esperanza matemática y proporcionalidad inversa entre probabilidad y ganancia.

Para evaluar las respuestas de los estudiantes también se requiere una comprensión de que la frecuencia relativa de los diferentes resultados del juego se igualan, aproximadamente, en una serie larga de repeticiones; pero en una serie corta de ensayos, puede haber oscilaciones importantes en dichas frecuencias. La única respuesta correcta es la del alumno B1. El alumno B2 comprende que María tiene más casos favorables, pero no cuantifica correctamente las probabilidades de cada jugador y da un valor incorrecto del premio que tendría que recibir Esteban. El estudiante B3 calcula correctamente la probabilidad de ganar cada jugador y, aplicando una probabilidad inversa, calcula correctamente el valor del premio, aunque añade una condición innecesaria para que el juego sea equitativo (repetir el juego tres veces); esta exigencia podría indicar una concepción incorrecta de la convergencia, que consistiría en esperar la convergencia en una serie de ensayos corta. Los alumnos B4, B5 conciben el juego equitativo como aquél en que los dos jugadores tienen las mismas probabilidades, no relacionando la equitatividad del juego con el valor del premio.

3.2. Método de recogida de datos

Los datos se recogieron dentro de una asignatura de Matemáticas y su Didáctica, que forma parte del plan de formación de estos profesores, a lo largo de dos sesiones. En la primera, se proporcionó a los estudiantes los dos problemas presentados en la Figura 1, pidiéndoles que resolvieran por escrito el apartado (a), con el objetivo de evaluar su conocimiento común del contenido matemático. El motivo que nos llevó a elegir estos problemas, a pesar de haber sido diseñados para investigaciones con niños, fue disponer de respuestas típicas a los mismos, obtenidas en nuestras propias investigaciones con alumnos de Educación Primaria. A partir de ellas, se han seleccionado las incluidas en cada uno de los ítems, que serán analizadas por los futuros profesores en los apartados (c) y (d) de los mismos.

En la segunda sesión, se pidió que resolvieran por escrito el resto de los apartados, trabajando en pequeños grupos (31 grupos en total). El apartado (b) pide analizar el contenido matemático necesario para resolver el ítem. De acuerdo con Godino (2009), esta pregunta lleva a reflexionar sobre los diferentes procedimientos posibles de resolución, modalidades de expresión, conceptos y propiedades que se ponen en juego en su formulación, y sobre maneras de justificar los procedimientos y por tanto evalúa el conocimiento especializado del contenido. En el apartado (c) se debe decidir, entre una serie de respuestas dadas por niños de Educación Primaria a los mismos ítems, cuáles de ellas son correctas, y en el (d) indicar las posibles intuiciones o estrategias incorrectas que han llevado a los estudiantes a dar una respuesta errónea evaluando por tanto, el conocimiento del contenido matemático y los estudiantes.

 

4. CONOCIMIENTO COMÚN DEL CONTENIDO

Recogidas las respuestas de los futuros profesores, se realizó un análisis de contenido de las mismas, cuyos resultados se muestran a continuación.

4.1. Análisis de resultados en el ítem 1

El 70.6% de los futuros profesores (Tabla 1) consideró que el juego propuesto en el ítem 1 es equitativo. Esta alta proporción indica que los futuros profesores muestran un buen razonamiento probabilístico en este ítem y una concepción adecuada del juego equitativo. Las estrategias empleadas para comparar las probabilidades de los dos jugadores se analizan a continuación.

Comparación del número de casos favorables: Un 14.4% de futuros profesores empleó esta estrategia incorrecta, que según Piaget e Inhelder (1951) corresponde a la etapa preoperatoria e indica una comprensión incorrecta de la probabilidad, pues sólo se usan dos de los cuatro datos proporcionados en el problema. Un ejemplo de respuesta dada por un participante es la siguiente: "La probabilidad de ganar Luis es mayor que la de Eduardo, pues tiene más bolas blancas; por tanto es más sencillo sacar una al extraer una bola al azar". La proporción de uso de esta estrategia por los participantes en nuestro estudio es alta, dada la sencillez del problema y tratarse de futuros profesores.

Comparación del número de casos desfavorables: Los sujetos eligen la caja que tenga menos casos desfavorables, estrategia que corresponde, según Piaget e Inhelder (1951), al final del nivel preoperacional. Un ejemplo es el siguiente: "No estoy de acuerdo, porque en ese caso Luis tiene menos probabilidades de ganar, ya que tiene más bolas negras". Aunque la proporción de uso de esta estrategia por los participantes en nuestro estudio fue pequeña, consideramos que no debiera darse en futuros profesores.

Estrategia de correspondencia: Consiste en establecer un criterio de proporcionalidad en una fracción, por ejemplo, ver que el numerador es el doble que el denominador y ver si en la otra fracción la razón entre numerador y denominador es mayor o menor. Como se ha indicado, esta estrategia no se desarrolla en su totalidad hasta el periodo de las operaciones formales (Piaget e Inhelder, 1951). Un ejemplo es el siguiente: "Creo que el juego es equitativo pues los dos tienen la misma probabilidad de ganar: el número de bolas blancas y negras guarda la misma proporción". El 36.5% de futuros profesores empleó esta estrategia, que sería válida para este problema pues proporciona una solución correcta al mismo.

Estrategia multiplicativa: Consiste en compararlas dos fracciones. Según Piaget e Inhelder (1951) esta estrategia, propia del período de las operaciones formales, es muy elaborada y requiere del dominio del cálculo con fracciones, puesto que se aplicaría explícitamente la regla de Laplace, como cociente de casos favorables entre posibles. Un ejemplo es el siguiente: "Tienen las mismas probabilidades ambos; la probabilidad de obtener una bola blanca para Eduardo es y lo mismo para Luis 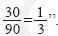. El porcentaje de utilización de esta estrategia por futuros profesores fue del 34.1%.

Dos participantes compararon sólo el número de casos posibles y otros tres consideraron aspectos irrelevantes, como el color favorito o la posición de las bolas en la urna o hicieron referencia a la suerte. El resto produjo una respuesta correcta, pero incompleta, al no explicar cómo llegaron a la conclusión de que el juego era equitativo.

Observamos, como resumen, que los futuros profesores en nuestro estudio hacen uso predominante de estrategias correctas, lo cual corresponde a un buen razonamiento probabilístico, aunque todavía hay un porcentaje importante que utiliza estrategias incorrectas.

4.2. Análisis de resultados en el ítem 2

La respuesta mayoritaria al ítem 2 (77.2%) fue la correcta (Ver tabla II). En cuanto a los argumentos empleados, el 69.5% de estas respuestas correctas se apoya en la comparación de las probabilidades de ganar de los contrincantes, como muestra la siguiente respuesta: "Esteban debe ganar 5 euros, porque su probabilidad es 5 veces mayor que la de María". El resto de futuros profesores que dieron la respuesta correcta, no compararon explícitamente las probabilidades de cada uno de los jugadores.

Con mucho menor frecuencia aparece la respuesta 6 euros (7.2%). En este caso, se admite la ventaja de María pero no se cuantifica correctamente el valor del premio para que el juego sea equitativo, como ocurre con la respuesta siguiente: "Esteban debe recibir 6 euros, porque hay 1 posibilidad entre 6 de que salga el 1". Aunque se calcula correctamente la probabilidad de ganar Esteban, no se compara con la de María; en lugar de ello, se compara con el número de resultados posibles en el juego y por tanto no se aplica la idea de esperanza matemática.

Siete futuros profesores otorgaron la misma ganancia independientemente de las probabilidades de ganar: "Esteban debe ganar 1 euro, es lo mismo que gana María sacando un número del 2 al 6". No son conscientes de que, al ser mayor la probabilidad de ganar María, el valor del premio ha de ser inversamente proporcional a dicha probabilidad. El mismo tipo de argumento sirve para apoyar las respuestas de los que indican que habría que dar 2, 3 o 4 euros. Otras respuestas han sido las que indican la correspondencia entre casos favorables y desfavorables: "por cada vez que gane Esteban, María ganará unas cinco veces", sin calcular el valor del premio, respuestas en que, al menos, encontramos razonamiento proporcional. No contestan el 4.8%. En resumen, destaca también el alto porcentaje de respuestas correctas, aunque todavía el 22.8% de los participantes no es capaz de encontrar el valor del premio para que el juego sea equitativo.

 

5. CONOCIMIENTO ESPECIALIZADO DEL CONTENIDO

Como hemos indicado, en la segunda sesión los futuros profesores trabajaron en pequeños grupos para resolver el resto de las cuestiones. A continuación, analizamos los resultados en el segundo apartado en que preguntamos por los conocimientos puestos en juego en la solución.

5.1. Análisis de resultados en el ítem 1

Los contenidos matemáticos mejor identificados por los futuros profesores en el ítem 1 (Tabla III), fueron la probabilidad y el cálculo de probabilidades mediante la regla de Laplace, que generalmente se citan juntas. El uso y comparación de fracciones, fue citado por pocos grupos, siendo también escasa la mención de la proporcionalidad, la aleatoriedad o los casos posibles (a veces denominados como posibilidades). Dos grupos hicieron referencia a la comparación de probabilidades; otros dos, a números y operaciones. No se identificaron en la tarea el espacio muestral, sucesos, casos favorables o desfavorables, juego equitativo, ni proporción, por lo que consideramos que el conocimiento especializado del contenido mostrado por los futuros profesores fue escaso.

5.2. Análisis de resultados en el ítem 2

El contenido matemático mejor identificado en el ítem 2 (Tabla IV) fue la probabilidad y el cálculo de probabilidades mediante la regla de Laplace, seguido por el juego equitativo, con menor frecuencia y las ideas de azar o aleatoriedad. También se citaron escasamente el razonamiento combinatorio, es decir, la capacidad de enumerar los resultados del experimento y la estimación de la probabilidad, mediante la realización del experimento un número grande de veces, tomando la frecuencia relativa como un valor aproximado de la probabilidad. Dos grupos identificaron la proporcionalidad; otros dos, la comparación de fracciones.

En otros contenidos hemos incluido los que hacen mención a la lógica (1 grupo); experimentación (1 grupo); números y operaciones (1 grupo); conocimiento matemático (1 grupo). No hubo referencia explícita al experimento aleatorio, casos favorables o posibles, esperanza matemática o proporcionalidad inversa entre probabilidad y ganancia. Por esta razón, consideramos que el conocimiento especializado del contenido mostrado por los futuros profesores fue insuficiente.

Los resultados en este apartado en los dos ítems corroboran la investigación de Chick y Pierce (2008), cuyos profesores no hicieron un uso adecuado de los recursos proporcionados por el investigador al planificar lecciones de estadística y probabilidad, pues fallaron en sacar a la luz los conceptos latentes, a pesar de la riqueza de conceptos de la situación didáctica planteada.

 

6. CONOCIMIENTO DEL CONTENIDO Y LOS ESTUDIANTES

En los dos apartados (c) y (d) se pidió a los futuros profesores evaluar las respuestas de estudiantes de Educación Primaria e indicar las causas de sus dificultades.

6.1. Análisis de resultados en el ítem 1

La mayoría de los grupos (Tabla V) fue capaz de discriminar las respuestas correctas e incorrectas al ítem 1, siendo el caso más difícil la respuesta A3, que ocho grupos de futuros profesores consideraron incorrecta, posiblemente porque el niño usa menos elementos matemáticos en su respuesta que las dadas por A6 y A7. Otros tres grupos de futuros profesores consideraron correcta la dada por el alumno A5, asumiendo que los dos jugadores tienen la misma probabilidad de ganar. Estos participantes muestran el sesgo de equiprobabilidad (Lecoutre, 1992), que también se observó en el estudio de Serrano (1996) con futuros profesores de primaria.

La tarea de detectar las respuestas correctas e incorrectas en el ítem ha sido más sencilla para los futuros profesores que la resolución del problema (Tabla I), lo que podría explicarse por la ventaja del trabajo en colaboración o porque los participantes hubiesen indagado personalmente las respuestas correctas después de resolver la primera parte. Sin embargo, pocos grupos detectaron las causas de los razonamientos erróneos (Tabla VI), dando explicaciones alternativas. La estrategia errónea de comparar solo casos favorables (alumno A2) fue la más reconocida, seguida de la de comparar solo casos desfavorables (alumno A1). Ningún grupo reconoció la estrategia aditiva (alumno A4) como errónea y sólo 3 grupos reconocen el sesgo de equiprobabilidad (alumno A5) como erróneo.

Entre las explicaciones alternativas aportadas por los grupos de futuros profesores destacan no tener en cuenta la proporción entre casos favorables y posibles en las dos urnas o el desconocimiento de la probabilidad por parte de los alumnos. Un alto número de grupos de futuros profesores no contestan o no saben explicar la causa del error de los diferentes alumnos de primaria. Así, por ejemplo, un grupo de futuros profesores afirma que "el alumno A1 ha realizado un razonamiento lógico a priori, comparando la cantidad de bolas negras de las dos urnas, pero inconscientemente ha asumido que los dos porcentajes son iguales". Esta explicación no es satisfactoria, porque el alumno A1 no ha comparado las dos proporciones, sino sólo el número de casos favorables en cada urna.

6.2. Análisis de resultados en el ítem 2

La mayor parte de los grupos fue capaz de discriminar las respuestas correctas e incorrectas al ítem 2 (Tabla VII), aunque hay un importante número de grupos que no las diferencian. Los casos más difíciles fueron el B5 y B4, donde once y nueve grupos de futuros profesores respectivamente consideraron correctas las respuestas, debido a la creencia de que el juego sólo es equitativo si los dos jugadores tienen las mismas probabilidades, no utilizando el valor del premio en su respuesta. Otro caso con cierta dificultad fue el B3, que siete grupos consideraron correcta, esperando que en tres jugadas se equilibre el juego, lo cual es poco probable en una serie tan corta. Para este ítem también ha sido mejor la detección por parte de los futuros profesores de las respuestas correctas e incorrectas que sus propias respuestas al mismo, al trabajar en grupos.

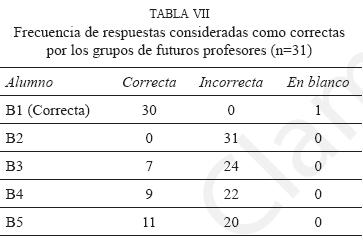
Fueron pocos los grupos que detectaron los razonamientos erróneos presentados (Tabla VIII), optando la mayoría por dar una explicación alternativa. El error mejor reconocido fue el fallo en la proporcionalidad inversa (alumno B2), seguido por el de considerar que el juego es equitativo solo si se juega varias veces (alumno B3). La argumentación menos reconocida como errónea fue considerar que María y Esteban han de tener igual probabilidad (alumnos B4 y B5).

También se observa un número muy alto de grupos de futuros profesores que no contestan o dan una explicación inadecuada, cuando intentan argumentar el razonamiento seguido por los diferentes alumnos de primaria. Lo más frecuente fue indicar que los alumnos hicieron un razonamiento correcto, sin saber explicarlo. Por ejemplo, un grupo de futuros profesores afirma que "(el alumno B5) ha razonado correctamente, pero no ha comprendido la pregunta que le hacen, ya que le preguntan cuánto dinero habría que darle para ser equitativo no de cuantos números le corresponden a uno y otro para ganar". Una explicación alternativa en todos los casos, menos en el B2, fue la del fallo en la estimación del valor del premio, sin justificar por qué se produce. En el caso B4, dos grupos indican que los niños no estiman correctamente la frecuencia: "podemos observar que el alumno B4 no se adecua a la estimación de frecuencia, lo que puede ser debido por no tener los conocimientos previos necesarios". Otros grupos identificaron incorrectamente las respuestas erróneas por fallo en su razonamiento probabilístico, por ejemplo, un grupo afirma: "la respuesta del alumno B3 es falsa, si a Esteban le dan tres oportunidades le tienen que dar 3 euros". Otro grupo indica que todas las respuestas son verdaderas menos la del alumno B2 "que piensa que al tener 6 caras el dado a Esteban le corresponden 6 euros pero a él solo le corresponde una cara".

     

7. DISCUSIÓN Y CONCLUSIONES

El estudio estuvo orientado a evaluar diversos componentes del conocimiento matemático para la enseñanza de los futuros profesores de Educación Primaria en relación con la idea de juego equitativo, siguiendo el modelo de Ball, Lubienski y Mewborn (2001) y Hill, Ball y Schilling (2008). Asimismo se utilizaron el tipo de preguntas sugerido por Godino (2009) para evaluar algunos componentes de dicho conocimiento. En lo que sigue discutimos nuestros resultados y mostramos las principales conclusiones respecto a cada uno de estos componentes.

Conocimiento común del contenido

Una primera aportación de nuestro trabajo es mostrar que la mayor parte de los futuros profesores participantes muestra un conocimiento común suficiente del contenido en relación al juego equitativo, mientras que Azcárate (1995) encontró que muchos participantes en su estudio tenían dificultad con esta idea. En nuestro estudio el 78.4% de los participantes clasifica correctamente el juego descrito en el ítem 1 y el 77.2% es capaz de encontrar el valor del premio necesario para transformar en equitativo el juego descrito en el ítem 2, aplicando correctamente la idea de esperanza matemática de la cantidad a ganar. Pensamos que la diferencia con los resultados de Azcárate se debe a que el juego propuesto por la autora (suma de puntos al lanzar dos dados) dificultó la tarea, en la que muchos participantes fallaron debido, no a falta de comprensión de la idea de juego equitativo, sino a falta de razonamiento combinatorio, (al considerar, por ejemplo, idénticas las combinaciones 56 y 65).

También las estrategias utilizadas para comparar probabilidades, con el objetivo de decidir si el juego es o no equitativo, han sido en su mayoría correctas, confirmando los resultados de Ortiz et al. (2006) pues predominan las estrategias de correspondencia o multiplicativas (70.6% en el ítem 1 y 69.5% en el ítem 2).

Hay, no obstante, errores, respuestas incompletas o no respuestas, en ambos ítems. En el ítem 1, alrededor de un 20% de futuros profesores llega a la conclusión de que el juego no es equitativo al aplicar estrategias incorrectas en la comparación de probabilidades, propias de niños en las etapas pre–operacional y concreta según Piaget e Inhelder (1951) y que serían improcedentes en estos problemas. En otros casos se obtiene la conclusión de que el juego es equitativo basándose en aspectos irrelevantes de la tarea, similares a los usados por niños en la investigación de Watson y Collis (1995) o en la de Cañizares et al. (1999). En el ítem 2, algunos futuros profesores, aunque calculan correctamente las probabilidades, no aplican la idea de esperanza matemática, ya que calculan el valor del premio en función del número de casos posibles, y no de la probabilidad de ganar (7.2%); comparan las probabilidades de ganar los dos jugadores sin llegar a establecer el premio (4.8%); o asignan el mismo premio, o un valor no relacionado con la probabilidad a los dos jugadores (6%).

Conocimiento especializado del contenido

Una aportación original de nuestro estudio es mostrar que el conocimiento especializado del contenido respecto a la idea de juego equitativo en los participantes es claramente insuficiente. Aunque, al pedir a los futuros profesores que identificaran los contenidos matemáticos en las tareas propuestas trabajando en grupo, muchos grupos fueron capaces de reconocer en las tareas las ideas de probabilidad y el uso de la regla de Laplace, sólo la tercera parte identifican la comparación de fracciones, y menos aún la proporcionalidad, aleatoriedad, espacio muestral, comparación de probabilidades, juego equitativo, esperanza matemática o proporcionalidad inversa implícitos en las tareas. En este punto, nuestros resultados apoyan las conclusiones de Chick y Pierce (2008), quienes, en un estudio sobre el trabajo con proyectos estadísticos, indican que algunos profesores no son capaces de identificar los conceptos latentes en una situación didáctica relacionada con la estadística o probabilidad.

La falta de capacidad para reconocer los objetos matemáticos necesarios para trabajar con una tarea, incluso cuando los por futuros profesores utilizaron dichos objetos al resolver correctamente los problemas planteados, es un motivo de preocupación, pues podría dificultar algunas de las actividades que realiza el profesor, tales como "indagar lo que los estudiantes conocen, elegir y manejar representaciones de las ideas matemáticas, seleccionar y modificar los libros de texto, decidir entre modos posibles de acción" (Ball, Lubienski, & Mewborn, 2001, p. 453). Estas tareas dependen claramente de su conocimiento especializado del contenido y, en vista de nuestros resultados, sería necesario mejorar este conocimiento en los futuros profesores, si queremos asegurar su éxito al realizar dichas actividades profesionales en la clase de probabilidad.

Conocimiento del contenido y los estudiantes

Para analizar el conocimiento del contenido y los estudiantes, se pidió a los futuros profesores, trabajando en grupos, que evaluasen las respuestas dadas por una serie de alumnos de Educación Primaria a los ítems propuestos. Al haber resuelto correctamente ellos mismos las tareas, fueron capaces de discriminar con facilidad las respuestas correctas e incorrectas de dichos alumnos a los ítems. Fue mucho menor el conocimiento mostrado de las posibles razones de los errores en las respuestas, ya que en muchos grupos hubo una inconsistencia entre la clasificación de una respuesta (como incorrecta) y la razón dada para explicar el error (indicando que la respuesta era correcta y el alumno no supo explicarse). Los razonamientos erróneos mejor identificados fueron el fallo en el razonamiento proporcional y el requerimiento de jugar varias veces para considerar un juego equitativo. En resumen, los futuros profesores en nuestro estudio muestran algunos conocimientos del contenido y los estudiantes, al reconocer las respuestas erróneas, pero la habilidad para explicar los errores de los estudiantes es insuficiente. Sería necesario mejorar la formación en este punto, dándoles a conocer los resultados de las investigaciones sobre didáctica de la probabilidad, que habría que transmitirles mediante una adecuada transposición didáctica previa.

Implicaciones del estudio

En este trabajo completamos los estudios previos sobre los conocimientos probabilísticos comunes de futuros profesores, y proporcionamos información original respecto a su conocimiento del juego equitativo, complementando el trabajo de Azcárate (1995). Proporcionamos también resultados originales sobre el conocimiento especializado y el conocimiento del contenido y los estudiantes, que no han sido tenidos en cuenta en la investigación previa. Estos resultados sugieren que dichos conocimientos podrían ser insuficientes y apoyan el interés de realizar una evaluación inicial de los futuros profesores al iniciar su periodo de formación, para detectar estas carencias, y proporcionarles un refuerzo sobre estos conceptos, en caso necesario.

Una implicación de interés para los formadores de profesores es la necesidad de reforzar la formación de los futuros profesores de Educación Primaria, tanto en su conocimiento especializado del contenido matemático como en el conocimiento del contenido y los estudiantes en el campo de la probabilidad. Respecto a la metodología, para llevar a cabo esta formación, se sugiere proponer a los futuros profesores una muestra de situaciones experimentales y contextualizadas, que sean representativas de juegos equitativos y no equitativos, pidiéndoles en el segundo caso, cambiar el premio o las condiciones del juego para transformarlos en equitativos. Para prepararlos en la componente didáctica, serán de gran ayuda situaciones relacionadas con la docencia, como las usadas en este trabajo. Las nuevas tecnologías y los foros de discusión pueden ser también un vehículo formativo, que permita a los profesores intercambiar experiencias y ganar conocimiento de la práctica educativa (Viseu & Ponte, 2009). Resaltamos también la necesidad de continuar la investigación sobre otros componentes del conocimiento del profesor en el campo de la probabilidad, como paso necesario para mejorar la formación de los profesores.

 

AGRADECIMIENTOS

Proyecto EDU2010–14947 (MICINN y FEDER) Grupo FQM–126, Junta de Andalucía, beca FPI BES–2008–003573 (MEC–FEDER) y Plan Propio de Investigación de la Universidad de Granada: Programa 20.

 

REFERENCIAS BIBLIOGRÁFICAS

Azcárate, R (1995). El conocimiento profesional de los profesores sobre las nociones de aleatoriedad y probabilidad. Su estudio en el caso de la educación primaria. Tesis de doctorado no publicada, Universidad de Cádiz, Cádiz, España.         [ Links ]

Ball, D. L., Lubienski, S. T., & Mewborn, D. S. (2001). Research on teaching mathematics: The unsolved problem of teachers' mathematical knowledge. In V. Richardson (Ed.), Handbook of Research on Teaching (pp. 433–456). Washington, DC: American Educational Research Association.         [ Links ]

Batanero, C. (2005). Significados de la probabilidad en la educación secundaria. Revista Latinoamericana de Investigación en Matemática Educativa 8 (3), 247–263.         [ Links ]

Batanero, C., Arteaga, P., Ruiz, B., & Roa, R. (2010). Assessing pre–service teachers conceptions of randomness through project work. In C. Reading (Ed.), Proceedings of the 8^th International Conference on Teaching Statistics. Lubjana: International Association for Statistical Education.         [ Links ]

Batanero, C., Burrill, G., & Reading, C. (Eds.) (2011). Teaching statistics in school mathematics. Challenges for teaching and teacher education. A joint ICMI and IASE study. New York: Springer.         [ Links ]

Batanero, C., Godino, J. D., & Cañizares, M. J. (2005). Simulation as a tool to train Pre–service school teachers. In J. Addler (Ed.), Proceedings of ICMI First African Regional Conference [CD ROM]. Johannesburgo: International Commission on Mathematical Instruction.         [ Links ]

Cañizares, M. J., Batanero, C., Serrano, L., & Ortiz, J. J. (1999). Comprensión de la idea de juego equitativo en los niños. Números 37, 37–56.         [ Links ]

Fischbein, E., & Gazit, A. (1984). Does the teaching of probability improve probabilistic intuitions? Educational Studies in Mathematics 15 (1), 1–24. doi: 10.1007/BF00380436        [ Links ]

Green, D. R. (1983). A survey of probabi/itic concepts in 3000 pupils aged 11–16 years. In D. R. Grey, P. Holmes, V. Barnett, & G. M. Constable (Eds.), Proceedings of the 1st International Conference on Teaching Statistics (Vol. 2, pp. 766–783). Sheffield, Reino Unido: Universidad de Sheffield.         [ Links ]

Chick, H. L., & Pierce, R. U. (2008). Teaching statistics at the primary school level: beliefs, affordances, and pedagogical content knowledge. In C. Batanero, G. Burrill, C. Reading y A. Rossman, Joint ICMI/IASE Study: Teaching Statistics in School Mathematics. Challenges for Teaching and Teacher Education. Proceedings of the ICMI Study 18 and 2008 IASE Round Table Conference. Monterrey: ICMI and IASE.         [ Links ]

Godino, J. (2009). Categorías de análisis de los conocimientos del profesor de matemáticas. UNIÓN 20,13–31.         [ Links ]

Hill, H. C., Ball, D. L., & Schilling, S. G. (2008). Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers' topic–specific knowledge of students. Journal for Research in Mathematics Education 39(4), 372–400.         [ Links ]

Jones, G. (2005) (Ed.). Exploring probability in school: Challenges for teaching and learning. New York: Springer.         [ Links ]

Jones, G., Langrall, C. & Mooney, E. (2007). Research in probability: responding to classroom realities. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (Vol. 2, pp. 909–956). Greenwich, CT: Information Age Publishing & NCTM.         [ Links ]

Lecoutre, M. P. (1992). Cognitive models and problem spaces in "purely random" situations. Educational Studies in Mathematics 23(6), 557–568.         [ Links ]

Lidster, S. T., Pereira–Mendoza, L., Watson, J. M., & Collis, K .F. (1995). What is fair for grade 6? Trabajo presentado en la Annual Conference of the Australian Association for Research in Education, Hobart, Tasmania.         [ Links ]

Lidster, S. T., Watson, J. M., Collis, K. F., & Pereira–Mendoza, L. (1996). The relationship of the concept of fair to the construction of probabilistic understanding. In P. C. Clarkson (Ed.), Technology in Mathematics Education, Proceedings of the 19^th Annual Conference of the Mathematics Education Research Group of Australasia, Melbourne (pp. 352—359). Sydney: MERGA.         [ Links ]

Llinares S., & Krainer K. (2006). Mathematics (student) teachers and teacher educators as learners. In A. Gutierrez & P. Boero (Eds.), Handbook of Research on the Psychology of Mathematics Education (pp. 429–459). Rotherdam/Taipei: Sense Publichers.         [ Links ]

Lopes, C. (2006). Stochastics and the professional knowledge of teachers. In A. Rossman y B. Chance (Eds.), Proceedings of the Seventh International Conference on Teaching Statistics [CD–ROM].Salvador (Bahía), Brasil: International Statistical Institute.         [ Links ]

MEC (2006). Real Decreto 1513/2006, de 7 de diciembre, por el que se establecen las enseñanzas mínimas de la Educación Primaria. Madrid: Boletín Oficial del Estado, n° 293.         [ Links ]

MEC (2007). Resolución de 17 de diciembre de 2007, de la Secretaría de Estado de Universidades e Investigación, por la que se publica el Acuerdo de Consejo de Ministros de 14 de diciembre de 2007, por el que se establecen las condiciones a las que deberán adecuarse los planes de estudios conducentes a la obtención de títulos que habiliten para el ejercicio de la profesión regulada de Maestro en Educación Primaria. Madrid: Boletín Oficial del Estado, n° 305.         [ Links ]

N. C. T. M. (2000). Principles and standards for school mathematics. Reston: VA, NCTM.         [ Links ]

Ortiz, J. J., Mohamed, N., Batanero, C.; Serrano, L., y Rodríguez, J. (2006). Comparación de probabilidades en profesores en formación. En P. Bolea, M. J. Gonzáles y M. Moreno (Eds,), Actas del X Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 267–276). Huesca, España: SEIEM.         [ Links ]

Piaget, J., e Inhelder, B. (1951). La genése de l'idée de hasard chez l'enfant. Paris: Presses Universitaires de France.         [ Links ]

Ponte, J. P., & Chapman, O. (2006). Mathematics teachers' knowledge and practices. In A. Gutierrez y P. Boero (Eds.), Handbook of reaserch on the psychology of mathematics education: Past, present and future (pp. 461–494). Roterdham: Sense Publishers.         [ Links ]

Schlottmann, A., & Anderson, N. H. (1994). Children's judgements of expected value. Developmental Psychology 30(1), 55–66.         [ Links ]

SEP (2006). Programa de estudio, educación secundaria. Dirección General de Desarrollo Curricular de la Subsecretaría de Educación Básica de la Secretaría de Educación Pública, México.         [ Links ]

Serrano, L. (1996). Significados institucionales y personales de objetos matemáticos ligados a la aproximación frecuencial de la enseñanza de la probabilidad. Tesis de doctorado no publicada, Universidad de Granada, Granada, España.         [ Links ]

Shulman,L. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher 15(2), 4–14.         [ Links ]

Stohl, H. (2005). Facilitating students' problem solving: Prospective teachers' learning trajectory in technological contexts. Journal of Mathematics Teacher Education 8(3), 223–254. doi: 10.1007/s10857–005–2618–6         [ Links ]

Thompson, A. G. (1992). Teachers' beliefs and conceptions: A synthesis of the research. In D. A. Grouws (Ed.), Handbook on Mathematics Teaching and Learning (Vol. 127, pp. 127–146). New York: Macmillan.         [ Links ]

Vahey, P., Enyedy, N., & Gifford, B. (1997). Beyond represen tativeness: Productive intuitions about probability. Comunicación presentada en la Annual Conference of the Cognitive Science Society. Stanford University, Palo Alto, CA.         [ Links ]

Viseu, F., & Ponte, J. P. (2009). Desenvolvimento do conhecimento didáctico do futuro professor de Matemática com apoio das TIC 's. Revista Latinoamericana de Investigación en Matemática Educativa 9(3), 383–413.         [ Links ]

Watson, J., & ColIis, K. F. (1994). Multimodal functioning in understanding chance and data concepts. In J. P. Ponte and J. P. Matos (Eds), Proceedings of the 18^th International Conference for the Psychology of Mathematics Education (Vol. 4, pp. 369–376). Lisboa, España: Universidad de Lisboa.         [ Links ]

Wood, T. (2008). The international handbook of mathematics teacher education. Rotterdam: Sense Publishers.         [ Links ]