Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.11 no.2 Ciudad de México jun. 2008
Artículos
PROPUESTA PEDAGÓGICA BASADA EN EL CONSTRUCTIVISMO PARA EL USO ÓPTIMO DE LAS TIC EN LA ENSEÑANZA Y EL APRENDIZAJE DE LA MATEMÁTICA
PEDAGOGICAL PROPOSAL BASED ON CONSTRUCTIVISM FOR THE OPTIMAL USE OF ICT IN THE TEACHING AND LEARNING OF MATHEMATICS
Sandra Castillo
Universidad Nacional Experimental de Guayana, Venezuela; scastillo@uneg.edu.ve
Recepción: Julio 16, 2006
Aceptación: Mayo 09, 2008
RESUMEN
Como consecuencia de la inminente incorporación de las Tecnologías de Información y Comunicación (TIC) a la enseñanza de las ciencias, y particularmente a la de la matemática, se ha visto transformada la práctica pedagógica de los docentes. Este artículo presenta una revisión bibliográfica que permitió dar respuesta a preguntas como ¿qué implicaciones tiene el constructivismo en Matemática Educativa? y ¿cómo se pueden vincular el constructivismo, la práctica pedagógica y la enseñanza de las matemáticas que promueven los docentes que utilizan las TIC? Lo anterior permitió establecer una propuesta que sustenta el uso de las TIC como soporte al proceso de enseñanza, y las transforma como medio para crear un ambiente apropiado que beneficie el aprendizaje de la matemática a través de proyectos.
PALABRAS CLAVE: Constructivismo, Matemática Educativa, práctica pedagógica, tecnologías de información y comunicación.
ABSTRACT
As a consequence of the imminent incorporation of Information and Communication Technology (ICT) in the teaching of the sciences, and particularly that of mathematics, teachers' pedagogical practice has been transformed. This article presents a bibliographical review that sought out answers to questions such as: What implications does constructivism have in Mathematics Education? And how can constructivism, pedagogical practice and the mathematics teaching promoted by teachers who use ICT, be connected? The above allowed a proposal to be established that sustains ICT use as an aid in the teaching process and transforms it into a means of creating an appropriate environment conducive to mathematics learning through projects.
KEY WORDS: Constructivism, Mathematics Education, pedagogical practice, information and communication technology.
RESUMO
Como conseqüência da iminente incorporação das Tecnologias de Informação e Comunicação (TIC) ao ensino das ciências, e particularmente a da matemática, viu–se transformada a prática pedagógica dos docentes. Este artigo apresenta uma revisão bibliográfica que permitiu dar resposta a perguntas como que implicações tem o construtivismo na Educação Matemática? E como se podem vincular o construtivismo, a prática pedagógica e ao ensino da matemática dos docentes que utilizam as TIC? Os resultados permitiram estabelecer uma proposta que sustenta o uso das TIC como suporte ao processo de ensino, e as transforma como meio para criar um ambiente apropriado que beneficie a aprendizagem da matemática através de projetos.
PALAVRAS CHAVE: Construtivismo, Educação Matemática, prática pedagógica, tecnologias de informação e comunicação.
RÉSUMÉ
Dû à l'imminente incorporation des Technologies de l'Information et de la Communication (TIC) à l'enseignement des sciences, particulièrement à celui des mathématiques, la pratique pédagogique des enseignants s'est transformée. Cet article présente une révision bibliographique, qui a permis de répondre aux questions telles que : Quelles sont les implications du constructivisme dans les Mathématiques Éducatives? Quels sont les liens possibles entre le constructivisme, la pratique pédagogique et l'enseignement des mathématiques pour les enseignants qui utilisent des TIC ? Ce qui précède a permis d'établir un choix portant sur l'usage des TIC comme support au processus d'enseignement, dans lequel ces ressources deviennent un moyen pour créer un environnement pour l'apprentissage des mathématiques à travers des projets.
MOTS CLÉS: Constructivisme, mathématiques éducatives, pratique pédagogique, technologies d'information et de communication.
1. INTRODUCCIÓN
Las Tecnologías de Información y Comunicación (TIC) están presentes en todos los sistemas que componen los diferentes ámbitos de la sociedad. En el campo de la educación se puede afirmar que, aunque ha sido lenta la inclusión de esas tecnologías, hay investigaciones que sustentan la importancia de su uso. Ya no se debate sobre su necesidad, sino sobre las ventajas que ofrece su utilización (la mejor manera de sacarles provecho, al ser medios o herramientas que contribuyen a enriquecer el proceso de enseñanza–aprendizaje), su incidencia en la cognición y procesos del pensamiento de los alumnos y la manera como impactan en la reestructuración del currículo educativo.
Aunado a estos estudios se buscan teorías, enfoques, metodologías y propuestas de enseñanza y aprendizaje que sustentan las acciones y funciones a seguir por parte de los docentes que enseñan matemáticas en diferentes niveles educativos para mejorar la calidad. Aquí, surgen preguntas como: ¿Se están formando los docentes para que utilicen las TIC en los diferentes ambientes de aprendizaje? ¿Cuáles son los roles y las funciones de los docentes que incorporan las TIC a su práctica pedagógica? ¿Qué implicaciones tiene el constructivismo en Matemática Educativa? Con el propósito de responder a tales interrogantes, este artículo ofrece una revisión bibliográfica sobre el constructivismo y lo vincula con la práctica pedagógica en Matemática Educativa, apoyada en tecnologías de información y comunicación.
El presente trabajo inicia con la definición, principios y postulados del constructivismo. Luego refiere sus implicaciones en Matemática Educativa y hace hincapié en la definición de práctica pedagógica, formulando su rediseño en la creación de ambientes de aprendizaje y en el establecimiento de competencias por los docentes. Posteriormente, trata las TIC con énfasis en el principio de la tecnología que propuso el Consejo Estadounidense de Profesores de Matemática (NCTM); realza el papel de la tecnología en el aprendizaje y la enseñanza efectiva; señala cómo usar las TIC con un enfoque constructivista, y presenta un ejemplo a través del Aprendizaje por Proyectos (ApP), explicando sus ventajas.
2. CONSTRUCTIVISMO: UNA PROPUESTA EPISTEMOLÓGICA
Coll (1999) señala que "se ha dicho varias veces que la concepción constructivista no es en sentido estricto una teoría, sino más bien un marco explicativo que, partiendo de la consideración social y socializadora de la educación escolar, integra aportaciones diversas cuyo denominador común lo constituye un acuerdo en torno a los principios constructivistas ". Asimismo, dice que existen diversas perspectivas sobre cómo el aprender se construye, lo cual implica a definir el constructivismo desde diferentes miradas, como plantea Sánchez (2000), y no encasillarlo en una única manera de pensarlo.
En este artículo se concibe al constructivismo como una propuesta epistemológica que surge en oposición al positivismo del conductismo y el procesamiento de la información; además, que se basa en la concepción que la realidad es una construcción interna, propia del individuo. Dicha forma de ver el constructivismo, indica Sánchez (2000), está justificada desde la perspectiva del uso de las tecnologías de información y comunicación para la construcción del conocimiento.
El Cuadro I muestra a algunos autores muy conocidos por sus aportes y concepciones constructivistas en los procesos de aprendizaje y enseñanza de las ciencias. Se puede observar que cada postura asume ciertos elementos que la distinguen y unos postulados que, aunque parecieran diferentes, convergen en precisar que el alumno es el principal protagonista de su propio aprendizaje. Desde luego, hay una serie de factores como el entorno social, manejo del lenguaje, cultura, desarrollo personal y otros que permiten que el cómo se aprende adquiera visiones diferentes. Jean Piaget aparece como representante del constructivismo cognitivo, Lev Vigotsky del constructivismo socio cognitivo, mientras que Von Glasersfeld y Maturana del constructivismo radical. A este último autor se le relaciona con el constructivismo biológico.
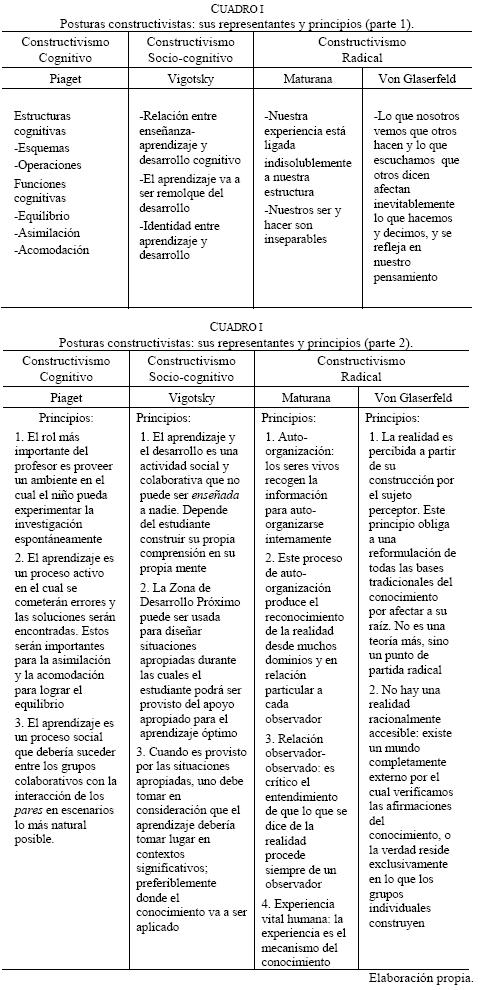
Ahora bien, independientemente de la postura que se asuma, una filosofía constructivista hará énfasis en cómo los aprendices construyen los conocimientos en función de sus experiencias previas, estructuras mentales y creencias o ideas que ocupan para interpretar objetos y eventos. La teoría constructivista postula que el saber, sea de cualquier naturaleza, lo elabora el aprendiz mediante acciones que hace sobre la realidad.
Esto implica que la construcción sea interna; el aprendiz crea e interpreta esa realidad. Von Glaserfeld (1990) afirma: "el saber es construido por el organismo viviente para ordenar lo más posible el flujo de la experiencia en hechos repetibles y en relaciones relativamente seguras". Tal aspecto debería ser tomado en cuenta por el docente, quien encuentra en la concepción constructivista un marco teórico para analizar y fundamentar muchas de las decisiones que toma en la planificación de sus actividades y práctica docente.
Por otro lado, cada una de las posturas constructivistas se guía por una serie de principios. Cabe mencionar que en la bibliografía consultada se enuncian tres de los seis que se consideran como rectores:
– El conocimiento no es pasivamente recibido e incorporado a la mente del alumno, sino activamente construido.
– Sólo el sujeto que conoce construye su aprender.
– La cognición tiene función adaptativa y para ello sirve la organización del mundo experiencial.
– La realidad existe en tanto existe una construcción mental interna interpretativa del que aprende.
– Aprender es construir y reconstruir esquemas, modelos mentales.
– Aprender es un proceso individual y colectivo de diseño y construcción/reconstrucción de esquemas mentales previos como resultado de procesos de reflexión e interpretación.
Cada uno de estos principios toma diferentes matices de acuerdo con la postura constructivista que se asuma. Empero, la esencia de cada principio se conserva, independientemente del modo en que se presente.
3. CONSTRUCTIVISMO Y SUS IMPLICACIONES EN MATEMÁTICA EDUCATIVA
El constructivismo como postura epistemológica también se encuentra en la Matemática Educativa. A continuación se expone un análisis sobre las implicaciones que el constructivismo ha traído consigo en esta área del conocimiento, refiriendo primero las características que han dado Kilpatrick, Gómez y Rico (1995):
– El conocimiento matemático es construido, al menos en parte, a través de un proceso de abstracción reflexiva.
– Existen estructuras cognitivas que se activan en los procesos de construcción.
– Las estructuras cognitivas están en desarrollo continuo. La actividad con propósito induce la transformación de las estructuras existentes.
Piaget considera que existen dos poderosos motores que hacen que el ser humano mantenga ese desarrollo continuo de sus estructuras cognitivas: la adaptación y el acomodamiento. Al conjugar estos elementos, se puede conocer la importancia de vincular un marco teórico con la práctica pedagógica que ha de ejercer un docente, al enseñar los contenidos matemáticos en el aula.
Adicionalmente, existe una característica muy particular en el ámbito de la matemática: la abstracción. Al respecto, Vergnaud (1991) considera tres puntos interesantes:
– La invarianza de esquemas, que se refiere al uso de un mismo esquema mental para diversas situaciones semejantes.
– La dialéctica del objeto–herramienta, que se refiere a que el uso proporcionado a aquello que abstrae inicialmente lo utiliza como herramienta para resolver algo en particular, pero posteriormente le da un papel de objeto al abstraer sus propiedades. Pero el proceso continúa, pues al obtener el sujeto un objeto a partir de una operación descubre nuevas cosas que, inicialmente, utilizará como herramientas para después abstraer sus propiedades y convertirlas en objetos, y así sucesivamente. De esta manera el individuo conceptualiza al mundo, y sus objetos, en diferentes niveles.
– El papel de los símbolos, que simplifican y conceptualizan los objetos al obtener sus invariantes sin importar el contexto en el que se encuentren.
Una postura constructivista no sólo permite advertir las dificultades que suelen tener los alumnos para aprender, sino también aporta una guía para desarrollar estrategias de enseñanza y aprendizaje más eficientes, empleando un proceso de enseñanza donde el protagonista central es el alumno, considerando sus intereses, habilidades para aprender y necesidades en el sentido más amplio.
El individuo que aprende matemáticas desde un punto de vista constructivista debe construir los conceptos a través de la interacción que tiene con los objetos y con otros sujetos. Tal parece que para que el alumno pueda construir su conocimiento y llevar a cabo la interacción activa con los objetos matemáticos es preciso que dichos objetos se presenten inmersos en un problema, no en un ejercicio.
Las situaciones problemáticas introducen un desequilibrio en las estructuras mentales del alumno, de tal manera que en la búsqueda de ese acomodamiento se genera la construcción del conocimiento. No obstante, este camino también implica errores, y por medio de ellos el sujeto cognoscente trata de encontrar el equilibrio que, con toda intención, le hizo perder el problema propuesto por el docente. Para lograrlo, y construir su conocimiento, el alumno debe retroceder para luego avanzar y re–construir un significado más profundo del conocimiento. Es entonces, en palabras de Vygotski, cuando la interacción social del alumno que aprende juega un papel primordial porque propicia que avance más en grupo que de manera individual. De allí la importancia del lenguaje, pues sirve como medio para estructurar el pensamiento y el conocimiento generado por el sujeto.
El constructivismo como postura epistemológica que adoptan los investigadores de matemática educativa es coherente con lo observable en el desarrollo mental de los individuos; sin embargo, afirma Larios (1998), en el momento en que se quiere aplicar esta teoría a la enseñanza de la matemática se tiene un salto mortal; por tanto, si se quiere aplicar el constructivismo en la enseñanza el docente debe ser cauteloso.
Por otro lado, hay propuestas didácticas que se basan en posturas constructivistas para abordar, por ejemplo, el álgebra básica casi exclusivamente a través de problemas. Empero, el desconocimiento y manejo de la base teórica puede llevar a una aplicación de dichas propuestas en la que se resuelvan problemas y/o ejercicios problematizados sin una sistematización en el trabajo del alumno, al ocupar procesos de tanteo y al azar con los cuales no se logre un verdadero desarrollo de los conceptos matemáticos.
El hecho de que los docentes no conozcan la teoría constructivista impide que la apliquen en forma adecuada, con lo cual se pierde la posibilidad de que hagan un estudio sistemático de su uso o, peor aún, se genera una adaptación ineficiente por las características cambiantes de los grupos de educandos. Por tanto, no sólo el conocimiento de la teoría constructivista permite que su uso, aplicación, implementación, estudio, análisis y evaluación sea lo más eficiente y real posible, sino también la ejecución efectiva de la práctica pedagógica que todo docente de matemática debe efectuar para combinar dos elementos esenciales en su acción: teoría y praxis.
Aplicar este tipo de propuestas conlleva a que el docente realice un esfuerzo mayor al que normalmente está acostumbrado, pues necesita romper su esquema de transmisor de conocimientos y convertirse en un organizador, coordinador, asesor y director del proceso de adquisición del conocimiento, el cual le pertenece primordialmente al alumno.
4. HACIA LA TRANSFORMACIÓN DE LA PRÁCTICA PEDAGÓGICA
Se concibe a la práctica pedagógica como el conjunto de actividades que permiten planificar, desarrollar y evaluar procesos intencionados de enseñanza mediante los cuales se favorece el aprendizaje de contenidos (conocimientos, habilidades, actitudes y valores) por parte de personas que tienen necesidades de formación (Wilson, 1996).
La práctica pedagógica incluye a todos aquellos procesos en los cuales se desarrolla la enseñanza con la intención de favorecer el aprendizaje. Está vinculada siempre y necesariamente a una teoría pedagógica y comprende todas aquellas situaciones donde haya personas que desean formarse. Dichas situaciones no son accidentales o casuales; están planificadas y representan lo que se llaman ambientes de aprendizaje (Marcelo, 2001). Enseñar y aprender, por tanto, son dos términos unidos por una sola intención: producir construcción y apropiación de conocimiento y competencia por parte de las personas que deciden implicarse en este juego.
El Cuadro II ofrece una comparación entre lo que se denomina práctica pedagógica tradicional y práctica pedagógica actual, que implica la práctica con el uso de las tecnologías.
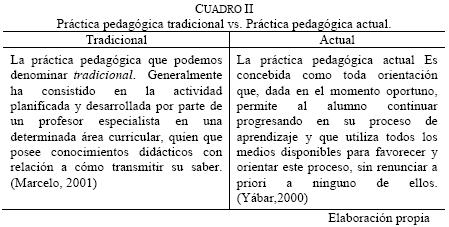
Indistintamente, sea cual fuere la práctica pedagógica que asuma cada docente, lo relevante del modelo constructivista radica en que el verdadero artífice en la construcción del conocimiento no es el profesor ni la computadora, sino el alumno.
En el párrafo precedente se mencionan los ambientes de aprendizaje, cuya creación tiene mucho que ver con las teorías de aprendizaje que se adopten:
– Si es constructivista, se requiere que se incorporen nuevos conocimientos a partir de la reestructuración y revisión de los conocimientos previos. Asimismo, se debe ofrecer a los alumnos estructuras conceptuales que les ayuden a ubicar los nuevos conceptos.
– Si se trata de aprendizaje situado, hay que dar posibilidades para aplicar el conocimiento en contextos auténticos mediante actividades de resolución de problemas, como parte de la presentación de contenidos.
– Si se adopta la flexibilidad cognitiva, los contenidos necesitan mostrarse desde múltiples perspectivas; hay que evitar la simplificación y fomentar el uso de diversas fuentes de información disponibles.
El rediseño de la práctica pedagógica implica que la instrucción deba basarse en el uso de casos prácticos que proporcionen experiencias de aprendizaje ricas, diversas y contextualizadas. La tarea de los docentes y formadores es diseñar ambientes de aprendizaje que ayuden a los alumnos a aprender; por tanto, hay que procurar que el aprendizaje sea, como plantea Marcelo (2001):
Activo: Los alumnos no pueden permanecer pasivos, a la espera de que el conocimiento les venga dado, sino tienen que ser participes en la construcción del conocimiento y desarrollar habilidades como la capacidad de búsqueda, análisis y síntesis de la información.
Autónomo: Se debería propiciar la capacidad de aprender en forma autónoma. Ello significa que no hay que ofrecerlo todo; es preciso que haya áreas de conocimiento que indaguen los propios alumnos.
Adaptado: A las posibilidades y necesidades de formación de diferentes alumnos.
Colaborativo: El alumno, además de adquirir conocimientos, tiene que desarrollar habilidades para relacionarse con los demás: saber escuchar, respetar a los demás, saber comunicar las ideas, etc.
Constructivo: La nueva información se elabora y construye sobre la anterior, contribuyendo a que el alumno alcance un verdadero aprendizaje.
Orientado a metas: Los objetivos de aprendizaje se hacen explícitos y el alumno tiene facilidad para elegir el camino que quiere seguir para alcanzar estas metas.
Diagnóstico: Se inicia con un diagnóstico para conocer el punto de partida de los alumnos, de forma que se puedan ir haciendo evaluaciones y comprobar el progreso en su aprendizaje.
Reflexivo: Se favorece la reflexión si los alumnos tienen la oportunidad de ir tomando conciencia sobre cómo aprenden, a fin de introducir mejoras en dichos procesos.
Centrado en problemas y casos: Estrategias adecuadas para conseguir que el alumno se involucre en el proceso de enseñanza y aprendizaje, lo cual ofrece nuevas alternativas para transmitir y facilitar el conocimiento, así como mejorar la calidad de la formación.
Para alcanzar dichos tipos de aprendizaje en los alumnos, se debe repensar el perfil y las tareas del docente que va a hacer uso de las tecnologías de la información y la comunicación. Marcelo (2001) apunta que el docente debe poseer competencias en al menos tres áreas:
Competencias tecnológicas: Son imprescindibles cada día más. Aunque por lo general se va a disponer de un técnico especialista, lo deseable es que el formador o docente alcance un nivel óptimo de autonomía en el manejo de aquellas herramientas de creación que le permitirán canalizar su formación a través de la red. Por ende, también tiene que conocer las aplicaciones de Internet.
Competencias didácticas: Atañen al conocimiento de las teorías de aprendizaje y sus principios, al igual que a las capacidades de adaptación a nuevos formatos de enseñanza; desarrollar ambientes de aprendizaje pensados para la autorregulación; crear materiales y plantear tareas relevantes para la formación del alumno, las cuales estén relacionadas con sus experiencias y sean aplicables a situaciones específicas.
Competencias tutoriales: Abarcan tanto a las habilidades de comunicación como a las capacidades de adaptación a las condiciones y características de los usuarios, y de trabajo y constancia en las tareas de seguimiento. Con ello, se busca crear un entorno social agradable en que se promuevan relaciones óptimas entre los participantes, se desarrolle en ellos el sentido de grupo y trabajen hacia un objetivo común. Además, que tengan mentalidad abierta para aceptar propuestas, sugerencias e introducir reajustes en la planificación inicial del curso; que posean capacidad de trabajo y constancia en las tareas de seguimiento del progreso de cada alumno, y faciliten de inmediato el feedback.
Semenov, Pereversev y Bulin–Socolova (2005) establecen las competencias que debe poseer el docente que usa las Tecnologías de Información y Comunicación para mejorar el proceso de enseñanza y facilitar el aprendizaje de las ciencias en general, y de las matemáticas en particular. Dichas competencias principales y esenciales para el uso efectivo de las TIC como herramientas de aprendizaje aluden a la pedagogía, la colaboración y trabajo en red, aspectos sociales y aspectos técnicos:
Competencias pedagógicas: Al implementar las competencias pedagógicas que permitirán incorporar la tecnología adquiere importancia fundamental el contexto local y el enfoque pedagógico individual del docente, que está vinculado al de su disciplina. A medida que se incremente el uso de las TIC como forma de apoyar el aprendizaje y favorecer la enseñanza, los docentes podrán:
– Demostrar una mayor comprensión de las oportunidades e implicaciones del uso de las TIC en la enseñanza y el aprendizaje dentro del contexto del plan de estudios.
– Planificar, implementar y dirigir el aprendizaje y la enseñanza en un entorno de aprendizaje más flexible y abierto, así como evaluar cada proceso.
Colaboración y trabajo en red: Las TIC ofrecen poderosas herramientas para apoyar la comunicación tanto dentro de los grupos de aprendizaje como fuera del salón de clase. El rol del docente se extiende al de facilitador de la colaboración y el trabajo en red entre comunidades locales y mundiales. Tal expansión de las comunidades de aprendizaje más allá de los límites del salón de clase requiere que se respete la diversidad, incluyendo la educación intercultural y el acceso igualitario a los recursos electrónicos de aprendizaje.
Durante este proceso, los docentes:
– Demostrarán una capacidad de comprensión crítica sobre los beneficios del aprendizaje en red y en colaboración dentro y entre las comunidades y los países.
– Participarán de modo efectivo en entornos de aprendizajes flexibles y abiertos, tanto en el rol de docentes como en el de alumnos.
– Crearán o desarrollarán redes de aprendizaje que traerán beneficios tanto a la profesión docente como a la sociedad (en los ámbitos local y mundial).
– Ampliarán el acceso a la educación y brindarán oportunidades de aprendizaje a todos los miembros de la comunidad, incluyendo a aquellos con necesidades especiales.
Aspectos sociales: Poder acceder a las tecnologías de información y comunicación implica un incremento en las responsabilidades de todos los miembros de la comunidad.
En particular, los docentes deben:
– Comprender y aplicar los códigos de práctica legal y moral, entre ellos el respeto a los derechos de autor y a la propiedad intelectual.
– Reflexionar y discutir acerca del impacto de la nueva tecnología en la sociedad actual, tanto en el ámbito local como en el mundial.
– Planificar y promover un uso adecuado y seguro de las TIC, incluyendo el asiento, la luz, el sonido y otras fuentes de energía relacionadas, como las señales de radio y electricidad.
Aspectos técnicos: Los aspectos técnicos que conciernen a la integración de las TIC al plan de estudios incluyen la competencia técnica y la disponibilidad tanto de la infraestructura como del apoyo técnico necesarios para ocupar la tecnología en el ámbito académico. Así, los docentes estarán capacitados para:
– Usar y seleccionar, entre una variedad de recursos tecnológicos, los más adecuados para mejorar su efectividad personal y profesional.
– Actualizar voluntariamente sus habilidades y conocimientos para acompasar los nuevos desarrollos y nuevos desafíos.
Con base en lo anteriormente expuesto, se puede afirmar que toda práctica pedagógica necesita estar en consonancia no sólo con los contenidos académicos a desarrollarse en el aula de clases, sino también con los cambios curriculares que en la educación se están dando en todos los niveles y en todas las áreas del saber. Por tanto, en el seno de la matemática educativa también se requiere hacer una revisión profunda.
Los docentes, desde la perspectiva de la enseñanza y el aprendizaje de las matemáticas, tienen que estar conscientes que las TIC les dan posibilidades de acceso a recursos, disponibles en línea o no, que utilizan una combinación de herramientas y elementos donde encuentran soporte para el manejo de audio, video o gráficos que favorecen el aprendizaje si las estrategias de enseñanza están diseñadas para garantizar el uso apropiado de dichas tecnologías.
5. INCORPORACIÓN DE LAS TECNOLOGÍAS DE INFORMACIÓN Y COMUNICACION. LA TECNOLOGÍA REALZA EL APRENDIZAJE Y APOYA LA ENSEÑANZA DE LA MATEMÁTICA
Martínez (2003) dice que las nuevas tecnologías precisan de unas necesidades previas, sin las cuales no puede hablarse de su incorporación a ningún ámbito de la enseñanza. Estas son:
El acceso técnico: Tiene que ver con la posibilidad material de disponer de acceso a estas tecnologías a los medios y servicios que proporcionan.
El acceso práctico: Se relaciona con la disponibilidad del tiempo necesario para el empleo de las tecnologías, al igual que con preparar el proceso de su uso como soporte para la enseñanza y como medio para el aprendizaje.
El acceso operativo: Referido a los conocimientos que van a permitir el manejo de la herramienta tecnológica.
El acceso criterial: La utilización de las tecnologías precisa de una actitud previa crítica con la propia tecnología y que facilita la toma de decisiones sobre su utilización. La posibilidad de responder a la pregunta de porqué esta tecnología aquí y ahora es una cuestión fundamental.
El acceso relacional científico tecnológico: Vinculado con los requisitos previos que necesitan tener del proceso de enseñanza en que se pretende incidir con las tecnologías.
Unidos a tales necesidades, se encuentran los principios que instituye el Consejo Estadounidense de Profesores de Matemática (NCTM), los cuales atañen a:
Equidad: La excelencia en matemática educativa requiere de equidad, expectativas altas y un fuerte apoyo para todos los estudiantes.
Currículo: Es mucho más que una colección de actividades. Debe ser coherente y centrado en temas matemáticos importantes que estén bien articulados en los diferentes grados escolares.
Enseñanza: La enseñanza efectiva de las matemáticas requiere de entender qué saben los estudiantes y qué necesitan aprender. A partir de ello, hay que retarlos y apoyarlos para que logren una buena formación.
Aprendizaje: Los estudiantes necesitan aprender matemáticas entendiéndolas e interpretándolas cognitivamente, deben construir conocimientos de manera activa, a partir de sus experiencias y el saber anterior.
Evaluación: La evaluación tiene que apoyar el aprendizaje de conceptos matemáticos importantes, además de suministrar información útil tanto a los docentes como a los estudiantes.
Tecnología: En su sentido más amplio, resulta esencial en la enseñanza y el aprendizaje, ya que influye en las matemáticas que se enseñan y mejora el proceso de aprendizaje de los estudiantes. Las tecnologías específicas como, por ejemplo, las electrónicas (calculadoras y computadoras) son herramientas muy útiles para enseñar, aprender y hacer matemáticas. De igual manera, ofrecen representaciones de instrucciones basadas en axiomas, teoremas y leyes matemáticas, facilitan la organización y análisis de los datos y permiten que se hagan cálculos de manera eficiente y exacta.
Las TIC pueden apoyar a las investigaciones de los alumnos en varias áreas de las matemáticas, como números, medida, geometría, estadística, álgebra, pues se espera que cuando dispongan de ellas logren concentrarse en tomar decisiones, razonar y resolver problemas. La existencia, versatilidad y poder de las TIC hacen posible y necesario reexaminar qué matemáticas deben aprender los alumnos, así como examinar la mejor forma en que puedan aprenderlas.
Este es el momento de establecer el vínculo entre el constructivismo y la matemática educativa asistida por las tecnologías de información y comunicación. Cabe preguntarse, entonces: ¿cómo usar las TIC con un enfoque constructivista en matemática educativa? Al respecto, Sánchez (2000) da los siguientes enunciados:
– Como herramientas de apoyo al aprender, con las cuales se pueden realizar actividades que fomenten el desarrollo de destrezas cognitivas superiores en los alumnos.
– Como medios de construcción que faciliten la integración de lo conocido y lo nuevo.
– Como extensoras y amplificadoras de la mente, a fin de que expandan las potencialidades del procesamiento cognitivo y la memoria, lo cual facilita la construcción de aprendizajes significativos.
– Como medios transparentes o invisibles al usuario, que hagan visible el aprender e invisible la tecnología.
– Como herramientas que participan en un conjunto metodológico orquestado, lo que potencia su uso con metodologías activas como proyectos, trabajo colaborativo, mapas conceptuales e inteligencias múltiples, donde aprendices y facilitadores coactúen y negocien significados y conocimientos, teniendo a la tecnología como socios en la cognición.
El conocer y el aprender lo hacen y construyen los aprendices Sánchez precisa que la tecnología sólo es una herramienta con una gran capacidad que, cuando es manejada con una metodología y diseño adecuado, puede ser un buen medio para construir y crear.
Al conocer los beneficios del uso de la tecnología en la enseñanza y el aprendizaje de las matemáticas, y tras revisar cómo usarla con un enfoque constructivista; surge otra interrogante: ¿Se puede construir conocimiento matemático usando las TIC? Si bien es cierto que los individuos adquieren información desde los ámbitos de la familia, la escuela y los medios de comunicación (Cebrián de la Serna, 1999), la función del educador será ayudar al individuo a que encarne estas tres corrientes de influencias en un mismo caudal, lo cual hará que potencie y desarrolle su personalidad (afectiva, social y cognitiva) en forma más equilibrada e integral con el mundo que lo rodea.
Por ello, se pretende que el conocimiento que los alumnos construyan en las aulas esté formado bajo la reflexión y fórmulas de trabajo colaborativo, así como que tenga miras hacia el surgimiento de un pensamiento racional y científico (Cebrián de la Serna, 1999). Esto parte del conocimiento previo, que abarca al que trae el alumno al aula producto de sus experiencias previas, donde residen muchos conocimientos que obtuvieron a través de medios de comunicación y otros recursos tecnológicos. El conocimiento previo es uno de los principios del aprendizaje constructivista; entre sus características podemos señalar:
– Implicación directa del alumnado en el aprendizaje y en la enseñanza al estar en contacto con situaciones del mundo real y cercano donde utilizan recursos tecnológicos.
– Surgimiento de nuevas temáticas en la investigación que despiertan el interés y la motivación del alumnado.
– Desarrollo de procesos y capacidades mentales de niveles superiores en proyectos informáticos.
Dichos rasgos implican la concepción de las TIC no sólo como medios, sino como elementos motivadores, creadores, que facilitan los procesos cognitivos de manera integrada con los demás elementos del currículo.
Por otro lado, es relevante el contenido matemático que desarrollará el docente al ocupar las TIC. Esto concierne a qué se debe abordar desde el punto de vista de los contenidos para que haya una comprensión del conocimiento matemático, mientras el docente usa las tecnologías de información y comunicación en sus prácticas pedagógicas.
Al respecto, Gallardo y González (2006) expresan que la comprensión del conocimiento matemático es un objeto de investigación que tiene un interés creciente en matemática educativa. No obstante, su elevada complejidad hace que los avances más recientes aún resulten insuficientes, lo cual implica la necesidad de ir adoptando enfoques más operativos y que se preocupen menos por el estudio directo de sus aspectos internos.
Esto conduce a los docentes que incorporan las TIC a determinar y clasificar el tipo de situaciones que propicien el aprendizaje y la comprensión del conocimiento matemático. Por tanto, la valoración precisa de un análisis situacional que inicia con una búsqueda de aquellas situaciones donde tiene sentido el uso del conocimiento matemático considerado, para lo cual se aconseja que se lleve a cabo una labor de categorización y selección de situaciones que organice, simplifique y haga más manejable el conjunto asociado.
Con base en argumentos de esta índole, algunos autores como Rojano (2006), opinan que para la enseñanza de la matemática se necesita de modelos específicos con tecnología, bajo los siguientes principios:
– Didáctico, mediante el cual se diseñan actividades para el aula siguiendo un tratamiento fenomenológico de los conceptos que se enseñan.
– De especialización, por el que se seleccionan herramientas y piezas de software de contenido. Los criterios de selección se derivan de la didáctica de la matemática.
– Cognitivo, por cuyo conducto se seleccionan herramientas que permiten la manipulación directa de objetos matemáticos y de modelos de fenómenos mediante representaciones ejecutables. Empírico, bajo el cual se seleccionan herramientas que han sido probadas en algún sistema educativo.
– Pedagógico, por cuyo intermedio se diseñan las actividades de uso de las TIC para que promuevan el aprendizaje colaborativo y la interacción entre los alumnos, así como entre profesores y alumnos.
– De equidad, con el que se seleccionan herramientas que permiten a los alumnos de secundaria el acceso temprano a ideas importantes en ciencias y matemáticas.
Entre el conjunto de la toma de decisiones para el diseño de los modelos, una de las más complejas reside en la selección de herramientas, ya que sus principios permiten formular criterios para elegir qué instrumentos deberían:
– Estar relacionados con un área específica de la matemática escolar.
– Contar con representaciones ejecutables de objetos, conceptos y fenómenos de la matemática.
– Permitir un tratamiento fenomenológico de los conceptos matemáticos y científicos.
– Ser útiles para abordar situaciones que no pueden abordarse con los medios tradicionales de enseñanza.
– Poder utilizarse con base en el diseño de actividades que promuevan un acercamiento social del aprendizaje.
– Permitir que se promuevan prácticas en el aula donde el profesor guía el intercambio de ideas y las discusiones grupales, a la vez que actúa como mediador entre el estudiante y la herramienta.
El hecho de conocer e identificar el conjunto de entornos tecnológicos de aprendizaje que cumplan con tales criterios hace posible el diseño de los modelos pedagógicos, de los tratamientos didácticos pertinentes en los temas de enseñanza, al igual que del aula, con la tecnología apropiada. Los diseños necesariamente se encuentran ligados al conocimiento didáctico, que el profesor pone en juego cuando realiza el análisis didáctico (Gómez y Rico, 2006). Asimismo, dicho saber tiene unos conocimientos disciplinares de referencia que se estructuran en tres ejes: noción de currículo, fundamentos de las matemáticas escolares y organizadores del currículo.
Si se toman en cuenta la descripción técnica de estos conocimientos de referencia, la planificación y estructuración del uso de las TIC y la forma como se espera que entren en juego al hacer el análisis didáctico, se podrá identificar y fundamentar los contenidos y objetivos de la asignatura. Por otra parte, la reflexión de cómo el profesor construye el conocimiento didáctico en la práctica y la postura sociocultural con respecto al aprendizaje de los futuros profesores permiten sentar las bases en las que se diseñan los esquemas metodológicos y de evaluación (Gómez y Rico, 2006).
Cabe señalar el papel preponderante que asume la interacción social a través del lenguaje y la comunicación entre docentes y alumnos, donde se puede evidenciar el aprendizaje colaborativo y cooperativo como una de las características que distingue al constructivismo.
Un ejemplo que ilustra el empleo de las TIC con un enfoque constructivista en la enseñanza de la matemática es el Aprendizaje por Proyectos (ApP), al que se conocía hace algunos años como aprendizaje por problemas. El cambio se debió a que el aprendizaje por problemas tenía un enfoque específico (abordaba un solo problema a la vez), mientras que el Aprendizaje por Proyectos soluciona diversos y numerosos problemas.
El ApP tiene como rasgo fundamental que cada proyecto no se enfoca a aprender acerca de algo, sino en hacer algo; es decir, involucra una acción.
Según Moursund (1999), el Aprendizaje por Proyectos tiene como objetivos:
Desarrollar competencia. Para los estudiantes, el objetivo del proyecto es aumentar su conocimiento y habilidad en una disciplina o en un área de contenido interdisciplinario. Con frecuencia, cuando el alumno realiza un proyecto alcanza un nivel de habilidad elevado en el área específica que está estudiando y hasta puede convertirse en la persona que más sabe sobre un tema específico. Algunas veces, su nivel de conocimiento puede exceder al del profesor.
Mejorar las habilidades de investigación. El proyecto requiere de aptitudes para investigar y ayuda a que se desarrollen.
Incrementar las capacidades mentales de orden superior. Capacidad de análisis y síntesis. Esto se logra cuando el proyecto es retador y va enfocado a que los estudiantes desarrollen tales habilidades.
Aprender a usar las TIC. Los alumnos incrementan el conocimiento y habilidad que tienen en las TIC a medida que trabajan en el proyecto. Un proyecto puede diseñarse con el objetivo específico de alentar en los estudiantes la adquisición de nuevas habilidades y conocimientos en las tecnologías.
Aprender a autoevaluarse y evaluar a los demás. Los estudiantes aumentan su habilidad de autoevaluación, con lo que se responsabilizan de su trabajo y desempeño. También aprenden a evaluar el trabajo y desempeño de sus compañeros y a darles retroalimentación.
Desarrollar un portafolio. Requiere que los estudiantes hagan un proyecto, una presentación o una función de alta calidad que forme parte del grado escolar que cursen.
Comprometerse en un proyecto. Los alumnos se comprometen activa y adecuadamente a realizar el trabajo del proyecto, de ahí que se encuentren motivados de manera interna: tal es una meta del proceso. El profesor puede efectuar observaciones diarias que permitan establecer si el estudiante tiene un compromiso con la tarea o si muestra una colaboración ejemplar.
Ser parte de una comunidad académica. Todos los estudiantes, profesores o grupo social se convierten en una comunidad académica donde se trabaja de manera cooperativa y se aprende uno de otro. Esta comunidad se expande para incluir a padres, alumnos de otras aulas y otras personas.
Trabajar en ideas que son importantes. El proyecto debe enfocarse a temas que tengan continuidad y sean relevantes para el profesor, el colegio y demás miembros de la comunidad. Por ejemplo, el trabajo interdisciplinario tiene que perfilarse como una de las metas que conformen los proyectos.
Dado que el constructivismo se afinca en la creciente comprensión del cerebro humano, pues atiende a cómo aprende o cómo el aprendizaje amplía el conocimiento previo, los profesores tienden a convertirse en mediadores. Sin embargo, como señala Moursund (1999), no todos los docentes enseñan de manera estrictamente didáctica ni constructivista, ya que recurren a los dos enfoques.
El Cuadro III presenta las áreas del currículo, la instrucción y la evaluación desde los enfoques didáctico y constructivista. En las tres se introducen las Tecnologías de Información y Comunicación como único componente educativo y su implicación en la instrucción didáctica y constructivista.
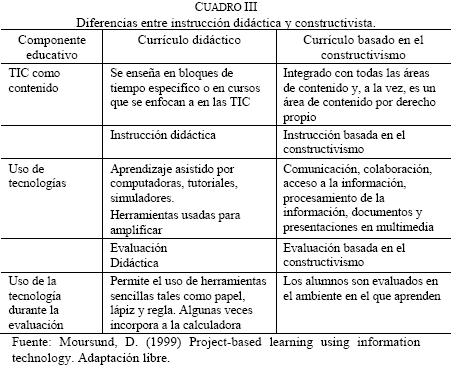
Desde el punto de vista del estudiante, el ApP promueve su motivación intrínseca; estimula el aprendizaje colaborativo y cooperativo; permite que le haga mejoras continuas; está diseñado para que el alumno se comprometa activamente en hacer cosas, en lugar de sólo aprender sobre algo, pues implica que realice una presentación o actuación; es retador, y va enfocado a las habilidades mentales de orden superior.
En cuanto a la perspectiva del docente, el ApP posee contenido y objetivos auténticos (del mundo real); utiliza una evaluación centrada en la valoración del desempeño; es proporcionado por el profesor; sus metas educativas son explícitas; afianza sus raíces en el constructivismo, y está diseñado para que el profesor también aprenda.
6. A MANERA DE CONCLUSIÓN
Con base en las ideas de Suchman (1987), Brousseau (1998) e Hinostroza (2000), y tomando en cuenta la relación que puede existir entre el constructivismo, la práctica pedagógica y la enseñanza de las matemáticas promovida por los docentes que ocupan las TIC, se establece que:
– Las teorías relacionadas con la innovación en la educación sugieren que las tecnologías actúan como catalizadoras del proceso de cambio. Tal efecto ayuda a producir una modificación en los métodos y procedimientos que utiliza un profesor, facilitando la adopción de estrategias pedagógicas diferentes que, eventualmente, son más efectivas.
– Desde una perspectiva distinta, que alude a las acciones del profesor, es posible argumentar sobre el potencial de estas tecnologías para actuar como mediadoras en la actividad profesional. Hay evidencia de su influencia en la forma como las personas estructuran su relación con el mundo que los rodea y de su consecuencia en la realidad que construyen (Suchman, 1987).
– En cuanto al aprendizaje, las tendencias actuales coinciden en argumentar a favor de enfoques constructivistas del aprendizaje, donde el alumno realiza actividades y proyectos que le permiten comprender los procesos y principios subyacentes. Estas tendencias implican que no basta con presentar un conjunto de contenidos, sino se deben entregar los medios necesarios para desarrollar actividades que tengan sentido para los alumnos en sus propios contextos y faciliten el desarrollo de habilidades superiores.
– Es posible afirmar que las Tecnologías de Información y Comunicación han cambiado el paradigma de los diseños para paquetes informáticos. Actualmente, como resultado de la integración de las comunicaciones con los multimedios, la computadora puede ser conceptualizada como vía de acceso a un espacio social distinto, lo cual permite concebir a un producto de software no como un interlocutor, sino como un instrumento de acción en un espacio en el que ocurren conversaciones con objetos reales o virtuales. Esto abre la posibilidad, como plantea Hinostroza (2000), de redefinir el rol de la tecnología, pues se transforma en un soporte al proceso de enseñanza que sirve para mejorar el aprendizaje.
– Desde la perspectiva de la didáctica de la matemática, como bien señala Brousseau (1998), los conocimientos pueden aparecer en situaciones originales, pero los saberes culturales están asociados necesariamente a prácticas sociales que les sirven de referencia. De esta manera, conociendo las bondades de las TIC en el área del aprendizaje y la enseñanza de las matemáticas, aunado a la concepción del constructivismo como postura epistemológica en la que el alumno es responsable de su propio aprendizaje, se establece que la práctica pedagógica de los docentes debe ir en consonancia con los cambios curriculares, donde los roles y funciones de los profesores se ven modificados siguiendo los cambios sociales.
– El conocimiento didáctico tiene unos conocimientos disciplinares de referencia que se estructuran en tres ejes: noción de currículo, fundamentos de las matemáticas escolares y organizadores del currículo. Si se toman en cuenta la descripción técnica de estos conocimientos de referencia, la planificación y estructuración del uso de las TIC, al igual que la manera como se espera que dinamicen al realizar el análisis didáctico, esto permitirá identificar y fundamentar los contenidos y objetivos de la asignatura en este caso particular de la matemática.
REFERENCIAS BIBLIOGRÁFICAS
Brousseau, G. (1998). ¿Qué pueden aportar a los enseñantes los diferentes enfoques de la Didáctica de las Matemáticas? Bordeaux, France: IREM–Université de Bordeaux. [ Links ]
Coll, C. y Solé, I. (1999). Los profesores y la concepción constructivista. En C. Coll, E. Martin, T. Mauri, M. Miras, Onrubia e I. Solé (Eds.), El constructivismo en el aula (pp. 7–23). Barcelona, España: Grao. [ Links ]
Cebrián de la Serna, M. (1999). La comunicación audiovisual y la informática en los planes de estudios de primaria y secundaria. En J. Cabero (Ed.), Tecnología educativa (pp. 151–161). Madrid, España: Síntesis. [ Links ]
Gallardo, J. y González, J. L. (2006). Una aproximación operativa al diagnóstico y la evaluación de la comprensión del conocimiento matemático. PNA. Revista de Investigación en Educación Matemática 1 (1), 21–31. Obtenido en junio, 2006, de http://www.pna.es/Numeros/pdf/Gallardo2006Una.pdf. [ Links ]
Gómez, P. y Rico, L. (2006). Análisis didáctico, conocimiento didáctico y formación inicial de profesores de secundaria. Trabajo no publicado. Universidad de Granada, España. [ Links ]
Hinostroza, E. (2000). Roles alternativos de TIC en educación: sistema de apoyo al proceso de enseñanza aprendizaje (Versión electrónica). Obtenido en octubre 3, 2003, del sitio web del Centro de Computación y Comunicación para la Construcción del Conocimiento, Universidad de Chile: www.c5.cl/ieinvestiga/actas/ribie2000/papers/265.html [ Links ]
Kilpatrick, J.; Gómez, P. y Rico, L. (1995). Educación matemática. México: Grupo Editorial Iberoamérica. [ Links ]
Marcelo, C. (2001). Rediseño de la práctica pedagógica: factores, condiciones y procesos de cambios en los teletransformadores. Conferencia impartida en la Reunión Técnica Internacional sobre el uso de TIC en el Nivel de Formación Superior Avanzada. Sevilla, España: 6–8 de junio. [ Links ]
Martínez, F. (2003). El profesorado ante las nuevas tecnologías. En J. Cabero, F. Martínez y J. Salinas (Coords.), Medios y herramientas de comunicación para la educación universitaria (pp. 207–222). Ciudad de Panamá, Panamá: Sucesos Publicidad. [ Links ]
Moursund, D. (1999). Aprendizaje por Proyectos con las TIC (capítulos I y II). Obtenido en diciembre, 2004, de http://www.eduteka.org/APPMoursund1.php. [ Links ]
Rojano, T. (2006). Incorporación de entornos tecnológicos de aprendizaje a la cultura escolar: proyecto de innovación educativa en matemáticas y ciencias en escuelas secundarias públicas de México. La Revista Iberoamericana de Educación 33. Obtenido en mayo, 2007, de http://www.campus–oei.org/revista/rie33a07.htm. [ Links ]
Sánchez, J. (2000). Nuevas tecnologías de la información y comunicación para la construcción del aprender. Santiago de Chile, Chile: LMA Servicios Gráficos. [ Links ]
Semenov, A.; Pereversev, L. y Bulin–Socolova, H. (2005). Las tecnologías de la información y la comunicación en la enseñanza. Manual para docentes. Montevideo, Uruguay: Trilce. [ Links ]
Suchman, L. (1987). Plans and situated actions: the problem of human machina communication. Cambridge, USA: Cambridge University Press. [ Links ]
Vergnaud. G. (1991) El niño, las matemáticas y la realidad. México: Trillas. [ Links ]
Von Glaserfeld, E. (1990). Introducción al constructivismo radical. En P. Watzlawick y otros, La realidad inventada (pp. 20–37). Barcelona, España: Gedisa. [ Links ]
Wilson, B. (1996). Constructivist learning environment. New Jersey, USA: Educational Technology. [ Links ]
Yábar, J. (2000). La computadora en la enseñanza secundaria. En C. Coll, (Comp.), El constructivismo en la práctica. Caracas, Venezuela: Laboratorio Educativo. [ Links ]














