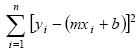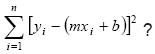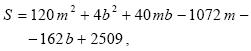El cálculo en carreras de ingeniería: un estudio cognitivo

 

Leopoldo Zuñiga ¹

 

¹ Escuela de Ingeniería y Ciencias Instituto Tecnológico y de Estudios Superiores de Monterrey Campus San Luis Potosí, México. E–mail: lzs@itesm.mx.

 

Fecha de recepción: 20 de Mayo de 2006
Fecha de aceptación: 24 de Noviembre de 2006.

 

RESUMEN

En este artículo se reporta un estudio cognitivo de carácter cualitativo en relación al aprendizaje de los conceptos de función de dos variables y de derivada parcial, en el contexto de la ingeniería. Se sostiene que en escenarios didácticos contextualizados se propicia un aprendizaje con significado para el estudiante, con sentido en el ámbito de su futura área profesional. Esto motivó la investigación sobre lo que sucede a nivel cognitivo en los alumnos en este tipo de ambientes didácticos. Se describen los referentes teóricos para el estudio del funcionamiento cognitivo en un acto mental de aprendizaje (como el proceso de resolución de un problema), y se presenta el análisis sobre los resultados de la puesta en escena del diseño de un escenario didáctico con un grupo de estudiantes de ingeniería.

PALABRAS CLAVE: Aprendizaje, contexto, funcionamiento cognitivo, ingeniería.

 

ABSTRACT

This paper reports a cognitive study of a qualitative character in relation to the learning of the two variable functions and partial derivative concepts in the engineering context. It defends the fact that didactic settings in context can be conducive to a logical meaningful learning for the student with sense in the future professional area. This motivated us to research what happened at cognitive levels for students in this type of didactic environment. The theoretical framework is described by the study of cognitive functioning in a mental act of learning (the process of resolving problem). The analysis reports the experience which results in the implementation of didactic setting designs with one group of engineering students.

KEY WORDS: Learning, context, cognitive functioning, engineering.

 

RESUMO

Este artigo se reporta a um estudo cognitivo de caráter qualitativo em relação a aprendizagem dos conceitos de função de duas variáveis e de derivada parcial, em um contexto de engenharia. Fundamenta–se que em cenários didáticos contextualizados se propicia uma aprendizagem com significado para o estudante, com sentido no âmbito de sua futura área profissional. Isso motivou a investigação sobre o que sucede a nível cognitivo, nos alunos, nesse tipo de ambiente didático. Descrevem–se os referenciais teóricos para o estudo do funcionamento cognitivo em um ato mental de aprendizagem (como o processo de resolução de um problema), e se apresenta a análise sobre os resultados de um local em cena do planejamento de um cenário didático com um grupo de estudantes de engenharia.

PALAVRAS CHAVE: Aprendizagem, contexto, funcionamento cognitivo, engenharia.

 

RÉSUMÉ

Dans cet article on fait le rapport d'une étude cognitif à caractère qualitative en ce qui concerne l'apprentissage des concepts à propos des fonctions à deux variables et des dérivées partielles, dans le contexte de l'ingénierie. Il en ressort que dans des situations didactiques en contexte, l'apprentissage acquiert un signifié, porteur de sens dans son environnement scolaire. Ceci a déclenché une recherche sur ce qui se passe chez les étudiants au niveau cognitif dans ce genre de situations didactiques. On décrit les référents théoriques pour l'étude du fonctionnement cognitif dans un acte mental d'apprentissage puis on présente les résultats de l'expérience de mise en oeuvre du design d'une situation didactique avec un groupe d'étudiants d'ingénierie.

MOTS CLÉS: Apprentissage, contexte, fonctionnement cognitif, ingénierie.

 

INTRODUCCIÓN

En el ámbito de la investigación en didáctica de las matemáticas es bastante conocido que la enseñanza habitual del cálculo se basa en la transmisión de conocimientos con un énfasis muy marcado en el desarrollo de habilidades algebraicas y se desatiende el discernimiento intelectual para la comprensión de ideas, nociones y conceptos. Tal situación ha sido abordada en diversos trabajos en los que se muestran desde argumentaciones teóricas hasta propuestas para mejorar la calidad del aprendizaje, las cuales incluyen tanto los conocimientos previos que necesitaría tener un estudiante para tener éxito en el estudio de cálculo, como la elaboración de materiales didácticos (Farfán, 1991 & 1994; Artigue, 1995; Dolores, 1999; Salinas et al., 2002).

Por ejemplo, Moreno (2005) indica que: "La enseñanza de los principios del cálculo resulta bastante problemática, y aunque seamos capaces de enseñar a los estudiantes a resolver de forma más o menos mecánica algunos problemas estándar, o bien a realizar algunas derivadas o integrales, tales acciones están muy lejos de lo que supondría una verdadera comprensión de los conceptos y métodos de pensamiento de esta parte de las matemáticas". Un problema importante ligado a esta situación es que el conocimiento generalmente se trata fuera de contextos apropiados. Así, cuando se pretende mostrar a los estudiantes la utilidad de los contenidos que se estudian, a lo más que se llega en un curso común de cálculo es a resolver los llamados problemas de aplicación que se proponen en los textos, que casi nunca corresponden a la realidad.

Esto tiene consecuencias negativas cuando los que aprenden son estudiantes que en el ejercicio de su profesión requieren de conocimientos y habilidades que les permitan resolver problemas de verdad. Tal es el caso de quienes se preparan en carreras de ingeniería. Camarena (1990) menciona que "parte de la problemática en ingeniería es que la matemática se encuentra totalmente desvinculada de las asignaturas de la ingeniería, y la realidad del ingeniero reclama esta vinculación que en materia de educación está en tierra de nadie".

Particularmente, en los programas de estudio correspondientes a los cursos de cálculo para ingeniería se puede leer, por ejemplo, que su objetivo consiste en proporcionar al alumno los conocimientos fundamentales del cálculo que serán utilizados en la interpretación, planteamiento y resolución de problemas específicos de su carrera; sin embargo, ni en dichos programas ni en los textos que se sugieren para los cursos son mencionados o tratados. Y más todavía: en comunicaciones personales con profesores que imparten dichos cursos señalan que, si bien tienen alguna idea, no conocen problemas o situaciones específicas de las carreras profesionales; por tanto, se limitan a enseñar, cuando mucho, el tipo de aplicaciones contenidas en los textos que llevan los alumnos.

Hay varios reportes en torno a esta situación de los profesores de matemáticas en el nivel superior de enseñanza. Moreno (2005) hace referencia a una investigación sobre las creencias de los docentes e indica que algunos maestros de matemáticas de las carreras de biología y química reconocen su "deficiente formación alejada de los modelos químicos y biológicos, y la influencia que esto tiene en su enseñanza, pues les impide dar explicaciones convincentes de algo que ni dominan ni conocen suficientemente".

Por otra parte, en entrevistas con profesores que imparten cursos de especialidad en ingeniería, donde se supone que emplean sus conocimientos de cálculo, afirman que realmente necesitan muy poco de estos conceptos, debido a que no se involucran con las deducciones de métodos o fórmulas, sólo las usan. Y como el tipo de problemas no van más allá de los rutinarios –ejercicios típicos que se presentan en los libros de texto de uso común–, no se necesita más.

Estas situaciones, producto de la experiencia, creencias y costumbres de los profesores, así como de su inmersión en el sistema didáctico habitual², repercuten directamente en el aprendizaje de los estudiantes y crea ideas falsas tanto sobre lo que se debe (qué y cómo) aprender como sobre la importancia de la matemática en su formación.

En diversos trabajos se mencionan las consecuencias negativas de estas situaciones. Artigue (1995) señala:

"Numerosas investigaciones realizadas muestran, con convergencias sorprendentes, que si bien se puede enseñar a los estudiantes a realizar de forma más o menos mecánica algunos cálculos de derivadas y primitivas y a resolver algunos problemas estándar, se encuentran grandes dificultades para hacerlos entrar en verdad en el campo del cálculo y para hacerlos alcanzar una comprensión satisfactoria de los conceptos y métodos de pensamiento que son el centro de este campo de las matemáticas. Estos estudios también muestran de manera clara que, frente a las dificultades encontradas, la enseñanza tradicional y, en particular, la enseñanza universitaria, aún si tiene otras ambiciones, tiende a centrarse en una práctica algorítmica y algebraica del cálculo y a evaluar en esencia las competencias adquiridas en este dominio. Este fenómeno se convierte en un círculo vicioso: para tener niveles aceptables de éxito, se evalúa aquello que los estudiantes pueden hacer mejor, y esto es, a su vez, considerado por los estudiantes como lo esencial, ya que es lo que se evalúa..."

Esta problemática condiciona el ambiente en el aula, la disposición de los estudiantes para aprender y su actitud ante los nuevos conocimientos. Saber matemáticas significa, para los alumnos, tener alguna habilidad en la resolución de ecuaciones, desarrollar procedimientos, aplicar fórmulas y métodos. Rara vez un estudiante concibe a las matemáticas como algo que le pueda ser útil más allá de eso, y cuando llega a suceder, no es del todo claro. ¿Qué se puede hacer? ¿Cómo vincular los contenidos matemáticos con las áreas que puedan interesar al estudiante? Al respecto, Camarena (2000) menciona:

"La matemática en contexto: ayuda al estudiante a construir su propio conocimiento de una matemática con significado, con amarres firmes y no volátiles; refuerza el desarrollo de habilidades matemáticas, mediante el proceso de resolver problemas vinculados con los intereses del alumno..."

De esta manera, atendiendo a la idea de que los estudiantes de ingeniería serán en su futura vida profesional usuarios de la matemática, y que requieren en su formación de situaciones que les muestren la utilidad de los conocimientos matemáticos en su área de especialidad, este trabajo se inscribe en la línea de investigación que aborda la problemática de la enseñanza de las matemáticas en contexto. Particularmente, su objetivo consiste en dotar de significado a los objetos y procesos matemáticos del cálculo, mediante el diseño de una situación–problema en el contexto de la ingeniería, a fin de investigar su impacto en el aprendizaje de los estudiantes dentro del aspecto cognitivo.

Cabe señalar que entre los antecedentes de estudios sobre matemática en contexto realizados en México se cuenta con el Diseño de un curso de ecuaciones diferenciales en el contexto de los circuitos eléctricos (Camarena, 1987), el Análisis de Fourier en el contexto del análisis de señales eléctricas y electromagnéticas (Camarena, 1993) y La serie de Fourier en el contexto de la transferencia de masa (Muro, 2000), mientras que en el ámbito mudial podemos mencionar a Riordan & Noyce (2001) y Meyer & Diopolus (2002). Incluso se están desarrollando algunos proyectos, como el Core–Plus Mathematics Project, llevado a cabo por investigadores de las instituciones Western Michigan University, University of Michigan, University of Maryland y University of Iowa. Sus productos didácticos han sido publicados bajo el título Contemporary mathematics in context: a unified approach (Hirsch et al., 2003).

Sin embargo, para los fines de este trabajo es elemental considerar que prácticamente no se han realizado estudios sobre el cálculo en el contexto de la ingeniería, atendiendo a las funciones cognitivas que están involucradas en el aprendizaje de los estudiantes. Se entiende por funciones cognitivas a los prerrequisitos básicos para que se den en forma satisfactoria las operaciones mentales y, en general, el procesamiento de la información en situaciones de aprendizaje, por ejemplo, al resolver un problema (esto se describe con mayor detalle en el marco teórico del trabajo).

Las investigaciones citadas proponen argumentos teóricos, estudian el impacto del diseño y la puesta en escena de situaciones–problema en contexto y hacen propuestas didácticas, mas no reportan un estudio específico y detallado de lo que sucede en las funciones cognitivas de quien aprende. Todo parece indicar en dichos trabajos que, cuando el aprendizaje ocurre en situaciones contextualizadas, se obtienen mejores resultados; de manera concreta, por la motivación que se provoca en los alumnos y el significado específico en el área de interés que, se supone, adquieren las nociones, ideas y conceptos matemáticos. Pero si esto es así, ¿qué sucede en la mente del estudiante?, ¿qué elementos de orden cognitivo están implicados en el aprendizaje?

 

EL PROBLEMA DE INVESTIGACIÓN

Para atender la problemática de la enseñanza y el aprendizaje de las matemáticas en carreras profesionales de ingeniería es necesario construir propuestas sobre estructuras didácticas alternativas que posibiliten un mejor aprendizaje, que tenga significado en los procesos ingenieriles prácticos cercanos al interés de los estudiantes y donde el estudio del cálculo adquiera sentido.

En aras de tal propósito, resulta indispensable indagar sobre el funcionamiento cognitivo de los estudiantes cuando se enfrentan a un escenario de aprendizaje del cálculo contextualizado en ingeniería, para tener elementos que den luz sobre la forma en que sucede el aprendizaje de nociones y conceptos matemáticos en ese tipo de escenarios. Se entiende que el funcionamiento cognitivo en un acto de aprendizaje que está determinado tanto por las operaciones mentales –comparaciones, síntesis, análisis– que posibilitan la interiorización y codificación de conocimientos, como por las funciones cognitivas –descritas en el marco teórico– que subyacen en el nivel operativo; es decir, las funciones que posibilitan la maniobra–bilidad para transformar y adecuar las representaciones mentales en juego durante el acto de aprendizaje.

De tal modo, se definió el problema de investigación mediante la pregunta ¿qué sucede en el aspecto cognitivo en los estudiantes de cálculo cuando el proceso de aprendizaje se realiza en escenarios contextualizados de la ingeniería? Esto surgió como respuesta a la necesidad de estudiar los aspectos cognitivos mencionados en experiencias de aprendizaje, dentro del contexto de la ingeniería. Además, se reconoce que la situación en la práctica educativa que reclama tal investigación está marcada por un hecho que revela la experiencia en las aulas, al menos en los primeros niveles de educación superior: la creencia generalizada (o al menos una duda constante) en los estudiantes de que las matemáticas poco les serán útiles en su futuro ámbito profesional.

Se sabe que un antecedente directamente ligado a este hecho radica en que el proceso de aprendizaje que han vivido los estudiantes en los niveles básicos está caracterizado por las tendencias de enseñanza tradicional; en ese sentido, su experiencia con las matemáticas no ha sido tal vez la más conveniente. Aquí, se cree que uno de los factores con influencia decisiva es que tanto los programas de estudio como las ideas didácticas en los textos de cálculo están basados en una estructura que propicia diversos conflictos en el aprendizaje, como señalan Cantoral & Mirón (2000): "la enseñanza habitual del análisis matemático logra que los estudiantes deriven, integren, calculen límites elementales sin que sean capaces de asignar un sentido más amplio a las nociones involucradas en su comprensión. De modo que aun siendo capaces de derivar una función, no puedan reconocer en un cierto problema la necesidad de una derivación".

Ahora bien, situaciones como ésta provocan que los estudiantes se formen una imagen conceptual restringida, y en muchos casos errónea, sobre el estudio y utilidad de las matemáticas. En particular, parece ser que para ellos el cálculo sólo es una serie de fórmulas, reglas o métodos sin beneficio, lo cual predispone su funcionamiento cognitivo. La actitud de los estudiantes hacia el aprendizaje de las matemáticas no es la misma cuando no hay motivación o interés por estudiar algo que, desde su perspectiva, no les resulta provechoso ni en su formación profesional ni en su futuro campo laboral.

Entonces, se considera que el aspecto cognitivo es fundamental en la investigación didáctica actual, ya que puede ofrecer información respecto a lo que sucede en la mente del que aprende. Se hace pertinente investigar cómo un sujeto obtiene conocimiento cuando se enfrenta a una situación problemática nueva, en un escenario de su interés, e interactúa con os recursos de que dispone en su memoria, tanto de orden cognitivo funcional y operativo –el estado de sus capacidades, en términos de funciones cognitivas y operaciones mentales– como los que atañen a sus conocimientos matemáticos previos.

Dado el problema de investigación en esta forma, el objetivo de nuestro trabajo fue analizar las funciones cognitivas³ de los estudiantes de cálculo en experiencias de aprendizaje de sus contenidos en el contexto de la ingeniería.

Cabe señalar que se supone que los estudiantes tienen mejor comprensión cuando los contenidos se tratan en contexto y, por consiguiente, se entiende a su vez que los estudiantes logran un mejor aprendizaje si es significativo (Ausubel et al., 1978); es decir, si los nuevos conocimientos se tratan en un proceso consistente en que los pensamientos, expresados simbólicamente de modo no arbitrario y objetivo, se unen con los conocimientos ya existentes en el sujeto para producir el aprendizaje. Por ello, el diseño de experiencias didácticas tiene que permitir una relación intencionada (no arbitraria) y sustancial (no al pie de la letra) con los conocimientos e ideas del alumno, pues el individuo debe desarrollar una serie de estrategias que le permitan adquirir un conocimiento, almacenarlo y recuperarlo cuando sea necesario. La eficacia de este aprendizaje se encuentra en función de su significatividad, no de las técnicas memo–rísticas, lo cual es acorde con las ideas sobre la matemática en contexto.

De esta forma, resulta esencial la investigación sobre cómo se logra ese aprendizaje, en términos de los elementos cognitivos implicados en el proceso donde se adquiere el conocimiento. Esto justifica el interés por abordar el análisis de las funciones cognitivas que soportan los procesos de pensamiento y posibilitan el nivel de operatividad mental adecuado para que suceda el aprendizaje.

 

MARCO TEÓRICO

El propósito de estudiar el aprendizaje en situaciones contextualizadas obligó a realizar una búsqueda de referentes teóricos que soportaran el análisis de todos los factores implicados en el desarrollo del proceso donde se implantan las experiencias de aprendizaje del cálculo en contexto y, por ende, en el propio proceso de conceptuación que concierne a las nociones matemáticas.

Por tanto, el soporte teórico debía tener como componente central al análisis de los aspectos cognitivos que ocurren en cada etapa del proceso de resolución de un problema contextualizado (Camarena, 2000). Estos son: planteamiento del problema; determinación de las constantes y variables del problema; incorporación de los temas y conceptos matemáticos necesarios para abordar el problema; obtención del modelo matemático del problema; solución matemática del modelo matemático; solución e interpretación en términos del problema. Aquí se incluye la comprensión de la situación, el proceso de resolución y la emisión de la respuesta.

Hay teorías que han sido pensadas (al menos en su origen) para estudiar los procesos de conceptuación progresiva de las estructuras matemáticas (Piaget, 1978; Vergnaud, 1990), lo cual implica un análisis en función de las etapas del desarrollo mental, como indica Vergnaud (1990), cuando explica el objetivo de su teoría: "Su principal finalidad es la de proporcionar un marco que permita comprender las filiaciones y las rupturas entre conocimientos, en los niños y los adolescentes". Y aclara que "las ideas de filiación y de ruptura se refieren igualmente a los aprendizajes del adulto, pero estos últimos se efectúan bajo restricciones que son más del orden de los hábitos y de sesgos de pensamiento adquiridos que relativos al desarrollo del aparato psíquico".

El interés de esta investigación estuvo directamente relacionado con esa aclaración de Vergnaud; es decir, con lo que sucede respecto a los efectos, en el nivel cognitivo, de tales hábitos y sesgos de pensamiento en situaciones de aprendizaje, sobre todo considerando que el presente trabajo se hizo con estudiantes de cálculo en carreras de ingeniería, que se supone han alcanzado la madurez cognitiva.

De este modo, para atender al objetivo del trabajo se decidió basar sus estudios en dos ideas esenciales: (1) incluir aspectos del comportamiento psíquico; es decir, para el análisis del funcionamiento cognitivo se recurrió a la idea de la analogía entre mente y ordenador como base científica de estudio, pero se incorporaron elementos teóricos que nos dieran luz sobre los factores internos en que se basan los procesos mentales y que influyen en las conductas de aprendizaje de los estudiantes; (2) implementar una forma sistemática de analizar lo concerniente a la conceptuación de nociones matemáticas en una experiencia de aprendizaje en contexto.

Para la primera consideración, se tomó la teoría de las funciones cognitivas, como la concibe Feuerstein (1977), y para la segunda tanto el modelo teórico de la tripleta conceptual fenomenologías–generalizaciones–notaciones, de Godino & Recio (1998), como las nociones de acto matemático–cognitivo y escenario didáctico. Se describen a continuación estos recursos teóricos.

Las funciones cognitivas son consideradas como los prerrequisitos básicos de la inteligencia, subyacen en las operaciones mentales, ayudan a la interiorización de la información y permiten la autorregulación del organismo. La interiorización es el pilar básico del aprendizaje y de la adaptación y, por tanto, de la inteligencia. "Las funciones cognitivas como actividades del sistema nervioso explican, en parte, la capacidad del individuo para servirse de la experiencia previa en su adaptación a nuevas situaciones" (Feuerstein, 1979).

Particularmente, este estudio sigue el esbozo teórico presentado en un trabajo anterior (Zúñiga, 2004), en el cual se describen las características de cada fase en el procesamiento de la información sobre las funciones cognitivas⁴ de Feuerstein, que aparecen en el acto mental de aprendizaje implicado en la resolución de un problema, y que se presenta a continuación:

En la fase de entrada:

• La comprensión implica tener una percepción clara tanto de los datos que se ofrecen en el enunciado como del estado final o meta a la que se quiere llegar (los datos proporcionan una descripción completa del contexto del problema y de los parámetros bajo los cuales se debe operar).

• A su vez, para el logro de la percepción clara es necesario que las funciones cognitivas de exploración sistemática de una situación de aprendizaje y de organización de la información aparezcan en forma eficiente.

En la fase de elaboración:

• La resolución del problema implica la búsqueda de una vía de solución (que conecte el estado inicial con el estado meta), pero antes es necesario que el sujeto sea capaz de percibir y definir con precisión el problema, lo cual implica que su función cognitiva de percepción y definición de un problema surja en forma eficiente. Este es un momento crucial en el proceso porque constituye el enlace entre la comprensión de la situación problemática y lo que es propiamente la resolución del problema. Se pueden tener dificultades en el desarrollo de la fase de elaboración cuando no se define con precisión el problema en términos de la meta a la que se quiere llegar.

• La búsqueda de una vía de solución implica la planificación de la conducta (una función cognitiva que está presente en todo el proceso de resolución), así como la recuperación de esquemas en la memoria a largo plazo que involucran conocimientos matemáticos, lo cual a su vez requiere de una conducta comparativa.

• El proceso de pensamiento para el uso, adecuación o modificación de esquemas previos en la construcción de las nuevas ideas, nociones o conceptos matemáticos involucra, al menos, la capacidad de pensamiento hipotético y la conducta comparativa.

• La construcción de conocimiento requiere para la codificación de la información correspondiente a las nuevas ideas, nociones y conceptos de la función cognitiva de interiorización y representación mental, que es una de las más importantes. Como señala Prieto (1992): "La interiorización es el pilar básico del aprendizaje y de la adaptación y, por tanto, de la inteligencia".

En la fase de salida:

• La respuesta ha de emitirse utilizando un lenguaje claro y preciso en función de la meta final del problema formulado; es decir, se debe observar una comunicación explícita de tal respuesta.

• Se debe observar capacidad para pensar y expresar la respuesta correcta al problema, así como para reflexionar antes de comunicarla. Debe haber precisión y exactitud en la respuesta y un control en su emisión.

Las etapas de la matemática en contexto (Camarena, 2000), mencionadas al inicio de esta sección, están contempladas dentro del esbozo teórico. En la fase de entrada: planteamiento del problema y determinación de las constantes y variables. En la fase de elaboración: incorporación de los temas y conceptos matemáticos necesarios para abordar el problema; obtención del modelo matemático del problema, y solución matemática del modelo matemático. En la fase de salida: solución e interpretación de la solución en términos del problema.

Además, para el análisis del aprendizaje sobre los conceptos matemáticos involucrados en la experiencia, se empleó como apoyo un modelo teórico particular para estudiar las relaciones dialécticas entre pensamiento, lenguaje matemático y situaciones–problema, el cual incluye los elementos concepto, signo/símbolo y objeto/contexto (Godino & Recio, 1998). Este modelo tiene las siguientes entidades básicas: las fenomenologías, donde se considera a las situaciones–problema, las aplicaciones, las tareas específicas y, en general, a las entidades extensionales que inducen actividades matemáticas; las notaciones, que abarcan a todo tipo de representaciones materiales ostensivas que ocupa la actividad matemática (términos, expresiones, símbolos, gráficos, tablas, diagramas, etc.; en general, a entidades notacionales), y las generalizaciones, como ideas matemáticas o abstracciones (conceptos, proposiciones, procedimientos, teorías; esto es, entidades intencionales).

Cabe señalar que, si bien este modelo semiótico ha sido pensado para el estudio de los procesos de interpretación y comunicación en educación matemática, en este trabajo se le hace una interpretación y adecuación personal para analizar los elementos conceptuales sobre los que debe transitar un estudiante cuando ha comprendido una noción matemática; es decir, si es capaz de reconocer y transitar por las fenomenologías, notaciones y generalizaciones que lo caracterizan.

Esta investigación también es acorde con la idea de que el estudio matemático tanto de los fenómenos del mundo real como del matemático coloca al que aprende ante situaciones–problema. Asimismo, que las generalizaciones matemáticas en esas situaciones son producto de los procesos de generalización de las acciones realizadas; es decir, de la generalización de esquemas o invariantes de sistemas de acciones, así como de las condiciones de realización y los resultados de tales acciones, apoyados por el uso de sistemas de signos. De igual modo, que las entidades notacionales pueden ser cadenas de letras o números, pero también gráficos, diagramas o incluso objetos físicos, y no tienen sólo una valencia semiótica, sino que a la vez son instrumentos ostensivos para la actividad matemática (Godino & Recio, 1998).

Respecto a las nociones de acto matemático–cognitivo y escenario didáctico, constituyen recursos teóricos propios que fue necesario definir en el desarrollo de la experiencia (esto se comenta más adelante, en la sección sobre el diseño y las actividades en el aula):

El escenario didáctico está constituido por todos los elementos que conforman el contexto de la situación problemática, y es el que determina y da sentido al estudio de las ideas, nociones y conceptos matemáticos necesarios para la resolución del problema que se plantea en tal contexto. Esto incluye también los factores extramatemáticos y extraescolares que dan origen al diseño de la situación–problema en contexto.

Con acto matemático–cognitivo nos referimos al hecho concreto del acto mental en que sucede el aprendizaje de una idea, noción o concepto matemático (o incluso un proceso algorítmico). Se encuentra constituido por al menos un proceso interpretativo que, a su vez, contiene las tres entidades básicas del modelo conceptual de Godino & Recio (1998): fenomenologías, notaciones y generalizaciones.

Un proceso interpretativo es cada elemento simbólico que interviene en el acto mental de resolver un problema, y está conformado tanto por la notación simbólica como por lo que representa en el ámbito de ese problema (interpretación personal sobre el término proceso interpretativo, usado por Godino & Recio, 1998).

Por último, es importante precisar la concepción de problema que se maneja, pues es un elemento central en el análisis de la investigación. Un problema representa un reto o dificultad que no tiene resolución inmediata y posibilita la búsqueda de procedimientos por parte del alumno a partir de sus conocimientos previos. Esta concepción de problema implica la novedad, tanto en el sentido de una tarea que tiene elementos nuevos que no se comprenden, como en la idea de construir procedimientos o estrategias para su resolución.

 

DESCRIPCIÓN DE LA EXPERIENCIA

La investigación se realizó en el ámbito de la carrera de Ingeniería Industrial y de Sistemas que ofrece el Instituto Tecnológico y de Estudios Superiores de Monterrey (ITESM), Campus San Luis Potosí, México. Se trabajó con un grupo de 12 estudiantes, entre 19 y 21 años de edad, que habían cursado y acreditado dos cursos de cálculo, uno de diferencial y otro de integral, ambos en una variable real.

La investigación se efectuó de acuerdo con dos fases: la primera comprendió un estudio previo de carácter didáctico sobre las áreas de especialidad en ingeniería donde se usan conocimientos de cálculo, y la segunda a la puesta en escena del diseño y al propio análisis sobre las funciones cognitivas.

El estudio de la primera fase se circunscribió al análisis de los textos en que están basados los cursos de esas áreas, la consulta a los profesores responsables y la revisión del plan de estudios de la carrera de Ingeniería Industrial y de Sistemas (con especial atención en los programas analíticos). Los resultados permitieron observar que hay áreas de especialidad de la ingeniería industrial –como el análisis de regresión y el análisis y diseño de experimentos– donde se ocupan conocimientos de cálculo. De manera particular, se identificó un conocimiento de especialidad, el método de mínimos cuadrados para el ajuste de curvas, en el que aparecen conocimientos de cálculo como las funciones de dos variables independientes, la derivada parcial y el cálculo de extremos de funciones.

La segunda fase comprendió las siguientes etapas:

a) Se diseñó la situación–problema en contexto que fue presentada a los estudiantes y se determinaron las actividades específicas del proceso a realizar en el aula.

b) Se realizó la experiencia de aprendizaje, mediante la aplicación de la situación problemática contextualizada al grupo de estudiantes ya mencionado, que llevaba el curso de Matemáticas para Ingeniería III (cálculo multivariable y una introducción al cálculo vectorial). Fueron conformados equipos para trabajo colaborativo y se abordó la situación problemática.

c) Se llevó a cabo el análisis cognitivo–cualitativo en el proceso de implementación de la experiencia, desde la perspectiva de Feuerstein, así como respecto al modelo teórico del triángulo fenomenologías–generalizaciones–notaciones. La recolección de datos se hizo mediante grabaciones en video y de los materiales que escribieron los alumnos.

Esta última fase se enfoca en el diseño de una experiencia de aprendizaje en el contexto de la Ingeniería Industrial y de Sistemas, particularmente en el método de ajuste de curvas llamado de mínimos cuadrados (resultado de la primera fase), como se describe a continuación.

 

EL DISEÑO Y LAS ACTIVIDADES EN EL AULA

En atención a los objetivos de la investigación y los resultados del estudio previo –primera fase–, se decidió aprovechar una situación que desde hace años es un problema ambiental en ciertas zonas aledañas a la ciudad de San Luis Potosí: la contaminación por residuos de sustancias químicas que realizan algunas empresas. De hecho, algunos casos han sido documentados y dados a conocer a la opinión pública en medios informativos como la prensa y la televisión. Inclusive, científicos de la Universidad Autónoma de San Luis Potosí han efectuado estudios experimentales (toma de muestras y su análisis) que han sido tema para estudios de posgrado.

Esta problemática se dio a conocer y se discutió con los estudiantes, previo al desarrollo de la experiencia, y constituyó uno de los factores que dieron sentido al problema matemático estudiado en el aula; además, situó el escenario didáctico global en el contexto específico de la ingeniería industrial.

El diseño de la experiencia fue el siguiente:

Uno de los problemas más desafiantes para el control de la contaminación del agua lo presenta la industria del curtido de pieles. Los deshechos de esta industria son químicamente complejos. Se caracterizan por valores elevados en la demanda de oxígeno bioquímico, los sólidos volátiles y otras mediciones de contaminación. Actualmente, se tiene un problema serio con este tipo de contaminación en las cercanías de la ciudad de San Luis Potosí, y se les está invitando a contribuir en la solución del problema. De acuerdo con los estudios realizados, lo que se necesita en estos momentos es determinar un modelo matemático para el comportamiento de este fenómeno y poder entonces estimar elementos en relación con la contaminación producida.

Considérense los datos experimentales de la tabla (ver Tabla 1), los cuales se obtuvieron de 33 muestras de desperdicios que se tratan químicamente en un estudio realizado en la empresa potosina Pieles Naturales del Centro, durante el periodo comprendido entre agosto de 2001 y enero de 2002. Se presentan las lecturas de la reducción porcentual del total de sólidos (x) y de la reducción porcentual de demanda de oxígeno químico (y) para esas 33 muestras.

¿Qué modelo matemático propondrían para el comportamiento de estos datos experimentales?

Se organizó al grupo en cuatro equipos de trabajo, con tres integrantes, mientras que el trabajo se realizó en seis sesiones de 75 minutos cada una.

Es importante mencionar que presentamos a los estudiantes el escenario diseñado antes de abordar cualquier contenido de cálculo diferencial en varias variables, con el objetivo de que la situación problemática motivara y diera sentido al estudio de los conocimientos matemáticos necesarios para resolverla.

 

La secuencia de actividades para la resolución del problema fue la siguiente:

1era. sesión:

• Presentación de la situación problemática (por escrito).

• Los estudiantes leen y discuten sobre ella (trabajo colaborativo).

• Se pide a los estudiantes que describan por escrito lo que se solicita, lo que conocen y lo que desconocen, así como el planteamiento de una estrategia de solución.

• Se les encarga que investiguen en torno a lo que desconocen de la situación (extra clase).

2a. sesión:

• Se discute sobre lo investigado y, con base en ello, se induce a los estudiantes a trabajar la idea básica del método de mínimos cuadrados.

• Se deduce en interacción grupal y por equipos la expresión matemática (*)⁵ que resulta al usar dicha idea.

• Se cuestiona a los estudiantes sobre qué se debe hacer para continuar el proceso de resolución.

• Se discute la naturaleza de la expresión última (*).

• Se pide a los estudiantes que realicen un ejercicio particular con sólo cuatro datos numéricos (extra clase).

3ra. sesión:

• Se discute el trabajo extra clase y la expresión (*).

• Se dedica la sesión al estudio de funciones de dos variables.

4a. sesión:

• Se discute acerca de las condiciones para que ocurra un valor extremo (en términos de pendientes de rectas y planos).

• Se estudia el concepto de derivada parcial y la forma de calcularla.

5a. sesión:

• Se continúa la última actividad de la sesión anterior.

• Se deduce el criterio para determinar valores extremos.

• Se solicita a los estudiantes que analicen la expresión (*) ya escrita como función y en términos de todo lo estudiado hasta el momento.

6a. sesión:

• Se determina en forma general el sistema de ecuaciones para determinar la pendiente y la ordenada al origen, y se resuelve.

• Se pide a los estudiantes que entreguen por escrito todo el proceso de resolución del problema.

Antes de presentar el desarrollo de la experiencia y el estudio cognitivo correspondiente, cabe resaltar un hecho que resultó fundamental durante el proceso de implementación de las actividades diseñadas: la necesidad de definir los elementos teóricos con base en los cuales se habría de realizar el análisis cognitivo respecto a los actos de aprendizaje en todo el proceso de resolución de la situación–problema en contexto.

Para el diseño particular en cuestión, era necesario precisar el papel que jugaban los actos concretos; por ejemplo, reconocer o interpretar la expresión:

como un ente matemático susceptible de diferenciación, las ideas y nociones matemáticas involucradas en la conceptuación de la derivada parcial, y el acto de aprendizaje del método para calcular un extremo de una función de dos variables.

Sin embargo, no había un término, ni en la teoría de Feuerstein ni en la tripleta conceptual de Godino & Recio (1998), con el que se pudieran ubicar en el marco teórico esos actos de aprendizaje. Entonces, para vertebrar los elementos centrales del análisis cognitivo (las funciones cognitivas implicadas, así como los conceptos matemáticos de estudio y sus relaciones en términos de generalizaciones, fenomenologías y notaciones), hubo necesidad de asignarle nombre a dichos actos y definir lo que significaban en el análisis. Así, se definió el término acto matemático–cognitivo y se precisó lo que se entiende por escenario didáctico y procesos interpretativos (ya mencionado en la sección del marco teórico).

El escenario didáctico descrito, que es la base de nuestra investigación, está conformado por el problema de contaminación ambiental en las cercanías de la ciudad de San Luis Potosí. Aquí, el contexto en la ingeniería queda determinado tanto por los resultados del estudio previo sobre las áreas de especialidad en ingeniería donde se usan conocimientos de cálculo como por la situación social del problema de contaminación, que atañe al área de especialidad de la ingeniería industrial. Esto implica que la noción de contexto se conforma por dos elementos: el ámbito institucional (planes y programas analíticos de estudio) y el ámbito extraescolar (situaciones o problemas vinculados al quehacer de un ingeniero).

El uso de los elementos teóricos en la investigación es como se presenta enseguida.

 

PROCESOS INTERPRETATIVOS PARA EL ANÁLISIS DE LAS FUNCIONES COGNTIVAS

Las palabras y expresiones matemáticas que aparecen tanto en el enunciado del problema en contexto como en el proceso de resolución, y que desencadenan procesos interpretativos, son las siguientes: Modelo matemático, %, x, y, los números (de la tabla), gráfica, puntos coordenados, función de una variable, función de dos variables, superficie, diferencia de ordenadas, pendiente, ordenada al origen, variables, constantes, sumatoria, igualdad, cuadrado (de potencia), derivada parcial, ecuación y solución de un sistema de ecuaciones lineales.

En cuanto a los procesos interpretativos, son:

1. Sobre el enunciado:

1a, modelo matemático significa función; 1b, % representa porcentaje; 1c, las letras x, y designan valores numéricos (datos experimentales); 1d, los números en las tablas representan valores porcentuales.

2. Sobre el proceso de resolución:

2a, d representa las diferencias verticales entre la recta que se busca y los datos numéricos. Se coloca junto al segmento de recta que une un punto con la representación gráfica de la recta que se pide;

2b, x, y designan los datos numéricos;

2c, m y b simbolizan la pendiente y la ordenada al origen de la recta que se busca, respectivamente;

2d, y = mx + b traduce la expresión "forma de una función líneal" (también puede interpretarse como "la ecuación pendiente–ordenada al origen de la recta");

2e, y_i – mx + b es la diferencia entre la ordenada y de cada punto dato numérico y la ordenada de un punto de la recta y = mx + b;

2f, d_i = y_i (mx_i+b) figura la equivalencia entre los procesos interpretativos 2a y 2e;

2g, representa una suma de términos, del primero al n–ésimo;

2h, significa la suma de todas las diferencias entre los puntos, datos experimentales y la recta buscada;

2i, determina una forma válida y conveniente para el trabajo en el registro algebraico y figura la suma de las diferencias entre los puntos datos experimentales y la recta, al cuadrado;

2j, una función en las variables independientes m, y b, (f (m, b) resulta de una extensión –generalización– de la notación f (x));

2k, simbolizan las derivadas parciales de f respecto a m y a b;

2l, o son la pendiente nula de f tocante a m y la pendiente nula de f en relación a b;

es la derivada parcial respecto a m, y

la derivada parcial que atañe a b;

es el sistema de ecuaciones que permite determinar m y b, bajo el conocimiento de que la igualación a cero proporciona los valores de m y b, dondef (m, b) toma su valor extremo mínimo.

En cada proceso interpretativo se puede reconocer la dialéctica entre las ideas (generalizaciones), el lenguaje simbólico (notaciones) y la situacion matemática en que sucede (fenomenologías).

Por ejemplo, en 2c la idea (generalización) de incógnita o variable está "encapsulada" en la notación m, b, y el hecho fenomenológico queda constituido por la representación geométrica donde se ubica (plano cartesiano), la cual es producto de la idea que genera el método. Otro ejemplo: en 2e la idea de diferencia (como una distancia en el registro gráfico) está representada por la expresión y_i (mx_i+b), y el hecho fenomenológico es la situación geométrica en que se enmarca (resulta de la idea que origina el método).

 

LOS ACTOS MATEMÁTICOS–COGNITIVOS

El análisis se centra en los actos matemático–cognitivos de aprendizaje fundamentales en el proceso de resolución del problema en estudio:

1. La interpretación de:

como una función de dos variables.

2. La conceptuación de la derivada parcial.

3.  El proceso para determinar un valor mínimo de una función de dos variables

Cabe señalar que en este último acto el análisis se hace considerando los conocimientos matemáticos que entran en juego; es decir, se analiza en función de las ideas, nociones y conceptos en que se basa el proceso al cual se refiere, no sólo en términos del proceso como tal.

 

RESULTADOS Y ANÁLISIS

Todo el análisis se efectúa con base en las observaciones sobre el desarrollo de las experiencias de aprendizaje, así como en el material de los videos y los escritos en papel de los estudiantes sujetos a las experiencias. Las frases en letra cursiva y entre comillas corresponden a transcripciones literales de los alumnos.

Fase de entrada

1era sesión

Al inicio no se observan dificultades para comprender lo que plantea el enunciado; sin embargo, en el tránsito al proceso de resolución surgen problemas en la función cognitiva de percepción y definición de un problema, ya que los alumnos comprenden lo que trata la situación problemática, mas no es inmediata su percepción del problema por los siguientes desequilibrios:

• Desequilibrio causado por el enfrentamiento con información novedosa: "hay cosas que no se conocen y no es claro lo que se pide".

• Las condiciones en que se aborda la situación problemática hace que los estudiantes tengan un desequilibrio en sus concepciones sobre las formas de enseñanza–aprendizaje a las que han estado expuestos (primero se han de estudiar los contenidos matemáticos, después las aplicaciones). Aparecen comentarios como "pero si todavía no hemos visto nada del curso, ¿cómo lo vamos a resolver?"

Estas dificultades se van superando a medida que los sujetos piensan reflexivamente el problema y lo discuten para buscar una definición conveniente; asimismo, descartan aquellos aspectos incompatibles e incongruentes y utilizan todo tipo de información previamente almacenada que tenga cierta relación con el problema, lo cual implica el uso de las funciones cognitivas de exploración sistemática de una situación de aprendizaje y de organización de la información. De manera particular, los estudiantes recuperan sus esquemas sobre el concepto de función, los de representación simbólica y gráfica y, sobre todo, la idea de lo que hay que hacer cuando lo que se tiene es una colección de puntos (en una tabla): graficar los puntos en un plano coordenado. Esa es la primera idea que aparece en prácticamente todos los equipos de trabajo.

Los esquemas previos de representación de funciones de una variable hacen que los estudiantes tengan confianza para elaborar una definición precisa del problema; además, les crea un sentimiento de competencia para abordarlo.

Por otra parte, se nota un aspecto de suma importancia en esta fase de entrada: hay una gran motivación en el grupo por tratar un problema asociado a una situación real, ligada al área de su formación profesional. Se percibe en el aula un ambiente propicio para el aprendizaje y existe disposición en cada alumno por abordar el problema y colaborar con sus compañeros de equipo. Cabe señalar que ésta era una situación ya esperada (debido a los resultados de investigación con que se contaba en este aspecto, mencionados en la introducción de este trabajo); sin embargo, se considera importante comentarla porque determina la conducta de los estudiantes para las fases siguientes en el desarrollo de la experiencia. Sin embargo, no se puede presuponer el éxito en cuanto al aprendizaje de los contenidos de cálculo involucrados sólo porque hay motivación y disposición de los alumnos para hacer las actividades diseñadas.

 

Fase de elaboración

1era. sesión

Una vez que los estudiantes han graficado los puntos en el plano xy, aparecen ideas diversas sobre la estrategia para determinar el modelo que pide el problema. Sin embargo, en todas se observan patrones de comportamiento muy similares en los estudiantes: planifican lo que van a hacer, siguen hipótesis, realizan comparaciones y utilizan la evidencia lógica. Por ejemplo, un equipo, luego de discutir, escribe: "intentamos graficar los datos dados en el problema y nos dimos cuenta que la gráfica no correspondía a una función, puesto que se repiten varios valores en el eje x".

Al platicar con ellos al respecto, señalan que planearon (planificación de la conducta) graficar para ver si podían determinar la forma de la función, lo cual implica la suposición (pensamiento hipotético) de que los datos numéricos representan, precisamente, una función. Luego, les surgieron ideas como unir los puntos con segmentos de recta, y uno de los estudiantes dijo que eso se parecía a una gráfica como las de códigos de barras, que no recordaba cómo eran, pero se hacían con funciones trigonométricas, hecho que implica una conducta comparativa; finalmente, advierten que la colección de puntos no representa una función porque hay pares ordenados donde se repite la abscisa. Esto significa que recurren a su conocimiento previo sobre el concepto de función y usan la evidencia lógica para describir el comportamiento de los datos y descartar la posibilidad de una función, como habían supuesto inicialmente.

Otro de los equipos anota: "Primero vimos que es bidimensional, después graficamos para darnos una idea de la tendencia que tiene la gráfica de la función; al verla, se nos ocurre trazar dos líneas paralelas entre las que se encuentran todos los puntos y después trazar una nueva recta paralela, exactamente entre las dos primeras rectas".

Nuevamente, se planea graficar y se supone que los datos representan una función. Sin embargo, la estrategia para tratar de hallar el modelo es diferente. Estos alumnos suponen que es una buena idea, dado el comportamiento de los puntos, dirigir sus esfuerzos a encontrar una recta que pase entre los datos numéricos; tal conducta implica el pensamiento hipotético y el uso de la evidencia lógica. Suponen que es una buena idea pensar en un modelo lineal, considerando la evidencia de la forma en que se comportan los datos.

Aquí, se invita a los estudiantes a reflexionar sobre lo que conocen y lo que desconocen de la situación problemática. En discusión, primero en equipos y después grupal, se delibera sobre la posibilidad de que existan métodos para realizar lo que se pide se acuerda investigar al respecto.

2a. sesión

Se presentan por equipo los resultados de la tarea encomendada en la sesión anterior.

Los estudiantes presentan diversos métodos numéricos (el nombre y alguna idea de cómo funciona) tanto de correlación como de interpolación y extrapolación, entre otros. El profesor, dentro de todas las posibilidades, induce al uso del método de mínimos cuadrados, y explica sus ventajas en relación con el problema que se está tratando y con los objetivos del curso. Se decide que se intente hallar un modelo lineal para los datos, recuperando la idea de uno de los equipos (ya mencionada).

Una vez estudiadas las ideas básicas en que se fundamenta el método, es decir, minimizar el cuadrado de la suma de las diferencias entre cada punto (dato experimental) y la mejor recta de ajuste, y determinan que la expresión que representa estas ideas es:

se prosigue con el análisis de las funciones cognitivas en términos de los actos matemático–cognitivos y los procesos interpretativos descritos anteriormente.

 

ANÁLISIS PARA EL ACTO MATEMÁTICO COGNITIVO 1

Acto matemático–cognitivo:

La interpretación de:

como una función de dos variables.

Procesos interpretativos involucrados:

2i. determina una forma válida y conveniente para el trabajo en el registro algebraico. Representa la suma del cuadrado de las diferencias entre los puntos datos experimentales y la recta.

2j. indica una función en las variables independientes m; b, del símbolo f(m, b), resulta de una extensión –generalización– de la notación f(x).

En 2i hay una expresión algebraica, pero no tiene un significado conceptual (como función) para los estudiantes ni está enmarcada en una situación fenomenológica (que no sea el propio registro gráfico que la origina).

Respecto a 2j, establece una representación simbólica funcional en las variables m y b, con lo cual se tiene un proceso interpretativo en el que intervienen los tres componentes del modelo: una expresión simbólica (notaciones); una idea matemática (noción de función de dos variables), y una fenomenología implícita, que atañe al espacio (sistema tridimensional) y la situación que le dio origen (los puntos datos experimentales y la idea básica del método).

 

Análisis:

Se observan dificultades en algunos estudiantes para interiorizar la expresión en 2i como una función de dos variables, debido a concepciones previas. Por ejemplo:

• Las variables son x y y: conocimiento fijo en la memoria como producto del abuso en el uso de estas letras para denotar variables en el sistema común de enseñanza.

• No es lo mismo incógnita que variable. Para los estudiantes, las variables son x y y porque "son las que varían en los datos de la tabla". Esto es, x y y "toman diversos valores"; m y b, por su parte, son incógnitas porque "no toman distintos valores, simplemente no sabemos cuánto valen".

Estas concepciones son un obstáculo para la interpretación en 2j porque, por ejemplo, una función tiene variables independientes, no incógnitas independientes; además, los estudiantes comentan que "son muchas variables e incógnitas". Asimismo, se privilegian a los símbolos en la expresión sobre la forma en que se denota una función, debido a que el proceso interpretativo 2i no tiene una generalización ni una fenomenología implícitas asociadas.

También surge impulsividad (disfunción asociada a la función cognitiva de exploración sistemática de una situación de aprendizaje) ante la pregunta ¿qué tipo de expresión matemática es:

Los estudiantes dan respuestas inmediatas como "es la suma de las diferencias entre los puntos y la recta que se busca", con lo cual muestran una tendencia a contestar sin reflexionar sobre la pregunta; sólo lo hacen en términos de los aspectos previos en la deducción de la expresión (procesos interpretativos anteriores). Ante esta situación, se les insiste a que piensen en lo que representa:

como objeto matemático; es decir, si la expresión simboliza una ecuación, una función, una identidad, etc.

Algunos estudiantes contestan de manera impulsiva que la expresión representa una ecuación; otros, una función. Se puede inferir que en su razonamiento subyacen hipótesis particulares sobre la naturaleza de la expresión, y eso los motiva a ofrecer sus respuestas. A su vez, tal razonamiento implica comparaciones con sus esquemas previos sobre el tipo de expresión en cuestión. Las funciones cognitivas de conducta comparativa y pensamiento hipotético entran así en juego, en forma implícita, en la situación de aprendizaje.

Es importante señalar que la impulsividad de algunos estudiantes ocurre, en ciertos casos, porque no efectúan una exploración sistemática y reflexiva sobre las características de la expresión en estudio, no porque no tengan el conocimiento para identificar los símbolos asociados a las notaciones comúnmente usadas para una ecuación o una función.

Además, se observa que esta impulsividad surge por el deseo de participar en el proceso de aprendizaje, ya que algunos estudiantes que comúnmente no colaboran en el grupo aportando ideas, ofreciendo respuestas o discutiendo, lo hacen ahora. La motivación que subyace en la experiencia de aprendizaje al abordar el problema crea un ambiente donde estos alumnos encuentran sentido a lo que se está estudiando, ponen toda su atención y muestran disposición a participar en las discusiones.

Se debe aclarar que las situaciones de disfunción cognitiva observadas no son generalizadas en el grupo, pues tanto los conflictos iniciales respecto al conocimiento previo como la impulsividad aparecen sólo en algunos estudiantes dentro de los equipos de trabajo. Otros, de inicio, proponen que la expresión "no es una ecuación porque no está igualada con nada", o "sí representa una función, pero le falta el nombre", etc.

En esta parte, para situar las características involucradas en el tránsito del proceso interpretativo 2i al 2j, necesario para la conceptuación de:

como una función de dos variables, se propuso a los estudiantes que consideraran el siguiente ejercicio:

Considera los puntos coordenados (2, 2), (4, 11), (6, 28) y (8, 40). Aplica la idea del método de mínimos cuadrados vista en la sesión de clase (sustituye estos valores en la expresión que estamos estudiando), desarrolla la sumatoria, simplifica y grafica en Maple la expresión resultante. Imprime una perspectiva gráfica donde se aprecie lo mejor posible el valor extremo que tiene.

Una vez que los estudiantes han simplificado y obtenido la expresión:

comprenden que ésta siempre es la forma que se obtiene, y que no depende de los números en los pares ordenados. Además, cuando se les cuestiona acerca de la forma geométrica de dicha expresión, algunos recuperan sus conocimientos sobre graficación de funciones en una variable y dan argumentos como "es una cuadrática general que tiene sus términos cuadráticos positivos y entonces debe abrir para arriba,... como una cosa tipo parábola". Si se trabaja con analogías y comparaciones de tal índole, a los estudiantes no se les dificulta aceptar que este tipo de expresión siempre tendrá un valor extremo mínimo.

Cuando los alumnos capturan la expresión en el software Maple reflexionan sobre su naturaleza, ya que la instrucción Plot3d grafica funciones (parte del trabajo extraclase consistía en investigar cómo utilizar el Maple para graficar este tipo de expresiones). Algunos escriben en su reporte de tarea:

donde S representa la sumatoria de la cual se obtuvo la parte derecha de la ecuación. Los demás estudiantes del grupo aceptan esta notación sin dificultad. Entonces, se les pregunta ¿de cuántas variables depende esta expresión?, y prácticamente todos están de acuerdo en que depende de dos: m y b. Aparecen explicaciones como "la sumatoria depende de m y de b".

En cierta forma, los estudiantes descubren que trabajan con una expresión que designa un nuevo tipo de función, y su representación geométrica es una gráfica en el sistema coordenado rectangular tridimensional.

Hasta este momento, el trabajo de tránsito entre los procesos interpretativos 2i y 2j se encuentra en una etapa donde la expresión matemática en 2i tiene una etapa donde la expresión matemática en 2i tiene una notación explícita asociada, la ecuación:

y una fenomenología que la soporta, la situación que le dio origen y el registro geométrico tridimensional. Sin embargo, no se ha alcanzado la generalización, ya que si bien los estudiantes intuyen aspectos de las características de este nuevo tipo de función, todavía no cuentan con una definición.

3a. sesión

Esta sección se dedica a estudiar el concepto de función en su definición, notaciones, representaciones gráficas y numéricas. Al término de esta actividad, los estudiantes, en el proceso interpretativo 2j, también tienen una generalización para el concepto de función de dos variables, en particular para la expresión:

4a. y 5a. sesiones

En estas sesiones se abordan las actividades que propician el aprendizaje de las nociones, ideas y definiciones que conforman el concepto de derivada parcial.

El acto matemático–cognitivo local y los procesos interpretativos en juego son los siguientes:

Acto matemático–cognitivo:

La conceptuación de la derivada parcial.

Procesos interpretativos involucrados:

2k. simbolizan las derivadas parciales de f respecto a m y b.

2l. son la pendiente nula de f respecto a m y la pendiente nula de f respecto a b.

2m. es la derivada parcial respecto a m, y

la derivada parcial respecto a b.

es el sistema de ecuaciones que permite determinar m y b, bajo el conocimiento de que la igualación a cero proporciona los valores de m y b, donde f (m, b) toma su valor extremo mínimo.

En 2k hay una notación asociada a una idea, la noción de derivada parcial como pendiente, y una fenomenología constituida por el espacio (tanto el sistema coordenado tridimensional en papel como el espacio real donde se desarrolla la experiencia; por ejemplo, considerando las paredes y el piso del aula como los planos que conforman el primer octante del sistema coordenado).

En 2l está encapsulada la idea de pendiente nula, que implica la idea de recta tangente horizontal respecto a m y b. La componente fenomenológica es la misma que en 2k.

Para 2m hay una notación explícita para las derivadas parciales de:

que se asocia con la idea de pendiente de las rectas tangentes en las direcciones de m y b en algún punto arbitrario. La componente fenomenológica es la misma que en los dos procesos anteriores.

En 2n se tiene una notación general asociada a pendientes nulas de rectas tangentes a la superficie f. La componente fenomenológica es la misma que en los otros procesos.

 

Análisis:

Se retoma el ejercicio usado en la sesión anterior y se cuestiona a los estudiantes sobre qué estrategia o procedimiento seguirían para determinar el punto (m, b), que corresponde al valor más pequeño de la superficie. Se discute en los equipos de trabajo y dan respuestas como:

"Derivando la ecuación con respecto a m y b. Como es de estilo parabólico y abre hacia arriba, no tiene máximos, por lo cual al derivar resultará el valor más pequeño de la superficie. Después de derivar, se iguala a cero. El valor obtenido será el más pequeño porque es la tangente, es decir, en ese punto la inclinación es cero".

Se observa que estos alumnos toman una conducta comparativa sobre la nueva situación con respecto a sus conocimientos previos del cálculo diferencial en una variable, en particular los de su noción de derivada como pendiente y la tangente. Aunque en este momento no saben cómo derivar la función, suponen que su procedimiento se puede realizar, lo cual implica un pensamiento hipotético.

Otros estudiantes van más allá en sus hipótesis al escribir:

"Creemos que una opción es derivar la función e igualar la derivada a 0 para obtener los valores extremos de m y b.

Después podemos sacar la segunda derivada para saber si los extremos son mínimos o máximos. Un resultado (+) revela una concavidad hacia arriba, es decir, un mínimo. Lo contrario sucederá con un resultado negativo.

Por otro lado, podemos tomar valores cercanos a los puntos que obtuvimos de la primera derivada (un valor a la izquierda y uno a la derecha) y sustituirlos en la 1era. derivada. Con ello veremos si la pendiente crece–decrece (+,–) = máximo, o lo contrario (–, +) = mínimo".

Los supuestos que asumen estos estudiantes los llevan a transferir características de las funciones en una variable a las de dos, pero sin reflexionar sobre las implicaciones propias del sistema tridimensional. Por tanto, aparece implícita una percepción borrosa de la situación, ya que no se reflexiona, por ejemplo, sobre el significado de izquierda o derecha en el espacio. Si bien parecen claros los conocimientos de dichos alumnos sobre los criterios para determinar valores extremos en funciones de una variable, en la nueva situación que enfrentan hacen una exploración sistemática deficiente. Este hecho puede ser consecuencia de la impulsividad que surge de los desequilibrios tanto por el desconocimiento sobre el significado de la derivada para funciones en el espacio como por la forma de calcularla algebraicamente.

En esta parte interviene el profesor y explica la interpretación geométrica de la derivada parcial, la simbología que se emplea y el uso de las reglas de diferenciación, interactuando con los estudiantes en función de sus conocimientos previos.

Se logra sin dificultad la interpretación de:

como la situación geométrica de aquellos puntos (m, b) donde la pendiente de las rectas tangentes a la superficie f, en dirección del eje m y del eje b, respectivamente, es nula.

Por otra parte, se discute sobre posibles situaciones geométricas de superficies donde pueda ocurrir que:

pero que no exista un valor extremo (puntos silla). También se tratan superficies con valores extremos en puntos donde las derivadas parciales no existen (el "pico" de un cono, por ejemplo).

Inmediatamente después de este tratamiento de la derivada, se regresa a la resolución del problema de contaminación. De nuevo se les pide a los estudiantes que describan –en función de todo lo que se ha abordado– las funciones de dos variables y la derivada parcial, el tipo de función que es:

y el procedimiento a seguir para determinar sus valores extremos. Sus descripciones son muy similares. Por ejemplo, uno de los equipos señala:

"La función es una cuadrática como una hoja doblada hacia arriba, por eso tiene un punto mínimo solamente y se puede saber además porque al derivar una cuadrática siempre quedan ecuaciones lineales; entonces, al resolverlas, cuando se iguala a cero, nada más queda un solo valor de m y b, que es el crítico donde está el mínimo. No se necesita checar nada más de las derivadas parciales porque esta función no tiene picos ni puntos de silla. Además, es continua siempre".

Se observa que los alumnos interaccionan sin dificultad en las componentes conceptuales de notación, generalización y fenomenologías. Las ideas, nociones y definiciones provocan que los conceptos sean significativos en el ámbito en que se han estudiado. En este momento, han comprendido tanto el método de mínimos cuadrados como los conceptos de función de dos variables y la derivada parcial, desde la perspectiva teórica que se está manejando.

 

Fase de salida

6a. sesión

Es claro para los estudiantes que lo que resta por hacer es obtener las derivadas parciales y averiguar para qué valores de m y b se anulan. Se discute en los equipos de trabajo y advierten que, de seguir el procedimiento realizado con el ejercicio de los cuatro puntos, tendrían que trabajar demasiado en el desarrollo de la sumatoria. Entonces, sugieren que se debe tratar de encontrar las derivadas parciales en forma general, aplicando las fórmulas de diferenciación, y dejando indicados todos los símbolos que involucra f(m, b), a fin de igualar a cero y resolver el sistema para m y b. Así, se determinan las ecuaciones del proceso interpretativo 2n y los equipos de trabajo resuelven el sistema con el método que consideran más adecuado. Finalmente, después de algunas dificultades algebraicas, se llegan a establecer las ecuaciones que permiten determinar las variables m y b.

 

CONCLUSIONES

El análisis e interpretación de la información que se obtuvo mediante las teorías cognitivas utilizadas permitió lograr una descripción detallada sobre el funcionamiento cognitivo del grupo de estudiantes sujeto a la experiencia de aprendizaje. Todo parece indicar que las funciones cognitivas y los procesos mentales operativos⁶ propician una adecuada codificación e interiorización de la información tratada. De igual manera, aparecen en forma eficiente como producto de la atención y esfuerzo que los estudiantes brindan a las actividades de aprendizaje, lo cual se debe a la motivación cuando abordan el problema en un contexto de su interés.

Los resultados del trabajo muestran que, en el escenario contextualizado en la ingeniería que se utilizó, el funcionamiento cognitivo de los estudiantes propició la comprensión de los contenidos de cálculo en el ámbito de su área de especialidad. Tal comprensión se logró tanto por las características de la situación problemática (que fue una tarea potencialmente significativa) como por la actitud positiva de los estudiantes al tratarla, lo cual concuerda con lo que señalan Ausubel, Novak & Hanesian (1978), en el sentido de que un aprendizaje es significativo si el estudiante tiene "una disposición para relacionar de manera significativa el nuevo material de aprendizaje con su estructura existente de conocimiento", y si la tarea de aprendizaje "consiste en sí de un material razonable o sensible y si puede relacionarse de manera sustancial y no arbitraria con la estructura cognoscitiva del estudiante particular".

La eficiencia observada en el funcionamiento cognitivo de los estudiantes en esta experiencia en contexto también se debió, en una parte importante, al diseño del escenario y sus implicaciones didácticas; particularmente, a la idea básica de presentar el problema a los alumnos antes de cualquier contacto con los contenidos del cálculo diferencial de dos variables. Esto permitió que la situación problemática, además de proporcionar un contexto específico de interés, fungiera como elemento rector de las acciones a efectuar para resolver la propia situación y representara un verdadero problema. Así, el nuevo conocimiento fue resultado de la interacción entre los nuevos objetos matemáticos de estudio y el conocimiento previo sobre el cálculo diferencial de una variable real que los estudiantes poseían. El funcionamiento cognitivo estuvo siempre orientado hacia la obtención de nuevas metas y el aprendizaje de las herramientas matemáticas que permitieran a los alumnos solucionar el problema.

Además, el texto del escenario didáctico hace explícito el tema (la contaminación provocada por una empresa industrial) y proporciona, en parte, el contexto en la ingeniería. Este es uno de los factores más importantes sobre el aspecto afectivo en los estudiantes, principalmente cuando abordan una experiencia de aprendizaje y tratan de comprenderla. Varios autores lo reconocen, como Schunk (1997), quien señala:

"Uno de los factores dirigidos conceptualmente más importantes de la comprensión es el tema general del material. La expectativa del que comprende sobre el tema de un pasaje puede servir como un sistema para la comprensión del material. El tema global de un pasaje puede afectar notablemente a casi todos los aspectos de la comprensión".

Respecto al objetivo general de la investigación, se considera que se cumplió de acuerdo con lo planteado. La teoría cognitiva de Reuven Feuerstein permitió realizar el análisis cognitivo en términos de las funciones que subyacen –como prerrequisitos para el aprendizaje– en las operaciones mentales y el procesamiento de la información al resolver el problema en el contexto de la ingeniería, propósito central de la investigación. La explicación de algunas conductas como la impulsividad, la exploración sistemática, el pensamiento hipotético y la conducta comparativa no se hubieran podido estudiar sin esta teoría, al menos no con los elementos necesarios para justificar las observaciones realizadas.

A su vez, el modelo teórico para el análisis de significados locales en cada proceso interpretativo, que se empleó como soporte de apoyo en las experiencias de aprendizaje, resultó fundamental para interpretar las observaciones hechas al proceso de aprendizaje de las ideas, nociones y conceptos involucrados en cada acto matemático–cognitivo básico en la resolución del problema.

Durante el diseño de la experiencia, se detectó la necesidad de organizar el análisis en torno a los actos mentales de aprendizaje que implican los principales conceptos y procesos matemáticos centrales en la comprensión y desarrollo del método de mínimos cuadrados: los conceptos de función de dos variables y de derivada parcial, así como el proceso para determinar un valor mínimo.

En razón de sus características, se llamó actos matemático–cognitivos de aprendizaje a dichos actos mentales. Tal elemento teórico permitió orientar las observaciones en la investigación y la descripción de los elementos de aprendizaje involucrados en la experiencia. Los procesos interpretativos para el análisis de las componentes conceptuales, es decir, las nociones e ideas matemáticas (fenomenologías), las definiciones conceptuales (generalizaciones) y el sistema de símbolos (notaciones) resultaron en cierta forma insuficientes por sí solos para el tipo de estudio que se quería realizar. Los actos matemático–cognitivos de aprendizaje permitieron identificar, definir y analizar los puntos medulares en el proceso de resolución del problema, como se concibió en el diseño.

Respecto a los elementos teóricos usados en la investigación para el análisis de las ideas, nociones y conceptos matemáticos, se considera que los actos mentales de aprendizaje ocurren cuando el estudiante transita adecuadamente por los procesos interpretativos involucrados en cada uno; es decir, cuando tiene la capacidad de interactuar entre las fenomenologías, notaciones y generalizaciones que constituyen cada proceso interpretativo en el acto mental.

De esta forma, considerando la teoría cognitiva de Feuerstein utilizada para analizar un acto mental de aprendizaje específico en la fase de elaboración de la resolución de un problema, se debe establecer el acto matemático–cognitivo de interés, identificar los procesos interpretativos y definir las fenomenologías, notaciones y generalizaciones para cada uno de ellos. Una vez que se realiza la experiencia de aprendizaje, hay que abordar el funcionamiento mental operativo (uso de analogías, comparaciones, análisis, síntesis, etc.) en términos de las funciones cognitivas que le subyacen.

Estas observaciones son importantes porque muestran la forma en que se integraron los elementos teóricos específicos para el estudio de contenidos matemáticos con los de la teoría cognitiva de Feuerstein en el desarrollo del trabajo. El uso de las teorías que soportaron la investigación permitió, como se ha señalado, indagar en el funcionamiento cognitivo de los estudiantes sujetos a las experiencias, desde las funciones cognitivas que permiten la operatividad mental en cuanto a capacidades hasta la forma en que ocurre el aprendizaje concreto de conceptos matemáticos. Además, son importantes porque esta investigación no tenía como objetivo estudiar el logro del aprendizaje en sí mismo, sino el análisis específico del funcionamiento cognitivo.

Sin embargo, aunque no era un propósito en el trabajo, esta forma de integración de los elementos teóricos utilizados posibilita el estudio y, a la vez, ofrece los referentes para interpretar y explicar, aunque sea en forma incipiente, las capacidades que debe mostrar un sujeto cuando ha realizado satisfactoriamente un acto mental de aprendizaje. Esto implica el logro del aprendizaje mismo (aun siendo parcial), dado que el acto mental de aprendizaje implica un proceso cognitivo y el aprendizaje en sí mismo es su consecuencia.

Otro aspecto que se desprende de esta investigación es la importancia que, en este tipo de experiencias, tiene la mediación del profesor en el proceso de aprendizaje. Por ejemplo, se pudo notar que algunos estudiantes tuvieron disfunciones cognitivas que, sin la intervención del profesor, probablemente no hubieran superado y tal vez no hubieran reflexionado, por ejemplo, sobre la importancia de comprender la naturaleza de los objetos que estaban tratando. Un estudiante bien podría derivar la expresión:

(una vez que conoce la forma algebraica para determinar una derivada parcial) y proseguir el proceso de resolución en términos operativos, sin reparar en la naturaleza de tal expresión y sin considerar, en particular, si representa una función o no. Esta situación, de acuerdo al modelo teórico y el propósito del trabajo, resultó uno de los actos matemático–cognitivos de aprendizaje básicos en el análisis.

De hecho, se puede indicar como resultado del trabajo que el diseño de una situación problemática en contexto (y de todo el escenario didáctico y la secuencia de actividades a realizar) con fines de aprendizaje –en el sentido como se ha concebido en esta investigación– implica necesariamente la mediación del profesor. Requiere de su intervención para guiar el proceso, explicar aspectos particulares de las ideas, nociones y conceptos que se tratan cuando es necesario, y sobre todo, ayudar al estudiante cuando se enfrenta a una situación de disfunción o ineficiencia de alguna función cognitiva en los actos de aprendizaje.

Finalmente, a manera de reflexión general sobre el trabajo, se puede señalar que constituye un esfuerzo por entender y explicar el funcionamiento cognitivo de estudiantes sujetos a una experiencia en el contexto de la ingeniería, considerando no sólo el aspecto mental operativo, sino también las funciones cognitivas subyacentes, que conforman los prerrequisitos básicos en el procesamiento de la información al resolver un problema.

Esta última consideración, más la definición y uso de los actos matemático–cognitivos de aprendizaje, los procesos interpretativos y la tripleta conceptual fenomenologías–generalizaciones–notaciones, posibilitó un análisis cognitivo más completo en las experiencias de aprendizaje realizadas. Se tiene la intención de que el cuerpo teórico utilizado en este trabajo pueda ofrecer una opción en la matemática educativa para realizar estudios cognitivos sobre el aprendizaje de las matemáticas en contexto.

 

BIBLIOGRAFÍA

Artigue, M. (1995). La enseñanza de los principios del cálculo: problemas epistemológicos, cognitivos y didácticos. En P. Gómez (Ed.), Ingeniería didáctica en educación matemática (pp. 97–140). México: Grupo Editorial Iberoamérica.        [ Links ]

Ausubel, D., Novak, J. & Hanesian, H. (1978). Psicología educativa. Un punto de vista cognoscitivo. México: Trillas.        [ Links ]

Camarena, P. (1987). Diseño de un curso de ecuaciones diferenciales en el contexto de los circuitos eléctricos. Tesis de maestría no publicada, Cinvestav, México.        [ Links ]

Camarena, P. (1990). Especialidad en docencia de la ingeniería matemática en electrónica. México: ESIME–IPN.        [ Links ]

Camarena, P. (1993). Curso de análisis de Fourier en el contexto del análisis de señales eléctricas. México: ESIME–IPN.        [ Links ]

Camarena, P. (2000). Etapas de la matemática en el contexto de la ingeniería (Reporte técnico de investigación). México: ESIME–IPN.        [ Links ]

Cantoral, R. & Mirón, H. (2000). Sobre el estatus de la noción de derivada: de la epistemología de Joseph Louis Lagrange al diseño de una situación didáctica. Revista Latinoamericana de Investigación en Matemática Educativa 3 (3), 265–292.        [ Links ]

Dolores, C. (1999). Una introducción a la derivada a través de la variación. México: Grupo Editorial Iberoamérica.        [ Links ]

Farfán, R. M. (1991). El curso de precálculo: un enfoque gráfico. Publicaciones Latinoamericanas en Matemática Educativa 5 (1), 206–211.        [ Links ]

Farfán, R. M. (1994). Ingeniería didáctica en precálculo. Acerca de la puesta en escena de los resultados de investigación en el sistema de enseñanza. Publicaciones Latinoamericanas en Matemática Educativa 8 (1), 457–462.        [ Links ]

Feuerstein, R. (1977). Mediated learning experience: a theoretical basis for cognitive human modificability during adolescence. En P. Mittler (Ed.), Research to practice in mental functions (Vol. 2). USA, Baltimore: University Park Press.        [ Links ]

Feuerstein, R. (1979). The dynamic assessment of retarded performes: the learning potential assessment device, theory, instruments and techniques. USA, Baltimore: University Park Press.        [ Links ]

Godino, J. D. & Recio, A. M. (1998). A semiotic model for analyzing the relationship between thought, language and context in mathematics education. Proceedings of the 22^nd Conference of the International Group for the Psychology of Mathematics Education. Research Forum (Vol. 3, pp. 1–8). South Africa: University of Stellenbosch.        [ Links ]

Hirsch, C. R., Coxford, A. F., Fey, J. T. & Schoen, H. L. (2003). Contemporary mathematics in context: a unified approach. USA: Glencoe/McGraw–Hill.        [ Links ]

Meyer, M. R. & Diopoulos, G. (2002). Anchored learning in context. Mathematics Teaching in the Middle School 8(1), 16.        [ Links ]

Moreno, M. (2005). El papel de la didáctica en la enseñanza del cálculo: evolución, estado actual y retos futuros. En A. Maz, B. Gómez & M. Torralba (Eds.), IX Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 81–96). Córdoba, España: Universidad de Córdoba.        [ Links ]

Muro, U. C. (2000). La serie de Fourier en la transferencia de masa. Tesis de maestría no publicada, UAEM, México.        [ Links ]

Piaget, J. (1978). The principles of genetic epistemology. USA, New York: Columbia University Press.        [ Links ]

ITESM (2000). Planes y programas de estudio de la carrera de Ingeniería Industrial y de Sistemas del Sistemas. México        [ Links ]

Prieto, S. D. (1992). Modificabilidad cognitiva y P. E. I. Madrid, España: Editorial Bruño.        [ Links ]

Riordan, J. E. & Noyce, P. E. (2001). The impact of two standards–based mathematics curricula on student achievement in Massachusetts. Journal for Research in Mathematics Education 32(4), 368.        [ Links ]

Salinas P., Alanís, J. A., Pulido, R., Santos, F., Escobedo, J. C. & Garza, J. L. (2002). Elementos del cálculo. Reconstrucción conceptual para el aprendizaje y la enseñanza. México: Trillas.        [ Links ]

Schunk, D. H. (1997). Teorías del aprendizaje. México: Pearson Educación.        [ Links ]

Vergnaud, G. (1990). La teoría de los campos conceptuales. Recherches en Didactique des Mathématiques 10(2–3), 133–170 (Trad. al español de Juan D. Godino).        [ Links ]

Zúñiga, L. (2004). Funciones cognitivas: un análisis cualitativo sobre el aprendizaje del cálculo en el contexto de la ingeniería. Tesis de doctorado, Cicata–IPN, México.        [ Links ]

 

NOTAS

¹ Escuela de Ingeniería y Ciencias, Instituto Tecnológico y de Estudios Superiores de Monterrey (ITESM), Campus San Luis Potosí, México. regresar

² Se entiende por sistema didáctico habitual a aquel en que el profesor tiene el rol principal en el proceso de enseñanza–aprendizaje, mientras que los estudiantes asumen una actitud pasiva. El aprendizaje sucede principalmente por repetición, no por descubrimiento, lo cual conduce a un aprendizaje producto del énfasis en la mecanización del saber (esto no significa que el aprendizaje por repetición sea erróneo o inadecuado, sino que resulta insuficiente); además, la didáctica empleada está determinada por el discurso de los libros de texto. Las sesiones de clase se diseñan para el cumplimiento a los programas de estudio (que, en muchos casos, están elaborados en función a la estructura de contenidos de los libros de texto). En buena medida, tales situaciones se deben a que los profesores de matemáticas no tienen una capacitación profesional en docencia (mucho menos en didáctica de las matemáticas), lo cual provoca que su trabajo como docentes se guíe casi exclusivamente por las experiencias vividas como estudiantes, su percepción de lo que significa ser un buen profesor, y lo que dictan los programas y libros de texto oficiales. regresar

³ De acuerdo a la teoría de funciones cognitivas utilizada en la investigación, y que se describirá en los siguientes párrafos. regresar

⁴ Percepción clara: conocimiento exacto y preciso de la información. La disfunción cognitiva: percepción borrosa consiste en un proceso pobre e impreciso de los datos de la información. Exploración sistemática de una situación de aprendizaje: capacidad para organizar y planificar la información. La disfunción de la exploración sistemática es la impulsividad ante una situación de aprendizaje, consistente en una incapacidad para tratar la información de manera sistemática y planificada. Organización de la información: capacidad para utilizar diferentes fuentes de información a la vez. Percepción y definición de un problema: consiste en la habilidad para delimitar qué pide el problema, qué puntos hay que acotar y cómo averiguarlos. Interiorización y representación mental: capacidad para utilizar símbolos internos de representación. La falta o deficiencia de la interiorización se manifiesta en la conducta demasiado concreta y sin generalización apropiada. Planificación de la conducta: capacidad para prever la meta que se quiere conseguir utilizando la información adquirida previamente. Conducta comparativa: consiste en la capacidad para realizar todo tipo de comparaciones y relacionar objetos y sucesos anticipándose a la situación. La deficiencia en la conducta comparativa consiste en la incapacidad para establecer relaciones de semejanza y diferencia entre objetos y sucesos. Pensamiento hipotético: capacidad para establecer hipótesis y comprobarlas, aceptando o rechazando la hipótesis previamente establecida. Comunicación explícita: consiste en utilizar un lenguaje claro y preciso que responda al problema formulado en la tarea. Esto supone un cierto nivel de comprensión por parte del sujeto. La disfunción es la comunicación egocéntrica. Precisión y exactitud en las respuestas: capacidad para pensar y expresar la respuesta correcta a un problema o situación general de aprendizaje. Control de las respuestas: consiste en la capacidad para reflexionar antes de emitir cualquier tipo de respuesta. El control y la autocorrección implican procesos metacognitivos. regresar

^{5 (*)} regresar

⁶ Clasificación, análisis, síntesis, etc. regresar