Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.10 no.1 Ciudad de México mar. 2007
Lectura e interpretación de gráficas socialmente compartidas1
Crisólogo Dolores2 Ithandehuil Cuevas2
2 Centro de Investigación en Matemática Educativa Universidad Autónoma de Guerrero México E–mail: cdolores@prodigy.net.mx.
Fecha de recepción: 15 de agosto de 2006
Fecha de aceptación: 8 de diciembre de 2006
RESUMEN
En este artículo presentamos una investigación de carácter cualitativo, en la cual exploramos qué lecturas o interpretaciones hacen los estudiantes de educación básica sobre las gráficas que se comparten socialmente; es decir, aquellas utilizadas por los medios de información y que van dirigidos a amplios sectores de la sociedad. Las gráficas puestas en el escenario de la lectura están referidas a temáticas poblacionales, financieras y una al contexto matemático. Este trabajo, que involucró a estudiantes de primaria y secundaria, nos permitió detectar interpretaciones en las que la mayoría de los alumnos identifican lo que cambia (las variables), hacen lectura de dato por dato o punto por punto (según corresponda), privilegiando a los máximos y mínimos, realizan descripciones cualitativas de cómo cambia algo, aduciendo que sube o baja. Sin embargo, no establecen relaciones covariacionales, no calculan cuánto cambian las variables ni se nota que usen las razones de cambio. Las evidencias obtenidas indican, además, un escaso conocimiento sobre los significados de los conceptos sociales representados en las gráficas.
PALABRAS CLAVE: Gráficas, lectura e interpretación, socialmente compartidas, pensamiento variacional.
ABSTRACT
In this paper we present a qualitative research, in which we explore what readings or interpretations are done by the students of elementary school on the graphs that are shared socially; it is to say, those used by the means of information and that are directed wide social sectors. The graphs put in the scene of the reading are referred to population, financial subject matters and one to the mathematical context. This work, which involved to students of elementary school, allowed us to detect interpretations in which the most of the students identify what changes (the variables), they do reading of data by data or point by point (according to it corresponds), favoring to the maximums and minimums, they make qualitative descriptions of how it changes something, adducing that rises or low. Nevertheless, they do not establish covariationals relations; they do not calculate how much they change to the variables nor note that use the change reasons. The evidences indicate, in addition, a little knowledge on the meaning of the social concepts represented in the graphs.
KEY WORDS: Graphs, reading and interpretation, socially shared, variational thought.
RESUMO
Neste artigo apresentamos os resultados de uma investigação de caráter qualitativo no qual exploramos que tipo de leituras ou interpretações fazem os estudantes da educação básica dos gráficos que se compartilham socialmente. Estes gráficos são aqueles utilizadas pelos meios de informação e que são dirigidos às várias camadas sociais. Os gráficos que surgiram da leitura se referem a temáticas populares, financeiras e um no âmbito precisamente matemático. Este trabalho envolveu estudantes do ensino fundamental e médio e nos permitiu detectar interpretações em que na maioria identificam o que muda (as variáveis), fazem leitura de dado por dado ou ponto por ponto (a que corresponde) privilegiando os máximos e mínimos, fazem descrições qualitativas de como muda alegando que sobem ou descem, não estabelecem relações co–variacionais nem calculam quanto mudam as variáveis, tampouco notamos o uso das razões de mudança. As evidências obtidas também indicam pouco conhecimento dos significados dos conceitos sociais representados nos gráficos.
PALAVRAS CHAVE: Gráficos, leitura e interpretação, socialmente compartilhadas, pensamento variacional.
RÉSUMÉ
Dans cet article nous rendrons compte d'une recherche qualitative dans laquelle nous explorons quels types de lectures ou d'interprétations font les étudiants d'école élémentaire sur les graphiques socialement partagés. Ces graphiques sont ceux utilisés pour les médias d'information qui ont un grand nombre d'impact sur les différents niveaux sociaux. Les graphiques mis dans le cadre de la lecture sont associés aux sujets de populations, de finances et aussi au domaine spécifiquement mathématique. Ce travail a été fait avec des étudiants de l'école primaire et du collège et cela nous a permis de détecter des interprétations dans laquelle la plupart des étudiants identifient ce qui change (les variables), font la lecture donné par donné ou point par point (selon corresponde) en privilégiant les maximums et les minimums, ils font de descriptions qualitatives de comment changer ce qui change en alléguant ce qui monte ou qui descend, ils n'établissent pas de rapports de covariance ni ne calculent de combien changent les variables, nous n'avons pas noté l'usage de raison de change.
Les résultats obtenus montrent une quasi nulle connaissance des significations et des concepts sociaux représentés dans les graphiques.
MOTS CLÉS : Graphiques, lecture et interprétation, socialement partagés, une pensée de variation
1. ANTECEDENTES
La graficación de funciones es una de las actividades sugeridas por el currículum matemático escolar de la educación media y superior. Es además, ampliamente tratada por los textos y los profesores en sus clases de matemáticas, desde la educación básica hasta el nivel superior. Las técnicas de graficación utilizadas van desde la tabulación hasta la graficación mediante el uso de la derivada: en la primera, las aproximaciones hacia la gráfica son todavía rudimentarias; en la segunda se gana más precisión y fineza, pues la derivada es un medio muy potente que permite tal fineza y precisión.
Después de los procesos sistemáticos de enseñanza sobre la graficación de funciones, los profesores creen que la mayoría de los estudiantes pueden representar e interpretar correctamente las gráficas. Sin embargo, hay diversos trabajos de investigación que dan cuenta de la persistencia de numerosas concepciones que no son congruentes con las aceptables en matemáticas.
Hemos estudiado en los últimos años las concepciones alternativas que tienen los estudiantes acerca de las gráficas de funciones elementales. En una investigación donde planteamos actividades de análisis sobre gráficas de funciones de coordenadas tiempo–distancia, que representaban fenómenos físicos (Dolores et al., 2002), detectamos concepciones alternativas como las siguientes:
• Asociación entre la mayor velocidad media con la representación gráfica de la ordenada de mayor altura, o con el intervalo al que le corresponden las ordenadas de mayor altura.
• Asociación entre la gráfica cartesiana que se asemeja a la trayectoria para el caso de la caída libre de los cuerpos con la trayectoria misma.
• La no aceptación de que una gráfica de coordenadas tiempo–distancia y otra de coordenadas velocidad–tiempo puedan representar al mismo movimiento.
A priori, se podría suponer que con gráficas sencillas como las rectas los estudiantes no encontrarían mayores problemas, mas no es así. Dolores y Catalán (2000) hallaron, en situación escolar, que cuando los estudiantes de bachillerato utilizaban gráficas para determinar los cambios sólo la mitad de ellos lo lograron hacer. Una cuarta parte de los estudiantes dieron muestras de interpretar consistentemente la ecuación de la recta, dada su pendiente y la ordenada al origen y representarla gráficamente, aunque no emplearon la relación de proporcionalidad implícita en el coeficiente m que da la pendiente. En general, se notó escasa capacidad para visualizar y analizar gráficas y mayor proclividad a realizar operaciones.
En otro trabajo, Dolores (2004) indagó de manera exhaustiva en las concepciones alternativas de los estudiantes cuando se les plantean actividades de análisis de funciones a través de sus gráficas, centrándose en la lectura e interpretación de gráficas escolares. Las concepciones alternativas identificadas fueron:
• La aceptación de que sólo las funciones cuyas gráficas poseen abscisas positivas tienen imágenes positivas; análogamente, sólo las gráficas con abscisas negativas pueden tener ordenadas negativas.
• La aceptación de una relación de concomitancia entre función positiva con función creciente, o bien entre función negativa y función decreciente.
• La consideración de que los puntos de corte de la gráfica con el eje de las x son puntos estacionarios. O bien de que si la gráfica pasa por el origen, entonces en tal punto la función no crece ni decrece.
• La asociación de intervalos con puntos de la gráfica.
Las concepciones alternativas podrían permanecer en los estudiantes si no se enfrentan con situaciones donde se haga explícita su contradicción con las teorías aceptadas, pero sobre todo si no hay interiorización de tales contradicciones y el reacomodo cognitivo que posibilite el asentamiento de las concepciones aceptadas en matemáticas.
Empeñados en investigar la estabilidad y cambio de estas concepciones alternativas, en Dolores & Valero (2004) se da cuenta de dichos procesos. Así, tras la puesta en escena de una experiencia instruccional diseñada ex profeso con estudiantes principiantes universitarios, hubo cambios conceptuales en la dirección deseada. Cuando las actividades fueron planteadas usando los registros verbal y gráfico, un 16% de los estudiantes manifestaron concepciones aceptables antes de la experiencia instruccional; con posterioridad a ella, tal porcentaje se incrementó a un 86%. Cuando las preguntas se plantearon con los registros analítico y verbal, los estudiantes que manifestaron concepciones alternativas pasaron, en promedio, de un 0% a un 55%.
Las concepciones alternativas que destacaron por su estabilidad fueron dos: 1) la consideración de que una función es positiva y creciente si, además de cumplir con estas dos condiciones, posee abscisas positivas; 2) la que considera que la derivada de una función en un punto es igual a la ordenada de ese mismo punto. Se notó también que los cambios en las concepciones no son lineales y se dan en distintos sentidos, así como se registraron avances y retrocesos.
La construcción de gráficas a partir de un enunciado verbal o una situación cercana a la realidad implica acciones derivadas del cambio de registro; a partir de esas producciones los investigadores detectan esas ideas. Algunos trabajos que involucran la construcción de gráficas se pueden dividir en los que usan tecnología (Yerushalmy & Shternberg, 1998), donde los estudiantes se ven precisados a pasar del contexto real al registro gráfico, y aquellos donde los alumnos construyen gráficas sin el uso de tecnología (Mevarech & Kramarsky, 1997; Carlson et al., 2002), transitando del registro verbal al gráfico, o como el estudio de Even (1998), donde algunas actividades suponen el paso de la representación simbólica a la gráfica. Otras investigaciones están más enfocadas al análisis de gráficas previamente construidas por el investigador; aquí, las interpretaciones están más influidas por lo que los estudiantes o profesores observan o interpretan sobre una gráfica dada. A esta categoría pertenece el trabajo de Hitt (1996), en el que los profesores examinados requirieron transitar del registro gráfico a la representación pictórica.
En investigaciones recientes (Cordero, 2005; Buendía & Cordero, 2005; Domínguez, 2003; Campos, 2003, Rosado, 2004; Flores, 2005), hechas bajo la perspectiva socioepistemológica, se ha estudiado la graficación en el discurso matemático escolar. Se parte de dos premisas fundamentales: por una parte, de que la matemática funcional es aquel conocimiento que deberá integrarse a la vida para transformarla, reconstruyendo significados permanentemente; por otro, de que el volumen y carácter de los conocimientos adquiridos por el hombre viene determinado por el nivel de desarrollo de las prácticas sociales; es decir, por el grado de su dominio sobre el mundo exterior. Bajo esta perspectiva, se ha encontrado evidencia sobre prácticas argumentativas gráficas en diversas situaciones, donde son resignificadas al debatir entre la función y forma de la graficación. Por ejemplo, el límite de un cociente se resignifica a través de la predicción, la analiticidad y la propia graficación; la derivada y la recta tangente debaten entre la comparación de dos estados y la sucesión simultánea de las derivadas, pero también contra la variación de parámetros y el comportamiento de la tendencia.
Los autores de dichos trabajos han relacionado las prácticas de graficación, modelación y predicción, donde el comportamiento de las curvas anticipa la tendencia de comportamiento local y global. Aquí, la derivada es resignificada en la linealidad del polinomio, mientras que la asintoticidad se resignifica a través de comparar las formas de comportamiento entre dos funciones. Contrario a las investigaciones que parten de premisas que colocan a la matemática formal en el papel central, éstas centran su atención en los usos y desarrollo de prácticas de la graficación y, de este modo, han posibilitado un acercamiento a la matemática funcional.
La interacción con las gráficas ha sido estudiada en el plano de su construcción o en el plano de su lectura e interpretación. Una buena parte de estos estudios han tenido como escenario al ambiente escolar. En este trabajo hemos orientado la mirada hacia las gráficas que no necesariamente son objeto de enseñanza en la escuela y que circulan libremente en los medios de comunicación o información. Nos planteamos una pregunta esencial: si la escuela, como se dice, prepara para la vida, en la vida diaria los individuos encontrarán seguramente gráficas que interpretar. ¿Estarán en condiciones de leerlas e interpretarlas adecuadamente?
2. OBJETIVO
Parte importante de las investigaciones descritas tratan el asunto de las gráficas desde el punto de vista cognitivo y enfocan su atención en las dificultades, los errores, las concepciones alternativas, el papel de las gráficas en la comprensión de los conceptos o propiedades matemáticas y en el desarrollo cognitivo del pensamiento.
El escenario donde se sitúan estos trabajos privilegia generalmente las condiciones escolares y, por tanto, el tipo de gráficas utilizadas son las que con frecuencia se emplean en las clases de matemáticas. Sin embargo, en nuestras investigaciones actuales nos planteamos como objetivo general el estudio de las gráficas, pero en contextos más amplios e integrales que incluyen los contextos sociales, más allá de considerar sólo el escenario escolar. Nos preguntamos cómo viven estos objetos fuera del aula, pues las gráficas son utilizadas no sólo por los matemáticos profesionales o profesores de matemáticas, sino también por personas con distintas profesiones y ocupaciones, no necesariamente cercanas a la matemática en un sentido convencional, como médicos, políticos, contadores, abogados o comunicadores. Además, son frecuentemente utilizadas y compartidas en los medios de comunicación e información –como revistas o periódicos–, informes médicos, oficinas gubernamentales o empresas.
En las revistas, periódicos u otros medios impresos se recurre a las gráficas para transmitir o comunicar información o datos; además, refieren la cuantificación y comportamiento de algún fenómeno en intervalos determinados; sin embargo, muchas gráficas que se difunden o comparten a través de estos medios parecen estar lejanas de las que utilizan los profesores en sus clases de matemáticas. ¿Qué lecturas e interpretaciones hacen los estudiantes sobre las gráficas socialmente compartidas? La búsqueda de respuestas a esta pregunta constituye la parte esencial del presente trabajo; a su vez, forma parte específica de las tareas globales que implican darle alcance al objetivo general enunciado en el párrafo anterior.
Así, el objetivo central del presente trabajo consiste en explorar qué lecturas o interpretaciones realizan los estudiantes de educación básica sobre las gráficas que circulan en ambientes extraescolares y se comparten a través de los medios de información. Cuando decimos extraescolar aludimos, por un lado, a que el tipo de gráficas sujetas a lectura son aquellas que circulan libremente fuera de la escuela, se comparten o son puestas a disposición de cualquier interesado para su libre uso; por otro, a que las lecturas que se piden no se supeditan al contrato didáctico establecido por sus profesores. Por tal razón, los profesores de los estudiantes participantes fueron ajenos a esta investigación; los alumnos no esperaban ninguna calificación o premio por las actividades planteadas.
3. ELEMENTOS TEÓRICOS
Al igual que muchos procesos matemáticos utilizados en la escuela, la graficación comprende la interpretación y la construcción. La interpretación se refiere a las habilidades de los estudiantes para leer una gráfica tanto local como globalmente, y darle sentido o significado (Leinhardt et al., 1990). En contraste, la construcción atañe al acto de generar algo nuevo, construyendo una gráfica o trazando puntos a partir de datos con una regla funcional o a partir de una tabla. Leindhart et al. plantean que la construcción de una gráfica es completamente diferente de la interpretación. Mientras que la interpretación ayuda y exige respuestas a partir de datos dados (por ejemplo, una gráfica, una ecuación, o un conjunto de datos), la construcción requiere generar partes nuevas que no están dadas.
La interpretación de gráficas precisa de procesos agudos de visualización, aunque Eysemberg & Dreyfus (1991) mostraron que muchos estudiantes poco utilizan el pensamiento visual. Prefieren el trabajo algorítmico al pensamiento visual, ya que éste requiere de procesos cognitivos superiores a los que demanda el pensamiento algorítmico.
Ahora bien, las interpretaciones de las gráficas pueden estudiarse desde diferentes puntos de vista. Hay quienes investigan las dificultades en la lectura de gráficas (Brassel & Rowe, 1993; Moschkovich et al., 1993; Yerushalmi & Shternberg, 2001); en el caso de Wainer (1992), identificó tres niveles de procesamiento de la información relacionados con la interpretación gráfica:
a. El nivel elemental: Implica la extracción de datos o la lectura de puntos aislados; por ejemplo, quién alcanzó la más alta calificación del grupo, quién alcanzó la calificación más baja, etc.
b. El nivel intermedio: Concierne a la detección de las tendencias observadas en intervalos determinados de las gráficas; por ejemplo, entre los años 1990 y 1993 qué compañía tuvo la razón más grande de crecimiento.
c. El nivel más alto: Es una comprensión profunda sobre la estructura de los datos y de su comportamiento; por ejemplo, las muchachas crecen más rápido que los muchachos.
En otras investigaciones sobre el pensamiento de los estudiantes de cálculo, cuando plantearon actividades de interpretación en torno a lo cambiante de la razón de cambio se percibió que esta habilidad es lenta de desarrollar; particularmente, se reportan problemas al interpretar la información gráfica de una función (Carlson et al., 2002). Muchas de estas dificultades están asociadas al escaso desarrollo de un razonamiento covariacional, que se define como aquel que involucra a las actividades cognitivas de coordinación de dos cantidades variables, atendiendo las formas en que cambian una en relación con la otra. Como puede notarse, este trabajo se orienta más hacia el estudio del pensamiento covariacional y tiene similitud con la visión matemática de la graficación.
Según Cantoral & Montiel (2001), hay dos formas clásicas de entender la enseñanza de la graficación: una asume que la graficación es una técnica o conjunto de técnicas que permiten bosquejar la gráfica de una función; otra, menos difundida, entiende la graficación como una forma de interpretar el sentido y significado de sus propiedades desde una perspectiva cognoscitiva. En tal enfoque se inserta nuestro trabajo.
Para explorar las interpretaciones que le dan sentido y significado a las gráficas, adoptamos las acciones sugeridas en el análisis de funciones planteadas en Dolores (1999), así como algunas desprendidas de Carlson et al. (2002). Dichas acciones son congruentes con las definiciones y objetivos de las gráficas de funciones que manejan los textos y programas de estudio de matemáticas y de estadística. Una gráfica cartesiana se define en los textos como una representación entre dos o tres variables, y se considera como herramienta visual útil porque posibilita la detección de tendencias, facilita las comparaciones y se constituye en un medio idóneo para analizar el comportamiento de fenómenos de variación. Las acciones sistemáticamente planteadas pueden resumirse en cinco: 1) ¿qué cambia?; 2) ¿cuánto cambia?; 3) ¿cómo cambia?; 4), ¿qué tan rápido cambia?; 5) ¿cómo se comporta globalmente la gráfica?
La primera acción concierne a identificar qué variables están representadas, ubicar puntos en el plano y determinar los intervalos de variación. Para poder determinar cuánto cambia eso que cambia hay que hacer comparaciones y operaciones de resta entre estados finales e iniciales, tanto para la variable dependiente como para la independiente, atendiendo a la correlación entre esos cambios. Para saber cómo cambian las variables representadas, es preciso determinar si la gráfica crece, decrece o se mantiene constante; en suma, la dirección del cambio. Para determinar la rapidez del cambio se requiere emplear la razón promedio de cambio, que involucra necesariamente cambios de la variable dependiente en relación con los de la variable independiente. El comportamiento global y preciso de la gráfica implica el uso de la razón de cambio instantánea (derivada) para precisar en qué intervalos crece o decrece, en qué puntos tiene máximos, mínimos o puntos de inflexión. Resulta claro que esta última no es tema de tratamiento en primaria y secundaria, pues se reserva para el bachillerato y la universidad.
4. ELEMENTOS METODOLÓGICOS
4.1. Características metodológicas de la investigación
El presente trabajo tiene naturaleza cualitativa y carácter descriptivo, en el sentido indicado por Hernández et al. (2003) y Pérez (1998). Su propósito es recoger información acerca de las interpretaciones que los estudiantes hacen de las gráficas socialmente compartidas. La recolección de los datos fue mayoritariamente verbal, pues las interpretaciones fueron solicitadas y emitidas verbalmente; dicha información se grabó en audio y video.
4.2. Estudiantes participantes
En la investigación participaron dos tipos de estudiantes: unos cursaban la primaria y otros la secundaria. Los de primaria, que estaban en la parte final del sexto grado, eran Amalia, Alfaro, Carmen, Andrés, Alondra, Luís y Daniel, mientras que los de secundaria eran Jazmín, Bernardo, Reina, Óscar e Irving, que iban en el tercer grado de este nivel. Los alumnos, considerados por sus profesores como de rendimiento aceptable, fueron seleccionados de dos escuelas primarias y dos secundarias ubicadas en la ciudad capital del estado de Guerrero, en el sur de México. La edad de los estudiantes de primaria oscilaba entre los 11 y 13 años; la de los de secundaria, entre 15 y 16 años.
Los estudios primarios en México se ciñen al currículo plasmado en el Plan y Programas de Estudio 1993 (SEP3, 1993a), articulándose con base en seis ejes: 1) Los números, sus relaciones y sus operaciones; 2) Medición; 3) Geometría; 4) Procesos de cambio; 5) Tratamiento de la información y 6), La predicción y el azar. La temática asociada al presente trabajo está más ligada a dos ejes temáticos: procesos de cambio y tratamiento de la información.
El eje Procesos de cambio, que inicia su tratamiento a partir del cuarto año, abarca la lectura, elaboración y análisis de tablas y gráficas donde se registran y analizan procesos de variación. El eje Tratamiento de la información contempla el análisis de la información estadística simple, presentada no sólo en forma de gráficas o tablas, sino también en el contexto de documentos, propagandas, imágenes u otros textos particulares. En los estudios de secundaria, la lectura e interpretación de gráficas atañen al eje temático Presentación y tratamiento de la información; a este respecto, el Plan y Programa de Estudios (SEP, 1993b) sugiere proponer a los alumnos situaciones y actividades muy diversas para que conozcan y se acostumbren gradualmente a la noción de función como una relación entre dos cantidades, al igual que a las diferentes formas de presentar una función. En segundo grado de secundaria se insiste en la lectura y elaboración de tablas y gráficas.
El currículo reseñado para la primaria y secundaria mexicanas es aplicable a todas las escuelas de esos niveles, sobre todo las públicas. Por tanto, los estudios que realizan los participantes en esta investigación se rigen bajo estas orientaciones, y el asunto de la construcción de gráficas y su lectura correspondiente no es un tema nuevo para ellos, pues vienen contemplados en los planes y programas de la SEP.
Los estudiantes participantes no fueron prevenidos sobre la lectura de las gráficas. Utilizaban libros de texto distintos, según la secundaria a la que asistían, pero estaban apegados a la curricula de la escuela pública, y todos fueron filmados individualmente por el investigador.
4.3. Instrumentos
Los instrumentos utilizados en la investigación fueron de dos tipos: mayoritariamente, gráficas que se comparten socialmente en ambientes extraescolares, y una que se comparte en los grupos escolares de los niveles medio y superior. El propósito fue estudiar cómo los alumnos interpretan gráficas libremente compartidas, en comparación con la lectura e interpretación de gráficas que suelen ser compartidas en los grupos escolares de los niveles medio y superior.
Para seleccionar las gráficas socialmente compartidas, se procedió de la siguiente manera. En primer lugar, fueron recopiladas cerca de 30 gráficas de revistas, periódicos, libros y páginas de internet. Se hizo una primera depuración, en la que quedaron alrededor de 15 gráficas, que se eligieron de manera que fuera factible su lectura e interpretación en tiempos razonables y no implicaran un trabajo continuo mayor a 30 minutos. La depuración llegó hasta cuatro gráficas, donde la de corte intramatemático, que se comparte en los grupos escolares del nivel medio, fue seleccionada de los textos de matemáticas utilizados en ese nivel.
Una vez seleccionadas y depuradas todas estas gráficas, se sometieron a lecturas previas a la lectura final. Las lecturas previas fueron practicadas en dos ocasiones e involucraron a estudiantes ajenos a la investigación, con el fin de tener validez y confiabilidad en los instrumentos a utilizar, observando qué gráficas eran más inteligibles y si permitían obtener información sobre su lectura e interpretación.
A continuación se describen cada una de las gráficas, en las que consignamos nuestras propias interpretaciones al extraer la información en ellas implícita. No son descripciones minuciosas ni detalladas, pero tratan de centrar la atención en lo esencial de la información.
La Gráfica 1 contiene información sobre el porcentaje de la población hablante de lengua indígena entre los 1895 y 1995. Las variables que intervienen son la cantidad de hablantes de lengua indígena, medida en porcentaje, y el tiempo, medido en años. En términos globales, la gráfica muestra el comportamiento de la población hablante de lengua indígena en un periodo de 100 años (1895–1995), en el que ha experimentado altas y bajas, prevaleciendo estas últimas.

La gráfica inicia en 1895 con un 16.2% y tiene una tendencia descendente hasta 1910, de modo que en tal lapso descendió 3.3%, para colocarse en 12.9%. Tiene un crecimiento muy notorio de 1910 a 1921; durante esos 11 años crece un 16%, por lo que en 1921 había más del doble de hablantes de lengua indígena que en 1910. Pero se nota un descenso drástico entre 1921 a 1930, etapa en la que desciende 19.5 puntos porcentuales, de manera que la población hablante de lengua indígena se redujo en 1930 a casi un tercio de la existente en 1921. La rapidez con la que decreció este tipo de población en el último intervalo fue mayor que con la que creció de 1910 a 1921. En el periodo restante el decrecimiento es predominante, a pesar de experimentar un ligero crecimiento de 1960 a 1970. De 1980 en adelante, la población hablante de una lengua indígena volvió a decrecer: de 1980 a 1990 disminuyó 1.6%; de 1990 a 1995 tuvo un descenso de 0.5. En términos globales, la población mexicana hablante de lengua indígena decreció 9.3% de 1895 a 1995. Por lo que se puede apreciar, la tendencia al descenso de la población hablante de lengua indígena es predominante en los 100 últimos años; si se mantiene, nuestras lenguas indígenas podrían desaparecer.
La Gráfica 2 es una gráfica en forma de pirámide que contiene información sobre la estructura de la población mexicana en el año de 1995. La población mexicana está clasificada en porcentajes y sus correspondientes grupos de edades. Pudiera decirse que las variables presentes son la cantidad de población (dada en porcentajes), las edades de esa población (dada por grupos de edades de cuatro en cuatro años) y el sexo de esa población. Es una gráfica sui generis que maneja números positivos tanto a la derecha como a la izquierda del cero, pues se trata de representar población existente.
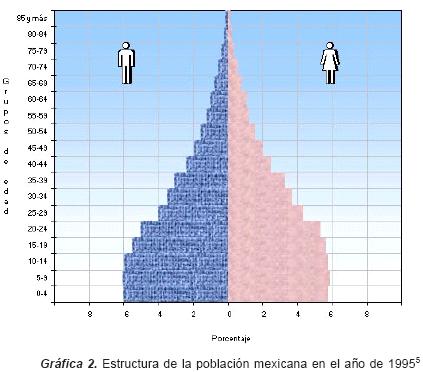
Al hacer una revisión global de esta gráfica, se deduce que la población mexicana estaba estructurada en 1995 mayoritariamente por gente joven; hay una ligera mayoría de hombres que de mujeres, aunque en ambos sexos no excede del 6%. Por gente joven nos referimos a aquella cuyas edades están comprendidas entre 0 y 24 años; en tal intervalo, la disminución de la población es casi imperceptible. A partir de esta última edad, los porcentajes de mujeres y de hombres empiezan a disminuir de manera más visible. En particular, cuando se pasa del intervalo 20–24 al 25–29 se percibe una notoria disminución de la población: es mayor en los hombres, con más de un punto porcentual, mientras que en el caso de las mujeres casi llega a un punto porcentual. Otra disminución sucede en el paso del intervalo de los 35–39 al de 40–44, que está próxima al punto porcentual y se acentúa nuevamente en los hombres. Los datos significan que las edades de mayor disminución en la población están centradas alrededor de los 25 y 40 años de edad. Nótese que la población entre 45 y 49, tanto en hombres como en mujeres, formaba el 2% de la población; después sigue disminuyendo, de ahí que en el intervalo de 60–64 llega al 1%. La población sigue disminuyendo en los restantes intervalos: las personas entre 70 y 74 años forman aproximadamente el 0.5% de la población.
La Gráfica 3 contiene información sobre el número de egresados de la UNAM7; las variables representadas son el número de egresados y la generación a la que corresponden. Los egresados, a su vez, son clasificados en dos categorías, los de bachillerato y los de licenciatura: el número de egresados de licenciatura corresponde a la línea café; el de bachillerato, a la línea naranja. Al analizar globalmente el comportamiento de los egresados de bachillerato, se puede apreciar que su comportamiento es irregular, tiene intervalos de crecimiento y de decrecimiento. El número de egresados de este nivel creció de 20 mil 598 en 1980 a 22 mil 848 en 2003; esos datos indican que en un periodo de 23 años el número de egresados no ha superado ni el 1 % de los que había inicialmente. Los crecimientos más notorios se dan en los periodos 1987–1988 y de 1999 al 2002. El descenso más notorio sucede de 1996 a 1999.

Un análisis global sobre el comportamiento de la gráfica de los egresados de licenciatura permite apreciar que es una gráfica de comportamiento irregular. El número de egresados de este nivel creció de 12 mil 347 en 1980 a 27 mil 470 en 2003, lo cual señala que en un periodo de 23 años el número de egresados superó el doble de los que había inicialmente. Los aumentos más notorios se dan en los periodos de 1990 a 1991, de 1993 a 1996 y de 1999 a 2002, mientras que los descensos más importantes suceden de 1991 a 1993 y de 1998 a 1999. Al comparar las dos gráficas, se nota que la cantidad de egresados de licenciatura es siempre menor a la de los egresados del bachille rato, a excepción de los periodos de 1990 a 1991 y de 1994 a 1999. Incluso se comportan de la misma manera y tienen los mismos valores en el lapso de 1999 a 2002. Esta información refuerza la idea de que, en los niveles superiores, los egresados son menos que los de educación media superior del país.
La Gráfica 4 muestra información sobre el tipo de cambio real del peso con respecto al dólar. Las variables representadas son el tipo de cambio y el tiempo, comprendido entre los años 1970 y 2005. La constante es la cantidad de dólares, pues durante todo el proceso la relación de cambio está hecha siempre con respecto a un dólar. En términos generales, la gráfica indica que el comportamiento de la cantidad de pesos por dólar ha disminuido, de 11.90 en 1970 a 10.90 en 2005. Asimismo, que en un periodo de 35 años (1970 a 2005) ha habido grandes devaluaciones para el peso respecto al dólar; las más notorias ocurrieron en los periodos de 1976 a 1977, de 1982 a 1983, de 1985 a 1987 y de 1994 a 1995. Al comparar los diferentes periodos se observa que el peso no ha tenido estabilidad; sin embargo, en los últimos 10 años una recta descendente marca la tendencia que podría seguir el comportamiento del tipo de cambio de nuestra moneda frente al dólar, apuntando hacia la franja 10 u 11 pesos por dólar.

Es notorio que las grandes devaluaciones de nuestra moneda están representadas por los crecimientos drásticos ocurrido en los periodos ya señalados; análogamente, las recuperaciones de nuestra moneda están indicadas por los decrecimientos, menos drásticos que aquéllos. El dibujo contiene tres gráficas: una punteada, que indica los promedios del tipo de cambio; una con doble línea, que representa el tipo de cambio real, y una continua de mayor grosor que la primera, la cual marca la tendencia del tipo de cambio, a partir de marzo de 1990 en adelante.
La Gráfica 5 es una gráfica de corte intramatemático, compartida socialmente en las clases de matemáticas a partir del último grado de la escuela secundaria, continuando en el bachillerato y el nivel superior. Las variables representadas son x y f(x). En el intervalo –4 < x < –1.2, la gráfica es decreciente; en el intervalo –1.2 < x < –2 la gráfica es creciente, y decrece nuevamente en el intervalo 2 < x < 6. La gráfica tiene un punto máximo en (2, 28), uno mínimo en (–1.2, –12) y uno de inflexión en el origen. En términos globales, la gráfica tiene un comportamiento sinusoidal y representa una función continua.

4.4. Aplicación de los instrumentos de exploración y análisis de los resultados
A los estudiantes se les proporcionaron por separado las cinco gráficas, en el orden que las describimos. Cada una fue impresa en hojas tamaño carta, a colores, para mejorar la claridad y distinción de los rasgos esenciales, y analizada individualmente, siguiendo la instrucción del entrevistador: analiza cuidadosamente esta gráfica y describe verbalmente qué información te proporciona.
No se indujo a los estudiantes a que centraran su atención en algún aspecto, pues se trataba de utilizar la observación no–participativa, donde el investigador observa y toma datos. Tampoco influimos en sus acciones porque deseábamos obtener sus propias lecturas, libres de la visión del profesor o del entrevistador. Procuramos hacerlo así porque estábamos interesados en darle énfasis a lo que los estudiantes sabían o entendían, no en lo que no conocían. Con ello dirigimos nuestra investigación a ver los procesos de interpretación o lectura de gráficas desde el punto de vista de los estudiantes, tomando en cuenta sus auténticos conocimientos o significados.
El grupo de las cinco gráficas fueron analizadas aproximadamente en 25 minutos por cada estudiante. Sus lecturas e interpretaciones se registraron por separado e individualmente, tanto en audio como en vídeo. Las actividades de lectura e interpretación se realizaron fuera del escenario escolar propio de los estudiantes, ajenos a sus profesores y al contrato didáctico impuesto por ellos. Los aplicadores y analistas de los datos fueron los propios investigadores, en tanto que los resultados y el trabajo en su conjunto se expusieron en al menos en tres seminarios donde participaron especialistas en matemática educativa. En dichos seminarios se hicieron observaciones y sugerencias que se tomaron en cuenta para el perfeccionamiento del trabajo y el reporte de los resultados.
Como la investigación tenía corte cualitativo y fines exploratorios, el análisis de los resultados también fue de carácter cualitativo, pues nos interesaba obtener de los estudiantes sus lecturas e interpretaciones de las gráficas socialmente compartidas. El proceso de análisis se efectuó de la siguiente forma:
a. Se captaron todas las lecturas e interpretaciones de los alumnos en audio y vídeo.
b. Se elaboró una matriz de datos, donde se almacenaron las lecturas e interpretaciones hechas por los estudiantes, gráfica por gráfica.
c. Se hizo un análisis, primero individual, después por gráfica, y luego uno global.
El análisis se llevó a cabo con base en las acciones que presentamos en el apartado 3 de este documento: ¿qué cambia?, ¿cuánto cambia?, ¿cómo cambia?, ¿qué tan rápido cambia? y ¿cómo se comporta globalmente la gráfica? Además, se exploró el sentido y significado de los conceptos y propiedades de las gráficas, así como las inconsistencias o errores exteriorizados por los estudiantes.
Para las gráficas socialmente compartidas, el sentido y significado va más allá de lo estrictamente matemático. Las variables no son abstractas, tienen nombres concretos y sus significados están asociados al tipo de fenómenos particulares que representan; incluso el sentido y significado que se les atribuye en estos contextos requiere de socializar y compartir los significados de los campos profesionales a los que pertenecen. Por ejemplo, cuando se muestra la gráfica del tipo de cambio real surge inevitablemente la pregunta: ¿qué es el tipo de cambio real? O bien, cuando nos muestran una gráfica alusiva al PIB de los países subdesarrollados, es razonable preguntarse ¿qué significa PIB? o ¿qué significa ser un país subdesarrollado ?
Las respuestas a estas preguntas trascienden el ámbito escolar y conducen a espacios de profesionalización particulares; sin embargo, es pertinente conocerlos o compartirlos socialmente si se quiere tener una interpretación o lectura adecuada. Los temas socialmente compartidos en las gráficas utilizan conceptos cuyos significados son ampliamente difundidos, pues hablan de la población hablante de lengua indígena, la estructura de la población mexicana en un año determinado, la cantidad de egresados de la UNAM, el tipo de cambio real del peso respecto del dólar y una que emplea las variables abstractas x, f(x). El sentido y significado atribuidos por los estudiantes a las variables concretas y su comportamiento fueron también considerados en el análisis de sus lecturas e interpretaciones.
5. LECTURAS E INTERPRETACIONES EXPRESADAS. EL CASO DE LOS ESTUDIANTES DE PRIMARIA
Gráfica 1. Porcentaje de la población hablante de lengua indígena entre 1895 y 1995.
En cuanto a la acción ¿qué cambia?, cinco de los siete estudiantes dan muestras de que identifican y utilizan las variables representadas, seguramente inducidos por el título y los letreros que etiquetaron a los ejes x, y.
Amalia y Andrés centran su atención en los datos máximos y mínimos, al decir: en el año 1921 se habló mayor lengua indígena, con 128.9; el año que menos se habló lengua indígena fue en 1960, con 3.8%; el porcentaje más alto fue en 1921 y el más bajo en 1960. Hubo otra época muy alta en 1895 y otra muy baja en 1950, en que los índices no han sido parejos. Alondra se dedica a leer la gráfica dato por dato: aquí, en la información que se me proporciona viene el porcentaje. Los años son de 1895 a 1995: en 1985 la lengua indígena se hablaba un 16.2% y en 1900 era de 15.3; en 1910 hablaban 12.9; en 1921, un 28.9; en 1930, un 8.4 y así sucesivamente; nada dice sobre el comportamiento de los datos, sólo lee uno por uno.
Alfaro, Carmen y Daniel hacen lecturas de los datos, mencionan los máximos y mínimos, pero también establecen comparaciones entre los datos, lo cual hace pensar que realizaron estimaciones visuales de los cambios: El porcentaje de la población que habla lengua indígena de 1895 a lo que sería un siglo parece que la población indígena aumentó más de 1910 a 1921 y la mayor descendencia fue desde 1950 a 1960, en esa década bajó mucho la población hablante indígena en esos 100 años; que aumentó entre 1921 y 1985 y ya después de 1921 disminuyó a 1960; aquí esta gráfica me indica que en 1895 casi 16.2% de la gente hablaba en lengua indígena y en 1900 el 15% y así se sigue... La más grande es de 1921, donde el 28.9% de la gente hablaba lengua indígena... igual puede aumentar o disminuir.
Las comparaciones que hacen estos estudiantes son sólo cualitativas, ya que no dan muestras de hacer restas para saber cuánto aumentó o disminuyó la población hablante de lengua indígena. Se nota que al menos uno de ellos centra su atención en la disminución más drástica de la variable representada en la gráfica. Hay manifestaciones explícitas sobre la acción derivada de la pregunta ¿cómo cambia?, pues los estudiantes mencionan que la variable población hablante de lengua indígena aumentó o disminuyó en determinados años. No hubo expresiones que indicaran la utilización de la idea de rapidez cambio de la variable representada.
Gráfica 2. Estructura de la población mexicana en el año de 1995
De acuerdo con lo expresado por los estudiantes, identifican qué es lo que cambia en esta gráfica, seguramente inducidos por el encabezado. Amalia y Andrés centran su atención en los datos más sobresalientes, que obtienen comparando con otros datos, pero no se nota en sus expresiones que hayan calculado cuánto cambió la variable en determinados intervalos: La mayor población de hombres y mujeres es de 5 a 9 años, o sea que hay más jóvenes que señores grandes porque ya baja mucho de 55 a 59, hay más de 20 para abajo en hombres y mujeres; esta es la estructura de la población mexicana en el año de 1995, por lógica hay menos gente cuya edad es de 85 años o más.... Son muy parejos los índices entre los 10 y 14 años; en las mujeres varía un poco, pero sigue siendo muy parejo, lo cual también me demuestra que en esa época había más hombres que mujeres en México.
Al leer la gráfica, Luis sólo dice el dato más alto relativo a la edad: Hasta qué edad pueden llegar... la mujer puede llegar hasta 85. Alfaro y Alondra se concretan a describir las variables representadas: Esto quiere decir qué porcentaje de la población pertenece a cada rango de edad y los están separando además por sexo; aquí lo que me muestra es del año de 1995 y acá son las edades de las personas... Lo que entiendo es que en estos años vivían más. Daniel lee algunos datos, empezando por el primero (de abajo hacia arriba), y menciona la tendencia hacia la disminución: Aquí dice que el 6% de hombres en 4 años es el 6%, hasta los 10 y 14 años tienen 15, y a los 19 años van disminuyendo. Por ejemplo, aquí nace la gente y aquí muere, igual con las mujeres. La lectura que Carmen hace es sólo que los hombres tienen menos edades que las mujeres.
Como puede apreciarse, algunos estudiantes hablan de que la población va disminuyendo al señalar la tendencia que sigue a medida que su edad avanza, mas no manifestaron acciones de cuantificación sobre los cambios. La acción asociada a la pregunta ¿cuánto cambia? en esta gráfica se sigue omitiendo; en cambio, sí expresan palabras que indican cómo cambia la variable.
Gráfica 3. Egresados de la UNAM
Cinco estudiantes identifican y utilizan las variables representadas. Amalia y Daniel leen algunos puntos: la primera lee los dos puntos iniciales de cada gráfica y el segundo sólo el punto inicial. En la licenciatura en el 1980 salieron 12 mil 347 y del bachillerato 20 mil 598, en el 82 más o menos como 13 mil de licenciatura, y en el 2003 hubo 27 mil 470; de bachillerato, en el 2003 hubo 22 mil 848, en el 2000 casi fue el mismo número los que salieron de licenciatura y bachillerato; acá en la generación 80 había 12 mil egresados de licenciatura.
Alfaro, Carmen y Daniel parecen no percatarse de que la variable que se representa es el número de egresados, pues al referirse a ella utilizan el término alumnos. Alfaro hace una lectura global: Esta gráfica nos menciona el número de alumnos que estudian en bachillerato y licenciatura y que también son egresados a la UNAM, pues están distribuidos por una poligonal y parece que han ido descendiendo a través de los años, pero se han mantenido parejas del 80 al 88 y del 92 al 93. En cambio, Andrés hace una lectura global de la gráfica de egresados del bachillerato, señalando que fue muy estable y resalta el hecho de que en 1999 volvió a bajar; en cambio, acerca de la gráfica de la licenciatura apunta que no es nada estable, subía y bajaba y resalta los descensos más grandes en 1993, 1999 y 2003. Por su parte, Luís sólo dijo una frase: los promedios. Nuevamente, en esta gráfica la mayor parte de los estudiantes identifican lo que cambia, no ofrecieron lecturas que indicaran algún cálculo de cuánto cambió la variable, mas hicieron caracterizaciones de cómo cambia la variable: dicen que desciende, sube, baja o es estable.
Gráfica 4. Tipo de cambio real de pesos por dólar
Varios estudiantes identifican lo que cambia y leen varios puntos representados en esta gráfica. Amalia, Alfaro, Carmen y Andrés, además de leer algunos puntos, enfocan su atención en los puntos máximos o mínimos y hacen comparaciones, lo cual nos induce a pensar que hicieron estimaciones visuales sobre cuánto cambia el valor del peso en dólares: En el año 76 ya bajó mucho más, en 83 subió más que en el año 77 y subió muchísimo más en 88 que en todos los años; descendió mucho en los años 70, pero aparentemente se recuperó en 78; recibió más en 96; aumentó más en 1988 y 2004 y sucesivamente fue disminuyendo a como antes lo pagaban.
Andrés denomina los intervalos donde la gráfica crece como momentos muy estables para el peso: del 86 al 88 hubo un momento muy estable para el peso y también en el 94 y en el 96, pero hasta la fecha, según lo que me marca aquí, creo que es el 2004, está muy bajo. Alondra solamente se dedica a leer los letreros que aparecen en la gráfica y Daniel dice que aquí el dólar diminuye y aumenta, disminuye y aumenta.
Las interpretaciones muestran que los estudiantes identifican lo que cambia. Para esta gráfica siguen apareciendo expresiones relativas a la acción cómo cambia eso que cambia, pues afirman bajó mucho más, subió más que. Eso indica comparaciones entre los ascensos y descensos, lo cual da una idea de que estimaron también cuánto aumenta la cantidad de pesos que se pagan por dólar. No se observaron indicios de que hayan efectuado restas para saber cuánto cambia, mucho menos expresiones que aludieran a la rapidez de cambio o a la razón promedio de cambio.
Gráfica 5. Sin nombre (gráfica de f(x))
Al interpretar esta gráfica, la mayoría de los estudiantes dicen no entiendo, pero algunos intentan dar alguna explicación. Parecen no darle sentido a las letras x y f(x); sin embargo, algunos les dan un significado concreto: me imagino que es la población que ha estudiado, es como el dinero... te lo gastas, trabajas... y te lo vuelves a gastar. Amalia dice no entiendo qué es f(x), no tiene la información, sólo vienen algunos números, números menos y de más; es como una gráfica, pero de cruz, tiene que ser por ejemplo 40–2 y 10 entre uno y dos menos. Alfaro dice: no estoy seguro, pero menciona cuántas personas o qué parte de la población ha estudiado en los últimos años; aquí es la universidad y aquí me parece que es antes de la universidad.
Carmen, Alondra y Luís sólo dicen: no entiendo. Andrés expresa: no le entendí muy bien debido a que no me dice de qué habla... la verdad está más difícil, pero si sé que subió y bajó, volvió a bajar, pero la verdad que no identifiqué de qué trata. Daniel señala: está en el 40% más o menos y disminuye hasta el 10 y luego aumenta otra vez y vuelve a disminuir. Es así como del dinero... tú tienes dinero, te lo gasta, trabajas, te pagan y tienes más dinero y luego te lo vuelves a gastar y así. En las lecturas se aprecia que para los estudiantes x y f(x) no tienen un significado de variables abstractas, ya que relacionan con alguna variable concreta que conocen. También expresan cualidades de comportamiento sobre la gráfica que indican cómo cambia: subió y bajó, volvió a bajar, aumenta otra vez y vuelve a disminuir.
6. LECTURAS E INTERPRETACIONES EXPRESADAS. EL CASO DE LOS ESTUDIANTES DE SECUNDARIA
Gráfica 1. Porcentaje de la población hablante de lengua indígena entre 1895 y 1995
Todos los estudiantes de secundaria que participaron en la investigación dieron muestras de apreciar qué era lo que cambiaba: el porcentaje de la población hablante de lengua indígena. Jazmín y Bernardo hacen lecturas dato por dato, realizan algunas comparaciones y mencionan cómo cambia la variable: Aquí nos dice los porcentajes y los años que tiene. Es un porcentaje de la población hablante de lengua indígena que nos marca de 1895 a 1995, nos dice que en 1895 hay un porcentaje de 16.2 que habla la lengua indígena; en 1900 hay el 15.3 que habla la lengua indígena, y en 1910 hay 12.9... en 1960 bajó un poco, al 3.8; en 1970 es el 7.8, en 1980 el 9%, en 1990 el 7.4 y en 1995 el 6.9; como podemos ver, en 1895 tiene aproximadamente 16.2%, también en 1990 bajó un poco, 15.3%; también en los diferentes años que corresponden hasta el año de 1995. Como podemos ver, hay una reducción en el porcentaje.
Reina e Irving efectúan lecturas globales, mencionando inclusive cómo cambia la variable: Es una información sobre el aumento y disminución de las lenguas indígenas. La primera gráfica es una información sobre el aumento y la disminución de las lenguas indígenas, muestra el porcentaje de la población que habla lengua indígena que ha disminuido del año 85 al 95. Sólo Óscar centra su atención en el dato más alto y el más bajo; además, emite caracterizaciones de cómo cambia la variable: En el año de 1921 había más porcentaje de población que hablaba la lengua indígena que fue bajando; en 1960 estaba en 3.8, de ahí subió poquito y en 1995 ya había un 6.9%; ahorita ya es más poca la gente que habla de ese tipo de lengua.
Las lecturas hechas por estos estudiantes indican que detectan lo que cambia (la variable). Son visibles las lecturas de dato por dato y en todas es notoria la caracterización de cómo cambia la variable: bajó un poco, aumento y disminución; en 1960 estaba en 3.8 y subió poquito en 1995, ya que había 6.9. No se externaron cuantificaciones del cambio, ni caracterizaciones relativas a la rapidez de la variación o a la razón de cambio promedio.
Gráfica 2. Estructura de la población mexicana en el año de 1995
Jazmín y Bernardo expresan que se trata de una gráfica que muestra la estructura de la población mexicana en 1995, seguramente inducidos por el encabezado de la gráfica. Jazmín lee los intervalos de los porcentajes de hombres y mujeres de derecha a izquierda, algunos datos y habla sobre la disminución entre ellos: Habrá un 5 de las mujeres y así sucesivamente nos va diciendo de las demás edades, y claro en la de 85 y más ya casi no hay porque casi no todas las personas llegan a esas edades.
Bernardo, Reyna e Irving hacen lecturas globales sucintas. Bernardo compara porcentajes de hombres y mujeres, y dice que el porcentaje de mujeres es un poco más alto que el de los hombres. Óscar e Irving centran su atención en los datos con valores más pequeños: El grupo de edades en 1995 de 85 años para arriba casi no había o había pocos, y de los hombres había más; muestra el índice de vida en porcentajes. Por ejemplo, de 85 en adelante se ve que hay poca gente. Para esta gráfica, los estudiantes consideran que lo que cambia es el porcentaje de la población y sus edades, leen algunos datos y hacen algunas comparaciones entre ellos, refieren tendencias indicativas de cómo cambian las variables, aduciendo que hay pocas personas de más edad. No se expresaron cuantificaciones de la variación ni de razones de cambio.
Gráfica 3. Egresados de la UNAM
La mayoría de los estudiantes sólo leen los datos iniciales y finales, ya que están dados en las gráficas de manera explícita. Todos se dan cuenta muy bien qué es lo que cambia (variables), de acuerdo con lo representado en la gráfica. Reina, Óscar e Irving hacen lecturas globales muy cortas: De alumnos que egresan del bachillerato y el aumento y disminución de alumnos y el año de egreso; el número de alumnos es muy alto que tiene la UNAM, los de bachillerato apenas alcanzaron un 20 mil 598 alumnos y los de la licenciatura fueron 27 mil 470, también la licenciatura es un poco más importante que el bachillerato y por eso es que es el mayor número de alumnos; muestra los egresados de la UNAM y se indica que se han elevado mucho.
De las lecturas se nota que los estudiantes saben qué es lo que cambia. Nuevamente leen algunos datos, expresan caracterizaciones sobre cómo cambia la variable (aumento o disminución), pero no formularon cálculos que nos hicieran pensar en la medición de los cambios ni en la rapidez de la variación.
Gráfica 4. Tipo de cambio real de pesos por dólar
Cuatro estudiantes señalan las variables que están representadas en la gráfica: el tipo de cambio real y pesos por dólar. Jazmín, Bernardo y Óscar presentan lecturas de algunos puntos específicos de la gráfica. Solamente Bernardo refiere la depreciación y las bajas del número de pesos por dólar: aquí podemos ver la depreciación cuando sube mucho el costo. Reina expresa una lectura global muy corta, al afirmar que se trata del aumento y disminución el dólar en pesos; Irving dice que habla de peso en dólar, que se nota que ha disminuido. De hecho, los estudiantes presentaron lecturas muy cortas sobre esta gráfica, identifican qué es lo que cambia y externan algunas cualidades del comportamiento de la variable.
Gráfica 5. Sin nombre (gráfica de f(x))
La mayoría de los estudiantes no le dio el sentido de variable a la x o f(x). Alguno la relacionó con variables concretas que conocía; otros emitieron caracterizaciones del comportamiento: bajó y subió. Jazmín afirmó: no tiene datos que debiera llevar arriba y abajo, pero nos dice que aquí hay una x. Bueno, es como un plano, pero no nos muestra una tabla de datos... lo que le faltaría a esta gráfica es la tabla de datos como las anteriores para saber qué es lo que nos está diciendo. Cuatro de los estudiantes dijeron: no sé o no le entiendo. Óscar además de indicar no le entendí, agrega: es como si fuera una tabla de dólar que también bajó y subió y otra vez descendió, bajó mucho en este tiempo. Irving también dijo no le entiendo porque no muestra algún título o encabezado.
7. RESULTADOS GLOBALES
Los hallazgos obtenidos en el presente estudio indican que no se detecta tabula rasa en la lectura e interpretación de gráficas socialmente compartidas, ya que los estudiantes centran su atención en aspectos diferentes; no obstante, percibimos ciertas preferencias y proclividades.
Cuando lo que cambia está expresado en términos de variables concretas –por ejemplo, la población hablante de lengua indígena, los grupos cambiantes de edades de la población, los egresados, etc.–la mayor parte de los estudiantes no tienen problemas en identificarlas, incluso en usarlas para sus descripciones; sin embargo, notamos interpretaciones erróneas en algunos estudiantes acerca de qué variables son las que están representadas en las gráficas, cuestiones que abordaremos más adelante. Ahora bien, cuando a los estudiantes se les muestra una gráfica cuyos ejes están etiquetados con las letras x y f(x) no le dan sentido de variable abstracta, sino la asocian con alguna variable concreta que conocen.
En las lecturas que los alumnos hicieron no encontramos indicios de que utilizaran la cuantificación aritmética del cambio, ni que correlacionaran los cambios de una variable con los cambios de la otra, en el sentido que marca el pensamiento covariacional. La acción relativa a la pregunta cuánto cambia eso que cambia no apareció en ninguna de las lecturas; sólo en algunos casos hubo comparaciones que sugieren estimaciones visuales de esos cambios. Por ejemplo, para la Gráfica 4 se dijo: en 83 subió más que en el año 77 y subió muchísimo más en 88 que en todos los años; para la Gráfica 1: la población indígena aumentó más de 1910 a 1921 y la mayor descendencia fue desde 1950 a 1960.
En cambio, aparecieron con mucha frecuencia caracterizaciones de la acción que hemos asociado con la pregunta cómo cambia eso que cambia. Fue muy frecuente hallar expresiones como aumentó, disminuyó, subió, bajó; incluso se emitieron calificativos cuantitativos del tipo aumentó poco, subió muchísimo más. Se nota en las lecturas e interpretaciones de los estudiantes la proclividad a leer dato por dato o punto por punto, según se trate, como si estuvieran leyendo un párrafo escrito en español cuya lectura inicia de izquierda a derecha. Muy pocos hacen comparaciones y describen sólo comportamientos cualitativos; ninguno deduce o calcula comportamientos cuantitativos de ¿cuánto aumentó?, ¿cuánto bajó? Mucho menos percibimos el cálculo de razones de cambio promedio, a pesar de que en el currículo y en los textos usuales de primaria y secundaria mexicanas las razones y proporciones son un tema de tratamiento obligatorio.
Varios estudiantes son proclives a leer sólo los datos inicial y final, omitiendo los datos intermedios. Incluso cuando las gráficas vienen acompañadas de letreros con datos específicos o palabras específicas, como el caso de la 4, se dedican a leerlas textualmente, aunque no compartan o comprendan el significado, por ejemplo, de los términos depreciación o tendencias. La gran mayoría de estudiantes hicieron caso omiso de la gráfica que indica el promedio del tipo de cambio 1970–2005, que está punteada, así como la recta de mayor grosor, que muestra la tendencia del tipo de cambio de 1990 a 2005.
La mayoría de los estudiantes, en particular los de primaria, prefieren centrar su atención en la lectura de los valores máximos o mínimos, sobre todo en la de la Gráfica 1. En el caso de la Gráfica 2, varios alumnos hacen notar los datos más pequeños, refiriéndose a la población de más de 85 años: ya casi no hay personas de más de 85 años. En los textos de primaria se plantean tareas de reproducción de construcción de trayectorias, análisis de información, ubicación y desplazamiento, distribución de puntos (Flores & Cordero, 2005), e incluso en primaria se empieza por estudiar la variación directamente proporcional y en secundaria se incorpora la variación inversamente proporcional, que implican el estudio de los cambios y las razones entre ellos. Sin embargo, en ninguno de los estudiantes notamos el uso del cálculo de las diferencias para medir los cambios, o de las razones de cambio para analizar la rapidez del comportamiento de las modificaciones.
En la lectura de aquellas gráficas consistentes de curvas o poligonales, los estudiantes ofrecen lecturas que denotan privilegio sobre la trayectoria de la curva en cuestión. Parecen centrar su atención más en la forma que en el contenido, lo cual es más notorio en los alumnos de primaria. En la Gráfica 3 indican siguiendo la trayectoria: la raya amarilla marca sobre el bachillerato y la café sobre la licenciatura; pues están distribuidas por una poligonal y parece que han ido descendiendo a través de los años. Para la Gráfica 4, algunos dicen: el aumento o disminución del dólar en pesos, aquí están los años y aquí lo que aumenta o lo que disminuye (señalan la trayectoria). Para la Gráfica 5 afirman: pero sí sé que subió y bajó, volvió a bajar, está en el 40% más o menos y disminuye hasta el 10, y luego aumenta otra vez y vuelve a disminuir.
En las gráficas socialmente compartidas generalmente no se representan variables abstractas. Las x y las f(x), comúnmente trabajadas durante las clases de matemáticas, en estas gráficas tienen nombres de variables concretas como el tiempo en años, cantidad de egresados, valor del dólar, población hablante de lengua indígena, etc. El nombre de las variables concretas depende del campo profesional a que correspondan; para el caso que nos ocupa, las gráficas 1, 2 y 3 atañen a estudios poblacionales; en la Gráfica 4, las variables son del tipo financiero, y en la 5 se representan variables abstractas. Para la lectura e interpretación de este último tipo de gráficas, se necesita dar sentido o significado más amplio y generalizado a las literales; por ejemplo, cuando intentaron leer la Gráfica 5, los estudiantes dijeron –principalmente los de primaria– que no entendían qué significaba la x porque sentían la necesidad de tener enfrente variables concretas.
Por otra parte, las gráficas que se comparten en espacios sociales muy amplios a través de los medios de comunicación e información, como los periódicos o internet, suelen ser muy expresivas, sobre todo si para leerlas no requieren de un alto grado de especialización, pues su objetivo es facilitar la comunicación. Las gráficas utilizadas en este trabajo contenían título, nombres de las variables y algunos letreros adicionales. Los estudiantes, de hecho, leían estos títulos o los letreros, pero manifestaron un escaso dominio sobre el significado del comportamiento de las variables. En la Gráfica 4; sólo un estudiante de secundaria emplea el término depreciación para indicar cuando aumenta mucho el costo. De igual manera, los alumnos hacen notar los máximos y mínimos, pero ninguno los relaciona con las devaluaciones del peso, quizá porque todavía no es parte de su información cultural.
La Gráfica 5 es diferente al resto, debido a que concierne al bachillerato o la universidad; además, no tiene título ni letreros sobre qué variables concretas están allí representadas. En sus lecturas e interpretaciones los estudiantes manifiestan extrañeza; la mayoría dijo no entiendo, e incluso para poderla leer consideran que debiera tener una tabla de datos; aseguran no entender qué es x y f(x) o que debiera tener algún encabezado. Quienes dan alguna interpretación dicen que es como la gráfica del dólar, me imagino que es la población que se ha estudiado; para ayudarse a darle sentido recurren a las variables concretas de las gráficas que habían leído. Esto es consistente con lo que señala King (1994): cuando los individuos encuentran nueva información usan su propio conocimiento y experiencia personal para ayudarse a dar sentido al nuevo material. Durante el proceso de construcción del significado pueden tener interferencias sobre la nueva información, dándole una nueva perspectiva a algún aspecto de su conocimiento existente y elaboraran el nuevo material por medio de adición de detalles. Así, generan relaciones entre el nuevo material y la información existente en su memoria.
8. INCONSISTENCIAS Y DIFICULTADES ENCONTRADAS
A pesar de que el presente estudio no se propuso la búsqueda de errores o inconsistencias en las lecturas de las gráficas, no podemos ignorarlos. Son de interés porque los profesores de matemáticas que intentan trabajar con gráficas de contextos reales a menudo no consideran las dificultades que conciernen a la interpretación y el significado de los conceptos. Por ejemplo, el trabajo muestra que la problemática de la depreciación monetaria no se puede tomar como un elemento de la información cultural de un alumno de educación básica, o al menos de los aquí cuestionados.
Notamos que en varias lecturas se expresaban frases que no correspondían a lo representado en las gráficas. Algunos estudiantes dijeron sobre las variables de la Gráfica 1 que aumentó las lenguas indígenas en 1921 a 1985 y que ya después de 1921 disminuyó hasta 1960; es una información sobre el aumento y disminución de las lenguas indígenas. Sus lecturas indican que la variable principal es el número de lenguas indígenas, en lugar del porcentaje de la población mexicana hablante de lengua indígena. Que los hombres tienen menos edades que las mujeres; hasta qué edad pueden llegar... la mujer puede llegar hasta 85; por ejemplo, aquí nace la gente y aquí muere, igual con las mujeres; el aumento de población de hombres y mujeres; muestra el índice de vida en porcentajes: de 85 en adelante se ve que hay poca gente. Tales expresiones muestran que interpretaron la variable principal de la Gráfica 2, como las edades de los hombres y las mujeres o el aumento de población por sexo.
En relación con la Gráfica 3, hubo frases como: Nos menciona el número de alumnos que estudian en bachillerato y licenciatura y que también son egresados; aquí empieza la gente a estudiar y aquí en el 2003, como sale cada año; el número de alumnos que tiene la UNAM es muy alto: los de bachillerato apenas alcanzaron 20 mil 598 alumnos y los de licenciatura fueron 27 mil 470. Esto evidencia la falta de correspondencia con la variable representada en la gráfica: número de egresados de licenciatura y bachillerato de la UNAM.
Respecto de la Gráfica 4, algunos dijeron: Es la cantidad de dólares que se cambia por pesos aquí y en el estado; habla del peso en dólar, que se nota que ha disminuido. En estas lecturas, sobre todo en la primera, se percibe que los estudiantes no repararon que la cantidad de dólares es constante y, en todo caso, lo cambiante atañe a la cantidad de pesos que se paga por cada dólar.
9. PERSPECTIVA DE FUTURAS INVESTIGACIONES
El estudio de las gráficas está siendo abordado por diversos grupos de investigadores; sin embargo, poco se sabe acerca de cómo viven estos objetos y procesos en contextos sociales, tanto dentro como fuera del ámbito educativo.
Aunque las gráficas son objetos de enseñanza en la escuela, su uso se ha expandido a amplios núcleos sociales. Son medios usuales para comunicar información y validar los argumentos, mientras que su papel en la escuela ha estado fuertemente influido por las concepciones y prácticas de los profesores sobre la enseñanza y aprendizaje de las matemáticas.
En el terreno de la investigación educativa se han dado explicaciones amplias sobre el papel de las gráficas en el ámbito escolar, mas poco se sabe del que desempeña en un contexto social fuera de la escuela, sobre todo qué repercusiones podría tener el uso social de las gráficas en el nuevo diseño curricular. La noción de contrato didáctico, elaborada por Brousseau (1997), impone ciertos comportamientos que implícitamente comparten estudiantes y profesores: si el estudiante no grafica la función o no resuelve los problemas con el método enseñado por su profesor puede que no apruebe la materia. Sin embargo, el ciudadano común, no el estudiante, como el periodista, el político o el funcionario, cuando lee o interpreta una gráfica, lo hace por motivaciones diferentes a las escolares, y creemos que con estrategias distintas de las aprendidas en las aulas. Sus interacciones con el mundo de las gráficas se dan en contextos y situaciones determinados por sus intereses o el uso profesional.
Compartimos la tesis de que las actividades matemáticas dependen del contexto social en el que se abordan, de que la matemática cobra vida y sentido en contextos sociales concretos. En esta perspectiva, indicada por Cantoral (2004) y Cantoral & Farfán (2003) interesa, a diferencia de otras investigaciones, las formas en que las gráficas viven y son movilizadas en las interacciones sociales. Desde este punto de vista no sólo es importante que un estudiante construya los conceptos matemáticos, sino también conocer cómo viven los conocimientos construidos, cómo son movilizados como argumentos o cómo se emplean como herramienta para intervenir en su entorno. En el trabajo aquí reportado, las tareas propuestas a los alumnos implicaban que sacaran información sin tener un objetivo práctico particular; quizá los resultados cambien si las tareas encomendadas obedecieran a razones prácticas o de carácter utilitario.
La relación entre las gráficas y los estudiantes en la escuela puede diferir de aquella que se establece entre las gráficas y las comunidades de profesionales, o incluso con la gente común y corriente. En el primer caso, la relación es regida por el contrato didáctico vigente; en el segundo predominan las relaciones utilitarias, prácticas o funcionales. Esta vertiente del uso social de las gráficas en nuestro país ha ocurrido bajo el enfoque socioepistemológico; en tal perspectiva se orientan nuestras investigaciones futuras.
1 Este artículo es uno de los resultados del proyecto GUE–2002–C0–7626, financiado por el Fondo Mixto Conacyt– Gobierno del Estado de Guerrero. regresar
BIBLIOGRAFÍA
Brassel, M. & Rowe, B. (1993). Graphing skills among high school physics students. School Science and Mathematics 93, 63–71. [ Links ]
Brousseau, G. (1997). Theory of didactical situations in mathematics. Dordrecht, The Netherlands: Kluwer Academic Publishers. [ Links ]
Buendía, G. & Cordero, F. (2005). Prediction and the periodical aspects generators of knowledge in social practice framework. A socioepistemological study. Educational Studies in Mathematics 58(3), 299–333. [ Links ]
Campos, C. (2003). La argumentación gráfica en la transformación de funciones cuadráticas. Una aproximación socioepistemológica. Tesis de maestría, Cinvestav, México. [ Links ]
Cantoral, R. (2004). Desarrollo del pensamiento y lenguaje variacional. Una mirada socioepistemológica. En L. Díaz (Ed.), Acta Latinoamericana de Matemática Educativa 17 (Núm. 1, pp. 1–9). México: Clame. [ Links ]
Cantoral, R. & Farfán, R. M. (2003). Matemática educativa: una visión de su evolución. Revista Latinoamericana de Investigación en Matemática Educativa 1(1), 27–40. [ Links ]
Cantoral, R. & Montiel, G. (2001). Funciones: visualización y pensamiento matemático. México: Prentice Hall. [ Links ]
Carlson, M.; Jacobs, S.; Coe, E.; Larsen, S. & Hsu, E. (2002). Applying covariational reasoning while modeling dynamic events: a framework and a study. Journal for Research in Mathematics Education 33(5), 352–378. [ Links ]
Cordero, F. (2005). La socioepistemología en la graficación del discurso matemático escolar. En J. Lezama (Ed.), Acta Latinoamericana de Matemática Educativa 18 (Núm. 1, pp. 477–482). México: Clame. [ Links ]
Dolores, C.; Alarcón, G. & Albarrán, D. (2002). Concepciones alternativas sobre las gráficas cartesianas del movimiento: el caso de la velocidad y la trayectoria. Revista Latinoamericana de Investigación en Matemática Educativa 16(3), 225–250. [ Links ]
Dolores, C. (1999). Una introducción a la derivada a través de la variación. México: Grupo Editorial Iberoamérica. [ Links ]
Dolores, C. (2004). Acerca del análisis de funciones a través de sus gráficas: concepciones alternativas de estudiantes de bachillerato. Revista Latinoamericana de Investigación en Matemática Educativa 7(3), 195–218. [ Links ]
Dolores, C. & Valero, M. S. (2004). Estabilidad y cambio de concepciones alternativas acerca del análisis de funciones en situación escolar. Epsilon 58(20–1), 45–73. [ Links ]
Dolores, C. & Catalán, A. (2000). El comportamiento variacional de la función lineal: Una experiencia didáctica con estudiantes del bachillerato. En R. M. Farfán, C. E. Matias, D. Sánchez & A. Tavares (Eds.) Acta Latinoamericana de Matemática Educativa 13, 36–41. [ Links ]
Domínguez, I. (2003). La resignificación de lo asintótico en la aproximación socioepis–temológica. Tesis de maestría, Cinvestav, México. [ Links ]
Eysemberg, T. & Dreyfus, T. (1991). On the reluctance to visualize in mathematics. En W. Zimmerman & S. Cunningham (Eds.), Visualization in teaching and learning mathematics (pp. 25–37). Washington, DC, USA: The Mathematical Association of America. [ Links ]
Even, R. (1998). Factors involved in linking representations of functions. Journal of Mathematical Behavior 17(1), 105–121. [ Links ]
Flores, R. & Cordero, F. (2005). El uso de las gráficas en los libros de textos. En J. Lezama (Ed.), Acta Latinoamericana de Matemática Educativa 18 (Núm.1, pp. 495–501). México: Clame. [ Links ]
Flores, R. (2005). El uso de las gráficas en el discurso matemático escolar. Un estudio socioepistemológico en el nivel básico a través de los libros de texto. Tesis de maestría no publicada, Cinvestav, México. [ Links ]
Janvier, C. (1998). The notion of chronicle as an epistemological obstacle to the concept of function. Journal of Mathematical Behavior 17, 123–134. [ Links ]
Hernández, R., Fernández, C. & Baptista, P. (2003). Metodología de la investigación. México: McGraw–Hill Interamericana. [ Links ]
King, A. (1994). Guiding knowledge construction in the classroom: effects of teaching children how to question and how to explain. American Educational Research Journal 31, 338–368. [ Links ]
Leinhardt, G., Zaslavsky, O. & Stein, M. (1990). Functions, graphs and graphing: tasks, learning and teaching. Review of Educational Research 60, 1–64. [ Links ]
Mevarech, Z. & Kramarsky, B. (1997). From verbal description to graphic representation: stability and change in student's alternative conceptions. Educational Studies in Mathematics 32(3), 229–263. [ Links ]
Moschkovich, J., Schoenfeld, A. & Arcabi, A. (1993). Aspects of understanding: on multiple perspectives and representations of lineal relations, and connecting among them. En T. Romberg, E. Fennema & T. Carpenter (Eds.), Integrating research on the graphical representation of function (pp. 69–100). Hillsdale, NJ: LEA. [ Links ]
Pérez, G. (1998). Investigación cualitativa: retos e interrogantes I. Métodos. Madrid, España: Editorial Muralla. [ Links ]
Rosado, P. (2004). Una resignificación de la derivada. El caso de la linealidad del polinomio en la aproximación socioepistemológica. Tesis de maestría no publicada, Cinvestav, México. [ Links ]
Secretaría de Educación Pública (1993a). Plan y Programas de estudio. Educación Básica. Primaria. México. [ Links ]
Secretaría de Educación Pública (1993b). Plan y Programas de estudio. Educación Básica. Secundaria. México. [ Links ]
Wainer, H. (1992). Understanding graphs and tables. Educational Researcher 21, 14–23. [ Links ]
Yerushalmy, M. & Shternberg, B. (2001). Charting a visual course to the concept of function. En A. Cuoco & F. Curcio (Eds.), The roles of representation in school mathematics (pp. 251–268). Reston, Virginia, USA: National Council of Teachers of Mathematics. [ Links ]
NOTAS
2 Centro de investigación en Matemática Educativa (Cimate) Universidad Autónoma de Guerrero, México. regresar
3 Secretaría de Educación Pública. regresar
7 Universidad Autónoma de México. regresar














