Vínculo entre el pensamiento proporcional cualitativo y cuantitativo: el caso de Paulina

 

Elena Ruiz ¹ Marta Valdemoros ²

 

¹ Centro de Investigación y de Estudios Avanzados del IPN, México. E–mail: elen_fruiz@yahoo.com.mx

² Departamento de Matemática Educativa, Centro de Investigación y de Estudios del IPN, México. E–mail: mvaldemo@cinvestav.mx

 

Fecha de recepción: Noviembre de 2005
Fecha de aceptación: Mayo de 2006

 

RESUMEN

El estudio de caso reportado aquí forma parte de un proyecto doctoral concluido. Hace referencia a una evaluación sobre la propuesta de enseñanza de razón y proporción desarrollada en la investigación doctoral. Tal propuesta se realizó con un grupo de sexto grado de educación elemental, conformado por 29 niños mexicanos que tenían 11 años de edad. La niña del estudio de caso, Paulina, reflejó el proceder de varios de estos niños, quienes resolvieron el cuestionario inicial con algoritmos manejados de un modo mecánico, sin darle sentido a sus elaboraciones, lo cual se vio ratificado al principio del programa de enseñanza. Dicho programa propició la ampliación del pensamiento proporcional cualitativo de Paulina, fortaleciendo su pensamiento proporcional cuantitativo en el terreno de la resolución de problemas. Así, la enseñanza, el cuestionario final y las entrevistas mostraron que el enriquecimiento del pensamiento proporcional cualitativo le permitió a Paulina ampliar las relaciones cuantitativas y mejorar el manejo de los algoritmos, enmarcándolos en aplicaciones plenas de sentido.

PALABRAS CLAVE: Pensamiento proporcional cuantitativo, pensamiento proporcional cualitativo, razón interna, razón externa, operador multiplicativo.

 

ABSTRACT

The case study reported here it is part of a doctoral project already concluded. It refers to the evaluation of the teaching proposal for rate and proportion developed in the Doctoral research. This proposal was carried out with a group of students of elementary school constituted by 29 eleven–year–old Mexican children. The girl of the case study (Paulina) express the behavior of various of these children, who resolved the initial questionnaire with algorithms handled on a mechanical way, without giving sense to its elaborations, which was ratified at the beginning of the teaching program. This program permitted the growth of the qualitative proportional thought of the student, fortifying its quantitative proportional thought, regarding problem solving. Thus, the teaching, the final questionnaire and the employed interviews, showed that the enrichment of the qualitative proportional thought permitted to Paulina to expand the quantitative relations and to improve the management of the algorithms, framing it in applications full of sense.

KEYWORDS: Quantitative proportional thought; qualitative proportional thought; internal rate; external rate; multiplicative operator.

 

RÉSUMÉ

L'étude du cas rapporté ici forme partie d'un projet de doctorat déjà conclu. Il fait référence a l'évaluation de la proposition d'enseignement de raison et de proportion, développée dans la recherche doctorale. Cette proposition s'est effectuée avec un groupe de sixième année d'éducation élémentaire composé de 29 enfants mexicains de onze ans. La fille de l'étude de cas particulier (Paulina) reflète le processus de plusieurs de ces enfants, qui ont résolu le questionnaire initial avec des algorithmes utilisés de façon mécanique, sans donner un sens à leurs élaborations, ce qui s'est vu ratifié au début du programme d'enseignement. Ce programme a permis l'amplification de la pensée proportionnelle qualitative de l'étudiante, en renforçant sa pensée proportionnelle qualitative dans le terrain de la résolution de problèmes. Ainsi, l'enseignement, le questionnaire final et les entretiens employés ont montré que l'enrichissement de la pensée proportionnelle qualitative a permis á Paulina d'élargir les relations quantitatives et d'améliorer l'usage des algorithmes, en les utilisant uniquement dans des applications pleines de sens.

MOTS CLÉS: Pensée proportionnelle quantitative ; pensée proportionnelle qualitative ; raison interne ; opérateur multiplicatif.

 

RESUMO

O estudo de caso aqui apresentado forma parte de um projeto de doutorado já concluído. Faz–se referência à avaliacão da proposta de ensino de razão e proporção desenvolvida na investigação de doutorado. Esta proposta se realizou com um grupo de quinta série da educação fundamental composto por 29 estudantes mexicanos de onze anos de idade. A estudande desse estudo de caso (Paulina) reflete o comportamento de vários outros, os quais responderam ao questionario inicial com algoritmos trabalhados muito mecanicamente, sem dar sentido a suas elaborações, o qual se viu ratificado no princípio do programa de ensino. Tal programa permitiu a ampliação do pensamento proporcional qualitativo da estudante, fortalecendo seu pensamento proporcional quantitativo, no terreno da resolução de problemas. Asim, o ensino, o questionário final e as entrevistas, mostraram que ol enriquecimento do pensamento proporcional qualitativo permitiu Paulina ampliar as relações quantitativas e melhorar o manejo dos algoritmos, enquadrando–os em aplicações plenas de sentido.

PALAVRAS CHAVE: pensamento proporcional quantitativo; pensamento proporcional qualitativo; razão interna; razão externa; operador multiplicativo.

 

MARCO TEÓRICO

A continuación, para establecer los antecedentes teóricos en este artículo, consideramos de manera preponderante a los autores Piaget y Streefland, quienes atienden a las manifestaciones del pensamiento proporcional cualitativo y cuantitativo de los sujetos. Asimismo, para sustentar la aproximación didáctica que aquí se desarrolla, nos apoyamos en el enfoque de la matemática realista, de Streefland.

Piaget e Inhelder (1978), a través de sus experimentos, señalan que el niño adquiere la identidad cualitativa antes que la conservación cuantitativa y hacen una distinción entre las comparaciones cualitativas y la verdadera cuantificación. Para Piaget e Inhelder (1972), la noción de proporción empieza siempre de una forma cualitativa y lógica antes de estructurarse cuantitativamente. Piaget define lo cualitativo a través de categorías o clases de palabras; de esta forma, se apoya en reconocimientos lingüísticos, creando categorías de comparación, como grande o pequeño. Consideramos que lo cualitativo también integra los aspectos intuitivos y empíricos que brindan los sentidos, apoyándonos en términos de la psicología.

Piaget (1978) indica que en el paso de lo cualitativo a lo cuantitativo aparece la idea de orden sin que todavía emerja la cantidad, a lo que llama cuantificaciones intensivas; desde nuestro punto de vista, esta noción destaca el tránsito del pensamiento cualitativo al cuantitativo. Van den Brink & Streefland (1979) coinciden con Piaget en cuanto a que lo cualitativo emerge antes que lo cuantitativo, pero Streefland comúnmente lo lleva al terreno de la enseñanza. Tal aportación la empleamos en el diseño de nuestro programa didáctico, así como en las tareas de las entrevistas que aplicamos para el estudio de caso.

Streefland (1984, 1985) lleva a cabo una investigación en la que enfatiza que la enseñanza temprana de la razón y la proporción debe partir de niveles cualitativos en los que haya un reconocimiento de ellas; además, hace uso de recursos didácticos (figuras, dibujos, expresiones) que favorecen el desarrollo de patrones perceptuales, en apoyo a los correspondientes procesos de cuantificación. Streefland comenta que el pensamiento cualitativo evoluciona cuando hay un avance en el pensamiento y el niño puede llegar a incorporar más elementos para un análisis que le permita considerar distintos factores conjuntamente.

Otros estudios sobre el pensamiento proporcional fueron realizados por el equipo de investigación de Hart (1988), quien en un estudio con un grupo de alumnos observó que la mayoría consideraba difícil resolver problemas matemáticos donde se involucra la proporción; sin embargo, hubo evidencia de que los estudiantes de menor edad y los alumnos de la secundaria con menos éxito tienen un sentido de lo que se ve correcto o lo que parece ser una distorsión. A esto Hart lo designó como una regulación desde el sentido común. Reconocemos que ese aspecto está íntimamente involucrado en el pensamiento cualitativo porque atañe a lo perceptual. Asimismo, Hart señala que lo más avanzado del pensamiento proporcional se da en el sujeto una vez que ha construido determinados conceptos.

Hacemos referencia al pensamiento proporcional cuantitativo del niño cuando puede hacer uso de las razones y proporciones y maneja indistintamente razones internas y externas para enfrentar problemas matemáticos. Al respecto, Freudenthal (1983) define a las primeras como relaciones establecidas entre distintos valores de la misma magnitud (distancia con distancia, tiempo con tiempo, precio con precio), y a las segundas como vínculos entre valores de diferentes magnitudes (por ejemplo, tiempo con distancia o litros de leche con precio).

En el terreno didáctico nos apoyamos fundamentalmente en Streefland (1993), quien habla sobre la educación realista de las matemáticas. Ésta ha llegado a constituirse en una teoría, según los seguidores de Freudenthal y Streefland, debido a que la realidad es, en primera instancia, una fuente de información; además, constituye el terreno donde se aplican modelos de enseñanza, esquemas, notaciones y producciones escolares que derivan en la práctica social. Por tanto, favorece el desarrollo de la investigación y la práctica de la enseñanza en la educación matemática. De igual modo, en esta teoría realista es fundamental entrelazar los tramos de aprendizaje de los estudiantes, apelando a la estrategia de cambio en perspectiva, que se caracteriza por el intercambio de una parte de la información en la situación–problema abordada. En consecuencia, las posibilidades para la reconstrucción y producción de problemas llegan a ser explícitamente reconocidas por los estudiantes, sin perder toda su riqueza conceptual multifacética.

 

PROBLEMA DE INVESTIGACIÓN

El presente estudio de caso forma parte de una investigación doctoral concluida, sobre la que se han efectuado trabajos previos referidos a otros aspectos y actividades del trabajo de campo, como lo reportado en Ruiz (2000, 2001) y en Ruiz y Valdemoros (2001, 2002, 2005), donde se abordan los modelos de enseñanza trabajados durante la propuesta, tras haber revisado las estrategias empleadas por los estudiantes al resolver problemas de razón y proporción simple y directa; también forma parte otro estudio de caso cuyo interés fue mostrar el paso de un registro de representación a otro en la resolución del tipo de problemas señalados.

En el seguimiento del caso de Paulina, aquí presentado, el problema de investigación concierne a que esta niña resolvía los problemas de razón y proporción utilizando algoritmos carentes de sentido y significado³. Es decir, tenía muy arraigado el procedimiento sin tener claro su uso, dados los problemas que se le presentaban referentes a razón y proporción. Ante tal situación, diseñamos una secuencia de actividades conformada por modelos de enseñanza⁴ que favoreció el establecimiento de sólidos enlaces entre su pensamiento proporcional cualitativo y cuantitativo, pretendiendo así que mejorara el manejo de sus algoritmos y los enmarcara en aplicaciones llenas de sentido. Ante el caso de Paulina, nos planteamos la siguiente pregunta de investigación:

¿El extenso manejo de lo cualitativo permite que la estudiante amplíe sus relaciones cuantitativas y mejore el manejo de sus algoritmos?

La hipótesis que fue la siguiente:

Ayudar a desarrollar el pensamiento cualitativo de la estudiante (al hacer uso de categorías verbales integradas, al reconocer las compensaciones que se plantean entre éstas y al involucrar los respectivos datos empíricos y perceptuales), favorece los procesos de significación desarrollados por ella cuando emplea algoritmos al resolver problemas de razón y proporción.

El método que usamos se describe a continuación:

El estudio de caso que muestra este trabajo integra los resultados que tuvo Paulina en el cuestionario inicial –cuyo propósito fue indagar el estado en que se encontraba el grupo en general–, el programa de enseñanza, de carácter constructivista–didáctico, el cuestionario final y las entrevistas de "naturaleza didáctica" (con base en lo señalado por Valdemoros, 1998). Los instrumentos metodológicos fueron piloteados a lo largo de un ciclo escolar anual; luego fueron desarrollados de modo definitivo, a través de los diez meses que duró el trabajo de campo. En las siguientes páginas se seleccionan ejemplos pertinentes sobre los instrumentos.

La utilidad del cuestionario inicial en nuestra investigación se manifestó predominantemente como un medio de recogida de información y como punto de partida para el uso de métodos cualitativos. (Woods, 1989). Una vez que se identificaron los temas de interés y fueron detallados en ítems los requisitos de información necesarios, nuestra tarea consistió en estructurar el cuestionario en sí mismo, atendiendo a la recomendación de Cohen y Manhion (1980), quienes señalan que hay evitar las preguntas que sugieran a los informantes que sólo hay una respuesta aceptable o las que sean complejas.

Para indagar en la manifestación del pensamiento cualitativo, requerimos primeramente de aplicar el cuestionario, que involucró tareas donde no se utilizaron cantidades para su solución, como actividades de comparación, lo cual le permitió a Paulina identificar relaciones de semejanza entre figuras. Consideramos pertinente incluir el cuestionario inicial –siendo el mismo que el final– para tener mayor claridad en el seguimiento de la metodología (Tabla 1).

Las dos primeras tareas exploraron los aspectos cualitativos en el terreno de la proporcionalidad.

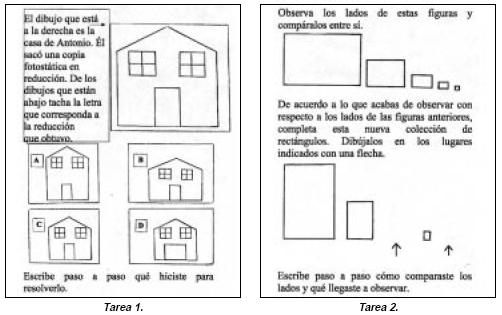
Las tres siguientes estuvieron enfocadas al tránsito de lo cualitativo a lo cuantitativo:

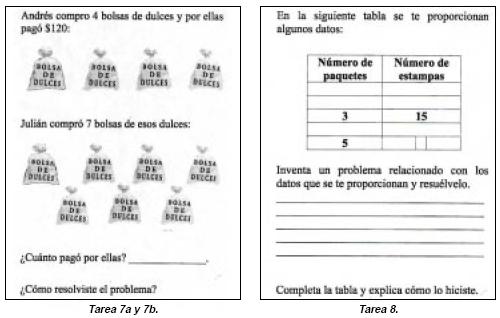
Las ocho tareas restantes del cuestionario se centraron en el campo cuantitativo del pensamiento del estudiante.

Para entrelazar los pensamientos proporcionales cualitativos y cuantitativos de Paulina en el programa didáctico, se diseñaron varias situaciones que estuvieron asociadas a modelos de enseñanza, según la definición de modelo que dan Figueras, Filloy y Valdemoros (1987): es el conjunto de estrategias de enseñanza que engloban significados, tanto en el lenguaje técnico como en el lenguaje cotidiano, tratamientos didácticos, modos específicos de representación y las relaciones que haya entre ellos. Trabajamos dichos en distintos momentos, lo cual se asemeja a lo señalado por Streefland (1993) en su teoría realista, tocante a la estrategia de cambio en perspectiva, pues creamos un modelo y lo tratamos de explotar al máximo a la luz de una idea, para luego retomarlo y utilizarlo en torno a otra idea.

Escogimos a Paulina porque caracterizó a aquellos estudiantes que mostraron en el cuestionario inicial un gran apego al manejo de algoritmos, pero carentes de sentido; además, tuvo pocas elaboraciones en el terreno cualitativo. A lo largo de la experiencia de enseñanza Paulina hizo notorio un enriquecimiento en su pensamiento cualitativo, logrando una conciliación en ambos campos; de igual manera, pese al progreso que alcanzó en el terreno numérico, no abandonó el aspecto cualitativo de la proporcionalidad.

 

ANÁLISIS DE LOS PROGRESOS DE PAULINA

Al contrastar el cuestionario inicial y el final se encontró lo siguiente:

El cuestionario inicial y el final estuvieron integrados por las mismas tareas, pero se diferenciaron en la finalidad de su aplicación, ya que el primero fue de naturaleza exploratoria y el segundo se centró en la evaluación del programa de enseñanza. Como el lapso entre la aplicación de ambos fue de ocho meses, no hubo ninguna influencia entre ellos.

Al resolver el cuestionario inicial, Paulina evidenció un predominio en el uso de los algoritmos de manera mecánica y poco trabajo en el terreno cualitativo; además, se observó en ella un escaso empleo de lo intuitivo, así como en el aspecto visual. De las 13 tareas de que constó el cuestionario inicial, tuvo nueve aciertos.

De las trece tareas, con las dos primeras buscamos que Paulina diera justificaciones más fundamentadas en la apreciación cualitativa, prescindiendo de cantidades explícitas asociadas a las relaciones de proporcionalidad dadas. En las tres siguientes empleamos la cuadrícula con la intención de favorecer la realización de un tránsito a la cuantificación. Las tareas restantes consistieron en situaciones de razón y proporción cuantificadas, ya que le dimos a Paulina algunos valores y le pedimos nuevos valores. Para algunas de estas tareas utilizamos una tabla como un modo de representación para el reconocimiento de razones externas o internas.

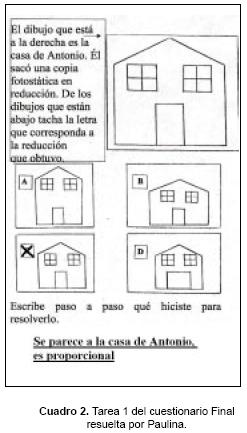
Con respecto a las cuatro tareas que Paulina respondió en forma errónea, hacemos referencia a ellas en las tareas 1 y 4. La tarea 1 aborda la elección de la reducción del dibujo de una casa; Paulina seleccionó aquella que no correspondía, dando como argumento "que era la más parecida a la original", mientras que en el cuestionario final eligió la casa reducida, basándose primero en su intuición y después en la medición de cada parte que la integraba. Así, obtuvo las razones entre las distintas magnitudes de la casa reducida con respecto al dibujo original, pero también volvió a mencionar en su explicación que la casa "C se parece a la casa de Antonio", agregando que "es semejante, es decir proporcional" (véanse Cuadros 1 y 2). Se puede notar que la expresión "se parece a" cambió de significado para ella entre la aplicación del cuestionario inicial y la del final, pues mostró una comprensión del término proporción como la relación de equivalencia entre dos razones, sin dejar de lado la parte intuitiva, que fue explotada a lo largo del programa de enseñanza. Hay otras evidencias para afirmar esto: Paulina resolvió de manera incorrecta la tarea 4 en el cuestionario inicial, pero de forma correcta en el final. Lo importante son las explicaciones que dio, las cuales se dan a conocer en los Cuadros 4 y 5.

Ahora, al señor Escalante le han pedido realizar una ampliación del siguiente dibujo original:

En la figura que aparece en el Cuadro 4 se observa que hay una parte del dibujo ampliado. Se solicitó que se amplificara de manera lineal la figura, basándose en lo que ya se tenía dibujado y haciendo hincapié en que conservara la misma forma que el diseño original

Paulina completó la figura, pero no se percató que sus lados los había amplificado al doble del diseño original, cuando debía ser al triple, como muestra la parte que se le dio dibujada.

En el Cuadro 5 Paulina muestra la equivalencia establecida entre dos razones, obtenidas a partir de la comparación de las dos magnitudes consideradas en la parte media del barco.

 

DURANTE LA ENSEÑANZA

Con el propósito de favorecer el pensamiento cualitativo de Paulina durante la enseñanza, requerimos de tareas en las que se utilizaran cantidades para ser resueltas, como actividades de comparación, que le permitieron a Paulina identificar relaciones de semejanza entre figuras en términos muy intuitivos, como "reducción" y "ampliación"; dichas nociones las trabajamos con referencia a situaciones concretas del tipo de la experiencia del dibujo a escala y la idea de la fotocopiadora.

En el paso de lo cualitativo a lo cuantitativo, Paulina generó un ordenamiento al hacer comparaciones, ya que empleó las frases "mayor que..." y "menor que...", lo cual coincide por lo señalado por Piaget (1978).

Posteriormente, usó la medida al hacer comparaciones: primero confrontó objetos entre sí, sobreponiendo una figura en otra; después aplicó un instrumento de medida. De acuerdo con Freudenthal (1983), los recursos desplegados por Paulina a este nivel se llaman comparadores.

Luego, Paulina estableció relaciones entre magnitudes, trabajó en el campo de los números naturales y también usó expresiones fraccionarias, incursionando de manera elemental en el campo de los racionales. Además, llegó a designar a la razón como la relación entre dos magnitudes y a la proporción como la relación de equivalencia entre dos razones, lo que concuerda con las definiciones dadas por Hart (1988).

La Tabla 2 presenta los modelos de enseñanza que utilizamos y sus propósitos.

A continuación, describiremos la manera en que fue trabajado el modelo de Blanca Nieves y los siete enanos con los estudiantes de sexto grado de primaria.

 

Modelo 2. El mundo de Blanca Nieves y los siete enanos

Se utilizó el cuento de la literatura clásica "Blanca Nieves y los siete enanos" durante siete sesiones. El modelo permitió ser trabajado a la luz de diferentes nociones; una de ellas, la de reducción, se apoyó en la experiencia del dibujo a escala y de la fotocopiadora, para lo cual se solicitó a los estudiantes que compararan la cama de Blanca Nieves con la de los enanos, con lo que producirían argumentos de carácter cualitativo. Se trató la noción de reducción a través de tres vías: escrita, oral y con el empleo del dibujo.

Posteriormente, el modelo fue utilizado al abordar la noción de ampliación, que también se basó en la idea de la fotocopiadora y del dibujo a escala. En este caso, se empleó otro mobiliario de la casa de los enanos (la mesa) y los alumnos debían seleccionar entre cuatro opciones la mesa que correspondía a Blanca Nieves, con lo que también generarían argumentos de carácter cualitativo.

En las siguientes sesiones, el modelo permitió que el estudiante verificara la reducción y la ampliación de las figuras con algún instrumento de medida para hacer comparaciones de naturaleza cuantitativa. Fue introducida la tabla como un recurso para organizar datos. Se emplearon las frases "cuántas veces cabe..." o "qué parte representa de..." al hacer referencia a la mitad y al doble de una magnitud.

 

• Planeación de las dos primeras sesiones, usando el modelo 2

Propósito: Abordar la noción de reducción. Trabajo del estudiante

– Observar el dibujo de la cama de Blanca Nieves y elegir, de 8 camas pequeñas, la(s) que correspondan a los enanos.

– Observar las camas y elegir aquella que sea la reducida a la de Blanca Nieves (reducción vista desde la idea de la fotocopiadora o la del dibujo a escala).

– Responder algunas preguntas en forma oral y escrita.

Dinámica del trabajo

Grupal–colectiva–individual.

Intervención en lo grupal

En principio, se solicita al grupo que recuerde el cuento de Blanca Nieves; entre todos los alumnos se reconstruye la historia.

Una vez que se llegue a la parte en que Blanca Nieves limpió la cabaña de los enanos y se sintió cansada, por lo cual recostó en la cama de los enanos, se pregunta si cabía en una de las camitas. Se continúa diciendo que los enanos le construyeron una cama a Blanca Nieves y se les muestra el dibujo.

Cada equipo saca el contenido del sobre, donde encontrarán dibujos de 8 camas pequeñas y una grande. Se les pide que busquen y elijan, entre esas camas, la que corresponda a la de los enanos. Se formulan varias preguntas: ¿cómo será la cama de los enanos?, ¿qué entienden por reducción de una figura? Esta última se hace porque se busca una cama reducida a la de Blanca Nieves.

Interesa saber la idea que tienen los alumnos sobre la reducción de una figura y las expresiones verbales que emplean al referirse a ella, así como a la forma y tamaño, ya que en la primera sesión, en los hechos, había una conjunción de forma y tamaño, no así en lo verbal. Cada equipo elige la cama de los enanos y se cuestiona el porqué de esa elección.

Intervención en lo colectivo

Se solicita a cada equipo que muestre la cama elegida y que den argumentos sobre su elección. Si hay discrepancias entre los equipos, se piden más argumentos, de tal forma que cada equipo esté convencido de la elección que hizo y no dude. Si llegase a haber un momento en que no se vea avance en los estudiantes, se intervendría con nuevas preguntas hasta que todos reconozcan cuál es la cama reducida.

Intervención en lo individual

Los alumnos darán respuesta a algunas preguntas que se han formulado colectivamente, pero por escrito. La retroalimentación se lleva a cabo en el momento colectivo:

– Comparando diversos resultados.

– Revisando las situaciones críticas.

• Planeación de las dos siguientes sesiones

Propósito: Abordar la noción de ampliación.

Trabajo del estudiante

– Observar el dibujo de la mesa de los enanos y seleccionar, entre cuatro mesas grandes, la que corresponda a la de Blanca Nieves.

– Observar las mesas y elegir aquella que corresponda a la amplificada, que es la de Blanca Nieves (ampliación vista desde la idea de la fotocopiadora o la del dibujo a escala).

– Responder algunas preguntas en forma oral y escrita.

Dinámica del trabajo

Grupal–colectiva–individual.

Intervención en lo grupal

Cada equipo revisa el contenido del sobre, donde se encuentran dibujos de cuatro mesas grandes y una pequeña. Se les pide que busquen y elijan la que corresponda a la de Blanca Nieves.

Se formulan varias preguntas: ¿cómo crees que es la mesa de Blanca Nieves?, ¿cómo se busca una mesa que sea la ampliación de la mesa de los enanos?, ¿Qué entienden por ampliación de una figura?

Interesa saber la idea que tienen los alumnos sobre la ampliación de una figura y las expresiones verbales que emplean al referirse a tal noción, así como a la forma y el tamaño. Cada equipo trabaja en la elección de la mesa de Blanca Nieves y se procede a preguntar el porqué fue seleccionada.

Intervención en lo colectivo

Se solicita a cada equipo que muestre la mesa elegida y que den argumentos sobre su elección. Si hay discrepancias entre los equipos, se piden más justificaciones de las posiblemente dadas, de tal forma que cada equipo esté convencido de la elección que hizo y no dude. Si hubiera un momento en que no se viera avance en los estudiantes, se intervendría con nuevas preguntas hasta que todos reconozcan cuál es la mesa amplificada.

Intervención en lo individual

Los alumnos responderán por escrito algunas preguntas que se han formulado colectivamente. La retroalimentación se lleva a cabo en el momento colectivo:

–Comparando las respuestas de los estudiantes.

–Revisando distintas situaciones que emergieran.

• Planeación de las tres últimas sesiones

Propósito: Hacer comparaciones de carácter cuantitativo.

Trabajo del estudiante

– Verificar que la cama elegida para los enanos es la correcta, haciendo uso de algún instrumento de medida.

– Medir los largos de las camas de los enanos y de Blanca Nieves y compararlos.

– Indicar si es el doble del largo de una cama con respecto al largo de la otra cama.

– Medir otras dimensiones (alto y ancho del respaldo) y hacer comparaciones.

– Responder algunas preguntas en forma oral y escrita.

– Escribir las relaciones entre las medidas obtenidas como una fracción.

Dinámica del trabajo

Grupal–individual–colectivo.

Intervención en lo grupal

Se cuestiona al grupo si hay otra forma diferente a la que se usó para comprobar que la cama elegida es la de los enanos.

Realizan mediciones, ya sea con una regla o poniendo la cama elegida de los enanos sobre la de Blanca Nieves.

Los estudiantes deben completar una tabla con los datos que se soliciten. Asimismo, responden a preguntas que se les formulen en forma oral, como: ¿si comparas los largos de las dos camas qué puedes decir?, ¿cuántas veces cabe el largo de una en el largo de la otra ?

Se hacen las mismas preguntas para el alto y el ancho de los respaldos de las dos camas.

Intervención en lo individual

Los alumnos contestan por escrito algunas preguntas que se han formulado colectivamente.

Intervención en lo colectivo

Se solicita a diferentes alumnos que lean y respondan las preguntas en voz alta. Se comparan las respuestas y donde haya discrepancias hay una discusión. La retroalimentación se lleva a cabo en el momento colectivo:

–Comparando las diferentes justificaciones dadas por los estudiantes.

–Llegando a un acuerdo que satisfaga a todo el grupo.

Intervención en la segunda parte individual del trabajo

Se solicita a los niños que dibujen una cama más grande y una más pequeña de la de Blanca Nieves y los enanos, respectivamente. Una cama será la ampliación de las dadas; la otra, una reducción de la de los enanos. Se les formulan preguntas en torno a qué medidas les dieron a las dimensiones de la cama ampliada y reducida, respectivamente, y cómo las obtuvieron.

Los alumnos completan una tabla con los datos solicitados y realizan comparaciones. Establecen relaciones entre las dimensiones de una cama con respecto a las dimensiones de la otra, utilizando la notación de fracción.

En lo anterior se expuso la forma de trabajo con el modelo de Blanca Nieves para dar una idea de cómo eran abordados los modelos, cuyo objetivo era hacer el tránsito del pensamiento proporcional cualitativo al cuantitativo.

Paulina, al finalizar las sesiones de trabajo, mostró una estrecha relación entre su pensamiento cualitativo y cuantitativo, lo cual implicó el sentido que le dio a su trabajo en el terreno numérico, circunstancia que al principio no se veía reflejada. Al término de la experiencia de enseñanza y con la aplicación del cuestionario final se enriquecieron en Paulina sus significados y sus procesos de cuantificación. A nivel de la designación, llegó a emplear un lenguaje técnico; de igual manera, alcanzó la generalización, mediante la cual se vieron favorecidas nuevas situaciones en torno a la razón y la proporción.

 

EN LAS ENTREVISTAS

Se aplicaron tres entrevistas a Paulina, una por semana, tras la realización de la enseñanza y la aplicación del cuestionario final. Las entrevistas –cuyo propósito central fue evaluar el programa de enseñanza– se integraron con tareas nuevas que tenían metas en común con el programa didáctico y el cuestionario; además, permitieron una retroalimentación en Paulina.

Con las tareas iniciales que propusimos en las entrevistas, revisamos la manera como Paulina mantuvo lo cualitativo a la luz de haber trabajado lo cuantitativo, el peso que tuvo la imagen visual y lo perceptual en la resolución de las tareas. Luego, con las entrevistas indagamos en el manejo que Paulina dio a las tablas, el reconocimiento en ellas de las razones y su expresión como fracciones; asimismo, pudimos observar cuándo empleó razones internas y externas, el pasaje de un sistema simbólico a otro y si planteó una situación que la condujera a utilizar una proporción para resolverla.

A continuación, presentamos el desarrollo y análisis de la primera entrevista, que tuvo relación con el modelo de enseñanza de Blanca Nieves y los siete enanos.

Paulina midió tanto el largo como el ancho del ropero de Blanca Nieves, así como los largos y anchos de los cuatro dibujos mostrados para que eligiera la reducción solicitada. Una vez hecho esto, obtuvo las razones en las que se encontraban las magnitudes de algunas partes de la reducción con las correspondientes al ropero original. Un segmento del diálogo que se sostuvo con ella en la entrevista se muestra a continuación:

– E: ¿En qué te basaste para elegir el ropero de los enanos?

– P: Medí y el ropero B es proporcional al de Blanca Nieves porque todas sus razones son equivalentes (señala lo que había escrito: 12/8=6/4=3/2).

– E: ¿Me puedes decir cómo obtuviste las razones?

– P: Comparando las medidas del ropero de Blanca Nieves con el ropero de los enanos. Los numeradores de cada fracción son los que miden distintas partes del ropero de Blanca Nieves; por ejemplo, el 12 es lo que mide de alto; 8 es lo que mide su base; 3 es lo que mide el largo de una ventanita (indica uno de los dibujos que representa un adorno del ropero); 1.5 es el ancho de esa ventanita. Los denominadores de las fracciones son las medidas de esas partes, pero del ropero de los enanos (las medidas mencionadas por Paulina están dadas en centímetros).

Paulina se basó en la medición para establecer vínculos y llegar de este modo a la determinación de razones. También en esta parte de la entrevista se hizo notorio el apoyo que tuvo en lo perceptual, ya que dijo: "El ropero A es larguísimo, el C es muy ancho y el D es muy chiquito. Aunque medí, también me fijé que esos tres no se ven proporcionales al de Blanca Nieves".

Asimismo, Paulina mostró un manejo de lo conceptual cargado de sentido, al identificar a la razón como una relación y a la proporción como la relación de equivalencia entre razones (Hart, 1988), y no abandonó el aspecto cualitativo, ya que usó categorías verbales y el sentido común para constatar que el ropero elegido era el correcto. Al respecto, escribió lo que se indica el Cuadro 8.

En la segunda parte de la entrevista, se pidió hacer un dibujo con las condiciones que se señalan:

2. Haz el dibujo de un ropero que sea proporcional al de Blanca Nieves, pero más grande.

¿Cómo obtuviste las medidas anteriores? ______________________.

Paulina tomó las medidas de cada parte que conformaba el ropero de Blanca Nieves y las duplicó para hacer el dibujo solicitado (Cuadro 9). Después de que Paulina leyó en voz alta las indicaciones, la entrevistadora le formuló algunas preguntas:

– E: ¿Cómo lo vas a dibujar?

– P: Podría ser que el ropero de Blanca Nieves sería la mitad de éste (señala la hoja donde iba a dibujarlo), la mitad del grande y el grande el doble del de Blanca Nieves.

– E: ¿El doble en cuanto a área o a dimensiones lineales?

– P: En cuanto a las dimensiones lineales.

– E: Entonces, ¿cuánto van a medir las dimensiones del ropero que vas a dibujar?

– P: Si la base del ropero de Blanca Nieves es 8 centímetros, aquí lo podemos hacer de 16 centímetros (midiendo con su regla traza el segmento de la base). Si esto mide 12 centímetros (refiriéndose a la altura del ropero de Blanca Nieves), sería 24 centímetros (traza el segmento utilizando su regla).

Paulina midió cada parte del ropero de Blanca Nieves y duplicó las medidas obtenidas, empleando el algoritmo de la multiplicación hasta terminar de hacer el dibujo, como se muestra a continuación. La acción de duplicar implica que Paulina tenía fluidez en el manejo de los operadores multiplicativos; en este caso, el (× 2).

Paulina no hizo operaciones por escrito, sino mentalmente, y en voz alta duplicó los valores de las magnitudes, lo cual indica su habilidad en el cálculo aritmético y en el uso del operador natural (× 2). Lo que dijo Paulina en la entrevista, respecto a que las dimensiones lineales del ropero de Blanca Nieves son la mitad del grande o que las dimensiones lineales de éste corresponden al doble de las de Blanca Nieves, evidenció una claridad en el manejo de la reciprocidad, lo cual coincide con lo que señala Piaget (1978a y b) en cuanto a tal modalidad de reversibilidad. El dominio de la reciprocidad muestra que Paulina tiene un pensamiento con mayor grado de abstracción.

Enseguida, Paulina dibujó un ropero más pequeño, pero proporcional al de los enanos, como se demandó en la entrevista:

3. Ahora haz un ropero que sea proporcional al de los enanos, pero que sea más pequeño.

¿Cómo obtuviste las medidas anteriores? ________________.

De las magnitudes obtenidas del ropero de los enanos, Paulina sacó la mitad de cada una empleando el algoritmo de la división, aunque no escribió ninguna operación, ya que las hizo mentalmente. Al respecto, escribió lo siguiente:

El dibujo que hizo se presenta a continuación:

Se notó que Paulina tiene claras las nociones tanto de reducción como de ampliación, vistas desde la idea del dibujo a escala y de la fotocopiadora. Además, al usar el operador natural (× 2) en la ampliación y el algoritmo de la división para la reducción, ocupó implícitamente el operador fraccional (× 1/2). Esto se toma de Dienes (1971 a y b, 1972) cuando los niños están multiplicando por uno y dividiendo entre dos. Más tarde aparece en lo formulado por Kieren (1985).

El hecho de que Paulina, por un lado, duplicara todas las magnitudes para hacer la amplificación y, por otro, obtuviera la mitad de las mismas para hacer la reducción, reflejó el significado adecuado del término proporción. Además, el señalamiento que hizo respecto a que una figura reducida o amplificada conserva la misma forma, sólo que cambia de tamaño, indicó que, aunque trabajó muy bien con algoritmos, no quedó opacado su pensamiento cualitativo.

Posteriormente, como parte de esta primera entrevista, se le pidió a Paulina lo que a continuación se presenta:

4. Completa la siguiente tabla:

Escribe las razones en las que se encuentran las medidas de los altos con respecto a los anchos de los roperos que tú quieras comparar ________________.

Compara las razones que escribiste y di cómo son entre sí ________________.

Paulina primero llenó la tabla con los datos que obtuvo de las medidas de cada ropero y después escribió las razones externas solicitadas, estableciendo la relación entre las magnitudes que obtuvo de la misma tabla. Al respecto, dijo:

– P: El ropero A es de veinticuatro dieciseisavos (escribió 24/16), el de Blanca Nieves es de doce octavos (escribió 12/8), lo que corresponde a medidas establecidas en centímetros.

– E: ¿Qué es lo que estás escribiendo?

– P: Las razones.

Continuó diciendo:

– P: El de los enanos es de seis cuartos (escribió 6/4) y el del ropero D es de tres medios (escribió 3/2), lo que también corresponde a medidas establecidas en centímetros.

– E: ¿Cómo obtuviste las razones?

– P: Leyéndolas de la tabla.

– E: ¿Qué leíste?

– P: Como me piden la razón del alto con respecto al ancho de los roperos que yo quisiera decir, primero leí cuánto mide el alto del ropero A y después su ancho, es decir, la razón es veinticuatro dieciseisavos y así para los demás.

De acuerdo con Freudenthal (1983), es posible interpretar que Paulina está adentrándose en un dominio incipiente de los racionales, ya que presenta un buen punto de partida para desarrollar el manejo de estos números; aunque no es sistemático, lo será más adelante. También logró relacionar ambas columnas de la tabla, lo cual indica que entendió a la razón como una relación entre magnitudes, como la define Hart (1988). Por otra parte, al comparar las razones entre sí, afirmó que son equivalentes y que los roperos son proporcionales y semejantes entre ellos.

Para determinar la equivalencia entre las razones, Paulina usó el algoritmo de la simplificación, al ir sacando mitades. Al respecto, escribió:

24/16=12/8=6/4=3/2, simplificando (lo que corresponde a medidas establecidas en centímetros).

Con el fin de saber si las razones eran equivalentes, Paulina recurrió a la división del numerador entre el denominador de cada fracción, dándose cuenta de que en todos los casos obtenía un entero y un medio. Esto implica que manejó el factor escalar como una constante, lo que coincide con lo dicho por Vergnaud (1991).

En la última parte de esta entrevista se pidió lo siguiente, que fue leído en voz alta por Paulina:

5. Ahora, escribe la razón en la que se encuentran las medidas de la altura de dos roperos y escribe la razón en que están las medidas de los anchos de esos mismos roperos que elegiste.

Compara ambas razones entre sí ¿cómo son? ________________.

Paulina eligió el ropero A y el de Blanca Nieves. Expresó como fracciones a las razones de sus largos con respecto a sus anchos; las magnitudes que relacionó las obtuvo de la tabla. Al respecto, mostramos un fragmento de esta parte de la entrevista:

– E: ¿Me puedes explicar qué es lo que vas a hacer? (Después de un momento de silencio y de que Paulina leyó en voz baja las instrucciones, dijo):

– P: Vamos a comparar entre dos roperos los largos y los anchos. Por ejemplo, aquí podría ser 24/12 y 16/8 (señala las dos columnas de tabla. Las medidas corresponden a centímetros).

Paulina tuvo cierta dificultad para identificar que las dos razones son equivalentes, lo que se nota en la trascripción:

–P: Porque 24 no es el doble de 16 ni 12 es el doble de 8 (señala tanto los numeradores como los denominadores de cada fracción). Para que sean equivalentes debo de simplificar; por ejemplo, 24/6 es equivalente a 12 /3 porque dividí arriba y abajo entre 2.

Finalmente, reconoció la relación de equivalencia entre ellas:

– P: 24 centímetros es el largo del ropero A, y 12 centímetros es lo que mide su base, mientras que 16 centímetros es el largo del ropero de Blanca Nieves y 8 centímetros es su ancho (señala los dibujos de los roperos). Si el largo del ropero A es el doble de su ancho (indica las magnitudes tanto en la figura como en la fracción), es decir, si 24 es el doble de 12 y 16 es el doble de 8 (señala en la tabla) entonces son equivalentes, pues están en la misma razón, es decir, al doble.

Al principio, se observó en Paulina un arraigo en el algoritmo referido a que dos fracciones son equivalentes si tanto el numerador como el denominador son multiplicados o divididos por un mismo número; es decir, tiene un buen manejo de los operadores multiplicativos. Sin embargo, al apoyarse en el dibujo, se dio cuenta que las magnitudes de los largos de los roperos con respecto a las de sus anchos eran el doble y que este consiste en otro procedimiento para determinar la equivalencia entre dos razones. Lo visual cobró mucha fuerza para que Paulina saliera del problema.

Esta situación mostró cómo Paulina pudo transitar de un registro a otro (del dibujo al numérico) y la conexión de ambos le permitió no sólo llegar a una respuesta correcta, sino dejar asentado lo visto durante las sesiones del programa de enseñanza.

 

CONCLUSIONES

Paulina mostró un fuerte avance en torno a dos aspectos importantes: el desarrollo de su pensamiento cualitativo sobre la razón y la proporción y la carga de sentido que le dio al empleo de algoritmos. Además, evidenció en la resolución de las distintas tareas la fuerza que cobró el dato perceptual y el apoyo en su experiencia, lo cual implicó el desarrollo alcanzado en el terreno cualitativo de la proporcionalidad.

El trabajo algorítmico nos permitió explorar el reconocimiento tácito de los operadores en los que Paulina estaba pensando, tanto naturales como fraccionarios. Estos últimos los aplicó en forma implícita, al multiplicar un valor por un número, como primer paso, luego al dividir lo obtenido entre otro número, o dividir primero y multiplicar después. Tal procedimiento remite a Dienes (1971 a y b, 1972) y a Kieren (1985).

A nivel de la construcción de significados, éstos fueron enriquecidos junto con los procesos de significación; en lo tocante a su designación, Paulina llegó a usar los términos matemáticos correspondientes. Finalmente, Paulina llegó a construir los conceptos de razón y proporción, lo que se notó por su aplicabilidad en distintos ámbitos y por el uso de los distintos modos de representación.

 

REFERENCIAS BIBLIOGRÁFICAS

Benveniste, E. (1971), Problemas de Lingüística. General. México: Siglo XXI. 91–100.        [ Links ]

Cohen, L. & Manion, L. (1980). Research Methods in Education. London, UK: Croom Helm.        [ Links ]

Dienes, Z. P. (1972). Estados y operadores. Operadores multiplicativos. Barcelona, España: Teide.        [ Links ]

Dienes, Z. P. (1971a). Cómo utilizar los bloques multibase. Barcelona, España: Teide.        [ Links ]

Dienes, Z. P. (1971b). Estados y operadores. Operadores aditivos. Barcelona, España: Teide.        [ Links ]

Figueras, O.; Filloy, E. y Valdemoros M. (1987). Some difficulties which obscure the appropriation of the fraction concept. In Proceedings of the 11th Conference International Group for the Psychology of Mathematics Education (volume 1, pp. 366–372). Montreal, Canada.        [ Links ]

Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrechet, Holland: Reidel Publishing Company.        [ Links ]

Hart, K. (1988). Ratio and proportion. In J. Hiebert & M. Behr (Eds.), Concepts and operations in the Middle Grades 2 (pp. 198–219). Reston, Virginia, USA: National Council of Teachers of Mathematics.        [ Links ]

Kieren, T., Nelson, D. & Smith, G. (1985). Graphical algorithms in partitioning tasks. The Journal of Mathematical Behavior 4, 25–36.        [ Links ]

Lesh, R. & Doerr, H. M. (2001). Foundations of a models and modeling perspective on mathematics teaching and learning. In H. M. Doerr & R. Lesh (Eds.), Beyond constructivism: A models and modeling perspective. Mahwah, NJ, USA: Lawrence Erlbaum Associates.        [ Links ]

Piaget, J. e Inhelder, B. (1978). Las operaciones intelectuales y su desarrollo. En J. Delval (Ed.), Lecturas en Psicología del niño (volumen 1, pp. 70–119). Madrid, España: Alianza Editorial.        [ Links ]

Piaget, J. (1978). Psicología del niño. Madrid, España: Morata.        [ Links ]

Piaget, J. e Inhelder, B. (1972). De la lógica del niño a la lógica del adolescente. Buenos Aires, Argentina: Paidós.        [ Links ]

Ruiz, E. F. (2002). Estudio de estrategias de solución y una propuesta para la enseñanza de razón y proporción. Tesis de doctorado no publicada, Cinvestav, México.        [ Links ]

Ruiz, E. F. (2001). Una propuesta de enseñanza de razón y proporción trabajada con estudiantes de educación primaria. Función Continua: Experiencias de Enseñanza de Matemática, 11, 5–19.        [ Links ]

Ruiz, E. F. (2000). Study of solving strategies and a proposal for the teaching of ratio and proportion. In María L. Fernández (Ed.), Proceedings of the twenty–second Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 395–396). Tucson, Arizona, USA.        [ Links ]

Ruiz, E. F. y Valdemoros, M. (2005). The relationship between the use of the representation and the development of ratio and proportion concepts: Nuria's case. Proceedings of the 27th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. Roanoke, Virginia: USA.        [ Links ]

Ruiz, E. F. y Valdemoros, M. (2002). Concepts of ratio and proportion in basic level students: case study. In Proceedings of the twenty–fourth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 1651–1657). Athens, Georgia, USA.        [ Links ]

Ruiz, E. y Valdemoros, M. (2001). A teaching proposal about ratio and proportion worked with students of elementary school. In Proceedings of the twenty–third Annual Meeting of PME–NA (volume 1, pp. 291–299). Snowbird, Utha, USA.        [ Links ]

Streefland, L. (1984a). Search for the roots of ratio: Some trought on the long term learning process (part I). Educational Studies in Mathematics 15 (3), 327–348.        [ Links ]

Streefland, L. (1984b). Search for the roots of ratio: Some trought on the long term learning process (part II). Educational Studies in Mathematics, 16 (1), 75–94.        [ Links ]

Streefland, L. (1993). The design of a mathematics course. A theoretical reflection. Educational Studies in Mathematics, 25 (1 –2), 109–135.        [ Links ]

Van den Brink, J & Streefland, L. (1979). Young children (6–8)– ratio and proportion. Educational Studies in Mathematics, 10, (4), 403–420.        [ Links ]

Valdemoros, M. (1998). La constancia de la unidad en la suma de fracciones: estudio de caso. En F. Hitt (Ed.), Investigaciones en Matemática Educativa II (pp. 465–481). México: Iberoamérica.        [ Links ]

Woods, P. (1989). La escuela por dentro. Barcelona, España: Paidós.        [ Links ]

 

Notas

³ El significado es una " entrada de diccionario" y "una categoría semántica universal", dice Benveniste (1971). El sentido, asegura, es un contenido semántico que se asocia a construcciones particulares del lenguaje, no conforma categorías universales y suele estar muy en relación con los modos específicos de articulación de los mismos. Además, cabe destacar que no hay una secuencia cronológica o de precedencia en el desarrollo, entre sentido y significado; son distintos componentes semánticos que se complementan.

⁴ Ver Figueras, Filloy y Valdemoros (1987). Un modelo de enseñanza engloba significados, tanto en el lenguaje técnico como en el lenguaje cotidiano, tratamientos didácticos, modos específicos de representación y las relaciones que existan entre ellos.