Introducción
La electricidad es uno de los pilares del desarrollo industrial y del bienestar de los individuos. La reforma energética de 2013 en México tiene entre sus fines el acceso incluyente a la energía así como imprimir dinamismo y competitividad en la economía. Varias razones motivan dichos fines, aunque de acuerdo a la Comisión Federal de Electricidad (CFE) la cobertura actual en México es de 98%, la inconformidad de la población ha aumentado debido a los altos costos de la energía eléctrica.
Por otra parte, las tarifas de la CFE no son competitivas a nivel internacional, aún con subsidio, son en promedio 25% superiores a las de Estados Unidos de América, con diferencias aún mayores en segmentos claves de la industria y el comercio; estos precios representan un freno a la economía mexicana.
Respecto a las tarifas residenciales del país, las cuales están subsidiadas, son 24% menores al equivalente en Estados Unidos, esto se logra con un alto costo sobre las finanzas públicas: el monto del subsidio asignado de 57 millones de pesos en el primer semestre del año 2013 fue cercano a 0,75% del Producto Interno Bruto en el mismo periodo. Con base en lo anterior, la reforma energética tiene entre sus objetivos reducir los costos de producción y las pérdidas técnicas, y no técnicas, a fin de disminuir las tarifas eléctricas y prevenir la pérdida de patrimonio y descapitalización de la CFE (Gobierno de la República, 2013).
En México, la demanda agregada de energía eléctrica asciende a 206,129 GWh, ésta se conforma de los sectores industrial, comercial, residencial, servicios y bombeo agrícola (cuadro 1). Históricamente, el sector que presenta el mayor consumo es el industrial, con 120,473 GWh en el año 2013, lo que representa 58,4% de la demanda total. Por su parte, el sector residencial se ha mantenido a través de los años en el segundo lugar como consumidor de energía eléctrica, con 52,369 GWh en el año 2013, representando 25,4% de la demanda total (Prospectiva del Sector Eléctrico de 2013). Durante la década 2002-2012, el sector residencial tuvo un crecimiento anual de 3,1% debido a la incorporación de nuevos usuarios a la región central del país, así como la regularización y la reducción de pérdidas en esta zona (CESOP, 2013).
Cuadro 1 Porcentajes de usuarios y ventas de electricidad por sector en México, 2013
| Tipo de usuario | Porcentaje de usuarios | Porcentaje de ventas |
|---|---|---|
| Residencial | 88,52 % | 25,41 % |
| Agrícola | 0,34 % | 4,99 % |
| Industrial | 0,76 % | 58,45 % |
| Comercial | 9,87 % | 6,67 % |
| Servicios | 0,51 % | 4,49 % |
Fuente: elaboración propia con datos del Sistema de Información Energética (SIE, 2013).
Si bien el sector industrial tiene una gran participación en la demanda agregada de energía eléctrica, sólo representa, para el 2013, alrededor de 0,76% de los 37 millones de usuarios del servicio provisto por la CFE, mientras que el sector residencial constituye 88,5% de los usuarios (SIE, 2013).
La concentración de usuarios que presenta el sector residencial lo convierte en uno de los sectores con mayor sensibilidad a la implementación de nuevas reformas o políticas que podrían generar cambios en uno o varios de los determinantes de su demanda. Es precisamente en el sector residencial donde existe una escasez de estudios económicos a propósito de la demanda de energía eléctrica a nivel nacional y estatal, particularmente en aquellos estados donde cambios en el precio u otro de sus determinantes tendrían un mayor impacto en el corto o largo plazo, dadas sus condiciones socioeconómicas (Maqueda-Zamora y Sánchez-Viveros, 2011). Según datos del SIE, en 2013 el Estado de México fue el estado con mayor consumo residencial y con mayor número de usuarios (cuadro 2).
Cuadro 2 Principales estados consumidores de energía eléctrica en el sector residencial, 2013
| Estado | Precio medio de la electricidad /1 |
Consumo /2 | Número de usuarios /3 |
|---|---|---|---|
| Estado de México | 132,820 | 4432,309 | 3616,997122 |
| Nuevo León | 132,820 | 4224,859 | 1508,583478 |
| Distrito Federal | 132,820 | 3634,928 | 2606,758379 |
| Jalisco | 132,820 | 3061,551 | 2331,934646 |
/1 ¢/kWh, /2 GWh, /2 (GWh), /3 Miles de usuarios
Fuente: elaboración propia con datos del Sistema de Información Energética (SIE, 2013).
La demanda de electricidad por el sector residencial en el Estado de México1 es influenciada por el número y nivel socioeconómicos de los usuarios, estacionalidad (Maqueda-Zamora y Sánchez-Viveros, 2011) y precio de la electricidad (Centro de Estudios de las Finanzas Públicas, 2005). Un mayor nivel de ingreso está relacionado con un mayor consumo y demanda de energía eléctrica (Maqueda-Zamora y Sánchez-Viveros, 2011).
Con respecto a la estacionalidad, la mayor demanda de electricidad en entidades como el Estado de México se presenta en enero y julio; donde la energía eléctrica es utilizada en gran medida para carga de iluminación y uso de electrodomésticos (refrigeradores, planchas, lavatrastos, lavadoras, bombas de agua, entre otros).
La demanda de electricidad también depende de los niveles tarifarios determinados por la Secretaria de Hacienda y Crédito Público (SHCP). Dicha tarifa se ajusta de manera mensual; durante el periodo 2002 a 2011 ha presentado una tendencia estable (SENER, 2013). Con respecto a la sustitución entre el gas y electricidad en el sector residencial, ésta se da básicamente entre los electrodomésticos y, en el caso de los estados ubicados en el centro del país, no es claro si se presenta una sustitución entre el gas y electricidad (Valenzuela-Parcero, 2011).
La relación entre el precio del servicio de agua y el consumo residencial de electricidad se explica a través del uso de electrodomésticos, donde un incremento en el precio del líquido conlleva una disminución en su demanda, y por consiguiente, una disminución en el consumo de energía eléctrica (Gómez-Ugalde et al., 2012). Con respecto a la relación entre el precio de los bienes durables y el precio de la energía eléctrica, Marshall (2010) señala que cuando el precio de los electrodomésticos se incrementa su demanda disminuye, y por consiguiente, su tasa de reemplazo. Lo anterior resulta en un decremento en el consumo de la energía eléctrica. Si no son reemplazados, directamente se traduce en una disminución de la energía eléctrica. Alternativamente, si son reemplazados, los equipos usan tecnología más eficiente o son de menor capacidad de consumo lo que resulta en un menor consumo de electricidad.
La demanda de energía eléctrica en el sector residencial ha sido analizada desde un punto de vista económico por una gran cantidad de autores en distintos países y en menor medida en México. A nivel internacional, autores como Castro (2000), Rosal-Fernández (1999), Dergiades y Tsoulfidis (2008) y Silk y Joutz (1997) han utilizado el método de cointegración de Johansen con objeto de probar la existencia de cointegración en variables integradas de orden uno I(1) e integradas de orden cero I(0) y así determinar la técnica de regresión a utilizar para estimar la demanda agregada de electricidad. En dichos estudios las elasticidades precio e ingreso encontradas han sido acordes a la teoría de la demanda. Benavente et al. (2005) y Espinoza-Acuña et al. (2013), aunque obtienen estimaciones acordes a la teoría de la demanda, a diferencia de los autores antes citados, asumen que las series económicas son estacionarias y aplican la técnica de mínimos cuadrados ordinarios.
A nivel nacional, Guzmán-Soria et al. (2011) y Saenz de Miera-Berglind (2004), asumiendo estacionariedad en las series económicas incluidas en sus respectivos modelos, utilizan la técnica de mínimos cuadrados ordinarios para estimar las elasticidades precio e ingreso de la demanda de energía eléctrica. Morales-Ramírez et al. (2012), por su parte, utilizan la técnica de cointegración de Engel-Granger, a partir de una función de demanda estilo Cobb-Douglas.
Con base en la revisión anterior se destaca lo siguiente. A pesar de que las elasticidades precio e ingreso reportadas en los estudios citados son acordes con la teoría económica, lo cual les otorga sustento y validez, éstas difieren entre sí. De acuerdo al meta-análisis realizado por Espey y Espey (2004) esto se debe principalmente a diferencias en las condiciones socioeconómicas de las áreas o países donde se realizaron dichos estudios, así como al tipo de información y técnica econométrica utilizada en las estimaciones. Adicionalmente, la mayoría de dichos estudios no son vigentes y en algunos casos las metodologías de regresión no toman en cuenta si cada una de las series económicas sigue un proceso estocástico estacionario, o alternativamente no evalúan si la combinación lineal de las mismas resulta ser estacionaria con base en el criterio de Engle y Granger (1987).
De esta manera, y ante la coyuntura de una nueva reforma energética en el país, la cual pretende disminuir el precio de la electricidad en todos sus sectores (Gobierno de la República, 2013), se justifica realizar un estudio de tipo económico en particular en el Estado de México, el cual estime un modelo de demanda residencial de energía eléctrica y determine sus correspondientes elasticidades de corto y largo plazo, con el fin de conocer con sustentos estadísticos los posibles efectos a través del tiempo en la demanda misma ante variaciones en el precio, el ingreso, la población y otros bienes relacionados como el agua y el gas LP; por consiguiente la pregunta de investigación a contestar en este estudio es la siguiente: ¿Qué tipo de efecto puede tener una disminución del precio medio de la energía eléctrica sobre su consumo en el sector residencial del Estado de México y que implicaciones económicas tendría para la población?
El presente estudio pretende brindar un antecedente que considere el comportamiento y el equilibrio que guardan a través del tiempo los distintos determinantes de la demanda de energía eléctrica en el sector residencial, esto con el fin de estimar la magnitud de los efectos que pueden tener en el futuro políticas enfocadas a desarrollar un proceso más eficiente de la generación y consumo de esta energía en los distintos sectores del país.
Esta investigación se encuentra integrada en cinco secciones: primero se presenta una sección de Materiales y métodos; posteriormente se incluye una sección con el Marco teórico. Se continúa con la sección de Resultados, seguido de una de Discusión de resultados; el artículo finaliza con las Conclusiones.
1. Materiales y métodos
De acuerdo a Castro (2000) y Morales-Ramírez et al. (2012), la demanda residencial de energía eléctrica en el Estado de México se puede representar aproximadamente por un modelo estilo Cobb-Douglas y posteriormente adoptar una forma funcional lineal logarítmica, ésta última permite obtener directamente las elasticidades de las distintas variables. Para establecer un modelo de la demanda residencial de energía eléctrica en el Estado de México se utilizaron series de tiempo mensuales de enero 2002 a febrero 2014, así como variables dicotómicas con el objeto de modelar el efecto estacional en la demanda de electricidad del Estado de México.
El modelo del que se parte es el siguiente:
En el cuadro 3 se describen las variables del modelo.
Cuadro 3 Descripción de las variables y su fuente de información
| Variable | Fuente |
|---|---|
| Qt (MWh) Consumo residencial de electricidad en el Estado de México | Sistema de Información Energética (SIE, 2013a) que provee la Secretaria de Energía (SENER, 2013) y de la Comisión Federal de Electricidad (CFE, 2013). |
| Y t ($/persona a precios 2003) Ingreso proxy, PIB per cápita mensual aproximado para el Estado de México | Elizondo (2012) y Gómez-Ugalde et al. (2012) |
| Pe t (cts/kWH) Precio medio real de la electricidad en el Estado de México | Sistema de Información Energética (SIE, 2013b) |
| Pa t ($/m3) Precio medio real del servicio agua en el Estado de México | Código financiero del Estado de México Sección quinta (Gobierno del Estado de México, 1998) |
| Pg t ($/kg) Precio medio real del gas L.P en el Estado de México | Sistema de Información Energética (SIE, 2013c) |
| U t Número de usuarios del servicio eléctrico en el sector residencial del Estado de México | Sistema de Información Energética (SIE, 2013d) |
| IPBD t Índice de bienes durables en México | El índice de precios de bienes durables aplica para todo México y se obtuvo de las estadísticas del Instituto de Estadística, Geografía e Informática (Inegi, 2014) |
| D it Variable dicotómica para el mes i | Se aplicó el valor de 1 para el mes correspondiente a ser modelado y 0 en los restantes. |
Fuente: elaboración propia.
2. Marco teórico: método de cointegración multivariado
Cuando las series económicas son no estacionarias, las técnicas convencionales de regresión son inadecuadas. Sin embargo si alguna combinación lineal de las series llega a ser estacionaria, las series no estacionarias pueden estar cointegradas, esto quiere decir que tienden a un equilibrio en el largo plazo. Para probar cointegración entre series de tiempo el procedimiento más adecuado, si bien es complejo, es el procedimiento de Johansen (1988).
Este procedimiento es aplicable a sistemas de ecuaciones, está basado en modelos VAR (vectores autoregresivos) (Sims, 1980), para su uso se requieren más de 100 datos y permite probar la existencia de múltiples vectores de cointegración entre las variables mediante la prueba de la traza y del eigenvalor máximo. Los coeficientes de los vectores de cointegración se pueden interpretar como las elasticidades de largo plazo.
Una vez obtenido el modelo VAR se construye un modelo de vector de corrección del error (VEC), que es un modelo VAR acotado con restricciones de cointegración incluidas en su especificación. Los coeficientes de los estimadores del modelo VEC permiten analizar el equilibrio de corto y largo plazo que existe entre las variables exógenas y la variable endógena (Boef, 2000). Debido a la complejidad de la metodología y para facilitar el seguimiento del análisis de resultados a continuación se describirá brevemente la metodología.
2.1. Enfoque de cointegración de Søren Johansen
El enfoque de cointegración multivariado de Johansen (1988) es utilizado para probar la existencia de cointegración en variables integradas de orden uno I(1) e integradas de orden cero I(0). Consta de los siguientes pasos: 1. Determinar el orden de integración de cada una de las series incluidas en el modelo. 2. Especificar un vector autoregresivo (VAR) con las series que resulten integradas del orden I(1). 3. Seleccionar las variables del modelo y las transformaciones de éstas, si las hubieran. 4. Determinar el retardo óptimo del VAR con la finalidad de que los residuos sean ruido blanco. 5. Diagnosticar el VAR estimado. 6. Aplicar el procedimiento de máxima verosimilitud al vector autorregresivo para determinar el rango (r) de cointegración del sistema, utilizando para ello la prueba de la traza y la prueba del eigenvalor máximo (valor propio). 7. Estimar el modelo vector de corrección de errores.
2.1.1. Integración de las series
Para determinar el orden de integración de las series a incluir en el modelo se pueden aplicar pruebas informales como la representación gráfica de las series y los correlogramas, y pruebas estadísticas como la prueba de Box-Pierce y la de Ljung-Box (Gujarati y Porter, 2010), que analizan la correlación de las series; la de Dickey-Fuller (DF) y la de Dickey-Fuller aumentada (DFA) que prueban si el parámetro de la pendiente del modelo es uno, lo que también se interpreta como que la raíz es unitaria. En la prueba DF se utiliza un modelo autorregresivo de orden 1, AR(1). La DFA se utiliza cuando la prueba de DF no pueda corregir la correlación serial en los residuos y añade al modelo usado en DF términos de diferencias de la variable.
2.1.2. Modelo VAR
Un modelo VAR es el punto de partida del enfoque de cointegración de Johansen, su forma general es la siguiente:
donde:
Yt Es un vector (N*1) de variables endógenas integradas de orden uno I(1)
α1,..., αρ, β Son matrices de coeficientes a ser estimados
ρ Es el número de retardos incluidos en el VAR
Xt Es un vector de variables exógenas (variables de intervalo y nominal)
εt Es un vector (N*1) de términos de errores normal e independientemente distribuidos
Una vez que se han seleccionado las variables endógenas que conformarán el vector Yt y las variables que conformarán el vector de variables exógenas Xt se realizan distintas pruebas estadísticas para determinar el retardo óptimo para el modelo VAR, con la finalidad de obtener residuos que sean ruido blanco. Existen varios criterios para determinar la longitud del retardo óptimo: a) criterio de Máxima Verosimilitud (LR), b) criterio de información de Akaike (AIC), c) criterio de información de Schwarz (SC), d) criterio de información de Hannan-Quinn (HQ).
Para el diagnóstico del modelo VAR se examinan las raíces inversas del polinomio autoregresivo con el fin de probar la estabilidad del modelo. Partiendo del supuesto de existencia de relaciones de cointegración, los valores propios del polinomio autorregresivo (eigenvalores) de la matriz del modelo deberían estar dentro de un círculo unitario, y el número de valores que se encuentren cercanos al límite del círculo determinarán el número de tendencias comunes.
Una vez que se determina que el sistema es estable y estacionario, se aplica el procedimiento de Máxima Verosimilitud al vector autorregresivo para determinar el rango (r) de cointegración del sistema utilizando para ello la prueba de la traza y la prueba del eigenvalor máximo (valor propio). El vector de cointegración con mayor valor propio es normalizado, se multiplica por -1 y se reordenan los coeficientes de modo que el vector se interprete como una función de consumo.
2.2. Modelo VEC
Un modelo de vector de corrección del error (VEC) es un modelo VAR restringido (habitualmente con sólo dos variables) que tiene acotaciones de cointegración incluidas en su especificación, por lo que se diseña para ser utilizado con series que no son estacionarias pero de las que se sabe que son cointegradas. En estos modelos se supone que existe una relación de equilibrio a largo plazo entre las variables económicas, aunque en el corto plazo puede haber desequilibrios (Boef, 2000). Con los modelos de corrección del error, una proporción del desequilibrio de un periodo (el error, interpretado como un alejamiento de la senda de equilibrio a largo plazo) es corregido gradualmente a través de ajustes parciales en el corto plazo.
3. Resultados
3.1. Cointegración de Søren Johansen
En esta sección se muestra la aplicación del procedimiento de Johansen a las seis series de tiempo del modelo
Para los análisis se utilizó el software estadístico Stata versión 10.1.
3.1.1. Integración de las series
A partir de la prueba de ADF se determinó si las series de tiempo en su nivel original fueron no estacionarias. De no ser estacionarias se aplican primeras diferencias a las series de tiempo para hacerlas estacionarias y por lo tanto integradas de orden 12 . Al respecto, Gujarati y Porter (2010) indican los diferentes procesos estocásticos que puede seguir una serie y determinar si es o no estacionario.
En general, una serie de tiempo no estacionaria puede seguir un proceso estocástico en particular, por ejemplo, camino aleatorio sin intercepto, camino aleatorio con intercepto, camino aleatorio con tendencia determinística, camino aleatorio con intercepto y tendencia determinística, camino aleatorio con intercepto y tendencia determinística y componente autorregresivo, etc. Comparando los valores absolutos de los estadísticos con los valores críticos se observa que en el caso de las series lnQt , lnYt , lnPet , lnPgt , lnUt y lnIPBDt se rechaza la hipótesis nula de “no estacionariedad” para la primera diferencia a un nivel de significancia de 1%. En la serie InPat se rechaza para la primera diferencia a un nivel de significancia del 10% (cuadro 4), por lo que las series de tiempo analizadas mediante la prueba de Dickey Fuller Aumentada (ADF) son integradas de orden 1, lo cual indica que no existe autocorrelación, lo cual es deseable en una prueba ADF.
3.1.2. Modelo VAR
Para determinar la longitud del retardo óptimo en el modelo que será utilizado en la prueba de cointegración se utilizan los criterios: a) criterio de máxima verosimilitud (LR), b) criterio de información de Akaike (AIC), c) criterio de información de Schwarz (SC), d) criterio de información de Hannan-Quinn (HQ). El cuadro 5 muestra los criterios para el modelo. Basado en el criterio de SC y HQ se seleccionó el primer retardo como el óptimo para estimar el vector de cointegración.
Cuadro 5 Criterios para determinar la longitud del retardo
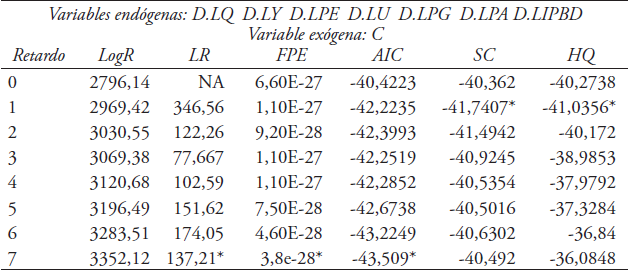
* Indica el orden de retardo seleccionado por el criterio
LR: Prueba estadística LR secuencial modificada (significante a nivel 5%)
FPE: Predicción final del error
AIC: Criterio de información de Akaike
SC: Criterio de información de Schwarz
HQ: Criterio de información de Hannan-Quinn
Fuente: diseño propio con base en los resultados del software estadístico Stata versión 10.1.
Para probar la estabilidad del modelo VAR se examinaron las raíces inversas del polinomio autoregresivo.
En la figura 1 se puede observar que todos los eigenvalores (valores propios) se encuentran dentro del circulo unitario y cinco de estos se encuentran al borde del círculo de la unidad, esto indica que existen diversas tendencias en común, por lo que se espera más de un vector de cointegración.
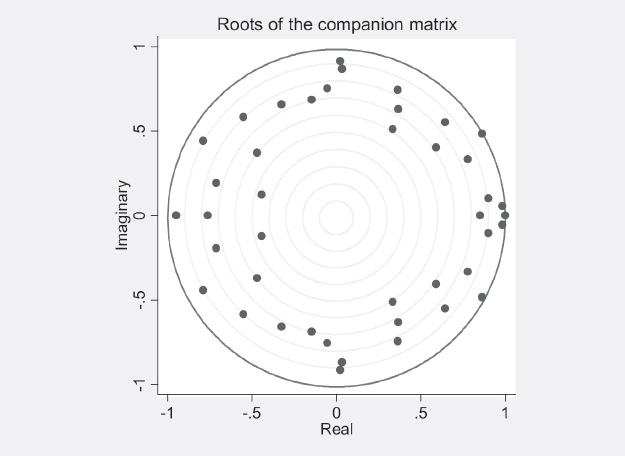
Fuente: elaboración propia con resultados del software estadístico Stata versión 10.1.
Figura 1 Raíces inversas del polinomio autorregresivo del VAR
Como el modelo resultó ser estable se determina el rango (r) de cointegración del modelo utilizando para ello la prueba de la traza y la prueba del eigenvalor máximo (valor propio). El cuadro 6 muestra los resultados de la prueba de la traza. La primera columna muestra el número de relaciones de cointegración, la segunda columna muestra el rango ordenado de los eigenvalores de la matriz, la tercera muestra el estadístico de la traza y el cuarto y quinto los valores críticos al 5% y 1 por ciento.
Cuadro 6 Prueba de la traza
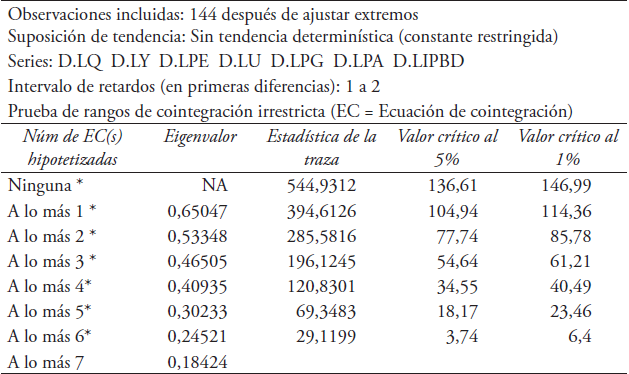
* denota rechazo de la hipótesis al nivel1%
La prueba de la traza indica 6 EC(s) al nivel 1%
Fuente: diseño propio con base en los resultados del software estadístico Stata versión 10.1.
La prueba de máximo eigenvalor mostrada en el cuadro 7 prueba la hipótesis nula de que el rango de cointegración es igual a r=0 contra que es mayor que 0. Dado que el valor del estadístico de máximo eigenvalor (109,031) es mayor que el valor crítico a 1% (48,17), se rechaza la hipótesis nula de que el rango de cointegración es igual a 1 (Greene, 2003). Basado en ambos resultados se concluye que existe más de una relación de cointegración entre el conjunto de series de tiempo incluidas en el modelo.
Cuadro 7 Prueba del eigenvalor máximo
| Núm de EC(s) hipotetizadas |
Eigenvalor | Estadística Max-Eigen |
Valor crítico al 5% |
Valor crítico al 1% |
|---|---|---|---|---|
| Ninguna * | 150.3186 | 48.45 | 54.48 | |
| A lo más 1 * | 0,65047 | 109,031 | 42,48 | 48,17 |
| A lo más 2 * | 0,53348 | 89,4572 | 36,41 | 41,58 |
| A lo más 3 * | 0,46505 | 75,2944 | 30,33 | 35,68 |
| A lo más 4* | 0,40935 | 51,4818 | 23,78 | 28,83 |
| A lo más 5* | 0,30233 | 40,2283 | 16,87 | 21,47 |
| A lo más 6* | 0,24521 | 29,1199 | 3,74 | 6,4 |
| A lo más 7 | 0,18424 |
* denota rechazo de la hipótesis al nivel1%
La prueba del eigenvalor máximo indica 6 EC(s) al nivel 1%
Fuente: diseño propio con base en los resultados del software estadístico Stata versión 10.1.
3.2. Modelo VEC
El modelo VEC (ecuación 3) se puede interpretar como una función de equilibrio de largo plazo de la forma (Greene, 2003):
Con base en la demanda residencial de energía eléctrica del Estado de México, los coeficientes de las variables incluidas con un retraso representan las elasticidades de largo plazo, y los coeficientes de las variables en niveles I(1) representan las elasticidades de corto plazo. El modelo obtenido incluyó sólo las variables que resultaron significativas, y fue estimado de manera dinámica mediante el software Stata. A continuación se presenta el modelo:
La interpretación de los coeficientes de largo plazo del modelo VEC para la demanda residencial de energía eléctrica del Estado de México se presenta en el cuadro 8. Las magnitudes de los coeficientes estimados para aquellas variables que resultaron significativas a 5% y 10% son los esperados y sus signos son congruentes con la teoría de la demanda.
Cuadro 8 Clasificación de elasticidades de largo plazo del modelo
| Elasticidades | Coeficientes | Error estándar | Elasticidad$ | Tipo |
|---|---|---|---|---|
| Precio de la electricidad | -0,0455 | 0,0556*** | -0,060 | Inelástica< 1 |
| Ingreso de la población | 0,1608 | 0,0961* | 0,213 | Bien normal de primera necesidad< 1 |
| Cruzada gas L.P | -0,0595 | 0,2085*** | -0,079 | Bien sustituto(+) |
| Cruzada agua | -0,1169 | 0,2508*** | -0,155 | Bien complementario(-) |
| Número usuarios del servicio | 0,3205 | 0,0528* | 0,425 | (+) |
| Índice del precio para bienes durables | -0,4832 | 0,4905*** | -0,640 | (-) |
| Mes enero | 0,0000 | 0,0190*** | 0,000 | (+) |
| Mes mayo | 0,0247 | 0,1500*** | 0,033 | (+) |
* denota significancia al nivel de 5 por ciento.
*** significancia mayor al nivel de 10% por lo que se consideran variables estadísticamente no significativas.
$ Se obtiene al dividir cada coeficiente por el factor de corrección del modelo ().
Fuente: elaboración propia con resultados del software estadístico Stata versión 10.1.
La interpretación de los coeficientes de corto plazo del modelo VEC se presenta en el cuadro 9. Las magnitudes de los coeficientes estimados son los esperados y sus signos son congruentes con la teoría del consumidor (demanda). En la figura 2 se puede apreciar el ajuste del modelo VEC.
Cuadro 9 Clasificación de elasticidades de corto plazo del modelo
| Elasticidades | Coeficientes | Error estándar | Tipo |
|---|---|---|---|
| Precio de la electricidad | -0,1391 | 0,0617* | Inelástica< 1 |
| Ingreso de la población | 0,3461 | 0,2252*** | Bien normal< 1 |
| Cruzada gas L.P | 0,4609 | 0,3151*** | Bien sustituto(+) |
| Cruzada agua | -0,7192 | 0,3020* | Bien complementario(-) |
| Número usuarios del servicio | -0,1746 | 0,5280*** | (+) |
| Índice del precio para bienes durables | -3,4524 | 1,5634* | (-) |
| Mes enero | 0,0013 | 1,6620*** | (+) |
| Mes mayo | 0,0200 | 0,0117** | (+) |
* denota significancia al nivel del 5%
** denota significancia al nivel del 10%
*** significancia mayor al nivel del 10% por lo que se consideran variables estadísticamente no significativas
Fuente: elaboración propia con resultados del software estadístico Stata versión 10.1.
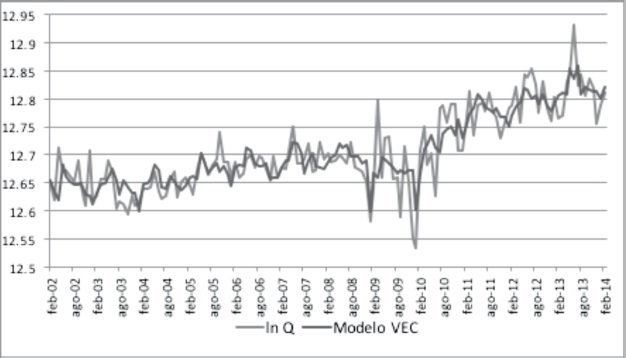
Fuente: elaboración propia con datos obtenidos de Sistema de Información Energética (SIE, 2013a) y CFE (2013) así como de los resultados del software estadístico Stata versión 10.1.
Nota: las magnitudes graficadas están expresadas en logaritmos, por tanto el eje de las ordenadas carece de unidades.
Figura 2 Consumo residencial de energía eléctrica en el Estado de México y modelo vector de corrección de errores
Finalmente, se procedió a probar la existencia de cointegración del modelo VEC, es decir, confirmar la existencia de un equilibrio de largo plazo en el que los errores estimados deben ser estacionarios. Al respecto se aplicaron dos pruebas sobre los errores estimados, DFA y la prueba de Porstmanteu.
En el cuadro 10, para los errores estimados del modelo VEC, se rechaza la hipótesis nula de no estacionariedad a un nivel de significancia de 1 por ciento. Adicionalmente, bajo la prueba de Porstmanteu no se rechaza la hipótesis nula de ausencia de autocorrelación hasta el retraso 40. Con base en lo anterior, se afirma que el modelo VEC propuesto presenta un equilibrio de largo plazo.
4. Discusión de resultados
En este estudio se encontraron seis vectores de cointegración, sin embargo sólo uno de ellos es congruente con la teoría del consumidor. Mediante la estimación de un modelo de corrección de errores se estimaron los coeficientes que se interpretan como las elasticidades de largo y corto plazo.
Las magnitudes de las elasticidades de la demanda residencial de energía eléctrica que han sido estimadas en este estudio y en otros estudios similares realizados en México se muestran en el cuadro 11. Cabe señalar que los estudios realizados en el país son muy escasos y no existe en particular un antecedente llevado a cabo en el Estado de México con el cual se pudiera realizar una adecuada comparación de los resultados obtenidos.
Cuadro 11 Investigaciones realizadas en México sobre elasticidades de la demanda residencial de energía eléctrica
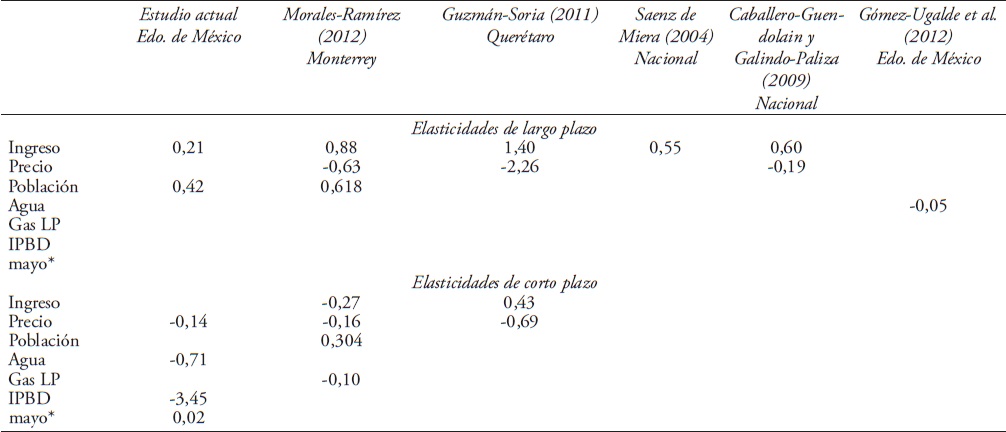
* Variable dicotómica. Aunque se probaron todos los meses de año, sólo el mes de mayo resultó significativo en el corto plazo.
Fuente: elaboración propia con base en los resultados del software estadístico Stata versión 10.1 y en los reportados en las investigaciones consultadas.
Como puede apreciarse en el cuadro 11, la elasticidad precio de la demanda resultó ser significativa e inelástica en el corto plazo con -0,14, lo que indica que al aumentar el precio en 1%, la cantidad demandada de energía eléctrica disminuirá en 0,14%. La magnitud de las elasticidad estimada en términos absolutos es menor a las reportadas por Guzmán-Soria et al. (2011)) y Morales-Ramírez et al. (2012), lo que indica una menor sensibilidad al precio a través del tiempo en el Estado de México que con respecto en entidades como Querétaro y Monterrey. Adicionalmente, dicha elasticidad es menor en magnitud a la elasticidad precio de largo plazo obtenida en otras investigaciones, por lo que se confirma lo referido por Espey y Espey (2004) y Pashardes (2014), en el sentido de que, la elasticidad precio de la demanda por electricidad de corto plazo es menor a la elasticidad correspondiente de largo plazo.
La elasticidad ingreso de la demanda resultó ser significativa, positiva y menor que uno en el largo plazo, por lo que se trata de un bien normal de primera necesidad (Pindick y Ribinfeld, 2013), es decir, al aumentar el ingreso del consumidor en 1% la demanda del bien aumenta en 0,21%. La magnitud de la elasticidad estimada es menor que la elasticidad estimada por el resto de los autores (Saenz, 2004, Caballero-Guendolain y Galindo-Paliza, 2009; Guzmán-Soria et al., 2011; Morales-Ramírez et al., 2012), lo que indica que en el Estado de México la demanda de electricidad es menos sensible a cambios inmediatos en el ingreso de la población que la que se presenta en entidades como Querétaro y Monterrey, lo cual se explica por las diferencias en el ingreso de las distintas zonas geográficas en que fueron realizados los estudios.
En la presente investigación, la elasticidad ingreso de la demanda de largo plazo resultó ser menor en magnitud a la elasticidad ingreso de la demanda de corto plazo estimada por Guzmán-Soria et al. (2011), lo cual no corresponde con lo referido por Espey y Espey (2004) y Pashardes et al. (2014). Sin embargo, es importante señalar que en el estudio de Guzmán-Soriaet al. (2011) aunque el estadístico Durbin Watson (1,82) muestra un bajo nivel de correlación de primer orden entre las variables de la ecuación de regresión, no implica que no exista un nivel de correlación de orden superior, y por consiguiente, que se tenga que estimar un modelo alternativo con objeto de que los errores estimados sean estacionarios.
En el caso de la elasticidad de la demanda respecto a la población (número de usuarios), ésta resulta ser significativa y menor en el largo plazo a la reportada por Morales-Ramírez et al. (2012). Esto se debe al perfil de consumo de los usuarios en el Estado de Monterrey, a diferencia del Estado de México. En el presente estudio, los resultados obtenidos indican que un incremento porcentual de 1% en el número de usuarios aumentaría en 0,42% la demanda de electricidad en el largo plazo.
En el caso de las elasticidades cruzadas, los resultados indican que el servicio público del agua es un servicio complementario al servicio eléctrico residencial en el corto plazo (-0,71). Con respecto a la elasticidad cruzada del precio del gas, ésta variable resultó no ser significativa en ambos horizontes de tiempo: largo y corto plazo.
En el caso del índice de precios de los bienes durables, en el presente estudio se obtuvo una elasticidad de corto plazo significativa y acorde con la teoría. El precio de dichos bienes tiene un comportamiento inverso con respecto a la demanda de electricidad (Marshall, 2010). De esta manera, cuando se incrementa el índice de los bienes durables en 1%, reduce la demanda por éstos, lo cual se traduce en una disminución en la demanda de electricidad en -3,45%. Esta elasticidad de corto plazo es significativamente mayor en términos absolutos comparada a la obtenida por Marshall (2010) de -0,37 en su estudio de consumo de electricidad en el sector residencial en Chile.
El coeficiente correspondiente a la demanda estacional en el consumo de electricidad resultó ser significativa y positiva para el mes de mayo (0,02) bajo un horizonte de corto plazo. Sin embargo, a pesar de dicho resultado, el valor de dicha elasticidad es cercano a cero.
Finalmente, con base en la ecuación (4) y aquellas elasticidades que resultaron significativas se determinó el impacto en la demanda de energía eléctrica, en el largo y corto plazo, cuando se da un efecto combinado en las elasticidades.
En el corto plazo, bajo el supuesto de un crecimiento de 1% en el precio del agua y del precio de los bienes durables respectivamente, se requiere de al menos un decremento del 37,2% en el precio de la energía eléctrica, esto permitiría un crecimiento del 1% en su demanda. Sin el crecimiento de los precios del agua y de los bienes durables, el decremento en el precio de la energía eléctrica tendría que ser del 7,2%. Respecto al largo plazo, un crecimiento del 1,6% en el ingreso de la población y del número de usuarios respectivamente, resulta en un crecimiento del 1% en la demanda de energía eléctrica. Cabe señalar, que dicho crecimiento en la demanda de electricidad de largo plazo es mayormente explicado por el crecimiento del número de usuarios.
Conclusiones
El presente estudio mostró la relevancia en cuanto al uso de los métodos de Johansen y de vector de corrección de errores. A partir de la integración de orden uno I(1) de las series económicas, incluidas en el modelo Cobb-Douglas de demanda residencial de energía eléctrica, fue posible estimar un vector autoregresivo restringido que a su vez cumpliera con la condición de que los residuos fueran ruido blanco. Los coeficientes de dicho vector indican que, en el corto plazo, un decremento en el precio de la electricidad, precio del servicio público del agua y precio de los bienes durables, incrementa la demanda de energía eléctrica. Por otra parte, en el largo plazo se mostró que, el aumento en el nivel de ingreso de la población y el crecimiento de usuarios son las variables que incrementan la demanda de energía eléctrica.
Finalmente, se concluye que los beneficios que pretende obtener la actual reforma energética mediante una disminución en el precio medio del servicio eléctrico serán mayores en la medida que los precios del servicio del agua y de los bienes durables disminuyan o, al menos, se mantengan constantes a través del tiempo. Variables como el ingreso de la población y el número de usuarios, tendrán un incremento en la energía eléctrica residencial sólo en el largo plazo.











 nueva página del texto (beta)
nueva página del texto (beta)




