Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería, investigación y tecnología
versión On-line ISSN 2594-0732versión impresa ISSN 1405-7743
Ing. invest. y tecnol. vol.7 no.3 Ciudad de México jul./sep. 2006
Educación en ingeniería
Criterios de energía específica mínima y momentum mínimo en el cálculo del régimen crítico en canales de sección compuesta
G. Sotelo–Ávila y A. Cafaggi–Félix
Departamento de Ingeniería Hidráulica.
División de Ingeniería Civil, Topográfica y Geódesica. Facultad de Ingeniería, UNAM
E–mails:
soteloa@servidor.unam.mx
acafaggi@servidor.unam.mx
Recibido: abril de 2005
Aceptado: agosto de 2005
Resumen
La selección del criterio de energía específica mínima o del momentum mínimo en el cálculo del régimen crítico toma particular importancia en canales de sección transversal compuesta, ya que una vez que el agua inunda las subsecciones laterales los coeficientes  de corrección del flujo de energía cinética y β de corrección del de cantidad de movimiento difieren de 1 y más entre ellos mismos, lo que aleja la coincidencia de los criterios. Este artículo presenta una comparación de los resultados obtenidos al calcular las condiciones críticas en canales de sección compuesta, empleando los métodos propuestos por Blalock y Sturm (1981) con el criterio de la energía específica mínima y por Chaudhry y Bhallamudi (1988) con el criterio del momentum mínimo y orienta en la preferencia de uno respecto del otro.
de corrección del flujo de energía cinética y β de corrección del de cantidad de movimiento difieren de 1 y más entre ellos mismos, lo que aleja la coincidencia de los criterios. Este artículo presenta una comparación de los resultados obtenidos al calcular las condiciones críticas en canales de sección compuesta, empleando los métodos propuestos por Blalock y Sturm (1981) con el criterio de la energía específica mínima y por Chaudhry y Bhallamudi (1988) con el criterio del momentum mínimo y orienta en la preferencia de uno respecto del otro.
Descriptores: Canal compuesto, tirantes críticos múltiples, régimen crítico en canales de sección compuesta, energía específica mínima, momentum mínimo.
Abstract
The discussion whether the condition of the critical regime must be calculated from the minimum specific energy criterion or the minimum momentum criterion, takes particular importance in the compound cross section channels, as once the water floods the lateral subsections, the coefficients  of kinetic energy flux correction and β of flux momentum correction differ from 1. This article shows a comparison between results obtained after calculating critical conditions in compound cross section channel, applying the method proposed by Blalock and Sturm (1981), with the minimum specific energy criterion, and the method proposed by Chaudhry and Bhallamudi (1989), with the minimum momentum criterion.
of kinetic energy flux correction and β of flux momentum correction differ from 1. This article shows a comparison between results obtained after calculating critical conditions in compound cross section channel, applying the method proposed by Blalock and Sturm (1981), with the minimum specific energy criterion, and the method proposed by Chaudhry and Bhallamudi (1989), with the minimum momentum criterion.
Keywords: Compound cross section channel, multiple critical dephs, critical regime in compound cross section channels, minimum specific energy, minimum momentum .
Introducción
Un canal compuesto consiste de un canal principal que conduce caudales base en la parte más profunda de la sección y de canales laterales más elevados que se inundan al desbordarse el primero, para conducir en conjunto los caudales de avenidas. La figura 1 muestra una sección compuesta, donde las subsecciones laterales suelen designarse como bermas que pueden ser simétricas o asimétricas.
El cambio brusco en la geometría de la sección compuesta cambia el flujo del canal principal a los laterales y da lugar a tirantes críticos múltiples, lo que dificulta ubicar la sección de control, así como la interpretación y el cálculo de los perfiles de la superficie del agua. En este tipo de canal, el coeficiente  de corrección del flujo de energía cinética y β de corrección de cantidad de movimiento son diferentes, por lo que el tirante crítico calculado con el concepto de energía específica mínima no es el mismo que el que se obtiene con el concepto de momentum mínimo, por lo cual, al definir la condición de régimen crítico se debe elegir sólo uno de estos criterios.
de corrección del flujo de energía cinética y β de corrección de cantidad de movimiento son diferentes, por lo que el tirante crítico calculado con el concepto de energía específica mínima no es el mismo que el que se obtiene con el concepto de momentum mínimo, por lo cual, al definir la condición de régimen crítico se debe elegir sólo uno de estos criterios.
Blalock y Sturm (1981), propusieron el uso de una nueva forma del número de Froude basada en el concepto de la energía específica mínima y establecieron un procedimiento de cálculo para determinar los tirantes críticos múltiples en canales de sección compuesta. Sturm y Sadiq (1996) propusieron un método para identificar el intervalo del gasto dentro del que existen tirantes críticos múltiples. Sotelo (1998) presentó un algoritmo sencillo para aplicar el método de Blalock, el cual se puede aplicar a canales de pendiente grande y toma en cuenta la variación del coeficiente n de Manning con el tirante, propuesta por Sturm y Sadiq (1996).
Chaudhry y Bhallamudi (1988), propusieron otro método de cálculo basado en el concepto del momentum mínimo, y que sólo se aplica a canales compuestos simétricos.
En este artículo se presenta una comparación de los resultados obtenidos al calcular los tirantes críticos en canales de sección compuesta empleando ambos métodos.
Principio de la energía específica mínima. Método de Blalock y Sturm (1981)
En este método se define un número de Froude FB para la sección compuesta. Al obtener dE/dy, es necesario considerar que  en toda la sección sea también función del tirante, aunque se considera que
en toda la sección sea también función del tirante, aunque se considera que  i en cada subsección sea constante. Por tanto, para el régimen crítico se obtiene
i en cada subsección sea constante. Por tanto, para el régimen crítico se obtiene
 ............................(1)
............................(1)
donde: E energía específica; y tirante; Q gasto; T ancho de superficie libre; A área hidráulica; θ ángulo que forma la plantilla de un canal de eje recto con la horizontal; g'=gcosθ.
El coeficiente  se expresa en términos de las variables de cada subsección i en que se subdivide el canal, en la forma
se expresa en términos de las variables de cada subsección i en que se subdivide el canal, en la forma
 .....................................................................(2)
.....................................................................(2)
donde

es el factor de conducción en la subsección i;
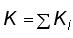
ni coeficiente de Manning en la subsección i; Pi perímetro mojado en la subsección i; Ai área hidráulica en la subsección i; Rhi radio hidráulico en la subsección i.
Al tomar en cuenta el desarrollo de d /dy, se llega a que el número de Froude sea
/dy, se llega a que el número de Froude sea
 ...............................................(3)
...............................................(3)
Para que se presente régimen crítico FB=1. Los coeficientes σ1, σ2, y σ3 se calculan con las siguientes expresiones:
 ........................(4)
........................(4)
 .......................................................................(5)
.......................................................................(5)
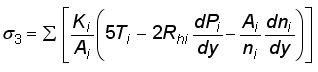 ...................................(6)
...................................(6)
Cuando la pared se comporta como hidráulicamente rugosa, se puede incluir la variación de n en cada subsección mediante la ecuación de Nikuradse y la de equivalencia de n con el factor de fricción f, esto es
 .........................................................(7)
.........................................................(7)
en que ks es la rugosidad equivalente en la pared del canal; al derivar n con respecto al tirante se llega a
 ..........(8)
..........(8)
Sturm y Sadiq (1996), usaron los coeficientes de Keulegan:  N=2 y c=12.64 para aplicarlos en el canal compuesto que utilizaron en sus experimentos y encontraron que el valor de n para el canal central se predice muy bien con la ecuación (7) siempre que el tirante sea menor que el nivel de desbordamiento; una vez rebasado este nivel, el valor de n en dicho canal resultó 1.19 veces mayor que el que resulta con dicha ecuación. El valor de n en los canales laterales también se ajustó bien al calculado con la ecuación (7).
N=2 y c=12.64 para aplicarlos en el canal compuesto que utilizaron en sus experimentos y encontraron que el valor de n para el canal central se predice muy bien con la ecuación (7) siempre que el tirante sea menor que el nivel de desbordamiento; una vez rebasado este nivel, el valor de n en dicho canal resultó 1.19 veces mayor que el que resulta con dicha ecuación. El valor de n en los canales laterales también se ajustó bien al calculado con la ecuación (7).
El número de Froude Fm del flujo cuando ocurre sólo en la subsección más profunda, es decir, para y=ym, (figura 1) se define en la forma convencional mediante la expresión:
 ..................................................................(9)
..................................................................(9)
donde el subíndice m se refiere a las condiciones de dicha subsección.
Para determinar el intervalo de gastos en el que existen tirantes críticos múltiples, la ecuación (3) se divide entre la (9) y se obtiene la relación adimensional
 .....................................(10)
.....................................(10)
Al considerar que el tirante crítico ocurre cuando FB=1 , existe un intervalo de valores 1/Fm y por tanto, un intervalo de gastos dentro del cual hay dos tirantes críticos, uno inferior en la subsección más profunda, yc1 < ym1 y uno superior yc2 > ym1. El gasto límite superior QU del intervalo, ocurre cuando yc1=ym1. El gasto límite inferior QL del intervalo es el último para el cual ocurre el tirante crítico yc2=ym1, es decir, Fm<1, FB=1, y (FB/Fm)max para Q=QL .
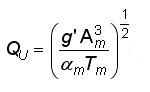 ....................................................................(11)
....................................................................(11)
 ...................................................................(12)
...................................................................(12)
Para que existan más de un tirante crítico, el gasto debe quedar, por tanto, dentro del intervalo: QL < Q < QU
Para determinar los tirantes críticos múltiples, se empleó en este trabajo el algoritmo de convergencia propuesto por Sotelo (1998).
Principio del momentum mínimo Método de Chaudhry y Bhallamudi (1988)
Al calcular el mínimo de la función momentum M y con la consideración que

en toda la sección sea también función del tirante, aunque en cada subsección se considera que βi; sea constante; con

se obtiene
 .....................................................(13)
.....................................................(13)
La ecuación (13) representa la condición general de régimen crítico en canales de sección compuesta, según el criterio de momentum mínimo.
En este método se incorpora una definición general del número de Froude basada en las ecuaciones de continuidad y momentum obtenidas por Yen (1973). En un canal de pendiente pequeña (cosθ =1), dicho número queda expresado como sigue
 ........................................(14)
........................................(14)
donde los términos se refieren a toda la sección; para que se presente régimen crítico el número de Froude FY debe ser igual a uno.
La sección compuesta en un canal simétrico se divide en tres subsecciones: la central (1) y dos laterales simétricas (2) como se muestra en las figuras 2, 3 y 4. De esta manera, se pueden definir las características geométricas de toda la sección como sigue:

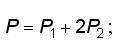



Además, se establece el parámetro
 .................................................................(15)
.................................................................(15)
por lo que
 ............................................................(16)
............................................................(16)
y
 ................(17)
................(17)
en que
 ......................(18)
......................(18)
Chaudhry (1988) propone en su artículo la obtención de los tirantes críticos mediante un procedimiento iterativo; otra manera de calcularlos es proponiendo tirantes y calculando FY hasta que éste sea igual a 1. En este trabajo, la solución se obtuvo de ambas maneras, pero se observó que el método original propuesto por el autor no converge rápidamente.
Chaudhry, a diferencia de Blalock, no propone ningún factor para el coeficiente de Manning del canal principal que tome en cuenta la interacción entre la subsección más profunda y las llanuras de inundación.
Comparación de ambos métodos
Comparación analítica
Al comparar las ecuaciones (1) y (13) se observa que la única forma que estos dos criterios proporcionen los mismos valores del tirante crítico se da cuando  =β=1 y constante para toda la sección transversal; lo cual no es posible que ocurra cuando se presentan diferentes rugosidades en el canal central y los laterales, además se requiere que d
=β=1 y constante para toda la sección transversal; lo cual no es posible que ocurra cuando se presentan diferentes rugosidades en el canal central y los laterales, además se requiere que d /dy=dβ/dy=0. Los estudios realizados muestran que los valores de
/dy=dβ/dy=0. Los estudios realizados muestran que los valores de  y β son distintos de uno en los canales de sección compuesta y cambian con el tirante del flujo, por lo que no es factible que ambos criterios coincidan en la práctica.
y β son distintos de uno en los canales de sección compuesta y cambian con el tirante del flujo, por lo que no es factible que ambos criterios coincidan en la práctica.
Dado que la comparación analítica no presenta evidencia suficiente, se presenta una comparación de los resultados obtenidos para tres canales simétricos diferentes, empleando ambos métodos.
Comparación de resultados
La geometría de cada canal se muestra en las figuras 2, 3 y 4 y los datos se resumen en la tabla 1. Por simplicidad y con fines de comparación entre los dos métodos, se considera que  i=1, que ni es constante en cada subsección, es decir, dni/dy=0. También se consideró que el valor de n es 1.19 veces mayor que el que se encuentra con la ecuación (7), una vez que es rebasado el nivel de desbordamiento.
i=1, que ni es constante en cada subsección, es decir, dni/dy=0. También se consideró que el valor de n es 1.19 veces mayor que el que se encuentra con la ecuación (7), una vez que es rebasado el nivel de desbordamiento.
Para cada canal se propusieron distintos gastos y los resultados se muestran en las tablas 2, 3, 4 y 5.
En figura 5 se muestra la curva FB – y que corresponde al caso de Q=141.58 m3/s en el canal 1, donde se presenta que FB=1 en tres puntos diferentes; sin embargo, el tirante cerca del nivel de berma no se considera como crítico, ya que representa más bien un máximo de energía específica. En la gráfica de la figura 6 se puede apreciar la curva FY – y, donde también se tiene FY=1 en tres puntos diferentes. Chaudhry considera válidos los tres tirantes, pero en este trabajo no se considera el cercano al nivel de berma.
Debido a que los resultados presentados en la tabla 5 son limitados, se analizaron varios canales para determinar la influencia de las relaciones n1/n2, b1/b2 y ym1/b2. Los tirantes críticos se obtuvieron para cada sección con cinco gastos diferentes propuestos dentro de los límites superior e inferior de gastos, de acuerdo con el criterio de Chaudhry, dado que el criterio de Blalock arroja un intervalo más amplio. Se calculó el promedio de las diferencias relativas para cada canal analizado. Los resultados se presentan en las tablas 6a, b, c y d.
Conclusiones
Con base en el análisis y los resultados mostrados en las tablas 6a, b, c y d, se concluye lo siguiente:
a) Las ecuaciones de la energía y de la cantidad de movimiento no conducen a los mismos resultados. La igualdad se logra sólo cuando
=β=l, lo cual es una simplificación inaceptable en un canal de sección compuesta.
b) El método de Blalock y Sturm es más general y sencillo en su procedimiento que el de Chaudhry y Bhallamudi.
c) El tirante crítico intermedio que proponen Chaudhry y Bhallamudi siempre es muy cercano al nivel de berma y más bien corresponde a un valor máximo de la energía específica; además, dicho valor se determina cuando el nivel del agua es muy bajo en la subsección lateral, para el cual no puede considerarse un flujo unidimensional plenamente formado. Por otra parte, para esta magnitud del tirante no se puede considerar flujo turbulento, y por lo tanto, no se pueden emplear coeficientes de fricción exclusivos de dicho flujo.
d) El algoritmo que presenta Chaudhry para calcular el tirante crítico no converge rápidamente. En este trabajo se modificó el método de convergencia para programar el cálculo o se determinó proponiendo tirantes y calculando su respectivo número de Froude FY hasta encontrar los valores para los cuales se cumple que FY=1.
e) El algoritmo propuesto por Sotelo (1998), para el cálculo de la condición crítica con el método de la energía específica mínima es de rápida convergencia.
f) El método de Chaudhry limita su aplicación a canales simétricos, no así el de Blalock.
g) El cálculo de los perfiles de flujo se realiza con la ecuación de la energía, por lo tanto, es recomendable que la condición crítica se calcule a partir de esta ecuación.
h) El método de Blalock y Sturm, proporciona valores del tirante crítico siempre mayores que el de Chaudhry y Bhallamudi.
i) La diferencia entre los tirantes críticos calculados con ambos criterios es aceptable cuando la relación entre las rugosidades del canal central y las bermas de inundación, n1/n2, es cercana a uno. Para que los resultados obtenidos con ambos criterios no difieran considerablemente, es necesario que la relación n1/n2 esté entre 0.5 y 1.0, independientemente de las dimensiones del canal. Esto en la práctica es difícil que se cumpla.
j) La diferencia de resultados también aumenta cuando la relación ym1/b2 tiende a cero, es decir, cuando el canal lateral es ancho.
k) Cuando los anchos de plantilla del canal principal y las bermas son muy similares, no importa el valor de las otras dos relaciones consideradas y la diferencia es despreciable.
l) No se puede establecer un intervalo específico en el que la relación ym1/b2 asegure resultados similares para ambos métodos.
Referencias
Blalock M.E. and Sturm T.W. (1981). Minimum Specific Energy in Compound Open Channel. ASCE J Hydraulics Division, 107 (HY6):699–717. [ Links ]
Chaudhry M.H. and Bhallamudi S.M. (1988). Computation of Critical Depth in Symmetrical Compound Channels. J. Hydraulic Research, IARH 26(4). [ Links ]
Sotelo–Ávila G. (1998). Algoritmo del método de Blalock y Sturm para determinar los tirantes críticos múltiples en canales compuestos. Ingeniería Hidráulica en México, Vol. XIII, enero–abril, pp. 51–60, México. [ Links ]
Sturm, T.W. and A. Sadiq (1996). Water Surface Profiles in Compound Channel with Multiple Critical Depths. ASCE, J. Hydraulic Engineering, 122(1 2): 703–709. [ Links ]
Yen Ben Chie. (1973). Open Channel Flow Equations Revisited. ASCE, Journal of the Engineering Mechanics Division, Vol. 99, No. EM5. [ Links ]
Semblanza de los autores
Gilberto Sotelo–Ávila. Es ingeniero civil, maestro en ingeniería, doctor en ingeniería con mención honorífica y Profesor Emérito de la UNAM. Asimismo, investigador nacional del Sistema Nacional de Investigadores del CONACYT. Recibió el Premio Universidad Nacional 1998, Docencia en Ciencias Exactas, en la UNAM, los Premios Nacionales Miguel A. Urquijo 1999 y José A. Cuevas 2002 a los mejores artículos técnicos publicados, así como el Premio Nacional Mariano Hernández Barrenechea a la Docencia del año 2003, los tres últimos, entregados por el Colegio de Ingenieros Civiles de México. El Consejo Técnico de la Facultad de Ingeniería de la UNAM le otorgó las cátedras especiales: Javier Barros Sierra para 1999 y Mariano Hernández Barrenechea para el 2000. La UNAM le entregó el reconocimiento Catedrático UNAM, nivel 2. Fue designado miembro de la Comisión Dictaminadora del Instituto de Ingeniería, jurado del "Premio Universidad Nacional" y "Distinción Universidad Nacional para Jóvenes Académicos", Docencia en Ciencias Exactas, para los a ños del 2001 al 2004. Fue también designado académico de honor de la actual Academia de Ingeniería. Es autor de los libros de texto, Hidráulica General e Hidráulica de Canales y coautor en cuatro más de consulta. Ha publicado 82 artículos de investigación y 13 de difusión, así como apuntes y notas de sus cursos. Es miembro de la Academia Mexicana de Ciencias, de la Sociedad de Investigación Científica Sigma Xi, presidente de la División Regional Latinoamericana de la Asociación Internacional de Investigaciones e Ingeniería Hidráulica, miembro del Colegio de Ingenieros Civiles de México, expresidente de la Asociación Mexicana de Hidráulica y del Consejo Académico del CENEVAL.
Amalia Adriana Cafaggi–Félix. Es ingeniera civil y maestra en ingeniería hidráulica por la Facultad de Ingeniería, UNAM. Actualmente es profesora de carrera en el Departamento de Ingeniería Hidráulica de la Facultad de Ingeniería y de cursos extracurriculares en el Colegio de Ingenieros Civiles y en la División de Educación Continua de la UNAM. Fue jefa del Laboratorio y del Departamento de Ingeniería Hidráulica. Ha participado y presentado ponencias en diversos congresos nacionales e internacionales, ha publicado artículos en revistas nacionales y es autora de instructivos de prácticas para el laboratorio de hidráulica. Es autora del Software Educativo: "Hidráulica Básica: prototipo de software interactivo de hidrostática". Fue representante del Departamento de Hidráulica en la Primer Mesa Directiva de Colegio del Personal Académico de Ingeniería Civil (1998–2001) y posteriormente presidenta de la segunda mesa Directiva de Colegio del Personal Académico de Ingeniería Civil (2001–2003). Fue distinguida con la Cátedra Especial "Mariano Hernández Barrenechea" en 1999 y en 2002, así como con el reconocimiento "Sor Juana Inés de la Cruz" en 2006.














