1 Introduction
Supercontinuum (SC) generation refers to coherent white light generated by spectral broadening of an injected spectrum and the generation of new frequency components within the pulse spectrum propagating in a nonlinear medium [5,4]. SC generation has recently attracted a great deal of attention because of its wide range of applications [4,8]. For that reason, it has been widely studied as a complex process introducing a variety of experimental and theoretical challenges in different waveguide types [4,8,6].
The theoretical study of the SC generation in optical dielectric waveguides has been possible with the use of the generalized nonlinear Schro-dinger equation (GNLSE) [1]. Broadly speaking, the GNLSE appropriately describes the coherent spectral broadening and the generation of new frequency components within the spectrum of high power optical pulses propagating in nonlinear dispersive waveguides [1,3].
However, in the context of photonic nanowires, i.e., waveguides with sub-micron transversal dimensions, the use of the GNLSE as an accurate and feasible method to describe the SC generation is questionable because it does not take into account, on one hand, the effect of the large longitudinal field component of the propagating electromagnetic waves generated due to the strong optical confinement and high optical powers [11,10], and on the other hand, the effect of the complete strong dispersion implicit in the propagation constant // of the propagating mode inside the spectral body of the optical pulses [1].
The importance of consider the effect of the large longitudinal electric field component of the propagating modes along photonic nanowires is because it can enhance the waveguide nonlinearity through the nonlinear parameter γ [7]. In this regard, nonlinear effects like SC generation can be modified along the photonic nanowires. This can be crucial in nano-photonic devices based on optical nonlinearities [2]. Therefore, to analytically study the SC generation in photonic nanowires is required to readapt the conventional GNLSE from the vectorial form of Maxwell's equations and does not neglect the longitudinal electric field.
Moreover, in the derivation of the conventional GNLSE the following approximation is used β + β 0 ≈ 2β 0, where β 0 is the wave number of the propagating optical pulse [1]. This approximation simplify the GNLSE but it is only valid when the optical field is assumed to be quasi-monochromatic. Therefore, when short pulses are launched into photonic nanowires, with large enough power such that supercontinuum generation is generated, that approximation is questionable.
In this theoretical approach, we despise before approximation and derive a new nonlinear pulse propagation equation considering the vectorial nature of Maxwell's equations and the longitudinal electric field component of the propagating mode. We investigate how the complete strong dispersion implicit in β of the propagating mode inside the spectral body of the optical pulses affects the SC generation in air-silica photonic nanowires waveguides.
2 Nonlinear Propagation Equation
Let us begin by considering an air-silica cylindrical photonic nanowire of core radius τ and length L. The photonic nanowire is initially pumped with an optical pulse, at the carrier frequency ω 0, such that it excites the fundamental mode. To describe the propagation of the optical pulse along the photonic nanowire, we use the Maxwell frequency-domain wave equation given by:
where
The Fourier transform of
where
Substituting Eq. (2) into (1) and applying the slowly varying envelope approximation, we obtain after associating terms:
where:
Here F
z is the longitudinal component and F
T
is the transverse part of the normalized electric field. Using the fact that
the fundamental mode distribution satisfies the equation:
Here the usual way to simplify this equation is to use the following approximation:
Multiplying Eq. (4) with F
*, using the vectorial identity
Considering that
From Eq. (6) and its complex conjugate, we obtain that
If we consider the generalized orthogonality condition given by
where we have expanded β(ω) in a Taylor series
about ω
0 and replaced by ω by
where
where
Figure 1 shows how the nonlinear parameter changes with the core radius of an air-silica photonic nanowire. For our calculations, we chose the following values: the nonlinear refractive index n 2 = 2.6 × 10-20 m2 W-1, the wavelength λ = 800 nm, and the relative core-cladding index difference Δ = 0.312.
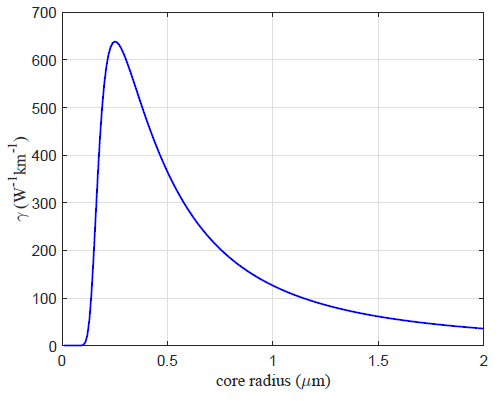
Fig. 1 Nonlinear parameter changes abruptly with the core radius of the air-silica photonic nanowire
To examine the main correction that our nonlinear pulse propagation model does to the SC generation in air-silica photonic nanowires, we compare in Fig. 2 the SC generation produced by the conventional GNLSE and by our new nonlinear propagation equation. Figure 2(a) and (b) shows the SC generation produced by the conventional GNLSE and Fig. 2(c) and (d) shows the SC generation produced by our new pulse propagation model. For this purpose, we have used the following value of the nonlinear parameter: γ = 0.182 W-1 m-1. We numerically simulate the SC generation in an air-silica photonic nanowire with length L = 35 cm, and core radius r = 900 nm. The input sech pulse has a central wavelength λ = 800 nm, peak power P 0 = 1 kW, and T 0 = 50 fs. Figure 2 shows that the additional shock terms in our new propagation equation (Eq. (10)) have the effect of reducing the long-wavelength edge of the supercontinuum spectrum.
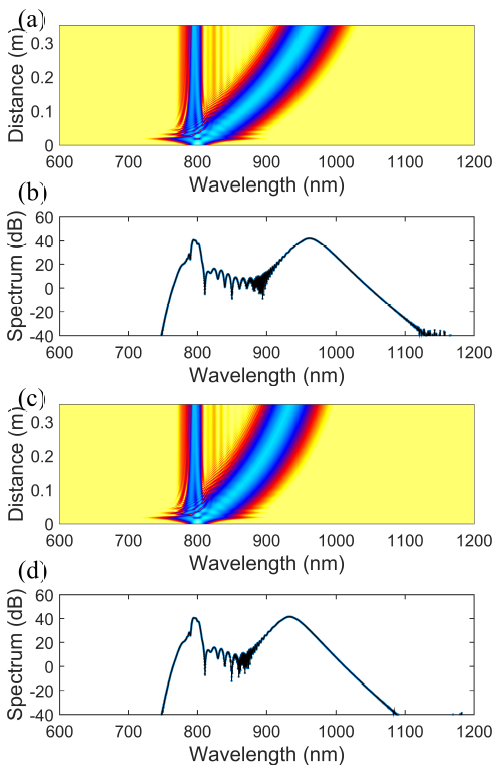
Fig. 2 (a) and (b) SC generation evolution and output spectra using the conventional model. (c) and (d) SC generation evolution and output spectra using our new pulse propagation model for L = 35 cm
Figure 3 shows that our new propagation model has more correction on the conventional model when the length of the photonic nanowire waveguide is larger, i.e., for higher legths there is a higher reduction of the extreme long-wavelength edge of the supercontinuum spectrum and therefore the spectrum becomes narrower. This result would be expected to be crucial for accurate comparison of simulations with experiments. In fact, our results
3 Conclusion
We have derived a new comprehensive evolution equation to describe the nonlinear propagation of high power optical pulses through photonic nanowires. (ur basic formulation part from the vectorial form of Maxwell's equations and take into account the effect of the complete strong dispersion implicit in the propagation constant β of the propagating mode inside the spectral body of the optical pulses.
Applying our new nonlinear propagation equation in air-silica photonic nanowires, we have showed evidence of additional effects that perturb the supercontinuum, reducing its extreme long-wavelength edge and making it narrower.











 nueva página del texto (beta)
nueva página del texto (beta)



