Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Computación y Sistemas
versión On-line ISSN 2007-9737versión impresa ISSN 1405-5546
Comp. y Sist. vol.8 no.2 Ciudad de México oct./dic. 2004
Routing with Wavelet–Based Self–Similarity Estimation
Ruteo con Estimación de Auto–Similaridad Utilizando Onduletas
Cesar Vargas–Rosales and Luis J. Manzanero
Center for Electronics and Telecommunications ITESM Campus Monterrey, Monterrey, N.L., C.P. 64849, México, E–mail: cvargas@itesm.mx ; lmanzanero@alestra.com.mx
Article received on June 20, 2002
Accepted on August 09, 2004
Abstract
The discovery of self–similar behavior in data traffic has initiated strong research in the area of traffic modeling. However, the way it affects the routing process is a subject not yet studied. This work presents the idea of providing intelligence to routers by estimating the Hurst Parameter using wavelets in a data link and uses this value as part of the routing metric. The motivation is to keep packets from using paths with high values of the Hurst Parameter, since in those paths the traffic tends to be bursty and therefore being more probable to drop packets and increase delay due to congestion. The algorithm is implemented for the Open Shortest Path First (OSPF) routing protocol in a simulation environment. Numerical results show that this technique is useful to provide traffic with low values of end–to–end delay and with smaller variance than those obtained when using traditional routing protocols.
Keywords: Self–similarity, Routing, Traffic.
Resumen
El descubrimiento de comportamiento auto–similar en el tráfico de datos, ha iniciado una enorme investigación en el área de modelado de tráfico. Sin embargo, la forma en la que afecta al ruteo en redes es un tema que todavía no se ha estudiado. Este trabajo presenta la idea de proporcionar inteligencia a los ruteadores por medio de la estimación del parámetro de Hurst utilizando onduletas en un enlace de datos, y utilizando ésta en la métrica de ruteo. La motivación es que los paquetes no utilicen trayectorias con altos valores del parámetro de Hurst, puesto que en esas trayectorias el tráfico tiende a contener ráfagas y a ser más probable que paquetes se pierdan y a que se incremente el retardo por congestión. El algoritmo es implementado para el protocolo de ruteo Open Shortest Path First (OSPF) en un ambiente se simulación. Resultados numéricos muestran que esta técnica es útil ya que proporciona tráfico con bajos niveles de retardo de extremo–a–extremo y con menor variación que aquellos valores obtenidos con el protocolo tradicional.
Palabras Clave: Auto–similaridad, Ruteo, Tráfico.
DESCARGAR ARTÍCULO EN FORMATO PDF
References
1. Abry, P., and Veitch, D., "Wavelet Analysis of Long–Range–Dependent Traffic," IEEE Transactions on Information Theory, Vol. 44, No. 1, January 1998, pp. 2–15. [ Links ]
2. Abry, P., Veitch, D., M.S. Taqqu and D. Veitch, "Wavelet for the Analysis, Estimation, and Synthesis of Scaling Data," Self–Similar Network Traffic and Performance Evaluation, Kihong Park and Walter Willinger editors, pp. 39–88, John Wiley and Sons 2000. [ Links ]
3. Beran, J., Statistics for Long–Memory Processes, Chapman and Hall, 1994. [ Links ]
4. Bertsekas, D., and R. Gallager, Data Networks, Prentice–Hall, Second Edition, 1992. [ Links ]
5. Burrus, C. Sidney, Ramesh A. Gopinath, and Haitao Guo, Introduction to Wavelets and Wavelets Transforms, a Primer, Prentice Hall, 1998. [ Links ]
6. Crovella, Mark E. and Azer Bestavros, "Self–Similarity in World Wide Web Traffic: Evidence and Possible Causes," IEEE/ACM Trans. on Networking, Vol. 5, No. 6, Dec. 1997, pp. 835–846. [ Links ]
7. Daubechies, L, Ten lectures on Wavelets, SIAM Philadelphia, 1992. [ Links ]
8. Erramilli, A., Onuttom Narayan, and Walter Willinger, "Experimental Queueing Analysis with Long–Range Dependent Packet Traffic," IEEE/ACM Transactions on Networking, Vol. 4, No. 2, April 1996, pp. 209–223. [ Links ]
9. Garrett, M. W., and W. Willinger. "Analysis, Modeling and Generation of Self–Similar VBR Video Traffic," In Proc., SIGCOMM94 Conference, pp. 269–280, London, UK, August 1994. [ Links ]
10. Graps, A., "An Introduction to Wavelets," IEEE Computational Science and Engineering, Vol. 2, No. 2, 1995, pp. 50–61. [ Links ]
11. Huitema, C., Routing in the Internet, Prentice Hall, Second Edition, 2000. [ Links ]
12. Korn, Granino A. and Theresa M. Korn, Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review, McGraw–Hill, Second Edition, 1968. [ Links ]
13. Labovitz, C., G. Robert Malan, and Farnam Jahanian, "Internet Routing Instability," IEEE/ACM Transactions on Networking, Vol. 6, No. 5, October 1998, pp. 515–528. [ Links ]
14. Leland, Will E., Murad S. Taqqu, Walter Willinger, and Daniel V. Wilson, "On the Self–Similar Nature of Ethernet Traffic (Extended Version)," IEEE/ACM Transactions on Networking, Vol. 2, No. 1, February 1994, pp. 1–15. [ Links ]
15. MIL3 Technologies, Opnet Modeling Concepts, 6th. edition. [ Links ]
16. Press, William H., Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery, Numerical Recipes in C, 2nd. edition, Cambridge University Press, 1992. [ Links ]
17. Roughan, M., Darryl Veitch, and Patrice Abry, "On–Line Estimation of Parameters of Long–Range Dependence," In Proc. of the GLOBECOM'98, Sidney, November 1998, pp. 3716–3721. [ Links ]
18. Van Jacobson and Sally Floyd. "The Synchronization of Periodic Routing Messages," IEEE/ACM Transactions con Networking, Vol. 2, No. 2, April 1994. [ Links ]
19. Veitch, D. and Abry, P., "A Wavelet Based Joint Estimator of the Parameters of Long–Range Dependence," IEEE Trans. on Information Theory, Vol. 45, No. 3, April 1999, pp. 878–897. [ Links ]
20. Willinger, Walter, Murad S. Taqqu, Robert Sherman, and Daniel V. Wilson, "Self–similarity Through High–Variability: Statistical Analysis of Ethernet LAN Traffic at the Source Level," IEEE/ACM Transactions on Networking, Vol. 5, No. 1, February 1997, pp. 71–86. [ Links ]
21. Willinger, Walter, V. Paxson and Murad S. Taqqu, "Self–similarity and Heavy Tails: Structural Modeling of Network Traffic," A Practical Guide to Heavy Tails, Birkhauser, 1998. [ Links ]
22. Zwillinger, D., editor, CRC Standard Mathematical Tables and Formulae, CRC Press, Third Edition, 1987. [ Links ]
Appendix. AV Estimator Algorithm
In this Appendix, we provide a brief description of the on–line AV wavelet estimator algorithm in Abry and Veitch (1998) and Roughan et. al., (1998). Let x(t) be the self–similar signal from which the parameters are to be estimated. In this case, the outgoing traffic in bits per second.
• Pass the input data by the filter bank shown in Figure 1. The number of stages of the filter is known as the number of octaves. The length of the response function of the bandpass function is the same as that of the low pass filter and it is known as the number of moments; the values of this vector are obtained from the coefficients of the wavelet family used, and for the band pass filter the coefficients are those of the wavelet with the sign of the elements in the odd position exchanged, while for the low pass filter the elements are the original wavelet coefficients transformed by flipping the original vector (i.e., swap the element in the n–th position with that at position one, the element in the (n–2)–nd position with that at position two and so on).
• The result of the convolution of the bandpass function and the signal is down–sampled (that is, the elements in the even positions are discarded) and the resulting vector is called the detail of the octave j, dx (j, i) with length len j . Make Sj
S j + dx (j, i)2 where i = 1...., K., lenj. Make nj
nj . + lenj . Continue introducing samples from the signal. The previous steps are performed on the arrival of any sample of the signal, while the next are only performed on a longer time scale, when the Hurst parameter wants to be estimated, in our case 60 seconds.
• Calculate for all the stages the following expressions
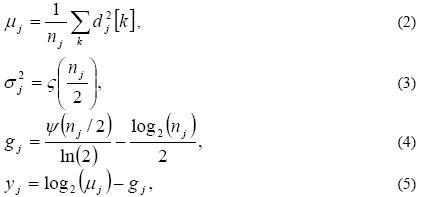
where ς(x) is the Riemann–Zeta function ς (x) =  see Zwillinger, (1987); ψ(x) = Γ'(x) / Γ(x) is the Psi function (also called the digamma function) see Korn, page 823, (1968) and Γ(x) =
see Zwillinger, (1987); ψ(x) = Γ'(x) / Γ(x) is the Psi function (also called the digamma function) see Korn, page 823, (1968) and Γ(x) =  dt is the gamma function with derivate Γ(x) .
dt is the gamma function with derivate Γ(x) .
•Calculate the next sums:

• For each value of j calculate
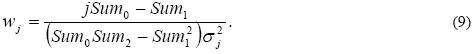
• Calculate

• And finally, the estimation of the Hurst Parameter  is given by
is given by

Table 1: Numerical Results for Medium Loaded Network: Topology One.
Table 2: Numerical Results for Highly Loaded Network: Topology One.















